1 Introduction

Photonics is recognized as a solution for various next-generation applications in communications, computation and sensing. The development of ever complex optical integrated circuits, at one hand requires the introduction of new exotic technologies, elements and approaches (e.g. Krupin et al. 2020; Calò et al. 2019; Fuschini et al. 2020; Alam et al. 2021). On the other hand, it is also important to optimize existing optical operations with new solutions (e.g. Bogaerts et al. 2020).

In this scenario, phase shifters are fundamental devices in many optical systems and components. These devices can be developed through a variety of technologies and may employ a plethora of mechanisms. Key parameters are tuning range, propagation loss, response time, integration density, control voltage (Kim et al. 2021). In particular, to evaluate the modulation efficiency a derived parameter is used: Vπ L, which is the product of the voltage and the phase-shifter length for a π-phase shift (smaller values indicating better modulation).

In order to achieve phase shifting in mainstream platforms (i.e. silicon photonics and InP based junctions), thermo-optic effect (Komma et al. 2012), electro-optic plasma dispersion effect (Reed et al. 2010), or actuated micro-electro-mechanical systems (MEMS) (Errando-Herranz et al. 2019) are commonly used, each with advantages and disadvantages. Thermo-optical approach requires the management of temperature propagation and dissipation, which often translates in lower modulation speeds and crosstalk. MEMS based devices often require complex fabrication processes and careful tuning in large scale circuits. Plasma dispersion effects through p-n junctions are the best choice for high speed modulation, although this solution is affected by high losses, and involves additional fabrication processes related to active components. While each type of mechanism presents in literature some specific configurations with small Vπ L down to 0.2 V mm, standard schemes show Vπ L values around 1–2 V cm, with lengths on the order of millimeters (Kim et al. 2021).

An interesting solution for phase shifting in integrated circuits is given by the electro-optical tuning of liquid crystals (LC) (Khoo 2022), which are materials allowing the development of low-power photonic devices, thanks to their large electro-optic response and nonlinear optical properties. LC can feature a high birefringence, which can be controlled through a molecular reorientation achieved by means of electric or optical fields. This characteristic can be used in both core and cladding of the optical devices (Asquini et al. 2005; Piccardi et al. 2011). In both cases, LCs have shown remarkable switching and tuning capabilities with low voltage and low propagation losses. The integration of LC cells proved to be compatible with both semiconductor and polymeric waveguiding systems.

LC dielectric anisotropy can be used to reorient their molecules through electric (Asquini et al. 2005) or optical (Piccardi et al. 2011) fields. Moreover, when used as cladding (Donisi et al. 2010; Gilardi et al. 2012), LCs show remarkable switching and tuning capabilities with low voltage and low propagation losses (Khoo 2022). The integration of LC cells proved to be compatible with both semiconductor and polymeric waveguiding systems (Pfeifle et al. 2012). Furthermore, the development of LC cells requires similar fabrication procedures and materials as those used for polymeric optical integrated circuit platforms. With this concept, LC cells are expected to greatly enhance performances and add new functionalities in sensing, computation, and communications (d’Alessandro et al. 2015). Thus, given some recent developments of new applications using SU-8 polymeric waveguides (Buzzin et al. 2021), we decided to perform a thorough investigation of the performance of a phase shifter exploiting the combination between LC and polymers such as SU-8.

In this work, a very efficient phase shifter based on a polymeric core and a LC cladding has been analysed and developed. The geometry of the waveguides, the distribution of the electrodes, and matching structures have been adapted with the goal of increasing the sensibility of the guided signal to the variations in the orientation of LC molecules. Furthermore, the materials forming this device have been selected after an evaluation of their compatibility during fabrication, and after taking into account production constraints. The present analysis is focused on the telecom wavelength of 1550 nm and on the TE00-like mode. It must be underlined that relevant performances can be obtained also with other wavelengths and modal choices. To analyse the phase shifting waveguides and validate our results, both a direct numerical 3D-Finite Difference Time Domain (FDTD) method and a semi-analytical approach with 2D-Finite Element Method (FEM) were used. Furthermore, to evaluate the electro-optical tuning voltages an analytical approach, combined to an electrostatic FEM simulation was used to confirm this study’s approximations. We show that combining LC cells and low index contrast polymeric waveguides with slot configuration enable the making of systems with strong modulation capabilities.

This manuscript is structured as follows. In Sect. 2, the physical characteristics of the device, its working principle, and some details on the simulation setups are described. In Sect. 3 the analysis of the electro-optic control of LC is shown. In Sects. 4 and 5 the calculations and the assumptions given for the 2D-FEM and 3D-FDTD analyses, are presented. In the final section, the conclusions are drawn.

2 Optical structure and working principle

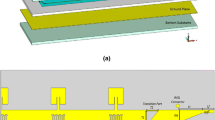
The device is designed to work at 1.55-μm wavelength with TE00-like mode. Fig. 1a shows a schematic representation of the phase-shifting section. It consists in a slot waveguide, obtained by positioning two parallel "rails" of SU-8 2000 (a polymer with refractive index n = 1.573) at a relatively small distance. The waveguides are fabricated upon a SiO2 substrate (n = 1.4657), which forms the bottom cladding, while the upper cladding is made of LC, which is birefringent. Both LCs E7 (ordinary refractive index no = 1.5, extraordinary refractive index ne = 1.689, Δn = 0.189) and 5CB (no = 1.511, ne = 1.678, Δn = 0.167) were investigated. While the claddings are physically finite (e.g. the LC is contained inside a polymeric cell), in the simulations those are considered infinite, so "perfectly matched layer" boundary condition was imposed in all directions.

Fig. 1
figure 1

a Phase shifting area with the slot waveguide, b the Y junction and c the top view of the entire structure of the device

Full size image

A co-planar configuration of 20 µm spaced electrodes was selected. The waveguide is optimized to support only TE00-like and TM00-like modes. The rails are 1.3-μm high and 1-μm wide, at 0.6 μm distance between them (slot gap). The choice of the slot configuration was due to the fact that a relevant part of the modes’ field is positioned in the gap, which is in a direct contact with the LC cladding. Such a choice improves the interaction between LC and the guided signal.

The correct starting alignment is granted by specific processing of the polymeric surfaces composing the LC cell, e.g. by using either a rubbed Nylon film or a photoalignment layer (Yaroshchuk et al. 2012). At rest, the LC molecules are expected to be aligned along the propagation direction of the waveguide. While this initial orientation is mainly granted from the aforementioned top processed polymer, it must be noted that this is also supported by the fact that during the infiltration stage the LC molecules tend to orient longitudinally to SU-8 ridges (Sadani et al. 2018), i.e. the slot gap. A voltage applied to the electrodes induces a reorientation of the LC molecules along the corresponding electric field direction: hence, the LC molecules twists in the xy plane. The amount of voltage necessary for the motion is affected by two parameters (Fig. 1): the height of the cell (d) and the distance between the electrodes (Le). The former needs to be relatively small (in our case 10 µm) for the correct alignment of LCs, while Le needs to be bigger than d to be consistent with the approximations shown in section 5. Since the electric field affects the refractive index experienced by the TE00-like mode, which depends on the final angle, then a phase shift is introduced along the waveguide.

Since most of the configurations developed so far are polymeric ridge waveguides (rectangularly shaped), and since a direct coupling with an optical fiber could be very challenging, an Y-splitter for the transition between ridge waveguide and the slot one (Fig. 1b) was developed. This Y-splitter can work in both directions. In Fig. 1c the developed top view of the phase shifting section is presented.

3 Voltage control over LC orientation

For this device a “coplanar” configuration of the electrodes was chosen, being disposed on the same plane of the waveguide. Thus, electric field lines parallel to circuit plane can be achieved, since by applying a control voltage the reorientation of the molecules will follow the direction of the electric field. The key parameters to determine the control voltage depend on the electromechanical properties of the LC and by the geometry of the cell. This device has been optimized to work with the TE modes. For TM modes, a vertical distribution of the electrodes should be adopted.

In Fig. 2 the “in-plane switching” configuration is represented, where the electrodes are planar to the waveguide. In Fig. 2a the molecular orientation is shown when no voltage is applied. Figure 2b reports reorientation of the molecules when the voltage is applied, and \(\mathrm{\varphi }\) is the twist angle, measured from x axis.

Fig. 2
figure 2

a Molecular orientation when no voltage is applied and b with applied voltage

Full size image

As mentioned in Sect. 2, the geometry of the cell is relevant for the electrical control of the LC. In particular, it is fundamental that the height of the cell d (cell gap) is smaller than the distance between electrodes (Le), due to the fringe fields generating near the electrodes. In fact, in this area the vertical component of the field is prevalent and generates an electrostatic torque, which tends to rotate the LC molecules along the z axis (which is perpendicular to the cell). This effect could compromise the phase shifting operation. Thus, a distance between electrodes of 20 µm and a height of the cell of 10 µm were chosen, since those values guarantee the correct orientation set by polymeric alignment layers (d’Alessandro et al. 2005).

3.1 Analytical relation between voltage and twist angle

The dielectric anisotropy for the E7 is ∆ε = 14.5, for the 5CB ∆ε = 11; their respective twist constant are K22_E7=\({9\times 10}^{-12} N\) and K22_5CB = \({3\times 10}^{-12} N\).

For the following calculations the electric field homogeneous in all the liquid crystal cladding was assumed, the density of elastic energy can be expressed as (Yeh and Gu 2009):

$${U}_{EL}=\frac{1}{2}{k}_{2}{\left(\frac{d\uptheta }{dz}\right)}^{2}$$
(1)

Assuming an uniform electric field, the electric field curl is \(\nabla \times E=0\), so it is independent from z. The density of electromagnetic energy can be expressed as:

$${\Delta U}_{EM}=\frac{1}{2}{\epsilon }_{\perp }{E}^{2}-\frac{1}{2}({\epsilon }_{\parallel }{sin}^{2}\left(\theta \right)+{\epsilon }_{\perp }{cos}^{2}(\theta )){E}^{2}$$
(2)

The total density of energy for each plane is given by the sum between \({U}_{EL}\) and \({\Delta U}_{EM}\), thus the total free energy in the cell is obtained from the integration over the whole cell of such a value:

$$U={\int }_{0}^{d}\frac{1}{2}\left[{k}_{2}{\left(\frac{d\theta }{dz}\right)}^{2}-({\epsilon }_{\parallel }-{\epsilon }_{\perp }){E}^{2}{sin}^{2}\theta \right]dz$$
(3)

Since \(\varphi\) must satisfy the condition of minimum energy (\(\delta U=0\)), and since we have the boundary conditions \(\theta \left(z=0\right)=0\) and \(\theta \left(z=d\right)=0\), we can solve (3) with a Lagrangian:

$$L\left(z,\theta ,\dot{\theta }\right)={k}_{2}{\left(\dot{\theta }\right)}^{2}-\left({\epsilon }_{\parallel }-{\epsilon }_{\perp }\right){E}^{2}{sin}^{2}\left(\theta \right);$$
$$\frac{\partial L\left(z,\theta ,\dot{\theta }\right)}{\partial \theta }-\frac{d}{dz}\frac{\partial L\left(z,\theta ,\dot{\theta }\right)}{\partial \dot{\theta }}=0$$
(4)

where \(\dot{\theta }=\frac{d\theta }{dz}\). The solution of (4) is given by:

$$\left({\epsilon }_{\parallel }-{\epsilon }_{\perp }\right){E}^{2}{sin}^{2}\left(\theta \right)+{k}_{2}{\left(\frac{d\theta }{dz}\right)}^{2}=constant$$
(5)

The angle \(\theta\) depends from the intensity of the E. To derive the relation between those, it is necessary to obtain the relation between \(d\theta\) and \(dz\), by considering the maximum value \({\theta }_{MAX}\) at z = d/2 and the electric field E:

$${k}_{2}{\left(\frac{d\theta }{dz}\right)}^{2}+\left({\epsilon }_{\parallel }-{\epsilon }_{\perp }\right){E}^{2}{sin}^{2}\left(\theta \right)=\left({\epsilon }_{\parallel }-{\epsilon }_{\perp }\right){E}^{2}{sin}^{2}\left({\theta }_{max}\right)$$
(6)

Then, to simplify the visualization it is useful to introduce new variables:

$$\upeta =\mathrm{sin}{\theta }_{max}; sin\Psi =\frac{\mathrm{sin}\theta }{\upeta };$$
(7)

From (6) and (7), it is useful to obtain the transformations for the differential terms \(d\theta\), \(d\Psi\), \(dz\), which can be used to refine (5) into (Yeh and Gu 2009):

$$\frac{1}{\sqrt{1-{\upeta }^{2}{sin}^{2}\Psi }}d\Psi =\sqrt{\frac{{\epsilon }_{\parallel }-{\epsilon }_{\perp }}{{k}_{2}}}Edz$$
(8)

Then we integrate the previous equation on both sides, with 0 < Ψ < π/2 and 0 < z < d/2:

$${\int }_{0}^{d/2}\sqrt{\frac{{\epsilon }_{\parallel }-{\epsilon }_{\perp }}{{k}_{2}}} Edz={\int }_{0}^{\pi /2}\frac{1}{\sqrt{1-{\upeta }^{2}{sin}^{2}\Psi }}d\Psi \ge \frac{\pi }{2}$$
(9)

The right member of the equation is an elliptic integral, whose result is always greater than π/2. In practice, this means that there is a threshold field, that induces a reorientation of LCs molecules (which is needed to win over the inertia of the LC molecules at rest). Remembering that E = V/distance, we obtain the threshold voltage \({V}_{t\mathrm{h}}\):

$${V}_{t\mathrm{h}}=\pi \frac{{L}_{e}}{d}\sqrt{\frac{{k}_{2}}{{\epsilon }_{\parallel }-{\epsilon }_{\perp }}}$$
(10)

where d is height of the cell and Le is the distance between electrodes, the relation between voltage applied and \({\theta }_{MAX}\) can be written as:

$$V={V}_{t\mathrm{h}}\frac{2}{\pi }{\int }_{0}^{\pi /2}\frac{1}{\sqrt{1-{\upeta }^{2}{sin}^{2}\Psi }}d\Psi$$
(11)

Using (11), for a given value of η (or equivalently \({\theta }_{MAX}\)), it is possible to estimate the needed voltage to get the desired reorientation. In Tables 1 and 2 the different values of V for the two different LCs are listed:

Table 1 Control voltage for LC E7 and the respective value of twist angle
Full size table
Table 2 Control voltage for LC 5CB and the respective value of twist angle
Full size table

The first value of voltage in each table represents the threshold voltage, which is the minimum voltage to apply to begin the reorientation of the molecules, a smaller value leading to no changes.

For the E7 to obtain the maximum twist angle (the one before the cut-off) a \(\Delta V=69.6\text{ mV}\) is needed. Instead for the 5CB, its dielectric anisotropy is lower than the E7, so as its maximum twist angle and overall the entire range of control voltage. In this case the \(\Delta V=27.9 {\text{mV}}\).

3.2 Evaluation of the constant field approximation

In the previous step and results, a uniform electric field in the entire LC was assumed. In order to validate this approximation, an electrostatic simulation to analyze the electric field lines was operated. In Fig. 3 the configuration of the 20 µm spaced electrodes is shown, between themselves and the height of the cell assumed as 10 µm. To take into account the fabrication process of the electrodes a thickness of 400 nm and a length of 1 µm were chosen. The dielectric constant of the SiO2 and SU-8 were set respectively to 3.6 and 3.2, while for the LC was used the following formula \(\overline{\epsilon }=\frac{(2{\epsilon }_{\perp }+{\epsilon }_{\parallel })}{3}\).

Fig. 3
figure 3

a The electric field lines for the LC cell. b A focus of the cross section of the device on the slot waveguide area (the arrows indicate the direction of the E field)

Full size image

In Fig. 3 the only not parallel electric field lines are near the external corner of the waveguide rails, so in this area the molecules of the LC will have, over the twist analyzed till now, a light tilt. Comparing the results obtained with the mode solver and the electrostatic simulation, it can be observed that the area of the slot mode is circumscribed; in this area the electric field has parallel lines and this verifies the approximation made before.

4 FEM analysis

In the first part of the analysis, 2D FEM were used to define correct sizes for the slot waveguides: the dispersion curves have been determined, along with the conditions for obtaining the propagation of only TE00-like and TM00-like modes. This study involved multiple mode solver simulations of the transverse direction of the slot waveguide (plane yz on Fig.1a), and the evaluation of the field distributions of the modes and the related effective indices. A finer mesh was assigned to the slot gap region, and boundary conditions were set to Perfectly Matched Layers (PML). After the waveguide modeling stage, the same type of simulation settings was further used, but with different values for the upper cladding, in order to map the possible phase shifts given by the LCs at hand. With this setup, various 2D-FEM simulations with isotropic upper cladding were carried out. From the resulting data, a parallel among the values of the refractive indices, effective indices and achievable angles was reported.

Given the molecules twist on the xy plane (parallel to the circuit), the general formula simplifies, and the LC refractive index becomes (Khoo et al., 2022):

$${n}_{e}\left(\theta \right)=\frac{{n}_{e}{n}_{o}}{\sqrt{{n}_{e}^{2}{cos}^{2}\left(\theta \right)+{n}_{o}^{2}{sin}^{2}(\theta )}}$$
(12)

where no is the ordinary index, ne is the extraordinary index, and θ is the twist angle (from axis x to y in Fig. 1).

Since the main part of the mode field distribution is concentrated in a small area, and given the large distance between electrodes, the electric field direction was approximated as being parallel to the circuital plane. Thus, the resulting index variations can be considered similar to an isotropic media. Given the relation (12) between the LC refractive index and the twist angle, middle values of n(θ) between ne and no were separately evaluated.

In Fig. 4 two results of the simulations are represented. In Fig. 4a, it can be noted the relation between the applied voltage, which induces an electric force, and the consequent twist angle from the molecule, which has been analytically computed as shown in section 3.

Fig. 4
figure 4

a Control voltage vs twist angle and b cladding refractive index vs twist angle for liquid crystal E7 and 5CB

Full size image

In Fig. 4b the relation between the twist angle and the index of the cladding is drawn. For a critical value n(θ) = ncut-off the slot mode exceeds the cut-off level, and the signal is no more guided. In this work, nco ≈1.526, corresponding to θ = 24° for E7 and θ = 19° for 5CB.

To evaluate the relative phase shift Δφ per length of the waveguide L, we have used the classical relations:

$$\varphi =k\cdot L=\frac{2\pi }{\lambda }\cdot {n}_{eff}\cdot L$$
$$\Delta \varphi =\Delta k\cdot L=\frac{2\pi }{\lambda }\cdot {\Delta n}_{eff}\cdot L=\frac{2\pi }{\lambda }\cdot \left({n}_{eff\left(\theta \right)}-{n}_{eff\left(0\right)}\right)\cdot L$$
(13)

where neff(θ) is the effective index of the mode, whilst neff(θ) is the one without excitation. Following (13), for a 1-mm reference length we get: \({\Delta \varphi }_{E7}=20\pi\) and \({\Delta \varphi }_{5CB}=13\pi\), for the highest modulated signal (close to the cutoff). The corresponding values for Vπ L are 0.086 V mm and 0.088 V mm, respectively, close to the cut-off values.

5 FDTD analysis

While the FEM approach was 2D, which is computationally more relaxed, the FDTD analysis was carried out in 3D by using a cubic mesh approximation, and was computationally more challenging. The model consisted in the two parallel SU-8 rails upon a SiO2 substrate and within the LC upper-cladding. All of the borders of the simulation volume were given the PML boundary conditions. The optical source consisted in a mode solver targeting the fundamental TE-like mode, and a length of 3 µm was considered as a transition inside the proper FDTD simulation. Similarly to the previous section, in the analysis the LC was treated as an isotropic media, with the refractive index value obtained from (12) as a function of the twist angle, which is related to the applied voltage by (11). Due to the high computational requirements, it was possible to compute the propagation only along a 20 μm waveguide segment.

The monitors used for the evaluation of the signal power report the time averaged power over the duration of the simulation, and the amount of power related to the mode of interest. It must be noted that the intermodal crosstalk was negligible, even when considering a non-isotropic model for LC. The transmission loss was computed in dB/cm through:

$$TL=10{\mathrm{log}}_{10}\left|\frac{{W}_{i}}{{W}_{t}}\right| [dB]$$
(14)

where Wi and Wt are the powers at the input and output monitors, respectively.

In Table 3 the results for both E7 and 5CB LCs are reported. As it can be seen, losses increase with the twist angle. The reason can be understood from Fig. 5, which shows the field distributions in various cut planes and in two situations: LC with no applied voltage (Fig. 5a, c) and LC close to cut-off (Fig. 5b, d). In the second case, the mode becomes more evanescent and lossy. For a 1-mm reference length, the results from 3D-FDTD are \({\Delta \varphi }_{E7}=18 \pi\) and \({\Delta \varphi }_{5CB}=8 \pi\). The corresponding values for Vπ L are 0.096 V mm and 0.143 V mm, respectively, close to the cut-off regions.

Table 3 Transmission losses for LC E7 and 5CB
Full size table
Fig. 5
figure 5

Electric field modulus on the xz plane (a, b) and on the yz plane (c, d) with no applied voltage (a, c) and with applied voltage (b, d)

Full size image

The slot waveguide has been optimized to be the operation part of the device, where the phase shift happens. In the remaining part of the circuit single waveguides can be used, by adopting Y junction in the transition between single waveguide and slot waveguide (and viceversa), as represented in Fig. 1.

Such a structure was simulated directly in 3D-FDTD method, with the goal of designing a low insertion loss optical element. The task was completed with a 14 μm long Y-splitter, and the related value for the losses is 0.2 dB in both directions. Such a small value of losses descends from the fact that this technology uses a low index contrast waveguide, where the optical signal does not experience strong variations as happens in platforms with higher index-contrasts and shorter lengths.

In Fig. 6 the light propagation in the longitudinal direction of the Y junction is represented, as taken from the middle of the waveguide’s thickness. As can be seen, the transition of the signal is stable without relevant oscillations.

Fig. 6
figure 6

Electric field modulus on the xy plane along the Y junction

Full size image

It is worth to note that for both LCs E7 and 5CB the simulations have been made only for the situation when the molecules are at rest (no voltage applied), their direction is along the propagation direction, that is because this element does not contribute to the phase shift achievable. In Table 4 are reported the insertion losses for both LCs E7 and 5CB, as you can see those are really low, therefore the Y junction does not affect negatively the entire system.

Table 4 Transmission losses for the Y junction
Full size table

6 Conclusions

In this work, after an analysis employing two different approaches, the configuration of phase shifter revealed a wide tuning range. Both methods have shown that, with a small voltage it is possible to have a very efficient modulation with polymeric waveguide platform and LC cells.

Through the less computationally demanding 2D-FEM simulations, and with the introduction of various approximations, it is possible to estimate the phase shift. Moreover, through the electrostatic simulation with the same method it was possible to validate the homogeneous electric field approximation for the entire process to determine the control voltage. Instead, 3D-FDTD method allowed to compute more directly the extension of the device; despite its precision, it could simulate only a limited length of the device, so it was still necessary to make an indirect estimation of the full length. Moreover, the same method allowed us to design easily the y-splitter. The final results of the two approaches fairly match in values and in trend for the two considered LCs, so this can be considered a mutual validation check.

The planar configuration of the electrodes, related to the tuning of the TE-like modes, has been defined, so the proposed device presents a phase shift of 18π and a needed voltage of just 1.73 V for E7, meanwhile for the 5CB the achievable phase shift is 8π for a 1.13 V. The best obtainable values for Vπ L, in both LC, are around 0.1 V mm. While those values were taken close to the cut-off of the waveguide, where the losses are high, there is space for margin control. Also, it must be noted that with the choice of LCs, E7 and 5CB, we were not able to use the full potential of the phase shifter. Choosing LCs with lower refractive indices would have further improved the tunability of the device.

Overall, our analysis shows the potentialities of the use of LC cells in polymeric waveguides, since the performance is very appealing. This adds up also to the fact that both technologies employ similar fabrication processes. On the long run, we expect an increased adoption of LCs in various polymeric optical circuits.