Abstract
On the basis of two optical fibers with an optional lateral and longitudinal displacement in a homogeneous background medium, we describe a general full-vectorial Wilson-basis discretized mode-matching method that evaluates the converged electromagnetic fields after all resonances in the possible gap cavity have settled. Wilson basis functions feature strong localization in both the spatial and the spectral domain, which allows for efficient modal electromagnetic field expansions, adequate truncation of field propagation operators, and sparse translation operators, which in turn allow to make ad hoc electromagnetic field-matching operators. For physical contact connections between single-mode fibers with a mode-field diameter mismatch, we obtain attenuation curves that are right between those obtained from approximation methods that either effectively match the electric field or the magnetic field under the assumption of a vanishing reflection. For fibers separated by a growing gap, constructive and destructive interference patterns in the cavity are computed by the successive application of Love’s equivalence principle and the propagation operator. By leveraging the physical width of the Wilson basis functions and the stepsize of the propagation operator, the initial operators may be reused in solving the interface problem for other wavelengths. For multi-mode fiber connections, we provide attenuation curves on a modal electromagnetic field level, as well as for overfilled and core-confined target encircled-flux compliant launches. A comparison to geometrical-optics based approaches shows attenuation differences in the order of several hundredth of a dB, and although that is small, it is significant for modern connection attenuation specifications. In the final example of connections between regular and trench-assisted multi-mode fibers, we notice that the relative change in the cumulative near-field power distribution can be significant, despite a marginally small attenuation. The influence of a core diameter and/or numerical aperture mismatch can be examined with a deliberate lateral misalignment.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Detachable low-attenuation optical fiber connections are indispensable to configure optical networks in a flexible manner. In optical systems that employ the space-division multiplexing technique to further increase the bandwidth of a single fiber (Richardson 2010), sub-micrometer fiber alignment is needed to preserve the specific linear combinations of the modal electromagnetic fields that span spatio-multiple transmission channels (Nagase 2014). In structured indoor cabling systems that rely on cascaded multi-mode fiber technology with a 50 \(\mu \,\hbox {m}\) core diameter, every connection should make and maintain physical contact between the accurately aligned fibers in order to keep the penalty on the power budget below several tenths of a dB. A further reduction of the connection attenuation would allow for more inline connections without sacrificing the total link length, and without exceeding the tight optical power budgets that are just shy of 2 dB for modern IEEE802.3 Ethernet networks (http://www.ieee802.org/3 2010) and will be tightened even further as data rates increase (Spurgeon 2000). Other (potentially) detachable optical interfaces that bring fiber optics closer to the transceivers or compute engines include free-space optics lenses inside a transmitter and receiver optical subassembly (Lam 2011), \(45^\circ\) mirrors that are integrated in board level optics (Fettweis et al. 2019), or direct butt-coupled fibers to rectangular waveguides on chip (Hauffe et al. 2001).
The examples mentioned above involve electromagnetic connections across planar interfaces. However, the actual material configurations in the half spaces on either side of those interfaces may be slightly, or very different. Even if the electromagnetic fields on either side of an interface may efficiently be described in terms of modal expansions, those modal expansions are generally mutually unrelated. Every time one would encounter such electromagnetic interface problems, one would have to expand one set of modes (including the radiation field) in terms of the other: a tedious task indeed. This can be circumvented by expressing every modal expansion in terms of the same complete set of orthogonal basis functions, i.e., a universal interface. We have discussed such a universal interface in terms of Wilson basis functions in (Floris and de Hon 2018a, b). The Wilson basis functions are duo-localized, i.e., they decay exponentially both in the spatial and in the spectral domain (Wilson 1987; Daubechies et al. 1991). In the Wilson basis, high-frequency electromagnetic wavefields can be represented through a parsimonious multidimensional set of coefficients (Arnold 2002; Floris and de Hon 2018a). In (Floris and de Hon 2018a, b), we introduced the Wilson basis universal interface approach, applied it to the electromagnetic scattering of incident modes at the end-face of a multi-mode fiber, and reciprocally, the coupling of light into a fiber. The major advantage of our Wilson-basis approach from a computational mode-matching perspective, is that it becomes irrelevant whether the coefficients represent fields that are associated with a round fiber, a rectangular dielectric waveguide or any other physical medium for which a complete set of (modal) transverse electromagnetic field solutions can be computed.
Below, we argue that the full benefits of the universal interface approach for computational electromagnetics really become manifest when two (or more) structures are connected along their planar interfaces. The main contribution of this paper is to demonstrate this through examples of two, not necessarily aligned nor identical, optical fibers that may be longitudinally separated by a homogeneous medium. In particular, we have devised a Wilson-basis discretized mode-matching method that relies on a recurrence scheme to accelerate the convergence of the electromagnetic fields that resonate in the cavity formed by two successive fiber interfaces with a possibly vanishing gap in between.
The effective duo-localization of the Wilson basis ensures the rapid convergence of the spectral Green’s function integrals, needed for the evaluation of the electromagnetic wavefields that emanate from Wilson-basis discretized electromagnetic source distributions in a homogeneous medium. From the Wilson-basis coefficients that describe a given transverse electromagnetic field at the end-face of the physical medium, it is possible to directly configure two electromagnetic source distributions that produce one-way forward and one-way backward propagating electromagnetic fields in a homogeneous medium in such a way that boundary conditions are satisfied at the interface (Floris and de Hon 2018b). The underlying Green’s function integrals constitute a propagation operator that synthesizes the electromagnetic field at a chosen distance from the source plane. The successive application of Love’s equivalence principle and the propagation operator allows for the evaluation of the electromagnetic fields at integer multiples of the selected distance almost effortlessly (de Hon and Floris 2018). It is convenient that the coupling matrix between Wilson basis functions and laterally displaced Wilson basis functions is sparse (Floris and de Hon 2018a), so that any adjustment of the lateral alignment of any of the the physical media (for instance a fiber) with respect to the interface is easily evaluated in the Wilson basis prior to executing the mode-matching procedure.
Our first aim is to demonstrate the effectiveness of the Wilson-basis universal interface computational framework in solving multiple interface problems. Our second aim is to discuss several interesting realistic fiber connection applications, outlined in Sect. 2. The main ingredients of our Wilson-basis interface framework: the Wilson basis, the Wilson-basis expansion of electromagnetic fields, and the construction of Wilson-basis discretized one-way propagating fields in homogeneous space are summarized in Sect. 3.
2 Optical fiber interconnect problems
In this manuscript, we aim to serve a diverse readership. If your primary interest is computational electromagnetic modeling of realistic interface problems, then you can find the theoretical underpinning in Sects. 4–6. Conversely, if you are mainly looking for a detailed discussion of modern optical fiber interconnect problems, you can find extensive practical simulation results in Sects. 7–11. Below, we present a roadmap to these sections to help navigate the paper.
In our Wilson-basis interface framework, all reflection-transmission problems that involve excitations and reflections that are spanned by the guided modal electromagnetic fields of a single optical fiber may be solved through the procedure described in Sect. 4. To cope with all other excitations, and to avoid having to discretize the continuous spectrum that constitutes the radiation field, we exploit the small transverse contrast in the refractive index profile to temporarily replace the fiber by a homogeneous background medium and solve the reflection-transmission radiation-field problem for two homogeneous half-spaces in Sect. 5.
In Sect. 6, we consider a cavity formed by two fiber interfaces separated by a slab of homogeneous material (e.g. air), and describe a loop operator that evaluates the evolution of electromagnetic fields that make a loop inside the cavity, i.e., that arrive back at the first interface after two successive reflections of respectively the first and the second slab-to-fiber interface. Particularly for configurations with highly reflective interfaces, we would like to avoid having to evaluate a Neumannn series through a direct term-by-term application of the loop operator in order to obtain the converged electromagnetic fields in the cavity, together with the reflection in the first fiber, transmission in the second fiber and the radiation fields. Instead, we describe an iterative method that decomposes the looped electromagnetic field in terms of the field in the previous loop and a residual field. The underlying Neumann-series for the converged electromagnetic fields reduces to evaluating geometric progressions of known vector fields, and evaluating the loop operator for a sequence of quickly decaying residual fields.
To test the approach, we consider single-mode fiber connections with a vanishingly small gap in Sect. 7 and compare the connection attenuation to the approximated case that spans the incident field in the first fiber by the guided modes of the second fiber by using projection (overlap) integrals under the assumption that the reflected field vanishes (Neumann 1988). There are two possible choices for the projection operation, one effectively matching the electric field, the other the magnetic field. As the mode-field diameter mismatch between the two fibers is increased, the effective impedance mismatch leads to two attenuation curves for the two choices of the approximate case, and interestingly we find that the curve produced by our mode-matching approach is right in the middle of the two. For the relatively small mode-field diameter mismatches that we considered here, the differences between the full mode-matching method and the approximation are only a few hundredths of a dB. However, in case of dissimilar waveguides or a significant separation, the assumption of a vanishing reflected field is no longer valid. We demonstrate examples of this for a fixed lateral displacement and a range of longitudinal separations in Sect. 8.
In Sect. 9, we apply the full mode-matching method to physical contact connections between two multi-mode fibers and give the attenuation curves for lateral misalignments up to 6 \(\mu \,\hbox {m}\) for each of the 342 guided modes of a regular multi-mode fiber. In order to make judicious, reproducible and repeatable attenuation measurements in practice, international standards organizations such as IEC (IEC 61280-4-1 2021) and TIA (TIA-455-203-A 0000) demand an encircled-flux compliant launch, which means that the cumulative near-field power distribution measured at the fiber end-face of the plug under test shall keep within tight bounds that are imposed on a handful of target levels. Even though there are commercially available mode conditioner devices that aid in achieving an encircled-flux compliant launch in practice, from a theoretical perspective the five prescribed targets are hardly restrictive in view of the 342 guided modal electromagnetic fields that one can mathematically choose from. To be able to study the impact of fiber alignment and fiber geometry parameters such as the fiber core diameter and numerical aperture on the attenuation, we follow a mode-continuum approximation (Daido et al. 1979) to narrow down to a sensible combination that employs all modes in such a way that the modal amplitudes are sampled from a smooth modal power distribution function.
In an earlier publication, we have shown that it is also possible to generate encircled-flux compliant ray-based launches in multi-mode fibers (Floris et al. 2019), and to determine design curves that balance core diameter mismatch, numerical aperture mismatch and lateral misalignment for reference-grade connectors specifications that achieve less than a tenth of a dB of attenuation when it makes a physical contact connection to another reference-grade connector (Floris et al. 2012). Here, we make a comparison between the vectorial full-wave mode-matching technique and geometrical optics, which reveals that both approaches are in agreement for lateral misalignments up to about 4 \(\mu \,\hbox {m}\), after which the attenuation curve produced by the geometrical optics method is a bit higher.
We evaluated the attenuation curves for each of the speckle patterns that together produce a spatio-temporal target encircled-flux compliant near-field pattern. The variation in the attenuation is a measure for modal noise, and in (Floris et al. 2019), we have shown that this coherent wavefield phenomenon can alternatively be studied in terms of incoherent rays with the aid of the cumulative near-field patterns of the individual speckle patterns. This is also discussed in Sect. 9.
In Sect. 10, we examine the attenuation and return loss for two longitudinally separated multi-mode fibers and a lateral offset. Such connections were also studied with ray-based methods (Di Vita and Rossi 1978; van Etten et al. 1985; Bude and Van Etten 1987) albeit for very large separations and for an overfilled launch. Here, we consider every mode as an individual excitation. Via weighted combinations of modal excitations, we construct realistic encircled-flux compliant launches. This approach enables us to study the response of the diverging fields in the cavity on the attenuation in the receiving fiber for the whole transition from small to very large separations.
We conclude in Sect. 12 with examples of connections between regular and trench-assisted multi-mode fibers. Even though additional core diameter and numerical aperture mismatches might not lead to significant changes in the attenuation, it does show up as a relative change in the cumulative near-field pattern in the sense that either the entire curve shifts upwards (narrower distribution) or downwards (wider distribution). The observation that a deliberate misalignment alters the shape of the curve suggests that relative encircled-flux measurements can reveal very subtle differences in the refractive index profile across the fiber connection interface. It may be possible to exploit this sensitivity for profile measurement purposes.
3 Decomposition of fiber modes to one-way propagating fields in homogeneous space
The Wilson basis consists of basis functions \(w_{\ell n}(x)\) that are trigonometric modulated and translated versions of a single window function \(\theta (x)\). The spatial translation is denoted by index n and the modulation by index \(\ell\). We adopted the algorithm of Daubechies et al. (Daubechies et al. 1991) for the construction of \(\theta (x)\) and gave a streamlined summary in (Floris and de Hon 2018a). With the aid of the forward Fourier transformation
the spectral counterpart of the Wilson basis functions are described by
The spectral basis functions have two peaks due to the trigonometric modulations of the Wilson basis functions. Further, the function \(\hat{\theta }= \mathcal {F}_T\left( \theta \right)\) decays exponentially for a Gaussian window function \(\theta (x)\) (Floris and de Hon 2018a).
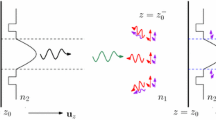
We proceed by giving a brief summary on the construction of one-way propagating fields in homogeneous space in the Wilson basis from (Floris and de Hon 2018b). In particular, we emphasize the construction of specific one-way forward propagating field \(\bar{\mathbf {f}}_\mathbf {i}^+\) (blue wiggles) and one-way backward propagating field \(\bar{\mathbf {f}}_\mathbf {i}^-\) (red wiggles) that match to the waveguide-specific guided mode \(\bar{\mathbf {f}}_\mathbf {i}\) (green wiggle) as shown schematically in Fig. 1.
For a fiber mode \(\bar{\mathbf {f}}_\mathbf {i}\) incident on a fiber end-face (single green wiggle in the fiber), a decomposition into a one-way forward \(\bar{\mathbf {f}}_\mathbf {i}^+\) (blue wiggles) and one-way backward \(\bar{\mathbf {f}}_\mathbf {i}^-\) (red wiggles) propagating fields in the homogeneous medium satisfy the boundary conditions. (Color figure online)
Let \(\mathbf {f}(\mathbf {r}_t,z)=\left[ E_x, E_y, H_x, H_y\right] ^T\) describe the transverse electromagnetic field components of an arbitrary wavefield along the transverse coordinate \(\mathbf {r}_t=x\mathbf {u}_x+ y\mathbf {u}_y\) at a longitudinal coordinate z. In the remainder of this section, we assume that \(\mathbf {f}\) represents an arbitrary guided mode in the fiber.
We expand the vectorfield \(\mathbf {f}\) in the Wilson basis by writing
where \(\bar{\mathbf {f}}_\mathbf {i}(z)\) is a four-vector containing Wilson basis coefficients and \(w_{\mathbf {i}}(\mathbf {r}_t) = w_{\ell _x n_x}(x)w_{\ell _y n_y}(y)\) is a 2D Wilson basis function. The multi-index \(\mathbf {i}=\left( \ell _x,n_x,\ell _y,n_y\right)\) is used to compress notation (and we shall also use the multi-indices \(\mathbf {j}\) and \(\mathbf {k}\) for this purpose), and the parameter d scales the Wilson basis function to the size of the modal electromagnetic fields. The Wilson basis coefficients \(\bar{\mathbf {f}}_\mathbf {i}(z)\) are computed numerically using fixed-point cubatures as detailed in (Floris and de Hon 2018a).
We proceed with the construction of a one-way forward propagating field \(\bar{\mathbf {f}}_\mathbf {i}^+(z)\) and a one-way backward propagating field \(\bar{\mathbf {f}}_\mathbf {i}^-(z)\), in such a way that the continuity of the transverse electromagnetic field \(\bar{\mathbf {f}}_\mathbf {i}(z_0) = \bar{\mathbf {f}}_\mathbf {i}^+(z_0) + \bar{\mathbf {f}}_\mathbf {i}^-(z_0)\) is satisfied across the interface \(z=z_0\). The field propagation in the positive and negative z direction are relative to the assumed \(\exp (j\omega t)\) dependence on time t, where \(\omega\) denotes the angular frequency.
In the first step, we invoke Love’s equivalence principle (Love 1901) and construct equivalent magnetic sources for the electric field of \(\bar{\mathbf {f}}_\mathbf {i}(z)\) at \(z=z_0\). This leads to a source distribution \(\mathbf {q}_\mathbf {j}=\left[ J_x,J_y,K_x,K_y\right] ^T\) in the Wilson basis
where the superscript K indicates that only magnetic sources are present.
In the next step, we configure a second electric source distribution by invoking Love’s equivalence principle again, but now on the magnetic field that was generated by the sources \(\bar{\mathbf {q}}_\mathbf {j}^{K}\) in Eq. (4), i.e.,
where the superscript J, K emphasizes that \(\bar{\mathbf {q}}\) contains a distribution of electric equivalent sources of the (magnetic) field that in turn was generated by magnetic sources. The source distribution \(\bar{\mathbf {q}}_\mathbf {j}^{J,K}\) in Eq. (5) generates the same electromagnetic field as the source distribution \(\bar{\mathbf {q}}_\mathbf {j}^{K}\) in Eq. (4) for \(z\ge z_0\). This becomes apparent upon inspection of the four-by-four matrix \(\bar{\mathsf {F}}_{\mathbf {i},\mathbf {j}}(\varDelta z)\) with \(\varDelta z = z - z_0\), which evaluates the double integral (Floris and de Hon 2018b)
In Eq. (6), \(\tilde{\mathsf {G}}_T(\mathbf {k}_t,\varDelta z) = \frac{1}{2}e^{-jk_z |\varDelta z|} \tilde{M}\) is the spectral dyadic Green’s function with,
in which the impedance \(Z=\sqrt{\mu _0/\varepsilon }=\sqrt{\mu _0/(\varepsilon _0 n^2)}\) relates to the refractive index n, permittivity \(\varepsilon _0\) and permeability \(\mu _0\). In view of the branch cut associated with the square root \(k_z(\mathbf {k}_t)=\sqrt{k^2-k_t^2}\), with the wavenumber \(k=\omega \sqrt{\mu _o\varepsilon }\) and with \(k_t=|\mathbf {k}_t|\), we define \({\text {Im}}(k_z)<0\), and \({\text {Re}}(k_z)\ge 0\) if \({\text {Im}}(k_z)=0\), associated with the physical Riemann surface. Furthermore, \(\tilde{M}\) in Eq. (7) depends on
For \(\varDelta z \rightarrow 0\), the magnetic \(\bar{\mathbf {q}}^{K}\) sources in Eq. (4) generate an electric field that changes sign across the \(z=z_0\) interface, whereas the electric \(\bar{\mathbf {q}}^{J,K}\) sources generate a magnetic field that changes sign across \(z=z_0\). Hence, the electromagnetic field
with the \(+\) subscript is one-way propagating in the positive z-direction and matches the electric field of \(\bar{\mathbf {f}}_\mathbf {i}\) at the positive side of the interface at \(z\downarrow z_0\). On the opposite side of the interface for \(z<z_0\), the electromagnetic fields vanish due to destructive interference of the fields generated by the sum of the sources \(\bar{\mathbf {q}}^K_\mathbf {j}\) and \(\bar{\mathbf {q}}_\mathbf {j}^{J,K}\). The − subscript denotes a one-way propagating electromagnetic field in the negative z-direction for \(z<z_0\) that matches the electric field of \(\bar{\mathbf {f}}_\mathbf {i}\) at the interface \(z\uparrow z_0\), while the field vanishes for \(z>z_0\).
In a similar fashion, one can deploy equivalent electric sources
supplemented with magnetic sources
to achieve a one-way propagating electromagnetic field
that has the same transverse magnetic field as \(\bar{\mathbf {f}}_\mathbf {i}\) at the interface.
Upon combining Eqs (9) and (12), the fiber mode \(\bar{\mathbf {f}}_\mathbf {i}\) is matched to two one-way propagating fields \(\bar{\mathbf {f}}_\mathbf {i}^+\) and \(\bar{\mathbf {f}}_\mathbf {i}^-\) in homogeneous space by choosing (Floris and de Hon 2018b)
The sum \(\bar{\mathbf {f}}_\mathbf {i}^+(z) + \bar{\mathbf {f}}_\mathbf {i}^-(z)\) at \(z=z_0\) matches \(\bar{\mathbf {f}}_\mathbf {i}\), because the sum of the fields \(\bar{\mathbf {f}}_\mathbf {i}^{E+}(z)+\bar{\mathbf {f}}_\mathbf {i}^{E-}(z)\) describes the desired electric field of \(\bar{\mathbf {f}}_\mathbf {i}\) (albeit with a factor 2), and has a zero magnetic field, whereas the sum of fields \(\bar{\mathbf {f}}_\mathbf {i}^{H+}(z)+\bar{\mathbf {f}}_\mathbf {i}^{H-}(z)\) describes the desired magnetic field of \(\bar{\mathbf {f}}_\mathbf {i}\) (albeit with a factor 2), and has a zero electric field.
To evaluate these fields at an arbitrary longitudinal z coordinate, one only needs to evaluate the matrix \(\bar{\mathsf {F}}_{\mathbf {i},\mathbf {j}}(z-z_0)\) for a compact set of source Wilson source distributions (Floris and de Hon 2018b). As an added bonus, the fields may be evaluated at subsequent longitudinal coordinates \(z=m\varDelta z\), with \(m=1,\dots ,M\) almost effortlessly by the repetitive application of Love’s equivalence principle and re-use of the propagation operation \(\bar{\mathsf {F}}_{\mathbf {i},\mathbf {j}}(\varDelta z)\) as shown in (de Hon and Floris 2018). Moreover, by ensuring that the quantities \(d/\lambda\) and \((\varDelta z)/d\) are left unchanged, one can re-use the pre-computed coefficients \(\bar{\mathsf {F}}_{\mathbf {i},\mathbf {j}}(\varDelta z)\) for other wavelengths too.
We proceed with a brief notation-consistent summary of the solution strategy to reflection-transmission problems at the end-face of an optical fiber from (Floris and de Hon 2018b).
4 Reflection-transmission problems for fiber end-faces
For fiber end-face reflection-transmission problems as sketched in Fig. 2, we now apply the field decomposition method of Sect. 3. For the forward propagating fiber mode \(\bar{\mathbf {f}}_{\mathbf {i},m}^+\) that is incident from the left on the interface at \(z=z_0\) in the top sketch of Fig. 2, the decomposition results in a one-way forward field \(\bar{\mathbf {h}}_{\mathbf {i},m}^+\) and a one-way backward field \(\bar{\mathbf {h}}_{\mathbf {i},m}^-\) in the homogeneous medium. For brevity, we denote the mode number m for the combined radial and angular indices of the pertaining fiber mode.
Top: a one-way forward propagating fiber mode \(\bar{\mathbf {f}}_{\mathbf {i},m}^+\) is decomposed into a one-way forward propagating field \(\bar{\mathbf {h}}_{\mathbf {i},m}^+\) and a one-way backward propagating field \(\bar{\mathbf {h}}_{\mathbf {i},m}^-\) in homogeneous space. Bottom: a backward propagating fiber mode \(\bar{\mathbf {f}}_{\mathbf {i},m}^-\) is decomposed into a one-way forward propagating field \(\bar{\mathbf {p}}_{\mathbf {i},m}^+\) and a one-way backward propagating field \(\bar{\mathbf {p}}_{\mathbf {i},m}^-\)
In a similar fashion for the backward propagating \(m^{\mathrm{th}}\) fiber mode \(\bar{\mathbf {f}}_{\mathbf {i},m}^-\) in the fiber (second sketch in Fig. 2), the one-way forward field \(\bar{\mathbf {p}}_{\mathbf {i},m}^+\) and one-way backward field \(\bar{\mathbf {p}}_{\mathbf {i},m}^-\) in the homogeneous medium satisfy the boundary conditions. As we use the homogeneous-space wavefields \(\bar{\mathbf {h}}_{\mathbf {i},m}^+\), \(\bar{\mathbf {h}}_{\mathbf {i},m}^-\), \(\bar{\mathbf {p}}_{\mathbf {i},m}^+\), and \(\bar{\mathbf {p}}_{\mathbf {i},m}^-\) as building blocks, we deliberately chose to assign two separate symbols \(\bar{\mathbf {h}}\) and \(\bar{\mathbf {p}}\) to emphasize that the associated fiber modes are propagating forward and backward in the fiber, respectively.
Consider an excitation \(\bar{\mathbf {f}}_\mathbf {i}^I=\sum _m c^I_m\bar{\mathbf {f}}_{\mathbf {i},m}^{+}\) written as a linear combination of forward propagating guided fiber modes \(\bar{\mathbf {f}}_{\mathbf {i},m}^+\) weighted with coefficients \(c^I_m\) (green wiggle in Fig. 3). In the homogeneous medium, the transmitted field \(\bar{\mathbf {f}}_\mathbf {i}^{T,\mathrm{guided}} = \sum _m c^I_m \bar{\mathbf {h}}_{\mathbf {i},m}^+\) is associated with the forward-propagating fiber modes (blue wiggles).
For a fiber mode \(\bar{\mathbf {f}}_\mathbf {i}^I\) incident on a fiber end-face (green wiggle), a specific linear combination of backward-propagating guided modes \(\bar{\mathbf {f}}_\mathbf {i}^{R,\mathrm{guided}}\) (black wiggles) are chosen in a minimum-norm sense so that the associated backward propagating fields \(\bar{\mathbf {p}}^-\) (bottom situation in Fig. 2) cancel the one-way backward propagating fields \(\bar{\mathbf {h}}^-\) (top situation in Fig. 2) that are associated with the excitation \(\bar{\mathbf {f}}_\mathbf {i}^I\). Any mismatch fields \(\bar{\mathbf {f}}_\mathbf {i}^{R,\mathrm{rad}}\) and \(\bar{\mathbf {f}}_\mathbf {i}^{+,\mathrm{rad}}\) (purple wiggles) are radiating fields. In the transmitted field, \(\bar{\mathbf {f}}_\mathbf {i}^{T,\mathrm{guided}}\) is spanned by \(\bar{\mathbf {h}}_{\mathbf {i},m}^+\) in Fig. 2, and \(\bar{\mathbf {f}}_\mathbf {i}^{-R,\mathrm{guided}}\) is spanned by \(\bar{\mathbf {p}}_{\mathbf {i},m}^+\) in Fig. 2. (Color figure online)
We aim to cancel the unphysical one-way backward field \(\sum _m c^I_m \bar{\mathbf {h}}_{\mathbf {i},m}^-\) from the homogeneous medium by expanding it in terms of one-way backward fields \(\bar{\mathbf {p}}_{\mathbf {i},m}^-\), for which we already determined the scattered fields (viz. second schematic in Fig. 2). This gives rise to a reflection in the fiber \(\bar{\mathbf {f}}_\mathbf {i}^{R,\mathrm {guided}} = \sum _m c^R_m \bar{\mathbf {f}}_{\mathbf {i},m}^-\) (black wiggles) and the second contribution to the transmission \(\bar{\mathbf {f}}_\mathbf {i}^{-R,\mathrm {guided}}=\sum _m c^R_m \bar{\mathbf {p}}_{\mathbf {i},m}^+\) (dark red wiggles). All that remains is a (typically small (Floris and de Hon 2018b)) residual field \(\sum _m\left( c^I_m \bar{\mathbf {h}}_i^- - c^R_m \bar{\mathbf {p}}_{\mathbf {i},m}^-\right)\) that is incident from the right, which in turn excites the fields \(\bar{\mathbf {f}}_\mathbf {i}^{R,\mathrm {rad}}\) in the fiber and \(\bar{\mathbf {f}}_\mathbf {i}^{+,\mathrm {rad}}\) in the homogeneous medium (purple wiggles) that are associated with the radiation spectrum of the fiber. The solution strategy to the evaluation of these residual fields is discussed in Sect. 5.
The vector \(\mathbf {c}^R\) that contains the coefficients \(c_m^R\) of the guided reflected modal electromagnetic fields is obtained by solving the system of equations \(A\mathbf {c}^R=\mathbf {b}\), where the matrix A has elements \(A_{u,v}=\langle \bar{\mathbf {p}}_u^{-},\bar{\mathbf {p}}_v^{-} \rangle\), and the vector \(\mathbf {b}\) has elements \(b_r=\langle \bar{\mathbf {p}}_r^-, \sum _m c^I_m \bar{\mathbf {h}}_{\mathbf {i},m}^- \rangle\). The (Poynting-vector based) scalar product between two transverse electromagnetic wavefields in the Wilson basis are evaluated through
where \(*\) denotes complex conjugation.
A similar approach may be followed in case the excitation \(\bar{\mathbf {f}}_\mathbf {i}^I\) is incident from the homogeneous medium. First, a minimum norm expansion \(\bar{\mathbf {f}}_\mathbf {i}^I \approx \sum _m c^I_m \bar{\mathbf {p}}_{\mathbf {i},m}^-\) with coefficients \(c^I_m\) constructs a (guided) transmitted field \(\sum _m c^I_m \bar{\mathbf {f}}_{\mathbf {i},m}^-\) in the fiber and a reflected field \(\sum _m c^I_m \bar{\mathbf {p}}_{\mathbf {i},m}^+\) in the homogeneous medium. Then, the residual field \(-\bar{\mathbf {f}}_\mathbf {i}^I + \sum _m c^I_m \bar{\mathbf {p}}_{\mathbf {i},m}^-\) excites the radiation fields in the fiber and the homogeneous medium.
Previously (Floris and de Hon 2018b), we considered situations where the excitation of the residual fields in the radiation spectrum of the fiber was negligibly small. However, for large excitations from the homogeneous medium, for example due to multiply scattered resonating fields in a gap between two fibers, the power carried by the residual fields can be substantial.
To avoid the burden of discretizing the radiation spectrum of the fiber modes just for the computation of the residual fields, we exploit the small contrast in the (transverse) refractive index profile by replacing the fiber by an effective homogeneous background medium, and solve the residual-field reflection-transmission for this effective medium. We adopt this approach below to evaluate the reflected field in the Wilson basis for an interface between two homogeneous half-spaces.
5 Reflection-transmission problems of two homogeneous half-spaces
For an interface between two homogeneous, isotropic, lossless, dielectric media, the spectral representation of the reflection is directly related to the incident electromagnetic field through Fresnel reflection coefficients for the s-polarized and p-polarized field components. The well-established approach has recently allowed the identification of conditions for incident evanescent plane-wave excitation to experience total internal reflection (Lakhtakia and Mackay 2008).
The incident Wilson-basis discretized transverse electromagnetic field formulation in Eq. (3) has a spectral representation
with the four-vector \(\bar{\mathbf {f}}_\mathbf {i}^I = [ \bar{\mathbf {f}}_\mathbf {i}^{I,E}, \bar{\mathbf {f}}_\mathbf {i}^{I,H}]^T\) containing two transverse electric Wilson-basis coefficients \(\bar{\mathbf {f}}_\mathbf {i}^{I,E}\) and two transverse magnetic Wilson-basis coefficients \(\bar{\mathbf {f}}_\mathbf {i}^{I,H}\) oriented along Cartesian unit vectors. Without loss of generality, we assume that the interface between two homogeneous media is located at \(z=0\).
To distinguish between the s- and p-polarisation in Eq. (15), we introduce polar coordinates \(k_x = k_t \cos \varphi\) and \(k_y = k_t \sin \varphi\), and rewrite the unit vectors \(\mathbf {u}_x\) and \(\mathbf {u}_y\) as
where \(\mathbf {u}_{k_t}= \mathbf {k}_t/|k_t|=\cos \varphi \mathbf {u}_x+ \sin \varphi \mathbf {u}_y\) is the unit vector in the \(\mathbf {k}_t\) direction. By substituting Eq. (16) in Eq. (15), we recognize the s- and p-polarizations of the electric field
with amplitudes \(a_{s,\mathbf {i}}\) and \(a_{p,\mathbf {i}}\) in the Wilson basis
Here, the numbers 1 and 2 between the square brackets denote the Wilson-basis discretized Cartesian \(E_x\) and \(E_y\) electric field components. In a similar fashion, we write the transverse magnetic field as
with Wilson basis coefficients
Here, the numbers 3 and 4 between the square brackets denote the Wilson-basis discretized Cartesian \(H_x\) and \(H_y\) magnetic field components.
The spectral representation of the reflected field is similar to Eq. (15) and reads (Lakhtakia and Mackay 2008)
and propagates in the negative z-direction. The reflection operator R produces a four-vector with components
and applies the Fresnel reflection coefficients
that depend on \(\mathbf {k}_t\). In view of the branch cut associated with the square root \(k_{z_1}(\mathbf {k}_t) = \sqrt{ k_1^2 - k_t^2}\), we define \(\mathrm {Im}(k_{z_1})<0\), and \(\mathrm {Re}(k_{z_1})\ge 0\) if \(\mathrm {Im}(k_{z_1})=0\). The wavenumber \(k_1\) of the incident and reflected fields in the first medium \(n_1\) are related to the free-space wavenumber \(k_0=\omega \sqrt{\mu _0\varepsilon _0}\) through \(k_1=k_0n_1\). Likewise for the square root \(k_{z_2}(\mathbf {k}_t) = \sqrt{ k_2^2 - k_t^2}\), we define \(\mathrm {Im}(k_{z_2})<0\), and \(\mathrm {Re}(k_{z_2})\ge 0\) if \(\mathrm {Im}(k_{z_2})=0\). The transmitted field in the second medium \(n_2\) has wavenumber \(k_2 = k_0 n_2\).
By applying the transformation in Eq. (16) to Eq. (22), and inserting the amplitudes in Eqs (18) and (20), the reflection operator \(R\left( \bar{\mathbf {f}}_\mathbf {i}^I\right)\) produces a spectral field representation with components
oriented along Cartesian unit vectors.
We wish to evaluate the integral in Eq. (21) and expand the field \(\mathbf {f}^R(\mathbf {r}_t,0)\) again in the Wilson basis through the inner-product
By inserting Eq. (21) into Eq. (25) and changing the order of integration, we arrive at the spectral integral representation for the Wilson-basis coefficients for the reflected field,
By bringing the coefficients \(\bar{\mathbf {f}}_\mathbf {i}^I\) outside the integral, we recognize from Eq. (24) that Eq. (26) can be written as a linear combination of six spectral integrals
with \(m \in \left( 1,\dots ,6\right)\), and where the reflections \(R_m\) are given by,
In (Floris and de Hon 2018b), we used fixed-point cubatures on a cylindrical polar grid of abscissae to evaluate the spectral Green’s function integrals in Eq. (6). Because the integrals in Eq. (27) have a similar form, we re-use the same approach to evaluate them. In particular, we make use of one, two or four non-overlapping cubatures, each cubature centered about a different peak of the Wilson basis source function \(\tilde{w}_\mathbf {i}\) in the \(k_x k_y\)-plane. For all Wilson-basis test functions \(\tilde{w}_\mathbf {j}\) under consideration in Eq. (21), we re-use the same cubature grids.
With the aid of the transformations \(k_x=k_t\cos (\varphi )\) and \(k_y=k_t \sin (\varphi )\) with the Jacobian \(\mathrm {d}\mathbf {k}_t= k_t \mathrm {d}k_t \mathrm {d}\varphi\), the \(k_t^{-2}\) singularities in Eq. (28) are conveniently removed. In view of the branch cuts at \(k_t = k_1\) and \(k_t = k_2\), we subdivide the integration over \(k_t\) in three regions. Without loss of generality, we assume \(n_1 < n_2\). In the opposite case, only the coefficients \(r_p\) and \(r_s\) in Eq. (23) change sign as \(n_1 \rightarrow n_2\) and \(n_2 \rightarrow n_1\). In the first region with \(k_t \in \left( 0,k_1 \right)\), we deployed 300 abscissae along the radial coordinate, and 1200 along the angular coordinate and applied the substitution \(u = \sqrt{ k_1^2-k_t^2}\) to aid the convergence of the six integrals. In the second region with \(k_t \in \left( k_1, k_2\right)\), we also deployed 300 radial and 1200 angular abscissae, however, we did not apply any substitutions. In the third region with \(k_t \in \left( k_2,\infty \right)\), we applied the substitution \(u=\sqrt{k_t^2-k_2^2}\) and again deployed 300 radial and 1200 angular abscissae.
Fortunately, we only need to evaluate the integrals for the non-displaced Wilson-basis source functions \(\tilde{w}_\mathbf {i}\), with \((l,n)=(0,0)\) and \(n \in (0,1)\) for \(1 \le \ell \le l_{\text {max}}\) applied to the pairs \((\ell _x,n_x)\) and \((\ell _y,n_y)\) (Floris and de Hon 2018b). The integrals with spatially displaced Wilson-basis source functions \(\tilde{w}_{\mathbf {i}+\mathbf {s}}\) with \(\mathbf {s}=(0,s_x,0,s_y)\) are the same as those for the non-displaced cases when the test functions are displaced according to \(\tilde{w}_{\mathbf {j}} \rightarrow \tilde{w}_{\mathbf {j}-\mathbf {s}}\) (Floris and de Hon 2018b).
Consider an interface between air with \(n_1=1\) and a glass material with \(n_2=1.452\) that resembles a fiber cladding at a wavelength of 850 \(\hbox {nm}\). To be able to adequately truncate the set of test function \(\tilde{w}_\mathbf {j}\) for the expansion of an arbitrary reflected field \(\bar{\mathbf {f}}_\mathbf {j}^R\) in Eq. (26), we visualize the behavior of the absolute maximum of the integrals \(I_m\) of Eq. (27) in Fig. 4 for all source functions \(\tilde{w}_{\mathbf {i}}\) with \(\ell \le 4\) and all test functions \(\tilde{w}_{\mathbf {j}}\) with \(\ell \le 6\).
For an air-glass interface, the absolute maximum of the integrals \(I_m\) in Eq. (27) decays rapidly as the distance \(|\varDelta \ell _x| + |\varDelta \ell _y|\) increases. The black curves are associated with the integrals \(I_m\), with \(m \in \{1,3,4,6\}\), whereas the red curves are those with \(m \in \{2,5\}\). (Color figure online)
As the distance \(|\varDelta \ell _x| + |\varDelta \ell _y|\) between the Wilson source function \(\tilde{w}_\mathbf {i}\) and the test function \(\tilde{w}_\mathbf {j}\) increases, the coupling decreases quite rapidly. The behavior for the integrals \(I_m\) associated with \(m\in \{2,5\}\) (red curves with \(\bullet\) markers) decay a bit differently due to the product \(k_xk_y\) in the integrand in Eq. (28), compared to the integrals with \(m \in \{1,3,4,6\}\) that either depend on \(k_x^2\) or \(k_y^2\) (black curves with \(+\) markers).
For an increasing spatial separation \(|\varDelta n_x| + |\varDelta n_y|\), the same integrals seem to decay very slowly as shown in Fig. 5, which indicates that the reflected field due to a confined incident field can potentially be very wide.
For an air-glass interface, the absolute maximum of the integrals in \(I_m\) in Eq. (27) decay relatively slowly as the spatial distance between \(|\varDelta n_x| + |\varDelta n_y|\) between the Wilson source and test functions increases
Although it may appear that an a priori truncation of \(|\varDelta n_x| + |\varDelta n_y| \le 12\) is inadequate, we want to emphasize that the actual reflected field depends on the specific linear combination of these integrals. For electromagnetic wavefields that resonate in a gap between two fibers, we estimate that we achieve an accuracy up to 5 digits judging from the power balance of the transmitted and reflected fields using the aforementioned truncations of the Wilson basis test functions.
We proceed in Sect. 6 with a procedure to evaluate the resonances in a gap between two fibers.
6 A resonating cavity between two fibers
Consider two optical fibers with flat end-faces that are displaced both laterally and axially with respect to each other in a homogeneous medium (see Fig. 6). The Wilson-basis discretized incident field \(\bar{\mathbf {f}}^I\) (green wiggle) in the first fiber propagates to the first interface at \(z=z_1\). For readability, we henceforth suppress the multi-index \(\mathbf {i}\) in the subscript of all Wilson-basis fields.
Sketch of a reflection-transmission problem comprising two laterally and axially displaced optical fibers in a homogeneous medium and an excitation by an arbitrary combination of guided fiber modes (green wiggle in the first fiber). The triple wiggles denote electromagnetic fields that are readily evaluated through one-way field decompositions and propagation (Sect. 3). The small purple wiggles represent approximated radiating fiber modes (Sect. 5). We wish to minimize the mismatch across the dashed interface at \(z_1^+ = z_1 +\delta\), with \(\delta \downarrow 0\), solving the multiple-scattering problem
Associated with the incident field \(\bar{\mathbf {f}}^I\), the first contribution to the reflection \(\bar{\mathbf {f}}_0^{R,\mathrm {guided}}\) (red wiggles) and the transmission \(\bar{\mathbf {f}}^{1+}_0\) (blue wiggles) in the homogeneous medium satisfy the boundary conditions at the first interface \(z=z_1\) as detailed in Sect. 4. The subscript 0 indicates that the reflection does not include contributions due to multiply scattered fields resonating in the gap. For convenience, we denote the propagation of a Wilson-basis discretized vector field \(\bar{\mathbf {f}}\) over a gap distance \(\varDelta z = z_2 - z_1\) as propagation operator \(\mathsf {P}(\bar{\mathbf {f}}, \varDelta z)\), which abbreviates the construction of equivalent sources in Eqs (4) and (5) to one-way field excitation in Eq (13) as discussed in Sect. 3. The field \(\bar{\mathbf {f}}_0^{2+}=\mathsf {P}(\bar{\mathbf {f}}_0^{1+},\varDelta z)\) (cyan wiggles) impinges on the second interface at \(z=z_2\) and excites the reflected field \(\bar{\mathbf {f}}_0^{2-}=\mathsf {R}(\bar{\mathbf {f}}_0^{2+})\) (gold wiggles), where \(\mathsf {R}\) is an abbreviation of the reflection operator (discussed in Sect. 4). In the second fiber, the guided transmitted field \(\bar{\mathbf {f}}_0^{T,\mathrm {guided}}\) (black wiggles) and the radiation field \(\bar{\mathbf {f}}_0^{T,\mathrm {rad}}\) (purple wiggles) are excited (as discussed in Sect. 4). By applying the propagation operator \(\mathsf {P}\) to the reflected field \(\bar{\mathbf {f}}_0^{2-}\), the field \(\bar{\mathbf {f}}_0^{1-} = \mathsf {P}(\bar{\mathbf {f}}_0^{2-}, -\varDelta z)\) denotes the first arrival on the right-hand side of the dashed interface at \(z=z_1+\delta\) with \(\delta \downarrow 0\) (orange wiggles). To improve readability, we let \(\bar{\mathbf {f}}_0 = \bar{\mathbf {f}}_0^{1-}\) denote the fields at the dashed interface, and suppress the superscript \(^{1-}\) in the remainder of this section.
We temporarily remove the excitation \(\bar{\mathbf {f}}^I\) from the first fiber and place equivalent sources for the field \(\bar{\mathbf {f}}_0\) (dark blue straight arrows) at \(z=z_1^+\) where \(z_1^+ = z_1 + \delta\) with \(\delta \downarrow 0\) as shown in Fig. 7. The evolution of the field \(\bar{\mathbf {f}}_0\) along the loop contour to \(\bar{\mathbf {f}}_1\) on the right-hand side of the dashed interface may be evaluated by a loop operator that we define as
The field \(\bar{\mathbf {f}}_0\) (dark blue wiggles) excites a backward-propagating guided field \(\bar{\mathbf {f}}_1^{R,\mathrm {guided}}\) (black wiggle) and a radiating field \(\bar{\mathbf {f}}_1^{R,\mathrm {rad}}\) (purple wiggles) in the first fiber and excites a forward-propagating reflected field \(\bar{\mathbf {f}}_1^{1+}=\mathsf {R}(\bar{\mathbf {f}}_0)\) (dark red wiggles) that propagates to the second interface and arrives as \(\bar{\mathbf {f}}_1^{2+}=\mathsf {P}(\bar{\mathbf {f}}_1^{1+})\) (red wiggles). At the second interface, it excites a forward-propagating guided field \(\bar{\mathbf {f}}_1^{T,\mathrm {guided}}\) (black wiggles) and a radiating field \(\bar{\mathbf {f}}_1^{T,\mathrm {rad}}\) (purple wiggles). The reflection \(\bar{\mathbf {f}}_1^{2-}=\mathsf {R}(\bar{\mathbf {f}}_1{2+})\) (blue wiggles) propagates back to the dashed interface and arrives as \(\bar{\mathbf {f}}_1 = \mathsf {P}(\bar{\mathbf {f}}_1^{2-})\) (cyan wiggles) and completes the loop operator.
Sketch of the reflected field in the first fiber and the transmitted field in the second fiber due to a specific excitation \(\bar{\mathbf {p}}_0\) at the dashed interface that was generated in Fig. 6. Along the trajectory of the first loop, the excitation \(\bar{\mathbf {p}}_0\) reflects off the first fiber \((\bar{\mathbf {p}}_0^{1+})\), propagates to the second interface \((\bar{\mathbf {p}}_0^{2+})\), reflects \((\bar{\mathbf {p}}_0^{2-})\), and propagates back to the dashed interface \(\bar{\mathbf {p}}_1\)
The application of the loop operator may be continued indefinitely to obtain \(\bar{\mathbf {f}}_l\) with \(l \in 2,3,\ldots\), and allows to accumulate all contributions to the scattered fields \(\bar{\mathbf {f}}_l^{R,\mathrm {guided}}\), \(\bar{\mathbf {f}}_l^{R,\mathrm {rad}}\), \(\bar{\mathbf {f}}_l^{T,\mathrm {guided}}\), and \(\bar{\mathbf {f}}_l^{R,\mathrm {rad}}\) in the process. The repeated application of the loop operator leads to a Neumann series \(\bar{\mathbf {f}}= \sum \limits _{n=0}^{\infty } \mathsf {L}^n(\bar{\mathbf {f}}_0)\) that describes the converged field we wish to evaluate. Depending on the gap configuration and the material properties, convergence of the Neumann series may be slow. Moreover, the finite numerical precision of the electromagnetic fields and the loop operator may interfere with reaching a stabilized situation in which all field resonances in the cavity have settled.
Our strategy is to rewrite the loop operator in an iterative form, where every step leads to a new geometric progression of a known field, and a residual field. By applying the Gram-Schmidt process, we separate the one-time looped field \(\bar{\mathbf {f}}_1\) in terms of the original field \(\bar{\mathbf {f}}_0\) and a residual field \(\bar{\mathbf {r}}_{1}\), i.e.,
By applying the loop operator on Eq. (30), the second loop \(\bar{\mathbf {f}}_2 = \mathsf {L}(\bar{\mathbf {f}}_1)\) can be written as
As the loop operator continues to iterate, the n-times looped field \(\mathsf {L}^n(\bar{\mathbf {f}}_0)\) reads
The total electromagnetic field at the dashed interface \(\bar{\mathbf {f}}=\sum _{n=0}^{\infty }\bar{\mathbf {f}}_n\) comprises the sum of geometric series for the vector fields \(\bar{\mathbf {f}}_0\), \(\bar{\mathbf {r}}_1\), \(\mathsf {L}(\bar{\mathbf {r}}_1)\), \(\mathsf {L}^2(\bar{\mathbf {r}}_1)\), \(\ldots\), all with a factor \(s_0\). Because \(|s_0|<1\), the total electromagnetic field converges to
We want to avoid the numerical computation of a large number of loops of the first residual field \(\mathsf {L}^n(\bar{\mathbf {r}}_1)\) for \(n=1,2,\ldots\) in Eq. (33). Therefore, we also make a decomposition of the loop of the first residual field by writing
which yields a second residual field \(\bar{\mathbf {r}}_2\) that generally carries less power than the first residual field \(\bar{\mathbf {r}}_1\), because in the loop \(\bar{\mathbf {r}}_1 \rightarrow \mathsf {L}(\bar{\mathbf {r}}_1)\), power is coupled into the two waveguides. Analogous to Eqs (30)–(32), we express the \(n^{\mathrm {th}}\)-loop of the first residual field \(\bar{\mathbf {r}}_1\),
which comprises geometric series with a factor \(s_1\) for the first residual field \(\bar{\mathbf {r}}_1\) and looped versions of the second residual field \(\bar{\mathbf {r}}_2\). Because the factor \(|s_1| < 1\), the infinite sum in Eq. (33) converges to
By substituting Eq. (36) in Eq. (33), the total electromagnetic field \(\bar{\mathbf {f}}\) becomes a weighted sum of \(\bar{\mathbf {f}}_0\), \(\bar{\mathbf {r}}_1\) and an infinite sum over looped versions of \(\bar{\mathbf {r}}_2\). For every subsequent loop, one can make a new decomposition according to Eq. (34) with \((\bar{\mathbf {r}}_1,s_1,\bar{\mathbf {r}}_2) \rightarrow (\bar{\mathbf {r}}_l,s_l,\bar{\mathbf {r}}_{l+1})\), where l denotes the loop number.
An iterative scheme for the evaluation of the Neumann series for the residual field is given by Eq. (36) by letting \((\bar{\mathbf {r}}_1,s_1,\bar{\mathbf {r}}_2) \rightarrow (\bar{\mathbf {r}}_l,s_l,\bar{\mathbf {r}}_{l+1})\). The converged total electromagnetic field is evaluated by
The sum over l should converge rapidly, because with every loop, the newly constructed residual field \(\bar{\mathbf {r}}_l\) carries less power than the previous residual field \(\bar{\mathbf {r}}_{l-1}\). For optical fiber connections, it suffices to evaluate the first three loops with \(\ell \in (1,2,3)\) in the sum in Eq. (37).
With the aid of Eq. (37), and by re-using the coefficients \(s_l\), the converged electromagnetic fields \(\bar{\mathbf {f}}^{1+}\), \(\bar{\mathbf {f}}^{2+}\) and \(\bar{\mathbf {f}}^{2-}\) are easily evaluated as well. The converged-state electromagnetic field \(\bar{\mathbf {f}}+ \bar{\mathbf {f}}^{1+}\) is the reflected field in the first fiber, whereas \(\bar{\mathbf {f}}^{2+}+\bar{\mathbf {f}}^{2-}\) is the converged transmitted field in the second fiber. Also, we have kept track of the contributions to the modal amplitudes of the guided modal electromagnetic fields in both fibers as the iterative scheme progressed.
Upon combining the excitation situation in Fig. 6, and the converged response due to the equivalent source at the dashed interface in Fig. 7, the multiple scattering problem is properly solved.
To give a feel for the speed of the convergence of the outlined approach, consider two identical standard single-mode fibers that are perfectly aligned along the transverse coordinates, and only separated by a vanishingly small gap of air with \(\varDelta z \downarrow 0\). Upon expansion of the fundamental mode in the Wilson basis (\(\bar{\mathbf {f}}^I\) in Fig. 6) at a wavelength of \(1310~\hbox {nm}\), we truncated the set of Wilson basis coefficients when unit power was achieved with an absolute accuracy of \(10^{-6}\) (further details on the expansion in Sect. 7). At the fiber to air interface at \(z=z_1\), the first reflected field carried by \(\bar{\mathbf {f}}_0^{R,\mathrm {guided}} + \bar{\mathbf {f}}_0^{R,\mathrm {rad}}\) is a factor \(\eta _r = 3.39\times 10^{-2}\) of the incident power. The power carried by the field \(\bar{\mathbf {f}}_0^{2+}\) that is incident on the air to fiber interface at \(z=z_2\) is \((1-\eta _r)=0.9661\). The associated reflected power is a factor \(\eta _r\) lower, rendering the power carried by the field \(\bar{\mathbf {f}}_0\) effectively \((1-\eta _r)\eta _r = 3.27\times 10^{-2}\).
After evaluation of the first intra-cavity loop \(\bar{\mathbf {f}}_0 \rightarrow \bar{\mathbf {f}}_1\), the power carried by \(\bar{\mathbf {f}}_1\) is as low as \((1-\eta _r)\eta _r^3 = 3.76\times 10^{-5}\). Due to the geometric progression in Eq. (33) with \(s_0=3.39\times 10^{-2}\) (obtained by means of Eq. (30)), all the fields have converged with an absolute accuracy of \(10^{-6}\) after a single loop correction! The power carried by the first residual field \(\bar{\mathbf {r}}_1\) is as low as \(6.67\times 10^{-8}\). Without the Neumann-series geometric progression, i.e. for \(s_0=0\) and a first residual field \(\bar{\mathbf {r}}_1\) carrying \(3.76\times 10^{-5}\) of power, it would take at least three loop evaluations to achieve the same level of accuracy.
We apply the mode-matching technique to single-mode fiber connections with a mode-field diameter mismatch in Sect. 7 and apply an axial misalignment in Sect. 8. In Sects. 9 and 10, we consider multi-mode fiber connections with lateral and axial misalignment respectively for encircled-flux compliant and overfilled launch conditions. As a closing example in Sect. 12, we evaluate the change in the near-field pattern when coupling a target encircled-flux compliant launch to a regular and a trench-assisted multi-mode fiber.
7 Single-mode fiber connections with a vanishingly small gap
To model a physical contact connection, we apply the mode-matching approach as outlined in Sect. 6 here for a vanishingly small gap of \(\varDelta z \downarrow 0\). We assume a perfect lateral alignment and an excitation by the fundamental mode at a wavelength of 1310 \(\hbox {nm}\) in the first fiber. For both the transmitting and receiving fibers, we assume a step-index profile comprising a pure silica cladding and a germanium-doped core with a core radius \(a=4.06\) \(\mu \,\hbox {m}\).
We define the mode-field diameter (MFD) of the fundamental mode as the diameter of the contour where the normalized power density distribution has decayed to \(\exp (-2)\). We model eleven different receiving fibers by choosing the germanium mole fraction at equidistant samples between 0.03 and 0.05, resulting in mode-field diameters between 10 and 8.7 \(\mu \,\hbox {m}\). With the aid of Sellmeier’s equation for optical glass (Bach and Neuroth 1998), we evaluate the refractive index at the wavelength of choice and compute the modal electromagnetic fields for the pertaining optical waveguide (Smink 2009).
The attenuation curves as a function of the MFD of the receiving fiber (\(\mathrm {MFD2}\)) in Fig. 8 are shown for a launch fiber with \(\mathrm {MFD1}=8.7\) \(\mu \,\hbox {m}\) (ascending curves) and for a launch fiber with \(\mathrm {MFD1}=10\) \(\mu \,\hbox {m}\) (descending curves). The attenuation is evaluated as \(-10 \log _{10}(P_2/P_1)\), where \(P_1\) and \(P_2\) denote the total power carried by the guided modes in the first and second fibers, respectively.
Single-mode fiber connection attenuation as function of the mode-field diameter of the receiving fiber (\(\mathrm {MFD2}\)) for two transmitting fibers with \(\mathrm {MFD1}\) respectively 8.7 \(\mu \,\hbox {m}\) (ascending curves) and 10 \(\mu \,\hbox {m}\) (descending curves). The solid red curves are obtained by the mode-matching technique, and are sandwiched between two approximation methods that effectively match either the electric field (blue \(+\) markers) or the magnetic field (green \(\circ\) markers) with overlap integrals. The red dashed curve is a Gaussian approximation by Marcuse (Marcuse 1977), and the thick black dashed curves that almost overlap our solid red curves are obtained with FIMMWAVE. (Color figure online)
The red solid attenuation curve (without markers) is obtained after solving \(\left. \left( \bar{\mathbf {f}}^I + \bar{\mathbf {f}}^R\right) \right| _{z_1^-} =\left. \bar{\mathbf {f}}^T\right| _{z_2^+}\) through the procedure as outlined in Sect. 6 for a Wilson-basis discretized launch \(\bar{\mathbf {f}}^I=\bar{\mathbf {f}}^{1}_{\mathrm {fun}}\) that excites the fundamental mode (\(\mathrm {fun}\) in subscript) in the first fiber (1 in superscript).
We have pre-computed a set of coefficients \(\bar{\mathsf {F}}_{\mathbf {i},\mathbf {j}}(\varDelta z)\) using Eq. (6) for \(\varDelta z \downarrow 0\) at a wavelength of \(850~\hbox {nm}\) for \(d=3~\mu \,\hbox {m}\) for the decomposition of the modal electromagnetic fields into their equivalent one-way propagating fields in homogeneous-space (cf. Eq. (13)). To be able to re-use the coefficients \(\bar{\mathsf {F}}_{\mathbf {i},\mathbf {j}}(0)\) at the wavelength \(\lambda =1310~\hbox {nm}\), we preserved the quantity \(\lambda /d\) by choosing the scaling parameter \(d\approx 4.6~\mu \,\hbox {m}\) for the expansion of the electromagnetic fields. Further, we included all the Wilson basis coefficients between the multi-indices \(\mathbf {i}_{\mathrm {min}}=(0,-22,0,-22)\) and \(\mathbf {i}_{\mathrm {max}}=(3,22,3,22)\) for all the field expansions, including the converged fields \(\bar{\mathbf {f}}^{1+}\), \(\bar{\mathbf {f}}^{2+}\), \(\bar{\mathbf {f}}^{2-}\) and \(\bar{\mathbf {f}}\) (as shown in Fig. 7), which in turn include all stabilized resonances due to the first three residual fields \(\bar{\mathbf {r}}_1\), \(\bar{\mathbf {r}}_2\) and \(\bar{\mathbf {r}}_3\).
For validation, we have chosen to compare our vectorial full-wave Wilson-basis discretized mode-matching results for this axisymmetric (aligned) full-contact case involving single-mode transmitting and receiving fibers with results obtained using a fully-licensed PhotonD suite (http://www.photond.com 2022). In particular, we have solved the pertaining \(\mathrm {HE}_{11}\) modes using the FIMMWAVE implementation of the EigenMode Expansion (EME) method (Gallagher and Felici 2003) with the full-vectorial General Fiber Solver (GFS), and have simulated the aligned full contact fiber connection through the Simple Joint operation. In FIMMWAVE one has to take care to set the (radial) cladding thickness judiciously. In this simple example, the difference in FIMMWAVE between setting it in the range \(15-20\) \(\mu \,\hbox {m}\) and a larger value of 50 \(\mu \,\hbox {m}\) is very small (about 0.01 dB). However, the results produced by FIMMWAVE are much more sensitive to the choice of cladding thickness for the case of two misaligned single-mode fibers with a gap to be discussed in Sect. 8.
The red solid line in Fig. 8 is sandwiched between two solid curves that are both obtained using approximation methods. When assuming a negligibly small reflected field \(\bar{\mathbf {f}}^R\), the transverse electromagnetic fields are continuous across the fiber interface when \(\left. \bar{\mathbf {f}}^T\right| _{z_2^+}=\;\left. \bar{\mathbf {f}}^I\right| _{z_1^-}\), rendering the transmitted field \(\bar{\mathbf {f}}^T\) directly proportional to the excitation \(\bar{\mathbf {f}}^I\). The transmitted field in the second fiber may be expressed as
where the fundamental mode \(\bar{\mathbf {f}}^2_{\mathrm {fun}}\) and radiating fields \(\bar{\mathbf {f}}^{2,\mathrm {rad}}\) are orthonormal with respect to the scalar product defined in Eq. (14). The coupling coefficient \(\eta = \langle \bar{\mathbf {f}}^{1}_{\mathrm {fun}}, \bar{\mathbf {f}}^{2}_{\mathrm {fun}}\rangle\) is the outcome of an overlap integral and effectively matches the electric field of the excitation \(\bar{\mathbf {f}}^1_{\mathrm {fun}}\) in the first fiber to the electric field in the second fiber in a minimum-norm sense (Neumann 1988), and results in the solid curve with blue \(+\) markers in Fig. 8. The overlap integrals are straightforwardly evaluated in the Wilson basis through a summation of scalar products of vectorfield coefficients in Eq. (14). One might just as well have chosen for an effective magnetic field matching by letting \(\eta \rightarrow \langle \bar{\mathbf {f}}^{2}_{\mathrm {fun}}, \bar{\mathbf {f}}^{1}_{\mathrm {fun}}\rangle ^*\), where \(*\) denotes complex conjugation. This choice results in the solid curve with green \(\circ\) markers in Fig. 8.
The differences between the full mode-matching approach and the approximation methods are relatively small, but increase as the mode-field diameter mismatch between the two fibers becomes larger. The effective electric (or magnetic) field matching with overlap integrals does not account for a difference in the impedance of the electromagnetic fields across the connection interface. The full mode-matching approach does achieve continuous transverse electric and magnetic fields across the connection interface. In case an approximation method using only overlap integrals is preferred, one would do best to combine both choices for the coupling coefficient by letting \(2\eta = \langle \bar{\mathbf {f}}^{1}_{\mathrm {fun}}, \bar{\mathbf {f}}^{2}_{\mathrm {fun}}\rangle + \langle \bar{\mathbf {f}}^{2}_{\mathrm {fun}}, \bar{\mathbf {f}}^{1}_{\mathrm {fun}}\rangle ^*\).
The red dashed curve in Fig. 8 is evaluated by Marcuse’s scalar approximation that uses a Gaussian electric field distribution (Marcuse 1977). To make a fair comparison, we configured the width of the Gaussian electric fields according to Marcuse’s approximation equation given in (Marcuse 1977) that depends only on the normalized frequency \(V=k_0 a \sqrt{n_{co}^2-n_{cl}^2}\). With this careful choice for the mode-field diameter, the attenuation due to Gaussian approximation is close to the full mode-matching model, albeit a bit on the high side.
8 Two misaligned single-mode fibers with a gap
As in Sect. 7, we start with two single-mode fibers with a MFD of \(8.7~\mu \,\hbox {m}\) at a wavelength of \(1310~\hbox {nm}\). Here, we consider a fixed lateral misalignment of \(3~\mu \,\hbox {m}\) and break the physical contact by gradually increasing the distance between the two fibers through a set of propagation operators \(\mathsf {P}(\bar{\mathbf {f}},\varDelta z)\rightarrow \mathsf {P}_{\mathrm {sweep}}(\bar{\mathbf {f}},m\varDelta z)\) with \(m=2,\ldots ,M\) that makes use of the repeated application of Love’s equivalence principle and re-use of the propagation operation \(\bar{\mathsf {F}}_{\mathbf {i},\mathbf {j}}(\varDelta z)\) for the first step (de Hon and Floris 2018). Specifically, we evaluated \(\bar{\mathsf {F}}_{\mathbf {i},\mathbf {j}}(\varDelta z)\) in Eq. (6) with \(\varDelta z=35.1~\hbox {nm}\) for Wilson basis functions that are scaled with \(d=3~\mu \,\hbox {m}\), and included all Wilson-basis test functions \(w_\mathbf {j}\) that satisfy \(|\varDelta \ell _x|+|\varDelta \ell _y| \le 6\) and \(|\varDelta n_x|+|\varDelta n_y| \le 6\) with respect to all the Wilson-basis source functions \(w_\mathbf {i}\). Re-use of \(\bar{\mathsf {F}}_{\mathbf {i},\mathbf {j}}(\varDelta z)\) is possible by preserving the quantities \(d/\lambda\) and \((\varDelta z)/d\), which results in step sizes \(\varDelta z=(54.1, 64.0, 67.1)~\hbox {nm}\) for the respective telecom wavelengths \(\lambda =(1310, 1550, 1625)~\hbox {nm}\) and electromagnetic field expansions using Wilson basis scalings \(d=(4.6,5.5,5.7)\) \(\mu \,\hbox {m}\).
The solid attenuation curves that are shown above the vertical scale brake in Fig. 9 are for \(\lambda =1310\) \(\hbox {nm}\) (blue \(\bullet\) marker), \(\lambda =1550~\hbox {nm}\) (black \(\times\) marker) and \(\lambda =1625~\hbox {nm}\) (red \(+\) marker) for four gap regions. The step from one region to the next is achieved by iterating an additional step operator \(\mathsf {P}_{\mathrm {step}}(\bar{\mathbf {f}},\varDelta z)\rightarrow \mathsf {P}_{\mathrm {step}}(\bar{\mathbf {f}},2\varDelta z)\) that was initialized by \(\mathsf {P}_{\mathrm {step}}(\bar{\mathbf {f}},\varDelta z)=\left. \mathsf {P}_{\mathrm {sweep}}(\bar{\mathbf {f}},\varDelta z)\right| _{\varDelta z = 0.85~\mu \,\hbox {m}}\) which became available after completing the sweep in the first region.
The attenuation as function of the gap size between two single-mode fibers with a 3 \(\mu \,\hbox {m}\) lateral offset for \(\lambda =1310\) \(\hbox {nm}\) (blue \(\bullet\) marker), \(\lambda =1550~\hbox {nm}\) (black \(\times\) marker) and \(\lambda =1625~\hbox {nm}\) (red \(+\) marker). The black solid curve is the \(\lambda =1310\) \(\hbox {nm}\) case simulated with FIMMWAVE. The attenuation due to power coupling into the fundamental mode of the receiving power is shown above the vertical scale brake, whereas the curves below the scale brake are due to the total received power including radiating fields. (Color figure online)
For the 1310 \(\hbox {nm}\) wavelength, laterally misaligned, variable gap case, the comparison of our vectorial full-wave Wilson-basis discretized mode-matching results (blue \(\bullet\) marker) with those generated using the PhotonD suite (solid black curve) is not as straightforward. In FIMMWAVE, the Simple Joint connection has to be replaced by a Free Space Joint based on a plane-wave expansion. It is probably due to the symmetry breaking offset that the FIMMWAVE results are now much more sensitive to the radial cladding index. FIMMWAVE produces results that match well with ours for a radial cladding thickness of 15 \(\mu \,\hbox {m}\). However, some caution is advised, since for cladding thickness values of 30 \(\mu \,\hbox {m}\) to \(50\, \mu \,\hbox {m}\), the attenuation curves deviate from about 0.3 dB to 6 dB.
We have demonstrated that for single-mode fiber interfaces both our method and FIMMWAVE/FIMMPROP produces rigorous full-wave solutions, where the GFS solver in the latter relies on a more traditional Bessel-function basis (or rather cylindrical harmonics in 2-D). We would like to point out that we expand the transverse fields in terms of a 2-D Wilson basis with the appealing effective localisation in both the spatial and spectral domains and the transverse shift properties. This basis serves as a universal interface. From Sect. 9 onwards, we shall discuss multi-mode applications of our method.
The three dashed curves below the scale brake represent the attenuation for the total power coupled into the receiving fiber. By including the radiating fields, this simulation effectively resembles the constructive and destructive interference in a gap between two glass materials. As the gap size increases, the spatial coherence slowly diminishes, whereas the attenuation to the guided mode attenuation increases significantly due to the fixed lateral misalignment of \(3~\mu \,\hbox {m}\) combined with the widening of the modal electromagnetic fields.
We checked with a separate propagation operator \(\mathsf {P}_{\mathrm {step}}\) that was evaluated with Eq. (6) directly for \(\varDelta z = 70~\mu \,\hbox {m}\) that the results in the fourth region were not impaired by the large number of concatenation operations that were applied to the relatively short-distance propagation operators. Furthermore, by keeping track of the total power carried by the fields in the cavity at every evaluated cross-section, we verified that the employed propagation operators properly conserve energy, confirming that sufficient interactions between Wilson-basis source and test functions were included.
In Fig. 9, the attenuation is highest for the \(\lambda =1310\) \(\hbox {nm}\) case due to the relatively small mode-field diameter. The fixed \(3~\mu \,\hbox {m}\) lateral offset is much less impactful on the coupling efficiency for the spatially wider fields associated with the longer wavelengths.
The total power that does not contribute to the transmission in the second fiber is reflected power in the first fiber. The part of the reflected power that is carried by the backward propagating fundamental mode is shown as the return loss in Fig. 10.
The return loss as function of the gap size between two single-mode fibers with a 3 \(\mu \,\hbox {m}\) lateral offset for \(\lambda =1310\) \(\hbox {nm}\) (blue \(\bullet\) marker), \(\lambda =1550~\hbox {nm}\) (black \(\times\) marker) and \(\lambda =1625~\hbox {nm}\) (red \(+\) marker). The solid black and green curves respectively indicate encircled-flux compliant and overfilled launches between two regular multi-mode fibers with a 3 \(\mu \,\hbox {m}\) lateral offset. (Color figure online)
We have interpolated the reflected power curve with a cubic spline prior to evaluating the logarithm, in order to preserve the deep dips in the return loss curves that are associated with the near-perfect transmission that occurs when the cavity length approaches integer multiples of the half wavelength. The return loss for the wavelengths \(\lambda =1310~\hbox {nm}\) (blue \(\bullet\) marker), \(\lambda =1550~\hbox {nm}\) (black \(\times\) marker) and \(\lambda =1625~\hbox {nm}\) (red \(+\) marker) respectively settle to \(-14.70~dB\), \(-14.75~dB\), and \(-14.77~dB\) as the gap size tends to infinity.
The solid black and green curves without markers respectively indicate an encircled-flux compliant and overfilled launch for a gap between two regular multi-mode fibers with a 3 \(\mu \,\hbox {m}\) offset that are discussed in Sect. 10.
9 Multi-mode fiber connections with a vanishingly small gap
We repeated the example in Sect. 7, but now for two identical cylindrically symmetrical graded-index multi-mode fibers with a parabolically-shaped germanium-doped core profile with a diameter of 50 \(\mu \,\hbox {m}\) and a numerical aperture \(\mathrm {NA}=\sqrt{n_{\mathrm{co}}^2-n_{\mathrm{cl}}^2}=0.2\) between the core refractive index \(n_{\mathrm{co}}\) and the homogeneous pure-silica cladding index \(n_{\mathrm{cl}}\). At a wavelength of 850 \(\hbox {nm}\), each fiber has 180 guided one-way forward propagating modal electromagnetic field solutions, or 342 when counting their complex conjugate counterparts which have the same field distribution but spiral in the opposite cylindrical angular direction.
We have expanded the transverse electromagnetic fields of the 180 fiber modes in a Wilson basis using \(d=3\) \(\mu \,\hbox {m}\) for the Wilson basis function scaling. For the expansion, we used all the Wilson basis coefficients between the multi-indices \(\mathbf {i}_{\mathrm {min}}=(0,-28,0,-28)\) and \(\mathbf {i}_{\mathrm {max}}=(3,28,3,28)\). We populated the dyad \(\bar{\mathsf {F}}_{\mathbf {i},\mathbf {j}}(\varDelta z)\) (Eq. (6)) in the propagation operator \(\mathsf {P}(\bar{\mathbf {f}},\varDelta z)\) with all Wilson-basis test functions \(w_\mathbf {j}\) that satisfy \(|\varDelta \ell _x|+|\varDelta \ell _y| \le 6\) and \(|\varDelta n_x|+|\varDelta n_y| \le 6\) with respect to all the Wilson-basis source functions \(w_\mathbf {i}\).
For every of the 180 guided modes in the first fiber as excitation, we have evaluated the total power coupled into the guided modes of the second fiber for lateral misalignments up to 6 \(\mu \,\hbox {m}\). Fig. 11 shows the attenuation (red \(\bullet\) symbols), and piece wise linear interpolations (black curves). The attenuation is defined as \(-10 \log _{10}(P_2/P_1)\), where \(P_1\) and \(P_2\) denote the total power carried by the guided modes of the first and the second fiber, respectively.
The curves are clustered in groups, and the left-most group consist of excitations by the high-order modes from the \(18^\mathrm {th}\) mode group. Every subsequent group is associated a lower mode group, which contain the more core-confined modes. The identification of the mode groups is discussed in Sect. 10 (and displayed graphically by the blue \(\bullet\) symbols in Fig. 15) in the context of an increasing gap between the fibers and a fixed 3 \(\mu \,\hbox {m}\) lateral offset.
It is interesting to note that some curves have strong oscillations and are not monotonically increasing. We verified that these dips are not artifacts due to the truncation in the Wilson basis expansion of the electromagnetic fields. They are not the result of the number of iterations for the residual fields in the cavity being too low either. The oscillations are due to the high spatial frequency of the modal electromagnetic fields that locally couple better to the relatively small number of guided modes in the receiving fiber for certain lateral offsets. For the lower-order excitations, the number of excited modes in the receiving fiber are much larger, effectively smoothing the pertaining curves.
Below, we proceed to study overfilled and encircled-flux compliant launches with the aid of the 342 modal electromagnetic fields, in order to arrive at practical attenuation curves.
9.1 Overfilled launch
A spatially and spectrally wide launch generated by a light-emitting diode (LED) has applications in legacy networks as well as in measurement instruments (Refi 1986), and optimum coupling may be achieved with a lens (Hasegawa et al. 1978; Park et al. 1999). We assume that such an overfilled launch is spatio-temporally incoherent and that the spatial interference of the 342 modal electromagnetic fields lead to speckle patterns that blend to a cylindrically symmetrical intensity pattern due to the large spectral width of the LED source. To simulate an overfilled launch incident on an interface between two fibers, we adopt the common assumption that all of the 342 modes are excited with equal power. Instead of adding the fields in a coherent manner and solving the reflection-transmission problem for a large number of speckle patterns, we treat the excitation of each fiber mode separately and then coherently add the results. The average of all the curves in Fig. 11 represents the attenuation curve of an overfilled launch which is shown with red \(+\) symbols in Fig. 12. For a lateral offset of about 2 \(\mu \,\hbox {m}\), the attenuation matches well with a simple approximation method (thin black solid line) given by Neumann and Weidhaas (Neumann and Weidhaas 1976).
The attenuation due to lateral misalignment of two multi-mode optical fibers with a vanishingly small \(1~\hbox {nm}\) gap. For an overfilled launch (red \(+\) marks), the results match an approximation method (thin black solid line) when the offset is larger than \(2~\mu \,\hbox {m}\). An incoherent target-EF compliant launch (blue \(\times\) symbols), and a coherent target-EF compliant launch (red solid line) produce identical attenuation curves. A geometrical-optics approach (blue dashed curve) leads to a slightly steeper curve. The purple solid vertical attenuation regions correspond to launches that touch the EF upper- and lower-bounds as shown in Fig. 13. (Color figure online)
Overfilled launches are no longer considered suitable for fiber connection measurements, because vertical cavity surface emitting laser (VCSEL) sources (deployed in large datacenter networks) generate strongly core-confined launches, leading to much higher optical power coupling efficiencies.
9.2 Encircled-flux compliant launch
Every launch may be distinguished by its time-averaged near-field pattern at the end-face of the multi-mode fiber and the associated normalized cumulative radial intensity distribution is known as encircled flux (EF). Specifically for connection attenuation measurements, international standards (cf. (IEC 61280-4-1 2009, 2021)) demand that the EF curve of the launch lies within tight bounds (between red keep-out zones) associated with four target power levels (green dots) that are defined at four prescribed radial coordinates as shown in the leftmost graph in Fig. 13.
The cumulative near-field distributions (shown left) of the launches are encircled-flux compliant when they do not cross the vertical red dashed lines. An overfilled launch (black dashed curve) exceeds the three lower bounds. The four encircled-flux targets are vertically centered between the respective upper- and lower bounds and are highlighted with four green \(\bullet\) marks. An incoherent launch configured by sampling a modal power distribution (blue solid curve) meets the targets. Also, the average (red solid curve) of 60 coherent launches (thin grey curves) as observed by a slow detector meets the targets. A geometrical-optics based launch (blue dashed curve) has a similar shape. Two extreme launches (purple solid curves) are configured to touch the EF upper- and lower bounds. The right figure shows the deviations of the EF compared to the geometrical-optics based launch. (Color figure online)
We want to avoid the burden of simulating a light source (either a VCSEL or a LED) that is connected to a specific (proprietary) mode scrambling device. Instead, we aim to describe an encircled-flux compliant incident field \(\bar{\mathbf {f}}^I=\sum _m c_m \bar{\mathbf {f}}_{m}^+\) by assigning appropriate modal amplitudes \(c_m\) to the modal electromagnetic fields \(\bar{\mathbf {f}}_{m}^+\), that individually propagate through a factor \(\exp (-j k_{z,m} z)\). Of course, the 342 modal amplitudes \(c_m\) cannot be uniquely determined by just five constraints that are imposed on the intensity distribution. However, by demanding that the launch is spatio-spectrally incoherent (Floris et al. 2019), it is possible to obtain a unique relation between the desired radial intensity distribution \(I(\rho )\) and the model power distribution \(\mathrm {MPD}(\delta )\) which is given by (Daido et al. 1979)
where \(\rho\) is the radial coordinate normalized with respect to the fiber core radius. The coefficient \(\delta \in (0,1)\) can be thought of as a continuous normalized mode group number that samples the modal power distribution function. The relation in Eq. (39) was derived by following the mode-continuum approximation, which assumes that all modes with comparable propagation coefficient carry equal power (Daido et al. 1979).
To make the connection between the modal amplitudes \(c_m\) and the modal power distribution function, we first write the propagation coefficients as
where \(k_0\) is the free-space wavenumber, and \(\varDelta _f = (n_{\mathrm{co}}^2 - n_{\mathrm{cl}}^2)/(2 n_{\mathrm{co}}^2)\) is the contrast in the refractive index profile. The parameter \(\delta _m\) is explained below.
In a related scalar problem with an infinite parabolic refractive index profile (Ghatak and Thyagarajan 1998), the propagation coefficients \(k_{z,m}\) of the linearly-polarized \(\mathrm {LP}_m\) modal electromagnetic fields are of the same form as given in Eq. (40). As \(m \rightarrow ({\mathrm {l},\mathrm {m}})\) with \(\mathrm {l}\) and \(\mathrm {m}\) respectively denoting the azimuthal and radial indices, the parameter \(\delta _m \rightarrow \mathrm {M}/\mathrm {M}_\mathrm {ub}\) directly connects the propagation coefficients \(k_{z,m} \rightarrow k_{z,(\mathrm {l},\mathrm {m})}\) to the mode group number \(\mathrm {M}=2\mathrm {m}+\mathrm {l}-1\) (Ghatak and Thyagarajan 1998). The upper bound \(\mathrm {M}_\mathrm {ub}=\lfloor k_0 n_{\mathrm{co}}R_f \sqrt{\varDelta _f/2}\rfloor\) equals 18 for a nominal multi-mode fiber that has a core radius \(R_f=25\) \(\mu \,\hbox {m}\) and numerical aperture of \(\mathrm {NA}=0.2\) at a wavelength of \(\lambda =850~\hbox {nm}\).
In the vectorial full-wave (VFW) case, the modes have comparable propagation coefficients that are clustered in 18 distinct groups, which we consider the vectorial full-wave counterpart of mode groups. We count the number of modes in each group as \(N_{\mathrm {mg}}(m)\) and sample the modal power distribution in Eq. (39) for each mode with the VFW variable \(\delta _m\) that is connected to the VFW propagation coefficients \(k_{z,m}\) in Eq. (40). With these ingredients, we select the modal amplitudes as
where \(\exp (j \varphi _m)\) is a phase term with \(\varphi _m \in (0,2\pi )\) that will be discussed below with respect to three different launches.
First, we assume a launch that is spatio-temporally incoherent in the sense that the contribution of every mode to the near-field pattern (and the reflection-transmission problem) is considered to be independent of the contributions of all other modes. The EF curve (blue solid curve in Fig. 13) that is obtained by summation of all the separate 342 cumulative near-field patterns that are weighted by \(|c_m|^2\) (rendering the phase \(\varphi _m\) of every mode irrelevant) nicely checks all four EF targets. The associated attenuation curve is shown in Fig. 12 with blue \(\times\) symbols. For reference, we have added the EF curve that is obtained by following a geometrical-optics approach (blue dashed curve) in Fig. 13 that also samples the modal power distribution in Eq. (39) as outlined in (Floris et al. 2019). The associated attenuation curve (blue dashed curve in Fig. 12) follows the vectorial full-wave approach very well, albeit that it develops a visible mismatch from lateral offsets larger than 2 \(\mu \,\hbox {m}\). Beyond an offset of 4 \(\mu \,\hbox {m}\), the mismatch is about \(0.05~\mathrm {dB}\). Despite a small mismatch in the shape of the encircled-flux distribution, the (real-ray) geometrical optics model yields a slightly pessimistic attenuation prediction because the guided rays are confined to the core region only, and can not represent the presence of a tail in the cladding region.
Second, we have configured a temporally incoherent launch that consists of a sequence of spatially coherent fields, where every field has has coefficients \(c_m\) according to Eq. (41) however with \(\varphi _m \in \mathcal {U}(0,2\pi )\) sampled arbitrarily from a uniformly distribution for all 342 modes. Every field represents a non-symmetric speckle pattern with its own radial intensity distribution as shown by the 60 thin grey curves in Fig. 13. The average intensity distribution as observed by a slow detector camera is cylindrically symmetric and also satisfies the EF targets (solid curve with red \(+\) markers in Fig. 13). The associated mean attenuation distribution (red curve overlapping the one with the blue \(\times\) markers), as well as the ensemble of individual field contributions (grey curves) are shown in Fig. 12. The variation in the attenuation among the thin grey curves for a fixed lateral offset connection can be observed as modal noise, and can deteriorate the eye diagram of a modulated signal generated by a spectrally narrow laser source (Epworth 1979; Efimov 2019; Koonen 1986).
As a third approach, we applied the Nelder-Mead minimization algorithm to the 342 unknown amplitudes in an attempt to minimize the absolute distance between the EF curve and the four EF targets. Although not shown here, the approach to solve the underdetermined system of equations leads to a solution (de Hon et al. 2015). Serving merely as an example, we applied this approach also to the upper and lower bounds of the target EF values and highlighted the results through solid purple curves in Fig. 13. The variation in attenuation associated with these two extreme EF launches are shown by vertical purple solid lines in Fig. 12. It is by coincidence that this range seems to align with the variations obtained by 342 spatially coherent speckle-pattern launches (from the second approach), because the EF bounds were originally determined to limit the variation in attenuation by no more than \(0.1~\mathrm {dB}\) for relatively low-loss connections.
We proceed with the introduction of an increasing gap between the two fibers.
10 Two multi-mode fibers with a gap
To break the physical contact between the two multimode fibers, we repeat the procedure as outlined in Sect. 9 but now for gap sizes that are integer multiples of \(\varDelta z = 70.2\) \(\hbox {nm}\). In this section, we consider a fixed 3 \(\mu \,\hbox {m}\) lateral offset between the transmitting and receiving fiber. By (again) using all the Wilson basis coefficients between the multi-indices \(\mathbf {i}_{\mathrm {min}}=(0,-28,0,-28)\) and \(\mathbf {i}_{\mathrm {max}}=(3,28,3,28)\), the total transmitted and reflected power (including radiating fields) deviates less than 0.1 dB compared to the unit launch power (for every launch mode), we could increase the gap size to 70 \(\mu \,\hbox {m}\). In this case, the diffracted field inside the open cavity formed by the gap extends to a region of about \(70*(28*3)^2/(0.850)^3 \approx 0.8\) million cubic wavelengths.
For each of the 180 guided modes in the launch fiber, the attenuation as a function of the separation \(\varDelta z\) are highlighted by red \(\bullet\) symbols in Fig. 14.
The attenuation into the guided modes in the receiving fiber (red \(\bullet\) symbols) is shown as a function of the longitudinal misalignment and a fixed \(3~\mu \,\hbox {m}\) lateral misalignment, upon launching each of the 180 guided modes in the transmitting fiber. The black solid curves are sinusoidal interpolations. The blue − symbols denote the attenuation for the total received power (including the approximated radiating fields). (Color figure online)
The solid black curves are sinusoidal interpolations, and the blue − symbols indicate the attenuation when considering the total received power (including radiating fields) with respect to the incident power.
It is interesting to observe that the attenuation curves are clustered in distinct groups. The highest cluster of attenuation curves are due to 19 modal excitations from the \(18^{\mathrm {th}}\) mode group. Due to the lateral offset of 3 \(\mu \,\hbox {m}\), these specific high-order modal launches couple about half of the power into the guided modes of the receiving fiber (attenuation about 3 dB at \(\varDelta z=0\)), whereas the other half couples into the (approximated) radiating fields (blue horizontal − symbols at 0 dB). Despite the 3 \(\mu \,\hbox {m}\) lateral offset, the excitation of radiating fields is insignificant for modal launches that are associated with the first 14 mode groups.
To better visualize the behavior of all 180 modes as the gap size increases, the minimum and the range of the attenuation curves are shown with blue \(\bullet\) symbols in Fig. 15 as a function of the propagation coefficient \(k_{z,m}\) of the respective modes. The number of modes in each mode group is denoted between parentheses above the bottom subfigure in Fig. 15. The smaller the propagation coefficient \(k_{z,m}\) for the cluster of modes, the higher the associated mode group number. Note that the fundamental mode, labeled \(m=1\), has the highest propagation coefficient \(k_{z,1}\) and is the only mode in the first mode group. The fundamental mode launch diverges slowly, and excites only guided modes in the receiving fiber, even if the gap size is increased to 71 \(\mu \,\hbox {m}\).
The top graph for 180 individual modal excitations (labeled by \(k_{z,m}\)) the minimum attenuation into the guided modes of the receiving fiber for the three gap ranges listed in the legend. The lower graph shows the variation in attenuation. The number of modes that form a mode group are given between brackets
The variation in attenuation is about 0.6 dB for all modes as shown by blue \(\bullet\) symbols in the bottom subfigure of Fig. 15. This 0.6 dB variation was also seen in the single-mode example in Fig. 9. It is noteworthy that the distribution of curves at \(\varDelta z\downarrow 0\) in Fig. 14 are identical to the distribution of curves in Fig. 11 along the vertical axis for a 3 \(\mu \,\hbox {m}\) lateral offset.
For a second region with a separation of \(\varDelta z = 17.5\) \(\mu \,\hbox {m}\), we employed a spatially larger propagation operator \(\mathsf {P}_{\mathrm {step}}(\bar{\mathbf {f}},\varDelta z)\) including interactions up to \(|\varDelta n_x|+|\varDelta n_y| \le 14\). This operator was evaluated directly using Eq. (6). The attenuation curves shown in Fig. 16 were made with an additional sweep operator \(\mathsf {P}_{\mathrm {sweep}}(\bar{\mathbf {f}},\varDelta z)\) that was configured for \(\varDelta z=35.1~\hbox {nm}\) and was chosen spatially smaller, including interactions up to \(|\varDelta n_x|+|\varDelta n_y| \le 6\).
The attenuation into the guided modes in the receiving fiber (red \(\bullet\) symbols) is shown as a function of the longitudinal misalignment and a fixed \(3~\mu \,\hbox {m}\) lateral misalignment, upon launching each of the 180 guided modes in the transmitting fiber. The black solid curves are sinusoidal interpolations. The blue − symbols denote the attenuation for the total received power (including the approximated radiating fields). (Color figure online)
The attenuation curves are still somewhat clustered for the mode groups 15 to 18, as can also be seen by the red \(\times\) markers in the top graph of Fig. 15. However, within these mode groups, the attenuation curves are very different and include curves that vary about 0.5 dB and include curves that are almost horizontal as seen by the spread of red \(\times\) markers in the lower subfigure of Fig. 15. Also, the sinusoidal interference patterns in Fig. 16 no longer synchronized.
More interesting are the peculiar near-constant attenuation curves for several mainly high-order modal launches. One might expect that the specific combination of a relatively large gap and a fixed \(3~\mu \,\hbox {m}\) lateral misalignment counteracts the interference in the cavity. However, the total received power in the receiving fiber is also near-constant for these specific launches. We are confident that we included sufficient Wilson-basis source and test functions in the expansions that rely on Eq. (6), because the power carried by the electromagnetic fields remains unchanged across the gap. Also, the sum of the transmitted and reflected power remains equal to the incident power for every step in the sweep. These power-balance checks are sensitive to incautious truncations of the field expansions and propagation operators.
As the gap-size is increased to about \(\varDelta z = 35\) \(\mu \,\hbox {m}\), the near-constant attenuation behavior is now also seen for relatively lower-order mode groups, as seen by the black \(+\) markers in Fig. 15. We suspect that the relatively diverging fields in the cavity cause the gap-size insensitivity for specific regions of \(\varDelta z\).
Although we also evaluated the curves for the region near \(\varDelta z = 70\) \(\mu \,\hbox {m}\), we do not want to clog Fig. 15 with more markers. For this distance, the diverging beam fields that are excited by the high-order modes in the first fiber start to noticeably exceed the edge of the truncated spatial domain.
To ascertain that the computational domain is large enough, we ran three simulations including all Wilson coefficients for which \(|n_x|,|n_y|\le 28\), or 30, or 32, and observed that the power loss of the residual fields (corrections to the first loop) for the most divergent \(m=18\) modal field excitation reduces from \(12\%\), to \(4\%\), and \(0.24\%\) respectively. Here it should be noted that this first residual field only carries about \(10^{-3}\) of the input power.
We have combined all computations in Fig. 17 for a spatio-temporal incoherent EF launch (blue curve with blue \(\times\) markers) and for an overfilled launch (black curve with red \(+\) markers).
The overfilled launch excites all modes equally strong (cf. Sect. 9.1), whereas the target EF launch is more core confined (cf. Sect. 9.2).
It is noteworthy that the attenuation curves at \(\varDelta z = 0\) for both launches agree with the curves in Fig. 12 for the physical contact case with 3 \(\mu \,\hbox {m}\) lateral offset. Although hardly noticeable from the figure, the envelope of the overfilled launch case decays slightly faster than the encircled-flux launch case, due the the stronger presence of the high-order modes.
We proceed with a few examples that show the evolution of the EF distribution when coupling a target launch from a regular fiber to a trench-assisted multi-mode fiber.
11 Regular multi-mode fibers connected to trench-assisted multi-mode fibers
Nowadays, trench-assisted multi-mode fibers are commonly deployed in datacenter networks and there they can get connected to regular multi-mode fibers that are already part of existing installed cabling infrastructure. To ensure that an optical link still meets the power-budget requirements when fiber types are mixed, the attenuation at each interface should be sufficiently low, preferably below several tenths of a decibel. To make a fair assessment on the connector performance of trench-assisted multi-mode fiber cables, a global debate has started on the applicability and functionality of an encircled-flux target launch (and the respective bounds) in trench-assisted multi-mode fibers.
Because trench designs are different among fiber suppliers, we did a preliminary study on the attenuation for various trench dimensions and trench positions in the cladding region (de Hon et al. 2015). In that assessment, we assumed that both the regular and trench-assisted fibers have a parabolic core refractive-index profile with a diameter of 50 \(\mu \,\hbox {m}\) and a numerical aperture of 0.2. Even though the presence of the trench effectively narrows to modal electromagnetic fields in the trench-assisted fiber, it hardly impacted the coupling matrix for connections to a regular fiber, resulting in attenuation values that were well below a tenth of a decibel.
Here, we redo some of those simulations with the aid of the mode-matching approach that was described in Sect. 6, and look at the impact on the cumulative near-field distribution as the target encircled-flux launch couples from a regular fiber to a trench-assisted fiber. We assume that a typical trench has a width of about 3 \(\mu \,\hbox {m}\) and a constant trench refractive index \(n_{\mathrm{tr}}\) that satisfies the ratio \((n_{\mathrm{cl}}-n_{\mathrm{tr}})\varDelta _f = 0.0045(n_{\mathrm{co}}-n_{\mathrm{cl}})\) relative to the core refractive index contrast \(\varDelta _f = (n_{\mathrm{co}}^2 - n_{\mathrm{cl}}^2)/(2 n_{\mathrm{co}}^2)\). The trench position is assumed to be 1 \(\mu \,\hbox {m}\) away from the parabolic core in the cladding region.
As shown by the blue solid curve (without markers) in the leftmost subfigure of Fig. 18, the tail of the near-field pattern is a bit more core confined (the curve is no longer horizontal). More importantly, it stays well within the bounds for a standards compliant launch, which means that its application can in principle be extended to connection attenuation measurements with modern multi-mode fibers. Even for an additional large lateral misalignment of 3 \(\mu \,\hbox {m}\) (black curve with \(+\) marker) and 6 \(\mu \,\hbox {m}\) (red \(\times\) marker), the launch remains EF compliant.
Both subfigures show the relative change in EF when a target EF launch in a regular multi-mode fiber couples into a trench-assisted multi-mode fiber. Left: both fibers have nominal dimensions and are perfectly aligned (blue curve without marker), with a 3 \(\mu \,\hbox {m}\) lateral offset (black curve with \(+\) marker) and with a 6 \(\mu \,\hbox {m}\) lateral offset (red curve with \(\times\) marker). Right: the trench-assisted multi-mode fiber has a 49 \(\mu \,\hbox {m}\) core diameter and has no lateral misalignment (blue solid curve without marker), or has a 3 \(\mu \,\hbox {m}\) lateral offset (black curve with \(+\) marker) or has a 6 \(\mu \,\hbox {m}\) lateral offset (red curve with \(\times\) marker). The blue dashed curve represents the EF change for a perfectly aligned trench-assisted multi-mode fiber with a 51 \(\mu \,\hbox {m}\) core diameter. The dashed curve with \(\Diamond\) markers represents a receiving fiber with a 51.75 \(\mu \,\hbox {m}\) core, a NA of 0.215 and a 10 \(\mu \,\hbox {m}\) lateral offset. (Color figure online)
In the rightmost subfigure of Fig. 18, the parabolic core of the trench-assisted multi-mode fiber is reduced to 49 \(\mu \,\hbox {m}\), and the three solid EF curves effectively move further upwards and touch the upper bounds. When the trench-assisted multi-mode receiving fiber has a 51 \(\mu \,\hbox {m}\) core diameter, the near-field pattern widens and the EF curve shifts downwards (blue dashed curve in Fig. 18), and gets close to the lower bounds.
A numerical aperture mismatch affects the width of the near-field distribution in the opposite way as a core diameter mismatch. The near-field pattern widens when the receiving fiber has a smaller numerical aperture than the launch fiber, whereas the near-field pattern becomes more core confined when the numerical aperture is larger.
The specific change in the cumulative near-field pattern due to a simultaneous mismatch in the core diameter and the numerical aperture might be revealed through deliberate lateral misalignments. Consider for instance the cumulative near-field pattern in a trench-assisted receiving fiber that has a core diameter of \(51.75\,\mu \,\hbox {m}\), a NA of 0.215, and a lateral misalignment of 10 \(\mu \,\hbox {m}\) with respect to the launch fiber. The larger receiving fiber CD (for equal NA) stretches the support of the EF towards larger radii, and the associated EF curve downwards, whereas the larger receiving fiber NA (for equal CD) shrinks the support of the EF towards smaller radii, and the associated EF curve upwards, albeit not in equal measure. That is to say, a receiving fiber CD increase is not fully cancelled by a simultaneous appropriate NA decrease. This is revealed by the asymmetric change in the EF (purple dashed curve in Fig. 18 for a deliberate lateral offset. Hence, it might be possible to unravel the two parameters by monitoring the EF changes across a connection interface, and thus provide an indirect measurement of such small-scale differences.
12 Discussion and conclusions
We have described a Wilson-basis discretized mode-matching technique that evaluates the converged electromagnetic fields for configurations that have two consecutive interfaces forming a resonating cavity. We gave examples of two optical fibers that are laterally and longitudinally misaligned in a homogeneous air medium. To avoid countless evaluations of fields that propagate forward and backward between the two interfaces (which we call looped fields), we devised an iterative method that yields a Neumann series of looped fields with every step.
The sum of these Neumann series converges very rapidly for fiber-air interfaces. For the limiting case of two identical and perfectly aligned fibers, the evaluation of the first Neumann series already yields the same level of accuracy as evaluating three consecutive loops of the initial looped field. To make sure all resonances have decayed, we included three Neumann-series (converged loops) for all simulations.
For single-mode fiber connections with a vanishingly small gap, we have evaluated the attenuation curves due to an impedance mismatch caused by a numerical aperture mismatch. The curves are right in the middle of those that are obtained with a common approximation technique that assumes a vanishing reflection and projects the transverse electric (or magnetic) field of the excitation to the transmitted field using overlap integrals. For the mismatches in the mode-field diameter that can occur for typical single-mode fiber applications (up to 2.5 \(\mu \,\hbox {m}\)), the attenuation difference between the approximation method and our approach is only a few hundredth of a dB.
However, the approximation methods are no longer applicable when the gap size increases. We have demonstrated the capability of the full mode-matching method by expanding the gap up to 70 \(\mu \,\hbox {m}\) and a 3 \(\mu \,\hbox {m}\) lateral misalignment for three telecom wavelengths. The consecutive application of Love’s equivalence principle and a propagation operator for just 32.1 \(\hbox {nm}\) allowed us to bridge the large gap of 70 \(\mu \,\hbox {m}\), sparing us the time-consuming effort to evaluate the propagation operator in Eq. (6) for every step. Even though the energy distribution among the Wilson-basis source and test functions in the propagation operator suggests that (spatial) truncations cannot be made (cf. Figs 4 and 5), we could truncate the operator due to the spatio-spectral confinement of the electromagnetic fields that are associated with the optical fibers. The conservation of the power carried by the fields that propagate across the gap are a valuable indicator for field degradations due to truncations. We were able to preserve the power balance to at least five digits. The attenuation and return-loss curves show strong interference effects for the short gap, but also decay of the resonances and increase in the overall attenuation as the gap size increases.
For multi-mode fiber connections, we have determined the attenuation curves for lateral and longitudinal misalignment for the excitation of each of the 180 guided modes (not counting complex conjugate counterparts). Particularly the high-order mode excitations reveal interesting attenuation dynamics, such as variations in the coupling efficiency as the lateral misalignment increases (cf. Fig. 11) or damping interference effects for the specific gap size near \(17~\mu \,\hbox {m}\) (cf. Fig. 16).
A multi-mode fiber launch in practice comprises a specific distribution of modal electromagnetic fields. We first evaluated a naive implementation of an overfilled launch that excites all modes equally strong and in a spatio-temporal independent manner. The resulting attenuation curve matches well to approximations by Neumann and Weidhaas. To construct a target EF launch, which is standardized for attenuation measurements, we sampled a modal power distribution to end up with a specific linear combination of modal amplitudes. By distributing the phases of every mode randomly, we generated a large number of speckle patterns, each with its own cumulative near-field pattern and attenuation. The average cumulative near-field pattern approaches the target encircled-flux levels, while the variation in the attenuation due to the speckle patterns is a measure for the modal noise (cf. Fig. 12). Similar to the single-mode fiber case, the repetitive application of Love’s equivalence principle and a short propagation operator of just 70.2 \(\hbox {nm}\), allowed us to cover a distance of 70 \(\mu \,\hbox {m}\). In this case, the diffracted field inside the open cavity formed by the gap extends to a region of about 1 million cubic wavelengths.
As a concluding example that couples a launch from a regular nominal multi-mode fiber to a modern trench-assisted multi-mode fiber, we have considered the impact on the cumulative near-field pattern rather than the attenuation. Even though the presence of the trench in the receiving fiber effectively narrows the intensity pattern, the EF curve stays within the standardized bounds for encircled-flux compliant launches. This means that existing modal conditioners can be extended with trench-assisted multi-mode fibers to generate a standards compliant launch that is in principle suitable for connection attenuation measurements with modern-day multi-mode fibers. If the receiving fiber has a smaller core diameter and/or a larger numerical aperture, the transmitted field shrinks further. Vice versa, if the receiving fiber with a larger core diameter and/or a smaller numerical aperture, the transmitted field widens. We have shown that a simultaneous core diameter and numerical aperture mismatch across a fiber connection can manifest in asymmetrical EF curves when applying a deliberate lateral misalignment. A model-based reconstruction is a promising means to determine the actual fiber geometry parameters of the receiving fiber.
Data Availability
The datasets generated during and/or analysed during the current study are available from the corresponding author on reasonable request.
References
Arnold, J.M.: Rays, beams and diffraction in a discrete phase space: Wilson bases. Opt. Express 10(16), 716–727 (2002)
Bach, H., Neuroth, N.: The Properties of Optical Glass. Springer Science & Business Media, Berlin (1998)
Bude, F., Van Etten, W.: Attenuation and interference in multimode fiber connections. Appl. Opt. 26(7), 1158–1161 (1987)
Daido, Y., Miyauchi, E., Iwama, T., Otsuka, T.: Determination of modal power distribution in graded-index optical waveguides from near-field patterns and its application to differential mode attenuation measurement. Appl. Opt. 18(13), 2207–2213 (1979)
Daubechies, I., Jaffard, S., Journé, J.-L.: A simple Wilson orthonormal basis with exponential decay. SIAM J. Math. Anal. 22(2), 554–573 (1991)
de Hon, B. P., and Floris, S. J.: Wilson basis expansion of electromagnetic fields and source distributions—wave decomposition and propagation tools for optical fibre scattering. In Proceedings of the 2018 20th International Conference on Electromagnetics in Advanced Applications (ICEAA), pp. 418–420, 2018
Di Vita, P., Rossi, U.: Theory of power coupling between multimode optical fibres. Opt. Quant. Electron. 10(2), 107–117 (1978)
Efimov, A.: Different measures of speckle and coherence at the output of a multimode optical fiber. J. Opt. Soc. Am. A 36(1), 1–11 (2019)
Epworth, R.E.: Phenomenon of modal noise in fiber systems. Optical Society of America, In Optical Fiber Communication (1979)
Fettweis, G.P., Dörpinghaus, M., Castrillon, J., Kumar, A., Baier, C., Bock, K., Ellinger, F., Fery, A., Fitzek, F.H.P., Härtig, H., Jamshidi, K., Kissinger, T., Lehner, W., Mertig, M., Nagel, W.E., Nguyen, G.T., Plettemeier, D., Schröter, M., Strufe, T.: Architecture and advanced electronics pathways toward highly adaptive energy-efficient computing. Proc. IEEE 107(1), 204–231 (2019)
Floris, S.J., de Hon, B.P.: Wilson basis expansions of electromagnetic wavefields: a suitable framework for fiber optics. Opt. Quant. Electron. (2018). https://doi.org/10.1007/s11082-018-1364-9
Floris, S.J., de Hon, B.P.: Electromagnetic reflection-transmission problems in a Wilson basis: fiber-optic mode-matching to homogeneous media. Opt. Quant. Electron. (2018). https://doi.org/10.1007/s11082-018-1368-5
Floris, S. J., de Hon, B. P., and Bolhaar, T.: Intrinsic attenuation in multi-mode fiber interconnects. In Proceedings of the 61st International Cable Connectivity Symposium (IWCS), 2012
Floris, S. J., de Hon, B. P., Bolhaar, T., and Tijhuis, A. G.: Standard and bend-insensitive multi-mode fiber connection modeling - A vectorial full-wave approach. In Proceedings of the 64th International Wire and Cable Symposium (IWCS), 6-8 October, Atlanta GA, United States of America, 2015
Floris, S. J., de Hon, B. P., Bolhaar, T., and Smink, R. W.: A geometrical optics approach to encircled-flux compliant source modeling for multi-mode fiber illumination and connection attenuation. Elsevier’s Journal of Optical Fiber Technology, 2019
Gallagher, D. F., and Felici, T. P.: Eigenmode expansion methods for simulation of optical propagation in photonics: pros and cons. In Integrated optics: devices, materials, and technologies VII, volume 4987, pp. 69–82. SPIE, 2003
Ghatak, A., Thyagarajan, K.: An Introduction to Fiber Optics. Cambridge University Press, Cambridge (1998)
Hasegawa, O., Abe, M., Yamaoka, T.: Efficient coupling of led and spherical-ended fiber. J. Appl. Phys. 49(8), 4353–4356 (1978). https://doi.org/10.1063/1.325489
Hauffe, R., Siebel, U., Petermann, K., Moosburger, R., Kropp, J., Arndt, F.: Methods for passive fiber chip coupling of integrated optical devices. IEEE Trans. Adv. Packaging 24(4), 450–455 (2001)
http://www.ieee802.org/3. IEEE standard 802.3ba, 2010
http://www.photond.com. Photon design products FIMMWAVE and FIMMPROP
IEC 61280-4-1. Fibre-optic communication subsystem test procedures—part 4–1: Installed cable plant - multimode attenuation measurement, June 2009
IEC 61280-4-1. Fibre-optic communication subsystem test procedures—part 1–4: General communication subsystems—light source encircled flux measurement method, 2021
Koonen, A.M.J.: Bit-error-rate degradation in a multimode fiber optic transmission link due to modal noise. IEEE J. Select. Areas Commun. 4(9), 1515–1522 (1986). https://doi.org/10.1109/JSAC.1986.1146487
Lakhtakia, A., Mackay, T.G.: Total internal reflection of evanescent plane waves. Eur. J. Phys. 29(6), N59–N61 (2008). https://doi.org/10.1088/0143-0807/29/6/n02
Lam, C.F.: Passive Optical Networks: Principles and Practice. Elsevier, Amsterdam (2011)
Love, A.E.H.: I. the integration of the equations of propagation of electric waves. Philosophical Transactions of the Royal Society of London. Series A, Containing Papers of a Mathematical or Physical Character 197(287–299), 1–45 (1901)
Marcuse, D.: Loss analysis of single-mode fiber splices. Bell Labs Tech. J. 56(5), 703–718 (1977)
Nagase, R.: How to connect multicore and multimode fibers. In OFC 2014, 1–3 (2014)
Neumann, E.-G.: Single-Mode Fibers. Springer Series in Optical Sciences. Springer, Berlin (1988)
Neumann, E.-G., Weidhaas, W.: Loss due to radial offsets in dielectric optical waveguides with arbitrary index profiles. Archiv Elektronik und Uebertragungstechnik 30, 448–450 (1976)
Park, E.-H., Kim, M.-J., Kwon, Y.-S.: Microlens for efficient coupling between led and optical fiber. IEEE Photonics Technol. Lett. 11(4), 439–441 (1999). https://doi.org/10.1109/68.752541
Refi, J.: Led bandwidth of multimode fibers as a function of laser bandwidth and led spectral characteristics. J. Lightwave Technol. 4(3), 265–272 (1986). https://doi.org/10.1109/JLT.1986.1074714
Richardson, D.J.: Filling the light pipe. Science 330(6002), 327–328 (2010)
Smink, R.W.: Optical Fibres: Analysis, Numerical Modelling and Optimisation. University of Technology, Eindhoven (2009)
Spurgeon, C.E.: Ethernet: The Definitive Guide. O’Reilly, Media Inc., Sebastopol (2000)
TIA-455-203-A. Light source encircled flux method
van Etten, W., Lambo, W., Simons, P.: Loss in multimode fiber connections with a gap. Appl. Opt. 24(7), 970–976 (1985)
Wilson, K.: Generalized Wannier Functions. Cornell University preprint, New York (1987)
Funding
The authors declare that no funds, grants, or other support were received during the preparation of this manuscript.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors have no relevant financial or non-financial interests to disclose.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Floris, S.J., de Hon, B.P., van Beurden, M.C. et al. Electromagnetic mode matching in a Wilson basis: optical fiber connections with a gap. Opt Quant Electron 54, 730 (2022). https://doi.org/10.1007/s11082-022-04135-3
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s11082-022-04135-3