1 Introduction

Photonic crystal fiber (PCF) (Russell 2003) has attracted a lot of research interest in different applications (Homola 2008; Hameed et al. 2010) instead of conventional optical fibers. This is due to the advantages of the PCF (Buczynskl 2004) including endlessly single mode guidance, large effective mode area and controlled dispersion. The PCF consists of core region surrounded by microstructure cladding of air holes. Therefore, PCF has large degrees of design freedom where the geometrical parameters can be controlled to achieve high sensor sensitivity (Rifat et al. 2015a; Singh 2016; Lu et al. 2018). Although, the conventional optical fiber sensors perform very well in telecom and non-telecom applications, but there is a series of fundamental limits related to their structures. In this context, the conventional fibers have rigid design rules such as limited core diameter for single mode guidance, modal cut-off wavelength, and limited material choice where the thermal properties of the core and clad glasses must be the same (Buczynskl 2004).

Surface plasmon resonance (SPR) has drawn enormous attention in different sensing applications. Surface plasmons (SPs) are united fluctuations of free electrons at the metal/dielectric interface. Originally, the SPR sensor was developed for gas sensing and biosensing (Liedberg et al. 1983). There are three common techniques for the SPs excitation including prism coupling, grating coupling, and waveguide coupling (Gwon et al. 2010). In the late 1970s, SPs were experimentally studied and characterized at thin film/metal dielectric interface (Pockrand et al. 1978). In this context, a gold thin film is deposited on a glass prism where a polychromatic collimated light beam was incident on gold/glass interface. Such arrangement was called Kretschmann-Raether configuration (Raether 1988; Foley et al. 2015). The SPs are highly sensitive to the dielectric constant of studied analyte which is the main principle of SPR sensor (De Leebeeck et al. 2007). The resonance coupling between the incident light and SPs is achieved when the incident light wave vector matches that of a surface plasmon wave (SPW). The resonance wavelength depends on the incident angle, operating wavelength, dielectric constant, and metallic geometry as well as sensing medium (Han et al. 2016; Colas et al. 2009). The Kretschmann configuration based on the attenuated total reflection configuration has higher sensitivity, lower cost, user friendly and real-time detection (Menon et al. 2018; Jamil et al. 2018) compared to other label-free methods. However, this approach suffers from its bulk size. Additionally, the frictional wear of the thin metal film strongly influenced the measurement accuracy (Maegawa et al. 2016). Therefore, plasmonic optical fiber sensors have been implemented with simple design. A concave shaped refractive index sensor (CSRIS) covered with multiple Au nanowires achieved sensitivity of 4471 nm/RIU over wide range of analytes refractive indices from 1.33 to 1.38 (Pathak et al. 2019, 2020) have also presented an optical fiber refractive index sensor using silver nanowire where high wavelength and amplitude sensitivity of 9314.28 nm/RIU and 1494 RIU−1, respectively are achieved within RI range from 1.33 to 1.38. Also, A highly sensitive RI sensor based on a microfluidic channel is presented and maximum wavelength and amplitude sensitivity of 13,700 nm/RIU and 1026 RIU−1, respectively are achieved (Pathak et al. 2021).

Plasmonic PCFs have been employed for sensing applications (Shuai et al. 2012; Zhao et al. 2014; Areed et al. 2017; Hameed and Obayya 2018). The PCF provides a perfect solution to the phase matching between the core modes and the SPR modes. The resonance wavelength depends on the analyte refractive index at the metal/dielectric interface. Therefore, the optical properties variation of the analyte can be detected with high sensitivity. The SPR has been utilized for the design of highly sensitive sensors based on PCF (Rifat et al. 2017), and D-shaped fiber (Wang et al. 2006). High sensor sensitivity can be achieved by tuning the geometrical parameters of the PCF or the plasmonic arrangement (Barnes et al. 2003; Homola 2008; Rifat et al. 2015a; Hameed and Obayya 2018). Gold and silver are the most preferable plasmonic materials. They have relatively low loss in the visible and near-infrared (NIR) ranges, and can be easily implemented in PCF structures (West et al. 2010; Gangwar and Singh 2017). Further, the silver (Ag) has the smallest dampening rate with sharp resonance peak (Momota and Hasan 2018). However, the Ag has a chemical instability problem. Hassani and Skorobogatiy (2006) have reported a SPR PCF with sensitivity of \(3000\) nm/RIU. Additionally, plasmonic PCF biosensor with an analyte-filled core has achieved sensitivities of \(2280\) nm/RIU and \(4354.3\) nm/RIU using two resonance wavelengths (Wei et al. 2014). Furthermore, plasmonic asymmetric PCF offered sensitivities of \(1700\) nm/RIU and \(2000\) nm/RIU, for the supported HEy11 and HEx11 modes, respectively (Otupiri et al. 2014). Compact PCF biosensor has been demonstrated for an aqueous environment sensing with sensitivity of \(4000\) nm/RIU (Akowuah et al. 2012a). High temperature sensitivity of 10 nm/°C has been obtained using liquid crystal (LC) SPR PCF sensor (Hameed et al. 2015). Additionally, spectral sensitivities of 2000 nm/RIU and 1500 nm/RIU were achieved using multi-channel PCF biosensor according to the HEx11 and HEy11 core modes, respectively (Akowuah et al. 2012b). Self-calibration highly sensitive PCF sensor was also proposed with sensitivities of \({ }6700\) nm/RIU and \(10000\) nm/RIU for y-polarized and x-polarized core modes, respectively (Hameed et al. 2016). However, the elliptical holes of this PCF will be difficult for fabrication. Moreover, maximum wavelength sensitivity of 3000 nm/RIU in the sensing range of 1.46–1.49 was achieved using y-polarized mode using plasmonic PCF (Rifat et al. 2015b). Further, bimetallic PCF biosensor achieved sensitivity of \(3200\) nm/RIU (Akowuah et al. 2012c). Multi-functional SP LC PCF biosensor has been reported for RI and temperature sensing with sensitivity of 3700 nm/RIU and 5 nm/°C, respectively (Azab et al. 2017). Further, Zhang et al. (2018) have reported D-shaped PCF coated partially by metallic layer with sensitivity of 3751.5 nm/RIU.

The excitation of the SPP wave at the dielectric/metal or metal/dielectric interfaces is not an easy process (Kamran and Faryad 2019). This is because the phase speed of the SPP wave is usually smaller than that of a plane wave in the dielectric material. In order to help excite the SPP waves and achieve the matching condition, a surface grating is used. In the grating based configuration, a periodic grating of a dielectric or metallic materials is used to create non-specular electromagnetic modes with various phase speeds. When the phase speed of one of the non-specular mode is equal to that of a SPP wave, a maximum power transfer occurs from the incident light and the SPP waves at a resonance wavelength. The use of metallic grating (Lu et al. 2018) is very attractive where the resonance wavelength can be tuned and maximize the sensor sensitivity using the different geometrical parameters. Lu et al. (2018) have also presented a D-shaped SPR PCF based on conventional gold grating with wavelength sensitivity of 3340 nm/RIU.

In this study, D-shaped PCF with gold grating is reported and analyzed. The geometrical parameters of the gold pyramid grating and PCF are tuned to improve the sensor sensitivity. The full vectorial finite element method (FVFEM) (Obayya et al. 2000a, b, 2002) is used to model the suggested design via the COMSOL Multiphysics software package. High sensitivity of 5200 nm/RIU is achieved for the quasi-TM mode using the suggested D-shaped PCF gold grating which is greater than 3340 nm/RIU and 3751.5 nm/RIU of the conventional grating design of (Lu et al. 2018; Zhang et al. 2018). Further, the reported D-shaped PCF holds great potential as a highly sensitive RI sensor with high linearity to detect an unknown analyte refractive index from 1.355 to 1.385. Also, the suggested design has a good tolerance to fabrication imperfection. It is worth noting that the basal normal cell and cancerous cells have refractive indices of 1.36 and 1.38, respectively. Therefore, the proposed sensor can be used for biomedical applications for basal cancer cell detection (Ayyanar et al. 2018; Sharma et al. 2015; Tsai et al. 2012; Yaroslavsky et al. 2012).

2 Design consideration and theoretical modeling

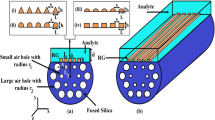
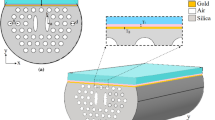
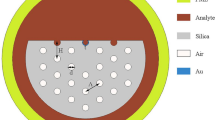
The cross-sectional view of the proposed SPR silica PCF sensor is shown in Fig. 1. The reported design has two rings of air holes arranged in hexagonal lattice. The inner ring has small air holes with radius of \(r_{1}\) while the second ring as large air holes of radius \( r_{2}\). The lattice pitch between all air holes is \( {\Lambda } = 2.3\) µm. The distance between the etched surface and the silica core is \({\text{ L}} = 3.2\) µm. The confinement of the supported modes through the core region can be controlled using the radii \(r_{1}\) and \(r_{2}\) of the air holes. Also, the D-shaped PCF has a channel of thickness \(d_{3} = 3\) µm to house the analyte. The nanopyramid gold grating is placed over the planar surface of the D-shaped PCF in order to enhance the sensor sensitivity. The gold grating constant is \(r\), with pyramid height of \(h\) and base width of \(w\).

Fig. 1
figure 1

a 2D Cross-section and, b 3D schematic diagram of the proposed PCF-SPR sensor, and, c the intensity distribution of the TM core mode and surface plasmon modes at wavelength of 1382 nm and analyte refractive index of 1.36

Full size image

The light confinement at nanoscale is one of the unique property of SPs. The resulted plasmonic modes have shown a high sensitivity towards ambient medium. The nanostructure and material nature can be adjusted to harness the sensing applications of SPs. In this context, D-shaped PCFs with gold planner layer and with rectangular gold grating have been previously studied in (Lu et al. 2018). The planer gold layer-based sensor has small sensitivity of 774 nm/RIU while the rectangular gold grating achieved sensitivity of 3340 nm/RIU. Therefore, it is aimed in the present design to increase the sensitivity by using the pyramid gold grating. This can be achieved by increasing the coupling between the core mode and surface plasmon mode with more light intensity in the analyte layer at resonance. The SPR and LSPR have high sensitivity to the dielectric refractive index change at the dielectric/metal interface (Reather 1988). The LSPR occurs when the frequency of incident photon is resonant with the collective oscillation of conduction electrons around small metallic particles (Bohren et al. 1998). However, the propagating SPR occurs at planar metal/dielectric interface such as Kretschmann configuration (Kretschm et al. 1968). It may be seen that the suggested design has metallic pyramid grating separated by a distance r. Therefore, the proposed design supports LSPR with improved sensitivity.

The refractive index of the fused silica background material is given by the following Sellmeier equation (Akowuah et al. 2012a):

$$ n\left( \lambda \right) = \sqrt {1 + \frac{{A_{1} \lambda^{2} }}{{\lambda^{2} - B_{1} }} + \frac{{A_{2} \lambda^{2} }}{{\lambda^{2} - B_{2} }} + \frac{{A_{3} \lambda^{2} }}{{\lambda^{2} - B_{3} }}} $$
(1)

where n is the refractive index of the silica and \({\uplambda }\) is the wavelength in \({\mu m}\). Further, \({\text{A}}_{1} = 0.696166300\), \({\text{A}}_{2} = 0.407942600\), \({\text{A}}_{3} = 0.897479400\), \({\text{B}}_{1} = 4.67914826\) µm2, \({\text{B}}_{2} = 1.35120631\) µm2, and \({\text{B}}_{3} = 97.9340025\) µm2. The complex dielectric constant of gold has the following frequency dependent relative permittivity (Azzam et al. 2016)

$$ \varepsilon_{Au} \left( \omega \right) = \varepsilon_{\infty } - \frac{{\omega_{p}^{2} }}{{\omega \left( {\omega + i\omega_{\tau } } \right)}} $$
(2)

where \(\varepsilon_{\infty } = 9.75\), \(\omega_{p} = 1.36 \times 10^{16} \,{\text{rad}}/{\text{s}}\), and \(\omega_{\tau } = 1.45 \times 10^{14} \,\,{\text{ rad}}/{\text{s}}\). The angular frequency can be expressed as \( \omega = 2\pi c/\lambda\), where c is the velocity of light in vacuum. The COMSOL-Multiphysics software package based on FVFEM is used to obtain the quasi-TM core-guided mode and SPR modes supported by the proposed sensor. The main component of the fundamental quasi-TM mode is \(H_{11}^{x}\) or \(E_{11}^{y}\). The computational window is set to 12 × 12 µm, where the number of triangular elements, degrees of freedom and minimum element size are equal to 109,154 elements, 765,109, and \(3.72 \times 10^{ - 9 } \,{\text{m}}\). Further, scattering boundary conditions (SCB) are used to truncate the computational domain and calculate the confinement losses of the supported modes.

The fabrication of the reported triangular lattice PCF can be made using the mature stake and draw method (Russell 2003). Additionally, the polishing of the PCF to realize the D-shaped configuration can be realized by using a fiber polish where splicing is applied for long PCF between two single-mode fibers (SMFs) as proposed in (Wu et al. 2017). The reported PCF will be spliced between the SMFs and is fixed by a pair of fiber holders. The polishing length and depth will be controlled accurately using computer-based program. Furthermore, the fused PCF can be strengthened by using a small weight which also supplies a suitable polishing force to speed up the polishing speed. A polishing paper is fastened around the mechanical wheel for polishing and abrasive the fiber. Then, the silica dust can be removed using an air-laid paper with water. If a power loss of 3 dB is obtained, the PCF polishing process will be stopped (Wu et al. 2017). The pyramid grating can be deposited on the D-shaped surface by focus-ion-beam (FIB) technology as reported in (Ding et al. 2014). A phase slab of various ion doses can be used for generating the array of the truncated pyramids using a pattern generator of direct milling. The multilayered metamaterial (MM) taper array is obtained by milling alternating dielectric–metal thin films with the focused-ion-beam (FIB) technology. The grayscale bitmaps are used to control the beam dose during the FIB milling by varying the beam dose pixel by pixel. By controlling the distribution of the beam dose with a carefully predesigned grayscale bitmap, the pyramid array can be successfully fabricated (Dang et al. 2020).

3 Numerical results

The PCF-SPR sensor is based on the interaction of the evanescent field of the core mode with the surface plasmon mode at the plasmonic grating. The geometrical parameters are taken as \(r_{1} = 0.4\) µm, \( r_{2} = 0.8\) µm,\( \Lambda = 2.3\) µm, \(d_{3} = 3 \) µm, \(r = 0.5\) µm, \(h = 0.4\) µm, \({\text{L}} = 3.2\) µm and \(w = 0.5 \) µm. Also, the analyte has a refractive index of 1.36. The initial parameters are chosen according to fabrication feasibility of the suggested PCF. Figure 2 shows the dispersion relation and confinement losses of the quasi TM core mode and neff of the SP mode at n = 1.36 and 1.37. The wavelength dependent confinement loss is expressed as:

$$ {\text{Loss}} = \frac{{40{\uppi }}}{{{\text{ln}}\left( {10} \right){\uplambda }}} \times {\text{Im}}\left( {{\text{n}}_{{{\text{eff}}}} } \right) \times 10^{4} { }\,\,{\text{dB}}/{\text{cm}} $$
(3)

where the \({\text{Im}}\left( {{\text{n}}_{{{\text{eff}}}} } \right)\) is the complex effective index imaginary part of the core-guided modes. It may be seen from Fig. 2b that the phase matching is obtained at \(\lambda = 1372.16\) nm where the effective indices of the core-guided mode and SPP mode coincide at \({\text{n}} = 1.36\). Then, the loss of the core mode will be maximum at the resonance wavelength as shown in Fig. 2a. It may be also seen that the resonance wavelength is shifted to \(\lambda = 1432.37\) nm at \({\text{n}} = 1.37\). Therefore, the suggested design can be used for detecting the variation in the RI of the analyte sample.

Fig. 2
figure 2

a Variation of the confinement losses of the quasi TM polarized core mode and, b variation of neff of the quasi TM core and SP modes with the wavelength at n = 1.36 and 1.37

Full size image

It is aimed to maximize the sensor sensitivity; therefore, the effects of the different geometrical parameters are analyzed. The SPR relies mainly on the gold grating constant r and gold grating pyramid height h. Therefore, the impact of the grating constant is firstly investigated. The loss spectra of the quasi-TM guided modes are shown in Fig. 3 at r = 0, 0.3, 0.4, and 0.5 µm at \({\text{n}} = 1.36\) and \(1.37\). It may be seen that the losses spectra are increased with decreasing the grating constant r where the SP effect will be increased. As \({\text{n}}\) changes from 1.36 to 1.37, the resonance wavelengths are shifted. At r = 0 and 0.5 µm, the resonance wavelengths of the quasi-TM mode are equal to 1632 and 1866 nm at n = 1.36. However, phase matching occurs at λ = 1640 nm and \(1908 \,{\text{nm}}\) at n = 1.37. Table 1 summarizes the effects of the geometrical parameters on the wavelength sensitivity.

Fig. 3
figure 3

The loss spectra at different grating constant r values at n = 1.36 and 1.37

Full size image
Table 1 Summary of the wavelength sensitivity at different geometrical parameters
Full size table

The sensitivity of the RI sensor can be calculated as follows (Homola 2003; Hautakorpi et al. 2008):

$$ {\text{S}}_{{\uplambda }} \left( {\uplambda } \right) = \frac{{\Delta {\uplambda }_{{{\text{peak}}}} }}{\Delta n}{ }\left( {{\text{nm}}/{\text{RIU}}} \right) $$
(4)

where \(\Delta {\uplambda }_{{{\text{peak}}}}\) is the shift in the resonant wavelength due to the analyte refractive index change \(\Delta n\). Therefore, the sensitivity of the proposed sensor are equal to 800, 2500, 3700 and 4200 nm/RIU at r = 0, 0.3, 0.4 and 0.5 µm, respectively. So, the highest sensor sensitivity is obtained at the largest gold grating constant. In addition, any further increase in that grating constant r will decrease the sharpness of the loss curves which decreases the detection accuracy. Therefore, r of 0.5 µm will be used in the upcoming simulations.

Next, the effect of the gold pyramid grating height h on the sensor sensitivity is studied as illustrated in Fig. 4 where h is varied from 0.1 to 0.4 µm at n = 1.36 and 1.37. It is evident that the losses spectra decrease with increasing the height h. When n is varied from 1.36 to 1.37, the resonant wavelength is shifted toward short wavelength region as revealed from Fig. 4. As h changes from 0.1 to 0.4 µm, the resonance wavelengths of the quasi-TM mode are shifted from 1866 to 1373 nm at n = 1.36 and from 1908 to 1423 nm at n = 1.37. The sensor has sensitivities of 4200, 4100, 4400 and 5000 nm/RIU for the quasi-TM at h = 0.1, 0.2, 0.3 and 0.4 µm, respectively. Therefore, the sensor sensitivity will be increased by increasing the grating height where h will be fixed at 0.4 µm in the next calculations.

Fig. 4
figure 4

Variation of the losses of the quasi-TM core mode with the wavelength at different grating pyramid heights h when the analyte refractive index changes from 1.36 to 1.37

Full size image

The impact of the small air hole radius is next studied as shown in Fig. 5 and Table 1. As r1 increases from 0.4 to 0.55 µm, the quasi-TM mode confinement through the core region increases which decreases the confinement losses. By changing r1 from 0.4 to 0.55 µm, the resonance wavelengths of the quasi-TM mode are shifted from 1373 to 1389 nm at n = 1.36 and from 1423 to 1441 nm at n = 1.37. Therefore, the sensitivity is slightly increased from 5000 to 5200 nm/RIU by increasing r1 from 0.4 to 0.55 µm. Consequently, r1 will be taken as 0.55 µm in the subsequent analysis with high quality factors of 10.5 and 10.11 at n = 1.36 and 1.37, respectively.

Fig. 5
figure 5

Variation of the losses of the quasi-TM core mode with the wavelength at different small air hole radius r1 values at n = 1.36 and 1.37

Full size image

The dependence on the large air hole radius r2 is also studied at different values of 0.8, 0.85, 0.9 and 0.95 as illustrated in Fig. 6 and Table 1. With increasing the large air hole radius, the loss of the quasi TM core mode is slightly deduced, and the resonance wavelength is shifted to shorter wavelength. Additionally, r2 has a slight influence on the wavelength sensitivity. By increasing r2 from 0.8 to 0.95 µm, the resonance peaks of the quasi-TM mode are shifted from wavelength of 1389 to 1375 nm at \(n = 1.36\) and from 1441 to 1426 at \(n = 1.37\). Additionally, high quality factors of 10.6 and 10.37 are achieved at \(n = 1.36\) and 1.37, respectively at r2 = 0.9 µm. The sensitivity is nearly constant at 5200 nm/RIU by increasing r2 from 0.8 to 0.95 µm. It should be noted that the achieved sensitivity is higher than 3340 nm/RIU of the conventional grating D-shaped PCF reported in (Junjie et al. 2018). It is worth mentioning that, the device achieves a maximum loss peak of 86.85 dB/cm at a resonance wavelength of 1431 nm. Thus, the proposed device length can be adjusted to meet the requirement of acceptable total leakage loss. As a result, the suggested device length of 10 µm can be used to have a total loss of less than 0.1 dB.

Fig. 6
figure 6

Variation of the losses of the quasi-TM core mode with the wavelength at different large air hole radius r2 values at n = 1.36 and 1.37

Full size image

Table 1 shows the optimum geometrical parameters where r = 0.5 µm, h = 0.4 µm, r1 = 0.55 µm, and r2 = 0.9 µm. The linear performance of the proposed sensor is next studied as shown in Fig. 7. It may be seen from Fig. 7 that the resonance wavelength increases with increasing the analyte refractive index from 1.355 to 1.385. Further, the resonance wavelength variation has a linear fitting given by:

$$ \lambda_{TM \,peak} \,\left( {{\mu m}} \right) = 6.157n - 6.994 $$
(5)
Fig. 7
figure 7

Linear fitting of the resonance wavelength for the quasi TM mode as a function of the analyte refractive index

Full size image

In this case, an average sensitivity of 6157 nm is achieved through the studied wavelength range. The achieved sensitivity is greater than 3340 nm/RIU of the D-shaped PCF with conventional gold grating (Lu et al. 2018). Further, the suggested pyramid grating offers higher sensitivity than 3751.5 nm/RIU (Zhang et al. 2018) of the D-shaped PCF coated partially by metallic layer.

The fabrication tolerance of the suggested design is also studied to ensure that the suggested sensor is robust to fabrication imperfection. In this study, only one parameter is studied while the other parameters are kept constant at their optimum values reported in Table 1. The tolerance results are summarized in Table 2. It may be seen that the different geometrical parameters have a good tolerance of ± 10% where the sensitivity is still better than 4800 nm/RIU.

Table 2 The tolerance study of the different geometrical parameters
Full size table

Table 3 shows the performance of the proposed sensor compared to the other results reported in the literature. It may be seen that the suggested sensor has higher sensitivity over wide range of refractive indices from 1.355 to 1.385.

Table 3 Comparison between the suggested RI sensor and those reported in the literature
Full size table

4 Conclusion

Modified D-shaped SPR PCF sensor with pyramid grating is suggested. The proposed sensor is numerically studied and its parameters are optimized to achieve maximum RI sensor sensitivity. The numerical results are obtained using full vectorial finite element method. High wavelength sensitivity of 5200 nm/RIU is achieved through RI range from 1.355 to 1.385 with high linearity. Therefore, the proposed SPR based PCF sensor is a promising structure for unknown analyte detection. In this context, the reported RI sensor can be used for basal cancer early detection.