1 Introduction

Oceanography is the branch of science that deals with the physical and biological properties and phenomena of the sea. It has more developments while it extends back to tens of thousands of years, which includes acquiring the knowledge of ocean tides, currents, and waves, because 97% of the Earth’s water covers the surface of the earth in the form of oceans as National Oceanic and Atmospheric Administration (NOAA) (2017). The desire to explore the undersea world has sparked a growing interest in underwater communication environment for many applications. This includes the study of oceanic living creatures, climate change, monitoring of oil rigs, and unmanned operations. Underwater conditions have a significant impact on electromagnetic signals, which has a significant impact on radio frequency (RF) propagation. On the other hand, the limited bandwidth due to high time latency at acoustic communication systems has a great effect on limiting the wide range of marine scientific applications in the commercial and naval sectors.

Because of that, underwater optical wireless communication (UOWC) becomes a technology that has received a considerable attention and is a very attractive topic to researchers worldwide due to high data rate and low time latency. It still has the challenge of increasing the limited link distance because of high channel path loss conspicuously increasing due to high attenuation effects (absorption/scattering) due to effects of water’s molecular and suspending particles. These effects include chlorophyll, water-soluble salts, and minerals while the fading caused by underwater optical turbulence (UOT) (Simpson 2008), which affects the refractive index fluctuation (scintillation) of water with random variations of temperature and pressure (Liu et al. 2015). Many underwater wireless communication (UWC) applications demand a way to communicate with internal communications or the outside world while submerged. This has been introduced in existing open literature such as climate change, oil and gas rig monitoring, the study of oceanic animals, surveillance, water pollution control systems, early detection warning of earthquakes, floods and unmanned operations. However, the interest of UOWC is still limited to military applications (Callaham 1981; Puschell et al. 1992; Wiener and Karp 1980). The massive market promotion of UOWC has not been achieved so far. In the early 2010s, just a few UOWC goods were commercialised (Zeng et al. 2016). However, these products are still constrained by link distance, which is inversely proportional to data transfer.

UOWC systems have been investigated in most of the recent existing works on UOWC systems and have considered channel effects due to scattering and absorption while most of them neglect the channel turbulence. J.A. Simpson presented a laboratory experiment (Simpson 2008). The system improvement was investigated by adopted only two light-emitting diodes (LEDs) and two photodiodes (PD) to enjoy the benefit of spatial diversity in UWOC. Single Input Multiple Output (SIMO) detection scheme was studied with a uniform circular array to reduce the signal scintillation caused by UOT (Liu et al. 2015). Multiple Input Single Outputs (MISO) was studied in Dong and Liu (2016). The authors combined the stochastic model in Dong and Liu (2016), with the log-normal turbulence model in Jamali et al. (2016), and evaluated the BER performance of these systems with weak turbulence turbid seawater (coastal water). They proved that the performance degradation can be reduced by spatial diversity at transmitter. The multiple-input multiple-output (MIMO) system was configured by Zhang et al. (2014), by combining the PDF of random sea surface slopes with the stochastic model in Dong and Liu (2016) to formulate the channel capacity depending on random sea surface slopes. The system was applied at more turbid water type coastal and harbor water and approved that more turbid water, larger link range and larger inter-spacing of Tx/Rx array will reduce the channel capacity. Transmission data rates of 5 Gbps up to link range 20 m were studied by Zhang et al. (2015), by MIMO using hybrid system spatial modulation with pulse amplitude modulation (PAM) at coastal water using the lognormal random variable modeled as a weak turbulence fading. They also studied the BER with SNR at different turbulence strengths. Aiping Huang et al. (2018) investigated the error performance of UOWC links over log-normal turbulence channels with spatial diversity technology and compared MIMO, SIMO, and MISO together, using the (RC) across the transmit apertures, and the optimal combiner (OC) was used for receiving apertures. The fading coefficient was modeled as a log-normal random variable for weak to moderate ocean turbulence. The numerical results demonstrated that multiple apertures at either transmitter or receiver enhance the quality of UOWC systems. However, at high transmission data rates, the destructive effect of intersymbol interference becomes extremely severe and the BEP of the system still cannot degrade even in the high SNR condition, especially in SIMO UOWC links.

Ali et al. (2019) compared the performance differences of radio-frequency RF-VLC and FSO-VLC dual-hop communications using decode-and-forward (DF) relay protocol. At different types of water, it was proved that the FSO-VLC combination has the superior BER performance in higher transmitted SNR condition compared to RF-VLC cooperative setup. Sarma et al. (2020) obtained the analytical expressions for outage probability and ABER for mixed triple hop RF-FSO-UWOC cooperative system. The RF link was acting as a backbone network while the FSO link was used for last mile access and the UWOC link was used for underwater users. The numerical results showed that the outage probability and BER of the system increases with the increase of the fading parameters of individual links such as atmospheric turbulence, pointing error, salinity, bubble level and temperature gradient. Sharma and Trivedi (2021) studied the performance analysis of UOT due to the variation in the temperature of seawater on the performance for pulse amplitude modulation (PAM) and quadrature amplitude modulation (QAM) under dual-hop underwater VLC system with receiver diversity with underwater cooperation relay assisted system works on half-duplex mode considering the channel state information (CSI) available at relay and destination with selection combining (SC) at the receiver. The results revealed that the increase in temperature of seawater degrades the performance of the system. However, by increasing the number of photodetectors, the degradation in the performance can be reduced. Jurado et al. (2022) combined terrestrial and underwater wireless optical links but with using an amplify-and-forward (AF) strategy. The first FSO link assumed a Málaga distributed turbulence and the second system was studied with a Weibull channel model selected to model the intensity fluctuations produced in UWOC. The authors obtained closed-form analytical expressions to evaluate the ABER for un-coded and coded transmissions for different turbulence conditions and several code rates by Monte Carlo simulations.

In this work, we reduced the signal scintillation caused by UOT and mitigate the channel fading using hybrid modulation PPM with a spatial diversity technique at the receiver. The system performance is enhanced by MISO-RC and the BER is evaluated with signal to noise ratio (SNR) at different turbulence strengths. The receiver of the FSO link should be upper top of the sea surface while the transmitter of the underwater optical link should be down the sea surface. The optimum link between both will be bending insensitive fiber optic cable according to International Telecommunications Union ITU.G657A2/B2 with low attenuation and dispersion.

The rest of this paper is organized as follows. We introduce the system model for FSO-FO-UWOC MISO in Sect. 2 The BER performance at the destination is studied in Sect. 3. Then, numerical evaluation of the BER performance is illustrated with various system parameters in Sect. 4. Section 5 is devoted to the main conclusions and the recommended future directions.

2 System model

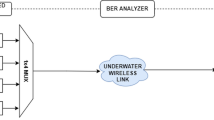
In this paper, we consider the three triple-connection hybrid on-shore, floating relay with fiber optic cable link and underwater cooperative communication systems as shown in Fig. 1.

Fig. 1
figure 1

Reference triple-hop hybrid FSO, FOC & UOWC link

Full size image

The proposed system consists of one terrestrial base station (TBS), a floating surface station (FSS) as a relay node with a bending insensitive fiber optic cable link inside (FOC), and a seabed station (SS) or autonomous underwater vehicle (AUV) as the destination node located in the underwater.

The TBS transmits the information to the underwater AUV via FSS using the decoding and forward (DF) protocol with the laser beam upper the sea surface wavelength \({\lambda }_{f}=1550\mathrm{ nm}\), which is same wavelength inside the FOC while we use wavelength \({\lambda }_{u}=530\mathrm{ nm}\) under water for optimum penetration inside the water.

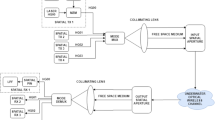
A schematic diagram for the triple connection of the considered system model is depicted in Fig. 2a and b. The white part represents the upper sea surface while the aqua part represents the undersea surface. It is assumed that the first two nodes are equipped with a full-duplex connectivity using FSO technology, which is one of a line of sight (LoS) innovation. The upper FSO system considers a single transmitter \({T}_{X}\) and a single receiver \({R}_{X}\). Source bits are modulated using on–off keying (OOK) pulsed modulation and are encoded by the OOK encoder. Here, \(S(t)\) denotes the transmitted symbols ∈ {0, 1} and an additive white Gaussian noise (AWGN) with zero mean and variance \({\sigma }_{n}^{2}= {N}_{0}/2\) is considered. At the underwater part, the encoder considers two techniques for transmission. Figure 2a represents the UOWC MISO communication system using SM as the investigated system has \({N}_{T}\) transmitters and \({R}_{T}\) single receiver. The PPM is employed to modulate the source bits through an active transmitter worked as SM. Both SM and PPM worked as MISO encoder. In Fig. 2b, the underwater OOK modulator transmits the same signal simultaneously from the \({N}_{T}\) available transmitters as RC system and at the receiver side, for RCs maximum-likelihood (ML) decoder is considered to decode the received signals.

Fig. 2
figure 2

a Schematic diagram for triple connection hybrid FSO, FOC and UOWC (Using spatial modulation). b Schematic diagram for triple connection hybrid FSO, FOC & UOWC (Using Repetition Code)

Full size image

The optimum use to link between the upper top of the sea surface and down sea surface is the bending insensitive FOC according to ITU.G657A2/B2 with very low attenuation and the dispersion is neglected for such lengths. One transmitting source and four photodetectors are used underwater to link optical wireless between the FSS and AUV/SS as a MISO communication with a spatial and hybrid modulation. The FSO in the upper sea surface communication link is used as system model 1 (SM1), The system model 2 (SM2) is related to the intermediate FOC link between SM1 and SM3, while the system model 3 (SM3) is used for undersea surface VLC communication links.

2.1 SM1-TBS to FSS (Source to Relay) communication FSO link

The channel power gain experience in the FSO terrestrial link in SM1 is represented as \({h}_{FSO}\) as per Eq. (1) which follows the log-normal channels. The received signals are affected by an additive white Gaussian noise (AWGN) with zero mean and variance \({\sigma }_{n}^{2}= {N}_{0}/2\), which is used to model noise between communication nodes. At the considered system, the normalized channel coefficient can be formulated as Sharma and Garg (2014)

$${h_{FSO}} = {h_{a}}{h_{p}}{h_{\beta}}$$
(1)

where \({h}_{a}\) is the channel fading coefficient due to atmospheric turbulence, while \({h}_{p}\) is the channel fading coefficient due to misalignment error and \({h}_{\beta }\) is the path loss which can be calculated by combining geometric losses with weather attenuation as Sharma and Garg (2014).

$$ h_{\beta } = 10^{ - \alpha \ell /10} \times \frac{{D_{R}^{2} }}{{\left( {D_{T} + \theta_{T} \ell } \right)^{2} }} $$
(2)

where ℓ is the link distance by (km) for SM1, α is the path attenuation coefficient in (dB/km) which is weather-dependent, \({D}_{R}\) and \({D}_{T}\) are the receiver and transmitter aperture diameters in (m), and \({\theta }_{T}\) is the optical beam divergence angle in (mrad). The misalignment error is another parameter of fading in LoS optical communications. In the FSO communication link, the pointing accuracy is considered a crucial factor for the system performance and reliability.

In our applications, wind and wave loads are the dominant weight at the pointing error. The pointing error fading coefficient can be written as Farid and Hranilovic (2007)

$$ h_{P} = A_{0} \exp \left( { - \frac{{2a_{r}^{2} }}{{\omega_{zeq}^{2} }}} \right) $$
(3)

where \({a}_{r}\) denotes the random radial displacement for the received beam and \({A}_{0}\) is the fraction of the collected power at the displacement randomness of \({a}_{r}=\pi {r}^{2}=0\). The displacement of randomness, \({a}_{r}\), depends on the vertical and horizontal movements of the received beam and the beam width is represented by \({\omega }_{zeq}\) The radial displacement can be modeled as (Abaza et al. 2016)

$$ f_{{a_{r} }} \left( {a_{r} } \right) = \frac{{a_{r} }}{{\sigma_{s}^{2} }}exp\left( { - \frac{{a_{r} }}{{2\sigma_{s}^{2} }}} \right) \cdot a_{r} > 0 $$
(4)

where \({\sigma }_{s}^{2}\) is the jitter variance at the receiver.

The probability density function, PDF, with log-normal channels is given by Farid (2007)

$$ f_{h} \left( h \right) = \frac{{\xi^{2} h^{{\left( {\xi^{2} - 1} \right)}} }}{{2\left( {A_{0} \beta } \right)^{{\xi^{2} }} }} \times {\text{erfc}}\left( {\frac{{ln\left( {\frac{h}{{A_{0} \beta }}} \right) + q}}{{\sqrt {8\sigma_{x} } }}} \right)\exp \left( {2\sigma_{x}^{2} \xi^{2} \left( {1 + \xi^{2} } \right)} \right) $$
(5)

where erfc(·) represents the error function, \(\beta \) is the normalized path loss coefficient, where \(\beta = {h}_{\beta }/{\beta }_{h}\) and \({\beta }_{h}\) is the path loss for the SM1, \(q\) = \(2{\sigma }_{x}^{2}\) (1 + 2 \({\xi }^{2}\)). At the receiver, \(\xi \) is the ratio between the equivalent beam width and the pointing error displacement standard deviation and \( \xi = \omega _{{zeq}}^{2} /2\sigma _{s}^{2} .\)

Back to (1), \({h}_{a}\) is the channel fading coefficient, where \({h}_{a }=\mathrm{exp}(2x)\) and \(x\) is identically and independently distributed Gaussian random variable with a mean \({\mu }_{x}\) and a variance \({\sigma }_{x}^{2}\). The fading coefficients are normalized to ensure that the channel fading does not amplify or attenuate the average power Abaza et al. (2015). Hence, based on Rytov theory, a plane wave propagation is assumed and the log-amplitude variance is calculated as a function of the distance (Ali et al. 2019)

$$ \sigma_{x}^{2} = 0.30545 k_{f}^{{{\raise0.7ex\hbox{$7$} \!\mathord{\left/ {\vphantom {7 {6 }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${6 }$}}}} C_{n}^{2} l^{{{\raise0.7ex\hbox{${11}$} \!\mathord{\left/ {\vphantom {{11} {6 }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${6 }$}}}} $$
(6)

where \({k}_{f}\) = \(2\pi /{\lambda }_{f}\) is the wave number, \({\lambda }_{f}\) is the FSO wavelength and \({C}_{n}^{2}\) is the refractive index constant.

2.2 SM2- Fiber Optic Cable (FOC) intermediate link

We used the optimized wide array for such water applications. An optical fiber delivers enhanced macro bending performance and neglected the effect of the waves vibration while maintaining compatibility with linked between both upper sea receiver and underwater transmitter for the floating body or may big boat. Our usage fiber optic recommendation is ITU-T G.657A2/B2 with maximum attenuation at wavelength 1550 nm is less than or equal 0.20 dB/km, The maximum induced attenuation due to fiber wrapped inside mandrel for a specified radius will not exceed 0.4 dB at wavelength 1550 nm. This is expected to use two wrapped at both transmitter and receiver for mechanical purpose at the floating relay with total attenuation of 0.8 dB. Also, two water proof connectors are used at the fiber optic link, which has an average loss of 0.5 dB. The best low-reflectance connector is the angle-polished connector (APC). The APC connectors specify reflectance of -65 dB or better. The low-reflectance connectors are important throughout the system and not strictly for the front end. The front-end connector, however, does not isolate strong reflections from other reflective components. It simply does not contribute a significant reflected signal itself. Hence, our maximum attenuation in the fiber optic link is 1.5 dB, while the polarization mode dispersion (PMD) is neglected for such communication length and (1) can be written adding the \({h}_{foc}\) effect as

$$ h_{FSO - Fo} = h_{foc} h_{a } h_{p} h_{\beta } $$
(7)

where \({h}_{FSO-Fo}\) represents the channel power gain for SM1 and SM2 and \({h}_{foc}\) is the channel fading coefficients due to FOC intermediate link.

The SNR at the relay can be expressed as Ali et al. (2019)

$$ \gamma_{Fso - FO} = \frac{{P_{so} \eta_{1}^{2} r_{1}^{2} h_{Fso - Fo}^{2} }}{{\sigma_{rn}^{2} }} $$
(8)

where \({P}_{so}\) is the power transmission signal of the on-shore base station, \({\eta }_{1}\) the electrical to optical conversion efficiency, \({r}_{1}\) is photodetector responsivity overwater and \({\sigma }_{rn}^{2}\) is the noise variance of the AWGN.

2.3 SM3-FSS to AUV/SS (Relay to Destination) communication UOWC link

We submit a static channel on assumption that both FSS and SS are symmetrically aligned. We consider a MISO communication system with underwater optical wireless using hybrid modulation pulse position modulation and spatial modulation (UOWC-MISO-SM-PMP) compared with (UOWC-MISO-RC-PMP). All possible combinations scheme for each symbol is tabulated in Table 1.

Table 1 SM-PMP possible symbol combinations scheme
Full size table

We assume that underwater system with \({N}_{T}\) transmitters (\({N}_{T}\) = 4) and \({N}_{R}\) receivers (\({N}_{R}\)=1) as an optical MISO system. The signals consist of a series of zeros and ones and are divided into a series of symbols. Each symbol has 4 bits \({N}_{N}\)= \({N}_{S}\)+ \({N}_{P}\) bits. The first \({N}_{S}\) bits are modulated to a given symbol duration for the only one active transmission sources (TXs), while the other TXs will be idle. The second \({N}_{P}\) bits are modulated to a given L-PPM signal pattern, where \(L\) denotes the number of time chips (slots) in a symbol duration. A total of \(M= {log}_{2}({N}_{T}L)\) bits is transmitted per data symbol. The SM-PPM encoding is illustrated in Fig. 3 for the case of \({N}_{T}\) = 4 and \(L\)= 4.

Fig. 3
figure 3

An illustration of the encoding mechanism of an optical SM technique to transmit the symbol 15 which has instance

Full size image

For instance, to transmit the symbol 15 which has a binary representation as 1110 where the first two most significant bits, 11 are used to select \({TX}_{4}\), while the last two bits 10 indicate that the pulse will be transmitted in the third time slot of the four-PPM pulse pattern. Therefore, the average optical power received signals \({P}_{r}\) is represented as (Liu et al. 2015; Zeng et al. 2016; Arnon and Kedar 2009)

$$ P_{r} = r.P_{t} {*}C\left( \lambda \right)\cdot{ }f\left( I \right) + N $$
(9)

where \({P}_{t}\) is the transmitted power of the active \({N}_{T}\) transmitter light source, \(r\) represents the receiver photodetector responsivity underwater. Here, we assume \(r\) = 1. \(N\) represents the additive white Gaussian noise (AWGN) with zero mean and variance\({\sigma }^{2}={N}_{0}/2\), where \({N}_{0}\) is the noise power spectral density. \(C\left(\lambda \right)\) is the salty water attenuation coefficient (also called the extinction coefficient), which is defined as the sum of absorption \(a\) and scattering \(b\) as (10) (Zeng et al. 2016), (11) (Liu et al. 2015) and (12) (Zeng et al. 2016), \(f\left(I\right)\) is the normalized channel fading, which satisfies a certain PDF under the influence of weak water turbulence.

2.4 VLC underwater attenuation model

At VLC link, the path loss is the attenuation coefficient \(C\left(\lambda \right)\), which is the summation of the two dominant factor absorption \(a\left(\lambda \right)\) and scattering \(b\left(\lambda \right)\) of photons underwater. Thus, the underwater extinction coefficient can be expressed as Zeng et al. (2016)

$$ C(\lambda ) = a(\lambda ) + b(\lambda ) $$
(10)

Both absorption and scattering are wavelength-dependent.

The values of \(a\left(\lambda \right)\) and \(b\left(\lambda \right)\) in different types of water medium are given in Table 2 (Hanson and Radic 2008). Thus, by considering Eq. (10), the pathloss of the underwater VLC link can be expressed as (Mobley et al. 1993)

$$ h_{l} = e^{C\left( \lambda \right)D} $$
(11)
Table 2 Absorption, scattering and attenuation coefficients in different water mediums (Hanson and Radic 2008)
Full size table

where \(D\) is the vertical LOS distance between relay buoy and the underwater destination.

2.5 Underwater VLC turbulence channel model

The UWOC system performance is also affected by channel fading due to the oceanic turbulence which is similar to the atmospheric optical turbulence (AOT) in FSO communication (Andrews et al. 2005; Khalighi et al. 2009). Underwater optical turbulence (UOT) is generally due to variations of water refractive index, which is caused by the changes of pressure, temperature, and salt concentrations (Simpson et al. 2009). UOT was neglected in most practical cases as shown in [21]. According to (Zeng et al. 2016), variations at temperature are usually very small in addition to the approximately constant level of salinity are generally on the deep seas. According to the theory of AOT (Hou Kedar), the spectrum density of UOT, following the classical Kolmogorov spectrum model of AOT, can be expressed as (Hou 2009),

$$ \Phi_{n}^{K} \left( k \right) = K_{3} k^{{{\raise0.7ex\hbox{${ - 11}$} \!\mathord{\left/ {\vphantom {{ - 11} 3}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$3$}}}} $$
(12)

where \(\Phi \) is the spectrum density of UOT, \({K}_{3}= \chi {\varepsilon }^{-1/3}\) as (\({\varvec{\chi}}\) is the gradient of temperature strength while ε is the dissipation rate for the kinetic energy) is considered constant that determines the turbulence strength which is similar to \({C}_{n}^{2}\) in AOT (Andrews et al. 2005). \({K}_{3}\) is several orders larger than \({C}_{n}^{2}\) as its range is from \({10}^{-14}\) to \({10}^{-8}\) m−2/3 (Bogucki et al. 2007). Generally, the light intensity received by random fluctuation due to the optical turbulence is quantitatively represented by the scintillation index and PDF. Three PDF models are adopted commonly, namely; K-distribution, lognormal distribution, and Gamma–Gamma (GG) distribution (Andrews and Philips 2001). For weak turbulence, the former two models are suitable while from weak to strong turbulence the latter is applied. At UOWC practical applications, the front end of a detector at each side will be behind a optical lens with aperture dimensions larger than transversal coherent length (\({\rho }_{0}\)). Also, with multiple light sources, separation should be larger than the transversal coherent length \({\rho }_{0}\). Under this condition, the fluctuation of received light will be remarkably weakened. At AOT, much numbers of field experiments have shown that, the PDF of the received light intensity can be represented by the log-normal distribution function even for strong turbulence conditions with considering the aperture averaging effect (Huang et al. 2018). Analogously, the PDF, \(f(I)\), for the UOT channel can also be expressed as the lognormal function (Liu et al. 2015).

$$ f\left( I \right) = \frac{1}{{I\sigma_{s} \sqrt {2\pi } }}\exp \left( { - \frac{{\left( {ln\left( {{\raise0.7ex\hbox{$I$} \!\mathord{\left/ {\vphantom {I {I_{0} }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${I_{0} }$}}} \right) - \mu } \right)^{2} }}{{2\sigma_{s}^{2} }}} \right) $$
(13)

where \({I}_{0}\) is the mean for the received light intensity, while μ is the mean for the logarithmic light intensity, and \({{\sigma }_{s}}^{2}\) is the scintillation index defined by (Liu et al. 2015).

$$ \sigma_{s}^{2} = { }\frac{{\left\langle {I^{2} } \right\rangle - \left\langle I \right\rangle^{2} }}{{\left\langle I \right\rangle^{2} }}{ } $$
(14)

where \(\langle \rangle \) is the mean operation.

By normalization, (4) tends to,

$$ \mu = {\raise0.7ex\hbox{${ - \sigma_{s}^{2} }$} \!\mathord{\left/ {\vphantom {{ - \sigma_{s}^{2} } {2{ }}}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${2{ }}$}} $$
(15)

Finally, the scintillation index can be expressed as (Morsy and Alsayyar 2020a, b).

$$ \sigma_{s}^{2} = \exp \left[ {\frac{{0.49\sigma_{r}^{2} }}{{\left( {1 + 1.11\sigma_{r}^{{{\raise0.7ex\hbox{${12}$} \!\mathord{\left/ {\vphantom {{12} 5}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$5$}}}} } \right)^{{{\raise0.7ex\hbox{$7$} \!\mathord{\left/ {\vphantom {7 6}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$6$}}}} }} + \frac{{0.51\sigma_{r}^{2} }}{{\left( {1 + 0.69\sigma_{r}^{{{\raise0.7ex\hbox{${12}$} \!\mathord{\left/ {\vphantom {{12} 5}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$5$}}}} } \right)^{{{\raise0.7ex\hbox{$5$} \!\mathord{\left/ {\vphantom {5 6}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$6$}}}} }}} \right] - 1 $$
(16)

where \({\sigma }_{r}^{2}\) is the Rytov variance.

Based on the traditional theory at FSO at the AOT, (6), with combination the UOT spectrum model defined by (3), can be expressed as (Andrews and Philips 2001).

$$ \sigma_{r}^{2} = 37.3K_{3} \left( {\frac{2\pi }{{\lambda_{u} }}} \right)^{{{\raise0.7ex\hbox{$7$} \!\mathord{\left/ {\vphantom {7 6}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$6$}}}} D^{{{\raise0.7ex\hbox{${11}$} \!\mathord{\left/ {\vphantom {{11} 6}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$6$}}}} $$
(17)

where \({\lambda }_{u}\) is the underwater wavelength and \(D\) is the length of light beam migration.

In this work, we neglected the salinity because it is generally has constant level on the deep seas as (Ali et al. 2019; Liu et al. 2015; Zeng et al. 2016).

3 BER performance at the destination

In the three proposed system models SM1, SM2, and SM3 over the different channel conditions at each receiver side, we assume ideal time synchronization and perfect knowledge of the channel statement. Therefore, we use the \({ABER}_{FSO-FO}\) the receiving node over SM1 and SM2 over the log-normal channel and thin fiber optic channel as derived in Abaza et al. (2016)

$$ ABER_{FSO - FO} \approx { }\frac{d}{2\sqrt \pi }\mathop \sum \limits_{i = 1}^{S} \frac{{\omega_{i} }}{2}exp\left( {\xi^{2} \overline{\psi } - s\sigma_{x}^{2} \xi^{4} } \right){\text{erfc}}\left( {\frac{{\overline{\psi }}}{{\sqrt 8 { }\sigma_{x} }}} \right) + { }\frac{d}{2\sqrt \pi }\mathop \sum \limits_{i = 1}^{S} \frac{{\omega_{i} }}{2}erfc\left( {\frac{{4\sigma_{x}^{2} \xi^{2} - \overline{\psi }}}{{\sqrt 8 { }\sigma_{x} }}} \right) \approx \frac{d}{2\sqrt \pi }\mathop \sum \limits_{i = 1}^{S} \omega_{i} I_{H} $$
(18)

where \(S\) is the order of the approximation, \({\omega }_{i}\) is the weights of the generalized Laguerre polynomial, and \(\overline{\psi }\) is given by Abaza et al. (2016)\(\overline{\psi }=ln\left(\frac{\sqrt{2{x}_{i}}}{{A}_{0}{\beta }_{hf}\sqrt{\overline{\gamma }c}}\right)+2{\sigma }_{x}^{2}\left(1+2{\xi }^{2}\right),\) \(H \in \left\{\mathrm{1,2}\right\}\) and

$$ I_{H} = { }\frac{1}{2}\left[ {exp\left( {\xi^{2} \overline{\psi } - 2\sigma_{x}^{2} \xi^{4} } \right)erfc\left( {\frac{{\overline{\psi }}}{{\sqrt 8 { }\sigma_{x} }}} \right) + erfc{ }\left( {\frac{{4\sigma_{x}^{2} \xi^{2} - \overline{\psi }}}{{\sqrt 8 { }\sigma_{x} }}} \right)} \right] $$
(19)

We use the \({ABER}_{UOWC}\) at the receiving node for SM3 over the log-normal distribution with assuming weak turbulence condition. Hence, for PDF, \(f(I)\) can be used and the average BER of SM-PPM-MISO system can be approximated by the union bound method as (Huang et al. 2018)

$$ ABER_{UOWC} \le { }\frac{1}{{LN_{T} log_{2} \left( {LN_{T} } \right)}} $$
$$ \mathop \sum \limits_{{m^{\left( 1 \right)} = 1}}^{L} \mathop \sum \limits_{{n_{t}^{\left( 1 \right)} = 1}}^{{N_{T} }} \mathop \sum \limits_{{m^{\left( 2 \right)} = 1}}^{L} \mathop \sum \limits_{{n_{t}^{\left( 2 \right)} = 1}}^{{N_{T} }} { }d_{H} \left( {b_{{m^{\left( 1 \right)} n_{t}^{\left( 1 \right)} }} .b_{{m^{\left( 2 \right)} n_{t}^{\left( 2 \right)} }} } \right). $$
$$ Q\left( {\sqrt {\frac{{r^{2} T_{s} }}{{4N_{0} N_{{R^{2} }} }}\mathop \sum \limits_{n = 1}^{{N_{R} }} \left| {I_{{m^{\left( 2 \right)} }}^{SM} \times h_{{nn_{t}^{\left( 2 \right)} }} - { }I_{{m^{\left( 1 \right)} }}^{SM} \times h_{{nn_{t}^{\left( 1 \right)} }} } \right|^{2} } } \right) $$
(20)

where \(Q\left(x\right)= \sqrt{2\pi } {\int }_{x}^{\infty }{e}^{-t^{2}/2} dt .\) It denotes the probability that receiver mistakes intensity \({I}_{{m}^{(1)}}^{SM}\) being transmitted by transmitter \({n}_{t}^{(1)}\) for intensity \({I}_{{m}^{(2)}}^{SM}\) being transmitted by transmitter \({n}_{t}^{(2)}. {b}_{{m}^{(1)}{n}_{t}^{(1)}}\) is the bit assignment which is encoded when intensity \({I}_{{m}^{(1)}}^{SM}\) is emitted by transmitter\({n}_{t}^{(1)}\), \({b}_{{m}^{(2)}{n}_{t}^{(2)}}\) is the bit assignment which is encoded when intensity \({I}_{{m}^{(2)}}^{SM}\) is emitted by transmitter \({n}_{t}^{(2)}\) and \({d}_{H}\left({b}_{{m}^{(1)}{n}_{t}^{(1)}}.{b}_{{m}^{(2)}{n}_{t}^{(2)}}\right)\) is the number of error bits when erroneously decoding the bit sequence \({b}_{{m}^{(2)}{n}_{t}^{(2)}}\) at the receiver instead of the actually transmitted sequence\({b}_{{m}^{(1)}{n}_{t}^{(1)}}\).

For a dual-hop system, an approximated BER, ABER, can be calculated by Morgado et al. (2010)

$$ {\text{ABER}} \approx { }\frac{1}{2}\left[ {\begin{array}{*{20}c} {1 - (\left( {1 - 2{ }ABER_{FSO - FO} } \right).} \\ {\left( {1 - 2{ }ABER_{UOWC} } \right))} \\ \end{array} } \right] $$
(21)

4 Results and discussion

In the analysis, the BER performance of SPPM and RC is compared with respect to the SNR in the form of \({E}_{b}\)/\({N}_{0}\). Different scenarios over log-normal channels are cascaded in our two transmission media while considering similar spectral efficiency for fair compared systems. We adopt Monte Carlo approach for simulation.

For S-PPM,

$$ \eta_{spec} = \frac{1}{L}log_{2} \left( {N_{T} L} \right) {\text{bits}}/{\text{s}}/{\text{Hz}} $$
(22)

where \(L=16\).

For PPM and RC,

$$ \eta_{spec} = \frac{1}{L}log_{2} \left( L \right){\text{ bits}}/{\text{s}}/{\text{Hz}} $$
(23)

where \(L=2\) which is similar to OOK modulation. The simulation results of the average BER in terms of the average SNR for different hybrid modulation techniques are illustrated displayed in Fig. 4, where \({K}_{3}= {10}^{-14}\) \({\mathrm{m}}^{-2/ 3}\).

Fig. 4
figure 4

Average BER versus average SNR for RC and SM

Full size image

We use same UOT model (Liu et al. 2015) which success to achive an effective communication range of more than 70 m in a strong UOT channel, using the Single Input Multiple Outputs (SIMO) system with LED with 1 W, which indicates promising applications in LED-based UOWC. While (Zhai et al. 2021) reached to FSO communication system with a transmission distance up to 3.9 km using our same similar system conditions as the laser wavelength 1550 nm with a SISO log-normal channel. To achieve an equal BER, the required average SNR for the RC-MISO system can be remarkably reduced compared with that for the OOK-SISO and SM-PPM systems. The obtained results show that RC achieved the target BER \({10}^{-6}\) at SNR = 22.8 dB. However, the SM-PPM and OOK-SISO failed to achieve the target for propagation distance 1000 m and 100 m for FSO and UOWC, respectively.

With the wavelength = 530 nm, using the maximum likelihood detection, and to validate the error performance analysis, we carry out the system simulation described in Section III. The BER as a function of SNR for both the simulation and theoretical analysis is compared in Fig. 4. It is observed that, in the region where the BER is less than \({10}^{-5}\), which is the region where any sufficient communication can be established, there exists an excellent agreement between the simulation and the theory. The slight deviation starts with lower BER.

Figure 5 illustrates the performance results of the average BER in terms of the average SNR for different turbulence strengths, where \({K}_{3}= {10}^{-8}\) \( {\text{m}}^{{ - 2/3}} \) to \({K}_{3}= {10}^{-14} {\text{m}}^{{ - 2/3}} \).

Fig. 5
figure 5

Contrasting BER performance of different turbulence strengths

Full size image

As expected, it can be noted from Fig. 5 that the turbulence levels are leading to a performance degradation. For instance, the obtained results show that MISO-RC at UOT \({K}_{3}= {10}^{-14}\) \( {\text{m}}^{{ - 2/3}} \) achieves the target BER \({10}^{-6}\) at SNR = 16.7 dB.

While MISO-RC at UOT \({K}_{3}= {10}^{-12}\) \( {\text{m}}^{{ - 2/3}}\) and SISO-OOK at UOT \({K}_{3}= {10}^{-14}\) \( {\text{m}}^{{ - 2/3}} \) are slight similar and achieves the target BER \({10}^{-6}\) at SNR = 22.7 dB. However, the SISO-OOK at UOT \({K}_{3}= {10}^{-8}\) \( {\text{m}}^{{ - 2/3}} \) and MISO-SM at all represented turbulence values failed to achieve the target.

Furthermore, the performance of MISO systems using RC and SM with \({N}_{T}\)= 4 is shown in Fig. 6. The performance of SISO employing OOK modulation is compared using commercially available fiber optic types ITU-T G.652D and ITU.G657A2/B2 with considering both traditional and low insertion loss connector. It is clear that, the enhanced fiber optic and fiber optic connector outperforms the traditional solutions at BER = \({10}^{-6}\) by 7 dB for SNR at MSIO-RC-PPM. Also at the same SNR.

Fig. 6
figure 6

Traditional vs. Enhancement FO link and FO connector impact

Full size image

A slight effect for the BER is noticed at the two fiber optic solutions at MISO-SM-PPM and SISO-OOK at underwater region. This demonstrates the role of the total link attenuation gradient in introducing severe or slight BER effect according to the type of modulations.

Figure 7 presents the results of the average BER versus average SNR for RC with varying propagation distance of light in water with moderate UOT \({K}_{3}= {10}^{-13}\) \( {\text{m}}^{{ - 2/3}} \). If we set the threshold BER to be\({10}^{-6}\), the effective communication range for the MISO-RC system can reach to 100 m at SNR = 22 dB.

Fig. 7
figure 7

Average BER versus average SNR for RC under different communication range

Full size image

Figure 8 displays the SNR for RC versus at varying propagation distances of the FSO link from 100 m to 1 km at the intermediate UOWC link for 50 m depth of light in water with moderate UOT \({K}_{3}= {10}^{-13}\) \( {\text{m}}^{{ - 2/3}} \). The effective communication link for the SISO-OOK-FSO/MISO-RC-UOWC system can reach to 50 m UOWC depth and 1000 m FSO link distance at SNR = 24.5 dB while SNR = 19.5 dB is in the middle of the FSO link at 500 m for the same UOWC depth.

Fig. 8
figure 8

FSO link distance versus SNR

Full size image

The error vector magnitude (EVM) is a new important metric for measuring the quality of the optical signal with BER and throughput performances (Morsy and Aly 2021). On the other hand, EVM is a measure of errors between the measured symbols and expected symbols (Shafik et al. 2006). The EVM of the detected signal can be calculated as (Zhang et al. 2021)

$$ EVM = \sqrt {\frac{1}{{N*max_{{j \left| {\widehat{{x_{j} }}} \right|^{2} }} }}. \mathop \sum \limits_{i = 1}^{N} \left| {x_{j} - \widehat{{x_{j} }}} \right|^{2} } \times 100\% $$
(24)

where \({{\varvec{x}}}_{{\varvec{j}}}\) and \(\widehat{{{\varvec{x}}}_{{\varvec{j}}}}\) are the transmitted and recovered data symbols respectevaly, and \({\varvec{N}}\) denotes the total number of detected symbols.

In order to establish a relationship between BER, SNR and EVM (Shafik et al. 2006) expressed it in terms of EVM as

$$ SNR \approx \frac{1}{{EVM^{2} }} $$
(25)

Figure 9 shows the inverse relationship that exists between BER and EVM at our optimum link MISO-RC with power term in log scale shown.

Fig. 9
figure 9

EVM% versus the BER for MISO-RC

Full size image

Finally, the performance comparison of different UOWC combining schemes with different turbulence strengths are summarized in Table 3.

Table 3 Performance comparison at different UOWC combining schemes and different turbulence strengths
Full size table

5 Conclusion and future directions

In this paper, the average BER performance of triple underwater hybrid system FSO, FO, and UOWC links with spatial diversity, PPM and RC is investigated over log-normal channels for both absorption, scattering for weak turbulence channel, with a statistical MC method for simulation. SM-MISO and RC techniques are considered. The obtained results are in favor of RC underwater links for same spectral efficiency applications and/or channel different turbulence effects, and the SM-PPM and OOK-SISO failed to achieve the target for propagation distance 100 m at UOWC. Our simulation results reveal that superiority systems as compared to their counterparts in terms of ABER. Moreover, our numerical results demonstrate that multiple transmitter apertures with PPM-RC enhances the quality of UOWC systems. At \({K}_{3}= {10}^{-14}\) \( {\text{m}}^{{ - 2/3}} \), and in comparison with the OOK-SISO scheme, a performance improvement of 6 dB is obtained at a BEP of \({10}^{-6}\) by using four transmit apertures in the MISO scheme. While at \({K}_{3}= {10}^{-12}\) \( {\text{m}}^{{ - 2/3}} \), a performance improvement of 10 dB is obtained at a BEP of \({10}^{-5}\) in a favor of MISO-PPM-RC. However, a bend insensitive FOC intermediate link reduces the SNR more than 7 dB at the target BER of \({10}^{-6}\) with MISO-PPM-RC scheme. We achieved an effective communication range of more than 100 m at UOWC system in a moderate UOT channel with SNR = 22 dB.

A future research should concentrate on underwater optical channel implementation in practical situations, such as deep ocean deployment with studing real system capacity. Also, tracking and positioning systems is to be considered that has been looked for issues with misalignment and pointing loss.