1 Introduction

The Brazilian Amazon is located in a tropical region on the planet, where mainly in the summer, intense rains occur. As a result, several areas suffer from floods and ebbs every year, especially cities located on the banks of rivers (Mansur et al. 2016, 2018). A high rainfall and high tides significantly contribute to the risk of flooding (Birkett et al. 2002). When there are floods at a high rainfall level, approximately 90% of the cities are submerged, causing great material damage and risks of transmission of diseases such as, Leptospirosis, Cholera and Hepatitis A. According to de Andrade and Szlafsztein, in the state of Pará many disasters were recorded between 1991 and 2010, several cities were hit by floods, affecting many families, agriculture and livestock (de Andrade and Szlafsztein 2015).

To avoid this type of scourge, it is necessary to develop a system to monitor the floods of rivers in areas that suffer from floods, which would contribute to the actions of the fire brigade, civil defense and alert the inhabitants of these risk areas.

In the literature it is possible to find some works that demonstrate flood monitoring systems that use FBGs sensors, as in Kuang et al., that built a system that remotely performed flood monitoring, the results were quite significant, but were performed with a vat of waves, away from a real environment (Kuang et al. 2008). In Ameen et al., they built a sensor, whose main element was a FBG coupled to a graphene diaphragm in order to measure temperature and water level simultaneously, the scheme showed good sensitivity results, but the tests were done by varying the water level from 0 to 1.0 m deep (Ameen et al. 2016). In Schenato et al., describe the implementation of a FBG sensor to measure water levels in a dike and it is based on a 3D printed mechanical transducer, where the external pressure is converted into longitudinal strain exerted on the fiber, another FBG integrated in the sensor measures the temperature and is used to compensate for the effects of temperature on the first FBG (Schenato et al. 2021). In Leal-Junior et al., they reported on the development of a temperature-insensitive pressure sensor based on a pair of Fiber Bragg Grating (FBGs) embedded in a polyurethane diaphragm. The sensor was tested for temperature, pressure and moisture absorption and showed high sensitivity and linearity for all analyzed cases, leading to a good pressure resolution for constant temperature conditions (Leal-Junior et al. 2020). In Schenato et al., they described a Fiber Bragg Grating (FBG) pressure sensor with high sensitivity. The sensor is a 3D printed mechanical transducer capable of converting external pressure very efficiently into strain, measured by a first FBG, while a second FBG is used for temperature compensation (Schenato et al. 2019). In Vorathin et al., the work reviewed recent methods of increasing pressure sensitivity among them with polymer FBGs, special fiber sensors, interferometric sensors and special grid sensors (Vorathin et al. 2020).

In addition to these works, some others were built for the purpose of just measuring the level of water, oil, etc. (Song et al., 2011; Sengupta and Kishore 2014; Marques et al., 2015; Sohn and Shim 2009; Li et al. 2016).

In this work, we propose a sensor that is capable of simultaneously measuring the variation in the level and the temperature of the waters of rivers in the Amazon at a limit depth of 3.95 m. FBGs sensors have intrinsic sensitivity to strain and temperature, so to obtain reliable results, temperature compensation must be performed (Wang et al 2006; Kumar and Chack 2018; Yucel, Ozturk and Gemci 2016; Zhou et al. 2008). The most suitable scheme is to use two FBGs, one to measure the strain and temperature and the other similar to the first to measure only the temperature, being used as a reference and free from any deformations (Tang and Wang 2006; Li et al. 2017; Meng et al. 2015).

The proposed sensor has a great potential for application, where it brings very interesting technological characteristics for the development of a monitoring scheme, such as its high sensitivity, high bandwidth with multiplexing features, where we can have several sensors monitoring different points of a same large city in real time and remotely, in addition to its immunity to chemicals dissolved in water, corrosion, radioactivity and electromagnetic interference (Koozekanani and Makouei 2017).

Due to the restrictions of the Covid-19 pandemic, it was not possible to physically build the device, but it was possible to perform numerical simulations using the OptiGrating and OptiSystem software, the first to parameterize and build the FBGs and the second to simulate the interrogation system. In this, we evaluate and analyze the efficiency of the sensors through variations in wavelengths simultaneously. In addition, we experimentally demonstrate the characterization of FBGs by simultaneously varying strain and temperature, with their sensitivities and graphic plot that delimit the maximum value of liquid level measurement by the sensors.

Thus, in this work we propose a sensor for monitoring the level and temperature of the rivers in the Amazon, with the main elements of the Bragg grating, with the objective of exploring this type of system in highly occurring environments and detecting flood risks.

2 Fundamental theory

2.1 Theory of FBG sensors

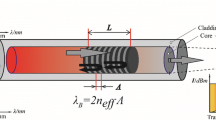
When there is a periodic variation in the refractive index along the core of a photosensitive optical fiber, which was inscribed by exposure to an intensity pattern of ultra-violet radiation, we have what we call FBG, Fig. 1.

Fig. 1
figure 1

Scheme of a uniform Bragg network with constant amplitude and modulation period. The incident, diffracted and grid wave spectra are shown as well

Full size image

Its main function is to select or reflect a narrow band from a broadband source that is coupled to an optical fiber, this is due to a special condition of propagation of modes in the fiber, known as the Bragg condition and is represented mathematically by (Othonos 1997):

$$\lambda_{B} = 2n_{{{\text{eff}}}} \Lambda$$
(1)

where Λ and neff the grating period and the effective refractive index in the fiber respectively.

Any change in the effective refractive index of the fiber, grating period or both, there is a variation in the Bragg wavelength, it is on this fact that the FBG sensors are based. In this way, any physical effect external to the fiber, such as deformation, temperature, pressure, tension, etc., that changes the fiber's refractive index or grating period can be revealed by an FBG, measuring the variation of the Bragg wavelength (Kreuzer 2006).

There is a very popular expression in the literature that relates the variation in Bragg wavelength to the physical parameters of strain με and temperature ΔT, such equation is described by (Othonos 1997; Kreuzer 2006; de Sousa et al. 2019):

$$\frac{{\Delta \lambda_{B} }}{{\lambda_{B} }} = (1 - p_{e} )\varepsilon + (\alpha_{n} + \alpha_{\Lambda } )\Delta T$$
(2)

where the first term of the second member of the Eq. (2) represents the deformation resulting from the applied force on the grating, \(p_{e} = (n_{{{\text{eff}}}}^{2} /2)[p_{11} - \nu (p_{11} + p_{12} )]\) is the effective photoelastic constant, ν is the Poisson's ratio,\(p_{11}\),\(p_{12}\) are the components of the tensor photoelastic. The second term describes the effect of temperature on the FBG, with \(\alpha_{n} = (1/n_{eff} )(\partial n_{eff} /\partial T)\), being the thermo-optical coefficient and \(\alpha_{\Lambda } = (1/\Lambda )(\partial \Lambda /\partial T)\), being the thermal expansion coefficient.

The Eq. (2) expresses the variation in wavelength as a function of strain and temperature, so we cannot guarantee whether the change in wavelength was due to deformation, temperature or both. To overcome this difficulty, we consider two FBGs on the same fiber, from which we will extract two different wavelengths, one with information on strain and temperature and the other only on temperature for compensation, thus, from Eq. (2) and some mathematical manipulations, the deformation of the FBG1 from the variation of its wavelength compensated by the temperature variation of the variation of the wavelength of the FBG2 can be written as (Oliveira et al. 2020):

$$\varepsilon = \frac{1}{{(1 - p_{e} )}}\left\{ {\frac{{\Delta \lambda_{B1} }}{{\lambda_{B1} }} - (\alpha_{n} + \alpha_{\Lambda } )\Delta T} \right\}$$
(3)

The Eq. (4) informs us about the temperature variation of the sensor for compensation from the variation of the FBG2 wavelength.

$$\Delta T = \frac{{\Delta \lambda_{B2} }}{{\lambda_{B2} \,(\alpha_{n} + \alpha_{\Lambda } )}}$$
(4)

In the next section, we will relate the ε strain to the physical measurement.

2.2 Sensor design and operation principle

The sensor proposed in this work uses the buoyant force in the longitudinal direction of a metallic cylindrical bellows to produce the deformation in a fixed FBG at one of its ends, Fig. 2.

Fig. 2
figure 2

Sketch of the proposal of the FBG sensor with the metal bellows as the mechanical connection element

Full size image

Its structure is formed by a cylindrical bellows made of stainless steel, two FBGs that are surrounded by a special cylindrical capsule also made of stainless steel with threaded ends, whose height is 400 mm and diameter 25 mm. The bellows is used as a mechanical connection element and can transfer the pressure applied inside it to the FBG fixed at its upper end, point C. It has a pressure opening of 5 mm in diameter and an average internal diameter of 10 mm with a length of 300 mm and a wall thickness of 0.2 mm. The main advantages of the metal bellows for the proposed structure are its elastic capacity, as it can be compressed or expanded when pressure is applied at great depths, its ability not to absorb torsional movements greater than fatigue and its sealing, as it does not allows the entry or flow of water inside the device, therefore not affecting FBGs with water flow noises.

When the device is immersed in a river, as the depth increases, the metal bellows expands, with this we have the mechanical transmission of pressure to the FBG1. Thus, the light signal, which comes through A is reflected when finding the FBGs that have undergone expansion and temperature variation, C. These reflections return to the interrogation system with the responses of the variations in Bragg wavelengths, where there is a linear relationship with the pressure variation suffered by the metal bellows.

The bellows have an elastic behavior when pressure is applied, thus, we will treat it here as a spring of smaller elastic constant in its axial direction compared to the radial direction (Pachava et al. 2015). Based on the Poisson principle, the pressure in the longitudinal direction of the bellows produces an axial strain, on the other hand, a pressure in the radial direction produces a longitudinal compression. Thus, the axial expansion of the metal bellows obeys Hooke's law and with each increase in distension along the bellows, produced by the pressure resulting from the increased depth of the device, it will deform the optical fiber longitudinally, which can be detected by the FBG (Pachava et al. 2015).

It is known that the buoyant force is directly proportional to the volume of the metal bellows immersed in the river water. As the metal bellows has a straight circular section that remains unchanged, the volume depends only on the height of the metal bellows immersed in the water, so the buoyant force can be expressed by (de Almeida et al. 2019):

$$F_{E} = \rho gA\,\Delta h = k\Delta x$$
(5)

where ρ the density of river water, g the acceleration of gravity, A = 78.53 mm2 the area of straight section of the metal bellows, k = 39.27 N/mm the spring elastic constant, in the case here of the bellows metallic, Δx the variation in the length of the bellows or the optical fiber and finally, Δh the variation in the level of the metallic bellows immersed in the river water.

The longitudinal deformation suffered by the optical fiber is given by ε = Δx/x, where x is the length of the fiber, which is fixed at C and D (Antunes et al. 2012), the length between these points is 300 mm, ie, the fiber has the same length as the metal bellows, so we can relate the longitudinal strain to Eq. (5), and write (Pachava et al. 2015):

$$\varepsilon = \frac{\rho gA\Delta h}{{kx}}$$
(6)

Thus, disregarding the lateral distension effect of the metal bellows, replacing Eq. (4) in (3), and adding (6), we arrive at:

$$\Delta h = \frac{k\,x}{{(1 - p_{e} )\rho gA}}\left( {\frac{{\Delta \lambda_{B1} }}{{\lambda_{B1} }} - \frac{{\Delta \lambda_{B2} }}{{\lambda_{B2} }}} \right)$$
(7)

The Eq. (7) shows a linear relationship between the variation of the sensor level with the variations in the wavelengths of the FBG1 and FBG2.

According to de Oliveira et al., a bare silica optical fiber that has an FBG inscribed and produced with conventional techniques supports a maximum deformation of approximately 0.5% (Oliveira et al. 2020). Therefore, for this proposal, the maximum rupture deformation would be above 1.5 mm. A beater was placed in B to prevent such breakage of the optical fiber.

2.3 Simulation model

The FBGs sensors underwent a construction and simulation process for a series of strain and temperature values. The numerical simulations were carried out in two moments, the first, using the OptiGrating 4.2 software, which allowed the construction and characterization of Bragg grating and the second, the data were exported in text format to the OptiSystem 17.0 software, the which simulated the interrogation system.

The sensitivity of FBGs to strain and temperature at a wavelength of 1550 nm, based on Eq. (2) are: \(\Delta \lambda_{B}\)/ ε = 1.2 pm/ με and \(\Delta \lambda_{B} /\Delta T\, = 14.2\,\) pm/°C. For the sensitivity values, we consider the Germanium-doped silica optical fiber in the values of: the components of the photoelastic tensor \(p_{11} = 0.121\), \(p_{12} = 0.27\); Poisson's coefficient \(\nu = 0.17\); photoelastic constant \(p_{e} = 0.22\). The thermo-optical coefficients \(\alpha_{\Lambda } = 0.55 \times 10^{ - 6}\)/°C−1 and \(\alpha_{n} = 8.3 \times 10^{ - 6}\)/°C−1 for the wavelength of 1550 nm and 25 °C of reference, Table 1 shows the parameters of the FBGs.

Table 1 Simulation parameters in the FBGs
Full size table

The FBG1 was centered at the wavelength of 1553.400 nm, responsible for the measurements of strain and temperature and the FBG2 was centered at 1549.500 nm, dedicated to measuring only the temperature for compensation.

2.4 Experimental setup

The Fig. 3 shows the experimental scheme for the interrogation, with a Laser Diode Controller transmitter (Model 6100), which emits a 0 dBm power band with a central wavelength of 1550 nm and a bandwidth of 50 nm that illuminates the FBGs through of an optical circulator.

Fig. 3
figure 3

FBG interrogation scheme using a broadband source, circulator and Optical Spectrum Analyzers (OSA)

Full size image

The signal coming from the transmission system enters through port 1 of the circulator and through port 2 it reaches the sensors, in which, the signal reflections occur according to the strain and temperature suffered by the sensors. The two narrow bands then return through port 3 of the circulator to the Optical Spectrum Analyzer—OSA (MS9740A), thus obtaining the wavelength responses of the modulated signal.

The communication between port 2 and the sensors and the sensors to port 3 of the circulator are made by two Single-Mode optical Fiber (SMF) optical fibers, both 1 km long. The Table 2 illustrates the parameters of SMF fibers.

Table 2 Optical parameters fiber
Full size table

The FBG2 transmit port was connected to the FBG1 input port and its reflection ports return the signal over the fiber, which transmits it through the second SMF to the OSA through port 3 of the circulator.

The data obtained from the performance of the sensors are visualized and analyzed through the OSA in the range from 1547 to 1559 nm. The FBGs were separated by 3.9 nm at wavelengths to avoid overlap after independent measurements of strain and temperature (Anfinogentov et al. 2021).

The image of the experimental setup used in interrogating the FBG sensors with all devices is shown in Fig. 4, where, in order to characterize and evaluate the sensors, deformation and temperature variation tests were performed. The FBG1 sensor was placed on two supports on the bench, with one end fixed and the other mobile that has a micrometer in steps. This allowed us, through a software connected to the micrometer, in steps to vary the deformation of the FBG1 from 0 to 2500 . In a first moment, FBG2, free of any deformation, experienced the temperature variation by the heater, and in a second moment both sensors. The modulated signal with the spectra of the wavelength variations due to deformation changes by the micrometer in steps and the temperature variation by the heater are shown by the (OSA). In the scheme, the thermometer has a function only for monitoring the temperature variation within the limits discussed in this work.

Fig. 4
figure 4

Image of the experimental configuration of the interrogation system of the FBGs sensors

Full size image

The Bragg gratings can be easily manufactured with relatively low cost, since the fiber used is an SMF and the chirp and apodization parameters of the grating have values close to those already available on the market (Tahir et al. 2006; Hehr et al. 2018). Although a broadband LED source offers a less complex alternative and a lower cost per mW delivered to the system when compared to the use of a Superluminescent Laser Diodo (SLD) as used in this work (Kressel et al. 1980), but for the experimental tests, we used the light source (SLD1005S – 22 mW), since it has better coupling in SMF fibers and greater temperature sensitivity in relation to broadband LED. The laser diode controller used was the 6100 Laser Diode and Temperature Controller. In addition, the use of only one circulator and an OSA can enable application in a large area through a association of sensors (Abdi et al. 2007).

3 Results and discussion

According to Ilha et al. (Ilha et al. 2018) and Dias et al. (Silva Dias et al. 2004), the average temperature of streams, headwaters and rivers in the Amazon are between 24 °C and 32 °C. And according to da Silva Gregório and Mendes, the average depth of the rivers is between 5 to 25 m at low sea, with high tides turning around 3.6 m (da Silva Gregório and Mendes 2009). Thus, both the temperature and strain ranges were chosen according to the parameters presented in these works, then the results of the performance of the FBG sensors were determined within the values of 0 °C to 50 °C, and 0 and 2500 .

The reflection and transmission spectra of the FBGs for temperature and strain values, from the OptiGrating software are shown in Fig. 5 and Fig. 6. In Fig. 5, for a constant temperature of 25 °C we have a strain from 0 to 2500 με , with the orange line being the transmission spectrum and the blue and red lines being the reflection spectra.

Fig. 5
figure 5

Reflection response and transmission of the initial FBG1 structure in relation to the applied

Full size image
Fig. 6
figure 6

Reflection response and transmission of the initial structure of FBG2 in relation to temperature

Full size image

Still in Fig. 5, the transmission spectrum (orange line) represents the wavelengths of the light signal that did not undergo changes when passing through the periodic variations of the refractive index of the Bragg grating, that is, these wavelengths do not obey Bragg condition, so all are transmitted. On the other hand, the peaks (blue and red lines) represent the wavelengths that obey the Bragg condition, at these points of the spectrum both are reflected by the periodic variation of the refractive index of the fiber core. Another important aspect is the spacing between the peaks, which are presented in this way, because the optical fiber is sensitive to some physical parameters such as temperature and strain, that is, at a temperature of 25 °C and free from deformation, the reflected Bragg wavelength is represented by the blue peak, maintaining the temperature at 25 °C and with a deformation of 2500 με the reflected Bragg wavelength is represented by the red peak.

In Fig. 6, we have FBG2, with the green and red lines being the reflection spectra for temperatures from 25 °C to 50 °C and free of any strain. The transmission spectrum (orange line) of Fig. 6 has the same physical meaning as the transmission spectrum of Fig. 5, as well as the reflection spectra, here represented in green and red. On the other hand, the spacing between the peaks, which here appears very reduced, is mainly due to the sensitivity of the optical fiber to the physical temperature parameter (green and red peaks), that is, the fiber free of deformation and at a temperature of 25 °C, the reflected Bragg wavelength is represented by the green peak, keeping the fiber free of deformation at a temperature of 50 °C, the reflected Bragg wavelength is represented by the red peak, the spacing between the peaks is not so accentuated due to the low temperature variation experienced by the optical fiber.

From the interrogation system, built in the OptiSystem software, we evaluated the proposed setup, which shows the reflection spectra of the FBG1 and FBG2 sensors, Fig. 7(a). In Fig. 7(b) we have the reflection spectra of FBG1 and FBG2 obtained by the experimental setup. Subfigures 7(a) and 7(b) have been placed side by side to show that the simulated and experimental data have a great match. The peaks in the figures represent the reflection of the light signal when they encounter periodic changes in the refractive indices inscribed in the fiber optic core, these changes are called Bragg gratings.

Fig. 7
figure 7

Optical spectrum of FBG1 and FBG2 obtained in, a OSA from the OptiSystem simulation software and (b) OSA (MS9740A) from the experimental results for a temperature of 25 °C

Full size image

Analyzing the data, we obtain the linear responses of the two sensors when we vary the parameters of strain and temperature. In the simulations, when we change the temperature by 5 °C, we obtain a variation of the Bragg wavelength of 0.06 nm, the linearity achieved with the FBG2 sensor is of the order of (\({\text{R}}_{1}^{2}\) = 0.9999). On the other hand, varying the temperature by 5 °C, the experimental results obtained with the FBG2 sensor are (\({\text{R}}_{2}^{2}\) = 0.9989), showing a very good correspondence relationship with the simulation results, Fig. 8.

Fig. 8
figure 8

Variation in wavelength versus temperature variation for compensation

Full size image

The determination of the FBG1 sensor response is given by varying the deformation from 0 to 2500 με and with 200 με intervals, in this way, for the simulated data, the corresponding wavelengths of FBG1 are measured by the OSA in the order of 0.14 nm. Figure 9, shows the experimental results, where for a temperature of 25 °C and within the strain range, the wavelengths of FBG1 ranged from 1553.40 nm to 1556.39 nm. Thus, we verified that the FBG1 wavelengths have a linear behavior with deformation and the linearity obtained with the FBG1 sensor is relatively higher, as can be seen by the linear coefficient (R2 = 0.9999) of the simulated results compared to the linear coefficient of the results experimental (R2 = 0.9961). The difference between experimental and simulated results can be explained by the inadequate fixation of the FBGs to the input and output devices of the interrogation system and to the parameter values used in the simulations, as they may not be 100% accurate. Therefore, in strain and temperature measurements, the FBGs sensors demonstrated good level of linearity, the sensitivity for temperature is 12.7 pm/°C and for the strain is 1.3 pm/ με.

Fig. 9
figure 9

Shifting wavelength as a function of applied strain from 0 to 2500 εµ

Full size image

The Fig. 10 shows the experimental results of the FBG1 sensor responses when we simultaneously vary the deformation from 0 to 2500 με with intervals of 200 με and the temperature from 0 to 50 °C with intervals of 10 °C. These results show, within the strain and temperature range, the wavelengths of FBG1 ranging from 1553.09 nm to 1556.78 nm. Once again, we verify that the FBG1 wavelengths have a very good linear correspondence with the simulated results (R2 = 0.9999) within the studied temperature range as seen by the linear coefficients of the experimental results (R2 = 0.9956, R2 = 0.9959, R2 = 0.9959, R2 = 0.9960, R2 = 0.9961 and R2 = 0.9960). As described above, we believe that the small difference between the linear coefficients of the experimental data and the simulated data are due to inadequate connections between the different devices present in the interrogation system and the values based on the simulated data that may not be as accurate.

Fig. 10
figure 10

Wavelength variation as a function of the strain applied to FBG1 to various temperatures

Full size image

The \(\Delta \lambda_{{{\text{FBG}}1}}\) and \(\Delta \lambda_{{{\text{FBG}}2}}\) variation measures, when we simultaneously change the temperature and the deformation, can be visualized by the Δh variation plane, where it is possible to identify two planes, the first plane above, representing the simulated data and the second plane representing the experimental data, this one slightly below the foreground, Fig. 11.

Fig. 11
figure 11

3D graph showing the plane of level variation as a function of the variations in wavelengths of the FBG sensors

Full size image

The sensitivity parameters of the two sensors establish the inclination of the plane. In Fig. 11, we highlight three points, the first referring to the point of lowest temperature without any strain, the second point, still without strain, but with a temperature of 25 °C and the third and last point of highest temperature, with strain of 2500 με. In the third point, where the temperature is 50 °C and 2500 με, for the simulated data the measurement of the level variation is of the order of 4.0 m and for the experimental data it is approximately 3.95 m, an optimal correspondence between the simulated data and experimental data, but it is important to note that this correspondence will depend on the calibration and depth at which the sensor is placed. It is worth mentioning that the calibration can be performed at a maximum depth of 30 m.

The sensitivity obtained in relation to the level was 9.3 pm/cm for the simulated data and 9.2 pm/cm for the experimental data, with a maximum height of variation of the level in the order of 3.95 m. The sensitivity obtained is very good, considering the levels tested, as summarized in Table 3.

Table 3 Comparison of the sensitivity and level of the proposed pressure sensor between various pressure sensors available
Full size table

The comparative in terms of structure, the proposed sensor, if built, may be better than diaphragm based structure sensors. Note that the sensitivity obtained is great compared to other works in the literature, but for the type of application that we are proposing, a high sensitivity is not such a relevant factor, since variations in the order of centimeters at river level is not the basis of this manuscript. It is important to note that, since the sensor system is designed for practical measurement in real rivers, the sensitivity to environmental noise in the experimental results, such as nearby water flow, sensor inclination and/or the influence of oscillations can be relevant and induce false interpretations in the obtained spectra.

The detection of changes in temperature and variation in the level of rivers can be measured with great precision, since the parameters are very close due to the grids being built with the same material and for having one of the FBGs with temperature compensation function.

The measurement of Δh and ΔT can be determined simultaneously given values of the changes in wavelengths of FGB1 and FBG2, using Eqs. (4) and (7). Because the two FBGs were built to give different responses in terms of strain and temperatures, this setup has the ability to eliminate the high cross sensitivity that are already part of the nature of Bragg gratings.

4 Conclusions

This work presented an approach for monitoring the water level and temperature of rivers in the Amazon with the use of two fiber optic sensors with Bragg grating. The scheme includes two FBGs coupled to a metal bellows structure covered by a stainless steel cylinder, which is in line with the questions and variables that limit the measurements of liquid levels by sensors. In the proposal, without the physical construction of the device, we obtain answers through simulations and experimental demonstration of simultaneous measurements of temperature and strain for the FBG sensors, spacing the sensor wavelengths at 3.9 nm. The experimental results presented values very similar to the simulated results and to several proposals of conventional liquid level sensors, exhibiting a resolution of the order of 1.6 mm, in addition to presenting an excellent linearity in relation to temperature and strain. It is clear that the results are in accordance with the proposed structure, whether the sensors or the cylinder that will condition them, however, it was not possible to build the device, which would be essential to carry out the tests in loco, which at the moment is unfeasible due to quarantine conditions and health restrictions imposed by health agencies in the face of the Covid-19 pandemic. Thus, the proposed sensor has an enormous potential for applicability in monitoring the level of rivers, in regions of the Amazon that are frequently affected by floods.