1 Introduction

In the last decades, many projects of laser optical communications have been proposed for free space and deep space communications due to the significant advantages in comparison with classical radio frequency microwave links for space communications in terms of link performance, system size and achievable transmission bitrates. The near-Earth orbits include low Earth orbits (LEO, 100–2000 km), medium Earth orbits (MEO, 2000–36,000 km) and geostationary Earth orbits (GEO, some 36,000 km). Lunar orbits are between 350,000–410,000 km. Deep space or interplanetary links range from 0.5 AU–3 AU (1 AU ~ 150,000,000 km). Generally a distance larger than 0.01 AU, or approximately 1,500,000 km from Earth, is considered as deep space. Many projects of laser optical communications have been proposed due to the above-mentioned significant advantages in comparison with classical radio frequency microwave links for space communications. ESA and NASA have also conducted projects like ARTEMIS, lunar laser communication demonstration project LLCD, and have planned projects like DOCS L5, and deep space optical communication links within the PSYCHE mission (Hemmati et al. 2011; Sans et al. 2012; Sodnik et al. 2014, 2017; Sodnik and Czichy 2005; Mendenhall et al. 2007; Cornwell et al. 2014; Biswas 2019) for the near future.

Numerous successful investigations have been performed especially for the near Earth orbit optical communications, proposing different modulation schemes and system parameters (Zech et al. 2018; Chaudhary et al. 2019; Dubey et al. 2020; Singh and Malhotra 2020a, b; Viswanath et al. 2018). On the other hand, deep space measurement results are still being expected during the PSYCHE and DOCS L5 missions.

Of course higher transmission bitrates can be achieved for relatively shorter distance of near-Earth constellations, where the signal-to-noise ratio could be designed high enough, so that higher-order modulation schemes could be applied. For deep space optical communications however, the most important requirement is to use extremely robust modulation schemes and forward error correction techniques (FEC) to enable reliable transmission of payload data or tracking and control data. This is because of the strongly reduced received optical power intensity or number of the signal photons in the so-called photon-starved conditions. Pulse position modulation (PPM) proved to be the appropriate modulation scheme in such situations and is therefore proposed by NASA and ESA for many laser communication projects (Sodnik et al. 2014, 2017; Sodnik and Czichy 2005; Mendenhall et al. 2007; Cornwell et al. 2014; Biswas 2019). This is also the reason that PPM is used throughout this paper.

Various system parameters have been investigated for laser optical communication demonstration projects, such as transmitter power, transmitter efficiency, telescope aperture gain, atmospheric loss, free space propagation loss and receiver efficiency. In photon-starved deep space optical communications, the very robust pulse position modulation scheme (PPM) in combination with Geiger-mode single photon counting avalanche photodiode (APD) receivers (Srinivasan et al. 2016) or superconducting nanowire single photon detectors (SNSPD) are used (Mendenhall et al. 2007; Natarajan et al. 2012). In case of the Geiger-mode APD, the single photon counting deadtime limits the slot widths and the total achievable bitrates. Besides the above-mentioned parameters, atmospheric turbulences should be considered (Andrews et al. 2005, 2001). The new results have been achieved by using the model verified by the ESA’s DOCS system design parameters (Sodnik et al. 2017) and the ESA’s Artemis measurement data (Sodnik and Czichy 2005; Chen 2021; Internal ESA Artemis OGS OPALE Measurement Results 2003–2004) as well as by the NASA LLCD results (Cornwell et al. 2014; Biswas 2019; Aboagye and Chen 2021) in order to investigate performance of all typical free space and deep space optical communications scenarios. In this paper the simulation procedures are explained first. Then the performance analysis results for (a) near-Earth laser optical communications; (b) lunar laser optical communications and (c) interplanetary laser optical communications are presented. In each section, the typical simulation parameters and the corresponding performance results like intensity, average received photons per pulse and data throughput are presented for both uplink and downlink.

2 Simulation procedures

In previous papers, the author and his co-workers have investigated (a) near-Earth short distance laser optical communications with dual polarization quadrature phase shift keying (DP-QPSK) and quadrature amplitude modulation (16-QAM) (Siegel and Chen 2020), (b) the link budget estimations for free space laser optical communications by also considering the atmospheric turbulences (Chen 2021) with comparison with the experimental data of the ESA ARTEMIS project (Internal ESA Artemis OGS OPALE Measurement Results 2003–2004) and with the design parameters of the ESA DOCS L5 project (Sodnik et al. 2017) and (c) the impact of the varying PPM orders on the characteristics of deep space laser optical communication downlinks (Aboagye and Chen 2021), partially with comparison with the NASA LLCD results (Sans et al. 2012; Sodnik et al. 2014; Cornwell et al. 2014).

The valuable measurement results achieved by ESA (Sodnik and Czichy 2005) in the ARTEMIS project for GEO satellite to Earth ground station (Internal ESA Artemis OGS OPALE Measurement Results 2003–2004), the design parameters of DOCS L5 project (Sodnik et al. 2017) and the valuable experimental results achieved by NASA in the LLCD (Lunar Laser Communications Demonstration) project (Sans et al. 2012; Sodnik et al. 2014; Cornwell et al. 2014) were used to verify the simulation models developed at the Darmstadt University of Applied Sciences in the last years. The good match between the simulation model (Chen 2021), the experimental data and the independent ESA planned mission parameters provides the confidence to apply these models in the investigations for different scenarios in this paper.

Based on these models, with some further developments, the author investigated different laser optical communication system performance characteristics depending on the varying distances during the missions and the telescope apertures. The very important noise factors reported in the above-mentioned papers were taken into account to ensure the sufficient signal-to-noise ratio and the required bitrates. These noise factors can be receiver circuit noises, direct and indirect Sun irradiances like blue sky brightness during daytime and Earth and Moon background light during nighttime. It should be noted, that the laser optical communication link can be designed more reliably, if the atmospheric turbulences characterized by the Rytov variance \(\sigma ^2\) are also considered. For the simulations in this paper, the altitude of the ground station is asummed to be 2393 m above sea level, same as the altitude of the ideal ESA groundstaion at the Observatorio del Teide at Izaña in Tenerife, Spain with average sunshine per year of 3700 hours. The corresponding structure parameter of the refractive index according to the Kolmogorov theory of turbulences and the Hufnagel-Valley Model will then be approximately \(C_n^2 = 5 \cdot 10^{-18} \text {m}^{-2/3}\) corresponding to a moderate wind velocity.

The detailed descriptions of link budget simulation parameters, atmospheric scintillations and PPM can be found in Siegel and Chen (2020), Chen (2021), Aboagye and Chen (2021) and therefore will not be explicitly repeated in this paper.

In case of interplanetary missions, the orbit constellations between the Earth ground station and the spacecraft could be extremely varying, so that only certain time frames allow the data transmission with sufficient signal-to-noise ratio. In this paper the reported Earth background, Moon background and blue sky brightness values for the above-mentioned missions are used for the corresponding range of distances as estimates. Also the previous investigation of atmospheric scintillation (Chen 2021) enables further analysis of the impact of the amplitude scintillation on laser optical communications in link budget estimations. On the other hand, the channel capacity limits depend strongly on the link budget parameters like available filter bandwidth, distance, PPM orders, the signal-to-noise ratio or the ratio of received signal photons to noise photons (Hemmati et al. 2011; Aboagye and Chen 2021). These limits represent the theoretical upper bounds, by no means the achievable bitrates. On the contrary, due to the special measures for forward error correction (FEC) like convolutional coding schemes, code rate, interleaving methods, repeat factor, and the deadtime constraints of the Geiger-mode APD single photon counting receivers, the bitrates will be much lower than the theoretical channel capacity limits.

The received power can be calculated by using the link budget formula

$$\begin{aligned} P_R(L) = P_T \cdot \eta _T \cdot g_T \cdot \eta _{Atm} (L) \cdot \eta _{FS}(L) \cdot g_R \cdot \eta _P \cdot \eta _R \end{aligned}$$
(1)

with \(P_T, P_R(L)\) as transmitted power and received power at a distance L; \(\eta _T, \eta _R\) as transmitter and receiver telescope aperture efficiencies, \(\eta _P\) as pointing efficiency, \(g_T, g_R\) as transmitter and receiver aperture gain; \(\eta _{Atm} (L)\) as the atmospheric transmittance due to absorption loss, Rayleigh scattering (size of the scatterers \(\ll \lambda\)) and Mie scattering (size of the scatterers \(\approx \lambda\)); \(\eta _{FS}(L)\) as free space propagation efficiency, corresponding to the beam divergence.

By considering these link budget estimations based on the above equation (1), the corresponding code rates, interleaving, PPM order and the corresponding meaningful slot widths \(T_s\) can be chosen, in order to achieve the channel capacity \(C_{PPM}\) for chosen PPM order M (Moision and Farr 2014) as:

$$\begin{aligned} C_{PPM} = {1 \over {E_{\lambda } \cdot {\ln 2}}} \cdot { {P_R^2} \over {P_N \cdot {1 \over {\ln (M)}} + P_N \cdot {2 \over {M-1}} + {{P_R^2 \cdot M \cdot T_s} \over {\ln (M) \cdot E_{\lambda } }}} } \end{aligned}$$
(2)

with \(P_R, P_N\) as received signal and noise power and \(E_{\lambda }\) as photon energy. In Aboagye and Chen (2021) all the components of \(P_N\) like shot noise, dark current noise, background noise and thermal noise were explained in detail and will be not repeated here again. By considering further the code rate for the forward error correction CR, the required data rate or maximum data throughput R can be estimated as:

$$\begin{aligned} R = C_{PPM} \cdot CR \end{aligned}$$
(3)

In the NASA LLCD project (Cornwell et al. 2014) a reliable laser optical communication with bitrates of 10–20 Mbps for uplink and 39–622 Mbps for downlink could be successfully demonstrated by using 4-PPM for uplink and 16-PPM for downlink, both with a code rate of 1/2 and interleaver.

Based on the received power \(P_R\), the PPM order M and the slot width \(T_s\) including the guard slots, also the number of signal photons per PPM pulse \(K_s\) can be estimated (Hemmati et al. 2011; Aboagye and Chen 2021).

In the space science community, there is an ongoing discussion about the limited aperture size due to the Fried parameter. Relatively small apertures are used for the pointing and acquisition beacon. Especially for the communication uplink for deep space either higher power or larger aperture will be needed, in order to receive enough signal photons. In both cases possibly the scintillation in the atmosphere will be increased, so it is very important to make trade-off decisions to choose the telescope apertures in an optimized way. A possible solution could be a larger aperture in combination with adaptive optics which is being investigated intensively nowadays. If this solution works out, possible further gain can be achieved. Nevertheless, in this paper we will not focus on this discussion but rather on the more important issue of performance analysis. Therefore we follow the recommendations of the experts to use smaller transmitter telescope apertures for the uplink, either single beam or multiple beams (Calvo et al. 2014).

3 Near-earth laser optical communications

In Tables 1 and 2, the near-Earth laser optical communications simulation parameters are listed for uplink and downlink. Basically the parameters are chosen only as an example, but are very similar to the ESA ARTEMIS project (Sodnik and Czichy 2005) for GEO orbits. In Figs. 1, 2 and 3 the uplink characteristics, like power intensity of the laser beam, received signal photons and achievable data throughput are displayed, whereas Figs. 4, 5 and 6 show the downlink characteristics. As an example the PPM orders 4 and 16 with a code rate of 1/2 are used to estimate the throughput for communcations uplink and downlink.

Table 1 Simulation parameters for near-Earth laser communications, uplink (Sodnik and Czichy 2005; Internal ESA Artemis OGS OPALE Measurement Results 2003–2004)
Full size table
Table 2 Simulation parameters for near-Earth laser communications, downlink (Sodnik and Czichy 2005; Internal ESA Artemis OGS OPALE Measurement Results 2003–2004)
Full size table
Fig. 1
figure 1

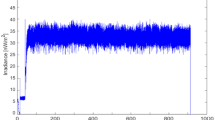
Near-Earth uplink intensity at the receiver depending on distance based on the parameters in Table 1

Full size image
Fig. 2
figure 2

Near-Earth uplink received signal photons per PPM pulse depending on distance based on the parameters in Table 1

Full size image
Fig. 3
figure 3

Near-Earth uplink maximum data rate depending on distance based on the parameters in Table 1

Full size image
Fig. 4
figure 4

Near-Earth downlink intensity at the receiver depending on distance based on the parameters in Table 2

Full size image
Fig. 5
figure 5

Near-Earth downlink received signal photons per PPM pulse depending on distance based on the parameters in Table 2

Full size image
Fig. 6
figure 6

Near-Earth downlink maximum data rate depending on distance based on the parameters in Table 2

Full size image

Figure 1 shows that uplink power intensity at the receiver onboard the spacecraft, with additional deviation \(\pm \sigma _I\) caused by the atmospheric scintillation in the troposphere up to about 11 km, decreases to about 0.02 mW/m2 for a larger distance up to 40,000 km. This intensity is still much larger than the Earth background brightness 43.6 nW/m2. The average numbers of the signal photons per pulse are between 80 and 70 depending on distance (Fig. 2). A maximum bitrate of about 9.5–0.2 Mbit/s can be achieved correspondingly by using the link parameters from Table 1 (Fig. 3).

Figure 4 shows the downlink power intensity at the receiver at the ground station, with additional deviation \(\pm \sigma _I\) caused by the atmospheric scintillation in the troposphere up to about 11 km, decreases to about 1 μW/m2 for a larger distance up to 40,000 km. This intensity is still much larger than the blue sky brightness 6 nW/m2 . The average numbers of the signal photons per pulse are between 112 and 100 depending on distance (Fig. 5). A maximum bitrate of about 500–470 Mbit/s can be achieved correspondingly by using the link parameters from Table 2 (Fig. 6).

4 Lunar laser optical communications

Tables 3 and 4 show the lunar laser optical communications simulation parameters for uplink and downlink. Basically the parameters are similar to the NASA LLCD project in cooperation with ESA (Sans et al. 2012; Sodnik et al. 2014; Cornwell et al. 2014). In Figs. 7, 8 and 9, the uplink characteristics, like power intensity of the laser beam at the receiver, received signal photons and achievable data throughput are displayed, whereas Figs. 10, 11 and 12 show the downlink characteristics. As an example the PPM orders 4 and 16 with a code rate of 1/2 are used to estimate the throughput for communcations uplink and downlink.

Table 3 Simulation parameters for lunar laser communications, uplink (Sodnik et al. 2014; Cornwell et al. 2014)
Full size table
Table 4 Simulation parameters for lunar laser communications, downlink (Sodnik et al. 2014; Cornwell et al. 2014)
Full size table
Fig. 7
figure 7

Lunar uplink intensity at the receiver depending on distance based on the parameters in Table 3

Full size image
Fig. 8
figure 8

Lunar uplink received signal photons per PPM pulse depending on distance based on the parameters in Table 3

Full size image
Fig. 9
figure 9

Lunar uplink maximum data rate depending on distance based on the parameters in Table 3

Full size image
Fig. 10
figure 10

Lunar downlink intensity at the receiver depending on distance based on the parameters in Table 4

Full size image
Fig. 11
figure 11

Lunar downlink received signal photons per PPM pulse depending on distance based on the parameters in Table 4

Full size image
Fig. 12
figure 12

Lunar downlink maximum data rate depending on distance based on the parameters in Table 4

Full size image

Figure 7 shows that uplink power intensity at the receiver onboard the spacecraft, with additional deviation \(\pm \sigma _I\) caused by the atmospheric scintillation in the troposphere up to about 11 km, decreases to about 0.35 μW/m2 for a larger distance up to 0.003 AU. But it is strong enough compared with the required irradiance at the spacecraft of 63 nW/m2. The average numbers of the signal photons per pulse are about 99 (Fig. 8). A maximum bitrate of about 15.6 Mbit/s can be achieved correspondingly by using the link parameters from Table 3 (Fig. 9).

Figure 10 shows that downlink power intensity at the receiver at the ground station, with additional deviation \(\pm \sigma _I\) caused by the atmospheric scintillation in the troposphere up to about 11 km, decreases to about 7.8 nW/m2 for a larger distance up to 0.003 AU. But it is still strong enough compared with the required irradiance at the ground station of 1.7 nW/m2. The average numbers of the signal photons per pulse are about 99 (Fig. 11). A maximum bitrate of about 466 Mbit/s can be achieved correspondingly by using the link parameters from Table 4 (Fig. 12).

5 Interplanetary laser optical communications

The simulation parameters for interplanetary or deep space laser optical communications are shown in Tables 5 and 6. These are basically derived from the ESA DOCS L5 parameters (Sodnik et al. 2017). In Figs. 13, 14 and 15 the uplink characteristics, like power intensity of the laser beam and achievable data throughput are displayed, whereas Figs. 16, 17 and 18 show the downlink characteristics. As example the PPM orders 4 and 16 with a code rate of 1/2 are used to estimate the throughput for communcations uplink and downlink.

Especially in the photon-starved laser optical transmission over an extremely large distance of 1.5 AU to 3 AU, it is most important to apply high laser power, larger receiver telescope apertures to focus the beam at the transmitter with high gain and to collect as many signal photons as possible at the spacecraft terminals, in order to guarantee sufficient signal-to-noise ratio and to enable the photon counting device to achieve low BER and high throughput. Transmitter can use a coherent beam combiner with 4 apertures of 0.2 m, or 8 apertures of 0.1 m diameter, or a larger transmitter telescope aperture in combination with adaptive optics, where applicable.

Table 5 Simulation parameters for interplanetary laser communications, uplink (Sodnik et al. 2017; Sodnik and Czichy 2005; Biswas 2019)
Full size table
Table 6 Simulation parameters for interplanetary laser communications, downlink (Sodnik et al. 2017; Sodnik and Czichy 2005; Biswas 2019)
Full size table
Fig. 13
figure 13

DSOC uplink intensity at the receiver depending on distance based on the Table 5

Full size image
Fig. 14
figure 14

DSOC uplink received signal photons per PPM pulse depending on distance based on the Table 5

Full size image
Fig. 15
figure 15

DSOC uplink maximum data rate depending on distance based on the Table 5

Full size image
Fig. 16
figure 16

DSOC downlink intensity at receiver depending on distance based on the Table 6

Full size image
Fig. 17
figure 17

DSOC downlink received signal photons per PPM pulse depending on distance based on the Table 6

Full size image
Fig. 18
figure 18

DSOC downlink maximum data rate depending on distance based on the Table 6 with 4 m ground station receiver aperture

Full size image
Fig. 19
figure 19

DSOC downlink maximum data rate depending on distance based on the Table 6 with 10 m ground station receiver aperture

Full size image

Figure 13 shows that uplink power intensity at the receiver onboard the spacecraft, with additional deviation \(\pm \sigma _I\) caused by the atmospheric scintillation in the troposphere up to about 11 km, decreases from 3 nW/m2 to about 0.1 nW/m2 for a larger distance up to 3 AU. Even though the mean intensity is enough compared with the Earth background irradiance of 36.4 pW/m2 at 1.5 AU, the atmospheric scintillation could reduce the irradiance significantly for larger distance. The average numbers of the signal photons per pulse are between 84–70 (Fig.14). A maximum bitrate of some 14 Mbit/s at 0.5 AU-212 kbit/s at 3 AU can be achieved correspondingly by using the link parameters from Table 5 (Fig. 15).

Figure 16 shows that downlink power intensity at the receiver at the ground station, with additional deviation \(\pm \sigma _I\) caused by the atmospheric scintillation in the troposphere up to about 11 km, decreases from 11 pW/m2 to about 0.3 pW/m2 for a larger distance up to 3 AU. Even though the mean intensity is still enough compared with the blue sky irradiance of 0.08 pW/m2, the atmospheric scintillation could reduce the irradiance significantly for distance larger than 2 AU. The average numbers of signal photons per pulse are between 68–54 (Fig. 17). A maximum bitrate of about 0.57 Mbit/s at 0.5 AU to 559 bit/s at 3 AU can be achieved correspondingly by using a 4 m ground station receiver aperture from Table 6 (Fig. 18). If however a larger telescope aperture of 10 m could be used, then the maximum bitrates can be improved to 22 Mbit/s at 0.5 AU to 39 kbit/s at 3 AU (Fig. 19).

6 Conclusions

Simulation results by using previously verified algorithms for near-Earth, lunar and interplanetary laser optical communications are presented in this paper. Different realistic system parameters are considered like uplink and downlink transmit power, telescope apertures, different distances, atmospheric scintillations, blue sky brightness, Earth and Moon background noise as well as receiver noise factors. The results show the uplink and downlink characteristics like intensity, average received photons per pulse and the achievable data rates. Generally, by using the assumed mission parameters, the required received power or power density levels can be ensured, so that a throughput of 9.5–0.5 Mbit/s for uplink and 500–470 Mbit/s for downlink can be achieved for near-Earth laser optical communications. About 15.6 Mbit/s for uplink and 466 Mbit/s for downlink are possible in case of lunar laser optical communications. For deep space interplanetary laser optical communications, a throughput of 14 Mbit/s–212 kbit/s for uplink and 22 Mbit/s–39 kbit/s for downlink can be possible depending on the distance between the groundstation and spacecraft, and ground station receive antenna apertues. These investigation results give an overview and could possibly help to verify future mission planning and measurement data, and further improve the performance by modifying uplink and downlink parameters.