Silicon-based flat-topped wavelength filter for low crosstalk, high fabrication tolerance and wideband operating range for CWDM applications

Abstract

A flat-topped wavelength filter with low crosstalk and high productivity is proposed and theoretically analyzed. The proposed filter scheme is composed of multiple cascade-connected delayed interferometers with several multimode interference couplers with 50:50 and 28:72 split ratios and a directional coupler with a 92:8 split ratio. Theoretical results based on analytic and numerical simulations exhibit flatband spectra over a wavelength range of > 100 nm and low crosstalk of < −20 [dB] with potentially better production yield for fabrication imperfections.

1 Introduction

Wavelength division multiplexing (WDM) has been adopted as a key strategy to enhance the optical bandwidth in high-density interconnections (Novac et al. 2014; Dai et al. 2014). Especially, coarse WDM (CWDM) has been investigated as a prominent technology to relax the accuracy of laser oscillation wavelengths and lower the temperature sensitivity of the entire WDM system. Normally, wavelength filters are needed in WDM interconnects or passive optical networks (Sundar et al. 2015, Binoy Das et al. 2019) to multiplex and demultiplex the WDM optical signals. There are several material types such as semiconductors and dielectric materials. Among these, silicon (Si)-based wavelength filters have versatile strong points such as a small footprint and dense monolithic integrability with other photonic and electronic devices through a mature complementary metal–oxide–semiconductor (CMOS) fabrication process (Horikawa et al. 2018, Mogami et al. 2018, Littlejones et al. 2020, Siew et al. 2021).

Among various types of Si-based wavelength filters such as microring resonators, multiple delayed interferometers (MDIs), and arrayed waveguide gratings, the MDI-type wavelength filter (Horst et al. 2013; Jeong et al. 2014; Jeong et al. 2018; Xu et al. 2018; Mikkelsen et al. 2018; Xu et al. 2021) showed several advantages in terms of low insertion loss, low spectral crosstalk, and spectral flatness. Considering randomly fluctuating optical signal wavelengths from the semiconductor laser based optical sources, spectral flatness becomes one of the most important needs to minimize the system penalties in the WDM interconnections. To date, to make the MDI-type filter spectral response box-like, it has been reported that coupling ratios to bar and cross ports for 2 × 2 optical couplers were carefully adjusted to be 50(bar):50(cross), 80:20, 67:33, 92:8, 96:4, etc. (Horst et al. 2013; Jeong et al. 2014).

In many cases, the above-mentioned multiple coupling ratios in the MDI-based wavelength filters were achieved by adopting a directional coupler (DC) as a light splitter/mixer in the MDI (Horst et al. 2013; Jeong et al. 2014; Jeong et al. 2018; Xu et al. 2018; Mikkelsen et al. 2018). Usually, the coupling efficiency (i.e. coupling coefficient to cross port for DCs [${\kappa }_{DC}\left(\lambda \right)$]) sinusoidally varies against a input signal wavelength. In other words, it is fundamentally difficult to keep ${\kappa }_{DC}\left(\lambda \right)$ constant over a wide wavelength range, which means that a flat spectral range is restricted to be < 40 [nm] unless double filtering architectures (Jeong et al. 2018) are employed. These drawbacks on ${\kappa }_{DC}\left(\lambda \right)$ was relaxed by adopting bent-shaped DCs with a relatively narrow gap (125 nm) and polymer claddings (Xu et al. 2018), or by utilizing the silicon–nitride material system with a relatively low dispersion property (Mikkelsen et al 2018). However, in the former case, the narrow DC gap and polymer cladding material were accompanied by technical complexity in a standard CMOS process, while in the latter case, there remain difficulties for monolithically integrating silicon nitride with other photonic devices, such as Si-based optical waveguides, or optical modulators. As another way to overcome the shortcomings on ${\kappa }_{DC}\left(\lambda \right)$, multi-stage interferometric coupler scheme rather than a simple DC scheme was adopted, thus enabling to achieve parabolic-shaped (Jeong et al. 2018) and box-like filter response (Xu et al 2021) in a wide spectral range of > 80-nm. However, an extremely high control accuracy is required for the phase change value of the phase shifters in the interferometric coupler to attain desired filter response from the viewpoint of box-like spectral shapes and low crosstalk. Moreover, there has been little report on the prospects for fabrication tolerance.

Recently, to overcome the above problems, we reported a novel MDI-type wavelength filter based on multimode interference (MMI) couplers with symmetric and asymmetric coupling ratios (Jeong 2021). Although the reported scheme exhibited a wide operating range with flat spectral shapes over the 80-nm-wide spectral range, it compromised with slightly degraded spectral crosstalk at some output channels. In this paper, as an alternative device scheme to further reduce the spectral crosstalk for the previously reported scheme, we propose a CWDM-targeted MDI-based wavelength filter scheme, and theoretically verify the superior spectral behaviors in terms of spectral crosstalk and fabrication tolerance, compared with those for the conventional and the previously reported schemes.

2 Theoretical investigations

2.1 Device schemes for MDI-type wavelength filters

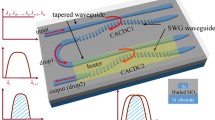
Figure 1 shows the schematic drawings of Si-based MDI-type 1 × 4 flat-spectral-band wavelength filters. In Fig. 1, $m\Delta L \left (m:\mathrm{positive \; integer}\right)$ indicates delay lines to determine the designed spectral shape and the channel spacing. Figure 2 indicates the schematics of optical couplers utilized in the MDI-type wavelength filters shown in Fig. 1 where (a) DC1: DC with ${\kappa }_{DC}=0.5$, (b) DC2: DC with ${\kappa }_{DC}=0.2$, (c) DC3: DC with ${\kappa }_{DC}=0.04$, (d) DC4: DC with ${\kappa }_{DC}=0.33$, (e) DC5: DC with ${\kappa }_{DC}=0.08$, (f) MMI1: MMI with ${\kappa }_{MMI}=0.5$, (g) MMI2: MMI with ${\kappa }_{MMI}=0.85$, and (h) MMI3: MMI with ${\kappa }_{MMI}=0.72$. To satisfy the phase matching between each MDI, proper phase shifter should be required depending on the interference condition. In this case, $\Delta L^{\prime}$ and $\Delta L"$ represent $\Delta L+\left(\pi /2\right) \left[rad.\right]$ and $\Delta L+\pi \left[rad.\right]$, respectively. As shown in Fig. 1a, the conventional MDI-type device scheme is composed of multiple DCs and optical delay lines with proper phase shifters. First-stage MDIs normally operate as spectral splicers defining channel spacing, whereas second-stage MDIs operate as channel selectors for differentiating wavelength components into spatially separated each output channel.

Fig. 1

Schematics of Si-based MDI-type flat-spectral-band wavelength filters: (a) conventional scheme based on all DCs with five types of ${\kappa }_{DC}$ (where ${\kappa }_{DC}$ stands for the optical ratio that couples to the DC cross port), (b) previously reported (Jeong 2021) scheme based on MMI couplers with three types of ${\kappa }_{MMI}$ (where ${\kappa }_{MMI}$ stands for the optical ratio that couples to the MMI cross port) and DCs with two types of asymmetric ${\kappa }_{DC}$, (c) proposed scheme based on MMI couplers with two types of ${\kappa }_{MMI}$ and a DC with a single type of asymmetric ${\kappa }_{DC}$

Fig. 2

Schematics of optical couplers used in the MDI-type wavelength filters: a DC1: DC with ${\kappa }_{DC}=0.5$, b DC2: DC with ${\kappa }_{DC}=0.2$, c DC3: DC with ${\kappa }_{DC}=0.04$, d DC4: DC with ${\kappa }_{DC}=0.33$, e DC5: DC with ${\kappa }_{DC}=0.08$, f MMI1: MMI with ${\kappa }_{DC}=0.5$, g MMI2: MMI with ${\kappa }_{DC}=0.85$, and h MMI3: MMI with ${\kappa }_{DC}=0.72$

In Fig. 1a, to make the spectral response flat around each CWDM channel grid, additional MDIs with different ${\kappa }_{DC}$ values and path lengths were connected within each MDI scheme (Horst et al. 2013; Jeong et al. 2014). For this, ${\kappa }_{DC}$ at the first-stage MDI was set to 0.5, 0.2, 0.2, and 0.04, and the path differences were set as $2\Delta L$, $4\Delta L$, and $4\Delta L"$. ${\kappa }_{DC}$ at the second-stage MDI was set to 0.5, 0.33, and 0.08 with similar path differences. It should be noted that the above-mentioned ${\kappa }_{DC}$ can only be satisfied at the operating center wavelength (${\lambda }_{CN}$) due to the sinusoidal dependence of ${\kappa }_{DC}\left(\lambda \right)$. Although the DC can accurately control the ${\kappa }_{DC}$ by optimizing the ${L}_{DC}$ and ${Gap}_{DC}$, the ${\kappa }_{DC}$ is susceptible to variations in a wavelength. The closer the ${\kappa }_{DC}$ is to 0.5, the more remarkable the rate of change of ${\kappa }_{DC}$ becomes. Thus, the MDI-type filter based on the conventional scheme shown in Fig. 1a has a narrower operating wavelength range.

As shown in Figs. 1b and 2, the reported scheme in NUSOD (Jeong 2021) mainly utilizes MMI couplers in each MDI. ${\kappa }_{MMI}$ at the first-stage MDI was set as 0.5, 0.85, and 0.85, and the coupling condition of ${\kappa }_{DC}$ was the same as that in Fig. 1a. From the viewpoint of optimal flat spectral band, the most desired ${\kappa }_{MMI}$ should be 0.8 rather than 0.2, because the coupling mechanism of MMI couplers is different from that of DCs. Usually, the interaction length of the DC (${L}_{DC}$) is proportional to ${\kappa }_{DC}$, while that of the MMI (${L}_{MMI}$) is vice versa. Irrespective of the coupler structure, it is desirable to reduce the coupling interaction length for keeping the DC coupling ratio (${\kappa }_{DC}$) nearly constant or for minimizing the excess loss by wavelength dependence of the MMI coupling ratio (${\kappa }_{MMI}$). In other words, when the MMI couplers are adopted in the MDI-type wavelength filter scheme, the coupling conditions shown in Fig. 1a inherently makes the insertion loss and the size of the wavelength filter much bigger. Thus, in case of the MMI-based MDI-type filter scheme, it is advantageous to design ${\kappa }_{MMI}$ to be larger than 0.5.

Furthermore, it should be noted that if we consider no fundamental excessive loss, ${\kappa }_{MMI}$ can be given as discrete values such as 0.85, 0.72, 0.5, 0.28, 0.15 (Bachmann 1995), which is why we used ${\kappa }_{MMI}$ of 0.85 rather than 0.8 that gives better spectral flatness. As will be theoretically discussed later, the above-mentioned parameter deviation from the optimum condition is accompanied with slight degradation of the degree of spectral crosstalk at the center wavelength of the filter (${\lambda }_{CN}$).

As seen in Figs. 1c and 2, the proposed scheme mainly employs MMI couplers. However, the device configuration is simpler than the case shown in Fig. 1b due to a smaller number of components. Except the parameter conditions for the delay lines at each MDI, ${\kappa }_{MMI}$ at the first and second stage of MDIs were identically set as 0.5, 0.72, and the coupling condition of ${\kappa }_{DC}$ was 0.08. Since the optical coupling condition shown in Fig. 1c is closer to the optimum condition for spectral flatness, the proposed scheme can make the spectral crosstalk from neighboring channels much lower. Additionally, the proposed scheme has a structural benefit due to a small number of the delay line with the discrete phase shifter.

In the case of the MMI-based wavelength filter schemes shown in Fig. 1b and c, the relatively longer path differences at each MDI were apparently different from those shown in Fig. 1a. Once again, this is due to different coupling mechanism between the DC and the MMI coupler. For the DC and MMI coupler, short interaction lengths (${L}_{DC}$ and ${L}_{MMI}$) are required to minimize the wavelength sensitivity of ${\kappa }_{MMI}\left(\lambda \right)$ and ${\kappa }_{DC}\left(\lambda \right)$. ${L}_{DC}$ becomes shorter as ${\kappa }_{DC}$ decreases, while ${L}_{MMI}$ tends to reduce as ${\kappa }_{MMI}$ increases (${L}_{MMI}$ with ${\kappa }_{MMI}=0.85 \; or \; 0.72$ is three times shorter than ${L}_{MMI}$ with ${\kappa }_{MMI}=0.15 \; or \; 0.28$). The device shown in Fig. 1b employs three kinds of MMI couplers with different ${\kappa }_{MMI}\left(\lambda \right)$ values of 0.5, 0.85, and 0.72. Although the asymmetric values of ${\kappa }_{MMI}$ are somewhat mismatched with the optimized condition, their values are sufficiently close to ensure the spectral response is box-like flat. A flat response also needs extremely asymmetric ratios of 0.04 and 0.08, which are not easy to attain by the MMI scheme. Fortunately, the closer the ${\kappa }_{DC}$ is to 0, the significantly smaller the rate of change of ${\kappa }_{DC}$ becomes.

On the other hand, the newly proposed device shown in Fig. 1c employs two kinds of MMI couplers with different ${\kappa }_{MMI}\left(\lambda \right)$ values of 0.5, 0.72, and a single DC with ${\kappa }_{DC}\left(\lambda \right)$ value of 0.08. Since the slight mismatch of optical coupling ratios generated in the device scheme in Fig. 1b is relaxed, the spectral crosstalk from neighboring channels of the proposed device scheme can be further reduced. Consequently, since all the coupling components have higher tolerances to wavelength, the proposed filter scheme can achieve wideband flat-topped response with a lower crosstalk and a good production yield.

2.2 Analytic and numerical calculations

The center wavelength (${\lambda }_{CN}$) and channel spacing in a wavelength domain ($\Delta \lambda$) for an MDI-type wavelength filter are normally given by the path length difference designated by $\Delta L$ defined in Fig. 1.

$${\lambda }_{CN}=\frac{{N}_{eq} \cdot 2\Delta L}{{m}_{diff}}$$

(1)

$$\Delta \lambda =\frac{{\lambda }_{CN}^{2}}{2\left({n}_{g} \cdot 2\Delta L\right)}$$

(2)

where ${n}_{eq}$, ${n}_{g}$, and ${m}_{diff}$ represent an equivalent index of the waveguide, a group index of the waveguide at the MDI region, and a diffraction order of the first-stage MDI, respectively. In this case, the spectral response for the first-stage of the proposed MDI-type device shown in Fig. 1c can be obtained as follows:

$$\left[\begin{array}{c}{p}_{1}\\ {p}_{2}\end{array}\right]=\left[{X}_{3}\right]\cdot \left[{F}_{2}\right]\cdot \left[{X}_{2}\right]\cdot \left[{F}_{1}\right]\cdot \left[{X}_{1}\right]\cdot \left[\begin{array}{c}0\\ {a}_{1}\end{array}\right]=\left[{T}_{M1}\right]\cdot \left[\begin{array}{c}0\\ {a}_{1}\end{array}\right]$$

(3)

where ${a}_{1}$, ${p}_{1}$, and ${p}_{2}$ stand for the electric field amplitudes for the input and two outputs shown in Fig. 1c ${X}_{n}$, and ${F}_{n}$ [$n$: positive integer] indicate the spectral response by optical coupling via the DC or MMI coupler, and by optical delay lines and phase shifters, where the subscript $n$ shows the sequence of the functional blocks from the input channel. $\left[{T}_{M1}\right]$ gives the transfer matrix for the first-stage MDI shown in Fig. 1c. In this case, ${X}_{n}$, and ${F}_{n}$ can be defined as follows:

$$\left[{X}_{1}\right]=\left[\begin{array}{cc}\surd {\kappa }_{bar}^{50:50}\left(\lambda \right)& -j\surd {\kappa }_{cross}^{50:50}\left(\lambda \right)\\ -j\surd {\kappa }_{cross}^{50:50}\left(\lambda \right)& \surd {\kappa }_{bar}^{50:50}\left(\lambda \right)\end{array}\right]$$

(4)

$$\left[{X}_{2}\right]=\left[\begin{array}{cc}\surd {\kappa }_{bar}^{28:72}\left(\lambda \right)& -j\surd {\kappa }_{cross}^{28:72}\left(\lambda \right)\\ -j\surd {\kappa }_{cross}^{28:72}\left(\lambda \right)& \surd {\kappa }_{bar}^{28:72}\left(\lambda \right)\end{array}\right]$$

(5)

$$\left[{X}_{3}\right]=\left[\begin{array}{cc}\surd {\kappa }_{bar}^{92:08}\left(\lambda \right)& -j\surd {\kappa }_{cross}^{92:08}\left(\lambda \right)\\ -j\surd {\kappa }_{cross}^{92:08}\left(\lambda \right)& \surd {\kappa }_{bar}^{92:08}\left(\lambda \right)\end{array}\right]$$

(6)

$$\left[{F}_{1}\right]=\left[\begin{array}{cc}{e}^{-{\beta }_{c}\cdot 2\Delta L}& 0\\ 0& 1\end{array}\right]$$

(7)

$$\left[{F}_{2}\right]=\left[\begin{array}{cc}{e}^{-{\beta }_{c}\cdot 4\Delta L}& 0\\ 0& 1\end{array}\right]$$

(8)

where $\left[{X}_{1}\right]$, and $\left[{X}_{2}\right]$ indicate the transfer matrices of the MMI coupler of ${\kappa }_{MMI}=0.5$ and ${\kappa }_{MMI}=0.72$ at $\lambda ={\lambda }_{CN}$. In the matrices, the subscripts give the coupling ratio to the bar and cross ports. $\left[{X}_{3}\right]$ denotes the transfer matrix of the DC with ${\kappa }_{DC}=0.08$. ${\beta }_{c}$ denotes a propagation constant, which is defined as $\left({2\pi n}_{eq}\right)/\lambda$ where ${n}_{eq}$ is an equivalent refractive index of the optical paths. By using similar approaches, we can also define the transfer matrices for the two second-stage MDIs in the following.

$$\left[\begin{array}{c}{q}_{1}\\ {q}_{2}\end{array}\right]=\left[{X}_{3}\right]\cdot \left[{F}_{4}\right]\cdot \left[{X}_{2}\right]\cdot \left[{F}_{3}\right]\cdot \left[{X}_{1}\right]\cdot \left[\begin{array}{c}{p}_{1}\\ 0\end{array}\right]=\left[{T}_{M2}\right]\cdot \left[\begin{array}{c}{p}_{1}\\ 0\end{array}\right]$$

(9)

$$\left[\begin{array}{c}{q}_{3}\\ {q}_{4}\end{array}\right]=\left[{X}_{3}\right]\cdot \left[{F}_{6}\right]\cdot \left[{X}_{2}\right]\cdot \left[{F}_{5}\right]\cdot \left[{X}_{1}\right]\cdot \left[\begin{array}{c}0\\ {p}_{2}\end{array}\right]=\left[{T}_{M3}\right]\cdot \left[\begin{array}{c}0\\ {p}_{2}\end{array}\right]$$

(10)

$$\left[{F}_{3}\right]=\left[\begin{array}{cc}{e}^{-{\beta }_{c}\cdot \Delta L}\cdot {e}^{-j\left(+\pi /2\right)}& 0\\ 0& 1\end{array}\right]$$

(11)

$$\left[{F}_{4}\right]=\left[\begin{array}{cc}{e}^{-{\beta }_{c}\cdot 2\Delta L}& 0\\ 0& 1\end{array}\right]$$

(12)

$$\left[{F}_{5}\right]=\left[\begin{array}{cc}{e}^{-{\beta }_{c}\cdot \Delta L}& 0\\ 0& 1\end{array}\right]$$

(13)

$$\left[{F}_{6}\right]=\left[\begin{array}{cc}{e}^{-{\beta }_{c}\cdot 2\Delta L}\cdot {e}^{-j\left(+\pi \right)}& 0\\ 0& 1\end{array}\right]$$

(14)

Consequently, the intensity of the spectral response for all channels in the proposed device is given by

$${I}_{s}\left(\lambda \right)={q}_{s}\left(\lambda \right)\cdot {q}_{s}^{*}\left(\lambda \right)$$

(15)

In Eq. (15), ${I}_{s}\left(\lambda \right)$ stands for the intensity for each output channel where $s$ indicates the channel number shown in Fig. 1c. Here, ${q}_{s}^{*}\left(\lambda \right)$ represents a complex conjugate of the ${q}_{s}\left(\lambda \right)$. As a matter of course, based on similar mathematical formulations, spectral response for the remaining two filter schemes shown in Fig. 1a and b can also be calculated.

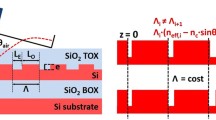
Usually, coupling efficiencies for the 2 × 2 DCs and MMI couplers cannot be preserved in a wavelength domain. In this case, coupling efficiencies for the two types of optical couplers with several kinds of $\kappa$ were calculated by using a 3-dimensional beam propagation method (3D-BPM, BeamPROP by Synopsys). As a waveguide model, we assumed 350-nm-wide and 220-nm-thick Si waveguides for operating in the O-band spectral regime. Figure 3 shows the simulation model for (a) DCs, (b) MMI couplers ($\kappa_{cross}=0.5 \; or \; 0.85$), and (c) MMI coupler ($\kappa_{cross}=0.72$) together with their corresponding intensity profiles in each coupler region simulated by the 3D-BPM ($\lambda=1.31 \: \boldsymbol{ }[\mu m]$). Figure 4 depicts the simulated coupling ratios with respect to the bar ($\kappa_{bar}$) and cross ports ($\kappa_{cross}$) for several kinds of (c) DCs and (d) MMI couplers. Table 1 specifies each parameter for DCs and MMI couplers used in the device schemes in Fig. 1.

Fig. 3

Simulation models for a DCs, b MMI couplers with $\kappa_{MMI}=0.5 \; or \; 0.85$ and c MMI coupler with $\kappa_{MMI}=0.72$ together with intensity distributions in each coupler scheme simulated by the 3D-BPM

Fig. 4

Simulated coupling ratios for the bar and cross ports for a DCs, and b MMI couplers for obtaining flat spectral response of each wavelength filter scheme

Table 1 Parameters for the DCs and MMI couplers indicated in Fig. 4

The gap between access waveguides defined as $Gap_{DC}$ and $Gap_{MMI}$ was commonly set to $0.2 \: [\mu m]$, which is a typically available value in standard fabrication processes (Littlejones, 2020; Siew 2021). For all design conditions of $\kappa_{DC}$, the curvature radius ($R_{DC}$) was set to $6.2 \: [\mu m]$. $L_{DC}$ and $L_{MMI}$ were properly optimized according to the coupling ratio. In the case of $\kappa_{DC}=0.04$, and $0.08$, the coupling efficiency was controlled by optimizing $L_{DC}=1.5 \: [\mu m]$ for $\kappa_{DC}=0.04$ and $L_{DC}=3.0 \: [\mu m]$ for $\kappa_{DC}=0.08$.

In the case of MMI couplers, to control the number of available excited modes within the MMI region and minimize the dispersion effect by higher modes, taper waveguide schemes were adopted for the input and output access waveguides, as shown in Fig. 3b and c. Other factors related to $\kappa_{MMI}=0.5,\boldsymbol{ }0.85$, and $0.72$ such as the MMI width ($W_{MMI}$), MMI length ($L_{MMI}$) and the relative position of input/output access waveguides to each MMI region were properly determined based on the MMI self-imaging principle. As schematically seen in Fig. 2, $\kappa_{MMI}$ of $0.5$ and $0.85$ can be given by optimizing only the $L_{MMI}$, while $\kappa_{MMI}$ of $0.72$ is additionally accompanied with inverse symmetrical positioning of the input and output access waveguides for the MMI region (Bachmann, 1995). For the DC and MMI couplers, $\lambda_{CN}$ for defining $\kappa_{bar}$ and $\kappa_{cross}$ was set as $1.31 \: [\mu m]$. For the proposed scheme shown in Fig. 1c, the design rule was the same as those used in the scheme shown in Fig. 1b, except not using the MMI coupler with $\kappa_{MMI}=0.85$ and the DC with $\kappa_{DC}=0.04$. Based on the parameters shown in Table 1, the device size can be estimated to $120 \: [\mu m] \times 220 \: [\mu m]$ for conventional scheme, $120 \: [\mu m] \times 300 \: [\mu m]$ for the previously reported scheme, and $120 \: [\mu m] \times 260 \: [\mu m]$ for the proposed scheme, respectively.

As shown in Fig. 4a, the DCs have sinusoidally-varying $\kappa_{cross}$ and $\kappa_{bar}$ whose wavelength sensitivities are more remarkable as $\kappa_{cross}$ gets close to 0.5. We can also confirm that the degree of sinusoidally-varying spectral behaviors was compatible with the experimentally measured spectral response. These results mean that the specific coupling condition for attaining flat-topped response is satisfied only at around $\lambda=1.31 \: [\mu m]$. As can be seen in Fig. 4b, both for the $\kappa_{cross}$ and $\kappa_{bar}$ values of all the MMI couplers are nearly constant over the 100-nm-wide spectral range. It should be noted that in the case of the MMI-based MDI-type filter schemes, the rate of change of $\kappa_{DC}$ (= 0.04, and 0.08) has reduced sensitivity to wavelength. That is, these results indicate that the proposed filter response does not degrade mainly by these DC coupling responses.

Subsequently, to analytically calculate the filter spectral response of the conventional, previously reported and proposed MDI-type wavelength filters, we used the transfer matrix method outlined in Eqs. (1)–(13). It is important to note that the optical coupling ratios, defined as $\kappa_{cross} (\lambda)$ and $\kappa_{bar} (\lambda)$ for all DCs and MMI couplers, numerically simulated by the 3D-BPM were applied to the transfer matrix for each MDI-type filter scheme. In the simulation, $n_{eq}$ and $n_{g}$ for the Si waveguides were set to 2.5766 and 4.3325 at $\lambda=1.31 \: [\mu m]$. Figure 5 shows the calculated spectral characteristics of the MDI-type filter based on the device scheme shown in (a) Fig. 1a, (b) Fig. 1b, and (c) Fig. 1c. Considering the set value of $n_{g}$, the path difference value of $\Delta L$ in the MDI region was set to $4.95 \: [\mu m]$ for achieving a $\Delta \lambda$ of 20-nm at $\lambda_{CN}=1.31 \: [\mu m]$.

Fig. 5

Simulated 20-nm-spaced spectral responses for the MDI-type wavelength filters based on a conventional scheme [Fig. 1a], b previously reported scheme [Fig. 1b], and c proposed scheme [Fig. 1c]

In Fig. 5a, the conventional scheme has an extremely better performance at around $\lambda =1.31 \left[\mu m\right]$. However, considering broad spectral ranges such as the CWDM targeted span, some channels (e.g., Ch-3 and Ch-1) inherently experience apparently higher crosstalk from neighboring channels. As seen in Fig. 5b, since the symmetric and asymmetric ratios of the MMI couplers are resilient to wavelength variations, the proposed device can operate without degrading the spectral crosstalk over the 100-nm-wide spectral range. Meanwhile, like the case of Fig. 5b, as can be seen in Fig. 5c, the proposed scheme exhibits prominent spectral advantages over the conventional scheme. Furthermore, as mentioned earlier, since the power coupling ratios for the MMI couplers are closer to the optimum condition, the spectral crosstalk tends to be much lower than the case shown in Fig. 5b by more than 10 [dB].

The shortcoming for the device structures shown in Fig. 5b and c is slightly inferior spectral flatness. If we define the degree of spectral flatness as the bandwidth ratio for −1 to −10 dB transmittances, the flatness factor is calibrated as 0.656 for the conventional scheme. Meanwhile, the flatness factor is estimated as 0.584 for the previously reported scheme, which can mainly be attributed to a slight mismatch of asymmetric coupling ratios by the MMI couplers from the ideal flatband coupling condition. Also, the proposed scheme has the flatness factor of 0.538, which is primarily due to a smaller number of MDI in the first-stage. However, the much lower spectral crosstalk and balanced spectral width for each WDM grid outweigh the aforementioned drawback, thereby ensuring that the proposed filter scheme is more practical than the conventional one.

2.3 Production yield

Real fabrication process implemented in commercially available CMOS-based photonics processes are normally accompanied with the deviation offset of the waveguide pattern width from the targeted values ($\Delta W$) through photo lithography, developing and dry etching process. In the case of the MDI-type wavelength filter scheme, the spectral shape and the spectral flatness are mainly influenced by multiple optical interferences via asymmetric intensity balances at each MDI. Consequently, the $\Delta W$ values on the pattern widths are directly responsible for the variations in splitting and coupling characteristics for DCs and MMI couplers, which leads to degradation on the spectral shapes and flatness factors.

Although the operation principles for the DC and MMI coupler are different with each other, as the $\Delta W$ has a negative value, the spectral behaviors shown in Fig. 4 tends to be shifted to the shorter wavelength side. In case of the DC, when $W$ of the waveguide is reduced, ${Gap}_{DC}$ becomes correspondingly wider. Since the optical confinement inherently becomes weaker, thus the optical field is easy to be coupled to the neighboring waveguide in the DC. In case of the MMI coupler, due to the reduction of the equivalent index at the MMI region forces the center wavelength shown in Fig. 4b to be shifted to the shorter wavelength side (Soldano 1995).

On the other hand, as the $\Delta W$ has a positive value, the spectral behaviors shown in Fig. 4 changes differently for the DC and MMI coupler. In case of the DC, when $W$ of the waveguide is widened, ${Gap}_{DC}$ becomes correspondingly narrower. Hence, the optical confinement inherently becomes stronger, which makes the optical field difficult to be coupled. However, the narrowed gap helps the optical field easily be coupled in the DC. As a result, the coupling behavior keeps nearly constant within a moderate range of < 10-nm of $\Delta W$. In case of the MMI coupler, due to the increase in the equivalent index at the MMI region forces the center wavelength shown in Fig. 4b to be shifted to the longer wavelength side (Soldano, 1995). Overall, as can be clearly seen in Fig. 4, since the MMI couplers have the wavelength insensitive coupling behavior more than the DCs, the spectral degradation by the above-mentioned $\Delta W$ can be much lower for the MMI-based filter schemes than for the conventional one. In other words, the proposed scheme is advantageous from the viewpoint of fabrication tolerance.

From another point of view, the absolute phase of optical waveguides is randomly fluctuated due to the line edge sidewall roughness of the waveguide during CMOS fabrication process. When the refractive indices of the core and cladding materials are constant, and the standard deviation of the random phase errors can be represented by (Goh 1997)

$$\sigma \left(\delta \phi \right)={k}_{0}\cdot \sigma \left(\delta w\right)\cdot \frac{d{n}_{eq}}{dw}\cdot \surd \left(L\cdot {L}_{c}\right)$$

(16)

where ${k}_{0}$, $\sigma \left(\delta w\right)$, $d{n}_{eq}/dw$, $L$, and ${L}_{c}$ stand for the wavenumber in free space, standard deviation of the line width roughness, the variation rate of the equivalent index against waveguide width, the interaction length and the correlation length related to spatial frequency of the line width roughness, respectively. The above-mentioned random phase variations within each MDI causes the intensity noise of the filter spectral response. Considering the above-mentioned random phase errors, we need to know statistical data of the line width roughness of the waveguide ($\updelta w$) and the thickness variation ($\updelta t$) across the silicon-on-insulator (SOI) wafer. By using an ArF-immersion lithography process technology on a 300-mm diameter SOI wafer, Horikawa et al. reported an extremely low standard deviation value of $\updelta t$ as ${\sigma }_{\updelta t}\approx 0.24 [nm]$ and $\updelta w$ as ${\sigma }_{\updelta w}\approx 1.3 [nm]$ (Horikawa et al. 2018).

It is noted that ${\sigma }_{\updelta w}$ and ${\sigma }_{\updelta t}$ are independent relation with each other. That is, although a large portion of $\Delta W$ leads to the direct increase in ${\Delta \lambda }_{CN}$, good spectral uniformity can be attained by reducing the ${\sigma }_{\updelta w}$. In this case, a wider waveguide width in the delay line regions helps have a better spectral distribution, because the value of $d{n}_{eq}/dw$ in Eq. (16) can be reduced by increasing $W$ (Jeong et al., 2018). Based on the similar analytic approaches depicted in Fig. 5, a 20-nm-spaced filter spectral response of the three kinds of MDI-type wavelength filters was calculated by considering the changes in coupling ratios for the DCs and MMI couplers in the main loop of the transfer matrices. In this simulation, $\Delta W$ was set as $-5 [nm]$ to $+5 [nm]$, considering the typical value of $\Delta W$ reported by the currently available silicon photonic foundry of $<\pm 7 [nm]$ (Siew et al 2021). Also, we assumed the following conditions: $W=0.8 [\mu m]$ for each delay line region (${n}_{\mathrm{g}}=3.7415$, $\Delta L=5.72 [\mu m]$), ${\sigma }_{\updelta W}=1.3 \left[nm\right]$ and ${\sigma }_{\updelta t}=0.24 \left[nm\right]$. Also, based on the experimental results (Jeong et al 2020) and the consideration of $\Delta L$ in this calculation model, a standard deviation of the phase error (${\sigma }_{\mathrm{\delta \phi }}$) was assumed as $0.1\pi \left[rad.\right]$. The results are shown in Fig. 6. Here, in addition to the feedback of the optical coupling behaviors of the DCs and MMI couplers into the transfer matrix, we also considered the filtering wavelength shift (${\Delta \lambda }_{CN}$) by $\Delta W$ and the spectral fluctuation by ${\sigma }_{\mathrm{\delta \phi }}$ based on a normal distribution. The spectra shown in Fig. 6 were superimposed by iterating the same simulation 11 times.

Fig. 6

Simulated 20-nm-spaced spectral responses for the MDI-type wavelength filters based on the device scheme shown in a Fig. 1a, b Fig. 1b, and c Fig. 1c when the coupling behaviors for DCs and MMI couplers, and phase variations at each MDI were considered as the entire pattern widths are randomly fluctuated based on the designated $\Delta W$, ${\sigma }_{\updelta W}$, and ${\sigma }_{\updelta t}$. The spectra were superimposed by iterating identical simulations 11 times

For the DC-based device scheme shown in Fig. 6a, although the insertion loss keeps nearly constant for all output channels, spectral crosstalk tends to be significantly deteriorated as the output wavelengths are deviated from ${\lambda }_{CN}$. Meanwhile, for the MMI-based device schemes shown in Fig. 6b and c, although the insertion loss tends to be slightly increased as the output wavelengths are deviated from ${\lambda }_{CN}$, spectral crosstalk is not influenced all output channels together with stably preserved spectral flatness.

Based on the filter spectral responses shown in Fig. 6, we calibrated the spectral crosstalk for three kinds of MDI-type wavelength filters. Figure 7 depicts the estimated crosstalk. In this case, the spectral crosstalk was obtained by summing up the transmittances for the neighboring channels, excluding that for the main output channel. From the results of Fig. 7, it is very clear that the spectral crosstalk property for the DC-based scheme is not satisfactory for all output channels in any case and tends to be prominently influenced by the fabrication imperfections.

Fig. 7

Calibrated spectral crosstalk from the 20-nm-spaced MDI-type wavelength filter responses shown in a Figs. 6a, b Fig. 6b, and c Fig. 6c

On the other hand, the MMI-based scemes shown in Fig. 7b and c can keep the crosstalk for each output channel essentially constant, showing the lower crosstalk of < −15 [dB] for all output channels. Table 2 specifies the estimated average crosstalk values at each CWDM grid wavelength for the three kinds of the devices shown in Fig. 7, considering statistical nature of $\Delta W$, ${\sigma }_{\updelta W}$, and ${\sigma }_{\updelta t}$. Table 3 also specifies the estimated average crosstalk values within 4-nm-wide and 8-nm-wide spectral range from each CWDM channel grid. As clearly seen in quantitative data, the proposed scheme shown in Fig. 7c enables that the crosstalk level can be further reduced to be < −23 [dB] at each CWDM grid. As can be seen Table 3, these advantages of the proposed scheme are firmly preserved within 4-nm-wide spectral range and tend to be marginally available within 8-nm-wide spectral range from each CWDM channel grid, which makes the proposed wavelength filter more practical from the viewpoint of minimizing system penalty in WDM optical interconnects.

Table 2 Estimated average crosstalk values for the three kinds of wavelength filters at each CWDM grid denoted by the dotted lines in Fig. 7

Table 3 Estimated average crosstalk values for the three kinds of wavelength filters within 4-nm-wide and 8-nm-wide wavelength ranges from each CWDM channel grid

Overall, based on MMI coupling mechanism whose coupling ratios is less sensitive to the wavelength variation compared with DCs, the proposed wavelength filter schemes provide a wider operating wavelength window together with a lower spectral crosstalk. Since the asymmetric MMI coupling ratios that are prerequisite to achieve flat spectral responses can be stably preserved with respect to the pattern width variations by fabrication imperfections, which contributes to better productivity. The reason why the degradation rate of crosstalk property for the proposed scheme was somewhat higher than the previously reported scheme was insufficient flatness factor caused by a smaller number of MDI in the first-stage interferometer. Further optimization of the MMI couplers by cascade-connecting the two MMI sections (Feng et al. 2007), or locally modulating the refractive index within the MMI region (Tseng et al. 2007) enables us to choose arbitrary MMI coupling efficiencies with low excessive loss, thus enabling to achieve the degree of flatness factor much higher by connecting additional MDI-stage in the filter scheme.

3 Conclusion

We proposed and theoretically verified novel broadband operating flatband MDI-type optical filters consisting of MMI couplers with symmetric and asymmetric split ratios and DCs with asymmetric split ratios. We implemented the device modeling based on the analytic calculation of cascade-connected MDIs combined with the 3D-BPM-based numerical simulation for spectral responses of the DCs and the MMI couplers operating in the O-band spectral regime, and theoretically clarified that the proposed device scheme provides flatband spectral response with a crosstalk of –20 [dB], which is lower than the conventional scheme by more than + 10 [dB] within 8-nm-wide CWDM wavelength span. These advantages of the proposed device scheme could also be available for arbitrary channel count and channel spacing if the designated phase and path difference relations are satisfied.