1 Introduction

Heisenberg spin chains are the archetype of quantum models describing magnetic properties of a wide range of compounds. In some metals and crystals these spin chain actually appear and describe the dominant physical behavior. Their intrinsically quantum mechanical nature and the large number of spins in macroscopic materials often leads to unexpected results and insights. The continuum limit is a valid approximation in the low temperature and long wavelength limit. In the presence of biquadratic interactions, the (2 + 1) dimensional HFSC continuum model equation, which is a NLSE with quartic dispersion and fifth degree nonlinearity, was constructed in Vasanthi and Latha (2015). In Niesen and Corboz (2018), the ground-state phase diagram of the nearest-neighbor spin-1 bilinear-biquadratic Heisenberg model on the triangular lattice was investigated. It is known that, the Heisenberg model for spin-1 bosons in one dimension presents multiple quantum phases with topological Haldane phase. The robustness of such phases in front of a SU(2) symmetry breaking field as well as the emergence of novel phases was studied (De Chiara et al. 2011). The chaotic dynamics of one dimensional Heisenberg ferromagnetic spin chain were studied, by constructing the Hamiltonian equations of motion (Gnana and Latha 2017). Theirin, the trajectory and phase plots of the system with bilinear and also biquadratic interactions. An algorithm for SU(2) symmetric matrix product states with periodic boundary conditions was implemented, where, it was applied to a study of the spectrum and correlation properties of the spin-1 bilinear-biquadratic Heisenberg model (Rakov and Weyrauch 2017).Very recently, it was shown that for a NLSE, whatever its formulation, is integrable (or completely integrable) when the real and imaginary parts are linearly dependent (Tantawy and Abdel-Gawad 2021; Abdel-Gawad 2021; Abdel-Gawad and Park 2021; Abdel-Gawad et al. 2021). In the absence of biquadratic interactions, the (2 + 1) dimensional HFSC was currently studied in the Literature. In this case it is (2 + 1) dimensional NLSE with quadratic dispersion and Kerr nonlinearity. In Sulaiman et al. (2018), the (2 + 1)-dimensional HFSC that describes the nonlinear dynamics of magnet was studied. Two mathematical approaches in constructing dark, bright, kink-type and singular soliton solutions to the HFSCS were presented. The NLSE in (2 + 1) dimensions, with beta derivative evolution, was considered to study nonlinear coherent structures for HFSC with magnetic exchanges (Uddin et al. 2020). In Inc et al. (2017), the NLSE in (2 + 1)-dimensions for the HFSC, with anisotropic and bilinear interactions in the semi classical limit,. where two integrating schemes were used, was studied. The (2 + 1)-dimensions HFSCS was considered for the objective of finding the exact solutions via a specific transformation and adopting a modified version of the Jacobi elliptic expansion method (Hosseini et al. 2021). An ansatz method,to solve The HFSC equation was used to get bright and dark 1-soliton solutions. Some conditions of integrability were given which guarantee the existence of solitons (Tang et al. 2017). In Osman et al. (2020), constructio0n of further exact soliton solutions of the (2 + 1)-dimensional HFSCE and investigating the nonlinear dynamics of magnets and explains their ordering in ferromagnetic materials were carried.. The collision dynamics of soliton in discrete classical ferromagnetic spin chain with Dzyaloshinskii-Moriya (DM) interaction in the classical limit are analyzed (Parasuraman 2019). In Guana et al. (2020), The conformable fractional derivative HFSCwas considered via the complete discrimination system for polynomial method. The rational combined multi-wave solutions were obtained for HFSCE by using the logarithmic transformation and symbolic computation with ansatz functions (Yusuf et al. 2020). The NLSE that describes the spin dynamics of (2 + 1)-dimensional inhomogeneous IHFSC with bilinear and anisotropic interactions in the semi classical limit was investigated (Douvagai et al. 2021). In Li and Ma (2019), Hirota bilinear method with appropriate polynomial functions in bilinear forms, the one-order rogue waves solution and its existence condition were obtained. Different methods and techniques were used to solve nonlinear evolution equations; Tan h and Exp-function (Wazwaz 2004; Ji-Huan 2006), \(\frac{G^{\prime }}{G}\) expansion (Bekir 2008), Darboux transformation (Bueno and Marcellán 2004), Kyrdiashov method (Hosseini and Ansari 2017), Hirota-bilinear transformation (Belmonte-Beitia et al. 2007), Lie symmetries of nonlinear partial differential equations (NLPDEs) (Abdel-Gawad 2012). Here, the unified method (UM) (Abdel-Gawad 2021a, b; Srivastava et al. 2021; Tantawy and Abdel-Gawad 2021; Abdel-Gawad 2022; Abdel-Gawad et al. 2022) is used. This method asserts that the solutions of nonlinear evolution equations are represented in polynomial or rational forms in an auxiliary function which satisfies an adequate auxiliary equation.

The outlines of this paper are as in what follows.

In Sect. 2 the mathematical model equations and the perspective of the UM are presented. Sections 3 and 4 are devoted to polynomial and rational solutions respectively, while discussions and conclusions are given in Sect. 5.

2 Mathematical formulation and perspective of the UM

2.1 Mathematical model equations

The continuum model equation to the (1 + 2) dimensional HFSC system was derived in Vasanthi and Latha (2015). It reads,

$$\begin{aligned} \begin{array}{l} iw_{t}-iw_{x}+wxx+w_{yy}-2w_{xy}+2w^{2}w^{*}+\sigma \{w_{xxxx}+w_{yyyy}\\ \quad -4(w_{xxxy}+w_{yyyx})+6w_{xxyy}+6w^{*}(w_{x}^{2}+w_{y}^{2}-2w_{x}w_{y})\\\quad +2w^{2}(w_{xx}^{*}+w_{yy}^{*}-2w_{xy}^{*})-4w(w_{x}w_{y}^{*}+wyw_{x}^{*})+4w(wxw^{*}x\\\quad +w_{y}w_{y}^{*})+8w^{*}w(w_{xx}+w_{yy}-2w_{xy})+6w^{2}w^{*2}w\}=0, \end{array} \end{aligned}$$
(1)

where \(w:=w(x,y,t)\) is a complex coherent amplitude function.assigned to the bosonic operator.

Here, we consider a generalized form (1), which is,

$$\begin{aligned} \begin{array}{l} iw_{t}-iw_{x}+wxx+w_{yy}-2w_{xy}+2w^{2}w^{*}+\alpha (w_{xxxx}+w_{yyyy}\\ \quad -4(w_{xxxy}+w_{yyyx})+6w_{xxyy})+\delta w^{*}(w_{x}^{2}+w_{y}^{2}-2wxwy)\\ \quad +\beta w^{2}(w_{xx}^{*}+w_{yy}^{*}-2w_{xy}^{*})-\gamma w(w_{x}w_{y}^{*}+wyw^{*}x)+\gamma w(w_{x}w_{x}^{*}.\\ \quad +w_{y}w_{y}^{*})+\nu w^{*}w(w_{xx}+w_{yy}-2w_{xy})+\delta w^{2}w^{*2}w=0. \end{array} \end{aligned}$$
(2)

We mention that when \(\alpha =\sigma ,\,\beta = 2\sigma ;\,\gamma = 4\sigma ,\,\delta =6\sigma ;\,\nu =8\sigma\), (2) reduces to (1). For the objective to find the exact solutions of (2), we introduce the transformation with complex amplitude,

$$\begin{aligned} \begin{array}{l} w(x,y,t)=(u(x,y,t+iv(x,y,t\})e^{i(k_{1}x+k_{2}y-\omega t)},\\ w(x,y,t)^{*}=(u(x,y,t-iv(x,y,t\})e^{-i(k_{1}x+k_{2}y-\omega t)}. \end{array} \end{aligned}$$
(3)

The transformation in (3) leads to inspect the effects soliton periodic wave collision. When inserting (3) into (2), we get the real and imaginary parts respectively by,

$$\begin{aligned} & u_{yy}\left( -6\alpha k_{1}^{2}+12\alpha k_{1}k_{2}-6\alpha k_{2}^{2}+1\right) \\ &\quad +\nu u_{yy}v^{2}+4\alpha k_{1}v_{yyy}-4\alpha k_{2}v_{yy}+\alpha u_{yyyy}-2\text {}v_{y}\text {}\left( 2\alpha (k_{1}-k_{2})^{3}\right. \\ &\quad -k_{1}+k_{2}\left. +v^{2}(k_{1}-k_{2})(\beta -\delta -\nu )+\delta v(u_{x}-u_{y})\right) +v_{x}(1-2k_{1}+2k_{2}\\ &\quad +4k_{1}^{3}\alpha -v_{t}-\beta u_{yy}v^{2}+\delta \nu u^{5}-12(k_{1}^{2})k_{2}\alpha +12\alpha k_{1}k_{2}^{2}\\ &\quad \left. +v^{2}(2\beta k_{1}-2\delta k_{1}-2k_{1}\nu -2\beta k_{2}+2\delta k_{2}+2k_{2}\nu )-4\alpha k_{2}^{3}\right) \\ &\quad -2\delta vu_{y}v_{x}+2\delta vu_{x}v_{x}+12\alpha k_{2}v_{\text {xyyy}}-4\alpha u_{\text {xyyy}}\\ &\quad +u_{xy}(-2+12k_{1}^{2}\alpha -24k_{1}k_{2}\alpha +12k_{2}^{2}\alpha +2\beta v^{2}-2\nu v^{2})\\ &\quad -12\alpha k_{1}v_{\text {xyy}}+(\gamma -\delta )v_{x}^{2}+(\beta +\nu )u_{yy}\\ &\quad +u_{xx}(1-6k_{1}^{2}\alpha +12k_{1}k_{2}\alpha -6k_{2}^{2}\alpha -\beta v^{2}+\nu v^{2})+u^{2}(2(k_{1}-k_{2})\\ &\quad (\beta -\gamma +\delta +\nu )v_{y}-2(k_{1}-k_{2})(\beta -\gamma +\delta +\nu )v_{x}-2(\beta +\nu )u_{xy}\\ &\quad +(\beta +\nu )u_{xx})+u(k_{1}-k_{1}^{2}+2k_{1}k_{2}-k_{2}^{2}+(k_{1}-k_{2})^{4}\alpha +\omega -(-2+(k_{1}-k_{2})^{2}\\ &\quad (\beta -\gamma +\delta +\nu ))v^{2}+\delta \nu v^{4}-u^{3}\left( (k_{1}-k_{2})^{2}(\beta -\gamma +\delta +\nu )-2\delta \nu v^{2}-2\right) \\ &\quad +(\gamma +\delta )u_{y}^{2}+\gamma v_{y}^{2}-\delta v_{y}^{2}-2(\gamma +\delta )u_{y}u_{x}+\gamma u_{x}^{2}+\delta u_{x}^{2}+2(-\gamma +\delta )v_{y}v_{x}\\ &\quad +2v(-(k_{1}-k_{2})(2\beta -\gamma )u_{y}+\beta v_{yy}+2k_{1}\beta u_{x}-2k_{2}\beta u_{x}-k_{1}\gamma u_{x}\\ &\quad +k_{2}\gamma u_{x}-2\beta v_{xy}+\beta v_{xx}))+\alpha (12k_{1}v_{xxy}\\ &\quad -12k_{2}v_{xxy}+6u_{xxyy}-4k_{1}v_{xxx}+4k_{2}v_{xxx}-4u_{xxxy}+u_{xxxx}=0, \end{aligned}$$
(4)
$$\begin{aligned} \begin{array}{l} \delta \nu u^{5}-u^{3}(-2+(k_{1}-k_{2})^{2}(\beta -\gamma +\delta +\nu )-2\delta \nu v^{2})-v_{t}\\\quad +u_{yy}(1-6k_{1}^{2}\alpha +12k_{1}k_{2}\alpha -6k_{2}^{2}\alpha )-\beta v^{2}u_{yy}+\nu v^{2}u_{yy}\\\quad +4k_{1}\alpha v_{yyy}-4k_{2}\alpha v_{yyy}+\alpha u_{yyyy}-2v_{y}(-k_{1}+k_{2}+2(k_{1}-k_{2})^{3}\alpha \\\quad +(k_{1}-k_{2})(\eta -\delta -\nu )v^{2}+\delta v(-u_{y}+u_{x}))+v_{x}(1-2k3\\\quad +2k3+4k_{1}^{3}\alpha -12k_{1}^{2}k_{2}\alpha +12k_{1}k_{2}^{2}\alpha -4k_{2}^{3}\alpha +2\delta vu_{x}v_{x}\\\quad +v^{2}(2k_{1}\beta -2k_{2}\beta )-2k_{1}\delta +2k_{2}\delta -2k_{1}\nu +2k_{2}\nu ))-2\delta u_{y}v_{x}\\\quad +u_{xy}(-2+12k_{1}^{2}\alpha -24k_{1}k_{2}\alpha +12k_{2}^{2}\alpha +2\beta v^{2}-2\nu v^{2})\\\quad -4\alpha u_{xyyy}+u_{xx}(1-6k_{1}^{2}\alpha +12k_{1}k_{2}\alpha -6k_{2}^{2}\alpha -\beta v^{2}+\nu v^{2})\\\quad +12k_{2}\alpha v{}_{xyyy}+(\beta +\nu )u_{yy}-2(\beta +\nu )u_{xy}+\omega \\\quad +u^{2}(2(k_{1}-k_{2})(\beta -\gamma +\delta +\nu )v_{y}-2(k_{1}-k_{2}(\beta -\gamma +\delta +\nu )v_{x}\\\quad +(\beta +\nu )u_{xx})+u(k_{1}-k_{1}^{2}+2k_{1}k_{2}-k_{2}^{2}+(k_{1}-k_{2})^{4}\alpha \\\quad -(-2+(k1-k_{2})^{2}(\beta -\gamma +\delta +\nu ))v^{2}+\gamma u_{x}^{2}+\delta u_{x}^{2}+2(-\gamma +\delta )v_{y}v_{x}\\\quad +\delta \nu v^{4}+(\gamma +\delta u_{y}^{2}+(\gamma -\delta )v_{y}^{2}-2(\gamma +\delta )u_{y}u_{x}+(\gamma -\delta )v_{x}^{2}\\\quad +2v(-(k_{1}-k_{2})(2\beta -\gamma )u_{y}+\beta v_{yy}+(2k_{1}\beta -2k_{2}\beta -k_{1}\gamma +k_{2}\gamma )u_{x}\\\quad -12k_{1}\alpha v_{xyy}-2\beta v_{xy}+\beta v_{xx}))+\alpha (2k_{1}v_{xxy}-12k_{2}v_{xxy}\\\quad +6u_{xxyy}-4k_{1}v_{xxx}+4k_{2}v_{xxx}-4u_{xxxy}+u_{xxxx})==0. \end{array} \end{aligned}$$
(5)

The objective is to find the traveling waves solutions of (4) and (5). To this end, we introduce the transformations; \(u(x,y,t)=U(z),\quad v(x,y,t)=V(z)\) and \(z=b(x+y)+ct.\) Eqs. (4) and (5) reduce to,

$$\begin{aligned} \begin{array}{l} -U^{3}(-2+(\beta -\gamma +\delta +\nu )(k_{1}-k_{2})^{2}-2\delta \nu V^{2})\\\quad +U(k_{1}-k_{1}^{2}+2k_{1}k_{2}-k_{2}^{2}+k_{1}^{4}\alpha -4k_{1}^{3}k_{2}\alpha +6k_{1}^{2}k_{2}^{2}\alpha -4k_{1}k_{2}^{3}\alpha \\\quad +k_{2}^{4}\alpha +\omega -(-2+(\beta -\gamma +\delta +\nu )(k_{1}-k_{2})^{2})V^{2}+\delta \nu V^{4})\\ \quad +2\alpha b^{4}\left( U^{(4)}-U^{(3)}\right) +(b-c)V'+\delta \nu U^{5}=0,\\ \end{array} \end{aligned}$$
(6)
$$\begin{aligned} \begin{array}{l} (k_{1}-k_{1}^{2}+2k_{1}k_{2}-k_{2}^{2}+k_{1}^{4}\alpha -4k_{1}^{3}k_{2}\alpha +6k_{1}^{2}k_{2}^{2}\alpha ]-4k_{1}k_{2}^{3}\alpha \\\quad +k_{2}^{4}\alpha +\omega -(-2+(\beta -\gamma +\delta +\nu )(k_{1}-k_{2})^{2})U^{2}+\delta \nu U^{4})V\\ \quad -(-2+(\beta -\gamma +\delta +\nu )(k_{1}-k_{2})^{2})-2\delta \nu U^{2})^{3}\\ \quad +2\alpha b^{4}\left( V^{(4)}-V^{(3)}\right) +(c-b)U'++\delta {{\nu }V}^{5}=0.\\ \\ \end{array} \end{aligned}$$
(7)

The solutions of Eqs. (6) and (7) are tackled by implementing the UM. It asserts that solutions of integrable nonlinear evolution equations can be represented by polynomial and rational forms in an auxiliary function with an adequate auxiliary equation.

2.2 Outlines of the UM

2.2.1 Polynomial forms

In this case the solutions of (6) and (7) are expressed by,

$$\begin{aligned} U(z)=\sum _{j=0}^{m_{1}}a_{j}g(z)^{j},\quad V(z)=\sum _{j=0}^{m_{2}}b_{j}g(z)^{j},g^{\prime }(z)=\sum _{j=0}^{r}c_{j}g(z)^{j}. \end{aligned}$$
(8)

The Eqs. (6) and (7) are integrable in the sense of the existence of the solutions (8) if there exist integers \(m_{i},i=1,2\) and r. To identify this, we use the balance and compatibility conditions are used. . In the present case, the balance condition reads \(m_{1}=m_{2}=r-1\). To determine the consistency condition, it is required to determine the following:

  1. (a)

    The number of equations that result from inserting (12) into (6) and (7) and by setting the coefficients of \(g(z)^{i}.,i=0,1,2,...\), (say \(h(r){=5r-4}).\)

  2. (b)

    The number of arbitrary parameters \({a_{i},b_{i},c_{i}}\), (say f(r)=\(2r+1\)). For integrable equations this condition is \({5r-4-(2r+1)\le s},\)where s is the highest order derivative (here \(s=4\)). Thus, in the present case the consistency condition reads \(1\le r\le 3.\)

2.2.2 Rational forms

In the UM the rational solutions are written,

$$\begin{aligned} \begin{array}{l} U(z)=\frac{\sum _{i=0}^{i=m_{1}}a_{i}g(z)^{i}}{\sum _{i=0}^{i=m_{1}}s_{i}g(z)^{i}},\quad V(z)=\frac{\sum _{i=0}^{i=m_{2}}b_{i}g(z)^{i}}{\sum _{i=0}^{i=m_{2}}s_{i}g(z)^{i}},\\ \\ g^{\prime }(z)=\sum _{j=0}^{r}c_{j}g(z)^{j}. \end{array} \end{aligned}$$
(9)

Here, the balance condition is \(m_{1}=m_{2}=1\).

Comparison of the method used here with the known methods, in the literature.

In this paper the unified method Bueno and Marcellán (2004) was used. It unifies all known methods such as, the tanh, modified , and extended versions, the F-expansion, the exponential, the G’/G expansion method, the Lie symmetries and the Kerdyashov methods. On the other hand, in the applications, it is established that the UM is of low time cost in symbolic computations. So, we think that it prevails the use of the Lie group to construct the symmetries of nonlinear partial differential equations which requires a hierarchy of long steps. Furthermore, it provides a wide class of solutions range from hyperbolic solutions, periodic solutions to elliptic solutions in Jacobi elliptic functions.

3 Polynomial solutions of (6) and (7)

Here, we consider the following cases.

3.1 When \(r=2\)

In this case (12) reduces to,

$$\begin{aligned} U(z)=a_{1}g(z)+a_{0},\quad V(z)=b_{1}g(z)+b_{0},\;g^{\prime }(z)=c_{2}g(z)^{2}+c_{1}g(z)+c_{0}. \end{aligned}$$
(10)

When inserting (10) into (6) and (7) and by setting the coefficients of \(g(z)^{i}.,i=0,1,2,...\) yields,

$$\begin{aligned} \begin{array}{l} \alpha =-\frac{(a_{1}^{2}+b_{1}^{2})^{2}\delta \nu }{48b^{4}c_{2}^{4}},\quad b_{0}=\frac{a_{0}b_{1}}{a_{1}},\quad a_{0}=\frac{a_{1}(-1+10c_{1})}{20c_{2}},\quad c_{0}=\frac{-6+25c_{1}^{2}}{100c_{2}},\\ \\ c:=\frac{400a_{1}bc_{2}^{4}+a_{1}^{4}b_{1}\delta \nu +2a_{1}^{2}b_{1}^{3}\delta \nu +b_{1}^{5}\delta \nu }{400a_{1}c_{2}^{4}},\quad \omega =\frac{1}{1920000b^{4}c_{2}^{8}(\beta -\gamma +\delta +\nu )^{2}}\\ \left( 625\delta \nu \left( a_{1}^{2}+b_{1}^{2}\right) ^{2}\left( \delta \nu \left( a_{1}^{2}+b_{1}^{2}\right) +16c_{2}^{2}\right) ^{2}\right. +12\text {}b^{4}\text {c2}^{4}(\beta -\gamma +\delta +\nu \text {)}\\ \left( 20000c_{2}^{2}\delta \nu \left( a_{1}^{2}+b_{1}^{2}\right) \right. \\ \left. \left. \quad\quad +529\delta \nu \left( a_{1}^{2}+b_{1}^{2}\right) ^{2}(\beta -\gamma +\delta +\nu )-160000c_{2}^{4}(k_{1}(\beta -\gamma +\delta +\nu )-2)\right) \right) ,\\ \\ k_{2}=\frac{\sqrt{c_{2}^{2}(\beta -\gamma +\delta +\nu )\left( \delta \nu \left( a_{1}^{2}+b_{1}^{2}\right) +16c_{2}^{2}\right) }}{2\sqrt{2}c_{2}^{2}(\beta -\gamma +\delta +\nu )}+k_{1},a_{1}=\sqrt{\frac{4\sqrt{3}\sqrt{\alpha }b^{2}c_{2}^{2}}{\sqrt{\delta }\sqrt{-\nu }}-b_{1}^{2}},\;\nu <0. \end{array} \end{aligned}$$
(11)

Finally the solutions of (4) and (5) are,

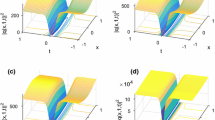
$$\begin{aligned} \begin{array}{l} u(x,y,t)=-\frac{\left( 2\sqrt{6}\tanh \left( \frac{1}{5}\sqrt{\frac{3}{2}}(\text {Ao}+z)\right) +1\right) \sqrt{\frac{4\sqrt{3}\sqrt{\alpha }b^{2}c_{2}^{2}}{\sqrt{\delta }\sqrt{-\nu }}-b_{1}^{2}}}{20c_{2}},\\ \\ v(x,y,t)=-\frac{b_{1}\left( 2\sqrt{6}\tanh \left( \frac{1}{5}\sqrt{\frac{3}{2}}(\text {Ao}+z)\right) +1\right) }{20c_{2}},\\ \\ z=b(x+y)+\frac{400a_{1}bc_{2}^{4}+a_{1}^{4}b_{1}\delta \nu +2a_{1}^{2}b_{1}^{3}\delta \nu +b_{1}^{5}\delta \nu }{400a_{1}c_{2}^{4}}t. \end{array} \end{aligned}$$
(12)

The results in (12) are evaluated numerically and they are used to display Rew against x and y for different values of t, \(\alpha\) (the coefficient of the biquadratic dispersion and \(\delta\) (the coefficient of the highest nonlinnearity) in Fig. 1 i–v. Where,

$$\begin{aligned} Rew(x,y,t)=u(x,y,t)cos(k_{1}x+k_{2}y-\omega t)-v(x,y,t)sin(k_{1}x+k_{2}y-\omega t). \end{aligned}$$
(13)
Fig. 1
figure 1

i–v. The 3D plots are displayed against x and y for different values of \(t,\,\alpha\) and \(\delta\) in Fig. 1i-iv, while in Fig. 1v shows the contour plot. When \(b = 5,b_{1} = 1.5,\nu = -0.7,\beta = 0.5,\gamma = 0.6,k_{1} = 2.5,c_{2} = 3,A_{0}=5\). In (i) \(\alpha =0.7,\delta =0.6,t=0.\) In (ii) \(\alpha =0.7,\delta =0.6,t=5.\) In (iii) \(\alpha =3.7,\delta =0.6,t=0.\) In (iv) \(\alpha =0.7,\delta =0.3,t=0.\) In (v) the same values as in (i)

Full size image

Figure 1i and ii show longitudinal and transverse “ continuum” solitons chains with tunneling along the characteristic line \(x+y=Const.\). Figure 1iii and iv show longitudinal and transverse “ continuum” solitons chains.The effects of varying the parameters \(\alpha\) and \(\delta\) is manifested via tunneling suppression when \(\alpha\) increases or when\(\beta\) decreases. While Fig. 1v shows complex lattice waves which are .

3.2 When \(r=3\)

In this the solutions take the form,

$$\begin{aligned} \begin{array}{l} U(z)=a_{2}g(z)^{2}+a_{1}g(z)+a_{0},\quad V(z)=b_{2}g(z)^{2}+b_{1}g(z)+b_{0},\;\\ \\ g^{\prime }(z)=c_{3}g(z)^{3}+c_{2}g(z)^{2}+c_{1}g(z)+c_{0}. \end{array} \end{aligned}$$
(14)

By substituting from (14) into (6) and (7), we have,

$$\begin{aligned} \begin{array}{l} \alpha \,{:=}\,-\frac{a_{2}^{4}\delta \nu \left( a_{1}^{2}+b_{1}^{2}\right) ^{2}}{768s_{1}^{4}b^{4}c_{3}^{4}},\quad b_{0}=\frac{a_{0}b_{1}}{a_{1}},\quad b_{2}=\frac{a_{2}b_{1}}{a_{1}},\quad a_{2}=\frac{3a_{1}c_{3}}{2c_{2}},\;a_{0}=\frac{3(-1+2\sqrt{6})a_{1}}{80c_{2}}+\frac{a_{1}c_{2}}{6c_{3}},\\ \\ c_{0}=\frac{(10c_{2}^{3}+9\sqrt{6}c_{2}c_{3})}{270c_{3}^{2}},\quad c=\frac{102400a_{1}bc_{2}^{4}+81a_{1}^{4}b_{1}\delta \nu +162a_{1}^{2}b_{1}^{3}\delta \nu +81b_{1}^{5}\delta \nu }{102400a_{1}c_{2}^{4})},\\ \\ \omega =\frac{1}{41943040000c_{2}^{8}(\beta -\gamma +\delta +\nu )^{2}}\left( \frac{16875\delta \nu \left( a_{1}^{2}+b_{1}^{2}\right) ^{2}\left( 9\delta \nu \left( a_{1}^{2}+b_{1}^{2}\right) +256c_{2}^{2}\right) ^{2}}{b^{4}}+1024\text {c2}^{4}(\beta -\gamma +\delta +\nu \text {)}\right. \\ \\ \left( 2880000c_{2}^{2}\delta \nu \left( a_{1}^{2}+b_{1}^{2}\right) \right. \\ +42849\delta \nu \left( a_{1}^{2}+b_{1}^{2}\right) ^{2}(\beta -\gamma +\delta +\nu )-40960000c_{2}^{4}(k_{1}(\beta -\gamma +\delta +\nu )-2))),\\ k_{2}=\frac{1}{16}\left( \frac{\sqrt{2}\sqrt{c_{3}^{2}\left( 9\delta \nu \left( a_{1}^{2}+b_{1}^{2}\right) +256\text {c2}^{2}\right) }}{c_{2}c_{3}\sqrt{\beta -\gamma +\delta +\nu }}+16k_{1}\right) ,\;c_{1}=\frac{\sqrt{3/2}}{5}+\frac{c_{2}^{2}}{3c_{3}},\\ \\ a_{1}=-\frac{b_{1}a_{2}}{\sqrt{a_{2}^{4}\delta \nu +768\alpha b^{4}c_{3}^{4}}}\sqrt{16\sqrt{3}\sqrt{\alpha }b^{2}c_{3}^{2}\sqrt{\delta }\sqrt{-\nu }-a_{2}^{2}\delta \nu }. \end{array} \end{aligned}$$
(15)

Finally the solutions of (4) and (5) are,

$$\begin{aligned} \begin{array}{l} u(x,y,t)=\frac{3\left( 10\left( 2\sqrt{6}+1\right) A_{0}e^{\frac{\sqrt{6}z}{5}}+2\sqrt{6}-1\right) \sqrt{16\sqrt{3}\sqrt{\alpha }b^{2}c_{3}^{2}\sqrt{\delta }\sqrt{-\nu }-a_{2}^{2}\delta \nu }}{80c_{2}\left( 10A_{0}e^{\frac{\sqrt{6}z}{5}}-1\right) \sqrt{a_{2}^{4}\delta \nu +768\alpha b^{4}c_{3}^{4}}},\\ \\ v(x,y,t)=-\frac{3\text {b1}\left( 10\left( 2\sqrt{6}+1\right) A_{0}e^{\frac{\sqrt{6}z}{5}}+2\sqrt{6}-1\right) }{80c_{2}\left( 10A_{0}e^{\frac{\sqrt{6}z}{5}}-1\right) },\\ \\ z=\frac{243\alpha b^{4}b_{1}^{5}c_{3}^{4}\delta \nu t\left( -32\sqrt{3}\sqrt{\alpha }a_{2}^{2}b^{2}\text {c3}^{2}\sqrt{\delta }\sqrt{-\nu }+a_{2}^{4}\delta \nu -768\alpha b^{4}c_{3}^{4}\right) }{400\text {c2}^{4}\left( a_{2}^{4}\delta \nu +768\alpha b^{4}c_{3}^{4}\right) ^{3/2}\sqrt{16\sqrt{3}\sqrt{\alpha }a_{2}^{2}b^{2}b_{1}^{2}c_{3}^{2}\sqrt{\delta }\sqrt{-\nu }-\text {a2}^{4}\text {b1}^{2}\delta \nu }}+bt+b(x+y). \end{array} \end{aligned}$$
(16)

The results in (16) are evaluated numerically and they are used to display Rew by varying t, x and yin Fig. 2i–v.

Fig. 2
figure 2

i–iv In 2(i)-(iv), the 3D plots of Reware carried by varying t, y and x, while Fig. 2 (v0 shows the contour plot. When \(\alpha =0.7,b:=5,b_{1}=1.5,\nu =-0.7,\beta =0.9,\gamma =0.6,\delta =0.6,k_{1}=2.5,c_{2}=3,A_{0}=5,a_{2}=2,c_{3}=1.7.\) (i) \(t=0\), (ii) \(t=5,\)(iii) \(y=5\)and (iv) \(x=5.\)(v) \(t=0.\)

Full size image

Figure 2i and ii show LT zig-zag SCs, with waves of higher amplitude propagate along the characteristic line \(x+y=Const.\)

Figure 2iii and v show LT zig-zag SCs, with waves of higher amplitude propagate along the characteristic line \(bx+ct=Const.\) (or \(by+ct=Const.\)).

4 Rational solutions of (6) and (7)

In this case we use the first Eq. in (9) and consider the following auxiliary equations.

4.1 When \(r=1\)

Thus, we have,

$$\begin{aligned} g^{\prime }(z)=c_{1}g(z)+c_{0}. \end{aligned}$$
(17)

By inserting (17) and (9) into (6) and (7) gives rise to,

$$\begin{aligned} \begin{array}{l} \\ \\ \quad \omega = \frac{1}{s_{1}^{4}}\left( s_{1}^{4}\left( -\alpha k_{1}^{4}+k_{1}^{2}\left( 1-6\alpha k_{2}^{2}\right) +4\alpha k_{1}^{3}k_{2}+k_{1}\left( 4\alpha k_{2}^{3}-2k_{2}-1\right) -\alpha k_{2}^{4}+k_{2}^{2}\right) -a_{1}^{4}\delta \nu \right. \\ -b_{1}^{4}\delta \nu +b_{1}^{2}s_{1}^{2}\left( k_{1}^{2}(\beta -\gamma +\delta +\nu )-2\left. k_{2}^{2}(\beta -\gamma +\delta +\nu )-2k_{1}k_{2}(\beta -\gamma +\delta +\nu )\right) \right. \\ \left. +a_{1}^{2}\left( s_{1}^{2}\left( \left( -2\left. +(k_{1}-k_{2})^{2}(\beta -\gamma +\delta +\nu )\right) \right. \right) -2b_{1}^{2}\delta \nu \right) \right) ,\\ \\ c=\frac{1}{a_{1}c_{1}s_{1}^{4}}\left( a_{1}b\text {c1}s_{1}^{4}+2\alpha b^{4}b_{1}c_{1}^{3}(c_{1}+1)s_{1}^{4}+4a_{1}^{4}b_{1}\delta \nu +4b_{1}^{5}\delta \nu -\right. \\ 2b_{1}^{3}s_{1}^{2}\left( -2\left. +(k_{1}-k_{2})^{2}(\beta -\gamma +\delta +\nu )\right) \right. \\ \left. +2a_{1}^{2}\left( 4b_{1}^{3}\delta \nu -b_{1}s_{1}^{2}\left( \left( -2\left. +(k_{1}-k_{2})^{2}(\beta -\gamma +\delta +\nu )\right) \right. -2\right) \right) \right) ,\\ c_{1}=-\frac{5}{69},\\ k_{2}=k_{1}-\frac{\sqrt{2}\sqrt{22667121a_{1}^{2}\left( 2b_{1}^{2}\delta \nu +s_{1}^{2}\right) +22667121a_{1}^{4}\delta \nu -4000\alpha b^{4}s_{1}^{4}+22667121b_{1}^{4}\delta \nu +22667121b_{1}^{2}s_{1}^{2}}}{4761s_{1}\sqrt{a_{1}^{2}+b_{1}^{2}}\sqrt{\beta -\gamma +\delta +\nu }},\\ \\ c_{0}=\frac{a_{1}s_{0}\left( 7555707\delta \nu \left( a_{1}^{2}+b_{1}^{2}\right) ^{2}-6500\alpha b^{4}s_{1}^{4}\right) -a_{0}s_{1}\left( 7555707\delta \nu \left( a_{1}^{2}+b_{1}^{2}\right) ^{2}+2000\alpha b^{4}s_{1}^{4}\right) }{117300\alpha a_{1}b^{4}s_{1}^{5}},\\ \\ s_{1}=-\frac{23\left( \frac{3}{5}\right) ^{3/4}\root 4 \of {\delta }\root 4 \of {\nu }\sqrt{a_{1}^{2}+b_{1}^{2}}}{2\sqrt{2}\root 4 \of {\alpha }b},\;b=\frac{23\left( \frac{3}{5}\right) ^{3/4}\left( 11135\sqrt{\alpha }+\sqrt{2}\left( 1-15903\root 4 \of {\alpha }\right) a_{0}\root 4 \of {\delta }\root 4 \of {\nu }\sqrt{a_{1}^{2}+b_{1}^{2}}\right) }{19072\sqrt{\alpha }a_{1}s_{0}}. \end{array} \end{aligned}$$
(18)

The solutions of (4) and (5) are,

$$\begin{aligned} \begin{array}{l} u(x,y,t)=\frac{1}{Q}\left( 11135\sqrt{\alpha }+(-15903\root 4 \of {\alpha }+1)\sqrt{2}a_{0}\root 4 \of {\delta }\root 4 \of {\nu }\sqrt{a_{1}^{2}+b_{1}^{2}})\right. \\ \left( 3e^{\frac{5z}{69}}\left( 11135\sqrt{2}\sqrt{\alpha }+(-41342\root 4 \of {\alpha }+2)a_{0}\root 4 \of {\delta }\root 4 \of {\nu }\sqrt{a_{1}^{2}+b_{1}^{2}}\right) \right. \\ \left. \left. +162112\root 4 \of {\alpha }A_{0}a_{1}\root 4 \of {\delta }\root 4 \of {\nu }\sqrt{a_{1}^{2}+b_{1}^{2}}\right) \right) ,\\ Q=5e^{\frac{5z}{69}}\left( 11135\sqrt{\alpha }+\sqrt{2}a_{0}\root 4 \of {\delta }\root 4 \of {\nu }\sqrt{a_{1}^{2}+b_{1}^{2}}(1+\right. \\ \left. \left. -20671\sqrt{2}\root 4 \of {\alpha }\right) +20264\sqrt{2}\root 4 \of {\alpha }a_{1}A_{0}\root 4 \of {\delta }\root 4 \of {\nu }\sqrt{a_{1}^{2}+b_{1}^{2}}\right) \root 4 \of {\nu },\\ v(x,y,t)=\frac{b_{1}}{a_{1}}u(x,y,t),\\ z=\frac{23\left( \frac{3}{5}\right) ^{3/4}\left( 11135\sqrt{\alpha }+\sqrt{2}\left( 1-15903\root 4 \of {\alpha }\right) a_{0}\root 4 \of {\delta }\root 4 \of {\nu }\sqrt{a_{1}^{2}+b_{1}^{2}}\right) }{19072\sqrt{\alpha }a_{1}s_{0}}(x+y)+ct.. \end{array} \end{aligned}$$
(19)

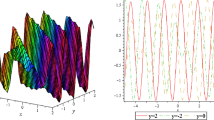
The results in (19) are used to display Rew in Fig. 3i–iii.

Fig. 3
figure 3

The 3D plots are carried in (i) and (ii), while the contour plot is shown in Fig. 3iii. When \(\alpha \,{:=}\,0.7,\nu \,{:=}\,0.7,\beta \,{:=}\,1.3,\gamma = 0.6,\delta = 0.8,k_{1}=2.5,a_{1}=0.7,A_{0}=5,\text {b1} = 1.5,a_{0}=1.6,s_{0}=1.2\). (i) \(t=0,\)(ii) \(t=5.\)

Full size image

Figure 3i and ii show longitudinal SC with small magnitude and transverse SC with higher magnitude. Figure 3iii shows lattice waves with gap.

4.2 When r = 2

Here, we write,

$$\begin{aligned} g^{\prime }(z)=c_{2}g(z)^{2}+c_{1}g(z)+c_{0}. \end{aligned}$$
(20)

From (20) and (9) int (6) and (7), we get,

$$\begin{aligned} \begin{array}{l} \omega =\frac{1}{a_{1}b_{1}s_{1}^{4}}(a_{1}^{2}(b-c)c_{2}s_{0}s_{1}^{3}-2a_{0}\text {}b^{4}b_{1}c_{2}s_{1}\left( c_{1}^{2}s_{1}^{2}(s_{1}-14c_{2}s_{0})\right. \\ +c_{1}^{3}s_{1}^{3}+8c_{1}c_{2}c_{0}s_{1}^{3}+6c_{1}c_{2}s_{1}s_{0}(6c_{2}s_{0}-s_{1})\\ \left. +6c_{2}^{2}s_{0}^{2}(s_{1}-4c_{2}s_{0})++2c_{2}c_{0}s_{1}^{2}(s_{1}-8c_{2}s_{0})\right) \alpha \\ a_{1}^{5}b_{1}\delta \nu +a_{1}^{3}\left( b_{1}s_{1}^{3}\left( (k_{1}-k_{2})^{2}(\beta -\gamma +\delta +\nu )-2\right) -2b_{1}^{3}\delta \nu \right) +a_{1}\left( a_{0}c_{2}^{2}s_{1}^{4}(c-b)\right. \\ +b_{1}\left( (k_{2}^{2}-\alpha k_{1}^{4}+4\alpha k_{2}k_{1}^{3}-\alpha k_{2}^{4})s_{1}^{4}+2b^{4}c_{2}s_{0}\left( c_{1}^{2}s_{1}^{2}(s_{1}-14c_{2}s_{0})\right. \right. \\ +(c_{1}^{2}+8c_{1}c_{2}c_{0})s_{1}^{3}+c_{1}^{2}s_{1}^{2}(s_{1}-14c_{2}s_{0})+6c_{2}^{2}s_{0}^{2}(s_{1}-4c_{2}s_{0})\\ +2c_{2}c_{0}s_{1}^{2}(s_{1}-8c_{2}s_{0})+6c_{1}c_{2}s_{1}s_{0}(6c_{2}s_{0}-\text {s1}))\alpha +k_{1}^{2}s_{1}^{4}\left( 1-6\alpha k_{2}^{2}\right) \\ \left. +k_{1}s_{1}^{4}\left( 4\alpha k_{2}^{3}-2k_{2}-1\right) \right) -b_{1}^{5}\delta \nu +b_{1}^{3}s_{1}^{2}\left( k_{1}^{2}(\beta -\gamma +\delta +\nu )\right. \\ \left. \left. \left. -2k_{1}k_{2}(\beta -\gamma +\delta +\nu )-2+k_{2}^{2}(\beta -\gamma +\delta +\nu )\right) \right) \right) ,\\ k_{2}=\frac{1}{Q}\left( 60000a_{0}^{3}b_{1}c_{2}^{5}k_{1}s_{0}^{2}(\beta -\gamma +\delta +\nu )+1350a_{0}b_{1}^{3}c_{2}^{3}k_{1}s_{0}^{2}(\beta -\gamma +\delta +\nu )\right. \\ +\sqrt{5}\surd \left( \frac{a_{0}^{2}b_{1}^{2}c_{2}^{4}\text {so}^{2}\left( 400a_{0}^{2}c_{2}^{2}+9b_{1}^{2}\right) (\beta -\gamma +\delta +\nu )}{c_{1}+1}\left( \left( 8\text {ao}^{2}(80\text {c1}+7)\delta \nu +45(8\text {c1}+1)\text {so}^{2}\right) \right. \right. \\ 1800b_{1}^{2}c_{2}^{2}+162b_{1}^{4}(80c_{1}+7)\delta \nu +c_{2}^{4}\text {}\left( 3600000a_{0}^{2}(8c_{1}+1)s_{0}^{2}\right. \\ +81\alpha b^{4}\left( 2800000c_{1}^{5}-1570000c_{1}^{4}+61000c_{1}^{3}+19200c_{1}^{2}+590c_{1}-183\right) s_{0}^{4}\\ \left. \left. \left. \left. +320000a_{0}^{4}(80c_{1}+7)\delta \nu \right) \right) \right) \right) ,\\ Q=150a_{0}b_{1}s_{0}^{2}\left( 400a_{0}^{2}c_{2}^{2}+9b_{1}^{2}\right) (\beta -\gamma +\delta +\nu ),\\ c=\frac{9\alpha b^{4}b_{1}\left( 2000c_{1}^{3}-300c_{1}^{2}-390c_{1}+49\right) }{200a_{0}(40c_{1}-19)\text {c2}}+b,\\ \delta =\frac{3\left( 2400000c_{1}^{5}-1660000c_{1}^{4}+63000c_{1}^{3}+55100c_{1}^{2}+917c_{1}+1371\right) }{7200000c_{1}^{5}-4480000c_{1}^{4}+401500c_{1}^{3}+69050c_{1}^{2}-11865c_{1}+988},\\ \nu =-\frac{27\alpha b^{4}(10c_{1}-1)\left( 180000c_{1}^{4}-26500c_{1}^{3}-2550c_{1}^{2}+515c_{1}-52\right) c_{2}^{4}s_{0}^{4}}{(20c_{1}+3)\left( 400a_{0}oc_{2}^{2}+9b_{1}^{2}\right) ^{2}},\\ c_{0}=-\frac{m(\text {so}(c_{2}s_{0}-c_{1}s_{1}))}{\text {s1}^{2}},\;a_{1}=\frac{a_{0}c_{2}\left( 120m^{2}-4m-1\right) }{12m^{2}(2m-1)},\;s_{1}=\frac{a_{1}(2m-1)s_{0}}{a_{0}},\;m:=-\frac{1}{4},\\ s_{0}=\frac{\root 4 \of {20c_{1}+3}\root 4 \of {-\nu }\sqrt{400a_{0}^{2}c_{2}^{2}+9b_{1}^{2}}}{3^{3/4}\root 4 \of {\alpha b^{4}\left( 1800000c_{`}^{5}-445000c_{1}^{4}+1000c_{1}^{3}+7700c_{1}^{2}-1035c_{1}+52\right) c_{2}^{4}}}. \end{array} \end{aligned}$$
(21)

The solutions of (4) and(5) are,

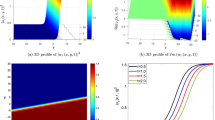
$$\begin{aligned} \begin{array}{l} u(x,y,t)=-\frac{P_{1}}{Q_{1}},\quad P_{1}=2a_{0}\root 4 \of {\frac{\alpha b^{4}\left( 1800000c_{`}^{5}-445000c_{1}^{4}+1000c_{1}^{3}+7700c_{1}^{2}-1035c_{1}+52\right) c_{2}^{4}}{(20c_{1}+3)\left( 400a_{0}^{2}c_{2}^{2}+9b_{1}^{2}\right) ^{2}}}\\ (\sqrt{100c_{1}^{2}+10c_{1}-1}\tanh \left( \frac{1}{20}\sqrt{100c_{1}^{2}+10c_{1}-1}(A_{0}+z)\right) +10c_{1}+3),\\ Q_{1}=\root 4 \of {3}\root 4 \of {-\nu }\left( \sqrt{100c_{1}^{2}+10c_{1}-1}\tanh \left( \frac{1}{20}\sqrt{100c_{1}^{2}+10c_{1}-1}(A_{0}+z)\right) +10c_{1}-2\right) ,\\ v(x,y,t)=\frac{b_{1}}{a_{1}}u(x,y,t),\;z=\frac{1}{50000\text {ao}(8c_{1}+1)(20c_{_{1}}+3)\text {c2}}\left( 50000a_{0}b\left( 160c_{1}^{2}+44c_{1}+3\right) \right. \\ c_{2}(t+x+y)-b^{4}b_{1}t\alpha \left( 14400000c_{1}^{5}(\delta -1)-40000c_{1}^{4}(89\delta -69)\right. \\ \left. \left. +8000c_{1}^{3}(\delta -36)+416\delta +9+100c_{1}^{2}(616\delta -381)-30c_{1}(276\delta -581)\right) \right) . \end{array} \end{aligned}$$
(22)

The solutions in (22) are used to display Rew in Fig. 4i–v.

Fig. 4
figure 4

i–v In Fig. 4 (i) and (ii) 3D plot is carried for different values t. In (iii) and (iv) y and x are taken fixed respectively. While Fig. 4(v) shows contour plot. When \(\alpha = 0.7,b = 5,b_{1} = 1.5,\nu = -0.7,\beta \,{:=}\,0.9,\gamma = 0.6,\delta = 0.6,k_{1} = 2.5,c_{2} = 3,t = 5,A_{0} = 5,c_{1} = 0.09,a_{0} = -1.5\)

Full size image

Figure 4i–iv show longitudinal-transverse solitons chains modulation along y and x axes respectively. On the other hand they exhibit different structure of cable waves. While Fig. 4v shows lattices waves.

4.3 Results and discussion

The results found in Sects. 3 and 4 are summarized in what it follows.

  1. (a)

    Figure 1 shows longitudinal and transverse “ continuum” solitons chains (LTCSCs) in the presence or the absence of tunneling (which occurs along a characteristic line).

  2. (b)

    Figure 2 shows LTCSCs but with small and relatively higher magnitudes in space. In space-time the same result holds but with remarkably high magnitude soliton along a characteristic line.

  3. (c)

    Figure 4 shows LTCSCs modulation along yand x.

Thus, we deduce that the solutions of the continuum model equation of HFSC exhibit LTCSCs and this result is significant and completely new. Furthermore, the longitudnal and transverse lattice wave structures are of clear relevance to the (2 + 1) HFSC.

5 Conclusions

Here, the continuum model equation, analog to the Heisenberg ferromagnetic spin chain in (2 + 1) dimensional system is studied. The model equation is a nonlinear Schrodinger equation with biquadratic dispersion and fifth degree nonlinearity. A transformation for describing complex amplitude solution, is introduced. It leads to inspect the effects of soliton- periodic wave collision. Collisions are elastic when smooth waves are produced, which hold in the present case. The exact solutions are found by implementing the unified method. The solutions obtained are evaluated numerically and represented in figures. These figures exhibit longitudinal- transverse continuum solitons chains with different structures, analog to the Heisenberg ferromagnetic spin chain. Different pulses structures are observed, among them, Zig-zag solitons, in the presence (or absence) of tunneling, cable waves and solitons with self- phase modulation . It is also remarked that the contour plots show lattice (or complex lattice) waves.