1 Introduction

Visible light communications (VLC) are data transmission techniques that use light-emitting diodes (LEDs) to transfer information in the visible light spectrum. The use of VLC systems for wireless data transmission in indoor environments, particularly for low mobility and short-range applications, is becoming increasingly popular Mohammed and Abd Elkarim (2015); Ibrahim et al. (2020); Asmaa et al. (2021).As a result of its benefits over radio frequency (RF) communications, VLC is currently being evaluated with great attention in broad research. Compared to RF systems, these systems offer various advantages, including reduced implementation costs, unlimited license bandwidth, a significant advantage of VLC technology, improved privacy, and security, as light rays cannot propagate through walls Matheus et al. (2019). Additionally, VLC systems are immune to RF interference, consume less energy, no health hazard, provide better security and faster data rates. There are numerous uses for VLC, including localization, high-speed video streaming, high-bit-rate data broadcasting in indoor environments, and underwater data transmission. The use of this technology is also preferable in situations where electromagnetic interference (EMI) is a concern, such as aircraft, military, and vehicle-to-vehicle communications Hesham et al. (2020); Ismail et al. (2021); Hesham and Ismail (2022).

Orthogonal frequency division multiplexing (OFDM) is a multi-carrier modulation technique that enables the enhancement of overall spectrum efficiency, reduction of energy consumption, and reduction of transmission latency Mohammed et al. (2017). Additionally, the OFDM system simultaneously permits several users by allocating specific sub-carriers for time intervals. This enables the transmitter to dynamically adapt the required bandwidth according to resource availability. In conventional RF-OFDM, the transmitted signals have complex values and may even be negative, which is not feasible with an optical data transmission technique, whereas optical OFDM (O-OFDM) systems require the presence of real and non-negative components in the transmitted signals. Several O-OFDM systems have recently been developed, including DC-biased optical OFDM (DCO-OFDM) system, Asymmetrically clipped optical OFDM (ACO-OFDM), and asymmetrically clipped DC biased optical (ADO-OFDM). In DCO-OFDM, the non-negative values are accomplished by applying a constant dc-bias to the OFDM signal as described in Zhang and Zhang (2014). The ACO-OFDM modulates only the odd sub-carriers, resulting in a non-negative signal as presented in Dissanayake et al. (2011). The ADO-OFDM uses DCO-OFDM symbols to map the even sub-carriers and ACO-OFDM symbols to map the odd sub-carriers Chen et al. (2017); Eltoukhi et al. (2018); Samir et al. (2021). Furthermore, the main drawback of the OFDM system based on VLC is the high peak to average power ratio (PAPR) that degrades the system performance and the reduction of the system throughput due to the usage of cyclic-prefix (CP) and photo source requirements Svaluto Moreolo et al. (2010).

In VLC communication systems the PAPR problem can be illustrated as follows: LEDs are employed as transmitters, and high-power signals easily influence them. LEDs’ operational voltage range is limited, and the relationship between voltage and current (V-I) is non-linear. The non-linear V-I characteristic of LEDs causes the OFDM signal to be distorted, resulting in a high PAPR. LED devices tend to overheat due to their high peak power. In bipolar OFDM systems, the high PAPR values result in significant power consumption for the transmitter power amplifier (PA) Shawky et al. (2018). As a result, nonlinear distortion occurs, causing distortion both in-band and out-of-band, which significantly impacts the overall system performance. Furthermore, the nonlinear distortion arises in the absence of this condition, resulting in a loss of sub-carrier orthogonality and degradation of performance. Thus, due to the high PAPR of OFDM, system components with a broad linear range capable of accommodating the signal are required. Fig. 1 shows the effects of non-linear PA on linear response (a) and bit error rate (b). In reality, the PA has a limited linear region, beyond which it saturates to a maximum output level as shown in Fig. 1a.

Fig. 1
figure 1

Effects of non-linear power amplifier on: a amplifier response and b bit error rate

Full size image

In OFDM system, the signal may have high PAPR. The PAPR of an OFDM signal x(n) is the ratio of the peak instantaneous power to the average power of an OFDM signal. Mathematically, the PAPR measured in dB is expressed as follows Mohammed et al. (2019):

$$\begin{aligned} \text {PAPR}\{x(n)\}(dB)&= 10.\log _{10}\left( \dfrac{\max {|x(n)|^2}}{\mathbf{E }\{|x(n)|^2\}} \right) . \end{aligned}$$
(1)

where, \(\mathbf{E }\{.\}\) is the statistical expectation operator, max\(|x(n)|^2\) is the peak OFDM signal power and \(\mathbf{E }\{|x(n)|^2\}\) is the average power of the OFDM signal. As a result, it is necessary to minimize the high PAPR of the OFDM signal in order for it to be fed into the LEDs’ linear region Vappangi and Vakamulla (2018). Therefore, there are a variety of PAPR reduction approaches, which can be broadly classified into three categories:

  • Distortion based techniques: Distortion-based techniques are the most straightforward PAPR reduction schemes. These schemes distort the spectrum, and the distortion of the spectrum can be corrected to a certain extent by using filtering operation Mohammed et al. (2018). These techniques are methods such as clipping, peak windowing, and non-linear companding.

  • Non-distortion techniques: This type of PAPR reduction technique does not distort the shape of the OFDM signal, and therefore no spectral distortion takes place Han and Lee (2005). The main idea of this type is generating multiple permutations of the OFDM signal and transmitting the one with minimum PAPR. However, this type has high computational complexity. Scrambling techniques, selective level mapping (SLM), and partial transmit sequences (PTS) are examples of non-distortion techniques.

  • Hybrid techniques: There are many hybrid techniques also available in the literature Hussein et al. (2020); Gahlot and Sukhijia (2020). These methods reduce high PAPR by combining two techniques, such as clipping with coding, SLM with coding, pre-coding with clipping, interleaving with companding, etc.

In Mohammed et al. (2021), the authors have proposed the IMADJS scheme for PAPR reduction in OFDM systems. The IMADJS scheme is used to generate a linear function to ensure that the transmitted signal’s average power before companding is about the same after companding. IMADJS scheme can operate with a linear dynamic range and a non-linear dynamic range. The IMADJS technique simultaneously adjusts the small and large amplitude while maintaining the same average power level before and after companding. Compared to alternative companding techniques such as \(\mu -\)law, Absolute exponential (AEXP) companding technique, and new error function (NERF), this allows for a reduction in PAPR without impacting the BER performance. The IMADJS has five parameters (low-in, low-out, high-in, high-out and \(\gamma\)). The impact of each parameter on PAPR and BER has been analyzed separately. The optimal value for the low-in parameter is zero (low-in \(=0\)), the low-out parameter is zero (low-out \(=0\)) and the optimal value for \(\gamma\) is 1 for the degree of companding (\(\gamma\)). As with the high-in and high-out parameters, reducing the high-in parameter limits large signals while changing the high-out parameter modifies small signals. A decrease follows this improvement in the performance of the BER. There is always a trade-off between PAPR improvement and BER degradation based on the above. In El-Bakry et al. (2017a, 2017b); Afifi et al. (2020); Mohamed Yasin Ibrahim Afifi, El-Sayed Soliman Ahmed Said (2020), the symbol time compression (STC) technique was proposed to reduce OFDM symbol by one-half.

The main contribution of this paper is the throughput enhancement and the PAPR reduction for OFDM systems based on VLC. Hence, the proposed STC-IMADJS technique is implemented via two steps on the transmitter side, the STC process for OFDM symbol compression and the IMADJS process for PAPR reduction. On the other hand, the inverse function for IMADJS is applied at the receiver side, and then the symbol time expansion (STE) process is applied for data recovery. The STC technique is implemented by using Walsh code for signal spreading and then a symbol mapping at the transmitter for symbol compression. As a result, the STC technique saves \(50\%\) of the symbol duration. Thus, the STC/DCO-OFDM, STC/ACO-OFDM, and STC/ADO-OFDM systems have twice more throughput than the traditional systems. After that, the IMADJS technique is modified to be compatible with the optical signal in the VLC system. As a result, the STC-IMADJS/DCO-OFDM, STC-IMADJS/ACO-OFDM, and STC-IMADJS/ADO-OFDM systems reduce the PAPR in comparison with the traditional systems. Finally, the proposed STC-IMADJS technique improves the system throughput, which are N, N/2, and N for the DCO-OFDM, the ACO-OFDM, and the ADO-OFDM systems, respectively. In addition to this, the PAPR for DCO-OFDM, ACO-OFDM, and ADO-OFDM systems will be reduced by 3.7 dB, 8.16 dB, and 1.81 without any effects on the BER performance in comparison with other companding techniques. The computational complexity of the proposed technique is calculated. The simulation results are applied using Matlab 20201a for the proposed STC-IMADJS technique based on the BPSK modulation scheme under additive white Gaussian noise (AWGN) channel. The evaluation methods are in terms of bit error rate (BER), time-domain waveform, and complementary cumulative distribution function (CCDF).

The structure of this paper is introduced as follows: In Sect. 2, the proposed STC-IMADJS scheme is introduced. Section 3 provides simulation results for validating the theoretical analysis. Finally, our conclusions are presented in Sect. 4.

2 Integrated STC-IMADJS technique in VLC

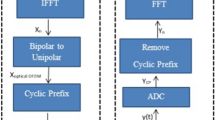
This section presents the integrated STC-IMADJS technique in associated with the DCO-OFDM, ACO-OFDM, and ADO-OFDM systems. The STC scheme is being used to improve the system throughput, while the IMADJS scheme is applied to minimize the PAPR. The block diagram of the transmitter and receiver for the proposed DCO-OFDM and ACO-OFDM systems, which employ the STC-IMADJS technique, is demonstrated in Fig. 2. The selection parameter (k) is used to determine the type of OFDM systems that are based on VLC. For example, if we choose \(k=1\), the block diagram represents the DCO-OFDM system, while selecting \(k=2\) indicates the block diagram illustrates the ACO-OFDM system. Also, the block diagram of the transmitter and receiver for the proposed STC-IMADJS/ADO-OFDM technique will be presented in Fig. 3. The block diagrams will demonstrate in more details in this section during the discussion.

Fig. 2
figure 2

Block diagram of the proposed STC-IMADJS/DCO-OFDM and STC-IMADJS/ACO-OFDM Techniques

Full size image
Fig. 3
figure 3

Block diagram of the proposed STC-IMADJS/ADO-OFDM Systems

Full size image

2.1 The STC scheme

Walsh spreading codes are used to accomplish the spreading procedure during transmission El-Bakry et al. (2017a).

$$\begin{aligned} c_{0}=\left[ \begin{array}{ll} 1&1 \end{array}\right] , \quad c_{1}=\left[ \begin{array}{ll} 1&0 \end{array}\right] \end{aligned}$$
(2)

Following the spreading procedure, the stream of bits on the mth sub-carrier is transformed into

$$\begin{aligned} a_{m}=b \oplus c, \quad m=0,1, \ldots , N-1 \end{aligned}$$
(3)

where b represents a bitstream and c is Walsh spreading code with chip rate\(T_{c}=T_{b} / 2\). After that, a unipolar to polar conversion is applied, and the total of each pair of consecutive sub-carriers is merged. As a result, the \(m^{\text{ th } }\) compressed symbol is introduced in the following form:

$$\begin{aligned} d_{m}^{c}=a_{m}+a_{m+1}, \quad m=0,1, \ldots , N-1 \end{aligned}$$
(4)

where \(d_{k}^{c}\) is the compressed data symbol with length N/2. Finally, symbol mapping is applied, and the \(k^{t h}\) sub-carrier of the complex data symbol is denoted as \(X_{k}^{c}, k = 0, 1, \ldots , N/2\) as shown in Fig. 2. Symbol demapping is used in receiving to demodulate the compressed data symbol obtained after the FFT operation \(Y_{k}^{c}, k=0,1, \ldots , N/2\) is accomplished. The bits on each sub-carrier will be reconstructed using similar codes that are used at the transmitter for despreading, and then summation is applied. The detected bit stream \({b}_{m}\) of the \(m{^th}\) demapped symbol \({\hat{Y}}_{m}^{c}\) is given by

$$\begin{aligned} {\hat{b}}_{m}=\sum {\hat{Y}}_{m} c_{0} \text{ and } {\hat{b}}_{m+1}=\sum {\hat{Y}}_{m} c_{1}, \quad m=0,1, \ldots , N-1 \end{aligned}$$
(5)

2.2 The IMADJS scheme

The IMADJS scheme is proposed in Mohammed et al. (2021) to reduce high PAPR in OFDM systems. This scheme reduces the PAPR by enlarging small signals and compressing peak signals simultaneously. The IMADJS companding function is defined as:

$$\begin{aligned} f(x)&= {\left\{ \begin{array}{ll} \, c \quad &{}\text{ if } x\le a,\\ \, \Bigg (\bigg (\dfrac{x-a}{b-a}\bigg )^{\gamma }(d-c)+c\Bigg ) &{}\text{ if } a< x < b,\\ d \quad &{}\text{ if } x \ge b. \ \end{array}\right. } \end{aligned}$$
(6)

where a is low input of the signal x, b is high input of the signal x, c is the low output of the signal x, d is the high output of the signal x, and \(\gamma\) is a positive number uses as a degree of companding. As it is proven in Mohammed et al. (2021), the optimum values for the parameters a, c and \(\gamma\) is zero, zero and one respectively (a=0, c=0 and \(\gamma\)=1). The parameters b and d are decreased carefully to reduce the high PAPR in the proposed system. The IMADJS function works and improves high PAPR when the parameters b and d are less than the peak of the signal. By substitution the values of a, c and \(\gamma\) in Eq. (6), we obtain the IMADJS linear function as follows:

$$\begin{aligned} f(x)= \left\{ \begin{array}{l l} 0&{} \text{ if } x \le 0,\\ \\ \dfrac{xd}{b} &{} \text{ if } 0< x < b,\\ \\ d&{} \text{ if } x \ge b. \end{array} \right. \end{aligned}$$
(7)

2.3 Integrated STC-IMADJS technique with DCO-OFDM

After completing the STC stage, the symbol will be compressed into one-half of its original length. As a result, the frequency domain of the modulated signal in the DCO-OFDM system is expressed as:

$$\begin{aligned} X_{k}^{c}=\Big [X_{0}^{c} , X_{1}^{c} ,\ldots , X_{{\frac{N}{2}}-1}^{c}\Big ]. \end{aligned}$$
(8)

where \(X_k^c\) is the modulated symbol obtained by the STC scheme, consequently, after Hermitian symmetry operation, the modulated signal can be presented as follows:

$$\begin{aligned} X_{k}^{\text {STC/DCO}}=\Bigg [\underbrace{0}_{\chi _{0}}, X_{0}^{c}, X_{1}^{c}, \ldots , \underbrace{0}_{X_{N / 2}}, X_{N / 2+1}^{*}, \ldots , X_{1}^{c *}, X_{0}^{c *}\Bigg ] \end{aligned}$$
(9)

As a result, compared to the conventional DCO-OFDM system, the number of transmitted signals is N instead of 2N. The time-domain sample of the function \(x_{n}^{\text {STC/DCO}}\) is provided by

$$\begin{aligned} \begin{gathered} x_{n}^{\text {STC/DCO}}=\frac{1}{N} \sum _{k=0}^{N-1} X_{k}^{\text {STC/DCO}} \exp \left( \frac{j 2 \pi k n}{N}\right) , \;\;\;\; 0 \le n \le N-1 \end{gathered} \end{aligned}$$
(10)

This is followed by appending the cyclic prefix (CP) to the beginning of the symbol. Finally, the transmitted signal will be companded by the IMADJS function in order to minimize the PAPR. As a result, the companded signal can be expressed as follows:

$$\begin{aligned} z_{n}^{\text {STC-IMADJS/DCO}}=f(x) \times x_{n}^{\text {STC/DCO}} \end{aligned}$$
(11)

The received signal with additive white Gaussian noise (AWGN) will be expressed by

$$\begin{aligned} \begin{aligned} y_{n}^{\text {STC-IMADJS/DCO}}=&z_{n}^{\text {STC-IMADJS/DCO}}+w_{n}, \;\;\;\;&0 \le n \le N-1 \end{aligned} \end{aligned}$$
(12)

where \(w_{n}\) is AWGN.The received signal \(y_{n}^{\text {STC-IMADJS/DCO}}\) will be decompanded as follows:

$$\begin{aligned} y_{n}^{\text {STC/DCO}}=f(x)^{-1}\times y_{n}^{\text {STC-IMADJS/DCO}} \end{aligned}$$
(13)

Following DC bias removal and FFT operation, the received signal can be represented as follows:

$$\begin{aligned} \begin{array}{r} Y_{k}^{\text {STC/DCO}}=\sum _{n=0}^{N-1} y_{n}^{\text {STC/DCO}} \exp \left( -\frac{j 2 \pi k n}{N}\right) , \;\;\;\; 0 \le k \le N-1 \end{array} \end{aligned}$$
(14)

The proposed STC-IMADJS/DCO-OFDM scheme utilizes the following data rate Mesleh et al. (2011)

$$\begin{aligned} \Re ^{\text {STC/DCO}} = \left( \frac{N - 2}{N + N_g}\right) \;\;\;\;\text {bits/s/Hz}, \end{aligned}$$
(15)

where B is the bandwidth, and \(N_g\) is the number of guard subcarriers employed in the CP.

2.4 Integrated STC-IMADJS technique with of ACO-OFDM

The ACO-OFDM signal following the STC and Hermitian symmetry operations can be expressed as follows:

$$\begin{aligned} \begin{aligned}&X_{k}^{\text {STC/ACO}} =\Bigg [\underbrace{0}_{\chi _{0}^{\text {ACO}}}, X_{0}^{c}, 0 , \ldots , X_{N / 2-1}^{c} , \underbrace{0}_{\chi _{N}^{\text {ACO}}}, X_{N / 2-1}^{c*}, \ldots , 0 , X_{0}^{c*}, \underbrace{0}_{\chi _{2N}^{\text {ACO}}}\Bigg ] \end{aligned} \end{aligned}$$
(16)

Following the IFFT operation, the time domain sample of \(x_n^{\text {STC/ACO}}\) is given by

$$\begin{aligned} \begin{array}{r} x_{n}^{\text {STC/ACO}}=\frac{1}{2N} \sum _{k=0}^{2N-1} X_{k}^{\text {STC/ACO}} \exp \left( \frac{j2 \pi kn}{N}\right) , \;\;\;\; 0 \le n \le 2 N-1 \end{array} \end{aligned}$$
(17)

Finally, the transmitted signal follows the insertion of the CP, and the operation of the IMADJS is as described as follows:

$$\begin{aligned} z_{n}^{\text {STC-IMADJS/ACO}}=f(x)\times x_{n}^{\text {STC/ACO}} \end{aligned}$$
(18)

The received signal with AWGN is given by

$$\begin{aligned} \begin{array}{r} y_{n}^{\text {STC-IMADJS/ACO}}=z_{n}^{\text {STC-IMADJS/ACO}}+w_{n}, \;\;\;\; 0 \le n \le 2 N-1 \end{array} \end{aligned}$$
(19)

The received signal after applying the decompanding IMADJS function is given by:

$$\begin{aligned} y_{n}^{\text {STC/ACO}}=f(x)^{-1}\times y_{n}^{\text {STC-IMADJS/ACO}} \end{aligned}$$
(20)

Following the FFT operation, the received signal is expressed as:

$$\begin{aligned} \begin{array}{r} Y_{k}^{\text {STC/ACO}}=\sum _{n=0}^{N-1} y_{n}^{\text {ACO}} \exp \left( -\frac{j 2 \pi k n}{N}\right) , \;\;\;\; 0 \le k \le N-1 \end{array} \end{aligned}$$
(21)

The data rate that the STC/ACO-OFDM can achieve is provided by Mesleh et al. (2011)

$$\begin{aligned} \Re ^{\text {STC/ACO}}= \left( \frac{N/2 - 2}{N + N_g}\right) \;\;\;\;\text {bits/s/Hz}. \end{aligned}$$
(22)

2.5 Integrated STC-IMADJS technique with ADO-OFDM

The block diagram of the proposed STCADO-OFDM with IMADJS system is presented in Fig. 3. After the input bitstreams have been mapped with the STC scheme, the Hermitian symmetry is applied as follows:

$$\begin{aligned} X_{k}^{\text {STC/HER}}=\Bigg [{0}, X_{0}^{c}, X_{1}^{c}, \ldots , X_{N / 2-1}^{c}, {0}, X_{N / 2-1}^{c*}, \ldots , X_{1}^{c *}, X_{0}^{c *}\Bigg ] \end{aligned}$$
(23)

Following Hermitian symmetry, the output signal is split into odd and even components as follows:

$$\begin{aligned} X_{k}^{\text {odd}}= & {} \Bigg [{0} , X_{0}^{c}, {0} , X_{2}^{c} , \ldots , X_{N/2-2}^{c}, {0} , X_{N / 2-2}^{c*} , {0} , \ldots , X_{2}^{c *} , {0} , X_{0}^{c *} ,{0}\Bigg ] \end{aligned}$$
(24)
$$\begin{aligned} X_{k}^{\text {even}}= & {} \Bigg [{0} , {0} , X_{1}^{c}, {0} , \ldots , X_{N/2-1}^{c}, {0} , {0} , {0} , X_{N/2-1}^{c*} , \ldots , {0} , X_{0}^{c *} ,{0}\Bigg ] \end{aligned}$$
(25)

Then, \(X_k^{\text {even}}\) and \(X_k^{\text {odd}}\) are applied to N-point IFFT to give two real bipolar signal vectors as follows:

$$\begin{aligned}&\begin{array}{r} x_n^{odd} = \text {ifft}(X_{k}^{\text {odd}}) , \;\;\;\; 0 \le n \le N-1 \end{array} \end{aligned}$$
(26)
$$\begin{aligned}&\begin{array}{r} x_n^{even} = \text {ifft}(X_{k}^{\text {even}}), \;\;\;\; 0 \le n \le N-1 \end{array} \end{aligned}$$
(27)

Hence, The ACO-OFDM signal is provided by clipping the negative values in \(x_n^{\text {odd}}\) to zero. On the other hand, the DC bias is added to \(x_n^{\text {even}}\) in order to generate the DCO-OFDM signal Eltoukhi et al. (2018). Finally, the STC/ADO-OFDM signal is generated by summing the ACO-OFDM and DCO-OFDM signals.

$$\begin{aligned} x_n^{\text {STC/ADO}} = x_n^{\text {even}}+ x_n^{\text {odd}} \end{aligned}$$
(28)

Following the insertion of CP, the transmitted signal will be combined using the IMADJS function in the following sequence:

$$\begin{aligned} z_{n}^{\text {STC-IMADJS/ADO}}=f(x)\times x_{n}^{\text {STC/ADO}} \end{aligned}$$
(29)

In reception operation, the received signal with AWGN \(y_{n}^{\text {STC-IMADJS/ADO}}\) will be decompanded as follows:

$$\begin{aligned} y_{n}^{\text {STC/ADO}}=f(x)^{-1}\times y_{n}^{\text {STC-IMADJS/ADO}} \end{aligned}$$
(30)

After FFT processing the signal is given

$$\begin{aligned} \begin{array}{r} Y_{k}^{\text {STC/ADO}}=\sum _{n=0}^{N-1} y_{n}^{\text {ADO}} \exp \left( -\frac{j 2 \pi kn}{N}\right) , \;\;\;\; 0 \le k \le N-1 \end{array} \end{aligned}$$
(31)

Then, the demodulation of the ACO-OFDM and the DCO-OFDM signals Eltoukhi et al. (2018). Finally, the STE process will be employed for the data recovery. The data rate that could be achieved by the STC/ADO-OFDM is given by

$$\begin{aligned} \Re ^{\text {STC/ADO}}=\left( \frac{3N/4 - 2}{N + N_g}\right) \;\;\;\;\text {bits/s/Hz}. \end{aligned}$$
(32)

3 Simulation results and discussions

This section The performances of the STC-IMADJS/DCO-OFDM, STC-IMADJS/ACO-OFDM, and STC-IMADJS/ADO-OFDM techniques compared to traditional DCO-OFDM, ACO-OFDM, and ADO-OFDM systems are analyzed analytically. This study includes the PAPR, BER, and computational complexity.

3.1 PAPR and BER performance analysis

The PAPR and BER performance of the proposed technique are analyzed using Matlab 2021a simulation software for 10\(^{-4}\) frames of BPSK symbols. The OFDM systems based on VLC used in the simulation are DCO-OFDM, ADO-OFDM, and ACO-OFDM systems with DC-bias \(-7\) dB. The number of sub-carriers, N used in simulation 1024. The IMADJS technique has five parameters: low-in (a), high-in (c), low-out (b), high-out (d) and \(\gamma\). Throughout the numerical results the parameters (a , c and \(\gamma\)) will be fixed to (\(a = 0\) , \(c = 0\) and \(\gamma = 1\)) Mohammed et al. (2021). While the parameters b and d will be varied through performing the PAPR and the BER of the proposed schemes. In addition, the communication channels in the VLC communication systems are almost line of sight (LOS). Hence, the AWGN channel will be considered for the BER performance of the proposed schemes.

Figure 4 shows the PAPR (a) and BER (b) for the proposed STC/DCO-OFDM technique utilizing the IMADJS companding scheme, which is compared to the conventional DCO-OFDM technique. As illustrated in Fig. 4a, the proposed scheme with IMADJS parameters (\(b = 0.114\) and \(d = 0.117\)) significantly improves the PAPR in comparison with the conventional DCO-OFDM. As a result, the proposed scheme reduces the PAPR by 3.7 dB (from 8 dB to 6.3 dB). The effect of the IMADJS companding scheme on the BER performance is presented in Fig.4b. It is important to note that the proposed scheme does not affect the BER performance and achieves the same BER compared to the conventional DCO-OFDM technique. As a result, the proposed scheme with the IMADJS companding scheme improves the PAPR without affecting the BER performance. Figure 5a and b shows the PAPR and BER performance of the STC-IMADJS/DCO-OFDM technique under different values of the parameters b, d . As shown in Fig. 5a, if the low-out and high-out parameters increase, the PAPR will be significantly enhanced as well as the BER decreases considerably as illustrated in Fig. 5b.

Fig. 4
figure 4

Performance comparison between conventional DCO-OFDM Eltoukhi et al. (2018) and the proposed STC-IMADJS/DCO-OFDM: a PAPR and b BER

Full size image
Fig. 5
figure 5

The effect of changing the parameter b and d for the proposed STC-IMADJS/DCO-OFDM: a PAPR and b BER

Full size image
Fig. 6
figure 6

Performance comparison between conventional ACO-OFDM Eltoukhi et al. (2018) and the proposed STC-IMADJS/ACO-OFDM: a PAPR and b BER

Full size image
Fig. 7
figure 7

The effect of changing the parameter b and d for the proposed STC-IMADJS/ACO-OFDM: a PAPR and b BER

Full size image

Figure 6 introduces the PAPR and the BER respectively for the STC-IMADJS/ACO-OFDM technique. As shown in Fig. 6a, the technique significantly improves the PAPR with a reduction of 8.16 dB (from 16.86 dB to 8.7 dB) while maintaining the same BER as conventional ACD-OFDM as presented in Fig. 6b. Figure 7 presents the PAPR and the BER of the STC-IMADJS/ACO-OFDM technique with different values of low-out (b), high-out (d) parameters. It is evident that as the low-out and high-out parameters grow, the PAPR is substantially enhanced as shown in Fig. 7a but at the penalty of BER degradation, as illustrated in Fig. 7b.

Figure 8 presents the PAPR and the BER for STC-IMADJS/ADO-OFDM technique, respectively. As shown in Fig. 8a, the STC-IMADJS/ADO-OFDM slightly improves the PAPR with 1.81 dB (from 10.48 dB to 1.81 dB) reduction with same BER as presented in Fig. 8b. The PAPR and the BER of the STC-IMADJS/ADO-OFDM technique are illustrated in Fig. 9 with different values of low-out (b), high-out (d) parameters. As the low-out and high-out parameters are increased, the PAPR improves, but the BER degrades, as illustrated in Fig. 7a and b, respectively.

Fig. 8
figure 8

Performance comparison between conventional ADO-OFDM Eltoukhi et al. (2018) and the proposed STC-IMADJS/ADO-OFDM: a PAPR and b BER

Full size image
Fig. 9
figure 9

The effect of changing the parameter b and d for the proposed STC-IMADJS/ADO-OFDM: a PAPR and b BER

Full size image

A summary of the evaluations of the following techniques is presented in a Table 1: (1) conventional DCO-OFDM and STC-IMADJS/DCO-OFDM, (2) conventional ACO-OFDM and STC-IMADJS/ACO-OFDM, and (3) conventional ADO-OFDM and STC-IMADJS/ADO-OFDM. The PAPR for STC-IMADJS/DCO-OFDM with (\(b = 0.105\), \(d = 0.108\)) decreases by 4.4 dB (from 8 dB to 3.6 dB) when compared to conventional DCO-OFDM at BER = \(2.15\times 10^{-4}\). Also, by using STC-IMADJS /ACO-OFDM with (\(b = 0.018\), \(d = 0.019\)), the PAPR is reduced by 8.57 dB (from 16.86 dB to 9.29 dB) when compared to conventional DCO-OFDM at BER = \(1.10 \times 10^{-4}\). Finally, the STC-IMADJS/ADO-OFDM with (\(b = 0.078\), \(d = 0.085\)) reduces the PAPR by 2.27 dB (from 10.48 dB to 8.21 dB) when it is compared with conventical ADO-OFDM at BER = \(5.1 \times 10^{-4}\).

Table 1 Summary with Comparison Among STC-IMADJS/DCO-OFDM, STC-IMADJS/ACO-OFDM, and STC-IMADJS/ADO-OFDM Techniques based on: PAPR and BER
Full size table

3.2 Computational complexity

The computational complexity is expressed in terms of the total number of arithmetic operations, either additions or multiplications required at the transceiver. The computational complexity for the various techniques is shown in Table 2. As shown, the proposed schemes decrease the computational complexity of the system compared to traditional DCO-OFDM, ACO-OFDM, and ADO-OFDM systems. Thus, as compared to conventional systems, the STC-IMADJS/DCO-OFDM, STC-IMADJS/ACO-OFDM, and STC-IMADJS/ADO-OFDM techniques reduced multiplication and addition operations by approximately \(50\%\).

Table 2 Computational complexity analysis Gallo et al. (2019)-Ahmad and Srivastava (2020)
Full size table

4 Conclusion

In this paper, the integrated STC-IMADJS technique is developed for throughput improvement and PAPR reduction of the OFDM-based VLC communication systems. The STC-IMADJS/DCO-OFDM, STC-IMADJS/ACO-OFDM, and STC-IMADJS/ADO-OFDM are developed to evaluate the proposed integrated technique. The simulation results are investigated for the BPSK modulation scheme under AWGN. As a result, the integrated STC-IMADJS technique improved the system throughput by \(50\%\). Additionally, it significantly reduced the PAPR for DCO-OFDM, ACO-OFDM, and ADO-OFDM schemes by 3.7 dB, 8.16 dB, 1.81 dB, respectively, compared to conventional schemes. Finally, the computational complexity of the integrated techniques is lower than the conventional techniques by approximately \(50\%\). Finally, we propose a higher constellation integrated with a filter bank multicarrier (FBMC) architecture in future work.