1 Introduction

Partial discharge is an important phenomena that occurs in high-voltage (HV) electric power systems (Niemeyer 1995). The PD measurement can be used to prevent the continuous deterioration of the insulation system of HV equipment which may cause a disruptive breakdown with an expensive loss (Zargari and Blackburn 1996). Thus, several methods have been developed for PD diagnosis and monitoring depending on the studied physical effect accompanying the PD (Chakravorti et al. 2013). Optical techniques are based on detecting the light radiation around the conductors, the insulator surfaces and the transformer oil. The light produced is due to various ionization, excitation, and recombination processes during the discharge. The UV wavelength of corona discharge radiation ranges from 200 to 400 nm owing to the air ionization spectrum (Grum and Costa 1976). It should be noted that optical detection methods provide many benefits in terms of high sensitivity and applicability. Subsequently, it can inhibit external electromagnetic interference (EMI) of traditional electric measurement (Zhou et al. 2019; Yaacob et al. 2014). Recently, several optical detection techniques have been developed for PD measurement such as optical fibers (Oliveira and Fontana 2009), fluorescent optical fiber (Mangeret et al. 1991; Tang et al. 2012), and silicon photomultiplier tubes (Zhou et al. 2018; Ren et al. 2017). The UV imagers are the most used technique for UV detection relying on the photon numbers parameter. However, the measurements are related to some factors such as imager gain besides observation distance and angle. Therefore, the measured values should be corrected which affects the accuracy of the PD detection (Kim et al. 2018; Li et al. 2016). Afterward, fiber-optic PD detection is an add-on to the conventional techniques to gain EMI resistance in addition to accurate detection (Zargari and Blackburn 1996). The conventional optical fibers have exhibited excellent performance in optical PD detection and many applications. However, they suffer from limitations regarding their structure. In particular, the optical fiber design should satisfy the design rules of core diameter limitation in single-mode operation, modal cut-off wavelength, and selection of core and cladding materials with similar thermal characteristics (Buczynski 2004).

Recently, photonic crystal fiber (PCF) sensors have gained high recognition as a new alternative technology to replace standard optical fibers (Russell 2003, 2006). The PCF has large degrees of design freedom due to the flexibility of air holes arrangement and diversity of filling materials such as appropriate liquids, gases, metals, or liquid crystals (Knight et al. 1998; Poli et al. 2007). Compared to standard optical fibers, PCFs have numerous outstanding properties such as high birefringence, endless single-mode propagation over a wide wavelength range, low-loss guidance, high nonlinearity, transfer of high power and low bending loss (Poli et al. 2007; De et al. 2019). PCF have been used in many applications including couplers (Hameed et al. 2009a), polarization rotators (Hameed and Obayya 2011, 2014), refractometers (Areed et al. 2017) and sensors (Azzam et al. 2016; Hameed et al. 2019). The PCF sensors have been used in a variety of applications. In that context, solid core PCF has been used as an interferometer to sense many physical changes, e.g., strain, pressure, besides the detection of hydrogen gas (Villatoro and Minkovich 2018). Furthermore, PCF filled with liquid crystal (Hameed et al. 2009b), placed between HV electrodes, is used to sense the electric field direction (Tefelska et al. 2015). For pressure sensing, Bragg grating-based highly birefringent microstructured optical fiber has been reported with sensitivity of 33 pm/MPa (Sulejmani et al. 2012). Likewise, polarization-maintaining PCF-based Sagnac interferometer has been investigated for downhole applications with sensitivity of 4.21 nm/MPa (Fu et al. 2010). Additionally, Tatar et al. have presented PCF sensor to sense UV light in addition to temperature variation. The cladding air holes were infiltrated with a fluorescein dye that was excited with the UV radiation with a detection limit of 0.24 mW.cm−2 (Tatar et al. 2016).

When an electromagnetic wave is incident on a metal/dielectric interface, surface plasmon wave will be excited. PCF sensors based on surface plasmon resonance (SPR) (Economou 1969) have been used for different applications. At resonance, coupling occurs between the surface plasmon (SP) mode and fundamental core mode. This leads to a dramatic increase in the confinement loss based on the surrounding medium's refractive index. Therefore, a shift occurs in the resonance wavelength with the refractive index variation. In particular, compact sensor size (miniaturization), real-time detection, remote sensing ability, and ultrahigh sensitivity are the advantages of PCF sensors (Rifat et al. 2017). In this context, Huang et al. have introduced a magnetic field PCF sensor with magnetic field sensitivity of 61.25 pm/Oe for the range 50–130 Oe (Huang et al. 2020). Hameed et al. (2015) have also reported a PCF temperature sensor with liquid crystal infiltration with high sensitivity of 10 nm/°C. Osifeso et al. designed a multi-core PCF temperature sensor with ethanol or benzene as a temperature sensing medium with a sensitivity of 360 pm/°C and 23.3 nm/°C for ethanol and benzene, respectively (Osifeso 2020). The TiN and ZrN were then introduced as alternative plasmonic materials to cover the silver layer in a bimetallic PCF SPR refractive index sensor. Yet, high sensitivities for quasi-transverse electric (TE) mode and quasi-transverse magnetic (TM) mode were 7000 nm/RIU and 6900 nm/RIU for the Ag/TiN configuration. Further, 5300 and 5400 nm/RIU have been achieved using Ag/ZrN configuration for the TE and TM polarized modes, respectively (El-Saeed et al. 2019).

The D-shaped PCFs attracted research interest for their ability to improve the sensing efficiency. In this type, the cladding is polished to form a flat surface. Then a metallic layer and the studied analyte are placed on top of the polished surface outside the PCF structure. In this regard, Ying et al. presented a magnetic field and temperature sensor where ethanol was selectively infiltrated in two holes while the magnetic fluid was placed on top of the gold layer. Sensitivities of − 1.25 nm/°C and 0.21 nm/Oe have been achieved (Ying et al. 2019) for temperature and magnetic field, respectively. In addition, Mollah et al. presented ultrahigh sensitive temperature sensor using benzene as a temperature sensing medium that was placed on top of the gold-coated surface. The sensor offered maximum sensitivity of 110 nm/°C (Mollah et al. 2020). Furthermore, TiN was used in a D-shaped refractive index SPR sensor within refractive index range of 1.44–1.52. The analyte was injected into the central hole giving a high sensitivity of 7571 nm/RIU through the studied RI range (Monfared 2020).

In this work, D-shaped PCF SPR sensor is proposed for the first time to the best of our knowledge for optical detection of PD in HV systems. The radiated light intensity from the PD reflects the charge quantity of the produced PD (Ren et al. 2016). The proposed sensor can detect the light intensity directly without the need for further calculations regarding its distance and angle from the PD source. In this study, the PCF is side-polished to form a flat surface covered by a silver film. The silver is chosen as a plasmonic material due to its sharp resonance peak. Although silver suffers from oxidation problems, another coating layer of TiN is added. The TiN is used as an alternative plasmonic material due to its properties such as resistance to corrosion, mechanical strength, high melting point, and chemically stable (Naik et al. 2013; El-Saeed et al. 2019). The sensing analyte is a photochromic spirooxazine dye-doped silica sol–gel which is sensitive to the UV emission. Hence, the analyte is placed over the TiN layer in direct contact with the UV radiated from PD in order to achieve an immediate response and real-time detection. The proposed sensor is analyzed via full vectorial finite element method via COMSOL Multiphysics software package (https://www.comsol.com). The different geometrical parameters are studied to maximize the sensor sensitivity. The numerical results show that high sensor sensitivity of 2.4 nm/mW.cm−2 is achieved with a simple design compared to other PD techniques (Zhou et al. 2018; Ren et al. 2017; Lee et al. 2018; Li et al. 2016).

2 Design considerations

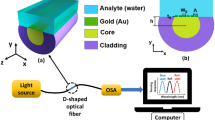
The reported optical sensor setup is shown in Fig. 1. The D-shaped PCF is connected to standard single mode fiber to couple the light source into the sensor. During the light propagation through the D-shaped PCF, the SPs are excited at bimetallic/dielectric interface. Then, maximum loss is obtained at the resonance wavelength which can be detected using the optical spectrum analyzer (OSA). Then, the spectrum response is transferred to a computer for enhanced analysis.

Fig. 1
figure 1

Schematic diagram of the proposed sensor setup

Full size image

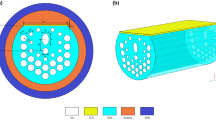
The sensing mechanism is explained as follows. According to the UV radiation, the refractive index of the sensing material will be changed. As a result, the resonance wavelength will be shifted which will be an indication of the light intensity corresponding to the magnitude of the PD. The stacked scheme is revealed in Fig. 2a while the 2-D cross-sectional view of the reported sensor is shown in Fig. 2b. The air holes of the three rings D-shaped PCF are arranged in hexagonal lattice with a hole pitch Λ = 2 µm and diameter of \({d}_{h}\)= 0.8Λ. The core consists of central hole with diameter \({d}_{c}\)= 0.3Λ. The center of the core hole is placed at \({h}_{c}\)= 0.5Λ. In order to achieve D- shaped configuration, side polishing is made to a distance of 0.45Λ. The thickness of the silver layer \({t}_{Ag}\)= 30 nm while the TiN layer \({t}_{TiN}\) = 5 nm. It is worth noting that an attenuator layer is used over the sensing material to keep the intensity at lower values to avoid the saturation of the sensing material. At high intensities, all molecules will be aligned (Fu et al. 2008) with no change in the refractive index due to radiation variation. Table 1 shows the initial chosen dimensions.

Fig. 2
figure 2

a Stacked scheme of the PCF and b A 2D schematic diagram of the D-shaped plasmonic PCF sensor after etching process

Full size image
Table 1 initial parameters
Full size table

For precise simulation, the dispersion of the material is considered. The background material is SF10 glass (Rahaman et al. 2020) which has the following Selmeier equation:

$$n^{2} \left( \lambda \right) = 1 + \frac{{A_{1} \lambda^{2} }}{{\lambda^{2} - B_{1} }} + \frac{{A_{2} \lambda^{2} }}{{\lambda^{2} - B_{2} }} + \frac{{A_{3} \lambda^{2} }}{{\lambda^{2} - B_{3} }}$$
(1)

where \(n\left( {\lambda } \right)\) is the wavelength dependent refractive index of the SF10, \(A_{1} = 1.62153902\),\(A_{2} = 0.256287842\),\(A_{3} = 1.64447552\),\(B_{1} = 0.0122241457\) μm2, \(B_{2} = 0.0595736775\) μm2 and\(B_{3} = 147.468793\) μm2. The first plasmonic material deposited on the D-shaped PCF surface is silver with thickness \(t_{Ag}\)= 30 nm. Further, the silver has the following relative permittivity (El-Saeed et al. 2019):

$$\varepsilon = \varepsilon_{\infty } + \frac{{\omega_{P}^{2} }}{{\omega \left( {\omega + i\omega_{\tau } } \right)}}$$
(2)

where \(\varepsilon_{\infty } =\) 9.84, \(\omega_{p} = 1.36 x10^{16} \,{\text{rad}}/{\text{s}}\) and\(\omega_{\tau } = 1.018 10^{14} \,{\text{rad}}/{\text{s}}\). The second plasmonic material adjacent to the UV sensitive material is TiN with film thickness \(t_{TiN}\) = 5 nm. The dielectric properties of the TiN films deposited at 500 °C is described by Drude- Lorentz model (Naik et al. 2013) as follow:

$$\varepsilon = \varepsilon_{b} - \frac{{\omega_{P}^{2} }}{{\omega \left( {\omega + i\gamma_{p} } \right)}} + \frac{{f_{1} \omega_{1}^{2} }}{{\left( {\omega_{1}^{2} - \omega^{2} - i\omega \gamma_{1} } \right)}}$$
(3)

where \({\varepsilon }_{b}=2.485\), \({\omega }_{p}=5.853 eV\),\({\gamma }_{p}=0.5142 eV\), \({\gamma }_{1}=2.4852 eV\), \({\omega }_{1}=3.9545 eV\) and \({f}_{1}=2.0376\).

The UV sensing ability is a reversible photoswitchable process between two forms with different absorption spectra which is known as photochromism (Lee et al. 2008). Under UV excitation, the photochromic mechanism produces a change in the absorption spectra due to the variation in the material refractive index (Lee et al. 2008; Alvarez-Herrero et al. 2008). Moreover, the reverse reaction to the initial form can take place by illumination to a visible light or heat (Malatesta et al. 1995). Spirooxazine dyes are famous for their photochromic behavior (Malatesta et al. 1995). Recently, Spirooxazines doped in polymers or sol-gels gained a substantial attention and were used in a variety of applications such as UV detectors (Goudjil 1996), reversible optical data storage (Fu et al. 2008), optical fiber switches (Huang et al. 2006), multiple holographic gratings (Fu et al. 2013), and nonlinear optics (Kim et al. 2005). In order to sense UV light radiation, a photochromic spirooxazine derivative, 1,3,3,5,6-pentamethyl-spiro[indoline-2–3′-[quinolino]oxazine], embedded in a sol–gel phenyl functionalized thin silica film can be used as a host matrix. The material preparation process and optical properties are described in (Alvarez-Herrero et al. 2007). Moreover, the dependence of the complex refractive index on the temperature is clarified in (Alvarez-Herrero et al. 2008).

3 Numerical results and analysis

The full vectorial finite element method (FEM) (Obayya et al. 2000, 2002; Koshiba and Tsuji 2000; Rahman et al. 2008) via COMSOL Multiphysics software package, is used to analyze the proposed sensor. Additionally, scattering boundary condition (SBC) is used to truncate the computational domain and calculate the confinement loss of the supported modes. The cross section is discretized with triangular elements with maximum and minimum element sizes of 0.05 μm, and 4 × 10–4 μm, respectively. The wavelength dependent modal confinement loss is calculated from the imaginary part of the mode effective index \(Im(n_{eff}\)) as follows (Crutchfield et al. 2004):

$$Loss = 8.686 \times {\text{Im}} \left( {n_{eff} } \right) \times \frac{2\pi }{{\lambda \left( {{\text{nm}}} \right)}} \times 10^{7} \left( {{\text{dB}}/{\text{cm}}} \right)$$
(4)

A coupling occurs between the y-polarized core mode and the SP y-polarized mode. Therefore, a substantial increase occurs in the confinement loss of the core mode as presented in Fig. 3. The real parts of the effective indices of the y-polarized core mode and SP mode are also shown in Fig. 3. Figure 4a–b show the modes at \(\lambda\) = 600 nm away from the resonance wavelength. Whereas, Fig. 4c–d describe the field plots at the phase matching point between the y-polarized core mode and the SP y-polarized mode at wavelength of 688 nm. It is evident that large power transfer occurs from the core guided mode and the surface plasmon mode. Therefore, maximum losses occur for the core guided mode at the resonance wavelength. The resonance wavelength depends on the sensing medium refractive index. Therefore, the sensitivity of the proposed sensor is calculated by the following equation

$$S_{I} \left( {{\text{nm}}/{\text{mW}}.{\text{cm}}^{ - 2} } \right) = \frac{{\Delta \lambda_{Peak} }}{\Delta I}$$
(5)

where \({\lambda }_{Peak}\) is the resonance wavelength shift and \(\Delta I\) is the change in the light intensity in mW/cm2. In this study, the UV source of the Ellipsometric analysis (Alvarez-Herrero et al. 2007) has an optical power of 5 mW/cm2. Thus, \(\Delta I\) is equal to 5 mW.cm−2.

Fig. 3
figure 3

Wavelength dependent effective indices of y-polarized core-guided and SP modes and the confinement loss spectra of the core-guided modes

Full size image
Fig. 4
figure 4

Field plot of the y-polarized a SP mode at 600 nm, b core mode at 600 nm, c SP mode at 688 nm and d core mode at resonance wavelength of 688 nm

Full size image

Another parameter to evaluate the sensing performance and detection accuracy is the signal to noise ratio (SNR), which is verified by the figure of merit (FOM). The FOM is the relation between the sensitivity and full-width at half-maximum (FWHM) which can be calculated as follows (Mollah et al. 2020).

$$FOM\left( {1/{\text{mW}}.{\text{cm}}^{ - 2} } \right) = \frac{{S_{I} \left( {{\text{nm}}/{\text{mW}}.{\text{cm}}^{ - 2} } \right)}}{{FWHM \left( {{\text{nm}}} \right)}}$$
(6)

where \({S}_{I}\) is the calculated sensitivity of the sensor in (nm/mW.cm−2). The sensitivity and FOM together are considered during the investigation to further enhance the sensing characteristics.

In order to achieve the best sensing performance of the proposed sensor, a numerical study of the structural parameter variation is accomplished. It is worth noting that the surface plasmons are strongly influenced by the metallic layer thickness. Therefore, the effect of the silver layer thickness \({t}_{Ag}\) is firstly investigated while the other parameters are kept at their initial values. Figure 5a shows the variation of the loss spectra with the wavelength when \({t}_{Ag}\) is varied from 25 to 40 nm with a step of 5 nm. By increasing the silver thickness, the resonance wavelengths are shifted to longer wavelength. Moreover, the loss peaks are changed after subjected to UV radiation. It is also observed from Fig. 5a that as the silver film increases from 25 to 30 nm, the loss spectra increases and narrows. If \({t}_{Ag}\) is further increased to 35 and 40 nm, a loss reduction is observed with a breadth of the loss spectra. As the metal thickness increases, the core guided mode will be screened from the SP mode. Therefore, the coupling efficiency and hence the sensor sensitivity will be reduced as illustrated in Fig. 5b. Maximum sensitivity of 2.2 nm/mW.cm−2 is achieved at \({t}_{Ag}\)= 25. However, the loss spectra shows large FWHM = 91 nm with low FOM = 0.024 mW−1.cm2. Meanwhile large FWHM may lead to uncertain detection due to spectral noise that affects the accuracy of detection. On the other hand, the highest FOM = 0.051 mW−1.cm2 is achieved at \({t}_{Ag}\) = 30 nm due to small FWHM = 39 nm. Thus, the thickness of the silver layer will be fixed at 30 nm in the subsequent simulations to assure accurate detection.

Fig. 5
figure 5

a Wavelength dependent losses of the core guided mode at different values of tAg and b the resonance wavelength and sensitivity at different values of tAg

Full size image

The central hole of the designed sensor has a significant influence on the coupling between core guided modes and plasmonic modes, and, hence the FOM. Based on this, the effect of the distance between the core hole and the metal \({h}_{c}\) is investigated. Here, \({h}_{c}\) changes from 0.40Λ to 0.55Λ with a step of 0.05Λ at constant \({t}_{Ag}\) = 30 nm, \({t}_{TiN}\) = 5 nm, \({d}_{h}\) = 0.8Λ, and \({d}_{c}\) = 0.3Λ. The change due to UV radiation is also studied. Figure 6 shows that by increasing \({h}_{c}\) from 0.40Λ to 0.55Λ, the power transfer from the core mode to the SP mode increases. Therefore, the loss spectra increases gradually to reach a sharp peak at \({h}_{c}\)=0.5Λ. Additional increase in \({h}_{c}\) will decrease the coupling between the core mode and the SP mode with reduced loss peak and broaden spectrum as may be seen in Fig. 7a. Moreover, a slight red shift to the resonance peak occurs. Furthermore, the numerical results reveal that high sensitivity of \({S}_{I}\) = 2.6 nm/mW.cm−2 is realized at \({h}_{c}\) = 0.4Λ as depicted in Fig. 7b. Although \({h}_{c}\) = 0.4Λ gives the higher sensitivity, it has a large FWHM = 89 nm with a low FOM of 0.0295 mW−1.cm2. Accordingly, choosing this value will definitely reduce the accuracy of the measurement. Thus, \({h}_{c}=0.5\Lambda\) is selected as an optimized value to achieve high FOM = 0.051 mW−1.cm2.

Fig. 6
figure 6

The field plots at different values of \({h}_{c}\) a 0.40Λ b 0.45Λ c 0.50Λ and d 0.55Λ

Full size image
Fig. 7
figure 7

a Wavelength dependent losses of the core guided modes at different hc values and b the resonance wavelength and sensitivity at varied values of hc

Full size image

To investigate the influence of the central core hole, the diameter of the central core hole \({d}_{c}\) is varied from 0.2Λ to 0.5Λ with a step of 0.1Λ while the other parameters are kept at \({t}_{Ag}\) = 30 n, \({t}_{TiN}\) = 5 nm, \({h}_{c}\) = 0.5Λ, and \({d}_{h}\) = 0.8Λ. Figure 8 clarifies the matching wavelengths between the core guided modes and SP modes at \({d}_{c}\) = 0.2Λ, 0.3 Λ and 0.4Λ. This is evident from Fig. 9a that illustrates that the increase of \({d}_{c}\) results in a red shift to the resonant wavelength and a gradual decrease in the confinement loss spectra. In Fig. 9b, design with \({d}_{c}\) = 0.2Λ shows high sensitivity \({S}_{I}\) = 2.4 nm/mW.cm−2 with a narrow loss spectra, small FWHM of 33 nm, and high FOM = 0.073 mW−1.cm2. Therefore, for the design to achieve high sensitivity along with high FOM, core hole diameter of \({d}_{c}\) = 0.2Λ is chosen in the subsequent simulations.

Fig. 8
figure 8

Wavelength dependent of the real part of the effective indices of the core guided modes and surface plasmon modes at different \({d}_{c}\) values

Full size image
Fig. 9
figure 9

a Wavelength dependent confinement loss at different values of dc and b the resonance wavelength change and sensitivity with the change of dc

Full size image

Next, the effect of the cladding holes on the confinement loss and resonant wavelength is studied to maximize the FOM. In this regard, the cladding holes diameter is changed from 0.6Λ to 0.9Λ in a step of 0.1Λ while the other parameters are kept at their optimized values \({t}_{Ag}\) = 30 n,\({t}_{TiN}\) = 5 nm, \({h}_{c}\) = 0.5Λ, and \({d}_{c}\) = 0.2Λ. It can be seen from Fig. 8a that as \({d}_{h}\) increases, the resonance is shifted to longer wavelengths with a narrow loss spectrum. It is also observed from Fig. 10b that \({d}_{h}\) = 0.7Λ shows the highest sensitivity with large FWHM of 68 nm and low FOM of 0.038. Selecting this design may lead to uncertain detection that influence the accuracy of the reported sensor. Since Sharp resonance peaks with a narrower FWHM can filtrate the noise in the realized spectrum and restrain non-resonant confinement loss. In terms of sensor performance, the design is optimized at holes diameter of 0.8Λ in order to obtain both high sensitivity and high FOM.

Fig. 10
figure 10

a Wavelength dependent confinement losses of the core guided modes at different values of dh and b The resonance wavelength and sensitivity with the change of dh

Full size image

Next, the TiN layer thickness \({t}_{TiN}\) is studied and optimized. In this investigation, \({t}_{TiN}\) thickness of 3, 5, 7 and 10 nm are tested while the other parameters are fixed at their optimized values. Figure 11a shows the wavelength dependent loss before and after UV irradiation at different values of TiN layer thickness. As \({t}_{TiN}\) increases, the confinement loss peak undergoes a red shift. In Fig. 11a–b, the numerical results reveal that at \({t}_{TiN}\) = 5 nm, high sensitivity is achieved with narrow loss spectra and small FWHM. Therefore, the optimized value for \({t}_{TiN}\) is 5 nm since it gives high sensitivity \({S}_{I}\) = 2.4 nm/mw.cm−2 and high FOM = 0.073 mW−1.cm2.

Fig. 11
figure 11

a Wavelength dependent confinement losses of the core guided modes at different values of \(t_{TiN}\) and b the resonance wavelength and sensitivity change with varying \({\mathrm{t}}_{\mathrm{TiN}}\)

Full size image

From the parametric study, the optimum parameters of the proposed sensor are defined and are listed in Table 2 where high sensitivity of 2.4 nm/mW.cm−2 and good FOM of 0.073 (1/mW.cm−2) are achieved.

Table 2 the optimized parameters of the reported sensor
Full size table

In order to proof the fabrication feasibility of the proposed design, a tolerance study is made as shown in Table 3 and Fig. 12. Table 3 shows the sensor sensitivity within a tolerance of ± 5% of the different geometrical parameters compared to that obtained using the optimized parameters. It may be seen from Fig. 12 that within a tolerance of ± 5%, a slight shift occurs in the resonance wavelengths of the optimized parameters. Therefore, the sensitivity of the proposed design is still better than 2.2 nm/mW.cm−2.

Table 3 The tolerance study of the different geometrical parameters within ± 5% and its effect on the sensor sensitivity compared to that obtained using the optimized parameters
Full size table
Fig. 12
figure 12

Fabrication tolerance study of the proposed sensor within a tolerance of ± 5% of the a Silver thickness \({t}_{Ag}\), b TiN thickness \({t}_{TiN},\) c cladding hole diameter \({d}_{h}\), d core hole diameter \({d}_{c}\) and e core height \({h}_{c}\)

Full size image

The proposed optical PD sensor offers significant advantages over conventional electrical methods (Yaacob et al. 2014) with a simple and compact construction, EMI immunity, fast response, and high sensitivity. The optical techniques include silicon photomultiplier tubes, which are expensive and can be only applied in laboratory experiments (Zhou et al. 2018; Ren et al. 2017). Likewise, the UV imagers, where the observed values require correction relative to numerous parameters which have an impact on the detection accuracy of the PD (Lee et al. 2018; Li et al. 2016).

The suggested PCF structure is a simple design with cladding air holes arranged in a hexagonal lattice surrounding a central core hole. The cladding air holes diameter is 1.6 µm while the core hole is 0.4 µm diameter which is sufficiently large for easy fabrication. Therefore, the PCF can be fabricated by stack and draw procedure using the improved technique presented in (Mahdiraji et al. 2014). In this context, a handle is connected to preform that doesn't require a high-temperature glass working lathe and only requires a fiber drawing tower. Further, the PCF can be fabricated by 3D printing technique presented in (Bertoncini and Liberale 2020). In that context, high-resolution 3D printing demonstrated for single-step fabrication of stacked ultrashort PCFs. This method allows exceptional design flexibility and precision in command of the transverse and longitudinal PCF geometry.

The D-shaped can be formed by applying the polishing technology introduced in (Wu et al. 2017). The grinding wheel of the fiber polishing system is mounted on a 3D mechanical platform that can move in the X, Y, and Z directions. The polishing length and depth can be easily set up and controlled using a computer program. For polishing fiber, abrasive paper wrapped around a mechanical wheel are used. To eliminate residual silica dust, the PCF polished surface is gently wiped with water and an air-laid paper. The polishing depth is 0.9 µm to enhance the SPR interaction between the light propagating in the core and the electrons on the metallic surface. Then, a plasmonic bimetallic layer of 30 nm silver film and 5 nm TiN film can be deposited on the flat plan by magnetron sputtering (Politano et al. 2018) or DC reactive magnetron sputtering (Jacob et al. 2012; Alishahi et al. 2016). Furthermore, the analyte of spirooxazine doped in silica sol–gel can be prepared as presented in (Alvarez-Herrero et al. 2007; Diaz and Yadid-Pecht 2019), which is photochromic dye sensitive to UV radiation. Meanwhile, after hydrolysis of the sol, the photochromic molecules is added in a tetrahydrofuran (THF) solution, yielding a photochromic-dye:Si molar ratio of 1:200.

Then, spin coating technique is used to coat the TiN layer by the studied thin film. The D-shaped configuration will permit direct contact between the thin film and the UV light radiation. A standard single mode fiber (SMF) is also spliced to the PCF from both ends where a light source with broadband spectrum can be coupled. An OSA and computer can be connected in order to analyze the spectrum.

4 Conclusion

A D-shaped SPR PCF sensor is utilized to sense the UV radiation from PD in HV systems. The sensing mechanism of the radiated light intensity relies on calculating the resonance wavelength shift of the transmitted optical spectra. The proposed D-shaped sensor is designed and investigated numerically using the FVFEM. The geometrical parameters are studied to improve the sensitivity and SNR to maximize the FOM. Therefore, the reported sensor offers high sensitivity of 2.4 nm/mW.cm−2 and good FOM of 0.073 (1/mW.cm−2). The standard PCF fabrication technologies can be used to fabricate the reported sensor owing to its simple design and structure. Further improvements of the sensor could be a study at different UV intensities.