1 Introduction

The ring laser has been proposed in the last years for different applications, ranging from the optical gyroscope (Taguki et al. 1999; Numai 2000), its main achievement, to the optical flip–flop (Trita et al. 2014) and the clock generator (Li et al. 2016).

The behavior of the ring laser has been studied both numerically and experimentally (Numai 2000; Marchal et al. 2000; Sorel et al. 2002a). Because of mode coupling due to cross-saturation, the laser exhibits bidirectional regimes, where both the clockwise (CW) and the counter-clockwise (CCW) modes are active, as well as unidirectional regimes, bistability and chaos. Also, optical feedback effects have been investigated (Friart et al. 2017), as well as methods to reduce the laser sensitivity to feedback (Khoder et al. 2018; Van Schaijk 2018; Lenstra and Schaijk 2019), or to select the laser operating wavelength and mode (Khoder et al. 2016; Vershaffelt and Khoder 2018).

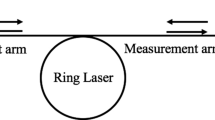
Recently, we have proposed the application of a ring laser to distance measurement (Aromataris et al. 2020). In the suggested scheme, shown in Fig. 1, a laser, working in the quasi-unidirectional regime, is further subject to delayed optical feedback both from a local and from a remote mirror. Differently from most time-of-flight telemeters (Donati 2004), this instrument, which combines time-of-flight and optical injection, does not require special provisions or processing to tackle the ambiguity problem. It is very simple to implement, since, in addition to a d.c. pumped ring laser, it only requires two mirrors, and collimation or focusing optics. Also, electronic processing only consists of measuring the period or frequency of laser mode switching generated by the optical feedback in proper operating conditions.

Fig. 1
figure 1

Scheme of the semiconductor ring-laser subject to double delayed optical feedback (M1–M2: mirrors)

Full size image

Later, Lombardi et al. (2021), we have investigated the various regimes taking place for different arm lengths (i.e., for different time of flight from laser to reflectors) in the scheme of Fig. 1. Our findings are reported in more detail in this paper.

2 Numerical model

The model used in our simulations was introduced in Aromataris et al. (2020) and is basically that of (Numai 2000) with the addition of two terms describing the optical feedback as in the Lang–Kobayashi model (Lang and Kobayashi 1980) for the standard semiconductor laser. We assume that the isolated laser (i.e., the laser without optical feedback) is in the quasi-unidirectional regime, produced by the mode cross-saturation (Sorel et al. 2002b). We will focus, in particular, on regimes in which the ring laser can be used as a telemeter, i.e., where the switching period between CW and CCW modes is linearly related to the distance of one or both reflectors from the ring laser.

In Aromataris et al. (2020), we have proposed two different equation sets, which describe the scheme of Fig. 1 with different level of accuracy. One (the three-equation model) is directly derived from that by Numai, and includes the dynamics of the carrier concentration N. In the other (the simplified two-equation model) the equation for N is adiabatically eliminated, by the reasonable assumption that the carrier dynamics is dominated by the faster photon dynamics.

In our study, we have used both models, confirming that they are equivalent, at least in the conditions of our investigations. Most simulations have been performed with the two-equation model, which allows for faster numerical integration. The three-equation model has been used to validate the other, i.e., to confirm that the regimes investigated in detail with the fast model are indeed found also with the more complete model.

The three-equation model is shown here below for convenience:

$$\frac{{{\text{d}}S_{1} }}{{{\text{d}}t}} = \left[ {G - \beta S_{1} - \theta S_{2} } \right]S_{1} - \frac{{S_{1} }}{{\tau_{ph} }} + \frac{{\eta_{2} }}{{\tau_{in} }}S_{2} (t - \tau_{r} )$$
(1)
$$\frac{{{\text{d}}S_{2} }}{{{\text{d}}t}} = [G - \beta S_{2} - \theta S_{1} ]S_{2} - \frac{{S_{2} }}{{\tau_{ph} }} + \frac{{\eta_{1} }}{{\tau_{in} }}S_{1} (t - \tau_{m} )$$
(2)
$$\frac{{{\text{d}}N}}{{{\text{d}}t}} = \frac{J}{ed} - [G - \beta S_{1} - \theta S_{2} ]S_{1} - [G - \beta S_{2} - \theta S_{1} ]S_{2} - \frac{N}{{\tau_{n} }}$$
(3)

In these equations, S1, S2 are CW and CCW photon densities, N is the carrier concentration, J is the current density, G = G0(N − N0) is the linearized gain and G0 is the modal gain coefficient, β and θ are the (assumed symmetrical) direct- and cross-saturation coefficients, and e is the electron charge.

The last terms of Eqs. (1) and (2) describe the optical feedback, where η1, η2 account for the total attenuations from the laser to each mirror and back, τin is the round trip time in the laser cavity, and τr, τm are the round trip times from the laser to the local reflector and to the measuring mirror and back, i.e., twice the time of flight of each arm. Other symbols are listed in Table 1.

Table 1 System parameters
Full size table

In simulations we have added noise sources, i.e., the Langevin noise (Ju et al. 2004) and the shot noise (not shown in the equations).

Photon density S can be converted into optical power P by P = kS, where:

$$k\, = \,h\nu \upsilon_{{\text{g}}} S_{{\text{b}}} ,$$
(4)

h being the Plank constant, ν = c/λ the optical frequency (c speed of light in vacuum), while vg and Sb are defined in Table 1.

3 Ring laser regimes

We have assumed the same parameter values (Table 1) as in Aromataris et al. (2020). These parameters are as in Numai (2000), except for adding the mirror reflections η1 = η2 = η = 0.3, not present in his paper, and then selecting β and θ in order to get a laser output power of approximately 1 mW. The pump current is I = JSa 5.3 mA as in the previous paper. This working point has been chosen to obtain robust switching regimes between CW and CCW modes for all investigated arm lengths L1, L2.

We have found five different regimes, which are described in the following. These regimes have been observed for a variety of arm lengths. Their exact boundaries depend on the arm lengths and on the laser parameters.

To exemplify, in Fig. 2 we show the period of the ring laser switching as a function of one arm length, in the range 50 μm–45 cm, when the other is fixed to 15 cm. Since in the description of the regimes it is convenient to assume that L1 is the length of the shorter arm, and L2 is that of the longer arm, as in Fig. 1, the abscissa of Fig. 2 thus corresponds to L1 (shorter arm) up to 15 cm, and to L2 (longer arm) over 15 cm.

Fig. 2
figure 2

Switching period as a function of one arm length, while the other arm is 15 cm, for the ring laser regimes (marked I to V) described in this paper

Full size image

3.1 Regime I

An arm is very short (50 μm–2.5 mm), while the other is significantly longer (1 cm to tens of meters). In these conditions, the system exhibits an asymmetrical bidirectional regime, i.e., the CW and CCW modes are both oscillating at the same time, but with remarkably different mode amplitudes (Fig. 3). The dominant mode is alternatively CW or CCW. Switching of the dominant mode takes place periodically, with a period T = 2τm, i.e., twice the roundtrip time, or four times the time of flight, of the long arm (L2 in Fig. 1). This regime is described in detail in Aromataris et al. (2020). It is represented by the inset of Fig. 2, and it exhibits a small dependence on the length of the short arm (L1 in Fig. 1). It is however characterized by a very good linearity for the measure of L2, as shown in Fig. 4, and it is thus suitable to make a telemeter. Provided that the condition of short (and constant) L1 is met, L2 = cT/4 (c: speed of light) with good accuracy, which increases with L1. For example, the error for L2 = 15 cm is 0.8%, when L1 > 2 mm, i.e., next to the short arm maximum value for this regime (Fig. 5). We would like to point out that correcting this accuracy error requires only a scale factor and a zero-bias trimming, because the system response is remarkably linear (Fig. 6). In this regime, the system has been tested as a telemeter up to L2 = 32 m, and for different values of L1 in the above-mentioned range.

Fig. 3
figure 3

Sample of power time series for CW (black, red online) and CCW (grey, blue online) modes in Regime I (L1 = 100 μm, L2 = 5 cm)

Full size image
Fig. 4
figure 4

Linearity plot in Regime I (L1 = 100 μm)

Full size image
Fig. 5
figure 5

Relative error in the distance measurement in Regime I (L2 = 15 cm)

Full size image
Fig. 6
figure 6

Distance measured in Regime I as a function of real distance L2 for different values of L1 (ideal: measured distance is real distance)

Full size image

3.2 Regime II

Both arms are relatively long (one is > 2.5 mm, the other > 1 cm) and their ratio is approximately in the range 0.05–0.15 with our parameter set. Also in this case, an asymmetrical bidirectional regime is found. The dynamics is complex, and, at first sight, the switching period seems nonlinearly related to the times of flight of the two arms (Fig. 2). A more accurate analysis shows that different sub-regimes can be detected within this regime, being separated by step discontinuities. Each sub-regime exhibits an approximately linear relation of the switching period vs. the arm lengths, i.e., T = a (τr + τm), with different slope a in the range 3–8. This regime is not suitable to make a telemeter, because of the short arm length range where each sub-regime is observed.

3.3 Regime III

Both arms are long (> 1 cm), and their ratio is larger than in the previous case (0.15–0.5 approximately, with our parameter set): this regime is still asymmetrical and bidirectional, but now the switching period is approximately the sum of the times of flight, or half the sum of the round trip times, of the two arms, i.e., T = 0.5 (τr + τm). The linearity, however, is rather poor.

3.4 Regime IV

Both arms are long (> 1 cm) and their ratio is approximately in the range 0.5–2. In these conditions, we find an asymmetrical bidirectional regime except for L1 = L2, where the laser regime is unidirectional (Fig. 7).

Fig. 7
figure 7

Sample of power time series for CW (black, red online) and CCW (grey, blue online) modes in Regime IV (L1 = L2 = 8 cm)

Full size image

In both cases, the switching period is well approximated by T = (τr + τm), i.e., the sum of the round trip times of the two arms, or twice the sum of the flight times of the two arms, and L1 + L2 = cT/2. This regime exhibits an approximately linear behavior (Figs. 2 and 8), and can be considered for distance measurements, even though with limited accuracy, which cannot be corrected by a simple linear scaling. It offers the possibility of measuring the distance L1 + L2 between two moving reflectors by locating the laser approximately halfway, with a dynamic range of about 50 to 150% of the starting distance.

Fig. 8
figure 8

Linearity plot in Regime IV (L1 = 8 cm)

Full size image

This regime has been experimentally demonstrated by other authors, and proposed to implement an optical flip–flop (Trita et al. 2014) and an optical clock (Li et al. 2016).

3.5 Regime V

Both arms are long (> 1 cm) but one is much longer that the other (their ratio is outside the range 0.5–2). We find several bidirectional incoming subregimes (Figs. 2 and 9), and the mean switching period T is approximately linearly related to the sum of the roundtrip times (Fig. 9), i.e., T = a (τr + τm). However, different values of the scale constant a hold for each specific sub-regime (Fig. 9). Differently from regime II, for L2 ≫ L1 (or L1 ≫ L2), slope a tends to a constant value (a ≈ 0.5, as in regime III). Nonetheless, implementing a telemeter in these conditions would be still a difficult task.

Fig. 9
figure 9

Switching period as a function of L2 for Regime V, showing different subregimes (L1=15 cm)

Full size image

As we see in Fig. 2, the above-described regimes are separated by steep jumps of the switching period vs. the arm length curve. It interesting to observe that these regimes are all bidirectional (but in the very special case of identical arm lengths in Regime IV) with alternating dominant modes. This means that the optical feedback provided by the two reflectors breaks the stable quasi-unidirectional regime of the isolated laser produced by the cross-saturation coefficients θ (Sorel 2002a).

As already observed, because of the linear relation holding between the switching period T and the time/times of flight, Regime I (with good accuracy) and IV (with lower accuracy) can be exploited to build a telemeter with the ring laser. This can be done, in practice, by detecting the mode power by a photodiode located behind one (semitransparent) mirror or by reading the voltage across the laser junction, and then measuring the period T of its square wave modulation, as suggested in Numai (2000) and Aromataris et al. (2020).

We would like to point out the different switching mechanism of Regime I and IV. In Regime I the period is twice the roundtrip time of the long arm only. This is the time required for the laser emission to fill and leave the longer arm. After one roundtrip time (i.e., twice the time of flight), the laser switches. The short arm fills almost immediately. However, a new commutation does not take place until the light stored in the long arm stops injecting the laser, and this requires another roundtrip time.

In Regime IV, instead, the period is the sum of the round trip times of the two arms, which means that switching between modes takes place as soon as light of one mode, travelling along one arm, reaches the laser, and starts the counter-propagating mode. This different laser behavior in different feedback conditions is not surprising, since the strong dependence of the laser regime on the feedback delay has been already observed in standard lasers (Donati and Mirasso 2002). Indeed, both Regime I (Marchal et al. 2000, in somewhat different conditions), and Regime IV (Li et al. 2016; Trita et al. 2014) have been observed experimentally in ring lasers.

On the other hand, Regimes II, III and V are not well-suited for distance measurement, because the relation of the time of flight vs. the switching period is less accurate and may change between incoming sub-regimes, making this task very difficult in practice. Nevertheless, these regimes could be considered for applications where reduced linearity is not an issue. For example, they may represent an alternative to regime IV to implement an optical clock or flip–flop.

As already pointed out in Aromataris et al. (2020), the ring laser should be designed and optimized to be suitable for the proposed telemeter application. Changing the laser parameters and working point may strongly affect the system behavior because (i) the isolated laser could leave the quasi-unidirectional regime and (ii) even if the laser is in this regime, mode switching cannot take place if we substantially modify the ring laser parameters (τn, τph, β, θ with respect to Table 1, or for too large attenuation η. On the other hand, the scheme of Fig. 1 is robust because (at least according to our numerical model) Regimes I and IV are found for a relatively large parameter range.

As for a practical implementation of this telemeter, we must consider that the present analysis is based on a rate equation model, which cannot take into account technological details and does not relate to a specific device.

However, as already observed, regimes I and IV can be physically explained, and experiments on Regime I and IV have been reported (Li et al. 2016; Trita et al. 2014; Marchal et al. 2000). Thus, we are confident that a telemeter based on our scheme can be successfully implemented.

A more accurate model is required to gain more insight, and get more details, on the regimes of a specific laser. Examples of technological implementations of ring lasers subject to delayed optical feedback are in (Li et al. 2016; Trita et al. 2014; Sorel et al. 2002b).

Though there is no fundamental limitation in the model as for the arm lengths, in a practical implementation a maximum operating distance is expected, due to available power and beam attenuation, also depending on focusing or collimating optics. Moreover, with a real device, the details of laser switching dynamics are expected to play a role. Typical expected switching times are of the order of 1.5 ns with a spread of 0.7% to 0.001%, depending on the feedback level (Li et al. 2016). This fluctuation would affect the telemeter accuracy on a single round trip. Since in our scheme we measure the switching frequency or period, a mean over different flight times is intrinsically performed, and the effect of fluctuations on the switching time is reduced. In a typical pulse time-of-flight telemeter the same result is obtained by taking the mean over several single measurements.

4 Conclusions

In this paper we have numerically investigated the regimes of a ring laser subject to delayed optical feedback from two reflectors, when the isolated laser is in the quasi-unidirectional regime. By rate equation models, we have found two regimes that are suitable for the design of a time-of-flight telemeter based on a properly designed ring laser, with different levels of accuracy. This scheme has a very simple optical arrangement, requiring only collimation or focalization of the laser emission, while electronic processing simply consists in photodetection and amplification of the laser emission, and in measuring the period or frequency of the square wave output signal.