Partial relay selection for two-way mixed RF/FSO DF networks in the presence of I/Q imbalance

Abstract

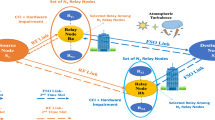
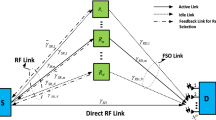
In this paper, the study of mixed radio frequency (RF)/ free space optical (FSO) communication decode and forward (DF) two way relaying (TWR) has been presented. In fact, it has been considered that multiple relays are present out of which the best operational relay is selected as per the partial relay selection (PRS) methodology in the presence of outdated channel state information (CSI). Importantly, the relay nodes are assumed to operate in the presence of in phase (I) quadrature phase (Q) imbalance (IQI). The atmospheric turbulence on the FSO link has been modeled using the Malaga distribution with pointing errors. In addition to this, the impact of type of optical demodulation has been considered in the analysis. For the system model, outage probability expression has been derived in terms of Meijer-G and Fox’s H-functions. In addition to this, for the TWR system, the outage probability expressions have been modified to present asymptotic results in terms of elementary functions. The numerical analysis of the research work suggests that the overall mixed RF/FSO DF TWR system is impacted by the image rejection ratio (IRR) due to IQI, correlation between outdated CSI, atmospheric turbulence, pointing error and type of optical demodulation in addition to the amount of fading on the RF link.

Appendices

Appendix A: Derivation of $F_{{\gamma _{\mathrm{RS2}}}}(x)$

In this section, the derivation of $F_{{\gamma _{\mathrm{RS2}}}}(x)$ has been presented. From the definition of $\gamma _{{\mathrm {{{RS2}}}}}(x)$ in (7), the expression for $F_{{\gamma _{\mathrm{RS2}}}}(x)$ can be defined using the relationship

$$\begin{aligned}F_{{\mathrm {\gamma _{RS2}}}}(x) = \text {Pr}\left[ \gamma _{RS2} < x \right] = \int _{0}^{\infty } F_{\hat{\gamma }_{\mathrm {RF}}}\left( \frac{x ((1+\text {IRR})\gamma _{FSO }+c)}{(1-x\text {IRR})\gamma _{FSO }} \right) f_{\gamma _{FSO}}(\gamma _{FSO }) d\gamma _{FSO } \end{aligned}$$

(23)

Substituting the requisites in the above integral, the expression for $F_{{\gamma _{\mathrm{RS2}}}}(x)$ can be deduced as

$$\begin{aligned} F_{{\mathrm {\gamma _{RS2}}}}(x)&= 1- j \left( {\begin{array}{c}N\\ j\end{array}}\right) \sum _{i=0}^{j-1} \frac{(-1)^{i} \left( {\begin{array}{c}j-1\\ i\end{array}}\right) }{[N-j+i+1] } \exp \Bigg (-\frac{A_1 x (1+x\text {IRR})}{(1-x \text {IRR})} \Bigg ) \frac{\xi ^2 A_3}{2^r \gamma } \sum _{m=1}^{\beta } x_2 \nonumber \\&\quad \times \, \int _{0}^{\infty } \gamma _{FSO}^{-1} \exp \Big (-\frac{xCA_1}{(1-\text {IRR} \gamma _{FSO})} \Big ) G^{3,0}_{1,3} \left. \left[ A_4 {\gamma _{FSO}}^{1/r} \Bigg \vert \right. {\begin{matrix} \xi ^2+1 \\ \xi ^2, \alpha , m \end{matrix}} \right] d \gamma _{FSO} \end{aligned}$$

(24)

The above integral can be further formulated as

$$\begin{aligned} F_{{\mathrm {\gamma _{RS2}}}}(x)&= 1- j \left( {\begin{array}{c}N\\ j\end{array}}\right) \sum _{i=0}^{j-1} \frac{(-1)^{i} \left( {\begin{array}{c}j-1\\ i\end{array}}\right) }{[N-j+i+1] } \exp \Bigg (-\frac{A_1 x (1+x\text {IRR})}{(1-x \text {IRR})} \Bigg ) \frac{\xi ^2 A_3}{2^r \gamma } \sum _{m=1}^{\beta } x_2 \nonumber \\&\quad \times \, \int _{0}^{\infty } \gamma _{FSO}^{-1} \text {G}_{1, 0}^{0, 1}\left[ \frac{{(1-\text {IRR} \gamma _{FSO})}}{xCA_1} \Bigg \vert \begin{array}{c} 1 \\ - \end{array} \right] G^{3,0}_{1,3} \left. \left[ A_4 {\gamma _{FSO}}^{1/r} \Bigg \vert \right. {\begin{matrix} \xi ^2+1 \\ \xi ^2, \alpha , m \end{matrix}} \right] d \gamma _{FSO} \end{aligned}$$

(25)

Applying Wolfram (2010, Eq. (07.34.21.0013.01)), a closed-form solution to the integral can be obtained which yields the expression for $F_{{\gamma _{\mathrm{RS2}}}}(x)$.

Appendix B: Derivation of $F_{{\gamma _{\mathrm{RS2}}}}(x)$

The overall CDF for $\gamma _{RS1}$ can be evaluated as

$$\begin{aligned}F_{{\mathrm {\gamma _{RS1}}}}(x) = \int _{0}^{\infty } F_{\gamma _{FSO}} \Big (x\Big \{\frac{(1+\text {IRR})y+C}{(1-x\text {IRR})y} \Big \} \Big ) f_{RF(j)}(y) dy \end{aligned}$$

(26)

Substituting the requites in the above expression, the above integral can be re-written as

$$\begin{aligned} F_{{\mathrm {\gamma _{RS1}}}}(x)&= j \left( {\begin{array}{c}N\\ j\end{array}}\right) \sum _{i=0}^{j-1} \left( {\begin{array}{c}j-1\\ i\end{array}}\right) \frac{(-1)^{i}}{(\bar{\gamma }_{RF })[(N-j+i)(1-\rho )+1] } A_5 \sum _{m=1}^{\beta } x_3 \nonumber \\&\quad \times \,\int _{0}^{\infty } \exp \left[ {-\frac{(N-j+i+1)}{((N-j+i)(1-\rho )+1 ) {\bar{\gamma }}_{RF } }} y \right] G^{3r,1}_{r+1,3r+1} \left. \left[ A_6 {\Bigg (\frac{(1+\text {IRR})y+C}{(1-x\text {IRR})y}\Bigg )} \Bigg \vert \right. {\begin{matrix} 1, \tau _1 \\ \tau _2, 0 \end{matrix}} \right] \end{aligned}$$

(27)

For finding the solution to the integral, the Meijer-G function can be expressed in contour integral form as per Wolfram (2010, Eq. (07.34.02.0001.01)) as shown below

$$\begin{aligned}G^{3r,1}_{r+1,3r+1} \left. \left[ A_6 {\Bigg (\frac{(1+\text {IRR})y+C}{(1-x\text {IRR})y}\Bigg )} \Bigg \vert \right. {\begin{matrix} 1, \tau _1 \\ \tau _2, 0 \end{matrix}} \right] = \frac{1}{2 \pi i} \int _{{\mathcal {L}}_1} \varTheta _1(s_1)A_6^{s_1} ((1+\text {IRR})y+C)^{-s_1} \times {(1-x\text {IRR})y}^{s_1} ds_1 \end{aligned}$$

(28)

Placing from (1) to (2), the integral required to be attended can be framed as

$$\begin{aligned}{\mathcal {I}}_1= \int _{0}^{\infty } ((1+\text {IRR})y+C)^{-s_1} {y}^{s_1} \exp \left[ {-\frac{(N-j+i+1)}{((N-j+i)(1-\rho )+1 ) {\bar{\gamma }}_{RF } }} y \right] dy \end{aligned}$$

(29)

Invoking identity (Wolfram 2010, Eq. (07.34.03.0271.01)), the integral can be again presented as follows

$$\begin{aligned}{\mathcal {I}}_1= \frac{C^{-s_1}}{\varGamma (s_1)} \int _{0}^{\infty } y^{-s_1} \text {G}_{1, 1}^{1, 1}\left[ \frac{(1+\text {IRR}y)}{C} \Bigg \vert \begin{array}{c} 1-s_1 \\ 0 \end{array} \right] \exp \left[ {-\frac{(N-j+i+1)}{((N-j+i)(1-\rho )+1 ) {\bar{\gamma }}_{RF } }} y \right] dy \end{aligned}$$

(30)

With the help of Wolfram (2010, Eq. (07.34.21.0088.01)), the solution to the above integral can be given as

$$\begin{aligned} {\mathcal {I}}_1&= \frac{C^{-s_1}}{\varGamma (s_1)} \Bigg ({\frac{(N-j+i+1)}{((N-j+i)(1-\rho )+1 ) {\bar{\gamma }}_{RF } }}\Bigg )^{s_1-1} \nonumber \\&\quad \times \, \text {G}_{2, 1}^{1, 2}\left[ \frac{(1+\text {IRR})}{C} {\frac{((N-j+i)(1-\rho )+1 ) {\bar{\gamma }}_{RF } }{(N-j+i+1)}} \Bigg \vert \begin{array}{c} s_1, 1-s_1 \\ 0 \end{array} \right] \end{aligned}$$

(31)

In order to establish a closed-form solution, the relationship (Wolfram 2010, Eq. (07.34.02.0001.01)) can be used to express the Meijer-G function into complex integral form, and therefore, the above integral can be further represented as

$$\begin{aligned} {\mathcal {I}}_1&= \frac{C^{-s_1}}{\varGamma (s_1)} \Bigg ({\frac{(N-j+i+1)}{((N-j+i)(1-\rho )+1 ) {\bar{\gamma }}_{RF } }}\Bigg )^{s_1-1} \frac{1}{(2\pi i)} \int _{{\mathcal {L}}_2} \varGamma (s_2) \varGamma (s_1-s_2) \nonumber \\&\quad \times \,\varGamma (1-s_1-s_2) \Bigg (\frac{(1+\text {IRR})}{C} {\frac{((N-j+i)(1-\rho )+1 ) {\bar{\gamma }}_{RF } }{(N-j+i+1)}}\Bigg )^{-s_2} ds_2 \end{aligned}$$

(32)

Combining together, the results from (B.2) and (B.7), the overall expression for $F_{{\mathrm {\gamma _{RS1}}}}(x)$ can be expressed in double contour integral form as given below

$$\begin{aligned} F_{{\mathrm {\gamma _{RS1}}}}(x)&= j \left( {\begin{array}{c}N\\ j\end{array}}\right) \sum _{i=0}^{j-1} \frac{1}{[(N-j+i)(1-\rho )+1]\bar{\gamma }_{\mathrm {RF(j)}}} \frac{1}{(2 \pi i)^2} \int _{{\mathcal {L}}_1} \int _{{\mathcal {L}}_2} \varGamma (s_1-s_2) \varGamma (1-s_1-s_2) \nonumber \\&\quad \times \frac{C^{-s_1}}{\varGamma (s_1)} \varTheta _1(s_1)A_6^{s_1} \Bigg ({\frac{(N-j+i+1)}{((N-j+i)(1-\rho )+1 ) {\bar{\gamma }}_{RF } }}\Bigg )^{s_1-1} ({(1-x\text {IRR})})^{s_1} \varGamma (s_2) \nonumber \\&\quad \times \Bigg (\frac{(1+\text {IRR})}{C} {\frac{((N-j+i)(1-\rho )+1 ) {\bar{\gamma }}_{RF } }{(N-j+i+1)}}\Bigg )^{-s_2} ds_1 ds_2 \end{aligned}$$

(33)

Comparing the obtained contour integral with the Mittal and Gupta (1972, Eq. (2.1)), the resulting CDF for $F_{{\mathrm {\gamma _{RS1}}}}(x)$ can be expressed as bivariate Fox’s H-function as given in (16).