Abstract
Given that, the exponential pace of growth in wireless traffic has continued for more than a century, wireless communication is one of the most influential innovations in recent years. Massive Multiple-Input Multiple-Output (M-MIMO) is a promising technology for meeting the world's exponential growth in mobile data traffic, particularly in 5G networks. The most critical metrics in the massive MIMO scheme are Spectral Efficiency (SE) and Energy Efficiency (EE). For single-cell M-MIMO uplink transmission, energy and spectral-efficiency trade-offs have to be estimated by optimizing the number of base station antennas versus the number of active users. This paper proposes an adaptive optimization technique focusing on maximizing Energy Efficiency at full spectral efficiency using a Genetic Algorithm (GA) optimizer. The number of active antennas is determined according to the change in the number of active users based on the proposed GA scheme that optimizes the EE in the M-MIMO system. Simulation results show that the GA optimization technique achieved the maximum energy efficiency of the 5G M-MIMO platform and the maximum efficiency in the trade-off process.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
5G cellular networks aim to provide 1,000-fold capacity increases without higher additional costs on today's networks. Since network energy varies significantly during the day, 5G networks must be capable of changing power usage (Navarro-Ortiz et al. 2020). Massive MIMO is required to be the primary applicant technology capable of handling extremely high capacity. In a massive MIMO system, each Base Station (BS) employs hundreds of antennas to support tens of user equipment (UEs) on the same time–frequency resource (Gampala et al. 2018).
Massive-MIMO relies on spatial multiplexing, which requires adequate channel information from the base station on both the up-link and down-link. Massive MIMO increases capability tenfold or more while also improving the radiated energy efficiency on a request by a factor of a hundred. Adjustment of Energy Efficiency (EE) plays a critical role in developing 5G massive MIMO systems.EE is estimated by the number of bits that can be realistically transmitted per joule as mentioned in Eq. (1), which has become a significant performance metric in wireless-communications (Salh, et al. 2019; Zappone and Jorswieck 2015).
where the service quality and associated costs are compared to power consumption, it is now a metric for the network's bit-delivery reliability. From another side, Spectral Efficiency (SE) can be defined as "The average number of bits of information, that can reliably have transmitted under consideration over the channel (Miao et al. 2016)" as indicated in Eq. (2).
Massive (MIMO) systems, which employ many receiving antennas at each base station, significantly increase SE in the cell network (Gupta and Jha 2015), potentially improving EE over single-antenna techniques. The EE is reliant not only on the SE but also on Circuit Power (CP) utilization. The usage of large numbers of BS antennas in massive-MIMO will significantly increase the power consumption of radio-frequency (RF) circuits and digital signal processing (DSP), which has an apparent effect on the EE (Rusek et al. 2013; Sarajli´c et al. 2017).
EE is one of the most important goals established for fifth-generation communications. As a result, many academics across the globe have been driving many studies on EE in communication systems. Various wireless methods have been proposed in the literature to enhance the EE of communication networks. When the SNR is low, Zhang et al. (Zhang et al. 2014) developed an improved adaptive power allocation method that provides optimal EE. Due to greater SNRs, their suggested method outperforms the conventional power allocation technique.
MIMO methods may, according to Gong et al. (Gong et al. 2017), lead to fair trade between EE and SE. However, the radio frequency connectivity issue was disregarded. Liu et al. (Björnson et al. 2015) proposed a resource distribution method for various users with varying power levels. Nevertheless, it leads to a great degree of difficulty. In addition, the authors of Ng et al. (2012, 2013) suggested a resource-allocation power-efficient method to resolve the energy consumption downlink problem in OFDM networks with a large number of base stations.
An adaptive massive MIMO optimization technique based on optimizing energy efficiency at full spectral efficiency is proposed in this paper. In order to achieve the optimum EE, the number of active antennas is adjusted based on the number of active-users in each network cell. Finally, Simulation results indicate that the proposed method has adjusted the number of active antennas based on changed active users in order to maximise EE of the 5G network Massive MIMO system.
The leftover of this paper is organized as follows: In Sect. 2, the Problem Formulation and system model are introduced. In Sect. 3, simulation analysis and results are considered. The conclusion of this paper is presented in Sect. 4.
2 System design
In this paper, EE and SE conditions and boundaries for data transmission are mainly being studied (Ibrahim Salah et al. 2021). The proposed system model consists of a single-cell (Wyner 1994; Xiao, et al. 2015) where one Massive-MIMO antenna BS simultaneously serving a set of User Equipment UE as shown in Fig. 1.
2.1 Impact of multiple BS antennas and users
While using Maximum Ratio (MR) combining with perfect channel information at the BS (Miao et al. 2016), the uplink (UL) SE of each UE is calculated according to Eq. (3)
where, M is the number of antennas per each base station, K is the number of user equipment’s UEs, p defines the transmit power, σ2 means the noise power, and β signify the average gain of channel of the active UE and it is assumed to be constant for all UEs in cell j. The corresponding EE of cell 0 is defined (Björnson et al. 2015) according to Eq. (4)
where, B denotes the bandwidth, and \(v_{0}\) is evaluated according to Eq. (5)
where, \(\mu\) is a factor accounts for the Effective Transmit Power (ETP), \(0 < \mu < 1\).
The Circuit Power (CP) model consumed by single UE is estimated according to:
where, PFIX is the fixed power and PBS refers to the power utilized by the circuit components (e.g., DACs, ADCs, Q mixers /filters, Local Oscillator, OFDM modulation/demodulation), and I in which they are needed for the operation of each BS antenna.
In order to calculate the additional Circuit Power (CP) consumed by all the active UEs (Miao et al. 2016), CP0 is estimated according to Eq. (7)
where, PUE, refers to the power required by all circuit components (e.g., I/Q mixer, DAC, filter, and so forth) of each UE’s single-antenna.
Derivative of Eq. (4), is obtained to get the Maximum Energy Efficiency (Max EE), (Björnson et al. 2015) yields the expression:
Equation (8) proves that, the maximum EE enhances logarithmically with the number of antennas per base station (M) and has an almost linear decreasing function with increasing PFIX.
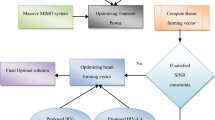
The block diagram of the proposed system is depicted in Fig. 2. The Maximum Energy Efficiency Estimator block is firstly supplied by the number of active users (Ibrahim Salah et al. 2021; Mabrook et al. 2019) served by the cell (Zhong et al. 2020) using the base station database or using spectrum sensing techniques (Mabrook et al. 2019, 2020). Then, Eq. (4) is used to estimate Max. EE values for different M antennas. Secondly, an Antenna selector-based Genetic optimizer is initiated to evaluate the optimum number of active antennas according to the Genetic algorithm optimization technique.
Finally, the RF chain switch operates the pre-evaluated number of active antennas and switches off the unnecessary antennas to maximize EE.
2.2 EE optimization based on Genetic Algorithm Artificial intelligence
In order to get the optimum number of massive MIMO antennas corresponding to the active users served by 5G cell, many optimization techniques are proposed [ 21]. However, GA optimization technique is mostly enrolled in massive MIMO networks as (Mabrook et al. 2020). GA technique supports selection, crossover, and mutation processes. GA's main concepts are focused on Charles Darwin's theory of evolution.
These concepts are then applied to a computational algorithm to find solutions to optimization problems with a given objective function. (Chou and Cheng 2017). A chromosome is a solution to such an optimization problem. Whereas a Population is a set of chromosomes.
The algorithm starts with an initial population of abnormal chromosomes, which are then determined using the fitness function (objective function) to choose the best ones, known as Parents Élite children have genes that donate the highest fitness value and are chosen to participate in the next generation. The remaining chromosomes would then be subjected to crossover and mutation processes to produce the next generation.
Regarding this mechanism, the target of the proposed technique is to optimize the EE in M-MIMO and improve the performance of 5G networks, as shown in Fig. 3 and Table 1.Then, the mentioned steps are refined till the optimum value of EE (the fitness function) is obtained. The number of antennas in M-MIMO grid is adopted to achieve the optimum EE in each cell. Therefore, we can reformat the optimization problem from Eq. (8) as,
GA is mainly used to get the optimization of its input objective functions. Therefore, in this work, EE and the number of users’ K are considered. The GA optimizers are used to optimize the consumed energy per cell and improve the M-MIMO system's EE in 5G networks.
3 Simulation and results
Using Matlab (ver. R 2019 a) with Simulink tools, numerically how the number of UEs (K), affects the (EE-SE) trade-off at different inter-cell interference (\({ }\beta^{\prime}\)) values (-3db, -15db) has been evaluated. In this scenario, EE is estimated at different numbers of users [5, 10, 30, and 40 users], the maximum EE is evaluated at each case at a constant number of active antennas where there are ten active antennas per array, according to parameters presented in Table 2.
Figure 3 shows the estimated EE values versus SE at various users [5, 10, 30, 40] while using ten active antennas. It is observed that the maximum EE value is obtained while serving ten users. Whereas for the proposed setup, the maximum value for (K = 10) is obtained where the sum spectral efficiency is a slowly increasing function of K in case of M = 10, while each additional UEs increases the PC by PUE = 0.5 W. Hence, the degradation in EE for a given sum SE increases as K grows up.
The proposed system is considered to be adaptive by changing the number of active-antennas while the change of the number of active-users to maintain the EE at its maximum point (EE = MaxEE).
Table 3, shows the estimates of EE based on different number of active-antennas while serving various number of users. It is observed that the maximum, highlighted values in each column, obtained energy efficiency is increased by increasing the number of active users at increased number of active antenna.
For example, the optimum number of active antenna for serving 5 users is 20 antennas in which the (MaxEE = 3.1262). Whereas, serving 10 UEs requires 30 antennas to get the (MaxEE = 3.8233). In addition, 30 UEs need 60 antennas to get (MaxEE = 4.8691) and 40UEs require about 70 active-antennas to achieve (MaxEE = 5.1015).
From the other side, the increased number of users increases the maximum EE value with more active antennas.
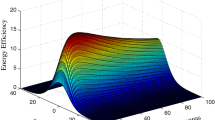
As shown in Fig. 4 The EE is increased by increasing the number of antennas for a constant number of users K = (5,10,30,40) until reach the maximum value of EE at a suitable number of antennas before decreasing again by increasing number of active antennas,where red points represents maximum EE for different values of inter cell interference (-3db,-15db). Hence, the EE is enhanced by increasing number of antennas at maximum SE.
When K = 10, the EE is shown in Fig. 5. For various values of the antenna-UE ratio M/K. The EE is an M/K unimodal function. It rises up to M/K = 2 for the investigated configuration and then gradually reduces as M/K becomes larger. In conclusion, servicing numerous UEs while concurrently expanding the number of BS antennas (to compensate for increased interference) may enhance network EE only if the advantages and costs of installing additional RF hardware are appropriately balanced.
We looked at the EE of Massive MIMO networks in the previous section at a constant number of UEs and a variable number of BS antenna. Hence, we consider the EE from a new perspective: we build the network to achieve maximum EE, without high-priority antennas for different UEs. This is accomplished via the use of adaptive antennas and GA optimization.
According to the simulation of the GA massive MIMO scheme for an active user (K = 10), the optimal number of active antennas at the optimum EE is determined to be (M = 20) at the best possible performance. However, when k = 20, M is estimated to be (M = 40). Therefore, this results is applicable as the antenna-UE ratio M/K = 2 as indicated in Fig. 6.
Additionally, every change in the number of active users results in a change in the number of antennas (M) in the 5G cell with the maximum EE while varying the number of active users. Based on the discussed simulation results, it has been proven that applying GA optimization algorithm on the proposed M-MIMO system improves the performance of the EE. However, the number of antennas in the M-MIMO grid is optimized based on the number of active users in the cell, as opposed to traditional wireless networks. It has also been possible to enhance the overall efficiency and dependability of the 5G system.
4 Conclusion
This paper suggests a scheme to minimize energy consumption in the 5G wireless network scenario where very complex antenna techniques such as massive MIMO technology are used. The proposed system has an adaptive number of active antennas in response to the change of the actual users within a cell. The number of available antennas is selected based on the maximum energy efficiency (EEmax) obtained using GA at a given spectral efficiency. By dynamically adjusting the number of antennas to achieve maximum energy efficiency, simulation results showed that the proposed system successfully saves energy and improves EE.
References
Björnson, E., Sanguinetti, L., Hoydis, J., Debbah, M.: Optimal design of energyefficient multi-user MIMO systems: is massive MIMO the answer? IEEE Trans. Wireless Commun. Inst. Elect. Electron. Eng. 14(6), 3059–3075 (2015)
Chou, H.-T., Cheng, D.-Y.: Beam-pattern calibration in a realistic system of phased-array antennas via the implementation of a genetic algorithm with a measurement system. IEEE Trans. Antennas Propag. 65(2), 593–601 (2017)
Gampala, G., Reddy, C. J.: "Massive MIMO — Beyond 4G and a basis for 5G," 2018 In: International Applied Computational Electromagnetics Society Symposium (ACES), Denver, CO, pp. 1–2 (2018)
Gong, S., Xing, C., Yang, N., Wu, Y.C., Fei, Z.: Energy efficient transmission in multi-user MIMO relay channels with perfect and imperfect channel state information. IEEE Trans. Wireless Commun. 16(6), 3885–3898 (2017)
Gupta, A., Jha, R.K.: A survey of 5G network: architecture and emerging technologies. IEEE Access 3, 1206–1232 (2015)
Mabrook, M.M., Khalil, H.A., Hussein, A.I.: Artificial intelligence based cooperative spectrum sensing algorithm for cognitive radio networks. Proc. Comput. Sci. 163, 19–29 (2019)
Mabrook, M.M., Taha, H.A., Hussein, A.I.: Cooperative spectrum sensing optimization based adaptive neuro-fuzzy inference system (ANFIS) in cognitive radio networks. J Ambient Intell Human Comput (2020). https://doi.org/10.1007/s12652-020-02121-9
Miao, G., Zander, J., Sung, K.W., Slimane, S.B.: Fundamentals of Mobile Data Networks. Cambridge University Press, Cambridge (2016)
Navarro-Ortiz, J., Romero-Diaz, P., Sendra, S., Ameigeiras, P., Ramos-Munoz, J.J., Lopez-Soler, J.M.: A survey on 5G usage scenarios and traffic models. IEEE Commun. Surv. Tutorials 22(2), 905–929 (2020)
Ng, W.K., Lo, E.S., Schober, R.: Energy-efficient resource allocation in OFDMA systems with large numbers of base station antennas. IEEE Trans. Wireless Commun. 11(9), 3292–3304 (2012)
Ng, W.K., Lo, E.S., Schober, R.: Wireless information and power transfer: energy efficiency optimization in OFDMA systems. IEEE Trans. Wireless Commun. 12(12), 6352–6370 (2013)
Rusek, F., et al.: Scaling up MIMO: Opportunities and challenges with very large arrays. IEEE Signal Process. Mag. 30(1), 40–60 (2013)
Salah, I., Mourad Mabrook, M., Hussein, A.I., Rahouma, K.H.: Comparative study of efficiency enhancement technologies in 5G networks - a survey. Proc. Comput. Sci. 182, 150–158 (2021)
Salh, A., et al.: Trade-off energy and spectral efficiency in a downlink massive MIMO system. Wireless Personal Commun. 106(2), 897–910 (2019)
Sarajli´c, M., Liu, L., Edfors, O.: When are low resolution ADCs energy efficient in massive MIMO? IEEE Access 5, 14837–14853 (2017)
Sivanandam, S.N., Deepa, S.N.: Introduction to Genetic Algorithms, Computational Intelligence and Complexity. Springer (2008)
Wyner, A.D.: Shannon-theoretic approach to a Gaussian cellular multiple-access channel. IEEE Trans. Inf. Theory 40(6), 1713–1727 (1994)
Xiao, H., et al.: CSI feedback for massive MIMO system with dual-polarized antennas. In: 2015 IEEE 26th Annual International Symposium on Personal, Indoor, and Mobile Radio Communications (PIMRC). IEEE (2015)
Zappone, A., Jorswieck, E.: Energy efficiency in wireless networks via fractional programming theory. Found. Trends Commun. Inform. Theory 11(3–4), 185–396 (2015)
Zhang, Q., Jin, S., Wong, K.K.: Power scaling of uplink massive MIMO systems with arbitrary-rank channel means. IEEE J. Select. Topics Signal Process. 8, 966–981 (2014)
Zhong, S., et al.: User oriented transmit antenna selection in massive multi-user MIMO SDR systems. Sensors J. MDPI (2020). https://doi.org/10.3390/s20174867
Funding
Open access funding provided by The Science, Technology & Innovation Funding Authority (STDF) in cooperation with The Egyptian Knowledge Bank (EKB).
Author information
Authors and Affiliations
Corresponding authors
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
This article is part of the Topical Collection on Optical and Quantum Sciences in Africa.
Guest edited by Salah Obayya, Alex Quandt, Andrew Forbes, Malik Maaza, Abdelmajid Belafhal and Mohamed Farhat.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Salah, I., Mabrook, M.M., Rahouma, K.H. et al. Energy efficiency optimization in adaptive massive MIMO networks for 5G applications using genetic algorithm. Opt Quant Electron 54, 125 (2022). https://doi.org/10.1007/s11082-021-03507-5
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s11082-021-03507-5