Focal beam structuring by triple mixing of optical vortex lattices

Abstract

On-demand generation and reshaping of arrays of focused laser beams is highly desired in many areas of science and technology. In this work, we present a versatile approach for laser beam structuring in the focal plane of a lens by triple mixing of square and/or hexagonal optical vortex lattices (OVLs). In the artificial far field the input Gaussian beam is reshaped into ordered arrays of bright beams with flat phase profiles. This is remarkable, since the bright focal peaks are surrounded by hundreds of OVs with their dark cores and two-dimensional phase dislocations. Numerical simulations and experimental evidences for this are shown, including a broad discussion of some of the possible scenarios for such mixing: triple mixing of square-shaped OVLs, triple mixing of hexagonal OVLs, as well as the two combined cases of mixing square-hexagonal-hexagonal and square-square-hexagonal OVLs. The particular ordering of the input phase distributions of the OV lattices on the used spatial light modulators is found to affect the orientation of the structures ruled by the hexagonal OVL. Reliable control parameters for the creation of the desired focal beam structures are the respective lattice node spacings. The presented approach is flexible, easily realizable by using a single spatial light modulator, and thus accessible in many laboratories.

1 Introduction

Ever since their discovery (Nye and Berry 1974), optical vortices have been subject of intense research interest. Due to their characteristic screw phase profiles, they are the only known truly two-dimensional (2-D) phase singularities. The phase at the singularity point of an optical vortex (OV) is not defined and, therefore, the intensity must vanish, leading to a doughnut-shaped bright beam (Rozas et al. 1997a; Desyatnikov et al. 2005). OVs were proven to carry orbital angular momentum (OAM) (Allen et al. 1992) which led to a new understanding of the relation between quantum effects and macroscopic optics. OAM is independent of the beams’polarization and can be transferred to matter (He et al. 1995; Padgett 2017). It is referred to as the topological charge (TC) m, i.e. an integer number with sign, describing the total phase change 2$\pi m$ around the OV beam axis in azimuthal direction. Although the entire physical picture is far richer, we will restrict our analysis to the canonical phase vortices, whose phase changes linearly in azimuthal direction.

In the past few decades, OVs have become a research topic in many areas of physics, including cold atoms in Bose-Einstein condensates (Matthews et al. 1999), nonlinear optics (Kivshar and Agrawal 2003; Hansinger et al. 2014, 2016), fluid dynamics (Brandt et al. 2002), optical communications (Li and Wang 2017), spectroscopy (Picón et al. 2010,Picón et al. 2010), interferometry (Fürhapter et al. 2005), and optical metrology (Wang et al. 2006b, a), just to mention a few. Ingenious applications include optical manipulation of small particles (Grier 2003), optical vortex coronagraph (Foo et al. 2005), high-resolution microscopy and lithography (Scott et al. 2009), and multiplexing of information for data transfer using complex optical fields (Trichili et al. 2016; Gregg et al. 2016; Wang et al. 2012; Larocque et al. 2017; Liu et al. 2018). OVs play an important role in super-resolution stimulated emission depletion (STED) microscopy (Hell and Wichmann 1994) and in the practical realization of optical tweezers (Grier 2003; Paterson et al. 2001).

For a better understanding of the obtained results presented here, we have to recall the basic results regarding the formation of stable elementary cells of OVs (Neshev et al. 1998; Stoyanov et al. 2019a) placed on a common background beam. This is a necessary step for the creation of rigid OV lattices (OVLs) of square or hexagonal type (Stoyanov et al. 2018a, b). Pairs of singly and equally charged OVs rotate and repel inside a laser beam as it propagates. When the TCs are opposite, the vortices attract each other and translate perpendicularly to an imaginary line connecting their cores (Rozas et al. 1997a, b). The smaller the OV-to-OV separation, the stronger the attraction/repulsion. The processes of rotation and repulsion within a rotational-symmetric ensemble composed of vortices with equal TCs can be cancelled by positioning an additional control OV with an opposite TC at its center (Neshev et al. 1998; Stoyanov et al. 2019a). Based on this, stable free-space propagation of large square-shaped and hexagonal OV lattices (even to the artificial far-field) was reported for the first time experimentally in (Neshev et al. 1998; Stoyanov et al. 2018a, b). These results were extended towards controllable beam reshaping in the focal plane of a lens by (twofold) mixing of square, hexagonal or square and hexagonal OV lattices with the same or different lattice constants (i.e. distances between two neighboring vortices in any vortex lattice) (Zhekova et al. 2019; Stoyanov et al. 2019b, c). The possibility for an additional beam structuring of each of the peaks of the focal arrays by hosting 1-D and quasi-2-D phase dislocations or even a singly-charged OV was also proven there. The potential control parameters for reshaping the desired bright beam focal pattern were discussed as well (Zhekova et al. 2019; Stoyanov et al. 2019b, c).

Here, we present a versatile method for beam structuring in the focal plane of a lens (artificial far field) based on a triple mixing of square (sq.) and/or hexagonal (hex.) optical vortex lattices (OVLs). The possibility for arranging different focal patterns is numerically simulated and proven experimentally. We present detailed data for three possible scenarios for OV lattices mixing-(i) triple mixing of square OVLs, (ii) triple mixing of hexagonal OVLs, as well as (iii) mixing of the type hexagonal-square-square OVLs. Additional data for square-hexagonal-hexagonal OVL mixing is provided in the Supplementary Material to this paper. Reliable control parameters for the creation of the desired focal beam structures are the OV node spacings of the individual OVLs and the sequence of the projection of the lattices on the spatial light modulators (SLMs), when hexagonal OV lattice is involved. In the Supplementary material to this work, we also demonstrate the possibility to additionally nest a phase singularity of desired type in each peak of the generated focal arrays. We believe that the reader will be convinced that the presented approach is flexible, easily realizable by using just a single SLM, and thus accessible in many laboratories.

2 Experimental setup and numerical model

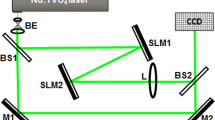
In Fig. 1 we schematically show the used experimental setup. Briefly, the continuous-wave Gaussian beam from a frequency-doubled Neodymium-doped Yttrium Orthovanadate (Nd:YVO$_4$) laser (wavelength $\lambda = 532$ nm) is expanded by a beam expander (BE). In order to apply the four-frame technique for interferogram analysis (Groves and Osten 2006; Dreischuh et al. 1996), a reference beam is split off by a beam splitter (BS) before the first spatial light modulator (SLM1). The object beam illuminates the first reflective SLM1. This SLM modulates the flat phase distribution of the input Gaussian beam. As a consequence, it also modulates the amplitude/intensity of the beam and redirects it to a second spatial light modulator (SLM2) of the same type. The singular beam reflected from SLM2 is then focused by a lens L ($f=75$ cm) onto a CCD camera chip. The CCD camera is placed at fixed position in the focal plane of the lens L. The object and the reference beams are recombined by a second beam splitter to interfere at the CCD chip. The respective intensity/interference patterns are recorded by blocking/unblocking the reference laser beam. The distance between SLM2 and the lens L is 30 cm, while the SLM1-to-SLM2 distance is 49 cm. The two SLMs are aligned in parallel and the angle of incidence of the laser beam with respect to the normal incidence is 4$^{\circ }$. The efficiency of the OVL generation from one of the SLMs is 71% resulting in an overall efficiency of nearly 45% in the focus of the lens L. The used experimental setup can easily be modified such that only one spatial light modulator is needed. In this case the two desired phase distributions have to be encoded on the respective half of the active pixels of the modulator.

Fig. 1

Experimental setup. Nd:YVO$_4$-continuous-wave frequency-doubled laser ($\lambda = 532$ nm); BE-beam expander; M-flat silver-coated mirrors; BS-beamsplitters; SLM-reflective spatial light modulator (Pluto, Holoeye Photonics); L-focusing lens ($f=$ 75 cm); CCD-charge-coupled device camera; SLM1-to-SLM2 distance $z_1=49$ cm. SLM2-to-lens distance $z_2=30$ cm

Another possibility is to perform imaging of SLM1 onto SLM2 and thereafter Fourier-transforming the plane of SLM2 by a thin lens. The reason not to use such imaging is to include in the experiment and in the numerical simulations the amplitude modulation resulting from the free-space propagation between the modulators and from SLM2 to the lens and, thus, to prove the stability of the demonstrated method. According to the choice to use two SLMs here, our numerical simulations considered the evolution of the manipulated light field by following the beam path SLM1-SLM2-lens until the artificial far field is reached. Since the propagation of the laser beam is linear, its evolution was numerically calculated by using the linear paraxial model equation for the slowly-varying optical beam envelope amplitude E

$$\begin{aligned} i\partial E/\partial (z/L_D) + (1/2)(\partial ^2/ \partial x^2 + \partial ^2/ \partial y^2)E=0. \end{aligned}$$

(1)

Here $L_D=ka^2$ is the diffraction length of an individual OV (the distance along the propagation direction of an unfocused beam, at which its intensity cross-section is doubled), k is the wavenumber in air, a is the half width at (1/e)-level of the amplitude of the individual optical vortex, x and y are the transverse Cartesian coordinates, and z the longitudinal coordinate. The used computational window spans 1024 $\times$ 1024 grid points. The half width at the $1/e^2$ intensity level of the incoming background Gaussian beam was 205 pix. By suitable programming of SLM1, we generated a single OV and recorded its profile right after SLM1 and at the position of SLM2. From the data we conclude that the distance between the modulators corresponds to 1.5$L_D$ and the SLM2-to-lens distance to 3.0$L_D$. The lens (focal length f) is accounted for by the transmission phase function T(x, y) at the appropriate step of the calculation,

$$\begin{aligned} T(x,y)=exp[-ik(x^2+y^2)/(2f)]. \end{aligned}$$

(2)

The beam evolution was numerically simulated by using the beam propagation method (known also as split-step Fourier method), which is proven to be fast and adequate for simulating nonlinear beam evolution. In the present case, we set the nonlinearity to zero.

3 Results and discussion

Throughout this paper we will use the terms node spacing and lattice constant as equivalent, denoting the distance between two neighboring vortices in any vortex lattice. With $\Delta$, followed by a subscript we denote the phase distributions sent to SLM1, with $\delta$-phase distributions sent to SLM2. The subscript will provide information regarding the specific type of the used OVL-sq for square-shaped, hex for hexagonal OVL. The OV lattice node spacing related to this OVL will be denoted afterwards. This style of notation will be kept also for the cases when the numerical sum of two phase distributions is programmed on one SLM.

In this prefatory section, we use one of the SLMs only. The second one was switched off, thus acting as a flat mirror. In Fig. 2 we show numerical results for the basic phase and intensity distributions of a square-shaped ((a), left panels) and a hexagonal optical vortex lattice ((b), left panels), resulting in the respective bright focal arrays. The white rhombi and the white triangles indicate one elementary cell of the respective lattices. OVs of unit topological charges with the same signs are placed in the apices of the square (triangular) elementary cell. In order to stabilize the elementary cell and thus the entire OVL, an OV with unit TC but with opposite sign is placed in the middle of each cell. In the right panel of Fig. 2a, we show the focal array resulting from the square-shaped OVL consisting of four peaks situated in the apices of a rhombus. The hexagonal OVL produces a triangular structure of bright peaks in the focal plane of the lens (Fig. 2b, right panels) (Stoyanov et al. 2018a, b). The bright peaks result from the Fourier-transformation of the bright portions of the background beam reaching the plane of the focusing lens. The bright portions of the background beams, however, crucially depend on the ordering of the nested optical vortices. Additional insight for this beam structuring is shown as pictorial representation in Fig. S1 in the Supplementary material. The white triangles in Fig. 2b denote the typical stabilized elementary cell of the hexagonal OV lattice – three equally charged OVs in the apices of a triangle and one oppositely charged OV in its center. It is worth mentioning that by inverting the signs of all TCs of the OVs of the hexagonal lattice the triangular focal structure can be rotated at 180$^{\circ }$ (compare Fig. 2b1, b2). The same can be achieved by changing the order of programming the OVLs on the two SLMs. In all described cases, all peaks in the focal plane of the lens have flat phases (Stoyanov et al. 2018a, b). By increasing/decreasing the OV lattices node spacing one can control the size of the focal arrays. The larger the OV node spacing, the smaller the bright focal arrays are. This is a nice manifestation of the similarity theorem of Fourier transformation. (“Wide” functions in the space domain correspond to “narrow” functions in the spatial frequency domain.)

Fig. 2

Numerical results. a Phase distribution of a square-shaped OV lattice (left), beam intensity distribution in front of the focusing lens L (down), and the obtained bright structure in the focal plane of a lens (right). b The same as in (a), but for a hexagonal OV lattice. b1, b2 Possibility to rotate the triangular structure coming from the hexagonal OVL. White rhombi and white triangles denote one elementary cell of the respective lattice

In (Zhekova et al. 2019; Stoyanov et al. 2019b, c) is shown that square-shaped and/or hexagonal OV lattices of different node spacings can be mixed to form various multi-spot focal arrays. In Fig. 3a–d, we show some examples for double mixing of OVLs, which could serve the reader as a guide to easily follow the triple mixing discussed later in this paper. Both SLMs are used in this and all subsequent cases. Let us remember the notations: $\Delta$ denotes the node spacing for the phase distribution sent on SLM1, $\delta$ the same for SLM2.

In Fig. 3a we show experimental multi-spot focal array obtained by mixing square-shaped OV lattices with different node spacings, in this case $\Delta _{sq} = 21$ pix. and $\delta _{sq} =121$ pix. Generally, when two OV lattices of any type and with different node spacings are mixed, the OV lattice with the smaller node spacing determines the large-scale structure of the focal array of bright beams. Respectively, the larger node spacing determines the small-scale focal structure. The multi-spot focal array in Fig. 3a is composed of 16 bright peaks resembling the basic form of the array coming from a single focused square-shaped OV lattice-square-shaped large-scale structure of square-shaped small-scale structures, each one consisting of 4 bright peaks. The same holds also for mixing OV lattices of a hexagonal type. The respective results are shown in Fig. 3b1, b2. Here the triangular large-scale structure consists of three triangular small-scale structures, each one composed of three bright peaks. In Fig. 3b1 we show results for $\Delta _{hex} = 41$ pix. and $\delta _{hex} = 151$ pix. By changing the ordering of the places of the phase distributions sent to the SLMs (equivalently - by inverting the signs of all OVs in both phase distributions) one can rotate the entire focal array by 180$^{\circ }$ (Fig. 3b2, see also Fig. S2 in the Supplementary material).

It is natural to expect that mixing of OVLs of different type is possible as well. The mathematical background of this operation is the convolution theorem of Fourier transformation (The Fourier transformation of a product of two functions is equal to the convolution of the Fourier transformations of the individual functions). This type of OVL mixing is demonstrated in Fig. 3c for $\Delta _{sq} = 41$ pix. and $\delta _{hex} = 101$ pix., and in Fig. 3d for $\Delta _{sq} = 151$ pix. and $\delta _{hex} = 61$ pix. On the basis of the similarity theorem, one can easily understand that the denser OVL will determine the large-scale structure, whereas the small-scale structure of the observed focal pattern results from the OVL with the larger array node spacing. The change in the symmetry between these two focal arrays (in simple words denoted as a square of triangles and a triangle of squares, respectively) is clearly seen in panels (c) and (d) of Fig. 3. Similar to the pattern rotation described for panels (b1) and (b2) of Fig. 3, the mixed focal patterns in panels (c) and (d) of this figure can also be rotated by 180$^{\circ }$ by changing the ordering of the phases programmed for the SLMs or by inverting all signs of the TCs. It is important to point out that the rotation of a focal structure is possible only for hexagonal OVLs and for OVLs mixed with at least one hexagonal lattice, since the square-shaped lattices are symmetric.

Fig. 3

Experimental beam reshaping by double mixing of OVLs. a Multi-spot focal array obtained by mixing square-shaped OV lattices with $\Delta _{sq} =21$ pix. and $\delta _{sq}=121$ pix. b1 The same for two hexagonal OVLs with $\Delta _{hex} =41$ pix. and $\delta _{hex} =151$ pix. b2 Rotation of the focal array at 180$^{\circ }$ by changing the ordering of the phase distributions sent to the two SLMs. c Mixing of square and hexagonal OV lattices with $\Delta _{sq} =41$ pix. and $\delta _{hex} =101$ pix. d The same but for different node spacings $\Delta _{sq} =151$ pix. and $\delta _{hex} =61$ pix

After this rather long but necessary introductory part, we start presenting the new results in this work. In Fig. 4 we demonstrate, both numerically and experimentally, the reliability of the method for triple mixing of square-shaped OV lattices with different node spacings. The input Gaussian beam, Fig. 4a, is reflected at SLM1, which is programmed with the phase of a square OVL with node spacing $\Delta _{sq} =21$ pix (Fig. 4b). The distance $z_1=49$ cm between the two SLMs is sketched in the figure. After passing this free-space propagation distance, the singular beam is phase modulated once more by the second SLM programmed with the phase distribution of a different OVL (Fig. 4c). The phase of this second lattice is the numerical sum (modulo 2$\pi$) of the phases of two square-shaped lattices with node spacings $\delta _{sq1} =41$ pix and $\delta _{sq2} =121$ pix. In panel (d) we present the intensity distribution of the structured beam right after SLM2. Because of the additional diffraction between the SLMs, it can clearly be seen that OVs created by SLM1 affect the intensity distribution stronger than the OVs created by SLM2, which form the denser grid. This is also due to the fact that no imaging system is used between the two SLMs. The respective distribution just in front of the focusing lens L at a distance $z_2 =30$ cm is shown in panel (e) of Fig. 4. For a better visibility, the marked portions of (d) and (e), are shown zoomed in frames (d2) and (e2), respectively. Notations for the position of the elementary cells formed by the OVL with different node-spacings are shown as well. The focusing of the structured beam by the lens is modeled by adding the phase distribution of a thin lens (panel (f); see Eq. 2).

In the left part of the second row of frames in Fig. 4 we show theoretically calculated (left) and experimentally recorded intensity distributions (right) of the triple mixed square-shaped OV lattices. As expected, the small-scale structure is in the form of a rhombus with four peaks situated in its apices. On both frames white solid rhombi mark the intermediate-scale structure typical for the double mixing of square-shaped OV lattices as shown in Fig. 3a. The large-scale structure is once again in the same form but it is consisting of four such intermediate-scale structures. The particular ordering of the phases on the SLMs was found to have negligible effect on the relative intensities of the peaks within the multi-spot focal array. As in the case of a double mixing, the small-scale structure of the observed patterns results from the OVL with the largest node spacing, whereas the large-scale structure is a result from the OVL with the smallest array node spacing. The intermediate-scaled structure comes from the OV lattice with medial node-spacing. This is, once again, a nice manifestation of the similarity theorem of the Fourier transformation. It will appear even more spectacular in the cases in which OVLs with different symmetries are mixed.

Fig. 4

Triple mixing of square-shaped OV lattices. Input Gaussian beam (a) is reflected from SLM1 programmed with the phase of an OVL (b) with node spacing $\Delta _{sq} =121$ pix. c SLM2 is encoded with the numerical sum of the phases of OVLs with node spacings $\delta _{sq1} =41$ pix. and $\delta _{sq2} =21$ pix. d Intensity distribution of the structured beam just after SLM2. e Respective intensity distribution in front of the focusing lens L at a distance $z_2 =30$ cm behind SLM2. f Phase distribution of a thin lens for modeling the focusing of the structured beam. Lower row-theoretically calculated and experimentally recorded focal intensity distributions of the triple mixed square-shaped lattices. Solid white rhombi-intermediate-scale structures discussed in the text. d2, e2 Zoomed marked portions of (d, e) with notations for the position of the elementary cells formed by the OVL with different node-spacings

In our numerical data we observe that the phase profiles of all 64 bright focal peaks are flat. The detailed analysis of one quarter of the experimental large-scale structure (i.e. one intermediate-scale structure) confirms this statement. In the left frames in Fig. 5 we show experimental interference patterns of one of the (in total four) intermediate-scale structures. Each one was obtained with a slightly inclined reference beam, at a controlled phase delay, and corresponds to the marked experimental intermediate-scale structure presented in Fig. 4 (bottom, left). The close inspection of the patterns reveals parallel interference lines across the bright beams, which indicate that their phases are flat. Nonetheless, in order to obtain quantitative information for the (horizontal) phase profiles of the beams in the sub-arrays in the left part in Fig. 5, we applied the four-frame technique for interferogram analysis (Groves and Osten 2006; Dreischuh et al. 1996). The graph in Fig. 5 represents the horizontal phase profiles of the sixteen bright peaks retrieved from the four frames to the left. One can clearly see that phase dislocations are absent. We attribute the small and similar curvature of the phase profiles in the graph in Fig. 5 to a possible slight offset of the CCD-camera chip from the focal plane.

Fig. 5

Quantitative reconstruction of the phase profiles of one intermediate-scale structure created in the focal plane by the triple mixing of the square-shaped OVLs (see also Fig. 4, bottom left panel). Left four panels-interferograms recorded at the indicated four relative phase offsets by overlapping the structured beam in the focus with an inclined plane wave. Graph-reconstructed horizontal phase profiles of the peaks located in the array

In Fig. 6, following the style of presentation used in Fig. 4, we show triple mixing of hexagonal OVLs with different node spacings. The phase (as well as the amplitude/intensity) of the unperturbed Gaussian beam (panel (a)) is modulated by SLM1. This modulator is programmed with a phase distribution, which is a sum of two hexagonal OVLs with node spacing $\Delta _{hex1} =41$ pix. and $\Delta _{hex2} =81$ pix. (panel (b)). After free-space propagation ($z_1$) to SLM2, this singular beam is additionally modulated by the phase of a third hexagonal OV lattice with node spacing $\delta _{hex} =21$ pix. (panel (c)). The computed intensity distribution of the obtained structured beam just after SLM2 is shown in panel (d), while the respective distribution in front of the focusing lens L at a distance $z_2$ is shown in panel (e) (magnified-in panels (d2) and (e2), respectively). The Fourier transform of this triple mixed hexagonal OV lattice is modeled by adding the respective phase of a thin spherical lens (panel (f)).

In the left part of the lower row of panels of Fig. 6 we compare the theoretically calculated and experimentally recorded intensity distributions of the triple mixed hexagonal lattices in the artificial far field. As seen, the large-scale bright beam focal structure exhibits the shape of an equilateral triangle composed of three smaller equilateral triangles (intermediate-scaled structure, marked by a ring). The basic small-scale structure is also in the typical form of a Fourier-transformed hexagonal OV lattice-three bright peaks situated in the apices of a triangle.

Unlike the case for triple mixing of a square-shaped OV lattice, here the particular ordering of the programmed phase on the two SLMs is important in view of controlling the direction of orientation of the obtained focal structures. All 9 small-scale structures forming the 3 intermediate-scale structures and the large-scale structure can be rotated by 180$^{\circ }$ by simply transposing the phase distributions encoded on the two SLMs. In addition to the OV lattices node spacing, this could also be used as a control parameter for generating the desired focal array of bright beams.

Fig. 6

Triple mixing of hexagonal OV lattices. Input Gaussian beam (a) reflected from SLM1, programmed with the phase of an OVL (b) with numerically added phases of OVLs with node spacings $\Delta _{hex1} =41$ pix. and $\Delta _{hex2} =81$ pix. Subsequently, it is phase modulated by a third hexagonal OV lattice with node spacing $\delta _{hex} =21$ pix. sent to SLM2 (c). The intensity distribution of the structured beam just after SLM2 is shown in (d) and the respective distribution in front of the focusing lens L at a distance $z_2$-in (e). The focusing of the structured beam is modeled by adding the respective phase of a thin spherical lens (f). Lower row of panels-theoretically calculated and experimentally recorded focal intensity distributions of the triple mixed hexagonal lattices. White rings-intermediate-scale structures discussed in the text. d2, e2 Zoomed marked portions of (d, e) with notations for the position of the elementary cells formed by the OVL with different node-spacings

Next, in Fig. 7, we report results regarding the triple mixing of square-shaped and hexagonal OVLs. For consistency, we continue using the style of presentation in the sequence of steps familiar from Figs. 4 and 6. The differences are: (i) SLM1 is programmed with the phase of a hexagonal OVL with $\Delta _{hex} =41$ pix. (Fig. 7b). (ii) SLM2 is programmed with the numerically added phase distributions (modulo 2$\pi$) of square-shaped OVLs with node spacings $\delta _{sq1} =21$ pix. and $\delta _{sq2} =121$ pix. (Fig. 7c).

In the lower left panels of Fig. 7 we show the obtained multi-spot focal pattern resulting from triple mixing of the described hexagonal and square-shaped OVLs. The obtained numerical data agree fairly well with the experimental result. The small-scale structure (in this case four bright peaks forming a diamond) is again resulting from the OVL with the largest node spacing $\delta _{sq2} =121$ pix. The intermediate-scale structure (triangle-like; Fig. 7, lower row, white rings) is ruled by the OV lattice with the medial node spacing, in this case $\Delta _{hex} =41$ pix. The rhomboidal large-scale structure consists of four intermediate-scale triangular structures, each one composed by four bright peaks resulting from the OV lattice with the smallest vortex-to-vortex node spacing. The classification small-, intermediate- and large-scale structure is independent on the type of the used OVLs (square or hexagonal) and on the particular ordering of the phase distributions on the two SLMs. The only important parameter is the OVL node spacing. As in the preceding case, by changing the order of the creation of the individual lattices on the SLMs one can rotate the direction of the intermediate-scale structure (and thus the entire focal array) by 180$^\circ$. In the Supplementary Material to this manuscript (Fig. S3) we also demonstrate the possibility to mix two hexagonal OVLs with a square-shaped one. Moreover, the numerical sum sent to either of the two SLMs can be the sum of two OVLs of different type (square or hexagonal).

Fig. 7

Triple mixing of one hexagonal and two square-shaped OV lattices. Input Gaussian beam (a) is reflected from SLM1, programmed with the phase (b) of a hexagonal OVL with $\Delta _{hex} =41$ pix. In the plane of SLM2 it is subsequently phase modulated with numerically added phases (c) of square-shaped OVLs $\delta _{sq1} =21$ pix. and $\delta _{sq2} =121$ pix. (d) Intensity distribution of the structured beam just after SLM2. The respective distribution in front of the focusing lens L is shown in (e). f Phase distribution of a thin lens. Lower row of frames-theoretically calculated and experimentally recorded focal intensity distributions of the triple mixed OVLs. Solid white rings-intermediate-scale structures discussed in the text. d2, e2 Zoomed marked portions of (d, e) with notations for the position of the elementary cells formed by the OVL with different node-spacings

Using the four-frame technique for interferogram analysis (Groves and Osten 2006; Dreischuh et al. 1996) in graphs (c) and (d) of Fig. 8 once again, we show the quantitative reconstruction of the phase profiles of the beam ensembles in the focal plane. The results refer to two different intermediate-scale structures marked with white rings in panels (a) and (b). The particular types of the used OVLs and the respective node spacings are denoted in the graphs. As seen from the data, one can conclude with reasonable accuracy that the reconstructed phases of the sub-beams are flat. In our view, the results in the graphs of Figs. 5 and 8 are remarkable in the sense that the flat phase profiles of the bright focal peaks are surrounded by hundreds of OVs with their dark cores and 2-D phase dislocations sitting in the dark neighboring area. The OVs are between and around the well-formed bright peaks in the focal plane of the lens. This can be also clearly seen in Figs. 3c, d and 5c, d in Stoyanov et al. (2019b). Additional data confirming these observation are presented also in (Stoyanov et al. 2018a, b).

Fig. 8

a Structured beam in the focus created using three hexagonal OV lattices of different periods (same as in Fig. 6, lower row). b Intensity of a structured beam in the focus created by mixing a hexagonal and two square-shaped OVLs. White rings in (a, b) denote the intermediate-scale structures used for the quantitative reconstruction of the phase profiles shown in graphs (c, d). The particular types of the used OVLs and the respective node spacings are also denoted in the graphs

As already stated the ratio between the lattice node spacings of the OVLs is an important control parameter. In Fig. 9, some more details confirming this are provided. In Fig. 9a–d we show four cases of triple square-shaped OV lattice mixing. OVL with a node spacing $\Delta _{sq} =21$ pix. is sent to SLM1. On the second SLM we encoded the numerical sum (modulo 2$\pi$) of OVLs with:

• (a) $\delta _{sq1} =41$ pix. and $\delta _{sq2} =61$ pix.;

• (b) $\delta _{sq1} =41$ pix. and $\delta _{sq2} =81$ pix.;

• (c) $\delta _{sq1} =41$ pix. and $\delta _{sq2} =101$ pix.;

• (d) $\delta _{sq1} =41$ pix. and $\delta _{sq2} =121$ pix.

In the graph to the right in Fig. 9, red open circles and red lines denote the vertical positions of the peaks from the top small-scale structures in panels (a-d). (For simplicity, only the top four peaks in panel (d) are marked.) As seen, the“center of the mass”of the small-scale structure remains unchanged (black hollow circles and black line), while the upper and the lower peaks tend to move towards its center with increasing the largest node spacing $\delta _{sq2}$. In other words, by increasing the node spacing of the least dense OV lattice in this triple combination, one can control the size of small-scale structure and, thus, the size of the whole focal array, without changing the position of the“center of mass”of the multi-peak structure. Because of the symmetry in the used square-shaped OVLs, in this case only, the summed phase distribution could be sent to either of the two SLMs without changing the symmetry of the obtained focal structures. The tendencies presented in Fig. 9a–d are clear manifestation of the already mentioned Similarity theorem.

Fig. 9

a–d Focal intensity distributions of structured beams created using square-shaped OV lattices with lattice constants $\Delta _{sq} =21$ pix. and the numerical sum of OVLs with $\delta _{sq1} =41$ pix. + $\delta _{sq2} =61$ pix. (a), $\delta _{sq1} =41$ pix. + $\delta _{sq2} =81$ pix. (b), $\delta _{sq1} =41$ pix. + $\delta _{sq2} =101$ pix. (c), and $\delta _{sq1} =41$ pix. + $\delta _{sq2} =121$ pix. (d), respectively. Graph: Vertical positions of the peaks from the top small-scale structure in (a–d) versus the largest node spacing $\delta _{sq2}$ ranging from 61 pix. to 121 pix

Independently of the type (square and/or hexagonal) of the used OVLs for triple mixing, the increase of the node spacing of the least dense OV lattice (i.e. the one with the largest OVL constant) leads to the shrinking of the small-scale structures. In Fig. 10 this is demonstrated for the case of triple mixing of hexagonal OVLs. The focal intensity distributions of bright beams is created using three hexagonal OV arrays with $\Delta _{hex} =21$ pix. (on SLM1) and with sums of phase distributions (panels (a)–(c)) corresponding to $\delta _{hex1} =41$ pix. + $\delta _{hex2} =61$ pix. (a), $\delta _{hex1} =41$ pix. + $\delta _{hex2} =81$ pix. (b), $\delta _{hex1} =41$ pix. + $\delta _{hex2} =101$ pix. (c), encoded on SLM2. The decreasing length of the effective cathetus of the encircled small-scale structures in panels (a–c) vs. increasing lattice period $\delta _{hex2} =61, 81, 101$ pix. is shown in the graph in Fig. 10 with blue open circles. The length of the catheta of the intermediate- and of the large-scale structures also decreases, however, at a slower rate. This tendency for the intermediate-scale triangular structure vs. $\delta _{hex2}$ is denoted on the graph with black hollow triangles, for the large-scale structure-with red solid triangles. The comparison between the data shows that the increase of the largest constant of the hexagonal OV lattice leads to shrinking of the whole multi-spot array. Obviously, the far-field scaling of the triple-mixed hexagonal OVLs is more complicated as compared to the one of the triple-mixed square-shaped OVLs.

Fig. 10

a–c Focal intensity distributions of structured beams created using three hexagonal OV arrays with lattice constants $\Delta _{hex} =21$ pix. and the numerical sum of $\delta _{hex1} =41$ pix. + $\delta _{hex2} =61$ pix. (a), $\delta _{hex1} =41$ pix. + $\delta _{hex2} =81$ pix. (b), $\delta _{hex1} =41$ pix. + $\delta _{hex2} =101$ pix. (c). Graph: Decreasing length of the cathetus of the small-scale (see white ring in (c); blue open circles in the graph), intermediate-scale (dashed triangles in (a–c); hollow black triangle in the graph), and large-scale structures in (a–c) (solid red triangles in the graph) versus increasing lattice period $\delta _{hex2}$

In panels (a–c) in Fig. 11 and in the corresponding graph we illustrate another possible approach for controlling the positions of the individual peaks within a focal array structure. Panels (a)–(c) present experimental data obtained using OVLs with period $\Delta _{sq} =21$ pix. (programmed on SLM1) and the numerical sum of the phase distributions sent to SLM2, $\delta _{sq} =41$ pix. + $\delta _{hex} =101$ pix. (a), $\delta _{sq} =61$ pix. + $\delta _{hex} =101$ pix. (b), and $\delta _{sq} =81$ pix. + $\delta _{hex} =101$ pix. (c). In other words, in this case the node spacing $\delta _{sq}$ of the intermediate-scale structure is changed. This structure is rhomboidal, with peaks forming triangles in its apices, as shown in the encircled area of Fig. 11a. The triangular small-scale structure is a result from the hexagonal OV lattice with the largest node spacing $\delta _{hex} =101$ pix. The intermediate-scale and the large-scale structures are in the form of rhombi determined by the corresponding node spacings of the square-shaped OVLs with smaller node spacings. The graph in Fig. 11 shows the decreasing horizontal size (peak-to-peak, red open circles and red curve) of the encircled intermediate-scale structure in panel (a) vs. the increasing intermediate lattice period $\delta _{sq}$. Black open circles and black line present the constant height of the small-scale triangular structure with $\delta _{hex} =101$ pix. Hence, in this way, by changing the medial node spacing of one the OV lattice, one can control the size of intermediate-scale structure without changing the size of the small-scale structures of the array but influencing the size of the large-scale structure of focal peaks.

Fig. 11

a–c Focal intensity distributions of structured beams created using square-shaped OV array with lattice constants $\Delta _{sq} =21$ pix. and with the numerical sum of a square-shaped and hexagonal OVL with $\delta _{sq} =41$ pix. + $\delta _{hex} =101$ pix. (a), $\delta _{sq} =61$ pix. + $\delta _{hex} =101$ pix. (b), and $\delta _{sq} =81$ pix. + $\delta _{hex} =101$ pix. (c). Graph: Decreasing horizontal size (peak-to-peak) of the encircled intermediate-scale structures in (a–c) versus increasing intermediate lattice period $\delta _{sq}$ (red open circles and red curve). Black open circles and black line-constant height of the small-scale triangular structure

4 Conclusion

The results presented in this paper for triple mixing of square-shaped and hexagonal OV lattices substantially expand previous published works and are clear manifestations for the possibility to create a rich variety of focal arrays composed of bright beams. The OV lattice node spacing, independently of the type of the used OV lattices and independently of its orientation (rotation), can serve as a control parameter. In agreement with the Similarity theorem of Fourier transformation, the largest node spacing determines the size of the small-scale structure, while the smallest node spacing controls the large-scale structure. As expected, by changing the OV lattice with the intermediate-scale node spacing, one can control the size and the position of the medial bright focal structure. When hexagonal OV lattices are involved in the triple mixing, an additional control parameter can be used. By reversing the phase distributions sent to the SLMs (or when all TCs are inverted), the orientation of the bright array structures coming from one or more hexagonal lattices are rotated at 180$^{\circ }$. This results in the rotation of the entire multi-spot bright array. The phases of the bright beams are flat. This is remarkable, since the bright focal peaks are surrounded by hundreds of OVs with their dark cores and 2-D phase dislocations sitting in the dark neighboring area. Additional structuring of the far-field intensity profiles of the discussed triple mixed OVLs by adding 1-D dark beam, a quasi-2-D dark beam, or by hosting an OV in each bright focal beam of the structure is shown in Figs. S4 and S5 in the Supplementary Material. Some of the potential applications of the presented method are controllable writing of optically-induced parallel waveguide structures (in e.g. photorefractive nonlinear media; see e.g. Stoyanov et al. 2017), multiplexing data transfer using complex singular beams (Li and Wang 2017; Wang et al. 2019), and creation of singular higher-order vector fields (Otte et al. 2017). For stimulated emission depletion (STED) microscopy, a potential modification (Xue and So 2018) could be based on the arrays of bright beams discussed in this work (with or without OVs nested in), in order to parallelize the scanning of adjacent sectors of one sample.