1 Introduction

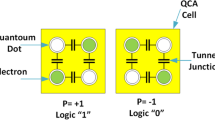
Power consumption and circuit size reduction are the major problems in digital electronics. CMOS technology that is used to design these circuits nowadays has problems such as high-power consumption, leakage current and short-channel effects (Lent et al. 1993). Landauer (1961) stated that for any bit of information loss, there is a KTln2 Joules of energy dissipation and this information cannot be retrieved in any way. This made researchers think about an alternative for CMOS. This new technology should have characteristics such as smaller size, higher speed, and lower power consumption than CMOS technology with same functionality. In 1944, Quantum-dot cellular automata (QCA) with same functionalities offered by Tougaw and Lent (1994). QCA Cell is the main and fundamental unit of QCA technology. Each QCA cell includes four quantum dots and two free electrons (Zhang et al. 2004). Logical zero and one states in this technology is determined by the location of electrons in the cells.

The most permanent state of a QCA cell is when two electrons are diagonal in cell. XOR gate is used as based gate in logic and combinational circuits design, like multiplexer (Sen and Dutta 2014; Rashidi et al. 2016), Converters (Beigh and Mustafa 2014), Full Adder (Ahmad et al. 2014; Shams and Bayoumi 2000; Hänninen and Takala 2010; Kianpour et al. 2014), as well as Comparator in QCA (Failed 2020a; Shiri et al. 2019). Therefore, the design of QCA-based XOR structure has been considered by researchers in recent years. The core idea of this study, is the offering of new QCA-based three-input XOR and two-input XNOR structures. To show that our proposed XOR structure is better than previous structures, we use this structure to design a Full Adder, 4-bit binary to gray (B2G) code converter, 4-bit Gray to Binary (G2B) code converter, and single comparator circuit, and compare the results with previous work. The proposed designs are simulated by QCADesigner and compared to the previous works. The major contributions of our work can be summarized as follows:

  • An efficient three-inputs XOR gate is proposed.

  • A novel Full Adder based on the proposed XOR is suggested and designed.

  • A novel single bit Comparator based on the proposed XOR is suggested and designed.

  • A novel B2G code converter based on the proposed XOR is suggested and designed.

  • A novel G2B code converter based on the proposed XOR is suggested and designed.

  • Simulation of the proposed structures by QCADesigner 2.0.3 (Walus et al. 2004) is done.

  • The proposed circuits improved in number of cells, occupied area and latency compared to previous works.

  • Our 1-bit simple proposed structures have no crossover.

  • Our 1-bit scalable proposed structured have crossover.

  • The total energy dissipation for proposed designs of 1-bit comparator is calculate by QCADesigner-E (https://github.com/FSillT/QCADesigner-E).

The structure of this paper is organized as follows: In Sect. 2, the previous works are discussed. Section 3 offers the new structures of XOR and XNOR gates, as well as One-bit Comparator circuit, Full Adder, 4-bit B2G converter, and 4-bit G2B converter based on them. In Sect. 4, the simulation results will be depicted. In Sect. 5, the proposed circuits will be compared with previous work. Finally, the Conclusions and future works are provided in Sect. 6.

2 Previous works

In this section, a number of studies conducted in recent years are reviewed. Akter et al. (2015) offered two comparator circuits using their proposed TR and QCA-based Feynman gates. The designed circuits using TR gate has 134 cells, 0.25 µm2 area, and 0.5 Clock Cycle latency; and the design using Feynman includes 87 cells, 0.11 µm2 area, and 0.5 clock cycle latency. Shiri et al. (2019), proposed and simulated a 1-bit comparator using Majority, XNOR, and NOT gates in QCA technology. Their proposed design has 38 cells, 0.03 µm2 of area, as well as 0.5 cock cycle latency. Ahmed et al. (2020a), introduced two QCA-based 1-bit comparator circuits. The first design has 55 cells and 0.0669 µm2 of area, and the second one has 42 cells and 0.0407 µm2 of area. Majeed et al. (2020b), offered new QCA-based XOR and XNOR gates with fewer cells and smaller areas compared to the existing designed gates. Also, they designed three one-bit comparator circuits with proposed structures. The designed comparators have 40, 35, and 33 cells, and the occupied area are 0.05, 0.04, and 0.04, respectively. The latency of the proposed designs was 0.75 clock cycle and the circuits were Irreversible. Save et al. (2020c), proposed QCA-based one-bit comparator using 3 Majority gates and a NOT gate. The proposed circuit includes 30 cells, and the occupied area is 0.05 µm2 and the latency is one clock cycle. This circuit was optimal in terms of cell counts, but it was not suitable in terms of area compared to previous works. Balali et al. (2017), designed a Full Adder using 3-inputs XOR. The proposed XOR consisted of 14 cells, with an area of 0.01 µm2 and a latency of 0.5 clock cycle. Roshany et al. ( 2019), proposed a 3-inputs XOR, and then by exploiting it, they designed and simulated a QCA-based multi-layer Full Adder. Majeed at el. (2020a), proposed a Full Adder using a novel XOR gate. The simulation results shown that the proposed design was better than previous works. Babaie et al. (2018) proposed a QCA Full Adder. The proposed circuit had only 26 cells and the outputs needed two clock zones to generate. Zhang et al. (2017), proposed a new-five majority to construct Full Adders. The proposed Full Adder had 35 cells and occupied area 0.0288, and also 1 clock cycle delay. Islam et al. (2018), proposed a new QCA circuit to convert 4-bit binary to 4-bit B2G and 4-bit G2B code using two input XOR gate. The proposed QCA B2G and G2B circuits has 37 and 47 cells, and 0.04 and 0.05 the occupied area, respectively. Karkaj et al. (2016), proposed a new XOR gate and also non-reversible 4-bit B2G and G2B converter based it in QCA technology. Shu et al. (2020), proposed a new 4-bit B2G converter by employing the proposed novel XOR structure as a basic building block in its circuit. Ahmadpour et al. (2018), proposed a novel 1-bit Full Adder based on their 3-input XOR structure. This circuit was simulated by only 20 cells and required three clock zones. Nuriddin et al. (2019), proposed new XOR structures and designed based on their simple and scalable Full Adders. The scalable form had 49 cells and four clock phases. Also, simple form had 35 cells and two clock phases. Sharma et al. (2020), proposed 1-bit comparator circuit that designed by only 26 cells. Wang et al. (2020), proposed a novel XOR/XNOR structure for modular design of QCA circuits. Then they designed and simulated 1-bit Full Adder and 1-bit Comparator circuits based on it. The design of 1-bit Full Adder used only 60 cells and had a delay of 0.75 clock cycle. The design of 1-bit comparator used 47 cells and had a delay of 0.75 clock cycle.

3 The proposed structures and designs

XOR and XNOR gates have very extensive applications in design of combinational and sequential circuits of arithmetic and logic units such as comparator, full adder, and B2G converter, G2B converter, as well as Reversible gates like Fredkin, Toffoli, Peres, and Feynman. Some of existing structures have a large number of cells and area, and also some have a long delay, which leads to an increase in the cost of the structure and the circuit designed by them. Therefore, design of such gates in QCA has a significant and critical importance. On the other hand, with optimal design of XOR and XNOR gates in order to use in combinational circuits, we can have circuits with fewer cell counts, as well as smaller area and less delay. The functionality accuracy of proposed designs are confirmed using QCADesigner (Walus et al. 2004). In the following subsections, new QCA-based XOR structure and also the Non-reversible 1-bit Comparator, Full Adder, B2G and G2B converters code are proposed.

3.1 Novel XOR and XNOR Structures in QCA

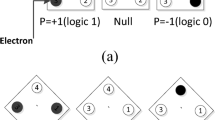
A novel XOR structure based on QCA technology is designed and simulated, as shown in Fig. 1. The inputs are A, B, and C, and Out is used as the output of the proposed structure. The proposed structure can be used in design of logic and computational circuits in QCA. This structure has 10 cells, area of 0.01µm2, and 0.5 clock cycle delay.

Fig. 1
figure 1

The proposed 3-inputs QCA XOR structure

Full size image

If the value of one of these inputs is set to − 1, then the proposed structure operates as 2-inputs QCA XOR. Also, if one of the inputs is set to + 1, the proposed structure will act as 2-inputs QCA XNOR. For instance, as illustrated in Fig. 2, by fixing one of the inputs, the structure of this gate becomes a 2-inputs QCA XNOR gate.

Fig. 2
figure 2

The proposed 2-inputs QCA XNOR gate structure

Full size image

3.2 The proposed 1-bit comparator

In digital circuits, in addition to subtraction and addition operations, sometimes it is necessary to compare inputs. A 1-bit comparator circuit has two inputs namely A and B, and three outputs namely G, E and L, which indicate that the input A is larger, equal or smaller compared to input B, respectively. The G, E, and L outputs are calculated according to relations in (1).

$$ \left\{ {\begin{array}{*{20}l} {L \left( {A < B} \right): }\; \hfill & {\overline{A}B ,} \hfill \\ {E \left( {A = B} \right):}\; \hfill & {A \odot B ,} \hfill \\ {G \left( {A > B} \right):}\; \hfill & {\left( {A \oplus B} \right).\overline{{\overline{A}B}} } \hfill \\ \end{array} } \right. $$
(1)

In this paper, we proposed 1-bit comparator circuit based on the logic diagram, as shown in Fig. 3.

Fig. 3
figure 3

The logic diagram of the proposed structure of a 1-bit comparator circuit

Full size image

The QCA structures of propose circuit are simulated using QCADesigner 2.0.3 (Walus et al. 2004) which is shown in Fig. 4. The proposed XNOR structure, as well as Majority gate and NOT gate is used in them. Simple design#1 and design#2 of 1-bit comparator has only 25 cells and 0.02µm2 area, as shown in Fig. 4a, b. The output of these designs obtains after 0.75 clock cycle delay. These proposed structure have no crossover. However, these designs of comparator are somewhat difficult to extend to an n-bit comparator. Therefore, we also propose a scalable form of the comparator. The scalable form is composed of 35 cells with four clocking phases. This structure occupies an area of only 0.028 μm2, as shown in Fig. 4c.

Fig. 4
figure 4

The proposed 1-bit comparator: a simple design#1 b simple design#2 c scalable design

Full size image

3.3 The proposed full adders

In this section, new designs for full adder in quantum-dot cellular automata technology is presented. The Full Adder circuit is a basic unit in digital arithmetic and logic circuits. Full Adder produces two outputs (SUM, Cout) by performing addition operation on three inputs values (A, B, Cin). We propose two QCA structures of 1-bit Full Adder, as shown in Fig. 5. The structure of the proposed design has three inputs (A, B, Cin) and two outputs (SUM, Cout). These structures are simple and scalable designs. The proposed XNOR structure, as well as Majority gate and NOT gate is used in them. Simple design of 1-bit Full Adder uses only 20 cells and 0.014 µm2 area. The output of this design obtains after 0.75 clock cycle delay. This proposed structure has no crossover. However, this Full Adder is somewhat difficult to extend to an n-bit adder. Therefore, we also propose a scalable form of the full adder for use as a ripple carry adder (RCA). The scalable form is composed of 29 cells with 0.75 clocking phases. This structure occupies an area of only 0.025 µm2, as shown in Fig. 5b.

Fig. 5
figure 5

The proposed Full Adder in QCA: a simple design b scalable design

Full size image

RCA is an adder circuit that by serially cascading 1-bit adders is constructed. A 2-bit RCA calculates the arithmetic sum of two 2-bit binaries and the circuit consists of two 1-bit full adder circuits, as shown in Fig. 6. The proposed 1-bit full adders are placed serially to successfully implement the design of the QCA 2-bit RCA, as shown in Fig. 6.

Fig. 6
figure 6

The proposed 2-bit RCA design in QCA

Full size image

3.4 The proposed 4-bit B2G code converter

Code converters are circuits that convert code into another. In this section, is proposed a novel QCA circuit to convert the 4-bit B2G code. This conversion method is useful to reduce the rapid switching activity. The logical structure of the proposed 4-bit B2G code converter is depicted in Fig. 7. Inputs are described as A3, A2, A1 and A0 and the corresponding gray outputs are P3, P2, P1, and P0. The logical equation of 4-bit B2G code converter is \(P_{3} = A_{3} , P_{2} = A_{3} \oplus A_{2} , P_{1} = A_{2} \oplus A_{1} { }\,{\text{and}}\,P_{0} = A_{1} \oplus A_{0}\).

Fig. 7
figure 7

The logical structure of 4 bit B2G code converter

Full size image

The main component of this converter is XOR gate. The proposed XOR structure is used for simulating B2G converter. The QCA diagram of the proposed 4-bit B2G code converter is depicted in Fig. 8. This structure has 29 cells and 0.02 µm2 area. It needs two clock zones to generate the correct outputs. Our proposed structure has no crossover.

Fig. 8
figure 8

The proposed structure B2G converter in QCA

Full size image

3.5 The proposed 4-bit G2B converter

In this section, a novel design of 4-bit G2B code converter based on the proposed two-input XOR gate in QCA is suggested. The logical structure of converting 4-bit G2B code is shown in Fig. 9. Inputs are described as A3, A2, A1 and A0 and the corresponding binary outputs are P3, P2, P1, and P0. The main component of this converter is XOR gate. The proposed XOR structure is used for simulating G2B converter. The QCA-based 4 bit G2B converter is shown in Fig. 10. This structure has 32 cells and 0.03 µm2 area. It needs two clock zones to generate the correct outputs. Our proposed structure has no crossover.

Fig. 9
figure 9

The logical diagram of 4 bit G2B code converter

Full size image
Fig. 10
figure 10

The proposed structure G2B converter in QCA

Full size image

4 The simulation results of proposed designs

In this section, the simulation results of proposed XOR structure, XNOR structures, the proposed single bit Comparator, Full Adder circuits, the proposed 4 bit B2G and G2B code converters based on QCA technology are shown. The simulation result of the proposed design of QCA XOR is shown Fig. 11. In this figure, A, B, and C are inputs and Out is the output.

Fig. 11
figure 11

The simulation result of the proposed design of QCA XOR

Full size image

The simulation result of the proposed design of QCA XNOR is shown Fig. 12. In this figure, A and B are inputs and Out is output.

Fig. 12
figure 12

The simulation result of the proposed design of QCA XNOR

Full size image

The simulation result of the proposed design of single bit Comparator is shown Fig. 13. In this figure, A and B are inputs and L (A is less than B), G (A greater than B) and E (A equal to B) are outputs.

Fig. 13
figure 13

The simulation result of the proposed design of single bit Comparator

Full size image

The simulation result of the proposed design of Full Adder is shown Fig. 14. In this figure, A, B and \({C}_{in}\) are inputs and SUM and \({C}_{out}\) are outputs.

Fig. 14
figure 14

The simulation result of the proposed design of Full Adder

Full size image

The simulation result of the proposed design of 4 bit B2G code converter is depicted Fig. 15. It has four inputs which are binary digits. The circuit has also four outputs which are the converted equivalent of the input vector into the gray code.

Fig. 15
figure 15

The simulation result of the proposed design of 4 bit B2G code converter

Full size image

The simulation result of the proposed design of 4 bit G2B code converter is depicted Fig. 16. As it can be seen in this figure, the output of the circuit is the binary equivalent of the input gray code. This circuit has four inputs and four outputs.

Fig. 16
figure 16

The simulation result of the proposed design of 4 bit G2B code converter

Full size image

5 Comparing results

In this section, comparison of the proposed structures with the existing designs are described. The proposed designs are validated by the QCADesigner version 2.0.3 and QCADesigner-E measures power consumption, respectively. In order to make comparison, some of the best previous circuits have been selected and compared. The evaluation parameters such as cell count, latency, occupied area, circuit cost, and power consumption are considered. The circuit cost is obtained by multiplying their area, cell count, and latency (Bahrepour and Maroufi 2018). The value of latency is calculated by counting the clocks from input to output. In Table 1, the proposed comparators with existing works are compared. It is clear that proposed designs has less cell count, lower occupied area, and less circuit cost compared to the existing works in recent years.

Table 1 Comparative study of the proposed 1-bit comparator with some of the previous researches
Full size table

In Table 2, the proposed Full Adders with existing works are evaluated based on the factors values listed in it. Simulation results show that the proposed circuits improves in number of cells, occupied area, circuit cost and latency compared to previous works.

Table 2 Comparative study of the proposed Full Adders with some of the previous researches
Full size table

In Table 3, the proposed B2G code converter with existing works is compared based on the factors values listed in it. Simulation result show that the proposed code converter improves in number of cells, occupied area and circuit cost compared to previous works.

Table 3 Comparative study of the proposed B2G code converter with some of the previous researches
Full size table

In Table 4, the proposed B2G code converter with existing works is compared based on the factors values listed in it. Simulation result show that the proposed code converter is better than the existing counterparts in terms of number of cells, occupied area and circuit cost compared to previous works.

Table 4 Comparative study of the proposed G2B code converter with some of the previous researches
Full size table

Energy analysis is estimated using QCA Designer-E tool. QCA Designer-E calculates the total energy for all possible coordinates. There are number of energy dissipation components in a QCA circuit such as bath of energy (E_bath), clock energy (E_clk), energy of a cell (E_io), input energy of a cell (E_in), and output energy of a cell (E_out). The total energy dissipation (Sum of Ebath) are 1.68e−002 eV and 1.75e−002 eV for the proposed 1-bit comparator design1 and design2, respectively. In this paper, the energy dissipation of 1-bit comparator circuits are compared with the available designs that reported the energy dissipation using QCA Designer-E, as shown in Table 5.

Table 5 Energy dissipation for the proposed 1-bit comparator circuit using QCADesigner-E
Full size table

6 Conclusions and future works

In recent years, QCA technology has attracted the attention of many researchers. Regarding to the important role of XOR and XNOR gates in design of logical and computational circuits such as Full Adder and Comparator, in this paper, a new three input XOR based on QCA technology are proposed. Also, we have proposed and simulated the 1-bit comparator circuit, both simple and scalable designs, 1-bit Full Adder circuit, B2G and G2B code converters circuits using the proposed XOR. The simulation results showed that the proposed designs had great improvements in terms of cell count, area and cost compared to previous designs. In the future, we can use the proposed XOR structure in the design of other combinational and sequential circuits.