1 Introduction

Quantum communication technology has become a research hot spot in the field of communication, which has been applied to a certain extent in commerce. Commercial banks have been using the information transmission mechanism of quantum cryptography. Security of communication technology are two important issues to be solved. One is identity authentication, the other is key distribution for encrypting information.

Identity authentication means that communication participants confirm whether the identities of other participants are their declared identities. In the identity verification process, one is the verifier and the other is the prover. The prover wants to send some information to enable the verifier to confirm whether his identity is authentic or conforms to a certain identity feature. Therefore, the first step in identity authentication is to establish an interactive identity system and assign an identity to each user. The second step is the identity verification process. The user as the prover can send information so that the verifier can confirm the user’s true identity. If the user has no identity, no matter what information is sent, the probability that the verifier will judge the prover as a real user is very small.

In the classic authentication system, relying on symmetric encryption technology and asymmetric encryption technology can be divided into two types of identity authentication systems. The symmetric encryption technology system is represented by Kerbroes Bryant (1988), which mainly relies on the unique key assigned to each user by the key distribution center as an identity. When a user is authenticated, the user first encrypts his identity information with a key, and then sends it to the key distribution center. The key distribution center decrypts the corresponding identity information and compares it with the identity of the key owner. If they are consistent, the identity authentication is successful. If they are inconsistent, authentication fails. Asymmetric encryption technology takes the identity information encrypted by public key and the private key (I’Anson and Mitchell 1990) signature of the certification authority as identity-a certificate. When the prover verifies identity, they only need to send their own certificates to the verifier, and the verifier can look up the certificates in the Certification Center for verification.The identity distribution method of the quantum identity authentication system is consistent with the classical authentication system. However, quantum technologies such as the principle of quantum non-cloning and the principle of quantum entanglement are used in the verification process, making the verification process more secure.

Real-time encryption of information is required in communication. In order to increase the rate of communication, a symmetric encryption system is usually used. Therefore, obtaining the real-time encryption key through two communications is the core issue.The traditional key distribution method relies on classic encryption technology, the risk of being cracked. Especially the emergence of quantum computers will make the classic encryption technology there have been significant defects. QKD uses the principle of quantum non-cloning and quantum uncertainty to realize unconditional secure key distribution. The unconditional security here is that if there is an attacker, he will either be found or unable to obtain key information. QKD started with BB84 protocol (Bennett and Brassard 1984), which has been deeply studied. BB84 protocol had been found that there were some technical flaws. After research, many solutions have also been discovered. However, one of the problems still exists, and that is the need for a classic authentication channel. Another problem is that the identity authentication of both parties cannot be performed during the communication process.

In this paper, we present a quantum key distribution protocol with two-way authentication. It uses some recent quantum technologies, such as QKD with pseudo-random number (Trushechkin et al. 2017), multi group quantum coding bases, Measurement-device-independent(MDI) QKD (Lo et al. 2012) and high-dimensional(HD) MDI QKD (Dellantonio et al. 2018). We prove the reliability of identity authentication and the security of quantum key distribution. When the traditional central authentication protocol is transformed into quantum central authentication and the key is distributed at the same time, the transformation is seamless and secure.

The structure of this paper is as follows. The second section introduces the basic technology used in this paper. The third section introduces the content of the protocol. The fourth section describes the security of the protocol. The fifth section describes some simulation experiments of the protocol. The sixth section is the conclusion.

2 Notation

This paper uses the methods and tools invented in the quantum field in recent years. In order to make the paper easier to read, they are explained in the order of the related technologies used in the paper.

2.1 BB84 protocol with multiple quantum coding bases

The invention of BB84 protocol (Bennett and Brassard 1984) is used to distribute the key used for encrypted information between authenticated communication parties. It uses the characteristics of quantum physics to achieve unconditionally secure key distribution. Unconditional security means that if a third party eavesdrops on the key during the key distribution process, either the eavesdropping of the third party is discovered and the communication is terminated, or the eavesdropper cannot obtain enough information to crack the key. Alice and Bob are celebrity in authenticated communication. In BB84 protocol, Alice first generates two true random strings, one is used to transmit key information, and the other is used to determine the coding basis of quantum state. Alice chooses two sets of conjugate bases as the coding bases. Each bit of one of random strings decides which sets of bases to choose, and then encodes bit of the other of random strings with the coding basis. Alice sends the single optical quantum encoded as a quantum state to Bob. Bob randomly selects one of sets of conjugate bases to measure it. After receiving all the information, Alice and Bob publicly compared their chosen coding basis and measurement basis on public channels. They discard inconsistent information and maintain consistent information. Through simple probability calculations, the probability that Alice and Bob choose a consistent base is 1/2. In fact, if there is an eavesdropper, then the coding basis of Alice that he can guess should also be 1/2. Due to the mutual influence of the two sets of conjugate bases, the eavesdropper has a 1/2 probability of correct guessing in the wrong part. A quarter error will be introduced in the total measurement result. Alice and Bob can take out a part of the retained coded information and compare them. If the error rate exceeds \(25\%\), they think there is an eavesdropper and stop the communication. If the error rate is less than \(25 \%\), they choose the appropriate error correction code to correct the information. Then, privacy amplification prevents the eavesdropper from obtaining the final encryption key information.

Multiple sets of quantum coding basis means that Alice has chosen more than two sets of coding basis. Usually, for convenience, she chooses sets. If we operate according to the idea of the BB84 protocol, the length of the reserved message is the length of the sent message. Eavesdropper guess the correct base probability is also reduced. However, since the number of keys to retain fewer, so the final key generation rate will decrease. In this case, if Alice and Bob can ensure that the coding basis is consistent with the measurement basis, then they will avoid the sifting process. The key generation rate will not decrease. At this time , when the eavesdropper cannot know the sequence of coding reference selection in advance, the eavesdropping accuracy will not improve. In addition, if we can judge whether the coding basis is consistent with the measurement basis, we will find eavesdroppers faster.

In the BB84 protocol, Alice and Bob use their true random string to select the corresponding basis from the two orthogonal bases (X, Z) for encoding and measurement respectively. The final key results from Alice and Bob choosing the same basis. Therefore, the number of the same basis directly determines the generation rate of the final key. Trushechkin et al. (2017) Alice and Bob use the shared secret key as a seed to generate long pseudo random numbers using the same pseudo-random number generation method to control the selection of quantum encoding and measurement bases. The quantum encoding bases may be two orthogonal bases in the BB84 protocol, and may be a plurality of sets of orthogonal bases evenly distributed in the Bloch sphere. This ensures that Alice and Bob always use the same basis for encoding and measuring, thus eliminating a sifting process which is to ensure the consistency of the base. Through rigorous proof, while guaranteeing security, this protocol provides a better key generation rate. ur Rehman et al. (2017) also uses a similar method, using a shared key generate a shared secret key. It also uses a pseudo-random number control encoding and measurement base. Here we give the mathematical definition of multiple sets of orthogonal bases. Assuming that the number of all bases is , , here \(\lceil \bullet \rceil \) is the ceil function,

(1)

is related to a random number whose m-bit is determined by k. We use the notation:

(2)

where \(\left\{ \left| 0 \right\rangle , \left| 1 \right\rangle \right\} \) is the quantum standard basis. One pair of basis is

(3)

Multiple bases are illustrated on the bloch sphere, as shown below Fig. 1.

Fig. 1
figure 1

Multiply basis

Full size image

2.2 MDI and HD-MDI

Since the birth of BB84 protocol, it has been gradually found that there are some defects. Among the defects related to Alice and Bob’s sending equipment and measuring equipment will lead to a basic problem of BB84 protocol, which will lead to the reduction of the randomness of coding, and ultimately affect the security of the key. The discovery of MDI protocol completely solves the problem of device defects. Its main method is that Alice and Bob are the prover of BB84 protocol, and send information to the third party(Center) of MDI. The third party publishes the verification results according to the program. According to the verification results, Alice and Bob determine what information they should keep. Due to the low generation rate of MDI protocol, high-dimensional MDI (Dellantonio et al. 2018) is invented, which makes the quantum state with more information and increases the key generation rate. In fact, in quantum theory, high-dimensional quantum states can be composed of multiple two-dimensional quantum states, which is the reason why high-dimensional quantum states can be converted into time-sharing two-dimensional MDI.

The MDI protocol (Lo et al. 2012; Tamaki et al. 2012) means that Alice and Bob are both senders in the BB84 protocol and randomly send some quantum states in the BB84 protocol. After a series of instrument conversions, they eventually pass through the beam splitter. Center uses some detectors to perform the bell state measurement. The result of the successful measurement correlates with the states sent by Alice and Bob. Then we get the relationship between random strings used by Alice and Bob before encoding. With appropriate adjustments, the random strings between Alice and Bob can be made consistent. Repeat the above process until the final key is obtained.

The idea of the MDI protocol comes from the “Time-Reversed EPR-Scheme” in Biham et al. (1996). In the actual transmission equipment, the 50:50 optical splitter is mainly used. The characteristics of this optical splitter are shown in the Fig. 2 below Nielsen and Chuang (2000).

Fig. 2
figure 2

Schematic of an optical 50/50 beamsplitter

Full size image

Decoy state Lo et al. (2005) is used in MDI, which makes it possible to prevent PNS attacks.This article assumes that Alice and Bob choose to use the basis in (3). Then the successfully measured bell state like Tamaki et al. (2012) ’phase encoding I’ is:

(4)

When the quantum states of Alice and bob are the same;

(5)

When the quantum states of Alice and bob are annihilated.

2.3 Central authentication protocol

The main content of Kerbroes authentication protocol is that the key distribution center (here simplified as Center) assigns a key bound with identity to each legitimate user. Alice and Center share this key. Each time Alice needs to do identity authentication, she uses the shared key to encrypt her identity and send it to the center. Center uses the shared key to decrypt the identity information. If the identity bounded with share key is consistent with the decrypted identity information, the authentication is successful. In practice, random number and time stamp should be added to prevent the attack of retransmission after interception. In this paper, the authentication protocol is modified slightly, which is also a commonly used authentication method. The information shared by Alice and Center includes identity information and key information. Alice can send the identity information and key information to Center directly through hash function. Center compares the received information with its own same information through the same hash function. If they are consistent, the authentication is considered successful. If they are inconsistent, the authentication fails. In the actual process, appropriate errors can be allowed, or error correction coding can be used to ensure the consistency of the above information. In this paper, the authentication information is connected with the coding base of quantum state to transfer the authentication information. Whether the authentication is successful or not can be determined by verifying whether the coding base is consistent with the measurement base. Because this paper uses MDI protocol, so we make a small technical adjustment to the measurement scheme, which will be explained in detail in the third section.

3 Quantum key distribution protocol with two-way authentication

This section will introduce the quantum key distribution protocol with two-way authentication in detail. Because this protocol uses a variety of technologies, in order to explain the process of the protocol more succinctly, we first need to state some parameters and devices used in the protocol.

3.1 Necessary equipment and parameters in the protocol

  • Participants of quantum key distribution protocol with two-way authentication: Alice, Bob, Center.

  • The basic channels in the agreement are classical channels and quantum channels. Whether the classic channel requires authentication is related to the security provided by the protocol. If it is necessary to prevent denial of service, authentication is required. If it is not necessary to prevent denial of service, no authentication is required. The quantum channel does not require pre-certification.

  • Basic equipment jointly owned by all parties to the protocol: This protocol takes light quantum as an example, and other types of quantum can also be adjusted appropriately. Alice and Bob have a polarized light quantum generator, which can produce polarized light quantum in any direction. There is a special interference spectrometer, detector and quantum circuit in the center, which can change the polarization direction of the light quantum at will.

  • The pre-negotiated parameters are as follows: the extraction method of the authentication information to be verified; the length of the session key to be generated; the number of coding bases; the selected pseudo-random function; the length of the true random number string

  • Authentication in the protocol: the authentication method has been explained in 2.3. With a little modification, Alice and Bob use the authentication information as the coding base to send the coding information to Center.

3.2 QKD protocol with two-way identity authentication

Here is the operational flow of the protocol, the device diagram is like Fig. 3. The detail of Fig. 3 can be seen in Tamaki et al. (2012) .

Fig. 3
figure 3

A simple figure of QKD with Center. In the figure: (PC) polarisation controller, (BS) 50/50 beamsplitter, (D0, D1) detector

Full size image
  1. Step 1

    The length of shared key and the number of bases to be used through key distribution protocol needs to be understood by Alice, Bob and center. Pseudo random functions \( {P_A(),P_B()} \) are negotiated by Alice, Bob and center respectively. Alice, Bob, and Center have shared keys, \({s_a,s_b} \) respectively. The selection method of the corresponding shared keys also needs to be negotiated. Of course, Alice or Bob can directly select all the shared information, and then use the one-way function to hash it as the seed of the pseudo-random number.

  2. Step 2

    Alice calculate the pseudo-random numbers \({k_a=P_A(s_a)}\) , where the length of \({k_a}\) is \({l=|P_A(s_a)| } \). Center also calculates the corresponding pseudo-random number. We have \({l/m \ge N }\), where . Bob uses the same information negotiated with Center to do the same thing.

  3. Step 3

    Alice and Bob generate their own true random numbers \({a_i,b_i, i \in \left\{ 1,\dots ,N\right\} }\) . Under the control of the pseudo-random number, select the corresponding basis to encode the true random number \( {\left| {\varphi _i}(k_a)+a_i \pi /2 \right\rangle , \left| {\varphi _i} (k_b)+b_i \pi /2 \right\rangle } \) where \({\varphi _i (k)}\) is determined by the \({m*(i-1)+1}\) to \({m*i}\) bits of , and send it to Center at the same time.

  4. Step 4

    Under the control of the Coin random number, Center randomly transforms Alice and Bob according to the differences between the bases selected by Alice and Bob, so that the bases selected by the two are consistent. \({\left| \varphi _i (k)+a_i \pi /2 \right\rangle }\) , \({\left| {\varphi _i}(k)+b_i \pi /2 \right\rangle } \) ,where or .

  5. Step 5

    Only D0 clicks or only D1 clicks is success events.If D0 is successful, it means that the Quantum States sent by both sides are consistent. If D1 is successful, it means that the Quantum States sent by both sides are just opposite. At this time, Alice and Bob decide to adjust whose random number according to another coin random so that their random numbers are the same. The random number sent by all successful events is retained as the raw key.If it is other detection results, it means that the quantum coding bases sent by both sides are inconsistent. This is where an error has occurred.

  6. Step 6

    when the error message in step 5 exceeds a certain number after verifying all authentication messages, abort communication. Otherwise, it repeats the previous five steps until enough information is obtained.

  7. Step 7

    Alice and Bob select a certain number of raw key and compare it in the classical channel. If the number of errors exceeds a certain limit, the communication will be aborted, which means that the center is not secure. At this time, Center is either attacked or blocked from communicating.

  8. Step 8

    Alice and Bob negotiate the error correction mechanism in the classical channel, eliminate the errors in the raw key. They generate the final key by the privacy amplification.

3.3 Key generation rate

If Alice and Bob are both legitimate users, they always have the same basis for the quantum states detected by Center’s intervention. The key sifted process is no longer needed, so the key generation efficiency will be improved. But in reality, this is impossible. Such as basis misalignment and dark count needs to be considered. The key generation rate in reality is

$$\begin{aligned} {R \equiv {Q^{\varphi }}(1-f_e({E^{\varphi }})H_2({E^{\varphi }}))} \end{aligned}$$
(6)

where is the raw key rate that Center declares a successful result when Alice and Bob send center photon each in the (3) basis. represents the quantum bit error rate(QBER) in the (3) basis when Alice and Bob send Center WCPS of intensity . is the error correction inefficiency function, and \({H_2()}\) is the binary entropy function. This conclusion is derived from Tamaki et al. (2012) the phase encoding scheme I. Because Center knows the bases of Alice and Bob, this conclusion can be drawn.

4 Security analysis

This protocol has two important characteristics. one is two-way authentication, the other is key distribution. So the security is mainly considered from these two aspects.

4.1 Reliability of two-way authentication

The reliability of identity verification is how we determine that the identity is authentic after passing the identity verification. There are two levels of meaning. The first layer is how much identity information the verified identity information represents. The second layer is whether the identity information is forged. The first layer here means that if all the identity information has been verified, it means that the authentication has a reliability of \(100\%\). For example, the symmetric authentication verifier receives all the identity information of the prover. The verifier compares whether the information is consistent with its own information. Only when all the information is consistent, the identity verification can be successful. This certification is \(100\%\) reliable. There is another method of verifying identity verification information, that is, verifying part of the identity information. For example, face recognition. It only needs to verify a part of the face to show whether the person is himself. This verification is not a full-face verification, and the reliability is not complete. Only a one-to-one correspondence between a part of a person’s face and the entire face is \(100\%\) reliable. In this protocol, all identity information can be verified. But for the security of identity information, some information can be extracted for verification.The process of extracting information can adopt the following scheme:

Pseudo random number seed key construction protocol(PRNSKC):

  1. 1.

    Alice and Center negotiate in the classical channel to select the starting position 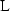of seed key from the registration information.

  2. 2.

    Alice and Center negotiate a true binary random string in the classical channel. The number of positions of the value 1 in the random string is greater than the length required by the seed key.

  3. 3.

    Alice and Center negotiate a time stamp in the public information channel.

  4. 4.

    Alice and center start from position in their own registration information, use the random number and registration information to do “the and operation”, take out the data of the corresponding position of 1, and then delete the number of positions of 0 in . The remaining number is .

  5. 5.

    Add a time stamp after the above data as the seed key of the pseudo-random number.

The length of \({k_a}\) can be determined in the following way: suppose the cyclic node of the pseudo-random function is t , l is the length of the desired pseudo-random number, \({l_{ka}}\) is the length \({k_a}\). \({l_{ka}}\)satisfies the following conditions.

$$\begin{aligned} {l_{ka}}\cdot {t}\cdot \alpha >{l} \end{aligned}$$
(7)

where \(0< \alpha <1\) is a security parameter like ur Rehman et al. (2017). The required length of \({k_a}\) in ur Rehman et al. (2017) is

$$\begin{aligned} 2^{{l_{ka}}\cdot {t}\cdot \alpha }>{l} \end{aligned}$$
(8)

Obviously the requirements in this article are higher and the security is better. It can choose as needed in actual use. The construction protocol of pseudo-random number seed key can ensure that the information sent by Alice and Center is different every time they need to authenticate and communicate. The selection of registration information is adjusted in location and length at the same time, which greatly increases the difficulty of eavesdropper guessing registration information.

Eavesdroppers can also steal Bob’s identity information by impersonating Alice. In this protocol, even if the eavesdropper has Alice’s identity information, he can only measure Bob’s quantum state and then guess his identity information. This situation is as difficult as attacking Alice. Therefore, this protocol can guarantee that the registration information of other users will not be leaked due to the disclosure of a few users’ information.We can use the following calculation to estimate the difficulty of Eve’s eavesdropping to crack Alice’s registration information in Center.

$$\begin{aligned} R\xrightarrow {PRNSKC} {{ k_a}} \xrightarrow {P()} l \xrightarrow {l/m}{\varphi (N)} \end{aligned}$$
(9)

Here refers to Alice’s registration information in the center. is the above protocol. \({k_a}\) is the seed of Alice’s pseudo-random number, which Cetner has the same information. is a pseudo-random function, is the pseudo-random number that determines the quantum base, is the final quantum state sent. Eve can only measure quantum states of . Because every time Alice and Center communicate, all the information will be changed, it is impossible for eve to guess the registration information through quantum state in terms of computational complexity. Since the basic knowledge of information theory can be obtained, it is necessary to obtain a sufficient number of correct bases to guess the pseudo-random numbers. This can be further proved by the strict proof that the probability of guessing pseudo-random numbers in the undiscovered situations is very low. The detail is in Trushechkin et al. (2017) appendix B and C.

4.2 Security of two-way authentication

In this protocol, Center can know the pseudo-random numbers of Alice and Bob. Under normal circumstances, Center can ensure that each measurement uses the same base, so it should be able to obtain a successful detection result every time. In the actual environment, due to interference and noise in the system, the detection must have a probability of failure. The proportion of detection failures can be used to judge whether there is eavesdropping. When sets of bases are selected, the proportion of false detection results is greater than , indicating that there is eavesdropping. Since the noise is always constant, the two parties in communication can also determine the magnitude of interference by choosing a different number of sets of base. Since one difference between this protocol and the other QKD protocol is that this protocol does not publish the encoding basis and measuring basis in the classical channel, eavesdroppers cannot obtain identity information. The authentication information is safe.

Because Alice, Bob, and Center have shared keys, Center can adjust the basis between Alice and Bob to the same basis before the measurement. Center knows what kind of bases Alice and Bob use. Therefore, the range of the final measurement result is also clear.If one of Alice and Bob is an illegitimate user, then the Center’s measurement result is equivalent to the case where two sets of bases are used in MDI. Due to Center’s rotation of the encoding base, the probability of a final successful measurement is less than that of a real user.

Let’s assume that Alice is an illegal user. The quantum state she sends is f \(\varphi _i \). Bob is a legitimate user. The quantum state he sends is f . Here i, j represent the base used by Alice and Bob respectively. Let a and b be the current their respective random numbers, and \({U^{coin}}\) represents the rotation operation of Center according to the coin random number. Set \({\left| {\varphi ^{\prime }}{}_i \right\rangle =U^{\textit{coin}}\left| \varphi _i +a\cdot \frac{\pi }{2}\right\rangle }\) ,\({\left| \varphi _j^{\prime }\right\rangle =U^{\textit{coin}+1}\left| \varphi _j +b\cdot \frac{\pi }{2}\right\rangle }\) , then the result of center is (Table 1):

Table 1 Illegal Alice or Bob
Full size table

The key generation rate at this time can be obtained from Tamaki et al. (2012) Phase Endconding Scheme I

$$\begin{aligned} {R^{\prime } \equiv \frac{1}{M}{Q^{\varphi }} - \frac{1}{M}{Q^{\varphi }}f_e({E^{\varphi }})H_2({E^{\varphi }})} = {\frac{1}{M}({Q^{\varphi }} - {Q^{\varphi }}f_e({E^{\varphi }})H_2({E^{\varphi }}))} \end{aligned}$$
(10)

The variable definition is the same as (5). \({R^{'} }\) is a very rough estimate because we assume that the probability of base selection is an average probability. Center can determine whether Alice or Bob is an illegal user through the measurement result. When both parties are illegal users, the probability of successful measurement is even smaller. From the above analysis, it can be seen that when illegal users occur, the key generation rate decreases rapidly as the number of cardinalities increases. First, the success measurements obtained are significantly reduced. When the probability of successful detection is abnormal, you can assume that an illegal user has occurred.

4.3 Security of key distribution

The security of key distribution refers to how much the key negotiated by the eavesdropper can be intercepted by the eavesdropper. Since this protocol adopts MDI scheme, the defects of the equipment can be completely removed. In addition, MDI protocol supports decoy state protocol (Lo et al. 2005), so the splitting attack can also be solved (Brassard et al. 2000). Therefore, the key security of this protocol needs to be considered in two cases. One is that the eavesdropper directly measures the information of Alice or Bob, the other is that the eavesdropper blocks the communication between Alice and Bob and directly sends false information to the center. In the first case, the eavesdropper passes the authentication under the probability of where M is the number of base and n is the length of key. This situation gradually becomes a small probability with the increase of n. In the second case, the eavesdropper has passed the authentication. At this time, the authentication Center is blocked, and the test results published at this time are not real. In general, the eavesdropper can get half of the information of one party, and then reduce it by half due to random adjustment. Even if the eavesdropper can get half of the correct information of both sides, because there is no real measurement result, he has no way to know which data is correct and which is wrong. Such data is actually useless.

When Alice and Bob randomly take out part of the data in the stage of checking the shared information, as long as the error message exceeds the noise, it means that there is an eavesdropper. At this time, the error message is related to the amount of data blocked by the eavesdropper. If the eavesdropper measures bits of data, then the error message has bits. So we can know that when the error message has bits, the data measured by the eavesdropper also has bits, who has correct bits. Because the eavesdropper does not know which of the measurement information is correct, as long as the error correction range of the error correction code is set to the boundary of terminating communication, the eavesdropper can not obtain enough information even if he has passed the authentication.

If an eavesdropper eavesdrops between Alice and Center or Bob and Center, it can be concluded from the analysis that the amount of information obtained by each eavesdropper measurement is consistent with that of non-eavesdropping direct guessing. Suppose Eve is between Alice and Center. Let’s set Alice’s initial value is 0, code is , Eve chooses . When Eve has no way to copy Alice’s state, the following theorem can be proved.

Theorem 1

When Alice’s coding basis is one of conjugate bases, Eve guesses the success probability of the key is only related to the probability distribution of the key and the probability distribution of the coding basis.

Proof

suppose Alice prepares a key of k, the code basis is , and Eve’s measurement basis is . Here we only prove the special case of the theorem, assuming that the key is at \(\left\{ 0,1 \right\} \) and the code base is (3). They all obey the uniform probability distribution. Eve guesses the success probability of the key through the measurement result is

so

(11)

\(\square \)

When the eavesdropper guesses the final key, the result published by Center has no effect on the eavesdropper’s guess. Because Center only announces whether their quantum states are equal, the eavesdropper cannot improve his judgment based on this information. The information and the quantum state are independent of each other. In the sense of information theory, the information has no effect on the information obtained from the quantum state. Can an eavesdropper eavesdrop on Alice and Bob’s information at the same time? The center will adjust the quantum state sent by both parties according to the random number of Coins, so that each bit of information will always be changed by one party. This means that the data generated by Alice and Bob are independent of each other, so obtaining both parties’ information at the same time will not increase the information for determining the final key.

As can be seen from the above discussion, if Alice and Bob authenticated, does not mean that key distribution success. If Alice and Bob either authentication fails, the key distribution fails. If Alice and Bob finally obtain the same key, then their identity authentication is also successful. Therefore, this protocol is called a quantum key distribution protocol with two-way authentication.

5 Simulation and channel

5.1 Comparison of key generation rates and authentication protocols

In many QKD protocols, key distribution requires four steps: original key acquisition, key sifting, error correction and privacy amplification. In a two-dimensional quantum space, the key generation rate is the ratio of the final key length to the length of the message sent. The length of the original key is related to physical factors, and the solutions of all QKD protocols are the same. Error correction and privacy amplification are only related to the selection method, and the solutions are basically the same. Improved key distribution agreement focused on the key sifting, because it determines the security of key distribution protocol, but also directly affect the production rate of the key. The key sifting of the BB84 protocol makes the key generation rate not more than 1/2. Because at least half of the encoding base and the measuring base are inconsistent, half of the quantum states must be sifted out. The MDI protocol has the same problem, because both Alice and Bob are used as the sending states of the BB84 protocol. At least half of the bases they send are inconsistent, so the original key generation rate is also less than 1/2.

HD-MDI can increase the original key generation rate of MDI when it takes a certain number of dimensions according to the detection performance of the device. The Hd-MID scheme is one of the high-dimensional quantum coding schemes. When the dimension is higher, the amount of information transmitted by each quantum state is more, and the key generation rate is higher. Quantum key distribution with two-way authentication also applies to Hd-MDI. Since what is obtained every time is a consistent basis, the key generation rate can be further on the basis of Hd-MDI. So the key generation rate is higher. Compared with other QKD protocols, the key generation rate is the highest because there is no sifting process.

Ghilen et al. (2014) introduced three types of authentication protocols. The first type is an authentication protocol based on entangled quantum and trusted third parties, using quantum channels. The second type is based on quantum entanglement and trusted third party, using the quantum channel and the classical channel authentication protocol. The third type is an authentication protocol that uses a quantum channel in the absence of an eccentric field quantum. The third type is an authentication protocol that uses a quantum channel without entangled quanta. The authentication method in this paper is an authentication protocol that uses a quantum channel with a trusted third party but no entangled quantum. Its computational complexity is consistent with the amount of authentication information. With the implementation of the key distribution protocol, the reliability of the authentication increases with the length of the key.

5.2 Channel problems

This protocol uses classic channels when negotiating basic parameters. After the parameter negotiation is completed, the classic channel is no longer used. When the quantum channel has a higher error rate, a quantum error correction code can be added to the code base. In this case, the authentication information can still play its original role, and can provide error correction check information by detecting failures. When successful detection means no error, the check code is 0. A failed detection indicates an error, and the check code is 1. Either Alice or Bob can correct the erroneous information in the coding base according to the check result and reduce channel errors. When the error rate is high (Khan 2009; Xu et al. 2020), high-dimensional quantum states can also increase the key generation rate. Hd-MDI (Dellantonio et al. 2018) is also a method to deal with high loss channels.

6 Conclusion

Quantum key distribution is considered to be the most important application of quantum technology. But some people have always doubted the reliability of this technology (https://www.nsa.gov/what-we-do/cybersecurity/quantum-key-distribution-qkd-and-quantum-cryptography-qc/). They believe that quantum key distribution technology has many flaws. In fact, this is true for any kind of technology in the early stages of development. We need to be enthusiastic and patient with new technologies. Invest more research to achieve ultimate success. This paper presents a quantum key distribution protocol with two-way authentication.After obtaining the shared information from the classic central authentication system, the original system can be transformed into a quantum key distribution system. It also realizes key distribution and identity authentication at the same time. We hope that through the discovery of this technology, we can achieve quantum key distribution under the guarantee of quantum authentication. This paper just completed the conversion of the symmetric key authentication system, and there is no solution for the asymmetric key authentication system. This paper uses the quantum encoding base and quantum state at the same time is a new idea, it should have a wider range of uses.