Impact of nonzero boresight and jitter pointing errors on the performance of M-ary ASK/FSO system over Málaga $\left( {\mathcal{M}} \right)$ atmospheric turbulence

Abstract

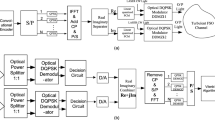
In free-space optical (FSO) communication, Distribution models such as lognormal, gamma-gamma, and k-distribution describe weak, moderate, and strong turbulence, respectively. Whereas Málaga $\left( {\mathcal{M}} \right)$ distribution is a powerful statistical model repeatedly mentioned in the literature due to its generality, Málaga $\left( {\mathcal{M}} \right)$ describes the three turbulence conditions while considering the pointing errors, represented by the jitter boresight displacement, of the communication beam. Exact and closed-form expressions for symbol error rate and outage probability are presented in this paper—furthermore, cases from these expressions are presented for various turbulence conditions. The proposed expressions describe the symbol error rate and outage probability performance of the FSO communication system with M-ary amplitude shift keying modulation over Málaga $\left( {\mathcal{M}} \right)$ atmospheric turbulence environments.

Appendices

Appendix A: Málaga composite PDF

(1) Composite PDF Approximation: We substitute (2) and (3) into (5) and write the composite PDF of the Málaga fading with nonzero boresight pointing error as

$$f_{M} \left( h \right) = \frac{{\gamma^{2} exp\left( {\frac{{ - s^{2} }}{{2\sigma_{s}^{2} }}} \right)}}{{\left( {A_{0} h_{l} } \right)^{{\gamma^{2} }} }}h^{{\gamma^{2} - 1}} A\mathop \sum \limits_{k = 1}^{\beta } a_{m} \mathop \smallint \limits_{{h/A_{0} h_{l} }}^{\infty } h_{a}^{{1 - \gamma^{2} }} I_{0} \left( {\frac{s}{{\sigma_{s} }}\sqrt {\frac{{ - w_{{z_{eq} }}^{2} }}{2}ln\;ln \left( {\frac{h}{{h_{a} A_{0} h_{l} }}} \right) } } \right)K_{\alpha - k} \left( {2\sqrt {\frac{{\alpha \beta h_{a} }}{{g\beta + \Omega^{\prime}}}} } \right)dh_{a}$$

(A.1)

Applying the change of variables rule $x = \sqrt {\frac{{ - w_{{z_{eq} }}^{2} }}{2}lnln \left( {\frac{h}{{h_{a} A_{0} h_{l} }}} \right) }$, Eq. (A.1) can be expressed as

$$f_{M} \left( h \right) = \frac{{4\gamma^{2} exp\left( {\frac{{ - s^{2} }}{{2\sigma_{s}^{2} }}} \right)}}{{\left( {A_{0} h_{l} } \right)^{2} w_{{z_{eq} }}^{2} }}A\mathop \sum \limits_{k = 1}^{\beta } a_{k} \mathop \smallint \limits_{0}^{\infty } x exp\left( {\frac{{2x^{2} }}{{w_{{z_{eq} }}^{2} }}\left( {2 - \gamma^{2} } \right)} \right)I_{0} \left( {\frac{s}{{\sigma_{s} }}x} \right)W_{\left( h \right)} dx$$

(A.2)

where $W_{\left( h \right)} = hK_{\alpha - k} \left( {2\sqrt {\frac{\alpha \beta h}{{g\beta + \Omega^{\prime}}}exp\left( {\frac{{2x^{2} }}{{w_{{z_{eq} }}^{2} }}} \right)} } \right).$

Using series expansion of modified Bessel function of the second kind (Wolfram 2020)

$$K_{v} \left( x \right) = \frac{\pi }{{2sin\left( {\pi v} \right)}}\mathop \sum \limits_{p = 0}^{\infty } \left[ {\frac{{\left( {x/2} \right)^{2p - v} }}{{\Gamma \left( {p - v + 1} \right)p!}} - \frac{{\left( {x/2} \right)^{2p + v} }}{{\Gamma \left( {p + v + 1} \right)p!}}} \right]$$

(A.3)

where it requires $v \notin Z$ and $\left| x \right| < \infty$, we can express $W_{\left( h \right)}$ as

$$W_{\left( h \right)} = \frac{\pi }{{2sin\left( {\pi \left( {\alpha - k} \right)} \right)}}\mathop \sum \limits_{j = 0}^{\infty } \left[ {\frac{{\left( {\frac{\alpha \beta }{{A_{0} h_{l} \left( {g\beta + \Omega^{\prime}} \right)}}exp\left( {\frac{{2x^{2} }}{{w_{{z_{eq} }}^{2} }}} \right)} \right)^{{j - \left( {\frac{\alpha - k}{2}} \right)}} }}{{\Gamma \left( {j - \left( {\alpha - k} \right) + 1} \right)j!}} - \frac{{\left( {\frac{\alpha \beta }{{A_{0} h_{l} \left( {g\beta + \Omega^{\prime}} \right)}}exp\left( {\frac{{2x^{2} }}{{w_{{z_{eq} }}^{2} }}} \right)} \right)^{{j + \left( {\frac{\alpha - k}{2}} \right)}} }}{{\Gamma \left( {j + \left( {\alpha - k} \right) + 1} \right)j!}}h^{j + \alpha - 1} } \right].$$

(A.4)

Substituting (A.4) into (A.2), and after some manipulation, we have

$$f_{M} \left( h \right) = \frac{{2\pi \gamma^{2} exp\left( {\frac{{ - s^{2} }}{{2\sigma_{s}^{2} }}} \right)}}{{\left( {A_{0} h_{l} } \right)^{2} w_{{z_{eq} }}^{2} sin\left( {\pi \left( {\alpha - k} \right)} \right)}}h^{{\frac{\alpha + k}{2} - 1}} A\mathop \sum \limits_{k = 1}^{\beta } a_{k} \left\{ {\left[ {\left( {\frac{1}{{\Gamma \left( {j - \left( {\alpha - k} \right) + 1} \right)j!}}\left( {\frac{\alpha \beta h}{{A_{0} h_{l} \left( {g\beta + \Omega^{\prime}} \right)}}} \right)^{{j - \left( {\frac{\alpha - k}{2}} \right)}} } \right)\mathop \smallint \limits_{0}^{\infty } x exp\left( {\frac{{2x^{2} }}{{w_{{z_{eq} }}^{2} }}\left( {k - \gamma^{2} + j} \right)} \right)I_{0} \left( {\frac{s}{{\sigma_{s} }}x} \right)dx} \right] - \left[ {\left( {\frac{1}{{\Gamma \left( {j + \left( {\alpha - k} \right) + 1} \right)j!}}\left( {\frac{\alpha \beta h}{{A_{0} h_{l} \left( {g\beta + \Omega^{\prime}} \right)}}} \right)^{{j + \left( {\frac{\alpha - k}{2}} \right)}} } \right)\mathop \smallint \limits_{0}^{\infty } x exp\left( {\frac{{2x^{2} }}{{w_{{z_{eq} }}^{2} }}\left( {\alpha - \gamma^{2} + j} \right)} \right)I_{0} \left( {\frac{s}{{\sigma_{s} }}x} \right)dx} \right]} \right\}.$$

(A.5)

In the following derivation, using integral identity (Gradshteyn and Ryzhik 2000) we get

$$\mathop \smallint \limits_{0}^{\infty } x^{{u - \frac{1}{2}}} e^{ - \alpha x} I_{2v} \left( {2\beta \sqrt x } \right)dx = \frac{{\Gamma \left( {u + v + \frac{1}{2}} \right)}}{{\Gamma \left( {2v + 1} \right)}}\beta^{ - 1} exp\left( {\frac{{\beta^{2} }}{2\alpha }} \right)\alpha^{ - u} M_{ - u, v} \left( {\frac{{\beta^{2} }}{\alpha }} \right)$$

(A.6)

where, $M_{ - u, v} \left( . \right)$ is the Whittaker function and with using another the identity (Wolfram 2020)

$$M_{{\frac{m - 1}{2}, \frac{m}{2}}} \left( z \right) = exp\left( {\frac{ - z}{2}} \right)z^{{\frac{1 - m}{2}}} m!\left( {exp\left( z \right) - \mathop \sum \limits_{k = 0}^{m = 1} \frac{{z^{k} }}{k!}} \right), \quad m \ge 0$$

(A.7)

We represent (A.5) as in (6). In our derivation, the (A.2) integral identity requires that $\left( {\alpha - \beta } \right) \notin Z$, and the integral identity (A.5) requires that the summation index $j$ in (A.4) must be equal to or lower than $J = \left\lfloor {\gamma 2 - \alpha } \right\rfloor$, where $\left\lfloor x \right\rfloor$ denotes the maximum integer not greater than $x$.

(2) PDF Near the Origin: To get the power series expansion of the Málaga composite PDF near the origin, $W_{\left( h \right)}$ could be expressed as

$$\mathop {\lim }\limits_{h \to 0} W_{\left( h \right)} = \frac{{\pi \left( {\frac{\alpha \beta }{{A_{0} h_{l} \left( {g\beta + \Omega^{\prime}} \right)}}\exp \left( {\frac{{2x^{2} }}{{w_{{z_{eq} }}^{2} }}} \right)} \right)^{{ - \left( {\frac{\alpha - k}{2}} \right)}} }}{{2sin\left( {\pi \left( {\alpha - k} \right)} \right)\Gamma \left( { - \left( {\alpha - k} \right) + 1} \right)}}h^{k - 1} + g_{k - 1} \left( h \right)$$

(A.8)

From (A.8) and (A.2), we can derive the PDF near the origin as

$$f_{M} \left( h \right) = A\mathop \sum \limits_{k = 1}^{\beta } \frac{{a_{k} \pi \gamma^{2} \left( {\frac{\alpha \beta }{{g\beta + \Omega^{\prime}}}} \right)^{{ - \left( {\frac{\alpha - k}{2}} \right)}} exp\left( { - \frac{{s^{2} }}{{2\sigma_{s}^{2} }} - \frac{{s^{2} \gamma^{2} /\sigma_{s}^{2} }}{{\left( {2k - 2\gamma^{2} + 2j} \right)}}} \right)}}{{2\left( {A_{0} h_{l} } \right)^{k} sin\left( {\pi \left( {\alpha - k} \right)} \right)\Gamma \left( { - \left( {\alpha - k} \right) + 1} \right)\left| { - \left( {k - \gamma^{2} + j} \right)} \right|}}h^{k - 1} + g_{k - 1} \left( h \right)$$

(A.9)

Appendix B: Lognormal composite PDF

For weak turbulence conditions, we use the lognormal turbulence model to characterize the atmospheric fading ha whose PDF is given by Yang et al. (2014)

$$f_{{h_{a} }} \left( {h_{a} } \right) = \frac{1}{{2h_{a} \sqrt {2\pi \sigma_{X}^{2} } }}\left( { - \frac{{\left( {lnh_{a} + 2\sigma_{X}^{2} } \right)^{2} }}{{8\sigma_{X}^{2} }}} \right)$$

(B.1)

where $\sigma_{X}^{2}$ is the log-amplitude variance given by $\sigma_{X}^{2} = \frac{{\sigma_{R}^{2} }}{4} = 0.31k^{7/6} C_{n}^{2} z^{11/6 }$, where $\sigma_{R}^{2}$ is the Rytov variance for a plane wave, $C_{n}^{2}$ is the index of refraction structure parameter of atmosphere, and $k = 2\pi /\lambda$ is the optical wave number with $\lambda$ being the wavelength. The parameters of the lognormal fading model can be measured directly for FSO systems.

After some mathematical derivation, we obtain a finite series approximation of the composite PDF as (Yang et al. 2014)

$$f_{LN} \left( h \right) = \frac{{\gamma^{2} exp\left( {u_{a} } \right)}}{{2\left( {A_{0} h_{l} } \right)^{{\gamma^{2} }} }}h^{{\gamma^{2} - 1}} erfc\left( {\frac{{ln\frac{h}{{A_{0} h_{l} }} + u_{b} }}{{u_{c} }}} \right).$$

(B.2)

where $u_{a} = \frac{{s^{2} }}{{\sigma_{s}^{2} }} + 2\sigma_{X}^{2} \gamma^{2} + 2\sigma_{X}^{2} \gamma^{4}$, $u_{b} = \frac{{6s^{2} }}{{\sigma_{s}^{2} }} + 2\sigma_{X}^{2} + 4\sigma_{X}^{2} \gamma^{2}$, $u_{c} = \sqrt {8\left( {\frac{{4s^{2} \sigma_{s}^{2} }}{{w_{{z_{eq} }}^{4} }} + \sigma_{X}^{2} } \right)} .$

We derive the average SER of lognormal fading with nonzero boresight pointing error by substituting (B.2) into (5). The BER expression can be written as

$$P_{e,LN} = \left( {\frac{M - 1}{{M log_{2} \left( M \right)\sqrt \pi }}} \right)\frac{{\gamma^{2} exp\left( {u_{a} } \right)}}{{2\left( {A_{0} h_{l} } \right)^{{\gamma^{2} }} }}\mathop \smallint \limits_{0}^{\infty } h^{{\gamma^{2} - 1}} erfc\left( {\frac{{ln\frac{h}{{A_{0} h_{l} }} + u_{b} }}{{u_{c} }}} \right)erfc\left( {\sqrt {\frac{{3log_{2} \left( M \right)R^{2} P_{t}^{2} }}{{\left( {M^{2} - 1} \right)\sigma_{n}^{2} }}h^{2} } } \right)dh.$$

(B.3)

Using a change of variable rule, (B.3) can be expressed as

$$\begin{aligned} & P_{e,LN} = \left( {\frac{M - 1}{{M log_{2} \left( M \right)\sqrt \pi }}} \right)\frac{{\gamma^{2} u_{c} exp\left( {u_{a} - \gamma^{2} u_{b} } \right)}}{2} \\ & \mathop \smallint \limits_{ - \infty }^{\infty } exp\left( {\gamma^{2} u_{c} x} \right)erfc\left( x \right)erfc\left( {\sqrt {\frac{{3log_{2} \left( M \right)R^{2} P_{t}^{2} }}{{\left( {M^{2} - 1} \right)\sigma_{n}^{2} }}} \frac{{A_{0} h_{l} }}{{exp\left( {u_{b} - xu_{c} } \right)}}} \right)dx. \\ \end{aligned}$$

(B.4)

(B.4) can be approximated as

$$\begin{aligned} & P_{e,LN} = \left( {\frac{M - 1}{{M log_{2} \left( M \right)\sqrt \pi }}} \right)\frac{{\gamma^{2} u_{c} exp\left( {u_{a} - \gamma^{2} u_{b} } \right)}}{2} \\ & \mathop \smallint \limits_{ - \infty }^{B} exp\left( {\gamma^{2} u_{c} x} \right)erfc\left( x \right)erfc\left( {\sqrt {\frac{{3log_{2} \left( M \right)R^{2} P_{t}^{2} }}{{\left( {M^{2} - 1} \right)\sigma_{n}^{2} }}} \frac{{A_{0} h_{l} }}{{exp\left( {u_{b} - xu_{c} } \right)}}} \right)dx. \\ \end{aligned}$$

(B.5)

where $B$ is an an auxiliary parameter.

Using a series expansion of the complementary error function (Wolfram 2020), Eq. (06.27.06.0002.01)]

$$erfc\left( z \right) = 1 - \frac{2}{\sqrt \pi }\mathop \sum \limits_{k = 0}^{\infty } \left[ {\frac{{\left( { - 1} \right)^{k} z^{2k + 1} }}{{k!\left( {2k + 1} \right)}}} \right].$$

(B.6)

And, an integral identity (Wolfram 2020), Eq. (06.27.21.0011.01)]

$$\smallint e^{bz} {\text{erfc}}\left( {az} \right)dz = \frac{1}{b}\left( {e^{bz} {\text{erfc}}\left( {az} \right) - e^{{\frac{{b^{2} }}{{4a^{2} }}}} {\text{erf}}\left( {\frac{b}{2a} - az} \right)} \right)$$

(B.7)

An infinite series expression of the SER can be written as

$$P_{e,LN} = \left( {\frac{M - 1}{{M log_{2} \left( M \right)\sqrt \pi }}} \right)\frac{{\gamma^{2} u_{c} }}{2}exp\left( {u_{a} - \gamma^{2} u_{b} } \right)\left\{ {\frac{1}{{\gamma^{2} u_{c} }}\left[ {exp\left( {\gamma^{2} u_{c} x} \right)erfc\left( B \right) + exp\left( {\frac{{\gamma^{4} u_{c}^{2} }}{4}} \right)erfc\left( {\frac{{\gamma^{2} u_{c} }}{2} - B} \right)} \right] - \frac{2}{\sqrt \pi }\mathop \sum \limits_{k = 0}^{\infty } \left[ {\frac{{\left( { - 1} \right)^{j} }}{{j!\left( {2j + 1} \right)}}\left( {\sqrt {\frac{{3log_{2} \left( M \right)R^{2} P_{t}^{2} }}{{\left( {M^{2} - 1} \right)\sigma_{n}^{2} }}} A_{0} h_{l} } \right)^{2j + 1} \frac{{exp\left( { - u_{b} \left( {2j + 1} \right)} \right)}}{{\left( {2j + 1 + \gamma^{2} } \right)u_{c} }}S_{j} } \right]} \right\}$$

(B.8)

where

$$S_{j} = exp\left( {\left( {\gamma^{2} + 2j + 1} \right)u_{c} B} \right)erfc\left( B \right) + exp\left( {\left( {\gamma^{2} + 2j + 1} \right)^{2} u_{c} /4} \right)erfc\left( {\left( {\gamma^{2} + 2j + 1} \right)u_{c} /2 - B} \right).$$

(B.9)

Appendix C: Gamma-gamma composite PDF

For medium to strong turbulence conditions, we use the Gamma-Gamma turbulence model to characterize the atmospheric fading ha whose PDF is given by (Yang et al. 2014)

$$f_{{h_{a} }} \left( {h_{a} } \right) = \frac{{2\left( {\alpha_{GG} \beta_{GG} } \right)^{{\left( {\alpha_{GG} + \beta_{GG} } \right)/2}} }}{{\Gamma \left( {\alpha_{GG} } \right)\Gamma \left( {\beta_{GG} } \right)}}h_{a}^{{\frac{{\left( {\alpha_{GG} + \beta_{GG} } \right)}}{2} - 1}} K_{{\alpha_{GG} - \beta_{GG} }} \left( {2\sqrt {\alpha_{GG} \beta_{GG} h_{a} } } \right).$$

(C.1)

Γ(·) is the Gamma function, and $K_{{\alpha_{GG} - \beta_{GG} }} \left( . \right)$ is the modified Bessel function of the second kind of order $\alpha_{GG} - \beta_{GG}$.The parameters $\alpha_{GG}$ and $\beta_{GG}$ are related to the small large scale eddies respectively. We obtain the composite PDF as (Yang et al. 2014)

$$f_{GG} \left( h \right) = \mathop \sum \limits_{j = 0}^{J} \frac{1}{j!}\left( {\frac{{\alpha_{GG} \beta_{GG} }}{{A_{0} h_{l} }}} \right)^{j} \left( {v_{j} \left( {\alpha_{GG} , \beta_{GG} } \right)h^{{\beta_{GG} - 1 + j}} - v_{j} \left( {\beta_{GG} ,\alpha_{GG} } \right)h^{{\alpha_{GG} - 1 + j}} } \right),$$

(C.2)

where

$$\begin{aligned} v_{j} \left( {\alpha_{GG} ,\beta_{GG} } \right) & = \frac{{\gamma^{2} \pi \left( {\frac{{\alpha_{GG} \beta_{GG} }}{{A_{0} h_{l} }}} \right)^{{\beta_{GG} }} exp \left( { - \frac{{s^{2} }}{{2\sigma_{s}^{2} }} - \frac{{s^{2} \gamma^{2} /\sigma_{s}^{2} }}{{\left( {2\beta_{GG} - 2\gamma^{2} + 2j} \right)}}} \right)\left( {\pi \left( {\alpha_{GG} - \beta_{GG} } \right)} \right) }}{{\Gamma \left( {\beta_{GG} } \right)\Gamma \left( {\alpha_{GG} } \right)\Gamma \left( {j - \left( {\alpha_{GG} - \beta_{GG} } \right) + 1} \right)\left| { - \left( {\beta_{GG} - \gamma^{2} + j} \right)} \right|}}, \\ v_{j} \left( {\beta_{GG} ,\alpha_{GG} } \right) & = \frac{{\gamma^{2} \pi \left( {\frac{{\alpha_{GG} \beta_{GG} }}{{A_{0} h_{l} }}} \right)^{{\alpha_{GG} }} exp \left( { - \frac{{s^{2} }}{{2\sigma_{s}^{2} }} - \frac{{s^{2} \gamma^{2} /\sigma_{s}^{2} }}{{\left( {2\alpha_{GG} - 2\gamma^{2} + 2j} \right)}}} \right)\left( {\pi \left( {\alpha_{GG} - \beta_{GG} } \right)} \right) }}{{\Gamma \left( {\beta_{GG} } \right)\Gamma \left( {\alpha_{GG} } \right)\Gamma \left( {j + \left( {\alpha_{GG} - \beta_{GG} } \right) + 1} \right)\left| { - \left( {\alpha_{GG} - \gamma^{2} + j} \right)} \right|}}. \\ \end{aligned}$$

By using (7) and (C.2) into (8)

$$\begin{aligned} P_{e,GG} & = \left( {\frac{M - 1}{{M log_{2} \left( M \right)}}} \right)\mathop \smallint \limits_{0}^{\infty } erfc\left( {\sqrt {\frac{{3log_{2} \left( M \right)R^{2} P_{t}^{2} }}{{\left( {M^{2} - 1} \right)\sigma_{n}^{2} }}h^{2} } } \right) \\ & \quad \times \mathop \sum \limits_{j = 0}^{J} \frac{1}{j!}\left( {\frac{{\alpha_{GG} \beta_{GG} }}{{A_{0} h_{l} }}} \right)^{j} \left( {v_{j} \left( {\alpha_{GG} ,\beta_{GG} } \right)h^{{\beta_{GG} - 1 + j}} - v_{j} \left( {\beta_{GG} ,\alpha_{GG} } \right)h^{{\alpha_{GG} - 1 + j}} } \right)dh. \\ \end{aligned}$$

(C.3)

The average SER is given by

$$P_{e,GG} \frac{M - 1}{{M log_{2} \left( M \right)\sqrt \pi }}\left[ {\mathop \sum \limits_{j = 0}^{J} \left\{ {\frac{1}{j!}\left( {\frac{{\alpha_{GG} \beta_{GG} }}{{A_{0} h_{l} }}} \right)^{ j} \left( {\frac{{\Gamma \left( {\frac{{ \beta_{GG} + j + 1}}{2} } \right)}}{{\beta_{GG} + j}}v_{j} \left( {\alpha_{GG} , \beta_{GG} } \right)\left( {\frac{{3log_{2} \left( M \right)R^{2} P_{t}^{2} }}{{\left( {M^{2} - 1} \right)\sigma_{n}^{2} }}} \right)^{{ - \left( {\frac{{\beta_{GG} + j}}{2}} \right)}} - \frac{{\Gamma \left( {\frac{{ \alpha_{GG} + j + 1}}{2} } \right)}}{{\alpha_{GG} + j}}v_{j} \left( { \beta_{GG} ,\alpha_{GG} } \right)\left( {\frac{{3log_{2} \left( M \right)R^{2} P_{t}^{2} }}{{\left( {M^{2} - 1} \right)\sigma_{n}^{2} }}} \right)^{{ - \left( {\frac{{\alpha_{GG} + j}}{2}} \right)}} } \right)} \right\}} \right]$$

(C.4)

Appendix D: K-distribution composite PDF

For medium to strong turbulence conditions, we use the K-distribution turbulence model to characterize the atmospheric fading ha whose PDF is given by

$$f_{{h_{a} }} \left( {h_{a} } \right) = \frac{2}{{\Gamma \left( {\alpha_{k} } \right)}}\alpha_{k}^{{\frac{{\left( {\alpha_{k} + 1} \right)}}{2}}} h_{a}^{{\frac{{\left( {\alpha_{k} - 1} \right)}}{2}}} K_{{\alpha_{k} - 1}} \left( {\sqrt {\alpha_{k} h_{a} } } \right).$$

(D.1)

where $h_{a}$ denotes the optical signal intensity $\alpha_{k}$ is the channel parameter related to the effective number of descrete scatterers, in this analysis $1 < \alpha_{k} < 2.$

We substitute (2) and (D.1) into (5) and write the composite PDF of the K-distribution fading with nonzero boresight pointing error as

$$f_{K} \left( h \right) = \frac{{2\gamma^{2} exp\left( {\frac{{ - s^{2} }}{{2\sigma_{s}^{2} }}} \right)}}{{\left( {A_{0} h_{l} } \right)^{{\gamma^{2} }} \Gamma \left( {\alpha_{n} } \right)}}h^{{\gamma^{2} - 1}} \mathop \smallint \limits_{{h/A_{0} h_{l} }}^{\infty } h_{a}^{{\frac{{\left( {\alpha_{k} - 1} \right)}}{2} - \gamma^{2} }} I_{0} \left( {\frac{s}{{\sigma_{s} }}\sqrt {\frac{{ - w_{{z_{eq} }}^{2} }}{2}lnln \left( {\frac{h}{{h_{a} A_{0} h_{l} }}} \right) } } \right)K_{{\alpha_{k} - 1}} \left( {2\sqrt {\alpha_{k} h_{a} } } \right)dh_{a}$$

(D.2)

After mathematical derivation, we obtain a finite series approximation of the composite PDF as

$$f_{K} \left( h \right) = \mathop \sum \limits_{j = 0}^{J} \frac{1}{j!}\left( {\frac{{\alpha_{k} }}{{A_{0} h_{l} }}} \right)^{j} \left( {v_{j} \left( {\alpha_{k} ,1} \right)h^{j} - v_{j} \left( {1,\alpha_{k} } \right)h^{{\alpha_{k} - 1 + j}} } \right),$$

(D.3)

where

$$\begin{aligned} v_{j} \left( {\alpha_{k} ,1} \right) & = \frac{{\gamma^{2} \pi \left( {\frac{{\alpha_{k} }}{{A_{0} h_{l} }}} \right)expexp \left( { - \frac{{s^{2} }}{{2\sigma_{s}^{2} }} - \frac{{\frac{{s^{2} \gamma^{2} }}{{\sigma_{s}^{2} }}}}{{\left( {2 - 2\gamma^{2} + 2j} \right)}}} \right) \left( {\pi \left( {\alpha_{k} - 1} \right)} \right) }}{{\Gamma \left( {\alpha_{k} } \right)\Gamma \left( {j - \left( {\alpha_{k} - 1} \right) + 1} \right)\left| { - \left( {1 - \gamma^{2} + j} \right)} \right|}}, \\ v_{j} \left( {1,\alpha_{k} } \right) & = \frac{{\gamma^{2} \pi \left( {\frac{{\alpha_{k} }}{{A_{0} h_{l} }}} \right)^{{\alpha_{k} }} expexp \left( { - \frac{{s^{2} }}{{2\sigma_{s}^{2} }} - \frac{{\frac{{s^{2} \gamma^{2} }}{{\sigma_{s}^{2} }}}}{{\left( {2\alpha_{k} - 2\gamma^{2} + 2j} \right)}}} \right) \left( {\pi \left( {\alpha_{k} - 1} \right)} \right) }}{{\Gamma \left( {\alpha_{k} } \right)\Gamma \left( {j + \left( {\alpha_{k} - 1} \right) + 1} \right)\left| { - \left( {\alpha_{k} - \gamma^{2} + j} \right)} \right|}}. \\ \end{aligned}$$

By using (7) and (D.3) into (8), it becomes

$$P_{e,K} = \left( {\frac{M - 1}{{M log_{2} \left( M \right)}}} \right)\mathop \smallint \limits_{0}^{\infty } erfc\left( {\sqrt {\frac{{3log_{2} \left( M \right)R^{2} P_{t}^{2} }}{{\left( {M^{2} - 1} \right)\sigma_{n}^{2} }}h^{2} } } \right) \times \mathop \sum \limits_{j = 0}^{J} \frac{1}{j!}\left( {\frac{{\alpha_{k} }}{{A_{0} h_{l} }}} \right)^{j} \left( {v_{j} \left( {\alpha_{k} ,1} \right)h^{j} - v_{j} \left( {1,\alpha_{k} } \right)h^{{\alpha_{k} - 1 + j}} } \right)dh.$$

(D.4)

The average SER is given by

$$P_{e,K} = \frac{M - 1}{{M log_{2} \left( M \right)\sqrt \pi }}\left[ {\mathop \sum \limits_{j = 0}^{J} \left\{ {\frac{1}{j!}\left( {\frac{1}{{A_{0} h_{l} }}} \right)^{ j} \left( {\frac{{\Gamma \left( {\frac{ 2 + j}{2} } \right)}}{1 + j}v_{j} \left( {\alpha_{k} ,1} \right)\left( {\frac{{3log_{2} \left( M \right)R^{2} P_{t}^{2} }}{{\left( {M^{2} - 1} \right)\sigma_{n}^{2} }}} \right)^{{ - \left( {\frac{1 + j}{2}} \right)}} - \frac{{\Gamma \left( {\frac{{ \alpha_{k} + j + 1}}{2} } \right)}}{{\alpha_{k} + j}}v_{j} \left( {1,\alpha_{k} } \right)\left( {\frac{{3log_{2} \left( M \right)R^{2} P_{t}^{2} }}{{\left( {M^{2} - 1} \right)\sigma_{n}^{2} }}} \right)^{{ - \left( {\frac{{\alpha_{k} + j}}{2}} \right)}} } \right)} \right\}} \right].$$

(D.5)