Abstract
The frequency-modulated continuous-wave radar is an ideal choice for autonomous vehicle and surveillance-related industries due to its ability to measure the relative target-velocity, target-range, and target-characterization. Unlike conventional microwave radar systems, the photonic radar has the potential to offer wider bandwidth to attain high range-resolution at low input power requirements. Subsequently, a frequency-modulated continuous-wave photonic-radar is developed to measure the target-range and velocity of the automotive mobile targets concurrently with acceptable rang resolution keeping in mind the needs of the state-of-the-art autonomous vehicle industry. Furthermore, the target-identification is also an important parameter to be measured to enable the futuristic autonomous vehicles for the recognition of the objects along with their dimensions. Therefore, the reported work is extended to characterize the target-objects by measuring the specular-reflectance, diffuse-reflectance, the ratio of horizontal-axis to vertical-axis, refractive index constants of the targets using the bidirectional reflectance distribution function. Furthermore, the reflectance properties of the target-objects are also measured with different operating wavelengths at different incident angles to assess the influence of the operating wavelength and the angle at which the radar-pulses incident on the surface of the targets. Moreover, to validate the performance of the demonstrated work, a comparison is also presented in distinction with the conventional microwave FMCW-RADAR.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Recent developments in sensor technology, imaging, radar, light detection and ranging, electronics, and artificial intelligence have enabled the state-of-the-art autonomous vehicles (AVs) to provide significant services including collision avoidance, blind-spot monitoring, lane departure warning, or park assistance (Bimbraw 2015; Self-Driving Cars Explained). To synchronize the operation of such systems through sensor-fusion allows the self-driving vehicles to monitor their surroundings and take evasive actions to prevent the probable road hazards (Self-Driving Cars Explained; Thrun 2010). To attain these objectives, the measurement of target-velocity and range concurrently with high precision is essential. This can be performed with the knowledge of signal processing Doppler shift (Tsui 2004; Haykin 2006; Scheer and Kurtz 1993). Therefore, most of the advanced AVs are equipped with various expensive signal processing modules, high precision cameras, and high-end sensors but still offer the target-detection to a few meters only. Thus, the automotive industry is looking for other cost-effective approaches in the last few years to improve the accuracy of the self-driving vehicles with extended target-range detection and range-visibility (Sharma and Sergeyev 2020). In contrast to the conventional microwave radar, Photonic-radar (PHRAD) offers accurate and improved range-speed resolution with low power requirements (Allen et al. 2002; Yang et al. 2007). Moreover, it is economical, small in size, and can be easily installed. However, PHRAD is susceptible to the noise because of the low-power of the returned pulses and wide-bandwidth of the detection electronics that lead to inaccuracies in the measurement of round-trip time. For these reasons, the frequency-modulated continuous-wave (FMCW)-PHRAD comes out as a cost-effective alternative. The FMCW-PHRAD continuously emits the frequency-modulated light pulses with sawtooth or triangular function towards the target through the free space (Karlsson and Olsson 1999).
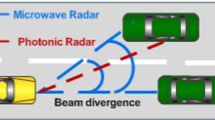
In addition to the target-detection, range, and relative radial-velocity measurements with required resolution, the target categorization, and identification is also highly required in AV related industry. To make optimal decisions according to the instantaneous situation promptly, the AV vehicles are required to differentiate and recognize the mobile or immobile targets. To meet this need, PHRAD has the potential to offer high-angular-resolution imagery due to its narrow beam divergence that allows better identification of the adjacent targets compared to the traditional microwave radar (Hata and Wolf 2016). To validate a target by a photonic-radar equipped self-driving vehicle is dependent on many variables, including distance, interrogation pattern and resolution, reflectivity, and the shape of the objects being examined. To classify and recognize a target, the laser radar cross-section (LRCS) parameter is usually computed by measuring the optical properties of the target. The radar cross-section is based on the bidirectional reflectance distribution function (BRDF), a radiometric concept used to recognize the objects based on electromagnetic wave reflection theory and to measure the high and/or low observability of an object (Cao et al. 2017). Several research methods have been reported for the measurements (Sevgi et al. 2013; Wong et al. 2006; Muth et al. 2005) and theoretical calculations (Lim 2011; Li 2016; Alfonzetti and Borzì 2000; Carpentieri 2007; Han et al. 2013; Rius et al. 1993; Ueng and Yang 2009; Liu et al. 2013) of LRCS considering the object-material, geometry, roughness, wavelength, incident angle, and other various parameters. To measure the LRCS of the natural and non-natural objects, BRDF relates the incident and reflected radiance and performs unproblematic scattering computations to evaluate the optical characteristics of the target (Cao et al. 2017). In literature, diverse surface models for BRDF have been developed and analyzed to measure the 3D light scattering characteristics. However, lofty data is required to accurately investigate the light scattering properties of a target in free-space which limits the experimental consciousness to put into practice. Hence, to overcome this setback, a five parameter BRDF function based on Torrance–Sparrow model, is developed (Zhang et al. 2010), including the specular reflectance, diffuse reflectance, the ratio of horizontal-axis to vertical-axis, and refractive index constants to observe the reflectance behavior of various targets. RCS is wavelength and surface material-dependent factor to determine the shape and type of the target. The majority of the prior research on the radar cross-section and BRDF is reported up to 1060 nm wavelength (Zhang et al. 2010; Wang and Ni-Meister 2019; Mungan 2000; Matthew et al. 2012; Li et al. 2016). Researchers in Hasan et al. (2015) used Walthall BDRF model to estimate the RGB color value associated with LiDAR cloud-point by applying point by point BRDF correction approach for homogenous areas and is focused on the improvement of LiDAR cloud-point data. Further, Li et al. (2014) presented an integration method to establish the relation between the intensity data of PHRAD and BDRF. Moreover, based on the physical background, the authors characterized the BRDF models into empirical, theoretical, and experimental categories. The empirical BRDF model provides a formulation for refection to reduce the computational complexity without considering the physical concepts. On the other hand, the theoretical BDRF models are physical concept-based models that lead to complex mathematical functions with the burden of computational efforts. Meanwhile, the experimental BRDF models have been carried out to show the relevance of the empirical and theoretical models. To integrate the advantages of various BRDF models, the hybrid BRDF models are also being developed. To calibrate the scattering model and the correctness of the intensity data, the reflection- and scattering-properties of different targets have been examined in the earlier reported literature for a radar system but the reflection properties beyond 1060 nm have not been explored extensively.
Therefore, the authors, in this work, develop a 77-GHz FMCW-PHRAD radar along with target-identification capability in 1550 nm band to carry out target-detection by computing the range-speed response pattern using MATLAB™ software. The target-characterization is attained by evaluating the BRDF function at different operating wavelengths and at different incident angles. The five-parameter based BRDF is computed by measuring the specular-reflectance, diffuse-reflectance, the ratio of horizontal-axis to vertical-axis, refractive index constants for two target-objects, i.e. the polyimide film and silver tin-foil, considered in this work. As the LiDAR cloud-point using the conventional BRDF function is not a storage-effective approach and requires thousands of coefficients to create an informative data-set, the authors modified the established photonic-radar by incorporating a logarithmic BRDF function to reduce the storage requirements. A contrast with the conventional BRDF approach is also presented. The rest of the manuscript is structured as Sect. 1 illustrates the introduction and earlier reported literature related to the automotive radar with its futuristic challenges and requirements. Section 2 describes the brief working principle of the demonstrated photonic-radar along with a detailed system description, whereas its observations are outlined in Sect. 3. The reflection characteristics of the targets by measuring the BRDF function are reported in Sect. 4 and is followed by the conclusion part of Sect. 5.
2 System modeling
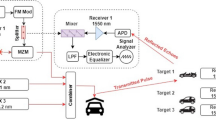
The FMCW-PHRAD system is developed using MATLABTM with the primary objective of avoiding the collision between the AVs by accurately estimating the distance between the target-vehicle and radar mounted vehicle simultaneously and unambiguously. To attain the secondary objective of measuring the LRCS of the different targets for their characterization and identification, the demonstrated system is further extended by incorporating the BRDF function. The basic principle of the PHRAD works on the Doppler Effect where the reflected signal is a time-delayed replica of the transmitted signal and by measuring this time-delay, the target-range is estimated. A triangular linear frequency modulated waveform (RF-LFM) is generated using a local waveform generator at 77 GHz in this work. As the signal is always a linear sweeping through a frequency band, the frequency difference between the Doppler-frequency and transmitted-frequency, known as the beat frequency remains constant. Thus, the time-delay can be easily calculated from the beat frequency which further translates into the target-range and velocity. As the FMCW signal occupies wide bandwidth signals, the sampling rate should be at least two times the bandwidth. However, this high sample rate imposes stress on the analog to digital converters due to the power constrains and restriction of a number of effective bits. To reduce the burden on analog to digital converter and to accommodate the power constrains and the effective number of bits issue, the sample rate is considered twice the maximum beat frequency in this work. Generally, the sweep-time for FMCW radar is preferred as five to six times of the round-trip time and in this work, the authors have considered the sweep-time as 5.5 of the round-trip time. Moreover, the maximum detection-range of 200 m of the demonstrated radar is considered and the maximum velocity of 230 km/h of each target-vehicle is modeled in this work. The demonstrated PHRAD is carried out with the parameters of sweep time = 7.33 µsec, sweep bandwidth = 150 MHz, and sample rate = 150 MHz. These RF-LFM generated waveforms are then widened by optical modulating over light pulses of a continuous laser of the operating wavelength of 1550 nm by means of an optical modulator. Since the short optical pulse is needed to attain maximum range resolution and it depends on round-trip time of the optical signals propagated between the transmitters and receivers (Harris et al. 2002; Mao et al. 2012), consequently, there is always as a tradeoff between the range- and velocity-resolution. To minimize the tradeoff between the range- and velocity-resolution, the optical treated RF-LFM signals of 77 GHz to realize an FMCW-PHRAD offers frequency chirped long optical-pulses with low peak power requirements (Harris et al. 2002; Mao et al. 2012). Moreover, the AV radars usually operate at both 24 GHz and 77 GHz frequency band. A high bandwidth (≈ 4 GHz) at the operating frequency of 77 GHz in distinction with 24 GHz band (≈ 200 MHz) can be attained. That is why the light-based radar manufacturers have moved towards the 77 GHz frequency band. This wide-bandwidth increases the range- and velocity-resolution to identify the closely spaced targets and improves the radar-accuracy (Ramasubramanian and Ramaiah 2018).
This intensity-modulated long optical pulses are amplified using an optical amplifier and then, transmitted over the free space channel towards the illuminated targets. A beam collimator is used to transmit and receives these optical modulated wider chirps via a free space channel without considering the adverse atmospheric fluctuations. The target scenario is modeled by assuming that the target-vehicles are moving at different distances ahead of the radar-mounted vehicle at different velocities to test and investigate the effectiveness of the demonstrated photonic-radar. The radar cross-section of the target is computed based on the distance between the radar-equipped vehicle and the target-vehicle (Karnfelt et al. 2009). The radar-equipped vehicle is modeled at a velocity of 100 km/h along the x-axis for all the considered scenarios in this work and the targets are approaching it at different relative speeds.
To measures the beat frequency signal, the received signal reflected from the target is mixed with the transmitted signal after re-converted into electrical signals using a photo-detector of Responsivity of 0.8 m/A. After the mixing, the dechirped signal contains only individual frequency components that correspond to the target-range. As it is not feasible to extract the Doppler information from a single sweep, a definite number of de-chirp signals is kept in a buffer, and in this work, the authors used 64 sweeps. Once the buffer is filled with 64 sweeps, the Fourier transformation is performed to extract the beat frequency and Doppler shift to measure the range and relative speed of the target vehicle (Gao et al. 2012; Adany et al. 2009). The single chirp FMCW waveform can be expressed as (Hinz and Zölzer 2011):
where ‘t’ is the variable time within the single chirp period, ‘fs’ is the start frequency of the chirp, and α indicates the sweep-rate, which is defined as the ratio of the chirp-bandwidth (B) divided by the chirp-duration (T). The received signal is a time delay replica of the transmitted signal which can be expressed as (Hinz and Zölzer 2011)
Where ‘A’ represents the attenuation during round-trip time of the signal to propagate from the radar system to the target and back. In mathematical terms, the beat frequency signal of a static point target is expressed in the following equation (Hinz and Zölzer 2011)
Then, the zero intermediate frequency echo signal is obtained as
This beat signal is sampled with frequency fs = 1/Ts during each ramp and can be expressed as (Song et al. 2014):
The Fourier Transform of Eq. (5) for each ramp can be represented as
where \(p = nT_{s} \left( {f_{\tau } + f_{d} } \right)\), fτ = Instantaneous frequency, fc = carrier-frequency, and fd = Doppler-frequency. Therefore, the information for range and velocity is stored in signal represented by Eq. (5) which is calculated for one modulation period. If the target speed is ‘v’, and its initial position is ‘R0’, then the delay ‘τ’ of the echo signal is measured as \(\tau = \frac{{2\left( {R_{0} + vt} \right)}}{c}\). By substituting the value of ‘τ’ in Eq. (4), the zero intermediate frequency echo of the FMCW signal is measured (Yue et al. 2019) as
3 Observations and discussions
To validate the effectiveness of the demonstrated photonic-radar system, a comparison with the conventional FMCW-RADAR is required to be established. Therefore, initially, a conventional microwave FMCW-RADAR is modeled and investigated at sweep bandwidth of 150 MHz and a range resolution of 1 m. The target-vehicle is assumed at a distance of 43 m from the FMCW-RADAR and is traveling at a velocity of 96 km/h, i.e. at a relative velocity of 1.11 m/s with respect to the radar equipped-vehicle. The power spectral density and range-response mapping for FMCW-RADAR is shown in Fig. 1. The radar equipped-vehicle is modeled at a speed of 100 km/h using MATLABTM for all the scenarios discussed in this work. The propagation channel is modeled without considering the influence of atmospheric fluctuations.
Further, three different target-scenarios are modeled to be tested using the demonstrated FMCW-PHRAD to validate its feasibility and potential in comparison with the FMCW-RADAR. In Scenario 1, the target-vehicle is modeled with the same distance and velocity as that of the above-mentioned Scenario. In Scenario 2, the target-vehicle is assumed at a distance of 70 m moving at a speed of 80 km/h, i.e. at a relative velocity of 5.55 m/s ahead of the PHRAD-equipped vehicle. The target-range is increased to 100 m moving at a speed of 50 km/h with a relative velocity of 13.88 m/s in Scenario 3. Figure 2 shows the power spectral density for beat frequency and the de-chirped signal corresponding to each modeled scenario. A decrease in the peak of beat frequency is observed corresponding with the distance between the target-vehicle and PHRAD-equipped vehicle. Moreover, a frequency-shift as a function of the relative velocity can be seen. The intensity of the beat frequency (Ib), is dependent on original wave intensity (Io), Doppler-shifted signal intensity (Io), and phase difference (Φ) between Doppler frequency and original frequency which can be expressed as (Yue et al. 2019):
As the range of target increased, the attenuation of the signal in the free-space propagation model elevated due to transmission impairments, hence the effect on beat frequency intensity is observed. Moreover, the beat frequency is an absolute difference of Doppler frequency and frequency of originally generated signal and proportional to target-velocity which leads to beat frequency shift as shown in Fig. 2. In comparison with the power spectra of FMCW-RADAR as shown in Fig. 1a, the FMCW-PHRAD as shown in Fig. 2a with the same target properties, offers a high peak-power of the measured beat signal and is, therefore, suitable for prolonged target-range. This is because of the potential of the photonic-radar to offer minimal beam-divergence, and thus, a smaller angular-resolution. Additionally, the range-Doppler response provides useful insight to measure the target position precisely. This is done by signal processing of FMCW systems which is quite helpful for the evaluation of range and relative velocity of the target vehicles. In this work, a range-Doppler mapping is carried out by using a two-dimensional fast Fourier transform (FFT). Figure 3 shows the range-Doppler response for all the modeled scenarios and displays the exact position of the targets as a function of the target distance and its relative velocity with respect to the PHRAD-equipped vehicle. In comparison with the range-Doppler response of conventional RADAR as shown in Fig. 1b, the established PHRAD measures the target-range and speed more unambiguously with high resolution.
The range resolution plays a vital role for target-detection as it decided the minimum detectable range of target and is directly proportional to the pulse-width and round-trip time. Thus, an extensive analysis is required to estimate the minimum target-range for unambiguous target-detection to obtain precision in real-world scenarios. Therefore, the work is extended to test the demonstrated FMCW-PHRAD at a range resolution of 0.25 m for all three scenarios. To attain the range-resolution of 0.25 m, the sampling rate is considered as 600 MHz with sweep-bandwidth of 600 MHz due to the inversely proportional dependence of the range-resolution on the sweep-bandwidth. The power spectral density and range-Doppler mapping measurements for the established FMCW-PHRAD are shown in Figs. 4 and 5. The outcomes reveal the ability of the photonic-radar to measure the target-range and velocity concurrently even at the increased resolution of 0.25 m with precision but at the cost of additional burden on ADCs.
4 Target-characterization
Besides the target-detection, the target-characterization is also quite imported to recognize the shape and target’s properties. The five parameters based BRDF function is a good choice to attain this objective by measuring the reflectance characteristics of the target-materials (Zhang et al. 2010). In addition to it, BRDF also plays an important role to improve the cloud-point data of the photonic-radar system. Therefore, it is necessary to examine the reflectance characteristics of the target-materials, and hence, the demonstrated system is carried out in this direction by incorporating a five parameter based BRDF function. Generally, the target surface consists of two or more than two materials. Also, the coating of these materials holds several random particles on the target surface. Several models have been developed in the last few years to measure the optical properties of the different target materials for their classification and identification. The demonstrated FMCW-PHRAD used the Torrance–Sparrow model to measure the BRDF function at an operating wavelength of 1550 nm of the proposed system at different incident angles. The BRDF estimation at 1550 nm will be beneficial to improve the cloud-point data of the projected approach for better estimation of the target-range and velocity along with their classification. Moreover, this wavelength band is also safe to human-eye, unlike the infrared band. The relation between α and γ in the rectangular coordinate system can be estimated as (Zhang et al. 2010):
By incorporating the specular- and diffuse-reflection, the five parameters based BRDF function according to the Torrance-Sparrow model can be deduced as
Where \(G\left( {\theta_{i} , \theta_{r} , \varphi_{r} } \right)\) is a shadowing function, which is estimated on the basis of the probability of shadowing and masking of the micro-facets with respect to the projections of \(\theta_{i} , \theta_{r} , \varphi_{r}\) denoted as \(\theta_{sph}^{i} , \theta_{sph}^{r} , \gamma_{sph}\) respectively which can be described as (Zhang et al. 2010)
where,
where \(\sigma_{r } = 0.0141,\sigma_{sph} = 0.0136, u_{sph} = 9.0,v_{sph} = 1\) are the empirical parameters to calculate the geometrical attenuation factor of the flux and the tangential factor of \(\theta_{sph}^{i} , \theta_{sph}^{r} , \gamma_{sph}\) which can be estimated as
In this work, the demonstrated FMCW-PHRAD is tested for BRDF measurements of the polyimide film and silver tin-foil as these are the most used material for the coating of targets in the automotive and aerospace industry. Polyimide is a type of polymer with high resistance to the temperature, mechanical-stress, radiation rays, and is widely used as an insulating and casing material in various areas like the automotive industry and aerospace due to its shiny nature. Therefore, it is a substantial material to be investigated at 1550 nm which is not much explored earlier. The five parameters for polyimide film at 1060 nm are measured as kb = 5.439, kr = 3.257, b = −23.098, a = 0.495, kd = 2.267 (Zhang et al. 2010), and as kb = 40, kr = 2.1, b = −500, a = 0.495, kd = 0.925 at 1550 nm. The peaks at 1060 nm and 1550 nm in Fig. 6 show that the BRDF function is measured with elevated peaks and wider specular-widths at 1550 nm at different incident angles compared to the operating wavelength of 1060 nm. It is also observed that the specular peak is high at the incident angle, i.e. 60°. Moreover, the laser radiations are safer at 1550 nm and show good results as well to characterize the target surfaces.
Another important target-material tested in this work is the silver tin-foil due to its ability to block the electromagnetic waves in the range of 100 kHz to 300 GHz and is widely used material in AV related industries. Thus, it is interesting to investigate the optical properties for this material at various wavelengths. In this work, a comparison of silver tin-foil is presented at a wavelength of 650 nm, 1060 nm, and 1550 nm at different incident angles to analyze the BRDF. The five parameter values at 650 nm wavelength are measured as kb = 20, kd = 0.082, kr = 0.9, b = −420, a = 0.875 (Sun et al. 2010), and as kb = 35, kd = 0.075, kr = 2, b = −410, a = 0.915 at 1060 nm (Sun et al. 2010). The measured values at 1550 nm are as kb = 40, kd = 0.075, kr = 2.1, b = −500, a = 0.925. The BRDF of the silver tin-foil is shown in Fig. 7 at different wavelengths and incident angles.
It is observed that the specular peak of BRDF is higher at 1550 nm as compared to other wavelengths and augments with the increase of the incident angle. This shows the suitability of 1550 nm to be used in the FMCW-PHRAD system to measure the reflection characteristics to offer an improved LiDAR cloud-point sensor data (Li and Liang 2015; Cui et al. 2019) for different target classifications. Moreover, the BRDFs often contain specular peaks that are several orders of magnitude higher than the nearby areas. Therefore, it is required to apply certain transforms that help in compressing the raw BRDFs and reduces the overload of the signal processing modules. The currently available approaches used for BRDF representation are inefficient, particularly in terms of storage-cost as they require tens of thousands of coefficients to represent a BRDF accurately. One of the simple approaches is to take the logarithm of the BRDF measurements. Subsequently, a logarithmic BRDF function is developed and used to measure the reflection coefficients of the silver tin-foil using the demonstrated PHRAD. It has been observed that the logarithmic BDRF reduces the specular peak at each wavelength and can be used as one of the simple and cost-effective approaches besides the other available complicated techniques (Tongbuasirilai et al. 2020).
5 Conclusion
In this work, an FMCW-PHRAD is demonstrated to measure the target-range and radial-velocity simultaneously and unambiguously for different scenarios to validate the effectiveness of the reported work. Further, the possibilities of the established system are examined for target-characterization using five-parameters based BRDF function at different operating wavelengths and at different incident angles. The outcomes show a significant improvement in range-Doppler response and peak-power for all the considered scenarios with the demonstrated FMCW-PHRAD in contrast with the conventional FMCW-RADAR. Moreover, a BRDF function is used to analyze the light scattering characteristics of the target-material. The investigation shows that the modeled FMCW-PHRAD at 1550 nm has the possibilities to be utilized to improve the colorization of the cloud-point data of the LiDAR sensor for the target-detection of different materials and dimensions. It is concluded from the outcomes that the simultaneously range and speed measurements depend upon the target-distance, target-speed, target-RCS, target-material, and incident-angle. Moreover, there are opportunities to explore the demonstrated system to be equipped with spatial-diversity schemes under the influence of different atmospheric conditions for different targets in more complex-scenarios as an extended work in the future.
References
Adany, P., Allen, C., Hui, R.: Chirped photonic-radar using simplified homodyne detection. J. Lightwave Technol. 27, 3351–3357 (2009)
Alfonzetti, S., Borzì, G.: A fast method for computation of the bistatic radar cross section. IEEE Trans. Magn. 36, 921–924 (2000)
Allen, C.T., Chong, S.K., Cobanoglu, Y., Gogineni, S.: Development of a 1319-nm Laser Radar Using Fibre Optics and RF Pulse Compression, Technical Report ITTC-RSL-FY2002-TR-18680-01 (2002)
Bimbraw, K.: Autonomous cars: past, present and future a review of the developments in the last century, the present scenario and the expected future of autonomous vehicle technology. In: Proceedings of the 2015 12th International Conference on Informatics in Control, Automation and Robotics (ICINCO), Colmar, France, 21–23 July 2015, Vol. 1, pp. 191–198 (2015)
Cao, Y., Du, Y., Bai, L., Wu, Z., Li, H., Li, Y.: Calculation method for laser radar cross sections of rotationally symmetric targets. Appl. Opt. 56(19), 5520–5525 (2017)
Carpentieri, B.: Fast large RCS calculation using the boundary element method. J. Electromagn. Waves Appl. 21, 1959–1968 (2007)
Cui, L., Jiao, Z., Dong, Y., Sun, M., Zhang, X., Yin, S., Ding, A., Chang, Y., Guo, J., Xie, R.: Estimating forest canopy height using MODIS BRDF data emphasizing typical-angle reflectances. Remote Sens 11, 2239 (2019). https://doi.org/10.3390/rs11192239
Gao, S., O’Sullivan, M., Hui, R.: Complex-optical-field Photonic-radar system for range and vector velocity measurement. Opt. Express 20, 25867–25875 (2012)
Han, Y., Sun, H., Li, Y., Guo, H.: Fast calculation method of complex space targets’ optical cross section. Appl. Opt. 52, 4013–4019 (2013)
Harris, M., Yong, R.I., Köpp, F., Dolfi, A., Cariou, J.-P.: Wake vortex detection and monitoring. Aerosp. Sci. Technol. 6(5), 325–331 (2002)
Hasan, S., Jansa, J., Pfeifer, N.: BRDF-based correction of colorized aerial photonic-radar point clouds. Joint Urban Remote Sens. Event (2015). https://doi.org/10.1109/jurse.2015.7120471
Hata, Y.A., Wolf, D.F.: Feature detection for vehicle localization in urban environments using a multilayer PHOTONIC-RADAR. IEEE Trans. Intell. Transp. Syst. 17(2), 420–429 (2016). https://doi.org/10.1109/tits.2015.2477817
Haykin, S.: Cognitive radar: a way of the future. IEEE Signal Process. Mag. 23, 30–40 (2006)
Hinz, J.O., Zölzer, U.: A MIMO FMCW radar approach to HFSWR. Adv. Radio Sci. 9, 159–163 (2011). https://doi.org/10.5194/ars-9-159-2011
Karlsson, C.J., Olsson, F.Å.A.: Linearization of the frequency sweep of a frequency-modulated continuous-wave semiconductor laser radar and the resulting ranging performance. Appl. Opt. 38, 3376–3386 (1999)
Karnfelt, C., Peden, A., Bazzi, A., El Haj Shhade, G., Abbas, M., Chonavel, T.: 77 GHz ACC radar simulation platform. In: 2009 9th International Conference on Intelligent Transport Systems Telecommunications (ITST). https://doi.org/10.1109/itst.2009.5399354 (2009)
Li, H.: Space target optical characteristic calculation model and method in the photoelectric detection target. Appl. Opt. 55, 3689–3694 (2016)
Li, X., Liang, Y.: Surface characteristics modeling and performance evaluation of urban building materials using photonic-radar data. Appl. Opt. 54(15), 4750–4759 (2015). https://doi.org/10.1364/ao.54.004750
Li, X., Liang, Y., Xu, L.: Bidirectional reflectance distribution function based surface modeling of non-Lambertian using intensity data of light detection and ranging. J. Opt. Soc. Am. A 31(9), 2055–2063 (2014)
Li, H., Lyu, H., Liao, N., Wu, W.: Measuring spatially varying, multispectral, ultraviolet bidirectional reflectance distribution function with an imaging spectrometer. Opt. Eng. (2016). https://doi.org/10.1117/1.oe.55.12.124106
Lim, H.: Radar cross section measurements of a realistic jet engine structure with rotating parts. J. Electromagn. Waves Appl. 25, 1000–1006 (2011)
Liu, J., Fang, N., Wang, B., Zhang, L.: An efficient ray-tracing method for RCS prediction in Greco. Microw. Opt. Technol. Lett. 55, 586–589 (2013)
Mao, X., Inoue, D., Kato, S., Kagami, M.: Amplitude-modulated laser radar for range and speed measurement in car applications. IEEE Trans. Intell. Transp. Syst. 13(1), 408–413 (2012)
Matthew, S.C., Claire, A.B., Féret, J.-B., Asner, G.P.: Mapping Savanna tree species at ecosystem scales using support vector machine classification and BRDF correction on airborne hyperspectral and photonic-radar data. Remote Sens. 4, 3462–3480 (2012). https://doi.org/10.3390/rs4113462
Mungan, C.E.: Infrared Spectropolarimetric Bidirectional Reflectance of PHOTONIC-RADAR Targets and Building Materials, Spring (2000). https://www.usna.edu/Users/physics/mungan/_files/documents/Publications/BRDFmeasurements.pdf
Muth, L.A., Wang, C.M., Conn, T.: Robust separation of background and target signals in radar cross section measurements. IEEE Trans. Instrum. Meas. 54, 2462–2468 (2005)
Ramasubramanian, K., Ramaiah, K.: Moving from legacy 24 GHz to state-of-the-art 77-GHz radar. ATZ Elektron Worldw 13, 46–49 (2018). https://doi.org/10.1007/s38314-018-0029-6
Rius, J.M., Ferrando, M., Jofre, L.: GRECO: graphical electromagnetic computing for RCS prediction in real time. IEEE Antennas Propag. Mag. 35(2), 7–17 (1993)
Scheer, J.A., Kurtz, J.L.: Coherent Radar Performance Estimation. Artech House, London (1993)
Self-Driving Cars Explained. https://www.ucsusa.org/clean-vehicles/how-self-driving-cars-work
Sevgi, L., Rafiq, Z., Majid, I.: Radar cross section (RCS) measurements. IEEE Antennas Propag. Mag. 55(6), 277–291 (2013)
Sharma, V., Sergeyev, S.: Range detection assessment of photonic-radar under adverse weather perceptions. Opt. Commun. (2020). https://doi.org/10.1016/j.optcom.2020.125891
Song, M., Lim, J., Shin, D.-J.: The velocity and range detection using the 2D-FFT scheme for automotive radars. In: 2014 4th IEEE International Conference on Network Infrastructure and Digital Content. https://doi.org/10.1109/icnidc.2014.7000356 (2014)
Sun, C., Yuan, Y., Zhang, X., Wang, Q., Zhou, Z.: Research on the model of spectral BRDF for space target surface material. Int. Symp. Opto-mech. Technol. (2010). https://doi.org/10.1109/isot.2010.5687369
Thrun, S.: Toward robotic cars. Commun. ACM 53, 99–106 (2010)
Tongbuasirilai, T., Unger, J., Kronander, J., et al.: Compact and intuitive data-driven BRDF models. Vis. Comput. 36, 855–872 (2020). https://doi.org/10.1007/s00371-019-01664-z
Tsui, J.B.: Digital Techniques for Wideband Receivers, 2nd edn. SciTech, London (2004)
Ueng, S.-K., Yang, F.-S.: Visual computing for scattered electromagnetic fields. In: Proceedings of the 5th International Symposium on Advances in Visual Computing: Part II, Vol. 5876, pp. 899–908 (2009)
Wang, Q., Ni-Meister, W.: Forest canopy height and gaps from multi-angular BRDF assessed with airborne photonic-radar data (short title: vegetation structure from photonic-radar a multi-angular data). Remote Sens. 11, 25–66 (2019). https://doi.org/10.3390/rs11212566
Wong, S.K., Riseborough, E., Duff, G., Chan, K.K.: Radar cross-section measurements of a full-scale aircraft duct/engine structure. IEEE Trans. Antennas Propag. 54, 2436–2441 (2006)
Yang, W., Zhao, J., Du, X., Zeng, Z., Wang, Q.: Laser diode transmitter for laser radar based on FM ranging principles. In: Proceedings of the International Symposium on Photo-electronic Detection and Imaging: Technology and Applications, pp. 662408–662408-9 (2007)
Yue, M., Chen, M., Yangying, Z., Wen, W.: An MIMO radar system based on the sparse-array and its frequency migration calibration method. Sensors 19, 3580 (2019). https://doi.org/10.3390/s19163580
Zhang, H., Wu, Z., Cao, Y., Zhang, G.: Measurement and statistical modeling of BRDF of various samples. Opt. Appl. 40(1), 197–208 (2010)
Acknowledgements
This work is carried out in Aston Institute of Photonic Technologies, School of Engineering and Applied Science, Aston University, Birmingham, UK and is supported by European Union-sponsored H2020-MSCA-IF-EF-ST Project No: 840267.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Sharma, V., Sergeyev, S., Kumar, L. et al. Range-speed mapping and target-classification measurements of automotive targets using photonic-radar. Opt Quant Electron 52, 438 (2020). https://doi.org/10.1007/s11082-020-02557-5
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s11082-020-02557-5