1 Introduction

The polarization multiplex (POL-MUX) optical system will play a major role in the design of future 5G integrated transport systems (Popovskyy and Iskandar 2016) since it is the evolution of the 4G network architecture. Using polarization multiplexing in an optical transmission system is to increase the capacity of the optical fiber network by transmitting information over two orthogonal polarization states (Rochat et al. 2004; Cybulski and Perlicki 2018; Gui et al. 2018). The two polarization modes carried by the fiber present an attractive avenue to double the fiber capacity.

In another case a major benefit is by using polarization multiplexing, that the effective symbol rate can be reduced to the half of that of single polarization transmission. That makes a high-speed transmission system possible by using lower speed electronics (Forbes et al. 2016; Wang et al. 2018). The advantages of this technique are: first, increasing the bit rate without increasing the penalties due to the phenomena of dispersion, second, there is simplicity of the equipment used.

While it is relatively simple to multiplex two optical beams on two orthogonal polarizations (X and Y) in the fiber, on the contrary, it is much more difficult to demultiplex them. The reason is attributed to the fact that while remaining orthogonal, the polarization states change continuously Do et al. (2012) since the single mode fiber cannot maintain these polarization states and polarization maintaining fiber requires only one single mode signal. The components Ex and Ey at each moment form a vector representing the electric field E whereas ω, \( \upsigma \) represents orientation angles:

$$ {\text{E}}\left( {{\text{z}},{\text{t}}} \right) = {\text{E}}_{\text{x}} \left( {{\text{z}},{\text{t}}} \right) + {\text{E}}_{\text{y}} \left( {{\text{z}},{\text{t}}} \right) \, = {\text{ E}}_{{ 0 {\text{x}}}} { \cos }\left( {\upomega{\text{t}} - {\text{kz}} +\upsigma_{\text{x}} } \right){\text{ e}}_{\text{x}} + {\text{ E}}_{{ 0 {\text{y}}}} { \cos }\left( {\upomega{\text{t}} - {\text{ky}} +\upsigma_{\text{y}} } \right){\text{e}}_{\text{y}} $$
(1)

Based on the propagation Eq. (1) we can obtain all possible polarization states of the polarization sphere.

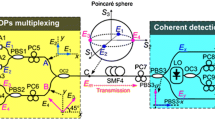
Figure 1 shows an example diagram for POL-MUX architecture, where polarization splitter and combiner (PBS and PBC) are used as multiplexers and demultiplexers. However, the obstacle is the polarization mode dispersion (PMD) (Badraoui and Berceli 2018a) which becomes very problematic in terms of bit rate limiting factor. To optimize the system operation, it is necessary to control the state of polarization (SOP) because it randomly fluctuates with time, making its study particularly complex. To control the state of polarization controllers (PC) should be used to ensure a high polarization extinction ratio (PER) for both orthogonal polarizations (Ito et al. 2019).

Fig. 1
figure 1

Optical link using polarization beam combiner (PBC), a polarization beam splitter (PBS) and polarization controller (PC)

Full size image

When the fiber length increases the differential group delay (DGD) increases as well (Badraoui and Berceli 2018b). That means the fiber length influences the quality factor (Q). Further, there is a decrease in the quality factor with increasing bit rate. Results show that for a bit rate of 40 Gbit/s Q = 6 is obtained, but with increasing bit rate the quality factor degrades. That means the bit rate is a factor that limits the performance of an optical fiber connection. Concluding the PMD coefficient values with ≤ 0.5 ps/km1/2 give a quality factor with (Q) > = 6. The other PMD coefficient values with (PMD > 0.5 ps/km1/2) degrades the quality. In addition, when the coefficient PMD increases the differential group delay also increases.

There is a relation between the PMD and DGD \( \tau \), the group time delay between the two-polarization modes. This relation is introduced in two equations the first is the Stock formalism of the PMD

$$ \vec{\tau } = \tau .\hat{q} $$
(2)

in which \( \hat{q} \) vector represents the slowest principal state of polarization. The next equation represents the DGD by Maxwellian probability equation:

$$ p_{\tau } \left( x \right) = \frac{8}{{\pi^{2} \left\langle \tau \right\rangle }}\left( {\frac{2x}{ \left\langle \tau \right\rangle }} \right)^{2} exp\left( { - \left( {\frac{2x}{ \left\langle \tau \right\rangle }} \right)^{2} \frac{1}{\pi }} \right) x \ge 0 $$
(3)

2 Compensation of polarization mode dispersion (PMD)

The PMD has a direct impact on signal quality (El-Nahal 2018). Therefore, all the parameters relating to the system performance can be used for the estimation of PMD (van den Borne et al. 2009; Al-Bermani et al. 2011). In this article, the following parameters have been used: bite error rate (BER), eye diagram, Q factor and optical signal to noise ratio OSNR. However because polarization multiplexing devices are very sensitive to linear and nonlinear effects, any modification to polarization controller will affect all system parameters, which require measuring all evaluation parameters as a whole not only a subset of them. There are four ways to compensate the PMD. The first one is the electronic compensation using either linear or nonlinear filters or using some complex techniques of signal processing. The advantage of this method is the low cost of electronic technology. The second method is the optical compensation of PMD that is based on polarization controllers. This method is applied in this article. The third one is based on the analysis of electrical spectrum. In that case, the spectrum analysis method is used to evaluate the differential group delay (DGD) by measuring PMD linear and non-linear spectral characteristics induced by signal distortion.

Finally, the last method is the measurement of polarization degree (DOP). The efficiency of this method depends on the ratio between the differential group delay (DGD) and the bit time. If the DGD is higher than the bit time a secondary maximum for the degree of polarization (DOP) is obtained. The advantages of the third and fourth methods are that they are analogue, fast and asynchronous.

3 Pre- and post-compensation

The simulation diagram in Fig. 2 represents a single mode optical link controlled by a polarization controller (PC). In the emission part CW laser, random signal generator, Mach–Zehnder modulator, an optical fiber with length equal to 100 km and PMD = 0.5 ps/km1/2 have been used. The power is 13 dBm. Then in the receiver part, an EDFA has been added to amplify the transmitted signal which compensates the attenuation. Further band pass Bessel optical filter, photodetector and low pass Bessel filter are also applied. The last one has 3 dB cut-off frequency of 0.75 bit rate. Finally, the result has been presented using BER analyses with the eye diagram.

Fig. 2
figure 2

Block diagram of double polarization link (pre- and post-compensation simulation)

Full size image

The first simulation is carried out without polarization controller. That means no compensation has been made to the polarization mode dispersion effects. In the second simulation, the PC was inserted before the optical fiber (OF). Finally, in the third one, the PC was inserted after optical fiber with azimuth equal to 90° and ellipticity 45°. In this simulation, a polarization mode dispersion (PMD) emulator was applied to show its effect on the quality factor with variable fiber length with the first and second order component of PMD. The result shows that the quality factor diminishes by l% for each 100 km of transmission. In the first propose, without using the polarization controller we get very noisy signal transmission when the Q factor is equal to 3 and BER is 1.35 × 10−3. A bad signal transmission has been detected due to PMD effects. The result is shown by the eye diagram in Fig. 5a.

3.1 Pre-compensation

The principle of this method is to adapt the parameters of the controller to transform the state of polarization from \( \hat{s}0 \) state to \( \hat{s} \) state which is parallel with the PSP (principal state of polarization) at the input of the fiber which is \( \hat{q}0 \) as shown in Fig. 3.

Fig. 3
figure 3

Diagram of the PMD pre-compensation method

Full size image

In the first part of the simulation, a polarization controller was inserted before the OF, the azimuth equal to 90° and ellipticity equal to 0°. We obtained just half of the optical signal and vice versa with the ellipticity when it is equal to 45°. The result is shown in the eye diagram when the Q factor equals to 6 after inserting the PC.

In Fig. 5b the eye diagram shows improvement in the quality of the signal. BER is equal to 10−8 because in this case the polarization for the first order was compensated.

3.2 Post-compensation

This technique is based on avoiding the total PMD. This technique requires a polarization controller to adjust the PMD orientation of the compensator (oriented signal \( \vec{\tau }_{2} \)) and the delay of PC element (time delay τ2) to adapt the amplitude of PMD in the optical fiber and M is the rotation matrix (Gordon and Kogelnik 2000). This method is expressed by the following vector Eq. (4):

$$ \hat{s}_{0} //\left( {\vec{\tau }_{0} + M_{t}^{ - 1} \vec{\tau }_{2} } \right) $$
(4)

In this simulation, a PC after OF with polarization delay of 1 s over X axis is used as shown in Fig. 4. The received signals are presented in Fig. 5c by the eye diagram. The enhancement of Q factor which is equal to 7 is remarkable. To obtain good signal transmission with PM compensation, both pre- and post-polarization compensations are used by inserting polarization controllers before and after the fiber.

Fig. 4
figure 4

Diagram of PMD post-compensation method

Full size image
Fig. 5
figure 5

Eye diagram without polarization compensation (a), with pre-compensation (b) and post-compensation (c) of PMD

Full size image

4 Polarization multiplexing (POL-MUX)

The novelty of polarization multiplexing technique (POL-MUX) is to use two orthogonal polarizations to carry different optical signals in the same optical fiber simultaneously. In our investigation at the transmitter side polarization controllers have been used after the continuous wave DFB laser providing 10 dBm output power at an emission wavelength of 1553 nm.

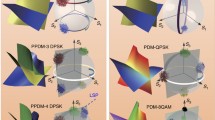
The modulator driving signal is a 1 Gbps 16QAM signal on the carrier frequency of 10 GHz for X-polarization, and 1 Gbps 64QAM signal with a carrier frequency of 10 GHz for Y-polarization. Then the two beams are combined by a polarization beam combiner (PBC). The dispersion is 18 e−6 s/m2 and dispersion slope is 0.08 e−3/s3. In the receiver, each polarization component is separated by a polarization beam splitter (PBS). The method of multiplexing two channels with two orthogonal polarizations has the major benefit of reducing the intermodulation distortion between them. In the POL-MUX approach, the polarization crosstalk can cause a significant impairment (Seimetz 2006; Gnauck et al. 2011). However because polarization multiplexing devices are very sensitive to linear and nonlinear effects, any modification to polarization controller will affect all system parameters, which require measuring all evaluation parameters as a whole not only a subset of them. As the polarization extinction ratio (PER) increases polarization crosstalk reduces resulting in better performance. To completely separate two polarizations, PER of 22 dB has to be applied. With low PER, the signal power coupling from the 64QAM/16QAM to 16QAM/64QAM will be high. The SER (symbol error rate) for 16QAM is better compared to 64QAM at low PER because 64QAM receiver detects more unwanted constellation points than the actual 16QAM due to the strong coupling of the 64QAM signal. Simulation with OptiSystem software simulator has been used for the link presented in Fig. 6. The optical signal is successfully transmitted over 150 km SMF with a power penalty of 8 dB (Chen et al. 2017). For each modulation, the resulted constellation is shown in Fig. 7. The bias voltage for the two MZM modulator is 4 V and the extension ratio is 25 dB. The phases of polarization controllers have been modified before and after the MZ modulator for both modulation types and in receiver part. The resulting constellations are shown in Fig. 8.

Fig. 6
figure 6

Block diagram of POL-MUX technique

Full size image
Fig. 7
figure 7

Constellation and eye diagram of 16QAM and 64 QAM without polarization multiplex

Full size image
Fig. 8
figure 8

I and II: constellation result for polarization multiplexing (16/64 QAM)

Full size image

Based on the sphere Eq. (5) the Stock parameters have been extracted. By using them we can characterise the polarization signal standards. Equation (6) presents the 4th Stock terms of intensity.

$$ \frac{{E_{x}^{2} \left( {z,t} \right)}}{{E_{{0_{x} }}^{2} }} + \frac{{E_{y}^{2} \left( {z,t} \right)}}{{E_{{0_{y} }}^{2} }} - 2\frac{{{\text{Ex}}\left( {{\text{z}},{\text{t}}} \right){\text{Ey}}\left( {{\text{z}},{\text{t}}} \right)}}{{E_{{0_{x} }} + E_{{0_{y} }} }}cos\delta = sin^{2} \delta $$
(5)
$$ \begin{aligned} S_{0} & = E_{{0_{x} }}^{2} + E_{{0_{y} }}^{2} \\ S_{1} & = E_{{0_{x} }}^{2} - E_{{0_{y} }}^{2} \\ S_{2} & = 2E_{{0_{x} }}^{2} E_{{0_{y} }} cos\delta \\ S_{3} & = 2E_{{0_{x} }}^{2} E_{{0_{y} }} sin\delta \\ \end{aligned} $$
(6)

In the case of 16 QAM modulation, a group of 4 bits [s3, s2, s1, s0] are mapped into the signal constellation as shown in Fig. 8 I-A. The signal constellation in Fig. 8 II-A shows the case of a 64-QAM modulation. A group of 6 bits is mapped into a single constellation symbol with real and imaginary parts mI(k) and mQ(k).

Each modulation symbol contains 4 bits, [s3, s2, s1, s0], where s2 and s0 must come from the base layer and s3 and s1 must come from the enhancement layer. For the energy ratio r between the base layer and the enhancement layer Eq. (7):

$$ \begin{aligned} \upalpha & = {\sqrt{ {\text{r}/(2 \, \left( {1 \, + \, r} \right)} )}} \\\upbeta & = \sqrt{{1/(2 \, \left( {1 \, + \, r} \right)})} \\ \end{aligned} $$
(7)

completely define the constellation. Figure 8 I shows the signal constellation of the layered modulator. The complex modulation symbols:

S = (mI, mQ) for each [s3, s2, s1, s0] represents only the real and imaginary parts respectively of the corresponding constellation symbol. For example, for [s3, s2, s1, s0] = 0000,

we get Eq. (8):

$$ \begin{aligned} {\text{m}_\text{I}} & =\upalpha +\upbeta\sqrt{ \cos \left( {{\theta + \frac{\pi} {2}}} \right)} \\ {\text{m}_\text{Q}} & =\upalpha +\upbeta\sqrt {\sin \left( {{\theta + \frac{\pi} {2}}} \right)} \\ \end{aligned} $$
(8)

In Fig. 8 II each modulation symbol contains 6 bits, [s5, s4, s3, s2, s1, s0], where s4, s3, s1 and s0 shall be from the base layer and s5 and s2 shall be from the enhancement layer.

For the energy ratio r between the base layer and the enhancement layer, we get Eq. (9):

$$\begin{aligned} \upalpha & = \sqrt{{{\text{r}}/(10\left( {1 + {\text{r}}} \right)})} \\\upbeta & = \sqrt{{1/(2\left( {1 + {\text{r}}} \right)})} \\ \end{aligned} $$
(9)

The complex modulation symbol S = (mI, mQ) for each [s3, s2, s1, s0] is the real and imaginary parts of the corresponding constellation symbol, respectively. For example: for [s4, s3, s2, s1, s0] = 000000, see Eq. (10):

$$ \begin{aligned} {\text{m}_\text{I}} & = 3\upalpha +\upbeta\sqrt {\cos \left( {{\theta + \frac{\pi} {2}}} \right)} \\ {\text{m}_\text{Q}} & = 3\upalpha +\upbeta\sqrt{ \sin \left( {{\theta + \frac {\pi} {2}}} \right)} \\ \end{aligned} $$
(10)

In many cases, we have a phase shift as an error in the signal transmission. In this investigation, the effect of some special phase shifts is presented by the constellation diagrams in Fig. 8. That shows the constellation of X polarization carrying 16QAM signal and Y polarization carrying 64QAM with a polarization phase shift of 45° in case of Fig. 8 II-B and phase shift of 90° in case of Fig. 8 II-C. It enhanced the transmission of the RF signal. We can see that the 64QAM constellation channel is noisier than the 16QAM channel. That is logical because the denser the channel the more noise we have due to linear and nonlinear effects like chromatic dispersion, polarization mode dispersion, crosstalk, crossphase modulation (XPM) (Badraoui and Berceli 2017), self-phase modulation (SPM), four-wave mixing (FWM), etc. Clearly if the polarization phase is equal to 45° that is better because both signals are more separated from each other. There is no collision between signal pulses. Each constellation is in its quadrature which makes the demodulation much easier. However, in this paper we use coherent detection because it has a better BER for the same energy per bit to noise power spectral density ratio (Eb/N0). The relation between BER and Q factor is shown by Eq. (11).

$$ {\text{BER}} = \frac{1}{2} {\text{erfc}}\left( {\frac{\text{Q}}{\sqrt 2 }} \right) $$
(11)

The Q value represents the system tolerance in dB before the B point (Fig. 9). For a smaller BER, a larger corresponding Q value is noticed, and better transmission is shown. In addition, the more the length of the connection increases the more the factor of quality decreases and BER decreases. Figure 10 shows the variation of BER and Q factor depending on the length of fiber. For a bit rate of 40Gbit/s, the lengths of connections cannot exceed 100 km so that the system has a good quality. It means that the length of fiber influences the PMD. When the length of transmission fiber increases the DGD also increases.

Fig. 9
figure 9

The relation between the BER and Q factor

Full size image
Fig. 10
figure 10

Variation of BER and Q factor depending on fiber length

Full size image

5 Conclusion

Using the polarization control to compensate the PMD by pre- and post-compensation techniques provides better transmission quality. Furthermore, using it in POL-MUX technique significant improvement has been achieved. In addition, integrating the beam splitters and beam combiners improve the POL-MUX structure, which improves the BER to 10 e−10 for less than 100 km. The impact of data sequence on the transmission performance has been investigated in terms of Q factor and BER considering different modulation formats like 16QAM and 64QAM and polarization phase shift of polarization controller.

In the example of modulation in 16QAM our results shows that its sequences give lower variability. A difference in variability between these two types of sequence modulation has been observed. By this study of the variability of performance as a function of data sequence type, the choice of polarization phase of polarization controller is extremely important to obtain a good transmission quality.