Polarisation non-reciprocity cancelling in Sagnac fibre ring interferometer: an attempt of realistic study

Abstract

Polarisation non-reciprocity (PNR) of Sagnac fibre ring interferometer (FRI) is one the fundamental limits of its long term bias stability. PNR value, being huge initially, then was reduced strongly, but after that PNR problem was left far from PNR cancelling. The latter may be defined as PNR reducing up to 10⁻¹⁰ deg/h when it does not prevent detecting the general relativistic Lense–Thirring effect. Clearly, such PNR cancelling may be treated only theoretically at this point. In this case, one has to model all practical defects of FRI. Present paper describes such kind of study for FRI of commercial fibre optic gyro implementing medium quality components. It is shown that for PNR cancelling, several meters fibre polariser is enough, despite of the stringent limitations of its standard polarisation extinction ratio. Also, a complete FRI configuration is treated for the first time in available literature, including an imperfect fibre coupler. This yields one more PNR component which is non-zero even for completely unpolarised light and which can be effectively suppressed by the fibre polariser too.

Appendices

Appendix 1: Polariser properties out of FRI and within it and its PER limitations

In this Appendix, a difference is illustrated between the “intensity” and “interferometric” PER concepts (Sect. 3.2) employing two polariser models with Jones matrices $P1$ and $P2$ having the following elements: (1) $P1_{11} = 1$, $P1_{12} = P1_{21} = 0$, $P1_{22} = \varepsilon$ (Kintner 1981); (2) $P2_{11} = 1$, $P2_{12} = ik_{1}$, $P2_{21} = ik_{2}$, $P2_{22} = 0$. For $P1$, PMC is absent, dichroism is finite ($\varepsilon \ne 0$); for $P2$, situation is reverse (close to long enough PZ-lightguide). For “intensity” PER measuring, when light passes the polarisers $P1$ and $P2$ in one direction, one has $PER1 = \varepsilon^{2}$ and $PER2 = \left| {k_{1} } \right|^{2}$, respectively. For opposite direction, $PER1 = \varepsilon^{2}$ and $PER2 = \left| {k_{2} } \right|^{2}$. Assuming that PER does not depend on direction, one yields $\left| {k_{1} } \right|^{2} = \left| {k_{2} } \right|^{2} = PER2$. Thus, when $\varepsilon = \left| {k_{1,2} } \right|$, one has $PER1 = PER2$, so these two polarisers look like identical.

However, if they are built into pair of FRI, identical in other respects, this is not the case. FRI Jones matrices are $M^{cw} = P^{T} \times U \times P$, $M^{ccw} = \left( {M^{cw} } \right)^{T}$. For spurious x-waves, one may write Eq. (7) as $\Delta E_{x} = \left( {{ \det }P1} \right)\Delta Ue_{y} = \varepsilon \Delta Ue_{y}$ and $\Delta E_{x} = \left( {{ \det }P2} \right)\Delta Ue_{y} = - k_{1} k_{2} \Delta Ue_{y}$ ($\Delta U \equiv U_{12} - U_{21}$). Thus, for $P1$, one has $PNR1\sim PER1^{1/2}$ (APNR), while for $P2$, one has $PNR2\sim PER2^{1}$ (IPNR); in other words, for identical “intensity” PER values, one has two radically different “interferometric” PER values.

Further, one may consider two polarisers, $Pol_{1}$ and $Pol_{2}$, at FRI input. They always have the axes misalignment (it should be small for low optical loss), so their Jones matrix is $Pol_{2} \times R \times Pol_{1}$ ($R$ is rotation matrix). Due to this, total “intensity” PER of these polarisers is not the sum of their own “intensity” PERs. At the same time, for these two polarisers within the FRI, one has $M^{cw} = Pol_{1}^{T} \times R^{T} \times Pol_{2}^{T} \times U \times Pol_{2} \times R \times Pol_{1}$. The difference of cw- and ccw-waves in this case will be described as

$$\begin{aligned} & \vec{E}^{cw} - \vec{E}^{ccw} = \left[ {Pol_{1}^{T} \times R^{T} \times Pol_{2}^{T} \times \left( {U - U^{T} } \right) \times Pol_{2} \times R \times Pol_{1} } \right] \times \vec{e} \\ & \sim det\left( {Pol_{2} \times R \times Pol_{1} } \right) = det\left( {Pol_{2} } \right)det\left( R \right)det\left( {Pol_{1} } \right) = det\left( {Pol_{2} } \right)det\left( {Pol_{1} } \right), \\ \end{aligned}$$

(9)

as if polarisers were aligned perfectly. This confirms the numerically established cooperation of PZ-lightguide and IOC guides in Sect. 6.2. In this case, waves $\vec{E}^{cw}$ and $\vec{E}^{ccw}$ by themselves do depend on axes misalignment angle, but depend identically. The latter is the consequence of the fact that light passes the polarisers twice in both directions within FRI. The same is right for any polarisers sequence.

Rest of this Appendix contains PER limitations description of PZ-lightguide.

One PER limit of PZ-lightguide is due to its PMC. In this case, primary x-wave generates the secondary y-wave which is suppressed by dichroism along the lightguide, except its final section of the length $\sim 1/\xi_{in}$. This y-wave intensity does not depend on $L_{in}$ (the same “intensity” PER for all $L_{in} > 1/\xi_{in}$). The difference between the “intensity” and “interferometric” PERs can be illustrated in this case analytically for lowest order PMC within PZ-lightguide. Jones matrices of quasi-minimal FRI have the form $M^{cw} = PZ^{T} \times U \times PZ$, $M^{ccw} = \left( {M^{cw} } \right)^{T}$, where $PZ$ is the Jones matrix of the input PZ-lightguide. For lowest-order PMC in PZ-lightguide, one may write: $PZ_{11} = a$, $PZ_{12} = ik_{1}$, $PZ_{21} = ik_{2}$, $PZ_{22} = Ga^{*}$, which is a generalised Jones matrix of PM-lightguide described by Kozel et al. (1986). For $\Delta E_{x}$ from Eq. (7), the following may be written (in the lowest order of $G$ and $k_{1,2}$): $\Delta E_{x} = det\left( {PZ} \right) \times \Delta Ue_{y} \approx G\Delta Ue_{y}$, containing no lowest order $k_{1,2}$ values (they do contribute to $E_{x}^{cw}$ and $E_{x}^{ccw}$, but identically for both of them); the same is right for $\Delta E_{y}$ from Eq. (7). Thus, PNR is proportional to $G$-value, so the “interferometric” PER of PZ-lightguide may be described by Eq. (5), at least for lowest order PMC. Numerical model reveals this for arbitrary order PMC (Sects. 6.1, 7.1).

Another PER limit is due to PZ-lightguide uniform twist with its elliptical polarisation eigenmodes, each of which has x- and y-components, major and minor (Sakai et al. 1982; Malykin et al. 2000). The latter can limit the “interferometric” PER, but only as $PER2$ which is twice the “intensity” PER. Moreover, it should be simply added to “interferometric” PER of IOC guides, according to Eq. (9). Therefore, this worst case scenario still allows PNR cancelling (Sects. 6.2, 7.2).

Finally, PER limitation is known due to the four-spot modal structure with orthogonal polarisation (Varnham et al. 1984; Vassallo 1987). This might explain the same “intensity” $PER\sim 43$ dB of bend-type fibre polariser for its all lengths exceeding 2 m described by Okamoto et al. (1984). However, within the FRI, this may affect only as $PER2 = 2 \times 43 = 86$ dB. Moreover, this four-spot structure excites only high-order y-modes in other components which do not interact with useful fundamental x-modes at PMC centres due to the fields zero overlap integral yielding, thus, no limitation of “interferometric” PER.

Bergh et al. (1981) reported about experimentally measured 60-dB “intensity” PER and at least 90-dB PER within the FRI (“interferometric” PER according to the above); Andreev et al. (1993), moreover, used FRI as a test bench for true PER measuring with the same results. This confirms the above conclusions, at least partially, but still this seems not to be a mainstream concept in available literature.

Appendix 2: General relationships for PNR

This Appendix starts from Eq. (6). Employing Jones matrix formalism, one may write $\vec{E}^{cw} \left( {\lambda ,t} \right) = M^{cw} \left( {\lambda ,t} \right)\vec{e}\left( {\lambda ,t} \right)$, $\vec{E}^{ccw} \left( {\lambda ,t} \right) = M^{ccw} \left( {\lambda ,t} \right)\vec{e}\left( {\lambda ,t} \right)$, where $\vec{e}$ is the electric field of an input light, $M^{cw}$ and $M^{ccw}$ are FRI Jones matrices for cw- and ccw-waves. This allows the following representation for PNR:

$$PNR_{0 - 3} \left( t \right) \approx \frac{{\int d\lambda \lambda^{ - 2} X_{0 - 3} \left( {\lambda ,t} \right){\text{Im}}A_{0 - 3} \left( {\lambda ,t} \right)}}{{SF\mathop \sum \nolimits_{k = 0}^{3} \int d\lambda \lambda^{ - 2} X_{k} \left( {\lambda ,t} \right){\text{Re}}A_{k} \left( {\lambda ,t} \right)}},$$

(10)

where $A_{0 - 3}$ are described by Eq. (8), and $X_{0} \equiv e_{x}^{*} e_{x} + e_{y}^{*} e_{y}$, $X_{1} \equiv e_{x}^{*} e_{x} - e_{y}^{*} e_{y}$, $X_{2} \equiv 2{\text{Re}}\left( {e_{y}^{*} e_{x} } \right)$, $X_{2} \equiv 2{\text{Im}}\left( {e_{y}^{*} e_{x} } \right)$. Values $X_{0 - 3} \left( {\lambda ,t} \right)$ are rapidly fluctuating instant Stokes parameters. Being averaged over infinite time, they become usual spectral Stokes parameters described by Perina (1972). However, PNR long-term drift is of primary interest which is due to the slow fluctuations of FRI parameters ($M_{i,j} \left( {\lambda ,t} \right)$). Smoothing the Eq. (10) with averaging time $T$ which is much less than the time scale of $A_{0 - 3} \left( {\lambda ,t} \right)$ slow drift (i.e. leaving them unaffected), one yields the values $\langle {X_{0 - 3}} \left( {\lambda ,t} \right)\rangle _{T}$ which can be written as $\langle X_{0 - 3} \left( {\lambda ,t} \right)\rangle_{T} \approx S\left( \lambda \right)s_{0 - 3}$ (“Appendix 3”), where $S\left( \lambda \right)$ is the spectral intensity of light, $s_{0 - 3}$ are the normalised conventional Stokes parameters (Perina 1972). This describes the input wideband light with the same polarisation state for all $\lambda$ (in general, it is elliptical) (Alekseev and Bazarov 1992). For instance, $\langle X_{0} \left( {\lambda ,t} \right)\rangle_{T}$ is the total spectral intensity of both polarisations in the form of a stable pattern at spectrum analyser display. As a result, Eq. (10) could be rewritten as Eq. (8) in Sect. 4.

Appendix 3: Derivation of the properties of thermal-type partially polarised light

The form of typical instant spectral intensity $I\left( {\lambda ,t} \right) = \left| {e\left( {\lambda ,t} \right)} \right|^{2}$ is shown in Fig. 5 which can correspond to x- or y-wave; its spectral components rapidly fluctuate independently of each other. Graph for $S\left( \lambda \right)$ shows the spectral intensity averaged over infinite time; however, this may also be the finite time $T$ which only should be much less than the time scale of FRI components slow drift.

Fig. 5

Instant spectral intensity ($I\left( {\lambda ,t} \right)$) and averaged spectral intensity ($S\left( \lambda \right)$) of simulated Erbium fibre light source

For PNR problem, one also has to treat the product $e_{x} \left( {\lambda ,t} \right)e_{y}^{*} \left( {\lambda ,t} \right)$ describing the instant interferometric patterns at photodetector generated by x- and y-waves after their interaction due to PMC. These patterns are chaotic in time, similar to $I\left( {\lambda ,t} \right)$ in Fig. 5; the difference is that corresponding averaged graph can be of another form comparing to $S\left( \lambda \right)$. E.g. for unpolarised light, it is zero.

Partially polarised light may be represented as a superposition of extreme cases of unpolarised and polarised light (Perina 1972). For the first case, one has the following electric fields:

$$e_{x,y}^{unpol} \left( {\lambda ,t} \right) = \left[ {I_{x,y}^{unpol} \left( {\lambda ,t} \right)} \right]^{1/2} \times { \exp }\left[ {i\varphi_{x,y}^{unpol} \left( {\lambda ,t} \right)} \right].$$

(11)

Here $I_{x,y}^{unpol} \left( {\lambda ,t} \right)$ and $\varphi_{x,y}^{unpol} \left( {\lambda ,t} \right)$ are four different random processes at each $\lambda$. It is reasonable to assume that they do not correlate with each other and, of course, with the processes at different $\lambda$ values. For spectral intensities in this case, one may write

$$\left\langle {e_{{x,y}}^{{unpol}} \left( {\lambda ,t} \right)e_{{x,y}}^{{unpol*}} \left( {\lambda ,t} \right)} \right\rangle \approx \left\langle {\left| {I_{{x,y}}^{{unpol}} \left( {\lambda ,t} \right)} \right|^{2} } \right\rangle = \left| {A_{{x,y}} } \right|^{2} S_{{x,y}}^{{unpol}} \left( \lambda \right),$$

(12)

where the angle brackets denote the averaging over time $T$, while $A_{x,y}$ are the x- and y-waves amplitudes, $S_{x,y}^{unpol} \left( \lambda \right)$ are their usual (averaged) spectral intensities. For unpolarised light, intensities of x- and y-waves are identical: $A_{x}^{*} A_{x} \int d\lambda S_{x}^{unpol} \left( \lambda \right) = A_{y}^{*} A_{y} \int d\lambda S_{y}^{unpol} \left( \lambda \right)$. When $S_{x}^{unpol} \left( \lambda \right) = S_{y}^{unpol} \left( \lambda \right)$, one has $\left| {A_{x} } \right| = \left| {A_{y} } \right|$; this corresponds to a common picture described above in the text. However, if $S_{x}^{unpol} \left( \lambda \right) \ne S_{y}^{unpol} \left( \lambda \right)$ (gain dichroism) this is not the case, so $PNR_{1}$ may grow. Spectra $S_{x}^{unpol} \left( \lambda \right)$ and $S_{y}^{unpol} \left( \lambda \right)$ could be equalised (Digonnet and Falquier 2002). But anyway, this does not break the Eq. (5).

Further, product $e_{x,y}^{unpol} \left( {\lambda ,t} \right)e_{x,y}^{unpol *} \left( {\lambda ,t} \right)$ can be written as

$$\begin{aligned} & \left\langle {e_{x}^{{unpol}} \left( {\lambda ,t} \right)e_{y}^{{unpol*}} \left( {\lambda ,t} \right)} \right\rangle \approx \left\langle {\left[ {I_{x}^{{unpol}} \left( {\lambda ,t} \right)I_{y}^{{unpol*}} \left( {\lambda ,t} \right)} \right]^{{1/2}} } \right\rangle \left\langle {\exp \left[ {i\varphi _{x}^{{unpol}} \left( {\lambda ,t} \right)} \right]} \right\rangle \otimes \\ & \quad \left\langle {\exp \left[ { - i\varphi _{y}^{{unpol}} \left( {\lambda ,t} \right)} \right]} \right\rangle \approx \left\{ {for\;RMS\left[ {\varphi _{{x,y}}^{{unpol}} \left( {\lambda ,t} \right)} \right] > 2\pi } \right\} \approx 0, \\ \end{aligned}$$

(13)

since $\langle{ \exp }\left[ { \pm i\varphi_{x,y}^{unpol} \left( {\lambda ,t} \right)} \right]\rangle \approx { \exp }\left\{ { - RMS^{2} \left[ {\varphi_{x,y}^{unpol} \left( {\lambda ,t} \right)} \right]/2} \right\}$; this is because all $\varphi_{x,y}^{unpol}$ are formed by a giant number of mutually independent atoms, leading to Gaussian distributions (central limit theorem).

As for polarised light, values $I_{x,y} \left( {\lambda ,t} \right)$ and $e_{x} \left( {\lambda ,t} \right)e_{y}^{*} \left( {\lambda ,t} \right)$ do not depend on time $t$, so the same polarisation occurs for all $\lambda$ (Alekseev and Bazarov 1992). For x- and y-waves fields, one has

$$e_{x,y}^{pol} \left( {\lambda ,t} \right) = e_{x,y}^{pol} \left( \lambda \right) = \left[ {S_{x,y}^{pol} \left( \lambda \right)} \right]^{1/2} { \exp }\left[ {i\varphi_{x,y}^{pol} \left( \lambda \right)} \right],$$

(14)

so $\langle I_{x,y}^{pol} \left( {\lambda ,t} \right)\rangle = I_{x,y}^{pol} \left( \lambda \right) = S_{x,y}^{pol} \left( \lambda \right)$, $\langle e_{x}^{pol} \left( {\lambda ,t} \right)e_{y}^{pol*} \left( {\lambda ,t} \right)\rangle = \left[ {S_{x}^{pol} \left( \lambda \right)S_{y}^{pol} \left( \lambda \right)} \right]^{1/2} \times { \exp }\left[ {i\Delta \varphi_{x,y}^{pol} \left( \lambda \right)} \right]$. For polarised light, x- and y-waves fields are completely correlated, so one has $S_{x}^{pol} \left( \lambda \right) = S_{y}^{pol} \left( \lambda \right) = S^{pol} \left( \lambda \right)$, $\Delta \varphi_{x,y}^{pol} \left( \lambda \right) = \Delta \varphi_{x,y}^{pol} = const$. This could be proved implementing the fields usual spectral representation $E_{x,y}^{pol} \left( t \right) = \int d\omega e_{x,y}^{pol} \left( \omega \right){ \exp }\left( {i\omega t} \right)$, where $E_{x,y}^{pol} \left( t \right)$ are electric fields in time domain; $e_{x,y}^{pol} \left( \omega \right)$ correspond to $e_{x,y}^{pol} \left( \lambda \right)$ from Eq. (14). Standard correlator for the fields has the following form:

$$\begin{aligned} & \left\langle {E_{x}^{{pol*}} \left( t \right)E_{y}^{{pol}} \left( t \right)} \right\rangle _{{T = \infty }} = \int d \omega d\omega ^{/} e_{x}^{{pol*}} \left( \omega \right)e_{y}^{{pol}} \left( {\omega ^{/} } \right)\left\langle {\exp \left[ {i\left( {\omega - \omega ^{/} } \right)t} \right]} \right\rangle _{{T = \infty }} \\ & \quad = \left\{ {\left\langle {\exp \left[ {i\left( {\omega - \omega ^{/} } \right)t} \right]} \right\rangle _{{T = \infty }} = 2\pi \delta \left( {\omega - \omega ^{/} } \right)} \right\} = 2\pi \int d \omega \left[ {S_{x}^{{pol}} \left( \omega \right)S_{y}^{{pol}} \left( \omega \right)} \right]^{{1/2}} \exp \left[ {i\varphi _{{x,y}}^{{pol}} \left( \omega \right)} \right]. \end{aligned}$$

(15)

Complete correlation of two complex fields means that

$$K = \left\langle {E_{x}^{{pol*}} \left( t \right)E_{y}^{{pol}} \left( t \right)} \right\rangle _{{T = \infty }} /\left[ {\left\langle {\left| {E_{x}^{{pol}} \left( t \right)} \right|} \right\rangle _{{T = \infty }}^{2} \left\langle {\left| {E_{y}^{{pol}} \left( t \right)} \right|} \right\rangle _{{T = \infty }}^{2} } \right]^{{1/2}} = \exp \left( {i\alpha } \right),$$

(16)

where $\alpha$ is the real number, so $\left| K \right| = 1$. This is fulfilled for Eq. (16) if $S_{x}^{pol} \left( \omega \right) = S_{y}^{pol} \left( \omega \right)$ and if $\alpha = \varphi_{x,y}^{pol} \left( \omega \right) = const$. It is also assumed that there is no difference between the above introduced finite time $T$ and $T = \infty$ from the point of view of emission processes in the light source.

Thus, for partially polarised light one may use the superposition of Eqs. (11) and (14):

$$e_{x,y} \left( {\lambda ,t} \right) = e_{x,y}^{unpol} \left( {\lambda ,t} \right) + \rho_{x,y} e_{x,y}^{pol} \left( \lambda \right),$$

(17)

where $\rho_{x,y}$ are real numbers, describing the partial intensity of polarised light. As a result,

$$\begin{aligned} & \left\langle {e_{{x,y}}^{*} \left( {\lambda ,t} \right)e_{{x,y}} \left( {\lambda ,t} \right)} \right\rangle \approx S_{{x,y}}^{{unpol}} \left( \lambda \right) + \rho _{{x,y}}^{2} S^{{pol}} \left( \lambda \right), \\ & \left\langle {e_{x}^{*} \left( {\lambda ,t} \right)e_{y} \left( {\lambda ,t} \right)} \right\rangle \approx \rho _{x} \rho _{y} S^{{pol}} \left( \lambda \right)\exp \left( {i\Delta \varphi _{{x,y}}^{{pol}} } \right). \\ \end{aligned}$$

(18)

Assuming $S_{x,y}^{unpol} \left( \lambda \right) = S^{pol} \left( \lambda \right) = S\left( \lambda \right)$, one may write the following

$$\left\langle {X_{{0 - 3}} \left( {\lambda ,t} \right)} \right\rangle \approx S\left( \lambda \right)s_{{0 - 3}} ,$$

(19)

transforming Eq. (10) into Eq. (8). Here the normalised Stokes parameters are introduced: $s_{0} = 1$, $s_{1} = Z\left( {\rho_{x}^{2} - \rho_{y}^{2} } \right)$, $s_{2} = 2Z\rho_{x} \rho_{y} { \cos }\left( {\Delta \varphi_{x,y}^{pol} } \right)$, $s_{3} = 2Z\rho_{x} \rho_{y} { \sin }\left( {\Delta \varphi_{x,y}^{pol} } \right)$, $Z \equiv 1/\left( {2 + \rho_{x}^{2} + \rho_{y}^{2} } \right)$. With Eqs. (11)–(14), one may yield the standard light coherence matrix (Perina 1972). For light with small DOP, one has $\rho_{x,y}^{2} \ll 1$, so $s_{1 - 3} \ll 1$. If $S_{x} \left( \lambda \right) \ne S_{y} \left( \lambda \right)$ (this case is not simulated in above text), one yields $\langle{\text{X}}_{0} \left( {\lambda ,t} \right)\rangle \approx S_{x}^{unpol} \left( \lambda \right) + S_{y}^{unpol} \left( \lambda \right) + \left( {\rho_{x}^{2} + \rho_{y}^{2} } \right)S^{pol} \left( \lambda \right)$, $\langle{\text{X}}_{1} \left( {\lambda ,t} \right)\rangle \approx S_{x}^{unpol} \left( \lambda \right) - S_{y}^{unpol} \left( \lambda \right) + \left( {\rho_{x}^{2} - \rho_{y}^{2} } \right)$ $S^{pol} \left( \lambda \right)$, $\langle{\text{X}}_{2} \left( {\lambda ,t} \right)\rangle \equiv 2\rho_{x} \rho_{y} S^{pol} \left( \lambda \right){ \sin }\left( {\Delta \varphi_{x,y}^{pol} } \right)$, $\langle{\text{X}}_{3} \left( {\lambda ,t} \right)\rangle \equiv$ $2\rho_{x} \rho_{y} S^{pol} \left( \lambda \right){ \cos }\left( {\Delta \varphi_{x,y}^{pol} } \right)$. For $\langle{\text{X}}_{1} \left( {\lambda ,t} \right)\rangle$, additional term $S_{x}^{unpol} \left( \lambda \right) - S_{y}^{unpol} \left( \lambda \right)$ occurs, which may contribute to $PNR_{1}$. However, this does not break the Eq. (5) and does not prevent the above described PNR cancelling.

Appendix 4: Fibre coupler and complete FRI Jones matrices

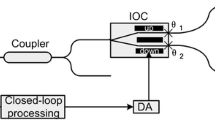
For simulation of the fibre coupler influence, the following steps are considered for cw- and ccw-waves propagating from the light source to photodetector (Fig. 6): (1) fibre lead $F_{11}^{coup}$ of the coupler; (2) coupler transmitting part; (3) fibre lead $F_{12}^{coup}$; (4) quasi-minimal FRI; (5) propagating backwards through the fibre lead $F_{12}^{coup}$; (6) coupling region of the coupler; (7) fibre lead $F_{21}^{coup}$. Therefore, one may write:

$$M^{cw} \left( {\lambda ,t} \right) = B\left( {\lambda ,t} \right)M\left( {\lambda ,t} \right)A\left( {\lambda ,t} \right),\quad M^{ccw} \left( {\lambda ,t} \right) = B\left( {\lambda ,t} \right)M^{T} \left( {\lambda ,t} \right)A\left( {\lambda ,t} \right).$$

(20)

where $M = U \times R_{12}^{in} \times F_{12}^{coup}$, $U$ is the quasi-minimal FRI Jones matrix, $R_{12}^{in}$ is the rotation matrix for axes misalignment of the fibre lead “12” with respect to those of the neighbouring input PZ-lightguide. For SM-coupler, this angle is set to be 45°, being out of control during FRI assembling; for PM-coupler, it is set to be 3°. The rest matrices from Eq. (20) are the following: $A \equiv Ctr \times F_{11}^{coup}$, $B \equiv F_{21}^{coup,T} \times Coup^{T}$, where $Ctr$ and $Coup$ are transmitting and coupling Jones matrices, $F_{i,j}^{coup}$ is the Jones matrix of fibre lead of the port $\left( {i,j} \right)$ (Fig. 6). These fibre leads have random twists and linear birefringence (10⁻⁶ for SM-coupler and 3 × 10⁻⁴ for PM-coupler). Clearly, $B \ne A^{T}$, because $Ctr \ne Coup$ and $F_{21}^{coup} \ne F_{11}^{coup}$, so for complete FRI, one has $M^{cw} \ne M^{ccw,T}$, unlike the minimal and quasi-minimal FRI.

Fig. 6

Coupler fibre leads illustration

Matrices $Ctr$ and $Coup$ cannot be of conventional form $C_{11} = C_{22} = 1/\sqrt 2$, $C_{12} = C_{21} = - i/\sqrt 2$, because the latter describes only the standard directional coupler 50 × 50 without polarisation effects consideration; instead, it takes into account only the light distributing between the output ports. At the same time, matrix $Ctr$ describes the transition “11” $\to$ “12” for halves of intensities of both x- and y-waves (without regard to port “22”), while $Coup$ does the same for transition “12”$\to$“21” (without regard to port “11”). These Jones matrices are equivalent to that for fibre sections with localised PMC, which corresponds to PMC within the coupler, along with its intrinsic 3-dB losses. Therefore, for fibre coupler, one may implement the elements from Sect. 5.3.

Direct multiplying in Eq. (20) leads to the following:

$$M_{1,1 - 2}^{ccw} = M_{1,1 - 2}^{cw} + a_{1 - 2} \Delta M,\quad M_{21}^{ccw} = M_{21}^{cw} + a_{3} \Delta M,\quad M_{22}^{ccw} = M_{22}^{cw} + a_{4} \Delta M,$$

(21)

where $a_{1} \equiv A_{21} B_{11} - A_{11} B_{12}$, $a_{2} \equiv A_{21} B_{21} - A_{11} B_{22}$, $a_{3} \equiv A_{22} B_{11} - A_{12} B_{12}$, $a_{4} \equiv A_{22} B_{21} - A_{12} B_{22}$. In turn, $\Delta M = det\left( {F_{12}^{coup} } \right)det\left( {R_{12}^{in} } \right)\Delta U = det\left( {F_{12}^{coup} } \right)\Delta U$, so coupler and its fibre leads do not contribute to PNR if $\Delta U = 0$, because this means identical cw- and ccw-waves at all stages. Clearly, $PNR\sim \Delta U$ in this case, so if it is cancelled for quasi-minimal FRI, it is cancelled for complete FRI too.

Appendix 5: Ergodicity hypothesis for PNR of Sagnac FRI

One ergodicity criterion requires a large number of PMC centres within the coherence zones; it is fulfilled in above described simulations because $l_{c} \ll L_{dec}$ (Sect. 5.5). Below, another ergodicity condition is discussed in the case of $PNR_{2}$ of minimal FRI taken for instance.

For large temperature fluctuations within {− 60; + 70} °C, PNR drift is shown in Fig. 7 by the graph 1. These thermal fluctuations correspond to those of $PNR_{2} \left( t \right)$ from Eqs. (6) and (8). Their zero mean value (solid horizontal line) and RMS deviation agree well with Eq. (1) derived for FRI ensemble (ergodicity).

Fig. 7

PNR under the large temperature fluctuations within {− 60; + 70} °C (graph 1) and under the small temperature fluctuation within {+ 25.0; + 25.2} °C (graph 2). Dashed horizontal line is non-zero PNR mean value for graph 2. Thin dotted horizontal lines are alternative mean values of PNR at small temperature fluctuations in other FRI realisations, or PNR mean values for the same FRI at different constant temperatures within the interval {− 60; + 70} °C

For small temperature fluctuations within {+ 25.0; + 25.2} °C, PNR drift is shown by the graph 2. Its RMS deviation is much smaller than for the graph 1 revealing the significant discrepancy with the ensemble approach. One more discrepancy results from the non-zero mean value of graph 2 (light dashed horizontal line upon graph 2). However, this mean value is unpredictable. Moreover, it can occur within the interval covered by the graph 1 (horizontal dotted lines at Fig. 7, which may be treated as different constant PNR components of different FRI realisations). Therefore, this mean value should be estimated within the ensemble approach. It is common to speak that it could be subtracted from FOG output as a part of its experimentally measured constant bias. However, for this, a much more accurate device is necessary, which is not the case when the most accurate device is only intended to be manufactured.

It should be noted that thin horizontal dotted lines at Fig. 7 also can be treated as PNR constant component of some single FRI at different constant temperatures within {− 60; + 70} °C, so graph 1 is nothing else than transitions between these lines due to the temperature variations.

Thus, ensemble approach is accepted, which at least does not underestimate PNR value.

Small RMS deviation of the graph 2 comparing to that of the graph 1 can be explained as follows. Only short fibre sections of length order of $L_{dec}$ contribute to $PNR_{2}$ of minimal FRI (Sect. 3.1). Fluctuations of the phase difference $\delta \varphi_{x,y} \left( t \right)$ of x- and y-waves within these fibre sections occur due to the temperature variations of corresponding refractive indices. One may write in this case $\delta \varphi_{x,y} \left( t \right) \equiv \delta \varphi_{x} \left( t \right) - \delta \varphi_{y} \left( t \right) \approx L_{dec} \delta \left[ {\beta_{x} \left( t \right) - \beta_{y} \left( t \right)} \right]$, where $\beta_{x} - \beta_{y}$ is the fibre modal birefringence. For Panda-type fibres, one has $\beta_{x} - \beta_{y} \approx k_{0} B$ (Kurbatov and Kurbatov 2016), where $B \equiv n_{x} - n_{y}$ is the material birefringence at the centre of the fibre cross section, $k_{0}$ is the light mean wavenumber. Thus,

$$\delta \varphi_{x,y} \left( t \right) \approx k_{0} L_{dec} \delta B\left( t \right) \approx k_{0} L_{dec} \left( {\partial_{T} B} \right)\delta T\left( t \right) \sim 2\left( {\partial_{T} B/B_{room} } \right)\left( {\lambda_{0} /\Delta \lambda } \right)\delta T\left( t \right),$$

where $B_{room}$ is the birefringence at mean room temperature. Ergodicity occurs if $\delta \varphi_{x,y} \left( t \right) > 2\pi$ rad, or if $\delta T\left( t \right) > \left( {B_{room} /\partial_{T} B} \right)\left( {\Delta \lambda /\lambda_{0} } \right)$. For Panda-type fibres, one has $\partial_{T} B \approx B_{room} /\left( {T_{B} - T_{room} } \right)$ (Chu and Sammut 1984); here $T_{B} \sim 800$ °C is the melting temperature of boron doped rods of Panda construction. Thus, for wideband light, $\delta \varphi_{x,y} \left( t \right)$ is large only for large $\delta T\left( t \right)$ (ergodicity) agreeing with Fig. 7.

Further, axes misalignments at splices/gluings are set the same for all FRI realisations, because they are not supposed to be changed in the certain FRI even under large temperature fluctuations.

In the same sense, IOC guide model could be simplified when assuming that its parameters are constant under temperature fluctuations, so there is no need to generate the random numbers $\alpha_{n}$ (Sect. 5.4). Instead, $\alpha_{n}$ may be set constant, equal to their RMS deviation, or, moreover, IOC guide may be treated as a uniform one with complex elements of its Jones matrix, similar to the fibre coupler in Sect. 5.3. However, simulation results will be the same, because PMC within the IOC does not contribute to PNR significantly in both cases; this is probably because IOC guides are too short for this.