1 Introduction

Chip Multiprocessors (CMPs), that exploit the potentialities of parallel computing, are the state of the art solution to face the constant need of increasing the computing system efficiency. A CMP consists of several smaller processing cores designed and replicated several times. They achieve performance gain through parallel code execution using multiple threads across the cores. As the number of cores in CMPs continues to scale, the efficient interconnection of these cores is becoming a major challenge, to avoid communication bottleneck and to meet the high bandwidth, low-power and low-latency requirements which, actually, cannot be matched by traditional point-to-point connections through dedicated wires. Network-on-chips (NoCs) have emerged as a technology enabling a high degree of integration in multi-core systems on chip (Benini and Micheli 2002). The NoCs were introduced to reduce the wiring complexity and to increase communication efficiency by designing regular topologies. However, an important performance limitation in traditional NoCs, which are mainly made by switching elements, network interfaces and inter-switch links, arises from multi-hop communications based on planar metal interconnects and to the consequent high latency and power consumption. In fact, at the physical level, the metal interconnects are responsible for depressing the on-chip data bandwidth while consuming an increasing percentage of power. Different approaches have been investigated to overcome these limitations which range from integrated optics to wireless on-chip communication. Architectures based on Optical Network-on-Chip (ONoC) rely on an optical layer, stacked with electronic layers, that allows the communication between different cores in the optical domain (Beausoleil et al. 2008; Shacham et al. 2008; Miller 2009). Optical networks significantly improve electronic technology, but at the expenses of complex layout, sophisticated routing algorithms, and high power budget. Moreover, as the network size scales up, signal losses and crosstalk due to waveguide crossings dramatically increase (Gambini et al. 2015; Fusella and Cilardo 2016; Ortin-Obon et al. 2017). An alternative emerging technology to overcome performance limitations of traditional NoCs is the Wireless Network-on-Chip (WiNoC), which exploits on-chip wireless transmission to perform an hybrid wired/wireless communication. In this approach silicon integrated antennas replace wired channels, so that transmission performance, power consumption and long distant communication problems of traditional wired NoCs can be addressed simultaneously (Lin et al. 2007; Ganguly et al. 2011; Deb et al. 2012; Matolak et al. 2012). Recent research has established characteristics of silicon integrated antennas operating in the millimeter-wave range of a few tens to one hundred gigahertz to be used for intra- and inter-chip communication. On-chip wireless communication links alleviate not only the latency issues of conventional technologies, but also the topological constraints. As a counterpart, on-chip antennas operating in the millimeter-wave range of a few tens to one hundred gigahertz suffer for low integrability and are not always viable solution at the CMP communication level; therefore, higher operating frequencies, at least in the THz range, should be required to reduce the size of the radiating elements (Matolak et al. 2012; Lee et al. 2009).

A completely new approach, which can combine the advantages of both the ONoC and the WiNoC, is the on-chip wireless connection through optical nanoantennas. Recent researches have proposed different plasmonic antennas for wireless communication such as dipole and horn antennas (Alù and Engheta 2010; Yang et al. 2016; Merlo et al. 2016; Solís et al. 2013), but the solutions proposed are based on all-plasmonic structures, which do not address the problem of integrating such devices within SOI-based optical networks on chip. In fact, with SOI integrated antennas, the optical signals could be either routed through waveguides or through wireless links, thus avoiding integration of electronic devices for electro-optical conversions, reducing complexity and energy costs. The elimination of electro-optical conversion has also the potential to guarantee bitrate transparency and distance independence of the photonic links.

The efficient coupling between optical antennas and SOI waveguides is non-trivial, especially when highly directive radiation is required for point-to-point connections. A very efficient coupling between SOI waveguides and plasmonic particle chains was demonstrated in Magno et al. (2016) and Fvrier et al. (2012). These particle chains can behave as directive radiators if suitably designed, but they are characterized by an out-of-plane radiation. Hybrid solutions using plasmonic antennas, with hybrid-waveguide feeding (Yousefi and Foster 2012; Yang et al. 2014; Saad-Bin-Alam et al. 2015), have been proposed for wireless applications. However, in order to guarantee a full compatibility with standard optical components, a silicon waveguide feed should be considered. For easy integration between optical wired and wireless connections, in Bellanca et al. (2017) the authors proposed a Vivaldi antenna coupled to a silicon waveguide, in which efficient power transfer to the antenna is achieved by an hybrid Si-plasmonic coupler. However, to cope with the problem of the high propagation losses due to signal spread (according to the Friis Equation (Kraus 1988), at optical wavelengths the attenuation introduced is of the order of 60 dB for a \(100~\upmu \mathrm{m}\) link), some improvements on the antenna performance are needed, to make this approach suitable. Based on the results of Bellanca et al. (2017), in this paper we propose the design of a double Vivaldi antenna, with the aim to improve the gain of both the transmitting and the receiving sections, thus reducing the power budget of an optical wireless link.

2 Double Vivaldi antenna coupled to Si waveguide

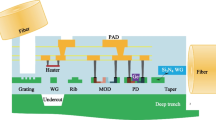
The proposed antenna configuration is shown in Fig. 1a and consists of a broadside array of two Vivaldi radiators fed through silicon waveguides. The excitation of the two antennas is provided by a three-waveguide coupler, which acts as a signal splitter. For a broadside excitation of the array, the signal must be equally split and arrive with the same phase at the two antennas. This is obtained by properly designing the three-waveguide coupler length and by the symmetry of the connections between the the antennas and the coupler ports (see Fig. 1a).

Fig. 1
figure 1

Scheme of the overall double Vivaldi antenna (a), detail of the antenna coupled to the Si waveguide, (b), and cross section of the hybrid Si-Plasmonic coupler feeding each antenna (c)

Full size image

The hybrid Si-plasmonic coupler feeding each element of the array is shown in Fig. 1b, with details of the geometry in Fig. 1c.

In the following sections, we will first consider the design of the hybrid Si-plasmonic coupler, which gives the constraints for the geometrical parameters of both the input signal-splitting region and the antennas. In fact, in order to properly feed the two Vivaldi antennas, it is of primary importance to assure an efficient power transfer between the silicon and the slotted plasmonic waveguides. After defining the optimal dimensions for the hybrid coupler, we will describe the design of the signal-splitting region and the optimization of the single Vivaldi antenna. Finally, the optimization of the double antenna array will be addressed.

2.1 Design of the hybrid Si-plasmonic coupler

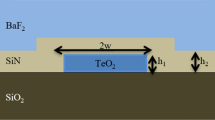
In order to design the Si-plasmonic coupler feeding each Vivaldi antenna, the results of the coupled mode theory (CMT) and of the normal mode analysis have been exploited (Yariv 1973; Calò et al. 2012). Although the CMT is not rigorous when strongly coupled waveguides are considered, it can be used to achieve the geometrical design with negligible computational effort, provided the validation with fullwave simulations. According to the CMT, the overall hybrid coupler, shown in Fig. 1c, can be regarded as the superposition of two single waveguides, i.e. the plasmonic slot waveguide and the Si one. To achieve the synchronism condition (\(\delta =\beta _2-\beta _1=0\) with \(\beta _1\) and \(\beta _2\) propagation constants of the fundamental modes of the two waveguides when considered uncoupled), the effective refractive indices of the two single structures must be equal. For this purpose, we have chosen to variate the width of the two waveguides, i.e. parameter w and p in Fig. 1c. The other geometrical parameters are considered as constants and equal to: \(h=220\), \(t=50\), and \(g=80\) nm, which are compatible with standard SOI waveguides and fabrication techniques.

Figure 2 shows the width p of the plasmonic waveguide, which guarantees the synchronism condition, as a function on the corresponding Si waveguide width w. In this case, the gap of the slotted plasmonic waveguide is \(s=30\) nm. Each point (p, w) of this design curve corresponds to possible couples of values of waveguide widths that guarantee the total power transfer between the Si and the plasmonic waveguides. In order to choose among the different possible solutions, we calculated the coupling length \(L_{c}\), for the different couples of width values, by evaluating the supermodes (i.e. the normal modes of the overall hybrid-coupler structure) by the Finite Element Method (FEM).Footnote 1 According to the normal mode analysis, once verified the synchronism condition, the coupling length \(L_c\) can be calculated as:

$$\begin{aligned} L_c = \frac{\lambda }{2\left( n_{c1}-n_{c2}\right) } \end{aligned}$$
(1)

where \(n_{c1}\) and \(n_{c2}\) are the effective refractive indices of the first two normal modes of the overall hybrid coupler. Figure 2 also reports, for some calculation points, the coupling length \(L_{c}\) and the value of the effective refractive index n\(_{eff}\) of the single waveguides at synchronism. Higher values of w correspond to lower p values and to longer coupling lengths.

Fig. 2
figure 2

Width p of the plasmonic waveguide, which guarantees the synchronism condition, as a function on the corresponding Si waveguide width w. For some calculation points (red dots), the coupling length \(L_{c}\) and the value of the effective refractive index \(n_{eff}\) of the single waveguides at synchronism are reported. (Color figure online)

Full size image

In this paper, we have chosen \(w = 380\) nm, \(p = 270\) nm and, therefore, \(L_c = 1.63~\upmu \mathrm{m}\). This configuration is a good compromise that assures a short coupling length without enlarging too much the width of the plasmonic waveguide. In this way, lower losses in the metal and better efficiency of the antenna are expected. Moreover, since the chosen configuration is near to the vertical part of the design curve in Fig. 2, a large tolerance in the choice of p is permitted (by changing p, the synchronism condition is still achieved for almost the same value of w). This condition definitely eases the fabrication process, where the control of the geometry could be difficult.

2.2 Design of the Si three-waveguide coupler

Provided the Si waveguide dimensions, the design of the three-waveguide coupler for the input signal splitting is straightforward. In fact, the device is a symmetric coupler where all the waveguides are equal. Therefore, in the case of excitation of the central waveguide, the length of the coupler \(L_0\) that guarantees an equal splitting of the signal in the two side waveguides, is given by the following equation:

$$\begin{aligned} L_0 = \frac{\lambda }{2\left( n_{1}-n_{3}\right) } \end{aligned}$$
(2)

where \(n_{1}\) and \(n_{3}\) are the effective refractive indices of the first and of the third normal modes of the three-waveguide coupler. The effective refractive indices of the normal modes of the three-waveguide coupler, calculated by FEM (See footnote 1), are equal to \(n_{1}=2.1975\), \(n_{2}=2.1504\) and \(n_{3}=2.0967\), respectively. The corresponding optimal coupler length is \(L_{0}=7.69~\upmu \mathrm{m}\). The coupler length \(L_{0}\) was finally optimized by the Finite Difference Time Domain (FDTD)Footnote 2 simulations, to take into account the presence of the curved waveguides, which are necessary to optimize the distance between the antennas in the two-element array. The calculated optimized length is \(L_{0}=7.35~\upmu \mathrm{m}\).

2.3 Single Vivaldi antenna design

The Vivaldi antenna has been designed by FDTD simulations (See footnote 2). The Vivaldi aperture profile is given by the following equations:

$$\begin{aligned} x = c_{1}e^{Rz}+c_{2} \end{aligned}$$
(3)

with

$$\begin{aligned} c_{1}=\frac{x_{2}-x_{1}}{e^{Rz_{2}}-e^{Rz_{1}}} \end{aligned}$$
(4)

and

$$\begin{aligned} c_{2}=\frac{x_{1}e^{Rz_{2}}-x_{2}e^{Rz_{1}}}{e^{Rz_{2}}-e^{Rz_{1}}} \end{aligned}$$
(5)

where R is the opening rate coefficient, \(x_{1}\) and \(x_{2}\) are the minimum and the maximum x coordinates of the Vivaldi profile, and, similarly, \(z_{1}\) and \(z_{2}\) are the minimum and the maximum z coordinates. Here, we report the optimization results obtained by varying the antenna length \(L_{a}\) for \(R=3.0~\upmu {\rm m}^{-1}\). The other geometrical parameters, such as the width p of the two metallic strips, their thickness t and the width s of the slot, are constrained by the hybrid Si-plasmonic coupler section. Further details on the antenna design can be found in Bellanca et al. (2017).

The antenna was optimized considering its gain defined as:

$$\begin{aligned} G(\theta ,\phi )=4\pi \frac{I(\theta , \phi )}{P_{in}} \end{aligned}$$
(6)

where \(I( \theta , \phi )\) is the radiation intensity and \(P_{in}\) is the power in input to the Si waveguide. The radiation intensity \(I( \theta , \phi )\) is calculated by the near-to-far-field projection of the FDTD simulated electromagnetic field. The gain is the most significant parameter to optimize the antenna, because it accounts for the radiation efficiency and, therefore, for the losses inside the antenna (either dielectric or conduction losses).

Figure 3a shows the maximum antenna gain as a function of the antenna length \(L_{a}\). In these simulations, we considered only a single antenna fed by its Si waveguide. The results in Fig. 3 were calculated from the gain radiation patterns obtained by the FDTD simulation of the overall structure (i.e. single antenna coupled to the Si waveguide). Standard near-to-far field projections of the fields recorded on a closed box, surrounding the antenna and the input hybrid plasmonic coupler, were calculated once applied Fourier transformations on time-domain FDTD field values (Taflove 2005). The minima and maxima in the gain curve of Fig. 3a are mainly due to resonances in the waveguide-to-antenna connection. In fact, although optimized, the connection is still subject to a residual mismatch which is a function of the structural dimension \(L_{a}\). Therefore, the design approach was to choose the optimal antenna length value \(L_{a}\) for which the gain is maximum. The optimal gain value \(G=9.9\) dB is achieved for \(L_{a}=1.75~\upmu \mathrm{m}\). It is worth noticing that, owing to the metal losses at optical frequencies, the maximum gain is not achieved for longer Vivaldi antennas as would be expected in the lossless case. Figure 3b shows the antenna gain as a function of wavelength for \(L_{a}=1.75~\upmu \mathrm{m}\) and \(R=3.5~\upmu \mathrm{m}^{-1}\), which is the optimized value for this parameter (see Bellanca et al. 2017). A good broadband behavior can be observed, since the gain varies of about 2.5 dB in the whole considered wavelength range (i.e. the C-band).

Fig. 3
figure 3

Maximum gain of the single Vivaldi antenna (a) as a function of the antenna length \(L_{a}\) and (b) as a function of the wavelength. In the first plot, \(R=3.0~\upmu \mathrm{m}^{-1}\) and \(\lambda =1.55~\upmu \mathrm{m}\). In the second plot, \(R=3.5~\upmu \mathrm{m}^{-1}\) and \(L_{a}=1.75~\upmu \mathrm{m}\)

Full size image

3 Double Vivaldi antenna radiation characteristics

The double Vivaldi antenna behaves as a two-element broadside array in which the two antennas are excited with signals of equal amplitude and phase. As anticipated, this condition is guaranteed by the design of the three-waveguide coupler and by the symmetry of the feeding section. The double Vivaldi antenna was designed and optimized by FDTD as before (See footnote 2). Figure 4a shows the directivity (blue curve) and the gain (red curve) of the double Vivaldi array with center-to-center distance between the antennas \(d_{2V}=2.0~\upmu \mathrm{m}\). This value of the distance between the antennas was chosen by parametric analysis, with the goal of maximizing the gain of the antenna array. Compared to the single Vivaldi antenna, a 3 dB improvement of the gain is achieved by this configuration.

Figures 4b and c show the double Vivaldi antenna radiation diagrams in the E-plane (horizontal plane) and H-plane (vertical plane), respectively. The aperture angle in the E-plane is \(\theta _{E}=13^{\circ }\) and in the H-plane is \(\theta _{H}=37^{\circ }\). Compared to the single antenna, \(\theta _{E}\) is reduced of \(\Delta _\theta = 16^{\circ }\), whereas \(\theta _{H}\) remains unchanged, as expected for a linear antenna array with antennas positioned along the x axis on the xz plane. The results in Fig. 4 were calculated by simulating the overall structure (i.e. input waveguide, signal splitter, hybrid couplers and antennas) and then applying near-to-far field projections to calculate gain and radiation patterns. Therefore, the calculation of the gain takes into account the mismatch losses due to the waveguide-to-antenna connection, the losses in the metal, and eventual losses due to the signal splitting region.

Fig. 4
figure 4

a Directivity (blue curve) and gain (red curve) of the double Vivaldi array as a function of the wavelength; in these simulations, the distance between the centers of the two antennas is \(d_{2V}=2.0~\upmu \mathrm{m}\). b E-plane and c H-plane radiation diagrams for the double Vivaldi antenna for \(\lambda = 1.55~\upmu \mathrm{m}\). (Color figure online)

Full size image

The performance of a wireless link between two double Vivaldi antennas, schematized in Fig. 5a, was evaluated by FDTD simulation. The transmitting and the receiving antennas are positioned at a distance \(d_{link}=50\) \(\upmu \mathrm{m}\), that verifies the hypothesis of far-field propagation. An homogeneous surrounding medium, i.e. silica with refractive index \(n_{SiO_{2}}=1.44\) has been considered in the simulations. The input and the output ports of the link are highlighted in Fig. 5a. These ports are defined on the Silicon waveguides, respectively, at the transmitter (TX) and at the receiver (RX); they allow to directly compute, through evaluation of the power fluxes, the power \(P_t\) supplied to the transmitting antenna and the power \(P_r\) collected by the receiver, and therefore to obtain the link power budget. Figure 5b shows the received power \(P_r\) for the \(50-\upmu \mathrm{m}\) link with single Vivaldi antennas (blue curve) and with the double Vivaldi arrays (red curve) at the TX and RX sections, respectively. The transmitted power is \(P_t=0.0\) dB. As it can be observed, with the two broadside arrays an improvement of the received power of about 6.0 dB at wavelength \(\lambda =1.55~\upmu \mathrm{m}\), is achieved. This result agrees very well with the received power increase that can be predicted by applying the well-known Friis formula for the calculation of the power budget of a wireless link (Bellanca et al. 2017; Kraus 1988).

Fig. 5
figure 5

a Scheme of the double Vivaldi antenna link; b received power \(P_r\) for the \(50-\upmu \mathrm{m}\) link with single Vivaldi antennas (blue curve) and double Vivaldi antennas (red curve) at the TX and RX sections. The transmitted power is \(P_t=0.0\) dB. (Color figure online)

Full size image

Figure 6 shows the patterns of the electric field intensity \(|E|^2\) for the \(50~\upmu \mathrm{m}\) optical link between the two double Viavaldi antennas. In particular, (Fig. 6)a pertains to the horizontal xz plane passing at the center of the metal layer, whereas (Fig. 6b) is for the horizontal xz plane passing at the center of the Si waveguides. The wavelength is \(\lambda = 1.55~\upmu \mathrm{m}\). In Fig. 6a we can clearly notice the effect of the two antenna arrays in the in-plane distribution of the electromagnetic field. Moreover, the decay of the field intensity with the distance is also apparent. Similarly, in Fig. 6b, we can observe the splitting of the input power in the three-waveguide coupler, and its recombination in the output section.

Fig. 6
figure 6

Patterns of the electric field intensity \(|E|^2\) for the \(50-\upmu \mathrm{m}\) optical link between the two double Viavaldi antennas: a horizontal xz plane passing at the center of the metal layer, b horizontal xz plane passing at the center of the Si waveguides

Full size image

By increasing the number of antennas, an increase in the directivity and in the gain is expected from antenna theory. In particular, we can calculate the array directivity from the multiplication of the single antenna directivity by the array factor. Figure 7 shows the array directivity as a function of the number of antennas N (red circles), analytically calculated through the array formula. Moreover, we simulated by the FDTD the cases of multiple antennas excited independently in-phase, i.e. without considering the signal splitter, but exciting each waveguide with its fundamental mode. In particular, Fig. 7 reports the maximum directivity values calculated by the FDTD, for N=1, 2, and 4 (red squares). We can see that the FDTD results agree well with the ones obtained from antenna theory (i.e. calculating the array directivity from the multiplication of the single antenna directivity by the array factor). Moreover, from the same FDTD simulations, we calculated the gain for N=1, 2, 4 (blue squares). In all the considered cases, the radiation efficiency is \(\eta =G/D=0.7\). It is worth mentioning that, when the signal splitter is included in the simulation, as in the case of N=2, the radiation efficiency reduces to \(\eta =G/D=0.6\). Moreover, the signal splitter also induces a reduction of the bandwidth as it can be noticed in Fig. 5b. Therefore, the actual gain of the N element array will be constrained by the performances of the N-ways signal splitting region.

The fabrication of the proposed device will require different steps for the realization of the dielectric waveguides and then of the plasmonic structures. In particular, electron beam lithography (EBL) can be used to fabricate the Si waveguide components (i.e. splitter and waveguides feeding the antennas) on a commercial SOI substrate. After the fabrication of the waveguides and the deposition of the middle dielectric layer, EBL exposure and lift-off techniques can be used to pattern the plasmonic components (i.e. plasmonic coupler and antennas) on the evaporated silver layer.

Fig. 7
figure 7

Array directivity as a function of the number of antenna N (red circles), calculated according to antenna theory; maximum directivity D (red squares) and gain G (blue squares) calculated by the FDTD, for N = 1, 2, and 4, exciting each waveguide with its fundamental mode. (Color figure online)

Full size image

4 Conclusion

In this paper we have proposed a double Vivaldi broadside antenna array for Optical Wireless Network on Chip applications. The antenna configuration is a two-element array fed by a silicon waveguide. The signal feeding section is made of a three-waveguide coupler, that behaves as a signal splitter. Moreover, two hybrid Si-plasmonic couplers guarantee an efficient excitation of the Vivaldi antennas. This design improves of 3 dB the gain of the single Vivaldi antenna. A point-to-point link has also been simulated, showing an increase of 6 dB of the received power with respect to the single antenna configuration. The increased gain makes this configuration suitable to realize longer links for inter- and intra-chip optical communications.