1 Introduction

Fiber optic transmission systems are typically deployed to achieve high bandwidth over large distances. The optical link may contain a concatenation of fibers, with interfaces that are either non-detachable fusion splices, or detachable connections with connector plugs in a coupler. At the transmitter or receiver, there may be butt-coupled fiber-to-chip couplings, lensed interfaces, longitudinal separations, or slabs of homogeneous material. Each interface affects the transmission and reflection characteristics of the entire link. The prediction of the optical performance comprises a significant electromagnetic challenge.

For example, indoor applications with multi-mode fiber require low attenuation at each interface in order to meet the optical power budget without sacrificing the transmission distance. The power budget may be as low as 1.9 dB for 100 gigabit per second IEEE802.3 compliant networks with a distance up to at least 100 m (IEEE 2010). To achieve that, one may constrain the mechanical alignment as well as the fiber geometry specification, including the core diameter and characteristics of the refractive index profile (Floris et al. 2012). Each connection that consists of two dissimilar fibers with a finite lateral alignment comprises a reflection–transmission problem. The maximum allowable attentuation per connection becomes very low, in the order of a few tenths of a decibel or less, to ensure that the power budget is met. In view of this development, we want to reconsider the full reflection–transmission problem for fiber connections. In particular, the traditional approach for optical fiber mode-matching ignores reflections, resulting in mode-projections by means of overlap integrals (Marcuse 1977), which may no longer be sufficiently accurate or adequate for the evaluation of the performance of the optical link.

Another example relates to the recent development of space-division multiplexing (SDM) technique to increase the capacity of a single optical fiber beyond the non-linear Shannon limit (Richardson 2010). The propagation of a specific linear combination of modal electromagnetic fields associated with a few-mode fiber is considered a separate transmission channel in that fiber. Optical multiple-input-multiple-output (MIMO) transmission systems may be further optimized by simulations of, for instance, the influence of imperfect optical connections on the modal power distribution of each transmission channel, or the effectiveness of mode multiplexing due to photonic lanterns (Birks et al. 2015).

In this paper, we consider reflection–transmission problems for interfaces consisting of a homogeneous half-space and an optical fiber. For flexibility, we expand the modal electromagnetic fields that span the discrete spectrum of all possible field solutions for the specific design of the optical fiber at the wavelength of choice, in a much more general orthonormal Wilson basis. Wilson basis functions have strong localization in both the spatial and spectral domain, which is achieved by the product of exponentially decaying window function with trigonometric functions (Daubechies et al. 1991). As a result, the basis function feature spectral duo-localization, in the sense that due to the trigonometric functions, the spectral basis functions peak at two coordinates positioned symmetrically about the origin. Due to the orthonormality, the expansion of vector fields in a Wilson basis is achieved by straightforward projection integrals, which we have demonstrated in a companion paper (Floris and de Hon 2018). Arbitrary lateral displacement of electromagnetic fields at the interface corresponds directly to sparse, diagonally dominant, translation operators in the Wilson basis.

With modal electromagnetic fields of optical fibers already discretized in a Wilson basis, we proceed with the construction of Wilson-basis discretized distributions of dipole sources that generate electromagnetic fields in homogeneous space in Sect. 4. At the observation plane, the generated electromagnetic fields are subsequently expanded in a Wilson basis, leading to double integrals consisting of spectral Wilson source- and test functions and the spectral dyadic Green’s function for homogeneous space. The duo-localization of the Wilson basis aids the convergence of these integrals.

In Sects. 6 and 7, we consider reflection–transmission problems for an interface consisting of a homogeneous half-space and an optical fiber, and an excitation from either side. The solution amounts to the construction of Wilson-basis discretized equivalent sources in the homogeneous medium at the interface, in such a way that the transverse electromagnetic fields are continuous across the interface. In particular, we show the reflection that is associated with the excitation of either the forward or backward propagating mode in the fiber. The results are the same up to the accuracy of the numerical quadratures.

A key ingredient to the recipe is the construction of source distributions at the interface in such a way that the electromagnetic fields (which include evancescent waves) propagate only on one side of the interface, thus leaving the fields zero at the other side of the interface. In Sect. 5, in a fashion similar to applying a Poincaré–Steklov operator (Knockaert and Zutter 2008), we construct the specific linear combination of electric and magnetic source distributions in homogeneous space that leads to one-way field propagation. Conveniently, the approach allows that we prescribe either the transverse electric or the transverse magnetic field distribution at the interface as well.

In Sect. 8, we show an example of a complex-source beam (CSB) in a Wilson basis at normal incidence on a few-mode fiber. A CSB is a Gaussian-shaped electromagnetic beam field obtained by inserting a complex source coordinate in the dyadic counterpart of the scalar Green’s function. The construction details and subsequent expansion in a Wilson basis is discussed in Floris and de Hon (2018). By application of the sparse translation operator, we show the change in the modal power distribution in a few-mode fiber as the CSB is displaced with respect to the center of the fiber in a number of steps.

We now proceed to describe the procedure to solve the reflection–transmission problem for a fiber to homogeneous space interface in Sect. 2 with a modal excitation in the fiber, followed by the excitation from the homogeneous half-space in Sect. 3.

2 Reflection–transmission problem for homogeneous space to a fiber

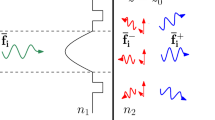
Consider an interface at \(z=z_0\) between a homogeneous half-space and an optical fiber as shown in the left schematic in Fig. 1. We denote the direction of the positive z-axis with the unit vector \({\mathbf {u}}_z\). In the fiber, we have highlighted an arbitrary guided mode that propagates away from the interface in the positive z-direction through a single wiggle.

Fig. 1
figure 1

The left schematic shows for a forward propagating fiber mode, the mode-equivalent incident and reflected field by blue and red wiggles respectively that generate the same transverse electromagnetic field at the interface \(z=z_0\). The arbitrary excitation, denoted through a green wiggle in the right schematic, is expanded in terms of mode-equivalent incident fields for which the situations in the left schematic serve as building blocks. The resulting transmission and reflection are highlighted trough blue and red wiggles respectively. The mismatch in the expansion, associated with the radiating part of the modal spectrum of the fiber, one may consider to compensate by the reflected and transmitted fields denoted by (smaller) purple wiggles, upon approximating the fiber by a homogeneous background medium. (Color figure online)

Full size image

To satisfy the boundary conditions, the transverse electric and magnetic field vectors, denoted by \({\mathbf {E}}_T\) and \({\mathbf {H}}_T\) respectively, need to be continuous across the interface and by extension into the homogeneous medium at \(z=z_{0^-}\) with \(z_{0^-} \uparrow z_0\). We temporarily remove the fiber, and make equivalent source distributions (indicated with blue and red arrows) that generate the same transverse electromagnetic field \({\mathbf {f}}_T = [{\mathbf {E}}_T, {\mathbf {H}}_T]^T\). The subscript \(_{T}\) denotes the transverse vector, whereas the superscript \(^T\) denotes the transpose operator.

We apply the Poincaré–Steklov operator to make a decomposition of the wavefield \({\mathbf {f}}_T\) at \(z=z_{0^-}\) into a one-way forward and backward propagating field, and then construct the associated two sets of equivalent source distributions. We emphasize that when we refer to one-way propagating fields generated by equivalent sources, evanescent waves are included as well. Generated by one set of equivalent sources, the one-way forward propagating field represent the mode-equivalent field that is incident on the interface. This field is indicated through (rightward pointing) blue wiggles, and is generated by a specific physical source somewhere on the left-hand side of the interface or at minus infinity. Generated by the second set of equivalent sources, the one-way backward propagating field emerges from the interface \(z=z_{0^-}\) and are highlighted through the (leftward pointing) red wiggles. For this specific incident field, when the fiber is placed back at the interface, the guided mode in the fiber is the transmission, and the one-way backward propagating field is the reflection, implying that the fields will be continuous from \(z\uparrow z_{0^-}\) to \(z\downarrow z_{0}\), thus eliminating the equivalent sources.

This decomposition to mode-equivalent incident and reflected fields may be repeated for all guided modal electromagnetic fields of the fiber. Serving as building blocks, an arbitrary incident field may be expanded in terms of the mode-equivalent incident fields, for which the reflection–transmission problem was already solved. In the second schematic of Fig. 1, an arbitrary incident field in homogeneous space is indicated by a (rightward pointing) green wiggle. Because the mode-equivalent incident fields are not necessarily orthogonal, we make a minimum-norm expansion of the arbitrary incident field to the mode-equivalent incident fields. The associated transmission is highlighted by (rightward pointing) blue wiggles in the fiber, and the reflection by (leftward pointing) red wiggles. In case the incident field is spanned by the mode-equivalent incident fields, then the reflection–transmission problem is solved.

However, for the expansion, we considered only the mode-equivalent guided modes and did not discretize the infinite set of radiating fields that complete the modal basis. Hence, a small part of the incident field may be associated with the radiating spectrum of the fiber modes. In general, we are not interested in the radiating fields in the fiber, because they do not contribute to the optical signal transmission over relatively long distances.

Although it is possible to discretize the radiating part of the spectrum, the oscillatory behavior at large distances radially away from the core make these fields more difficult to work with, and this track is usually avoided (Snyder and Love 1983). One could also consider to increase the set of modes, for instance by adding an artificial second cladding somewhere in the existing cladding region. The rationale is that the leaky mode part of the radiating spectrum have mode fields dominantly present in the core region (Snyder and Love 1983). Depending on the refractive index difference between the two cladding levers, this approach drastically increases the set of guided modes, as well the required computational effort to avoid numerical instabilities in obtaining the field solutions.

In view of the relatively small contrast in the index of refraction in the radial direction, one may decide to replace the fiber by a homogeneous background medium and illuminate it by the remaining part of the incident field that is not associated with the mode-equivalent incident wavefields. The associated transmitted and reflected field may respectively be generated by equivalent source distributions positioned on the left and right side of the interface \(z=z_0\) as shown in the schematic through purple arrows in Fig. 1. Because of the approximation, the one-way forward propagating field represented by the purple wiggles on the right side of the interface does not fully satisfy Maxwell’s equations for the optical fiber. Fortunately, due to the generally small contrast in the index of refraction between the core and cladding of optical fibers, that error should be small (Snyder and Sammut 1979). We will consider the reflection–transmission problem of an arbitrary incident field on an interface of two homogeneous half-spaces in the Wilson basis in a separate publication. Our main focus is to demonstrate mode-matching in a Wilson basis, and display the appealing features of the Wilson basis expansions. In the next section, we consider the reciprocal problem of the radiation from the end-face of an optical fiber.

3 Reflection–transmission problem for a fiber to homogeneous space

To keep the direction of propagation of the excitation in the positive z-direction, the fiber is now placed on the left-hand side of the interface \(z=z_0\), and the homogeneous medium on the right-hand side, as shown in the left schematic of Fig. 2. Effectively, this is the same situation as explained in Sect. 2 and shown in the left schematic of Fig. 1, in the sense that the guided mode still propagates in the positive z-direction, and the fields and equivalent sources in homogeneous space are now moved to the plane \(z=z_{0^+}\) with \(z_{0^+} \downarrow z_0\). In this configuration, there is also an incident field from the right, highlighted by the red wiggles, due to a physical source somewhere at the on the right-hand side of the interface, or at infinity.

Fig. 2
figure 2

The left schematic shows the configuration with the fiber and the homogeneous medium interchanged compared to the situation in the left schematic of Fig. 1. The equivalent sources (denoted by arrows) and associated fields (denoted by blue and red wiggles), are moved to the plane \(z=z_{0^+}\). The schematic on the right shows the same configuration again, but now with all the wavefields propagating in the opposite direction. (Color figure online)

Full size image

We aim to cancel this undesired mode-equivalent incident field originating in the half-space with the aid of a specific linear combination of backward propagating modes in the fiber. Consider the situation in the right schematic in Fig. 2, which is the same as the left configuration, except that all the wavefields now radiate in the opposite direction. This may for example be achieved by switching the sign of all the magnetic field components of all the wavefields. In this situation, for the specific backward propagating mode, highlighted through a black wiggle, we have readily obtained the backward-mode-equivalent incident and scattered field, respectively highlighted through the dark blue wiggles and the red wiggles.

For the undesired incident field on the right-hand side of the interface in the left schematic, we make a minimum-norm expansion to all the backward-mode-equivalent incident fields associated with all the guided modes of the fiber. Subsequently, we cancel the undesired incident field, by subtracting the associated backward-propagating modes in the fiber, and the associated scattered field in the homogeneous medium, as shown in Fig. 3. As discussed in Sect. 2, the mismatch is associated with the radiation field of the fiber, and may adequately be accounted for through fields generated by equivalent sources indicated in purple in the schematic.

Fig. 3
figure 3

For an arbitrary guided fiber mode incident on the interface, the reflected field is expanded in terms of backward-propagating guided modes. The reflected radiating field one may consider to approximate by fields due to equivalent-sources in a homogeneous background medium. The transmitted field consists of an incident-mode-equivalent transmitted field, backward-mode-equivalent scattered fields, and a rest field, highlighted with blue, dark red and purple wiggles (large to small), respectively. (Color figure online)

Full size image

Before we discuss the construction of one-way propagating fields in detail in Sect. 5, we give a brief summary of the construction of Wilson-basis discretized equivalent sources, to generate electromagnetic fields in a Wilson basis.

4 Electromagnetic fields due to Wilson-discretized sources

For various reasons, we favor a Wilson basis to make expansions of electromagnetic fields, to make dipole-like Wilson source distributions (in this section), and to solve electromagnetic reflection–transmission problems. The orthonormal basis has exponentially decaying basis functions in both the spatial and the spectral domain. Because of that, coefficients for field expansions are readily obtained using projection integrals in such a way that it allows for an expedient discretization of the phase-space information of optical wavefields (Arnold 2002). By means of examples, we demonstrate electromagnetic field expansions in a Wilson basis in a companion paper (Floris and de Hon 2018). Through a Wilson basis inner product parameter sweep, expanded fields may directly be spatially displaced with the aid of a sparse, diagonally dominant, translation operator. This is very valuable when multiple alignment configurations of interface problems are to be evaluated. The basis functions consist of translated and trigonometrically modulated versions of a single exponentially decaying window function \(\theta (x)\). The definition of the basis functions depend on the parity of the sum \(\ell +n\) for \(\ell \in {\mathbb {Z}}\), and \(n \in {\mathbb {N}}\), according to

$$\begin{aligned} w_{\ell n}(x) = \left\{ \begin{array}{ll} \theta (x-n/2), & \quad \ell =0, n\;{\mathrm {even}},\\ 0, & \quad \ell =0, n\;{\mathrm {odd}},\\ \sqrt{2} \theta (x-n/2)\cos (2 \pi \ell x), & \quad \ell>0, \ell +n\;{\mathrm {even}}, \\ \sqrt{2} \theta (x-n/2)\sin (2 \pi \ell x), & \quad \ell >0, \ell +n\;{\mathrm {odd}}. \\ \end{array} \right. \end{aligned}$$
(1)

We adopted the construction of the window function \(\theta (x)\) from the excellent, although highly mathematical paper by Daubechies et al. (1991). In Floris and de Hon (2018), we give a short, streamlined and notation consistent summary on its construction with examples. The inner product of two Wilson basis functions are orthonormal with respect to the norm

$$\begin{aligned} \left\langle w_{\ell n}(x),w_{\ell ' n'}(x)\right\rangle = \int \limits _{x \in {\mathbb {R}}} w_{\ell n}(x)w^{\ast}_{\ell 'n'}(x)\,{\mathrm {d}}x = \delta _{\ell \ell '}\delta _{nn'}, \end{aligned}$$
(2)

where the star \(^{\ast}\) denotes complex conjugation and \(\delta\) the Kronecker delta function. We introduce a scaling parameter d to match the width of the Wilson basis functions appropriately to the electromagnetic wavefields by letting

$$\begin{aligned} w_{\ell n}(x) \rightarrow d^{-1/2} w_{\ell n}(x/d), \end{aligned}$$
(3)

while preserving orthonormality. For consistency with a conventional formulation for electromagnetic wavefields, we define the forward Fourier transformation by

$$\begin{aligned} \tilde{w}_{\ell n}\left( \kappa \right) = \int \limits _{x \in {\mathbb {R}}} w_{\ell n}(x) e^{j\kappa x} \,{\mathrm {d}}x. \end{aligned}$$
(4)

Due to the trigonometric modulations in Eq. (1), the spectral Wilson basis functions \(\tilde{w}_{\ell n}(\kappa )\) have two peaks in the spectral domain, i.e.

$$\begin{aligned} \tilde{w}_{\ell n}(\kappa ) = \left\{ \begin{array}{ll} e^{j\kappa \frac{n}{2}}\hat{\theta }\left( \frac{\kappa }{2\pi }\right) , & \quad \ell =0, n \;{\mathrm {even}},\\ 0, & \quad \ell =0, n \;{\mathrm {odd}},\\ \frac{1}{\sqrt{2}} e^{j\kappa \frac{n}{2}} \left[ \hat{\theta }\left( \frac{\kappa }{2\pi }+ \ell \right) e^{j\pi \ell n} + \hat{\theta }\left( \frac{\kappa }{2\pi }- \ell \right) e^{-j\pi \ell n}\right] , & \quad \ell>0, \ell +n \;{\mathrm {even}},\\ \frac{1}{j\sqrt{2}} e^{j\kappa \frac{n}{2}} \left[ \hat{\theta }\left( \frac{\kappa }{2\pi } + \ell \right) e^{j\pi \ell n} - \hat{\theta }\left( \frac{\kappa }{2\pi }-\ell \right) e^{-j\pi \ell n}\right] , & \quad \ell >0, \ell +n \;{\mathrm {odd}}. \end{array} \right. \end{aligned}$$
(5)

The window function \(\hat{\theta }\) is constructed in the companion paper, albeit with a \(\kappa =2\pi \xi\) substitution in the exponent of the Fourier transformation in Eq. (4). We note that the basis functions have exponential decay in both the spatial and spectral coordinates away from the peaks.

To expand dipole source distributions and electromagnetic fields at a two-dimensional plane in a Wilson basis, we define two-dimensional scalar Wilson basis functions \(w_{\mathbf {i}}(\mathbf {r}_t)=w_{\mathbf {i}}(x,y) = w_{\ell _x n_x}(x)w_{\ell _y n_y}(y)\). The multi-index \({\mathbf {i}}=(\ell _x,n_x,\ell _y,n_y)\) and the transverse coordinate \({\mathbf {r}}_t=x{\mathbf {u}}_x+y{\mathbf {u}}_y\) are used to compress notation. These 2D Wilson basis functions are orthonormal and satisfy \(\langle w_{\mathbf {i}}, w_{\mathbf {j}}\rangle =\delta _{\mathbf {ij}}\). The inverse Fourier transformation of a 2D Wilson basis function satisfies

$$\begin{aligned} w_{\mathbf {i}}(x,y) = \frac{1}{(2\pi )^2} \int \limits _{\mathbf {k}_t\in {\mathbb {R}}^2} \tilde{w_{\mathbf {i}}}(\mathbf {k}_t) e^{-j{\mathbf {k}}_t\cdot {\mathbf {r}}_t} \,{\mathrm {d}}{\mathbf {k}}_t, \end{aligned}$$
(6)

where \({\mathbf {k}}_t= k_x{\mathbf {u}}_x+ k_y{\mathbf {u}}_y\) is the transverse wave vector and \({\text{d}}{\mathbf {k}}_t\) is short for the area element \({\text{d}}{{k}}_x\,\,{\text{d}}{{k}}_y\).

In view of the boundary conditions for reflection–transmission problems, it suffices to consider only the transverse electric and magnetic field components. Let \({\mathbf {f}}=[E_x,E_y,H_x,H_y]^T\), and \({\mathbf {q}}=[J_x,J_y,K_x,K_y]^T\). The transverse electromagnetic field \({\mathbf {f}}_{\mathbf {j}}\) at a plane z, generated by a electromagnetic current sheet \({\mathbf {q}}_{\mathbf {j}}\) at \(z=z_0\), is given by

$$\begin{aligned} {\mathbf {f}}_{\mathbf {j}}(x,y,z)=\int \limits _{\mathbf {r}_t' \in {\mathbb {R}}^2} {\mathsf {G}}_T({\mathbf {r}}_t- {\mathbf {r}}_t',z -z_0) \cdot {\mathbf {q}}_{\mathbf {j}}({\mathbf {r}}_t') \,{\mathrm {d}}{\mathbf {r}}_t', \end{aligned}$$
(7)

where the subscripts \({\mathbf {j}}\) denote the source coordinate multi-index. Let us exploit the convolution in Eq. (7) to rewrite \({\mathbf {f}}_{\mathbf {j}}\) in terms of the spectral quantities according to

$$\begin{aligned} {\mathbf {f}}_{\mathbf {j}}(x,y,z)= & {} {\mathcal {F}}_T^{-1} {\mathcal {F}}_T{\mathbf {f}}_{\mathbf {j}}(x,y,z) = {\mathcal {F}}_T^{-1}\left( \tilde{\mathsf {G}}_T({\mathbf {k}}_t,z-z_0) \cdot \tilde{{\mathbf {q}}}_{{\mathbf {j}}}({\mathbf {k}}_t) \right) \nonumber \\= & {} \frac{1}{4\pi ^2} \int \limits _{\mathbf {k}_t\in {\mathbb {R}}^2} e^{-j{\mathbf {k}}_t\cdot {\mathbf {r}}_t} \tilde{{\mathsf {G}}}_T({\mathbf {k}}_t,z-z_0) \cdot \tilde{\mathbf {q}}_{\mathbf {j}}({\mathbf {k}}_t) \,{\mathrm {d}}{\mathbf {k}}_t. \end{aligned}$$
(8)

We want to expand the transverse electromagnetic field \({\mathbf {f}}_{\mathbf {j}}(x,y,z)\) in the Wilson basis through \({\mathbf {f}}_{\mathbf {j}}(x,y,z) =\sum _{\mathbf {i}} \bar{\mathbf {f}}_{{\mathbf {i}},{\mathbf {j}}}(z) w_{\mathbf {i}}(x,y)\). Denoted by an overbar, \(\bar{\mathbf {f}}_{\mathbf {j}}\) is the electromagnetic field in the Wilson basis, and refers to the collection of Wilson basis coefficients \(\bar{\mathbf {f}}_{{\mathbf {i}},{\mathbf {j}}}\) for all coordinates \({\mathbf {i}}\), generated by a source distribution at coordinate \({\mathbf {j}}\). To generalize the evaluation of the electromagnetic fields in the Wilson basis due to the four specific electric and magnetic field components in \({\mathbf {q}}_{\mathbf {j}}\), we construct a 4\(\times\)4 matrix \(\bar{\mathsf {F}}_{\mathbf {i},{\mathbf {j}}}\) that consists of

$$\begin{aligned} \bar{\mathsf {F}}_{\mathbf {i},{\mathbf {j}}}= \left[ \,\bar{\mathbf {f}}_{{\mathbf {i}},{\mathbf {j}}}^{J_x}, \, \bar{\mathbf {f}}_{{\mathbf {i}},{\mathbf {j}}}^{J_y}, \, \bar{\mathbf {f}}_{{\mathbf {i}},{\mathbf {j}}}^{K_x}, \, \bar{\mathbf {f}}_{{\mathbf {i}},{\mathbf {j}}}^{K_y}\right] . \end{aligned}$$
(9)

At this point, we will not bother with additional indices to indicate each specific element in Eq. (9), but provide that the elements are obtained through an inner product of \({\mathbf {f}}_{\mathbf {j}}\) from Eq. (8) with a weight function \({\mathbf {q}}_{\mathbf {i}}\), i.e.,

$$\begin{aligned} \bar{f}_{{\mathbf {i}},{\mathbf {j}}} = \left\langle {\mathbf {f}}_{\mathbf {j}}, {\mathbf {q}}_{\mathbf {i}}\right\rangle = \frac{1}{4\pi ^2} \int \limits _{\mathbf {k}_t\in {\mathbb {R}}^2} \tilde{\mathbf {q}}_{\mathbf {i}}(-{\mathbf {k}}_t) \cdot \tilde{\mathsf {G}}_T({\mathbf {k}}_t,z-z_0) \cdot \tilde{\mathbf {q}}_{\mathbf {j}}({\mathbf {k}}_t) \,{\mathrm {d}}{\mathbf {k}}_t. \end{aligned}$$
(10)

Each of the elements in Eq. (9) is obtained by selecting one of the four elements of \({\mathbf {q}}_{\mathbf {j}}\) to be Wilson distributed by \(w_{\mathbf {j}}\), one of the four elements of \({\mathbf {q}}_{\mathbf {i}}\) to be distributed by \(w_{\mathbf {i}}\), and by letting the other components vanish. Hence, by choosing Wilson basis functions as source and test functions, we may express the entire matrix \(\bar{\mathsf {F}}_{\mathbf {i},{\mathbf {j}}}\) in Eq. (9) as the double integral

$$\begin{aligned} \bar{\mathsf {F}}_{\mathbf {i},\mathbf {j}}= \frac{1}{4\pi ^2} \int \limits _{\mathbf {k}_t} \tilde{w}_{\mathbf {i}}(-\mathbf {k}_t) \tilde{\mathsf {G}}_T(\mathbf {k}_t,z-z_0) \tilde{w}_{\mathbf {j}}(\mathbf {k}_t) \,{\mathrm {d}}\mathbf {k}_t \end{aligned}$$
(11)

for all observation coordinates \({\mathbf {i}}\) and source distributions \(w_{\mathbf {j}}\) of interest.

In the companion paper (Floris and de Hon 2018), we have briefly summarized the mathematical formulation of the dyadic Green’s function for the Helmholtz operator in three dimensional homogeneous space. In view of the inverse Fourier transformation in Eq. (6), the nabla operator \(\nabla\) reduces to \(\nabla \rightarrow -j{\mathbf {k}}_t+ {\mathbf {u}}_z\frac{{\mathrm {d}}}{{\mathrm {d}}z}\) in the spectral domain. With this transformation, the spectral dyadic Green’s function \(\tilde{\mathsf {G}}_T(\mathbf{k}_t,z-z_0)\) in Eq. (11) can be expressed in terms of the spectral counterpart of the scalar Green’s function given by

$$\begin{aligned} \tilde{G}(\mathbf {k}_t,z-z_0) = \frac{-j}{2k_z}e^{-jk_z |z-z_0|}. \end{aligned}$$
(12)

The associated spectral dyadic Green’s function \(\tilde{\mathsf {G}}_T\) is readily determined in Floris and de Hon (2018) with the transformation \(\nabla \rightarrow -j{\mathbf {k}}_t+ {\mathbf {u}}_z\frac{{\mathrm {d}}}{{\mathrm {d}}z}\), and reads

$$\begin{aligned} \tilde{\mathsf {G}}_T(\mathbf {k}_t,z-z_0)= \frac{M}{2}e^{-jk_z |z-z_0|} \end{aligned}$$
(13)

where the four-by-four matrix M reads

$$\begin{aligned} M= \left[ \begin{array}{c c c c} - \frac{Z k}{k_z}\left( 1 - \frac{k_x^2}{k^{2}}\right) &{} \quad \frac{Z}{k_z}\frac{k_x k_y}{k} &{} \quad 0 &{} \quad -\,{\mathrm {sign}}(z-z_0) \\ \frac{Z}{k_z}\frac{k_x k_y}{k} &{} \quad -\frac{Z k}{k_z}\left( 1-\frac{k_y^2}{k^2}\right) &{} \quad {\mathrm {sign}}(z-z_0) &{} \quad 0 \\ 0 &{} \quad {\mathrm {sign}}(z-z_0) &{} \quad - \frac{ k}{Z k_z}\left( 1 - \frac{k_x^2}{k^{2}}\right) &{} \quad \frac{1}{Z k_z}\frac{k_x k_y}{k} \\ -\,{\mathrm {sign}}(z-z_0) &{} \quad 0 &{} \quad \frac{1}{Z k_z}\frac{k_x k_y}{k} &{} \quad -\frac{k}{Z k_z}\left( 1-\frac{k_y^2}{k^2}\right) \end{array} \right] , \end{aligned}$$
(14)

in which \(Z=\sqrt{\mu_0/\varepsilon}\) and \(k=\omega\sqrt{\mu_0\varepsilon}=\omega n\sqrt{\mu_0\varepsilon _0}\) denote the plane-wave impedance and the wavenumber in the dielectric half-space.

In view of the large number of coordinates associated with the multi-indices \({\mathbf {i}}\) and \({\mathbf {j}}\), it seems daunting to evaluate all the integrals in Eq. (11). Fortunately, the integrals only need to be evaluated for a few Wilson-basis source distributions \(\tilde{w}_{\mathbf {j}}\). Specifically, we only need the displacements and modulations for the few cases \((\ell ,n)=(0,0)\) and \(n \in (0,1)\) for \(0\le \ell \le \ell _{\mathrm {max}}\), applied to the pairs \((\ell _x,n_x)\) and \((\ell _y,n_y)\) of \(\tilde{w}_{\mathbf {j}}\). These specific sources generalize the excitation due to spatially displaced source distributions. Consider for instance a source and observation displacement \(\tilde{w}_{\mathbf {j}}\rightarrow \tilde{w}_{{\mathbf {j}} + {\mathbf {s}}}\) and \(\tilde{w}_{\mathbf {i}}\rightarrow \tilde{w}_{{\mathbf {i}}+{\mathbf {s}}}\) due to a translation multi-index \({\mathbf {s}}=(0,s_x,0,s_y)\) with \(s_x,s_y \in {\mathbb {N}}\). By direct substitution in Eq. (11), we recognize that the coefficients \(\bar{{\mathsf {F}}}_{{\mathbf {j}}+{\mathbf {s}};{\mathbf {i}} + {\mathbf {s}}} = \bar{\mathsf {F}}_{\mathbf {i},\mathbf {j}}\) are readily obtained. We will show later that it generally suffices that the parameter \(\ell _{\mathrm {max}}\) is chosen equal to the maximum of \(\ell _x\) and \(\ell _y\) used in the electromagnetic field.

Depending on the distance between the source and observation plane \(|z-z_0|\), the number of test functions \(\tilde{w}_{\mathbf {i}}\) may be truncated as well. We will consider this truncation first in Sect. 5, where we evaluate the integrals at close proximity of \(z=z_0\), to be able to construct one-way forward or one-way backward propagating fields.

In particular we would like to mention that in the case the distance \(|z-z_0| \downarrow 0\), the antidiagonal in Eq. (13) is constant in \(k_x\) and \(k_y\), and the associated integrals in Eq. (11) are readily evaluated. Upon replacing the two 2D Wilson basis functions \(w_{\mathbf {i}}(x,y)\) and \(w_{\mathbf {j}}(x,y)\) in the orthonormality condition \(\left\langle w_{\mathbf {j}}(x,y),w_{\mathbf {i}}(x,y)\right\rangle =\delta _{{\mathbf {i}}{\mathbf {j}}}\) by their respective inverse Fourier transformations from Eq. (6), we infer that

$$\begin{aligned} \frac{1}{4\pi ^2}\int \limits _{\mathbf {k}_t\in {\mathbb {R}}^2} \tilde{w}_{\mathbf {i}}(-{\mathbf {k}}_t) \tilde{w}_{\mathbf {j}}({\mathbf {k}}_t) \,{\mathrm {d}}{\mathbf {k}}_t= \delta _{{\mathbf {ij}}}. \end{aligned}$$
(15)

Hence, the double integral in Eq. (11) for the antidiagonal of the dyadic Green’s function for \(|z-z_0| \downarrow 0\) is evaluated using Eq. (15).

We evaluate the double integral in Eq. (11) numerically with the aid of fixed-point cubatures that we explain in the companion paper (Floris and de Hon 2018). In view of the branch cut associated with the square root \(k_z({\mathbf {k}}_t) = \sqrt{k^2-k_t^2}\) with \(k_t=|{\mathbf {k}}_t|\), we define \({\text {Im}}\left( k_z\right) <0\), and \({\text {Re}}\left( k_z\right) \ge 0\) if \({\text {Im}}\left( k_z\right) =0\), associated with the physical Riemann surface. Furthermore, by the substitutions \(k_x = k_t \cos (\varphi )\), and \(k_y = k_t \sin (\varphi )\), we convert the double integral over \(k_x\) and \(k_y\) in Eq. (11) to a double integral over \(k_t \in (0,\infty )\) and \(\varphi \in (0,2\pi )\). In view of the branch point at \(k_t=k\), we divide the integration domain of \(k_t\) into two subregions. The region \(k_t \in (0,k)\) is associated with \({\text {Re}}(k_z) \ge 0\), and with the aid of the substitution \(k_t = k\sin (t)\), the \(k_z^{-1}\) singularity that occurs in the matrix M in Eq. (14) is removed. The region \(k_t \in (k,\infty )\) is associated with \({\text {Im}}(k_z) < 0\), and the substitution \(t=\sqrt{k_t^2-k^2}\) removes the \(k_z^{-1}\) singularity.

The integrand in Eq. (11) contains two 2D Wilson basis functions, \(\tilde{w}_{\mathbf {i}}\) and \(\tilde{w}_{\mathbf {j}}\). Each of these basis functions consist of the product of two one-dimensional basis functions. Each basis function consists of two evaluations for the function \(\hat{\theta }\) in Eq. (5) for \(\ell >0\). In turn, the evaluation of the function \(\hat{\theta }\) comprises the weighted sum of complex exponential functions. We show this in detail in Floris and de Hon (2018), and make use of 120 pre-computed weights to achieve an absolute accuracy of \(10^{-10}\).

One may decide to interchange the double integral in Eq. (11) and the sums associated with the function \(\hat{\theta }\) that occurs in each one dimensional Wilson basis function in Eq. (5). The sum of integrals comprise Wilson-basis specific complex exponential functions (Floris and de Hon 2018) and the Green’s functions in Eq. (13). Depending on the modulation parameters \(\ell\), associated with each one-dimensional Wilson basis function, there are at most sixteen cross-terms, leading to weighted sums over sixteen dimensions for the evaluation of each Wilson basis coefficient \(\bar{\mathsf {f}}_{\mathbf {i},{\mathbf {j}}}\).

To avoid that track, we make use of a finite fixed grid of cubature points where we sample the integrand in Eq. (11). More specifically, we employ multiple non-overlapping cylindrical polar cubature grids that are centered about the coordinates \(k_x\) and \(k_y\) where the localized basis functions \(\tilde{w}_{\mathbf {j}}\) peak. In view of Eq. (5), depending on the value of \(l_x\) and \(l_y\), it may be one, two or four non-overlapping cubatures, associated with cross-products that arise by the scalar multiplication of two Wilson basis functions in \(\tilde{w}_{\mathbf {j}}\), in terms of the function \(\hat{\theta }\) in Eq. (5). The cylindrical polar grids are convenient to limit the integration bounds in the \(k_t\) direction, so that we can integrate to the branch point at \(k_t=k\).

That completes the formulation of electromagnetic field in a Wilson basis, generated by Wilson-basis discretized distributions of dipole-like Wilson sources. A complex source beam (CSB) field may be generated by substituting a complex source coordinate in the argument of the Green’s function \(\tilde{\mathsf {G}}_T\), leading to an electromagnetic beam field that strongly resembles a vectorial Gaussian beam. We discuss the construction in detail in the companion paper (Floris and de Hon 2018). We now proceed with the construction of one-way propagating fields in homogeneous space.

5 One-way propagation in homogeneous space in a Wilson basis

As motivated in Sects. 2 and 3, the ability to excite one-way propagating electromagnetic fields is convenient, for instance for addressing reflection–transmission problems at interfaces with homogeneous space. Recall from Sect. 4 that we denote transverse electromagnetic fields in homogeneous media in the Wilson basis by \(\bar{\mathbf {f}}_{{\mathbf {i}},{\mathbf {j}}}^{J_x}\), \(\bar{\mathbf {f}}_{{\mathbf {i}},{\mathbf {j}}}^{J_y}\), \(\bar{\mathbf {f}}_{{\mathbf {i}},{\mathbf {j}}}^{K_x}\), and \(\bar{\mathbf {f}}_{{\mathbf {i}},{\mathbf {j}}}^{K_y}\). The multi-index \({\mathbf {i}}\) denotes the specific Wilson-basis field coefficient, the multi-index \({\mathbf {j}}\) denotes a specific Wilson-basis source distribution, and the superscript denotes the specific electromagnetic source component. The total electromagnetic fields \(\bar{\mathbf {f}}^{\mathbf {J}}_{\mathbf {i}}\) and \(\bar{\mathbf {f}}^{\mathbf {K}}_{{\mathbf {i}}}\) due to electric and magnetic source distributions with source amplitudes \(\bar{c}_{\mathbf {j}}^{J_x}\), \(\bar{c}_{\mathbf {j}}^{J_y}\) and respectively \(\bar{c}_{\mathbf {j}}^{K_x}\), \(\bar{c}_{\mathbf {j}}^{K_y}\) in the Wilson basis are equal to

$$\begin{aligned} \bar{\mathbf {f}}^{\mathbf {J}}_{\mathbf {i}}= & {} \sum _{\mathbf {j}} \bar{c}_{\mathbf {j}}^{J_x} \bar{\mathbf {f}}_{{\mathbf {i}},{\mathbf {j}}}^{J_x} + \bar{c}_{\mathbf {j}}^{J_y} \bar{\mathbf {f}}_{{\mathbf {i}},{\mathbf {j}}}^{J_y}, \end{aligned}$$
(16)
$$\begin{aligned} \bar{\mathbf {f}}^{\mathbf {K}}_{\mathbf {i}}= & {} \sum _{\mathbf {j}} \bar{c}_{\mathbf {j}}^{K_x} \bar{\mathbf {f}}_{{\mathbf {i}},{\mathbf {j}}}^{K_x} + \bar{c}_{\mathbf {j}}^{K_y} \bar{\mathbf {f}}_{{\mathbf {i}},{\mathbf {j}}}^{K_y}. \end{aligned}$$
(17)

In case \(|z-z_0|\downarrow 0\), the exponential function in the spectral Green’s function in Eq. (13) vanishes. Moreover, due to the Wilson-basis source discretization in Eq. (11), and the orthonormality of the Wilson basis in Eq. (15), the relation between source and field distributions on the anti-diagonal of matrix M in Eq. (14) is described through Kronecker delta functions \(\delta _{\mathbf {ij}}\). Furthermore, across the interface \(z=z_0\), we observe that the magnetic fields due to electric sources switch sign, whereas for magnetic sources, the electric field switches sign.

A strategy to achieve a one-way propagating field, is to construct equivalent electric and magnetic source distributions, in such a way that the associated electric and magnetic fields add constructively on one side of the interface, whereas they vanish through destructive interference on the other side.

For example, let the four-vector \(\bar{\mathbf {f}}=[\bar{\mathbf {f}}^{\mathbf {E}}, \bar{\mathbf {f}}^{\mathbf {H}}]^T\) describe a transverse field vector in a Wilson basis with \(\bar{\mathbf {f}}^{\mathbf {H}}\) the desired transverse magnetic field distribution for a one-way propagating wavefield in a homogeneous medium. We invoke Love's equivalence principle and introduce the equivalent transverse electric sources \(\bar{\mathbf {f}}^{\mathbf {H}}\times \mathbf {u}_z\) at z = z0 in the Wilson basis. This leads to the source amplitudes

$$\begin{aligned} \bar{c}_{\mathbf {i}}^{J_x} = -\, \bar{\mathbf {f}}^{\mathbf {H}}_{\mathbf {i}}(2), \quad {\text {and}} \quad \bar{c}_{\mathbf {i}}^{J_y} = \bar{\mathbf {f}}^{\mathbf {H}}_{\mathbf {i}}(1), \end{aligned}$$
(18)

where (2) and (1) indicate the second and first component of the two-vector \(\bar{\mathbf {f}}^{\mathbf {H}}_{\mathbf {i}}=\). The electromagnetic field \(\bar{\mathbf {f}}^{\mathbf {J}}_{\mathbf {i}}=[\bar{\mathbf{f}}_{\mathbf{i}}^{\mathbf{JE}}, \bar{\mathbf{f}}_{\mathbf{i}}^{\mathbf{JH}}]^T\), evaluated through Eq. (16) for \(z=z_{0^+}\) has the same magnetic field as \(\bar{\mathbf {f}}^{\mathbf {H}}\) (apart from a factor 1/2), whereas evaluated for \(z=z_{0^-}\), the magnetic field distribution switches sign. We generate the same magnetic field again, but now through equivalent magnetic sources \({\mathbf {u}}_z\times \bar{\mathbf {f}}^{\mathbf {J},{\mathbf {E}}}_{\mathbf {i}}\), leading to the source amplitudes in the Wilson basis

$$\begin{aligned} \bar{c}_{\mathbf {i}}^{K_x} = \bar{\mathbf {f}}^{\mathbf {J}}_{\mathbf {i}}(2), \quad {\text {and}} \quad \bar{c}_{\mathbf {i}}^{K_y} = - \, \bar{\mathbf {f}}^{\mathbf {J}}_{\mathbf {i}}(1). \end{aligned}$$
(19)

The electromagnetic field \(\bar{\mathbf {f}}^{\mathbf {K}}_{\mathbf {i}}\), evaluated through Eq. (17), also has the same magnetic field as \(\bar{\mathbf {f}}^{\mathbf {H}}\) (apart from a factor 1/2), but now at both sides of the interface \(z=z_0\). The electromagnetic field \(\bar{\mathbf {f}}^+_{\mathbf {i}} = (\bar{\mathbf {f}}^{\mathbf {J}}_{\mathbf {i}} + \bar{\mathbf {f}}^{\mathbf {K}}_{\mathbf {i}})\), is one-way forward propagating, because \(\bar{\mathbf {f}}^{\mathbf {J}}_{\mathbf {i}}\) and \(\bar{\mathbf {f}}^{\mathbf {K}}_{\mathbf {i}}\) are the same for \(z> z_0\), whereas for \(z<z_0\), the electromagnetic fields \(\bar{\mathbf {f}}^{\mathbf {J}}_{\mathbf {i}}\) and \(\bar{\mathbf {f}}^{\mathbf {K}}_{\mathbf {i}}\) carry an opposite sign and cancel in \(\bar{\mathbf {f}}^{+}_{\mathbf {i}}\).

Analogously, the electromagnetic field \(\bar{\mathbf {f}}^-_{\mathbf {i}} = (\bar{\mathbf {f}}^{\mathbf {K}}_{\mathbf {i}} - \bar{\mathbf {f}}^{\mathbf {J}}_{\mathbf {i}})\), is one-way backward propagating for \(z < z_0\), and is zero for \(z> z_0\). The electromagnetic fields \(\left. \bar{\mathbf {f}}^-_{\mathbf {i}}\right| _{ z\uparrow z_0}\) and \(\left. \bar{\mathbf {f}}^+_{\mathbf {i}}\right| _{ z\downarrow z_0}\) have the same magnetic field \(\bar{\mathbf {f}}^{\mathbf {H}}\), but electric fields with opposite signs. Because of that, both fields radiate away from the interface \(z=z_0\).

Likewise, following the same procedure, but starting with constructing equivalent magnetic sources to generate a known electric field \(\bar{\mathbf {f}}^{\mathbf {E}}\), one-way forward and backward propagating fields can be straightforwardly constructed in the Wilson basis as well.

6 Mode-matching for excitations from homogeneous media

In this section, we follow the approach as outlined in Sect. 2 to match an arbitrary incident field from a homogeneous medium to the guided modes in the fiber. As shown in the left schematic of Fig. 1, we first make a decomposition of an arbitrary guided mode in the fiber to a one-way forward and a one-way backward propagating field in the homogeneous medium. We proceed with the construction of equivalent sources that, when the fiber is removed, generate a forward and backward propagating field. Upon placing the fiber back at the interface, the forward and backward propagating fields respectively are the excitation and reflection of the interface, for which the guided mode is the transmission.

Let \(\bar{\mathbf {f}}_p^+ =[\bar{\mathbf {E}}_T^p, \bar{\mathbf {H}}_T^p]^T\) denote the transverse electromagnetic fields in the Wilson basis of an arbitrary guided mode p in the fiber that propagates in the positive z-direction. As a first step, we follow the procedure in Sect. 5, and construct two sets of electromagnetic sources at \(z=z_{0^-}\) that generate a one-way forward field \(\bar{\mathbf {h}}^+_{\mathbf {H}}\), and a one-way backward field \(\bar{\mathbf {h}}^-_{\mathbf {H}}\) in the homogeneous medium. In the remainder of this paper, we use the symbol \(\bar{\mathbf {h}}\) to emphasize the wavefield is a one-way propagating field in a homogeneous medium. Furthermore, the subscript \(_{\mathbf {H}}\) indicates that the wavefield has a transverse magnetic field that is equal to \(\bar{\mathbf {H}}_T^p\).

As pointed out in Sect. 5, \(\bar{\mathbf {h}}^+_{\mathbf {H}}\) and \(\bar{\mathbf {h}}^-_{\mathbf {H}}\) have the same magnetic field, but opposite signs for the electric fields. As a result, the total field \(\bar{\mathbf {h}}^+_{\mathbf {H}} + \bar{\mathbf {h}}^-_{\mathbf {H}}\) at \(z=z_{0^-}\) has the desired magnetic field \(\bar{\mathbf {H}}_T\), and has a zero electric field at the interface \(z=z_0\). In a similar fashion, we configure an additional two sets of electromagnetic sources at \(z=z_{0^-}\), generating a one-way forward field \(\bar{\mathbf {h}}^+_{\mathbf {E}}\), and a one-way backward field \(\bar{\mathbf {h}}^-_{\mathbf {E}}\). The total field \(\bar{\mathbf {h}}^+_{\mathbf {E}} + \bar{\mathbf {h}}^-_{\mathbf {E}}\) has the desired electric field \(\bar{\mathbf {E}}_T^p\), and has a zero magnetic field at the interface \(z=z_0\).

The combination of the four sets of equivalent source distributions generate a the one-way forward propagating field \(\bar{\mathbf {h}}^+= \bar{\mathbf {h}}^+_{\mathbf {E}} + \bar{\mathbf {h}}^+_{\mathbf {H}}\) that describes the incident field, and the one-way backward propagating field \(\bar{\mathbf {h}}^-= \bar{\mathbf {h}}^-_{\mathbf {E}} + \bar{\mathbf {h}}^-_{\mathbf {H}}\) describes the reflected field. By repeating this procedure for all guided modes \(\bar{\mathbf {f}}^p\) of the fiber, we construct the collection of all the mode-equivalent incident and reflected fields \((\bar{\mathbf {h}}^+_p, \bar{\mathbf {h}}^-_p)\) in the homogeneous medium that satisfy the boundary conditions at the interface \(z=z_0\) with the guided mode \(\bar{\mathbf {f}}_p^+\).

The inner-product of two transverse electromagnetic wavefields, evaluated by a double integral over the z-directed Poynting vector in the transverse plane, is readily evaluated in the Wilson basis through

$$\begin{aligned} \left\langle \bar{\mathbf {f}}_u, \bar{\mathbf {f}}_v \right\rangle = \frac{1}{2} \sum _{\mathbf {i}} \bar{\mathbf {f}}_{\mathbf {i},u}(1)\bar{\mathbf {f}}_{\mathbf {i},v}^{\ast}(4) - \bar{\mathbf {f}}_{\mathbf {i},u}(2)\bar{\mathbf {f}}_{\mathbf {i},v}^{\ast}(3). \end{aligned}$$
(20)

The set of guided modes are orthonormal in the sense that the inner product of two arbitrary modes \(\bar{\mathbf {f}}_p\) and \(\bar{\mathbf {f}}_q\) in the Wilson basis satisfy \(\left\langle \bar{\mathbf {f}}_p, \bar{\mathbf {f}}_q\right\rangle = \delta _{pq}\), The collection of mode-equivalent incident fields with elements \(\bar{\mathbf {h}}^+_p\) are in general not orthogonal under the norm in Eq. (20). Therefore, we avoid making projections to expand an arbitrary incident field in terms of mode-equivalent incidents field.

To demonstrate the reflection of a specific incident fields that couple into a specific mode of the fiber, we compute the return loss, which is defined as

$$\begin{aligned} RL[{\text {dB}}] = 10\log _{10}\left( \frac{\left\langle \bar{\mathbf {f}}^I,\bar{\mathbf {f}}^I\right\rangle }{\left\langle \bar{\mathbf {f}}^R,\bar{\mathbf {f}}^R\right\rangle }\right) . \end{aligned}$$
(21)

As an example, we have evaluated the mode-equivalent incident and reflected wavefields \(\bar{\mathbf {h}}^+_p\) and \(\bar{\mathbf {h}}^-_p\) in air that couple into each and every of the guided modes \(\bar{\mathbf {f}}_p^+\) of a standard multi-mode fiber at a wavelength of 850 nm. The associated return loss, evaluated through Eq. (20) are shown in Fig. 4. We assume a circularly cylindrical refractive index profile with a radial parabolic core \(n(r)=n_{\mathrm {co}} \sqrt{1-2\varDelta (r/R)^2}\), for \(0\le r \le R\), with \(n_{\mathrm {co}}=1.46647\), \(\varDelta =0.0093\), and \(R=25\,\upmu\)m. Outside the core, we assume a constant cladding \(n(r) = n_{\mathrm {cl}}=1.45276\), for \(r\ge R\). Following Floris and de Hon (2018), we have computed the 180 vectorial full-wave modal electromagnetic fields and subsequently expanded them in the Wilson basis using two numerical cubatures and using a scaling parameter \(d=3\,\upmu\)m in Eq. (3). For the cubature disc covering the core region, we used 200 points in the radial direction and 800 in the angular direction. For the cladding region, we used an annular cubature ring with an outer radius of 75 \(\upmu\)m, 346 radial points, and 1384 angular points. We used all Wilson basis functions between the multi-indices \({\mathbf {i}}_{\mathrm {min}}=(0,-\,24,0,-\,24)\) and \({\mathbf {i}}_{\mathrm {max}}=(3,24,3,24)\). Depending on the mode that is excited, the return loss varies between 14.45 and 14.7 dB. Along the horizontal axis, the excitation of each and every of the vectorial full-wave modes are numbered sequentially and are grouped by increasing angular index starting with zero. Excitations of modes with an even or odd angular index are respectively colored blue or black. Within each group, the modes are ordered by decreasing phase velocity. The excitation of the fundamental mode is highlighted through a red cross.

Fig. 4
figure 4

The return loss for 180 specific launches that excite each an every of the guided modes. Modes with an even angular index are the blue ● symbols, whereas modes with an odd angular index are the black + symbols. The excitation of the fundamental mode is indicated by a red \(\times\) symbol. (Color figure online)

Full size image

To solve the reflection–transmission problem for an arbitrary field \(\bar{\mathbf {h}}^I\) incident on the interface \(z=z_0\), as shown in the second schematic of Fig. 1, we make a decomposition

$$\begin{aligned} \bar{\mathbf {h}}^I = \sum _p c_p^I \bar{\mathbf {h}}^+_p + \bar{\mathbf {h}}^{I,{\mathrm {rad}}}, \end{aligned}$$
(22)

in terms of the mode-equivalent incident fields \(\bar{\mathbf {h}}^+_p\) for which we already solved the reflection–transmission problems. The part of the incident field \(\bar{\mathbf {h}}^I\) that may not be spanned by the mode-equivalent incident fields \(\bar{\mathbf {h}}^+_p\) is associated with the radiating spectrum of the optical fiber and denoted through \(\bar{\mathbf {h}}^{\mathrm {rad}}\). In this paper, we consider excitations for which \(\bar{\mathbf {h}}^{I,{\mathrm {rad}}}\) is not significant. The reflected field is then described by \(\bar{\mathbf {h}}^R = \sum _p c_p^I \bar{\mathbf {h}}_p^-\) and the transmission by \(\bar{\mathbf {f}}= \sum _p c_p^I \bar{\mathbf {f}}_p^+\).

The coefficients \(c^I_p\) in Eq. (22) are obtained by minimizing the system of equations \(\Vert A{\mathbf {c}}-{\mathbf {b}}\Vert ^2_2\), where the matrix A has elements \(A_{u,v} = \left\langle \bar{\mathbf {h}}^+_v,\bar{\mathbf {h}}^+_u\right\rangle\), and the vector \({\mathbf {b}}\) has elements \(b_r = \left\langle \bar{\mathbf {h}}^I,\bar{\mathbf {h}}^+_r\right\rangle\). The minimum-norm solution \({\mathbf {c}}\) with elements \(c^I_p\) may be obtained through a singular-value decomposition.

In Sect. 8 we solve the reflection–transmission problem for a CSB wavefield incident on an interface with a few-mode fiber, and demonstrate the illumination of the fiber through CSBs that are laterally displaced in the Wilson basis. We proceed in Sect. 7 with the same interface, but now for excitations from the fiber.

7 Mode-matching for excitations from the fiber

In this section, we follow the approach as outlined in Sect. 3 to solve the interface problem with an excitation from the fiber as shown in the left schematic of Fig. 2. Because we interchange the fiber and homogeneous medium compared to the situation treated in Sect. 6, we reuse the field combinations \(\bar{\mathbf {f}}_p^+\), \(\bar{\mathbf {h}}^+_p\) and \(\bar{\mathbf {h}}^-_p\). However, in the current situation, that leaves us with an undesired excitation \(\bar{\mathbf {h}}^-_p\) due to a source somewhere in the homogeneous medium.

Our strategy is to construct another excitation from the right, and designed to interfere destructively with \(\bar{\mathbf {h}}^-_p\), for which we subsequently solve the reflection–transmission problem. The resulting situation is sketched in Fig. 3.

Let \(\bar{\mathbf {f}}^-_p=[\bar{\mathbf {E}}_T^p,-\bar{\mathbf {H}}_T^p]^T\) denote backward propagating guided modes in the fiber, and \(\bar{\mathbf {p}}^p_-\) and \(\bar{\mathbf {p}}^p_+\) the associated modal fields incident on and reflected at the interface respectively. Note that \(\bar{\mathbf {p}}^p_-\) and \(\bar{\mathbf {h}}^p_+\) have the same transverse electric fields, but opposite transverse magnetic fields, because of the opposite direction of propagation. The same holds true for \(\bar{\mathbf {p}}^p_+\) and \(\bar{\mathbf {h}}^p_-\). The fields \(\bar{\mathbf {p}}^p_-\) and \(\bar{\mathbf {p}}^p_+\) are respectively highlighted through dark blue and dark red wiggles in the second schematic of Fig. 2.

We now want to make the decomposition

$$\begin{aligned} \bar{\mathbf {h}}_p^{-} = -\sum _q c_q^p \bar{\mathbf {p}}_q^- - \bar{\mathbf {h}}_p^{-{\mathrm {rad}}}, \end{aligned}$$
(23)

with coefficients \(c^p_q\) obtained by minimum norm expansion with the same procedure as was done for Eq. (22). We complete the reflection–transmission problem in Fig. 3, by adding the field \(\sum _q c_q^p \bar{\mathbf {f}}^q_-\) in the fiber, and by adding the field \(\sum _q c_q^p \bar{\mathbf {p}}^+_q\) to the forward-propagating field in the homogeneous medium.

For the same multi-mode fiber as defined in Sect. 6, we have evaluated the reflection carried by the backward propagating modes, due to the excitation of each and every forward-propagating mode. The results are shown in Fig. 5. The results are basically the same to those obtained in Fig. 4, for launches that excite only one-way forward propagating modes in the fiber. The error in the minimum-norm expansion in Eq. (23) is very small, and the power carried by \(\bar{\mathbf {h}}_p^{-{\mathrm {rad}}}\) is in the order of \(10^{-7}\). This is of the same order of accuracy of the Wilson-basis expansion of the original electromagnetic fields.

Fig. 5
figure 5

The return loss due to launching each and every of the 180 guided modes. The reflection is carried by the guided-modes only. Modes with an even angular index are colored blue, whereas modes with an odd angular index are colored black. The excitation of the fundamental mode is indicated by a red cross mark. (Color figure online)

Full size image

8 SDM fiber illumination by a complex-source beam

As an example related to space-division multiplexing (SDM), we have computed the vectorial full-wave modal fields of a few-mode fiber at a wavelength of 1.550 \(\upmu\)m, with a parabolic core given in Sillard et al. (2014), with a contrast \(\varDelta \approx 0.0055\). We subsequently expanded the fields in the Wilson basis and employed a scaling \(d=5.47\,\upmu\)m using Eq. (3). This choice assures that the ratio \(\lambda /d\) remains unchanged, and as a consequence, we may reuse the computed coefficients in \(\bar{\mathsf {F}}_{\mathbf {i},\mathbf {j}}\) in Eq. (9).

In Fig. 6, we show the return loss due to an interface with air, for the excitation of each and every of the guided modes of the few-mode fiber, equivalent to the situation in Sect. 7. The return-loss values are distributed over a range that is quite comparable to that of a standard multi-mode fiber, despite the reduced contrast and the number of supported modal electromagnetic fields of this fiber. Upon employing a scalar approximation, we indeed obtain 6 degenerate modes, confined in four mode-groups. Because the phase velocities of the vectorial full-wave modes are confined to four isolated small ranges, we were able to identify each vectorial full-wave mode to the associated scalar mode-group labeling.

Fig. 6
figure 6

The return loss due to launching each and every of the 12 guided modes. The reflection is carried by the guided-modes only. Modes with an even angular index are colored blue, whereas modes with an odd angular index are colored black. The excitation of the fundamental mode is indicated by a red cross mark. (Color figure online)

Full size image

In a second example, we evaluated the change in the received power distribution as an incident complex-source beam is laterally displaced with respect to the few-mode fiber in steps of 1 \(\upmu\)m. Due to the the sparse translation operator in the Wilson basis, we were able to straightforwardly evaluate the reflection–transmission characteristics of the normal incident CSB. We used the same complex-source beam that we generated in the companion paper (Floris and de Hon 2018), however this time, we placed the interface at only \(3\,\upmu\)m distance from the source disc, so that the beam is highly collimated. In Fig. 7, the black dashed curve shows the total power carried by the guided modes of the few-mode fiber through the black dashed curve. It starts at 96.6% and despite significantly large displacements, the total transmitted power remains above 96% up to an offset of \(7\,\upmu\)m. For greater offset, it starts to decrease as the tail of the complex-source beam starts to notably cross the core–cladding interface. Through the red dashed line, we highlight the efficiency of the minimum-norm expansion of Eq. (22). For small offsets, the difference in power between the black and red dashed lines is the reflection and is about 3.4% of the incident power (about 14.7 dB return loss). The four thin solid lines indicate the total power in each of the four mode-groups. The fundamental mode is dominantly excited for small offsets. The larger the offset, the larger the contribution to the mode-groups containing the higher-order modes. The four dashed lines deviate from the four solid lines for large offsets, are scaled to the total incident power, rather than the mode-matched incident power. The difference is due to the omitted radiation field.

Fig. 7
figure 7

For a normal incident CSB on a few-mode fiber, the power carried by the guided modes of the fiber as function of lateral offset is indicated by the black dashed line. The red dashed line shows the efficiency of the minimum-norm expansion. For large offsets, the beam crosses the core–cladding interface, and power couples into the radiating spectrum of the fiber modes. The modal power distribution among the four mode groups (labeled in the legend) is indicated by the thin colored lines. The dashed counterparts are normalized with respect to the power of the CSB. (Color figure online)

Full size image

9 Discussion

We have demonstrated that electromagnetically large reflection–transmission problems may be addressed in a flexible manner in the Wilson basis. Although we have specifically considered interfaces consisting of a homogeneous medium and a circularly cylindrical optical fiber, one may in principle connect with other devices as well. One of the appealing features of the Wilson basis is that it consists of functions that are strongly localized in both the spatial and the spectral domain. Apart from efficient electromagnetic field discretizations with basis functions that have a strong resemblence to optical wavefields, the localization and orthonormality aid for instance in the convergence of the spectral Green’s function integrals in Eq. (11).

We have demonstrated how to excite one-way propagating electromagnetic fields in homogeneous media. Moreover, the decomposition of an arbitrary wavefield in one-way forward and one-way backward propagating fields in a fashion similar to the Poincaré–Steklov operator allows for the construction of building blocks to solve electromagnetically large problems in a more flexible manner. The orthonormality of the basis in both domains aided in the ability to configure sources with minimum programming effort. Furthermore, lateral displacement is readily achieved in the Wilson basis through the application of a sparse diagonally-dominant translation operator.

As an example to space-division multiplexing, we have demonstrated the evaluation of modal power distributions as function of lateral displacement of a complex-source beam. Although it is just an example, it demonstrates the impact of the lateral alignment on the modal power distribution for a configuration that is a simple model for a photonic lantern connected to a few-mode fiber. The laterally displaced configurations were straightforwardly evaluated in the Wilson basis framework.

For interface problems consisting of a homogeneous medium and an optical fiber, we solved the reflection–transmission problem using one-way propagating fields in Wilson basis building blocks. In future work, we extend the approach to interfaces of two optical fibers, and to configurations with more than one interface.