1 Introduction

Vertical-cavity surface-emitting laser (VCSEL) constructions capable of direct modulation at bit rates in excess of 40 GBit/s have attracted considerable attention for future high speed long- and medium-haul networks. There are two main approaches to realizing this goal. The first one is the improvement in the direct modulation laser performance (Blokhin et al. 2009), (Karachinsky et al. 2013). For example, it was possible to have an error- free transmission up to 39 and 40 Gbit/bit/s direct modulation working in a temperature up to 100 °C using oxide-confined 850 nm VCSELs with InGaAlAs based active regions. Another method of improving direct (current) modulation is to modulate two active cavities simultaneously and out of phase (Chen et al. 2010). Reducing the photon lifetime by shallow surface etching of the top mirror reflectivity can also improve the direct modulation (Westbergh et al 2010, 2011). The second, fundamentally different, approach to increasing the modulation speed is by using the modulation of the photon lifetime in the cavity as an alternative to current modulation; see e.g. (Avrutin et al. 1993; Germann TD 2012; Panajotov et al. 2010; Paraskevopoulos et al. 2006; Shchukin et al. 2014; Stanley et al. 1994). Advanced semiconductor lasers involving direct modulation of the photon lifetime promise better dynamic properties than lasers with current modulation because their operating speed is less strongly limited by the electron-photon resonance. Several laser designs to implement this principle have been proposed, and initial measurements are all promising. For example, Germann and co-authors have experimentally demonstrated a modulation bandwidth of 30 Gbit/s with 100 mV and 27 dB electrooptic (EO) modulation changes in the voltage and the optical amplitude for small signal modulation, respectively (Germann TD 2012). Large-signal Non-return-to-zero (NRZ) modulation at 40 + GBit/s has been confidently and repeatedly demonstrated in (Shchukin et al. 2014). By using a non-absorbing EO modulator in the first known compound VCSEL (Paraskevopoulos et al. 2006), the electrical bandwidth up to 60 GHz and optical bandwidth more than 35 GHz, restricted by the photodetector response, have been achieved. Strain-compensated multiple quantum wells were used in the active gain region in the VCSEL cavity with 960 nm reference frequency and 3–4 nm blue shift in the modulator region. A more recent experimental achievement for photon lifetime modulation was conducted by utilizing the influence of the aperture size on the performance of 850 nm InGaAlAs oxide-confined VCSELs (Bobrov et al. 2015). When the aperture size is decreased to an optimum value of 4–6 μm and the photon lifetime is reduced from 4 to 1 ps, there is a saturation in the the maximum 3 dB modulation bandwidth at 21 GHz.

These experimental results have been supported, and partly stimulated, by theoretical studies using rate equation (RE) models (Avrutin et al. 1993; Germann TD 2012; Shchukin et al. 2008). Small-signal modulation at moderate frequencies has been analysed (Germann TD 2012) and showed signs of a broad, large resonant peak consistent with the formula presented in (Avrutin et al. 1993). Experiments and large-signal simulations show that the best performance of electrooptically modulated VCSELs is realised at moderately small rather than large bias currents (Shchukin et al. 2008), which is completely different to the case of current modulation, and not immediately obvious from the published small-signal analysis of photon lifetime modulation (Avrutin et al. 1993). We believe one reason for this is that the small-signal analysis of (Avrutin et al. 1993) considered the modulation of the photon density inside the laser cavity, rather than the measurable power outside the laser which is also influenced by the outcoupling loss modulation, particularly as the modulation subcavity may have some dynamic properties of its own. Another limitation of the existing theories, whether small-signal (Avrutin et al. 1993) or large-signal (Shchukin et al. 2008) is that they are based on “traditional” rate equations for the power of the output only without considering the frequency response, whereas in a complex resonator system such as a coupled-cavity laser, amplitude and phase/frequency modulation can be expected to be intricately interrelated. These limitations are addressed in the current paper. We start with explaining the design considered and the operating principle in Sect. 2. A modified rate equation model involving careful analysis of both amplitude and frequency/phase of laser emission, as well as the spectrally selective nature of the laser cavity, is presented in Sect. 3. The model is based on the analysis for complex eigenvalues (frequency detunings and amplitude variation rates) of the compound cavity modes and used it to describe the laser operation and predict the performance beyond current experimental conditions, under both small- and large signal modulation conditions. The photon lifetime in the modulator subcavity is found to be the ultimate limitation of the modulation speed. A summary of the findings concludes the paper in Sect. 4.

2 The design considered and the operating principle

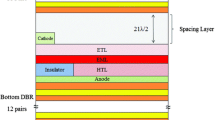
Figure 1 shows the schematic of a representative Compound Cavity Laser which we used in our analysis. The laser is formed by two subcavities; the top, modulator, subcavity is a passive Fabry–Perot resonator whose reflectivity R m (t) is modulated via electrooptically varying the optical properties of a modulator layer contained within the subcavity by applying time-varying reverse bias voltage. In a typical design, the intermediate Distributed Bragg reflector (DBR) has 25–35 periods of two layers of alternating composition, the top DBR consists of 15–25 periods; the resonator thus can be substantially asymmetric. It should be noted that the relatively low Q-factor modulator helps achieving efficient light coupling and low chirp (Paraskevopoulos et al. 2006). Throughout the analysis, we consider only refractive index modulation (no absorption modulation). Indeed, according to (Shchukin et al. 2008), the electrorefraction effect (Miller et al. 1985) plays a dominant role in modulating R m (t) as compared to electroabsorption.

Fig. 1
figure 1

Schematic of a compound cavity laser

Full size image

The bottom subcavity is the active one, containing the electrically pumped active layer and terminated by the bottom DBR whose reflectivity is assumed to be very large (about 0.999). Three electric contacts are used in our device to have a good control when changing the current in the active subcavity and the reverse bias voltage for the modulator subcavity as shown in Fig. 1.

In a realistic design (see e.g. (Shchukin et al. 2008)), the mesas containing the two subcavities have different lateral diameters; however, as in the previous analysis, we use a purely one-dimensional approach, which is justified because the diameter of the active part of the laser is determined by the current aperture and is thus smaller than the mesa diameter. In this design, we assumed the length confinement factor of 0.0209 and the enhancement factor due to the standing wave pattern of 1.83. As a result, the overall confinement factor in the active subcavity is assumed to be 0.0209 × 1.83 = 0.0382, as in (Coldren 1995; Rahman & Winful 1994; Wenzel et al. 1996). The fundamental principle of EO modulation is the modulation of the photon lifetime in the active subcavity, determined by the reflectance R m of modulator subcavity, which is calculated as:

$$R_{m} = r_{m} r_{m}^{*} ; r_{m} = r_{am} + \frac{{\theta_{am } \theta_{ma} r_{mt} e^{{ - j2K_{m} L_{m} }} }}{{1 - r_{ma} r_{mt} e^{{ - j2K_{m} L_{m} }} }}$$
(1)

Here r kl and θ kl are complex (and strictly speaking wavelength dependent, though the dependence is relatively weak) amplitude reflectances and transmittances of multistack DBRs, with the light incidence direction from layer k towards layer l. The layers are denoted k, l = a, m, t, where a is defined as inside the active subcavity, m as inside the modulator subcavity, and t as outside the top layer (see Fig. 1). The values are calculated at the wavelength λ. Furthermore, in Eq. (1):

$$K_{m} = \frac{{2\pi n_{m} }}{\lambda } = \frac{{n_{m} \omega }}{c}$$

is the spatially averaged wave vector in the passive (EO modulator) subcavity, n m being the average refractive index in this subcavity, λ = 2πc/ω the wavelength in vacuum (ω being the optical angular frequency) and c is the speed of light in vacuum. Then, EO variation of the average refractive index (n m ) of the modulator subcavity leads to a corresponding variation in the wave vector K which makes a change to R m according to Eq. (1); this changes the photon lifetime and the mirror transparency, both of which lead to the modulation of the output light.

Figure 2 shows the calculated reflectivity versus incident light wavelength for the EO modulator subcavity for a specific case of the GaAs/Al0.2Ga0.8As 80 \({\dot{\text{A}}}\) QW laser operating at λ = 0.9685 µm. Τhe reflectivity R m is very close to one for a broad range of the wavelength λ between 0.9 µm and 1.1 µm but has a narrow notch, in the case simulated at λ ≈ 0.9666 µm. The inset of Fig. 2 illustrates how the position of the notch, and thus the reflectance in the relatively narrow range of wavelengths within it, can be modulated by changing the reflective index. It can be seen that the notch can be shifted by 1 nm when the average refractive index is modulated by ~10−3. Figure 2 illustrates the fact that a substantial variation of the reflectance is possible with the average refractive index varied by about ~10−3, but also highlight the narrow wavelength range in which this variation occurs.

Fig. 2
figure 2

Calculated Reflectivity versus incident light wavelength for the EO modulator subcavity. Inset: Spectral shape of the reflectance notch with n m  = 3.620 (solid curve) and n m  = 3.621 (dashed curve) calculated using full transfer matrix analysis

Full size image

3 The modified rate equation model

3.1 The model

In designing the model, we follow the approach used previously for Distributed Feedback (DFB) lasers (see e.g. Wenzel et al. 1996) and for multimode compound cavity lasers (see e.g. Avrutin et al. 1999). Namely, the laser cavity is treated as a complex resonator, and a complex eigenfrequency of this resonator is found, which is then used to describe the laser dynamics. Τhe electrooptically modulated VCSEL is very naturally suited for such an approach, because the complex resonator in this case can be defined by considering the active subcavity as a quasi-Fabry–Perot resonator terminated, on one side, by the bottom reflector with a (complex, generally speaking) amplitude reflectance r b and on the other side, by the EO modulator subcavity treated as a passive, frequency-dependent reflector with a complex reflectance r m (ω), where ω is the complex eigenfrequency sought. The value of r m(ω) is calculated from Eq. 1 with the average wave vector in the form of:

$$K_{m} \left( \omega \right) = \frac{{\left( {n_{m} + \varGamma_{m} \Delta n_{EO} } \right)\omega }}{c}$$
(2)

Here \(\Delta n_{EO}\) describes the time-dependent correction to the refractive index of the modulator layer caused by EO modulation. \(\varGamma_{m} \approx \frac{{d_{m} }}{{L_{m} }}\) (assuming the modulator layer is thick enough that the standing wave factor is near one) is the confinement factor of the modulator layer, d m- being the modulator layer thickness and L m, the total physical thickness of the modulator subcavity, including any spacer layers between the modulator layer and the DBRs but not including the penetration into mirrors. The complex eigenfrequency is then found by solving the usual threshold/resonant condition of a Fabry–Perot type cavity (due to the short cavity length, the equation has only one solution):

$$r_{m} \left( \omega \right)r_{b} (\omega) \exp \left[ 2{\left( { - j\frac{{\left( {n_{a} + \Delta n_{a} } \right)\omega }}{c} + \varGamma_{a} \frac{g}{2}} \right)L_{a} } \right] = 1$$
(3)

It is convenient to write this solution in terms of a frequency correction \(\Delta \omega = \omega - \omega_{ref}\), where the (real) reference frequency \(\omega_{ref}\) is arbitrary but can be conveniently taken, for example, as the position of the reflectance spectrum notch (Fig. 2) in either on or off-state. Then, the complex instantaneous frequency correction \(\Delta \omega\) is defined from a transcendental equation:

$$\Delta \omega = v_{g} \left[ { - \frac{j}{2}\left( {\varGamma_{a} g - \frac{1}{{L_{a} }}\ln \frac{1}{{r_{m} \left( {\omega_{ref} + \Delta \omega } \right)r_{b} }}} \right) - \frac{{\Delta n_{a} \omega_{ref} }}{c} + \left( {\frac{q\pi }{{L_{a} }} - \frac{{n_{a} \omega_{ref} }}{c}} \right)} \right]$$
(4)

Here \(v_{g}\) is the group velocity, L a is the geometrical thickness of the active subcavity, \(\varGamma_{a}\) is the confinement factor for the active area, g is the time-dependent gain, n a is the refractive index of the active layer subcavity, averaged over the length in the same way as n m is averaged over the modulator subcavity. The refractive index varies in time primarily due to self-phase modulation in the active layer; its time-dependent part can be quantified as:

$$\Delta n_{a} \approx \frac{c}{{2\omega_{ref} }}\varGamma_{a} \alpha_{H} \left( {g - g_{th} } \right)$$
(5)

where \(\alpha_{H}\) is the Henry linewidth enhancement factor in the active layer and \(g_{th}\) is the gain at threshold which we used as a reference value.

The choice of reference frequency near the modal frequency to ensure that | \(\Delta \omega | \ll \omega_{ref}\) means that we can introduce a parameter q which is the number of half-wavelengths of light in material fitting (roughly) in the distance L a . It depends on the VCSEL design, mainly the thickness L a , and it is an integer number chosen in such a way that:

$$q \approx \frac{{2n_{a} L_{a} }}{\lambda } - \frac{1}{2\pi }\arg \left( {r_{m} r_{b} } \right)$$
(6)

where λ = \(2\pi c/\omega_{ref}\) is the operating wavelength, and r m can be estimated in the on- or off-state.

The frequency ω (or frequency correction Δω) has a real part, which determines the time-dependent spectral position of the lasing mode and thus the chirp of laser emission, and an imaginary part, which reflects the balance of gain and loss (the latter including the outcoupling loss, which is frequency dependent through r m (ω)). The imaginary part determines the dynamics of photon density (in the active subcavity) N p , giving a modified rate equation in the form:

$$\frac{{dN_{p} }}{dt} = - 2{\times} \text{Im} \left( {\Delta \omega \left( t \right)} \right)N_{p} \left( t \right) + \frac{{\beta_{sp} N}}{{\tau_{sp} \left( N \right)}}$$
(7)

where \(\beta_{sp}\) is the spontaneous emission factor. The dynamics of the carrier density N is determined by a standard rate equation:

$$\frac{dN}{dt} = \frac{{\eta_{i} I}}{eV} - \left( {\frac{1}{{\tau_{sp} \left( N \right)}} + \frac{1}{{\tau_{nr} \left( N \right)}}} \right)N - v_{g} \frac{g\left( N \right)}{{1 + \varepsilon N_{p} }}N_{p}$$
(8)

in which N and N p are the the electron and photon densities, respectively, \(\eta_{i}\) is the internal quantum efficiency, I is the injected current, e is electron charge, V is the volume of the active region; \(\tau_{sp} = \left[ {B_{1} N^{2} /\left( {1 + b_{1} N} \right)} \right]^{ - 1}\) and \(\tau_{nr} = \left( {A_{1} + C_{1} N^{3} } \right)^{ - 1}\) are the spontaneous and nonradiative recombination times of carriers, respectively, g(N) is the optical gain in the active layer, \(\varepsilon\) is gain compression factor (see Table 1).

Table 1 Compound VCSEL parameters
Full size table

Finally, the model includes a differential equation taking into account the electromagnetic resonance in the modulator subcavity. The equation is derived by considering the modulator section in frequency domain and then substituting the imaginary part of the frequency correction by a time derivative. The result is conveniently expressed as:

$$\frac{{d\tilde{E}_{t} }}{dt} = \left( { - \frac{1}{{2\tau_{cm} }} - j\left( {\Delta \omega^{\prime } (t{} )-\Delta \omega_{n0} + \varGamma_{m} \frac{{\Delta n_{EO} (t)}}{{n_{g} }}\omega_{ref} } \right)} \right)\tilde{E}_{t} + \frac{{\sqrt {2T_{i} T_{t} } }}{4}\frac{{v_{g} }}{{L_{eff,m} }}E_{a}$$
(9)
$$\tau_{cm} = \frac{{L_{eff,m} }}{{v_{g} \left( {1 - \sqrt {R_{i} R_{t} } } \right)}} \approx \frac{{2L_{eff,m} }}{{v_{g} \left( {T_{i} + T_{t} } \right)}}$$
(10)

Here \(\tilde{E}_{t} = E_{t} { \exp }\left( {j\varphi_{t} } \right)\) describes the complex amplitude of the output field emitted from the modulator subcavity (the top mirror), \(E_{a} = \sqrt {N_{p} }\) is the field amplitude inside the active subcavity. Note that in the equation written in the form above, E a is a real value, which means that the complex amplitude of the output light is actually \(\tilde{E}^{c}_{t} = \tilde{E}_{t} \exp \left( {j\smallint \Delta \omega^{\prime } dt} \right)\), where Δω′ = Re(Δω) is the instantaneous frequency correction in the active subcavity. Furthermore, Δω n0  = ω n0 −ω ref is the position of the notch in the modulator subcavity transmission in the absence of modulation (Δ nEO  = 0), τ cm is he effective photon lifetime in the modulator subcavity (which was neglected in the simple model since it was assumed to be very fast), \(R_{i} = \left| {r_{ma} } \right|^{2}\) and \(R_{t} = \left| {r_{mt} } \right|^{2}\) are the intensity reflectances of the intermediate and top reflectors (the two reflectors forming the modulator subcavity) respectively, \(T_{i} = 1 - R_{i}\), \(T_{t} = 1 - R_{t}\) are the transparencies of the intermediate and top DBR stacks, and

$$L_{eff, m} = L_{m} + \frac{{v_{g} }}{2}\left. {\left( {\left| {\frac{\partial }{\partial \omega }\arg \left( {r_{ma} } \right)} \right| + \left| {\frac{\partial }{\partial \omega }\arg \left( {r_{mt} } \right)} \right|} \right)} \right|_{{\omega_{ref} }}$$
(11)

is the effective thickness of the modulator section. The effective thickness is typically a fraction of a micron greater than the physical one, as it considers the penetration of the field into the mirrors. The power emitted from the laser can be calculated as:

$$P \approx v_{g} \hbar \omega A_{x} E_{t}^{2}$$
(12)

where \(A_{x}\) is the cross-section of the aperture. The instantaneous frequency determining the chirp of the output laser emission is:

$$\Delta \omega_{t} = \frac{d}{dt}\arg \left( {\tilde{E}^{c }_{t} } \right) = {\Delta \omega^\prime\left( t \right)} + \frac{d}{dt}\varphi_{t}$$
(13)

It is worth noting that an alternative formalism for describing the laser dynamics with phase included would consist of writing out an equation similar to Eq. (9) for the active subcavity, with an injection term representing light reflected from the modulator subcavity, rather than solving a transcendental Eq. (4) for the instantaneous frequency. A model of that type treats the laser as a system of two subcavities, one active, one passive but modulated, treated on the same footing. The results should be very similar to those of the current formalism so long as the dynamics of light inside the active subcavity remain slower than the modulator subcavity round-trip (which is the case for most realistic designs). We chose the formalism presented above as it represents an easy logical step from the simple rate equation model used previously by ourselves and other authors. Indeed, in the absence of the explicit expression for the frequency dependence of r m , interrelated with the laser chirp as described by Eq. (4), the detuning Δω becomes constant and Eq. (7) then gives the standard rate equation for photon density.

$$\left. {\frac{{dN_{p} }}{dt}} \right|_{RE \ model} = \frac{{\beta_{sp} N}}{{\tau_{sp} }} + \left( {\varGamma \frac{G\left( N \right)}{{1 + \varepsilon N_{p} }} - \left( {\tau_{ph - in}^{ - 1} + \tau_{ph - out}^{ - 1} } \right)} \right)N_{p}$$
(14)

\(\tau_{ph - in}^{ - 1} = v_{g} a_{\text{int}}\) and \(\tau_{ph - out}^{ - 1} \left( t \right) = \frac{{v_{g} }}{{2 L_{eff,a} }}\ln \frac{1}{{R_{b} R_{m} \left( t \right)}}\) being the photon decay rates (inverse photon lifetimes) due to internal (a int ) and outcoupling losses. Assuming in addition an infinitely fast photon lifetime of the modulator subcavity as is normal in standard rate equations, we get an instantaneous relation between the photon density and output power (P) as:

$$P_{RE \ model} = h\nu_{ph} V_{opt} \tau_{ph - out}^{ - 1} \left( t \right) N_{p} \left( t \right)$$
(15)

where hν ph  = hc/λ is the photon energy (\(h\) being Planck’s constant), and \(V_{opt}\) is the modal volume. Then, the modified rate equation model is reduced to the standard rate equation model used in our initial studies (Albugami 2015) and consisting of Eqs. (8, 14, 15).

The major additional capabilities offered by the full modified RE model, with the electromagnetic Eqs. (4) and (7) replacing Eqs. (14) and with (9) instead of (15), over the standard RE model are as follows. Firstly, by describing frequency and phases, as well as intensity, of the signal, we can evaluate the chirp and optical spectra, as well as recalculating the effect of the refractive index variation on the photon lifetime more accurately and consistently. Secondly, by including Eq. (9) rather than using the instantaneous relation (Eq. 15) between the photon density and the output power, we can take into account the speed limitations because of the spectral selectivity of the modulator subcavity (spectral width of the notch in Fig. 2); as will be shown later, this eliminates unphysical abrupt fronts in the eye diagram (Fig. 7). Most of the results obtained below are thus obtained with the full, modified rate equations model, but some results using the reduced, standard model are shown for comparison. The main parameters used in the simulations, together with their values where appropriate, are summarized in Table 1.

3.2 Small signal analysis

To analyse the small signal response, dynamic variables are separated into steady state values (denoted below by the subscript 0) and small harmonic variations denoted by the sign \(\delta\). The origin of modulation in this case is the electrooptically modulated refractive index:

$$\Delta n_{EO} = \Delta n_{EO0} + \delta n_{EO} \exp \left( {j\varOmega t} \right) + {\text{c}} . {\text{c}},$$

This leads to small-signal modulation of the electron density

$$N = N_{0} + \delta N\exp \left( {j\varOmega t} \right) + {\text{c}} . {\text{c}} .$$
(16)

and the field amplitudes in the active subcavity and outside the laser:

$$E_{a} = E_{a0} + \delta E_{a} \exp \left( {j\varOmega t} \right) + {\text{c}}.{\text{c}}.; E_{t} = E_{t0} + \delta E_{t} { \exp }\left( {j\varOmega t} \right) + {\text{c}}.{\text{c }}$$

which can be recalculated into photon density modulation variation, e.g. \(\delta E_{a} = \frac{{\delta N_{p} }}{{2\sqrt {N_{p} } }}\)

These are connected to the small-signal modulation of the lasing frequency \(\Delta \omega\) and the phase shift \(\varphi_{t}\) between the fields inside and outside the cavity \(\Delta \omega = \Delta \omega_{0} + \delta \omega \exp \left( {j\varOmega t} \right) + {\text{c}} . {\text{c}} .; \Delta \varphi_{t} = \varphi_{t0} + \delta \varphi_{t} \exp \left( {j\varOmega t} \right) + {\text{c}} . {\text{c}} .\)

(the latter only required if small-signal chirp is analysed).

The steady state values of the carrier and photon densities N 0 and N p0 as well as the operating frequency \(\Delta \omega_{0} ,\) have to be found from the steady state solutions of the rate equation system, including the transcendental Eq. (4), and so cannot be written in a closed form. The linear differential Eq. (9), on the other hand, can be easily solved in steady state, giving the transmission properties of the modulator subcavity:

$$E_{t0} = \frac{{\sqrt {2T_{i} T_{t} } }}{{T_{i} + T_{t} }}\cos \varphi_{t0} E_{a0}$$
(17)

where

$$\tan \varphi_{t0} = - 2\tau_{cm} \Delta \omega_{i}$$

and

$$\Delta \omega_{i} = \Delta \omega_{0} + \varGamma_{m} \frac{{\Delta n_{EO0} }}{{n_{m} }}\omega_{ref}$$

is the steady state detuning between the incident light and the position of the transmission notch in the modulator subcavity. A combination of the three equations above gives the steady-state relation between the internal and output intensity or power as:

$$\left| {\frac{{E_{t0} }}{{E_{a0} }}} \right|^{2} = \frac{{2T_{i} T_{t} }}{{\left( {T_{i} + T_{t} } \right)^{2} }}\frac{1}{{1 + \left( {2\tau_{cm} \Delta \omega_{i} } \right)^{2} }}$$
(18)

(which stems from the assumption Δω ≪ ωref and is a very good approximation for the actual form presented in Fig. 2 and Eq. (1); note that the result differs from the transmittance of the modulator section by a factor of two, as only half of the internal intensity is travelling in the output direction).

Linearising the differential Eq. (9), we can relate the small-signal modulations of light amplitude outside and inside the laser as:

$$\delta E_{t} = \frac{1}{{\left( {j\varOmega + \frac{1}{{2\tau_{cm} }}} \right)^{2} + \Delta \omega_{\iota }^{2} }}\times$$
$$\left[ {\left( {\frac{1}{{2\tau_{cm} }}\left( {j\varOmega + \frac{1}{{2\tau_{cm} }}} \right) - \Delta \omega_{i}^{2} } \right)} \right.\left. {\frac{{\sqrt {2T_{i} T_{t} } }}{{\left( {T_{i} + T_{t} } \right)}}\cos \varphi_{t0} \delta E_{a} + \Delta \omega_{i} E_{t0} \left( {\delta \omega + \frac{{\varGamma_{m} \omega_{ref} }}{{n_{m} }}\delta n_{{{\rm E}{\rm O}}} } \right)} \right]$$
(19)

Linearisation of the transcendental Eq. (4) gives a small-signal complex frequency variation in the form:

$$\delta \omega = - jv_{g} \frac{{\varGamma_{a} \left( {1 - j\alpha_{H} } \right)\delta g + \frac{1}{{2L_{a} }}\varGamma_{m} \frac{{\partial r_{m} }}{{\partial n_{m} }}\delta n_{EO} }}{{1 + j\frac{{v_{g} }}{{2L_{a} }}\left. {\left( {\frac{{\partial r_{b} }}{\partial \omega } + \frac{{\partial r_{m} }}{\partial \omega }} \right)} \right|_{{\omega_{ref} }} }}$$
(20)

Here variation of gain at the modulation frequency is determined in the same way in standard rate equations, namely

$$\delta g = \frac{\partial g/\partial N }{{1 + \varepsilon N_{p} }}\delta N - \frac{\varepsilon g}{{\left( {1 + \varepsilon N_{p} } \right)^{2} }}\delta N_{p}$$
(21)

With these notations, the expressions for photon (and electron) density variations can be obtained in a closed form (see the Appendix, which also shows the small signal formulas for the standard rate equation case).

As we found earlier (Albugami 2015), in the standard rate equation model, at high enough currents we get a situation when at high frequencies (above the electron-photon resonance) the laser response is higher than at low frequencies approaching DC. In terms of the 3 dB cutoff frequency, this means that this parameter tends to infinity as the current approaches a certain critical value and is not defined above this critical current within the standard rate equation approach, as seen in Fig. 3, which represents the small-signal modulation curves calculated using the standard RE model. This is however an artefact of using the instantaneous relation (15) between the internal and output power, and is thus removed in the full modified rate equation approach, as shown in Figs. 4 and 5. Figure 4 shows the small-signal response of EO laser modulation calculated using the full modified RE model at three different values of bias current (for 35 periods in the intermediate reflector and 17 periods in the top reflector). At low modulation frequencies, the figure, with the characteristic broad resonant peak, is fairly similar to the ones calculated using the standard rate equation model (Fig. 3). However at high frequencies, there is no plateau seen in Fig. 3, and the 3 dB cutoff modulation frequency can be determined in all designs. This is due to the limitation introduced by the modulator subcavity photon lifetime.

Fig. 3
figure 3

Small-signal response of electrooptic laser modulation calculated in the standard rate equation model at three different values of bias current

Full size image
Fig. 4
figure 4

Small-signal response of electrooptic laser modulation calculated in the modified rate equation model at three different values of bias current (for 35 periods in the intermediate reflector and 17 periods in the top reflector)

Full size image
Fig. 5
figure 5

Calculated small-signal response of electrooptic laser modulation for two different designs of top reflector. 35 periods in the intermediate reflector; current 10 mA

Full size image

The figure shows that the transfer function for the properly designed compound cavity laser is capable of providing 3 dB cutoff frequency as high as hundreds of GHz in a broad range of currents; the cutoff frequency is a rather weak function of total power/current. This can be expected since the roloff of the modulation curve at high frequencies, and hence the 3 dB cutoff frequency, are mainly determined by the lifetime of the photons in the modulator subcavity which does not depend on current in the active subcavity. With the optimised laser design (a large R i ensuring the external-modulator-type operation of the modulator section, and a more modest R t ensuring the value of τcm of the order of picoseconds), this limit is indeed of the order of hundreds of gigahertz, and thus not a concern for any realistic modulation scheme. The situation can be different however with a design of the modulator section less optimised for high speed operation. Figure 5 shows that with a large (but perfectly technologically achievable) number of periods in the top reflector (hence R t ), when the notch in the reflectance of the modulator section (the peak in the transmittance) becomes narrow meaning a large photon lifetime in the modulator subcavity, the 3 dB frequency drops as low as ~10 GHz. At the same time, the amplitude of output power modulation, given the same (small) refractive index modulation, increases with an increased number of top reflector periods, though this is not shown in Fig. 5 in which the transfer function is normalised to 0 dB at low frequencies. As will be discussed later, these effects of the reflector design manifest themselves also in the results of large signal modulation simulations (see Fig. 9).

3.3 Large signal analysis

For the large signal analysis, the rate equations, either modified or standard for comparison, are solved directly numerically for NRZ digital pseudorandom modulation. The results are used to construct an eye diagram as seen by an ideal receiver. In addition, since the modified RE model gives both the amplitude and phase/frequency of the output field, we can analyse the optical spectrum of the laser emission.

Figure 6 shows a typical calculated output spectrum at 40 GBit/s, with the spectrum near the main peak, with a smoothed line for easier evaluation of the spectral width. The smoothing is performed by adjacent averaging of points, as in, say, (Ryvkin et al. 2009). While the spectrum is somewhat asymmetric, implying that there is a bit of chirp in the output, the width at half maximum is 20 GHz, and at e −2 close to 40 GHz, or the bit rate, or the Nyquist limit for NRZ modulation, which implies that the chirp is low.

Fig. 6
figure 6

Amplitude spectrum of output field at 40 GBit/s

Full size image

Figure 7 shows the eye diagrams calculated using the standard and modified rate equation models, respectively, for the same amplitude of refractive index modulation. As can be expected, the modified RE model is free from unphysical abrupt changes from OFF to ON states; instead, it shows gradual transients with elements of oscillatory behaviour in the off state (which is associated with the frequency detuning between the light frequency and the resonator).

Fig. 7
figure 7

Amplitude spectrum of output field at 40 GBit/s

Full size image

To quantify the quality of modulation represented by eye diagrams, we calculated the modulation quality factor:

$$Q = \frac{{\overline{{P_{\left( 1 \right)} }} - \overline{{P_{\left( 0 \right)} }} }}{{\sigma_{\left( 1 \right)} + \sigma_{\left( 0 \right)} }}$$
(22)

where \(\overline{{P_{\left( 1 \right)} }}\), \(\overline{{P_{\left( 0 \right)} }}\) are the mean values of the power corresponding to the logical one and zero states, respectively; \(\sigma_{\left( 1 \right)}\), \(\sigma_{\left( 0 \right)}\) are the corresponding standard deviations. In all the figures below, the quality factor Q was calculated using the modified rate equation model.

Figure 8 shows Q as function of the number of layer pairs (periods) in the top reflector DBR stack. As seen in the figure, there is an optimum number, in this case around 17. When we increase the number of periods beyond that number, the photon lifetime in the modulator subcavity is increased, leading to longer transients and closing the eye diagram, hence bad quality factor. This is illustrated in Fig. 9. When the number of top reflector period becomes too low, on the other hand, the modulation of power (P 1−P 0) becomes lower, hence lower quality factor. We observe that the optimum number of periods is not a strong function of the current, so once optimised, a laser should be able to provide good modulation quality at all currents.

Fig. 8
figure 8

Modulation quality factor as function of the number of periods in the top reflector for three different currents

Full size image
Fig. 9
figure 9

Eye diagrams for I = 10 mA, 40 GBit/s, 35 periods in the intermediate reflector, 17 (a) and 23 (b) periods in the top reflector

Full size image

Figure 10 shows the modulation quality as a function of the number of periods in the intermediate reflector. Again, there is an optimum number of periods, in this case around 32. When the number of periods is increased beyond that value, there is less output power hence somewhat lower quality factor. When the number of periods is decreased below the optimum level, the width of the transmission notch increases, leading to less efficient modulation; as a result, the eye diagram deteriorates, hence the lower quality factor. This is illustrated by Fig. 11 which shows eye diagrams for I = 10 mA, 19 periods in the top reflector, 33 and 31 periods in the intermediate reflector, respectively.

Fig. 10
figure 10

Modulation quality factor as function of the number of periods for the intermediate reflector

Full size image
Fig. 11
figure 11

Eye diagrams for I = 10 mA, 40 GBit/s, 19 periods in the top reflector, 33 (a) and 31 (b) periods in the top reflector

Full size image

We study next the dependence of the modulation quality on current. Figure 12 shows the modulation quality factor as a function of current for bit rates of 40 and 80 GBit/s. At very low current values, the modulation quality decreases simply due to lower power, given a similar distribution of the on-state. There is an optimum (rather modest) current value, though at higher currents, the modulation quality is not far below optimum. Similar qualitative tendencies are observed for 40 and 80 GBit/s; quantitatively, the quality factor is smaller than at the lower modulation rate, but still acceptable for digital communications, particularly with the optimised current and design. Figures 13 and 14 show eye diagrams for a given structure and bit rates, for currents of 10 and 2 mA, illustrating the origin of the lower modulation quality at low currents seen in Fig. 12, which appears to be due to the spread of the “one” level being more important when compared to the overall small difference between the “zero” and “one”.

Fig. 12
figure 12

Quality factor as function of the bias current for 40 GBit/s modulation

Full size image
Fig. 13
figure 13

Eye diagrams for 40 GBit/s, 32 periods in the intermediate reflector, 19 periods in the top reflector for I = 10 mA (a) and I = 2 mA (b)

Full size image
Fig. 14
figure 14

Eye diagrams for 80 GBit/s, 32 periods in the intermediate reflector, 19 periods in the top reflector for I = 10 mA (a) and I = 2 mA (b)

Full size image

4 Discussion and conclusions

To conclude, we considered, for the first time to our knowledge, both amplitude and frequency (phase) dynamics of laser emission in an electrooptically modulated compound cavity VCSEL. As the standard rate equation model has limitations in describing high-frequency modulation, we introduced the modified rate equation model taking into account the spectrally selective nature of the laser cavity and the finite photon lifetime in the modulator. We found that the ultimate modulation frequency limit is determined by the photon lifetime of the modulator subcavity. Large signal simulations have shown that the quality of modulation depends non-monotonically on the numbers of dielectric grating periods in the top and intermediate mirrors, so that there is an optimum cavity design usable in a broad range of currents. High quality factors at modulation bit rates of up to 80 Gbit/s were predicted.

Note that in this paper, we concentrated on the electromagnetic/carrier kinetic model only, not considering the electrical circuit limitations. Indeed, Zujewski and co-authors have proved that the modulation speed limitation due to associated electrical circuit, as studied in (Zujewski et al. 2011), of coupled-cavity vertical-cavity surface-emitting laser (CC-VCSEL) can be avoided using a traveling wave electrode design (Zujewski et al. 2012). They were also able to make up for the low 50 Ω impedance of the modulator which allow the electrical cutoff frequency to go up to 330 GHz (Zujewski et al. 2012).

Comparison with other advanced modulation schemes in VCSELs is reserved for future work.