1 Introduction

The femtosecond laser based electrooptic sampling (EOS) is a very powerful tool for the characterization of ultrafast electronic devices. A very common way of EOS is the pump-probe approach in which the response of a device under test (DUT) to an optically generated short electric pulse (usually in picosecond range) is sampled with a laser beam using an EO crystal e.g. Pfeifer et al. (1995). An adequate number of studies have extensively covered the use of this technique for the THz characterization of transmission lines such as coplanar waveguides (CPWs) (Frankel et al. 1992). Despite the ultra-broadband capability of this technique, unfortunately, it has several drawbacks. Firstly, the transmission line as a test structure has to be sufficiently long to apply time windowing in order to distinct between the reflected and transmitted waves at circuit nodes. Secondly, one needs to carefully select DUTs as they need to be compatible with the pulse excitation and thirdly, incorporating of a photo-conductive switch on the transmission line, fort generating the pulse has to be considered. The latter can make the system cumbersome as the internal switch implementation is only feasible with photoconductive substrates and the external solution requires wire bonding that seriously influences parasitic effects to DUTs (Hjelme and Mickelson 1992).

In contrast, EOS for CW excited circuits, working with an external microwave signal source, is quite compatible with most of the devices, provided that they are planar and give sufficient space to the EO probe to samples their near-field. This method is also advantageous over the pump-probe technique, since it allows testing DUTs while they are under real operation. Despite this big advantages, unfortunately, the bandwidth of this method is strongly limited by the incoherency and jitter in the system and even measurements above tens of GHz without having a good synchronization is challenging (Giboney et al. 1994; Jamshidifar et al. 2012). To alleviate this problem, one needs to implement a fast synchronization between the DUT signal and the sampling laser pulse (Löffler et al. 1996; Jamshidifar et al. 2012; Jamshidifar and Bolívar 2013). Such a system using PLL solution is working quite well in the presence of nanosecond-scale jitter (Giboney et al. 1994). However, for fully recovering system bandwidth from the pulse to pulse and fast jitter, very coherent and stable alternative such as the work addressed by Jamshidifar and Bolívar (2013) is recommended.

Although synchronization of the EOS system is extremely important for maintain its measurement bandwidth, in some extent even an open-loop system can work. In this work, we demonstrate such an approach which only relies on the triggering of measurement without using any PLL system. This approach, in combination with snapshot sampling and post-processing of the data, has enabled achieving a measurement bandwidth of more than 230 GHz for a CMOS nonlinear transmission line (NLTL). However, it still performs far below a fully synchronized system.

2 Experimental setup

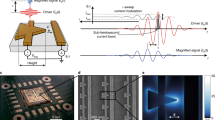
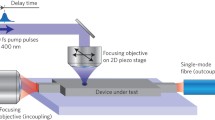
The schematic diagram of the setup is shown in Fig. 1. The femtosecond laser beam #1 is the sampling beam and the second beam #2 is only used for triggering of the measurements. The near-field signal of DUT is measured with an electrooptic (EO) sampling head (probe) consisting of a 50 μm-thick LiTaO3 crystal mounted on fused silica support and glued to a GRIN lens (Yang et al. 2001). This combination prepares a laser beam diameter of less than 8 μm at the probe tip, which determines the spatial resolution. A λ/2 plate placed in the path of beam #1 aligns the beam polarization with respect to the crystal optical axis. Inside the LiTaO3 EO crystal, field detection takes place based on Pockel's effect in which the evanescent electric field of the DUT alters the polarization state of the laser beam. The field induced variation of the laser beam polarization can be converted to the intensity with a combination of a λ/4 (analyzer) plate and a Wollaston prism (WP). A differential slow photodiode detector connected to a low-noise current amplifier provides the down-converted signal of the DUT in the baseband (BB) level. This signal is then filtered with a high pass analog filter (HPF) with the cut-off frequency of 4 kHz with 48 dB/decade roll-off and hence, amplified again to be measured with the oscilloscope. This configuration strongly reduces the flicker noise in the photodiode output current and prevents saturation of the second stage amplifier.

Fig. 1
figure 1

Schematic diagram of the open-loop EOS setup. The laser beam #1 samples electric field of devices which an EO probe, mounted on XYZ stage and beam #2 is used for triggering the measurement

Full size image

Tracing beam #2, the trigger signal is achieved by photoconductive mixing of the femtosecond laser pulse with a microwave signal which drives the DUT. The output signal offset frequency is given by \(\Delta f = f_{m} - n \times f_{l}\), where \(f_{m}\) and \(n \times f_{l}\) are microwave and nth harmonic of the laser repetition rate frequencies (≈76 MHz) respectively. In order to reduce the flicker noise on this trigger signal, it is also given to another HPF (not shown in Fig. 1) with about 1 kHz guard band below the signal frequency. Here, the system works with an open-loop feedback and therefore, no PLL system is used to synchronize the laser with this trigger signal. However, this increases jitter.

The DUT in this experiment is a 65 nm-CMOS-NLTL addressed in Tripodi et al. (2012) and Jamshidifar et al. (2012) which is terminated with an on-chip wideband antenna and its capability in generating harmonics from 10 to 300 GHz has already been verified by our fully synchronized setup (Jamshidifar et al. 2012). The aim of this work is to investigate on detection of the NLTL signal with an open-loop configured EOS system and compare it to other synchronized methods. In order to minimize the jitter and achieve the highest measurement bandwidth for this system, we decided to feed the DUT at 20 GHz as the second harmonic of a 10 GHz fundamental driving signal addressed in works (Jamshidifar and Bolívar 2013; Jamshidifar et al. 2012). However, due to the limitation of our signal generator in delivering the required 18.5 dBm of power to the NLTL, we shifted to 19.2 GHz.

3 Results

3.1 Real-time waveform and the temporal resolution

The EOS detected signal of the NLTL at the end of the line, where the on-chip antenna is connected, is measured with an oscilloscope and its RF translation is depicted in Fig. 2. The 500 MHz bandwidth and 14-bit resolution of our oscilloscope ensure accurate tracing of the signal fall-time which is of the most interest in terms of temporal resolution.

Fig. 2
figure 2

The output waveform of the NLTL which is fed at 19.2 GHz @ 18.5 dBm of power. The graph is the RF translated of the down-converted signal

Full size image

In these measurements unlike a fully synchronize setup with a lock-in amplifier (Jamshidifar and Bolívar 2013), averaging of the signal is not helpful due to a random phase which leads to a mean value of zero. Instead, we used capturing signal in a snapshot with a time <100 µs. The 52 picosecond in the signal trace accounts for the period of the fundamental signal @19.2 GHz and the 4.2 picosecond for the 90 to 10% fall-time is calculated accordingly. This is a quite good temporal resolution to assess the performance of our CMOS based NLTL.

3.2 The frequency domain observations

In this experiment, the NLTL down converted signal is given to a high dynamic range BB standard spectrum analyzer and its spectrum in RF translation is shown in Fig. 3. The main harmonic at 19.2 GHz represents an IF = 5 kHz in the BB level and hence, the instrument bandwidth of ≈ 100 kHz allows detecting up to 20th harmonic (i.e. 384 GHz at the RF level). Apparently, it worth nothing to try measuring the higher harmonics as the signal already is fallen into the noise for the harmonics beyond 12th. Since setting the IF frequency @ 5 kHz strongly get influenced by the system flicker (1/f) noise, the use of HPF, with a cut-off frequency of 4 kHz, is quite helpful and without that, even the 5th harmonic hardly could be detected.

Fig. 3
figure 3

RF translation spectrum of the NLTL signal measured with a baseband spectrum analyzer. The minimum noise level is measured while the NLTL is in off-state

Full size image

While the RF signal (of the NLTL) is turned off, the minimum system integrated noise floor in the 100 kHz bandwidth of the instrument for the BB electronics and optics is measured at 40 dB below the fundamental peak as shown in Fig. 3. An artifact appeared for both the signal and noise at 340 GHz is not originally an RF level signal but an oscillation of the high gain current amplifiers at 85 kHz which after translation to RF emerges at 340 GHz in the plot. Therfore, this is just a BB electronic artifact and can be neglected.

3.3 Retrieving the measurement bandwidth

Averaging of signals is a common way of increasing SNR. As mentioned above, due to jitter which drifts the frequency of the detected harmonics, a simple averaging of the measured signals will not help. Instead, we averaged only at the harmonic peaks of 200 snapshots. This is carried out by reading all data files, searching for the harmonics peaks and saving only the peak values for the averaging. This frequency resolved algorithm leads to a large reduction of the noise by \(- 20\log \left( {\sqrt {200} } \right) = - 23\,{\text{dB}}\). Nevertheless, the minimum achievable value is limited by the minimum noise level shown in Fig. 3. Unfortunately, most of the noise in EOS is the phase noise of the laser which cannot be reduced with this algorithm, but the good thing is that the pure amplitude noise and any conversion of the phase to the amplitude noise (PM–AM) can be minimized.

It is obvious that in on-state NLTL, additive RF noise increases the noise level of the measurement and therefore, finding the actual noise level is necessary. It is known that the phase noise, which increases with the square of harmonic number (Rodwell et al. 1989), is the dominant factor for limiting the EOS measurement bandwidth (Jamshidifar and Bolívar 2013). Therefore, it is very helpful to define its level in our open-loop system. Accordingly with an RF spectrum analyzer, we measured −104 dBc/Hz of phase noise for the microwave signal generator @10 GHz (@ 5 kHz offset frequency). Similarly, we observed −102 dBc/Hz for a ≈10 GHz signal generated from the incidence of the laser pulse on a fast photodiode (i. e, 132nd harmonic of the laser repetition rate). With this experiment, we came to a point to verify the laser phase noise as the dominant factor. Hence, this noise at harmonic #n of our fundamental (≈20 GHz) signal can be defined by

$$PN\left( n \right)\left[ {\text{dB}} \right] = PN_{0} + 20\log \left( {\sqrt {BW_{eff} } } \right) + 20\log \left( n \right) + 6\,{\text{dB}}$$

where PN0 and BW eff are the measured 1-Hz bandwidth phase noise @10 GHz and the effective measurement bandwidth for each harmonic respectively, whereas the added 6 dB accounts for the additive phase noise @ 19.2 GHz with respect to the measured value @ 10 GHz. Considering a BW eff  ≈ 10 kHz for each harmonic (see Fig. 3), the calculated phase noise, illustrated in Fig. 4 can be achieved. It can be seen that our EOS detection bandwidth is limited by this noise at 13th harmonic of the NLTL signal which in comparison to Fig. 3 reveals recovering at least 1 more harmonic from the noise.

Fig. 4
figure 4

Averages of 200 snapshots of the NLTL signal. The phase noise hampers the detection of higher harmonics

Full size image

3.4 Comparison of EOS synchronization methods

Having the same DUT, the open-loop setup plus the post-process algorithm in comparison to our fully synchronized setup (Jamshidifar and Bolívar 2013), with 300 GHz bandwidth for the same device, shows 23% less bandwidth. It also reveals 15% larger bandwidth compared to our PLL base setup. However, this gain has been mainly achieved by almost doubling of the fundamental frequency which increases the frequency span and reduces the phase noise simultaneously. A more meaningful comparison based on the harmonic number, and not the frequency, can be seen in Table 1.

Table 1 A comparison of different EOS methods
Full size table

3.5 Near-field scanning

An interesting feature of the EOS is near field scanning of devices (Hjelme et al. 1993; Pfeifer et al. 1998) measured by a freely positioned probe. As in this case, the integrated timing jitter extremely deviates the Δf, it is compensated with tuning the laser cavity with a kind of soft-synchronization. This is implemented by computer controlling of a voltage source which drives a rotation stage that holds an etalon in the laser path. In terms of simplicity and cost, this is very advantageous over the traditional use of piezoelectric stages for the cavity output coupler (Pfeifer et al. 1996). Although this is not a real-time synchronization technique, it can be upgraded by integrating with a PLL system. We also increased the offset frequency to Δf = 50 kHz which helps to prevent from fast fluctuation in the Δf frequency and overshooting of the control system. The final frequency drift can be tolerated with our 2 MHz bandwidth lock-in amplifier. With this setup, 1.2 × 1.0 mm2 area around the on-chip antenna was scanned multiple times (with 50 μm × 50 μm resolution or 480 pixels/image) and then averaged. The ultimate images at 1st, 5th, and 11th harmonic of the signal as well as the optical image of the antenna are depicted in Fig. 5.

Fig. 5
figure 5

The optical and EOS images of an on-chip wideband antenna connected to NLTL at signal harmonics of 1st, 5th, and 11th

Full size image

Slightly more than 210 GHz (11th harmonic) imaging bandwidth is achieved. At this point, it worth to notify that 10 µm lifting up the probe head from the DUT for safe scanning as well as the effect of jitter averaging in lock-in detection reducing SNR hampered the imaging bandwidth. Nevertheless, to the best of our knowledge, this is the broadest bandwidth achieved in EOS imaging of CW exited DUTs. The antenna images, containing both the amplitude and phase of the near-field, provide useful data for mode analysis and the resonance of the device.

4 Conclusion

An open-loop free-running electrooptic sampling system for real-time detection of sub-THz signals with picosecond temporal resolution was presented. The initial 210 GHz bandwidth of the setup has been enhanced to 230 GHz with a post-process algorithm. A simple soft-synchronization technique, instead of PLL and capable of very broadband imaging, was demonstrated. Also, the effect of noise as the dominant limiting factor for the system measurements bandwidth was quantitatively studied.