Influence of temperature on dispersion properties of photonic crystal fibers infiltrated with water

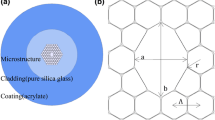
Abstract

Temperature change of the water infiltrated PCF is an interesting and practical method for a dynamical fine tuning of dispersion in active dispersion shift compensating systems. In this paper we present a numerical study on the influence of the temperature of infiltrated water on the dispersion and modal characteristics of photonic crystal fiber. We study regular hexagonal lattice photonic crystal fibers with various geometrical parameters using finite element method.

Introduction

The photonic crystal fiber (PCF) attracted a lot of attention over the last two decades and induced tremendous development in fiber optic technology. The PCFs differ from the conventional fibers with respect to their construction and optical properties. Usually PCF are composed of regular array of air holes along its entire length, similar to photonic crystal, with a defect in the center of the structure, which plays a role of a core. Two types of defects, solid or air hole, of various size and form are used as cores (Knight 2003). In the case of solid core the light is guided with modified effective refractive index and light witness a lower refractive index in the cladding. The use of the large air hole as a core offers the possibility of light guiding in the air. The guiding is based on the photonic band gap mechanism, which prevent light from penetration of photonic crystal structure. As a result light is trapped in the defect in photonic crystal. Solid core PCFs finds its applications in nonlinear fiber optics, fiber lasers, supercontinuum generation devices etc. (Moller et al. 2015; Dudley et al. 2006; Kibler et al. 2009; Petersen et al. 2014). On the other hand air-core PCF opens new perspectives in application of fibers for high energy transfer, particle guidance, and fiber sensors (Jin et al. 2013; Frazao et al. 2008; Wang et al. 2013).

Many valuable applications were already considered for PCFs, but still several of specific properties of these type of fibers need further study. One of the most important properties of photonic crystal fiber is related to easy tuning of its dispersion properties. Dispersion of photonic crystal fibers are determined by its structure, more specifically by lattice constant and air hole diameter. A proper choice of those parameters allows to modify whole dispersion characteristics and in particular shift a zero dispersion wavelength over hundreds of nanometres (Hansen 2003; Saitoh et al. 2003; Buczynski et al. 2011). The dispersion characterises can be further modified if air holes are replaced with another type of glass or liquids, or if the size of air holes vary along photonic crystal structure (Rasmussen et al. 2006; Buczynski et al. 2012; Martynkien et al. 2014).

In the context of tuning of dispersion characteristics it seems interesting to use liquids to infiltrate air holes (Kedenburg et al. 2012). Application of liquids with various refractive indexes allow for the modification of dispersion properties of the fiber without changing its geometrical parameters, which seems to be very practical (Pniewski et al. 2016). Moreover fiber properties can be further dynamically modified by means of temperature and pressure adjustment, since liquids are much more sensitive to these parameters than glass itself. It has been previously shown that change of temperature of liquid results in the zero dispersion wavelength (ZDW) shift (Karasawa 2012; Park et al. 2014). In both these studies the authors present numerical results for dispersion properties of fibers, where the role of the core is played by central capillary infiltrated with water. Park et al. considered a PCF with small constant hole diameter of 1.5 µm and very high filling factor between 0.81 and 91. A ZDW shift from 0.75 till 1.4 µm is reported for various geometrical parameters of the fibers. Karasawa reported results of simulations of ZDW shift from 1.15 till 1.23 µm for hollow core infiltrated with water in the PCF with small lattice constants varying between 0.6 till 2.1 and hole diameter between 0.5 till 2.0.

Practical use of infiltrated PCFs raises an issue of fiber sealing. In most of the reported work authors assume coupling from free space to PCFs with open holes infiltrated with liquids. Due to liquid evaporation this approach cannot be used in practical systems. A sealing of PCF is required instead. Successful sealing of PCF infiltrated with water was reported for example in (Nielsen et al. 2005; Bethge et al. 2010). They used a single mode fusion splicer for collapsing the holes in the cladding of the PCF. An UV curable adhesive was also successfully used to close holes in the cladding of PCF (Huang et al. 2004).

Temperature tuning of PCF infiltrated with liquids requires fast and stable system for temperature control. A resistant furnace can be used for this purpose (Stepniewski et al. 2016), however temperature change is relatively slow due to large thermal capacity of the system. A fast dynamic change of temperature can be obtained with Peltier plate, where the fibre is mounted with thermal conductive glue to the plate (Wolinski et al. 2014). Since thermal expansion of liquids is higher than glass one, we should consider this issue in the case of hermetically sealed PCF infiltrated with liquids. However mismatch of thermal expansion coefficients between glass and liquid can be neglected because volume of liquids in sealed microchannels is very low.

In this paper we present study on influence of temperature and infiltration of PCF with water on fiber dispersion characteristics. We consider infiltration with water because it is most common solvent used for biomolecules. Water can be further modified with bioluminescent particles used as nonlinear medium to stimulate supercontinuum generation (Cho et al. 2015). PCFs infiltrated with pure water were also successfully used for supercontinuum generation (Bethge et al. 2010; Bozolan et al. 2008). We use a fused silica solid core PCF with holes ordered in a hexagonal lattice, which consists of 8 rings of holes infiltrated with water. In our model we assume the lattice constant and various filling factors. Simulations are performed within the temperature range of water from 10 to 90 °C. We suppose that a temperature change of the water infiltrated PCF is interesting and practical method for a fine tuning of zero dispersion wavelength (ZDW). This new approach can be used in applications where fast dynamical compensation of dispersion shift is necessary.

Photonic crystal fibers infiltrated with water

The refractive index of water as a function of wavelength, temperature and pressure can be given by (Thormahlen et al. 1985)

$$\begin{aligned} n\left( {\lambda ,T,p} \right) & = \sqrt {\frac{{a_{1} }}{{\lambda^{2} - \lambda_{a}^{2} }} + a_{2} + a_{3} \lambda^{2} + a_{4} \lambda^{4} + a_{5} \lambda^{6} } + \left( {b_{1} + b_{2} \lambda^{2} + b_{3} \lambda^{4} } \right)\left( {T - T_{b} } \right) \\ & \quad + \left( {b_{4} + b_{5} \lambda^{2} + b_{6} \lambda^{4} } \right)\left( {T - T_{b} } \right)^{2} \, + \left( {b_{7} + b_{8} \lambda^{2} + b_{9} \lambda^{4} } \right)\left( {T - T_{b} } \right)^{3} \\ & \quad + \left[ {c_{1} + c_{2} \lambda^{2} + \left( {c_{3} + c_{4} \lambda^{2} } \right)T} \right]\left( {p - p_{b} } \right)\, + \left( {c_{5} + c_{6} \lambda^{2} } \right)\left( {p - p_{b} } \right)^{2} , \\ \end{aligned}$$

(1)

where λ ² _a  = 0.018085, a, = 5.743534 × 10⁻³, a ₂ = 1.769238, a ₃ = −2.797222 × 10⁻², a ₄ = 8.715348 × 10⁻³, a₅ = −1.413942 × 10⁻³, b ₁ = −8.454823 × 10⁻⁵, b ₂ = −2.787742 × 10⁻⁵, b ₃ = 2.608176 × 10⁻⁶, b ₄ = −2.050671 × 10⁻⁶, b ₅ = 1.019989 × 10⁻⁶, b ₆ = −2.611919 × 10⁻⁶, b ₇ = 8.194989 × 10⁻⁹, b ₈ = −8.107707 × 10⁻⁹, b ₉ = 4.877274 × 10⁻⁸, T _b  = 19.993 °C. Material dispersion of water for various temperatures is presented in Fig. 1.

Fig. 1

Refractive index of water as a function of wavelength for various temperatures (b)

The total fiber dispersion consists of material and waveguide dispersion. Unlike in the case of conventional fibers, the waveguide dispersion in PCF can substantially influence total fiber dispersion. Furthermore, the “effective” material dispersion is strongly modified by material dispersion of liquid infiltrating air holes in photonic cladding of PCF. In this case material dispersion is a combination of glass material dispersion and liquid material dispersion. Since photonic structure is very complex it cannot be simply treated as a direct sum of both dispersions.

A key parameter that describes properties of fibers is a group velocity dispersion (GVD). It is defined by the dispersion parameter:

$$D(\lambda ) = \frac{\lambda }{c}\frac{{d^{2} n_{eff} }}{{d\lambda^{2} }}$$

(2)

where λ wavelength and n_eff—effective refractive index for the considered mode defined as:

$$n_{eff} = \frac{{\beta \left( {\lambda ,n(\lambda )} \right)}}{{k_{0} }}.$$

(3)

Additionally dispersion characteristics in PCFs can be controlled by lattice constant, hole size, liquid and glass material as well as temperature. It is a main purpose of this study to investigate these characteristics.

For modelling we used finite difference method, which is commonly used to treat optical properties of fibers with complex structures. A commercial software Mode Solution by Lumerical is used (Mode Solution 2016). The model allows to take into account dispersion properties of the materials used for development of PCF and determine the mode parameters that may propagate in the considered structures. We calculate its effective refractive index, effective mode area and propagation losses for every mode. The analysis is performed in wide range of wavelengths determined by available parameters of used materials.

In our simulations we considered fibers with regular hexagonal lattice and various hole diameters. We assume that glass is fused silica and the liquid is pure water. The ambient temperature is 10 °C as the lower one (Fig. 2). A PCF with holes ordered in a hexagonal lattice, which consists of 8 rings of holes infiltrated with water is considered. As a reference we consider the PCF with empty air holes in the photonic cladding. In order to keep flexibility of choice of the diameter of water’s hole, we assume the lattice constant Λ is 5 μm. Then we choose diameter of holes infiltrated with water as d = 1, 2, 3, and 4 µm. Simulations are performed within the temperature range of water from 10 to 90 °C. We have selected lattice constant of 5 μm to obtain effective mode area similar to standard step-index single mode fibers, having in mind fusing splicing connection of standard fibres with liquid infiltrated PCFs, since it is the most reliable, compact and straightforward methods. A mode field diameter of standard SMF28 fiber is 9.2 μm for 1310 nm, while for the considered PCFs with the lattice constant of 5 μm the mode filed dimeter vary between 7.4 and 12.6 μm depends on air hole dimeter in the cladding when infiltrated with water (Fig. 3).

Fig. 2

Layout of analysed hexagonal lattice PCFs with lattice constant Λ = 5 μm and air hole diameter d = 1 μm (a), 2 μm (b), 3 μm (c), 4 μm (d). The air holes are infiltrated with water

Fig. 3

The intensity distribution of fundamental guided mode of PCFs with lattice constant Λ = 5 μm and different diameter of holes hole diameter d = 1 μm (a), 2 μm (b), 3 μm (c), 4 μm (d). The air holes are infiltrated with water

In our study we observe that the effective mode area of fundamental mode decreases when hole diameter increases (Fig. 3). The dispersion characteristic calculated using Eq. (2) is presented in Fig. 4. Our results show that infiltration with water of air holes in photonic cladding in PCFs shifts dispersion characteristics toward lower values and flatten dispersion for longer waves. If we consider a change of diameter in PCF infiltrated with water we observe that the decrease of the diameter of holes infiltrated with water shift all dispersion curvature down towards normal dispersion range and also shits ZDW into longer wavelength range (Table 1).

Fig. 4

The dispersion characteristic of proposed PCF with different diameter of holes infiltrated with water (a) and without water (b)

Table 1 The dependence of the zero dispersion wavelength on the size of the holes infiltrated with and without water

In the case of the PCF infiltrated with water decreasing hole diameters from 4 to 1 μm results in a shift the ZDW by 151 nm within the range from 1.199 to 1.048 μm. The obtained changes in dispersion characteristics are rather small, below 65 nm. It limits practical use of water infiltration as a potential dispersion engineering method when a relatively large lattice constant (Λ = 5 μm) is considered. In case of PCFs with small, hollow core infiltrated with water a shift of ZDW up to 750 nm can be obtained (Park et al. 2014). However structures with filling factor of 0.97 are not robust and can be considered only as a reference. Moreover water has high absorption in proximity of 1.1 and 1.3 μm, which might limit practical application of fibers with water core for supercontinuum generation. In our simulation water infiltrates only photonic cladding and its influence on attenuation is limited since overlap between fundamental mode and holes infiltrated with water is very small. As a result we can gain in flat dispersion characteristics due to water presence in photonic cladding and high transmission due to mode guidance in fused silica solid core.

Tuning zero-dispersion wavelength with temperature

In the next step we consider a change of temperature in tested PCF structures in the range between 10 and 90 °C. To understand the influence of temperature on dispersion characteristics we first consider a fiber with small filling factor (Λ = 5 and = 1 μm). The obtained results show that dispersion characteristics are shifted up toward anomalous dispersion range when temperature increase (Fig. 5). This behaviour can be easily explained since when temperature increases density of water decreases. Consequently, the effective refractive index of water also decreases (Eq. 1). Similar behaviour of red shift ZDW we observed for dispersion characteristics of the PCF infiltrated with air and water, respectively.

Fig. 5

Zero-dispersion characteristics with temperature for PCF with lattice constant Λ = 5 μm and hole’s diameter d = 1 μm

Note that observed changes are small when we compare them with an effect of change of hole diameters (Fig. 4). The ZDW is blue shifted with increase of the temperature. The total shift of ZDW is only 12 nm. It means that by changing temperature we can obtain a very fine tuning of ZDW. This mechanism can be very useful when we shift ZDW pump wavelength and observe nonlinear phenomena in case of excitation in normal and anomalous dispersion shift, or offer a method for accurate dynamic dispersion compensation. This mechanism can also be used to tune ZDW of fiber to zero in order to form a shape of ultrashort pulses propagating over the fiber.

The similar study were performered for other PCF structures with various hole sizes. A combination of both effects; change of air hole diameter and temperature allows to dramatically modify position of dispersion characteristics, influence its flatness and position of ZDW. The ZDW obtain for different parameters of structure and temperature are summarized in Table 2, dispersion characteristics obtained for various hole diameters are presented in Figs. 6, 7, 8 and 9.

Table 2 Zero dispersion wavelength for PCF with various diameters of water infiltrated holes in photonic cladding at different temperatures. The lattice constant is Λ = 5 µm

Fig. 6

Dispersion characteristics of PCF with lattice constant Λ = 5 μm and hole’s diameter d = 1.5 μm infiltrated with water at different temperatures

Fig. 7

Dispersion characteristics of PCF with lattice constant Λ = 5 μm and hole’s diameter d = 2 μm infiltrated with water at different temperatures

Fig. 8

Dispersion characteristics of PCF with lattice constant Λ = 5 μm and hole’s diameter d = 3 μm infiltrated with water at different temperatures

Fig. 9

Dispersion characteristics of PCF with lattice constant Λ = 5 μm and hole’s diameter d = 4 μm infiltrated with water at different temperatures

The obtained results suggest that we can control the ZDW position by changing temperature relative to the room temperature in the range up to 27 nm. A selection of hole diameter determine the wavelength region where the fine tuning of ZDW with temperature is obtained. For example, PCFs with the hole diameter of 4 µm allow to tune of ZDW in proximity of 1040 nm (Fig. 9), while PCFs with the hole diameter of 1 µm allow to tune of ZDW near 1205 nm (Fig. 5). The ZDW shift-temperature characteristics are shown in Fig. 10. As a reference we took values of ZDW at the temperature of 10 °C.

Fig. 10

The ZDW shift vs temperature of PCF with lattice constant Λ = 5 μm and various diameter of holes infiltrated with water

We observe that for all PCFs, the ZDW shift-temperature characteristics show similar behaviour. The relation between ZDW and temperature is non-monotonic since one can identify three different factors that contribute simultaneously, namely: material dispersion of water, refractive index change with temperature and spatial distribution of refractive index in the fiber. The strongest effect of ZDW shift we observe for PCFs with a small core. It is easy to explain this behaviour, because in this case the mode field strongly overlap with water and therefore change of temperature strongly influence on propagation parameters of the mode. For the PCF with hole’s diameter of 1 μm, ZDW is up to 12 nm blue shifted with increasing of water’s temperature from 10 to 32 °C and 65 to 90 °C. In the temperature range 32–65 °C a red shit of ZDW is observed. We noticed similar behaviour for PCFs with larger hole’s diameters >1 μm. However in this case ZDW shift with temperature decreases when size of the core increases.

Conclusions

We simulated the dispersion properties of the PCFs with the regular hexagonal lattice photonic cladding infiltrated with water. PCF structures with a hexagonal lattice constant of Λ = 5 µm and various diameters of the holes: d = 1, 2, 3, 4 µm were analysed. The results show that zero dispersion wavelength (ZWD) of PCF can be tuned over 179 nm when the diameter of holes infiltrated water changes within the range of 1–4 µm and water’s temperature changes in the range of (10–90) °C. A change of water’s temperature in the range of (10–90) °C allows dynamic and very accurate shifts of the ZDW by 27 nm for a PCF with geometrical parameters of d = 1 µm and Λ = 5 µm. The ZDW is blue shifted with increasing water’s temperature. In conclusion: the PCF infiltrated with water can be used for the precise adjustment of ZDW; the latter can be easily modified by changing the temperature of water infiltrating holes in photonic cladding.