Langevin-like method for modelling the noise currents in HgCdTe barrier LWIR detectors

Abstract

This paper presents the modeling of the spectral density of noise current in semiconductor structures. Basing on P. Handel’s theory we have considered a wide range of sources of 1/f noise caused both by generation–recombination (G–R) and scattering processes. In addition to the shot G–R noise caused by different mechanism, the diffusion noise and temperature fluctuations are also included. Moreover, we have found the place where the noise current is mainly generated in HgCdTe barrier long wavelength detectors.

1 Introduction

Photoelectric characteristics of long wavelength infrared radiation (LWIR) barrier detector are relatively easy to estimate theoretically. The key to this is to solve the transport equations numerically by using iterative methods. For this purpose we use our own computer programs, where as a discretization method, the cell-centered finite volume method (FVM) is applied to approximate a set of nonlinear transport equations. Next the Newton iterative method is used to solve them. Another possibility would be to use one of many commercial programs. However, analysis of the fluctuation phenomena is still an open problem. The possibility of numerical modelling of the spectral density (SD) of noise currents in semiconductor devices gives a lot of information about the influence of generation–recombination (G–R) mechanisms and scattering mechanisms on fluctuation phenomena. Knowing the principal place of generation of noise currents in the semiconductor structure and the participation of different mechanisms of generation, we can find optimal design solutions reducing the noise current. In this work we present a numerical method which gives these possibilities. We show the result of our calculations for cylindrical HgCdTe LWIR barrier detector working at room temperature.

2 Numerical method

The applied method is similar to the sinusoidal steady state analysis (S3A) used for semiconductor device simulation (Kurata 1971, Temple and Shewchun 1973, Laux 1985). S3A method involves the use of complex sinusoidal perturbation of the generation rate with infinitesimal amplitudes to excite the device in the frequency domain. In Langevin-like method these sinusoidal excitations of device parameters (electrical potential Ψ, quasi Fermi energy for electrons and holes Φ_n and Φ_p and temperature T) are caused by perturbation amplitudes connected with spectral density of random source terms (noise sources). Knowing the spectral density of noise sources, we can determine the modules of these complex amplitudes. The equations obtained in this way are called the transport equations for fluctuations (TEFF) (Jóźwikowski 2001). These equations were modified and developed in subsequent works (Jóźwikowski et al. 2004), eventually taking the form of Eq. (4) in (Jóźwikowski et al. 2016). Let the set of transport Eqs. (1)–(4) in (Jóźwikowski et al. 2016) at the node k in the computation mesh be symbolically given [similarly as in (Laux 1985)] by:

$$\begin{aligned} F_{\Psi }^{k} \left( {{\text{N}}_{\text{D}}^{ + } ,{\text{N}}_{\text{A}}^{ - } ,{\text{n}},{\text{p}}} \right) = 0 \hfill \\ \frac{\partial n}{\partial t} - F_{n}^{k} \left( {{\text{n}},{\text{p}},\upmu_{\text{e}} ,({\text{G}} - {\text{R}})} \right) = 0 \hfill \\ \frac{\partial p}{\partial t} - F_{p}^{k} \left( {{\text{n}},{\text{p}},\upmu_{\text{h}} ,({\text{G}} - {\text{R}})} \right) = 0 \hfill \\ \frac{\partial T}{\partial t} - F_{T}^{k} \left( {{\text{n}},{\text{p}},\upmu_{\text{e}} ,\upmu_{\text{h}} } \right) = 0 \hfill \\ \end{aligned}$$

(1)

In the first step the set (1) is solved to obtain steady-state values by using the Newton iterative method. The system is obtained by expressing the intensive parameters in the form $\varPsi = \varPsi^{0} +\updelta\varPsi$, $\varPhi_{\text{n}} = \varPhi_{\text{n}}^{0} +\updelta\varPhi_{\text{n}} ,\varPhi_{\text{p}} = \varPhi_{\text{p}}^{0} +\updelta\varPhi_{\text{p}}$ and $T = T^{0} + \delta T$. 0 superscript denotes the steady-state solution for the device, and δ refers to small time dependent terms. All physical quantities which depend on intensive parameters may be properly expanded: for example the electron mobility may be expressed as

$$\mu_{e} = \mu_{e}^{0} + \delta \mu_{e} = \mu_{e}^{0} + \left( {\frac{{\partial \mu_{e} }}{{\partial {\text{n}}}}\frac{\partial n}{\partial \Psi } + \frac{{\partial \mu_{e} }}{{\partial {\text{p}}}}\frac{\partial p}{\partial \Psi }} \right)\delta \Psi + \frac{{\partial \mu_{e} }}{{\partial {\text{n}}}}\frac{\partial n}{{\partial \Phi_{\text{n}} }}\delta \Phi_{\text{n}} + \frac{{\partial \mu_{e} }}{{\partial {\text{p}}}}\frac{\partial p}{{\partial \Phi_{\text{p}} }}\delta \Phi_{\text{p}} + \left( {\frac{{\partial \mu_{e} }}{{\partial {\text{n}}}}\frac{\partial n}{{\partial {\text{T}}}} + \frac{{\partial \mu_{e} }}{{\partial {\text{p}}}}\frac{\partial p}{{\partial {\text{T}}}}} \right)\delta \text{T}$$

(2)

To analyze the noise problem we treat them as fluctuations and introduce additional noise sources.

For electron mobility it looks as follows:

$$\mu_{e} = \mu_{e}^{0} + \delta \mu_{e} + \frac{{\partial \mu_{\text{e}} }}{{\partial\uptau_{\text{rel}}^{\text{e}} }}\delta\uptau_{\text{rel}}^{\text{e}} .$$

(3)

In this way we can obtain Eq. (4), which is the matrix–vector notation of Eq. (4) in (Jóźwikowski et al. 2016) at each analyzed node k.

$$\begin{aligned} \left[ {\begin{array}{cccc} {\frac{{\partial F_{\Psi }^{k} }}{{\partial \Psi }}} & {\frac{{\partial F_{\Psi }^{k} }}{{\partial \Phi _{{\text{n}}} }}} & {\frac{{\partial F_{\Psi }^{k} }}{{\partial \Phi _{{\text{p}}} }}} & {\frac{{\partial F_{\Psi }^{k} }}{{\partial {\text{T}}}}} \\ {\frac{{\partial n}}{{\partial \Psi }}\frac{\partial }{{\partial t}} - \frac{{\partial F_{{\text{n}}}^{k} }}{{\partial \Psi }}} & {\frac{{\partial n}}{{\partial \Phi _{{\text{n}}} }}\frac{\partial }{{\partial t}} - \frac{{\partial F_{{\text{n}}}^{k} }}{{\partial \Phi _{{\text{n}}} }}} & { - \frac{{\partial F_{{\text{n}}}^{k} }}{{\partial \Phi _{{\text{p}}} }}} & {\frac{{\partial n}}{{\partial {\text{T}}}}\frac{\partial }{{\partial t}} - \frac{{\partial F_{{\text{n}}}^{k} }}{{\partial {\text{T}}}}} \\ {\frac{{\partial p}}{{\partial \Psi }}\frac{\partial }{{\partial t}} - \frac{{\partial F_{{\text{p}}}^{k} }}{{\partial \Psi }}} & { - \frac{{\partial F_{{\text{p}}}^{k} }}{{\partial \Phi _{{\text{n}}} }}} & {\frac{{\partial p}}{{\partial \Phi _{{\text{p}}} }}\frac{\partial }{{\partial t}} - \frac{{\partial F_{{\text{p}}}^{k} }}{{\partial \Phi _{{\text{p}}} }}} & {\frac{{\partial n}}{{\partial {\text{T}}}}\frac{\partial }{{\partial t}} - \frac{{\partial F_{{\text{p}}}^{k} }}{{\partial {\text{T}}}}} \\ { - \frac{{\partial F_{{\text{T}}}^{k} }}{{\partial \Psi }}} & { - \frac{{\partial F_{{\text{T}}}^{k} }}{{\partial \Phi _{{\text{n}}} }}} & { - \frac{{\partial F_{{\text{T}}}^{k} }}{{\partial \Phi _{{\text{p}}} }}} & {\frac{\partial }{{\partial t}} - \frac{{\partial F_{{\text{T}}}^{k} }}{{\partial {\text{T}}}}} \\ \end{array} } \right]\left[ {\begin{array}{c} {\delta \,\Psi } \\ {\delta \,\Phi _{{\text{n}}} } \\ {\delta \,\Phi _{{\text{p}}} } \\ {\delta \,T} \\ \end{array} } \right] \hfill \\ = \left[ {\begin{array}{c} {\frac{{\partial F_{{p}}^{k} }}{{\partial {\mu }_{{\text{e}}} }}\frac{{\partial {\mu }_{{\text{e}}} }}{{\partial {\tau }_{{{\text{rel}}}}^{{\text{e}}} }}\delta {\tau }_{{{\text{rel}}}}^{{\text{e}}} + \frac{{\partial F_{{\text{n}}}^{k} }}{{\partial ({\text{G}} - {\text{R}})}}\left( {\delta ({\text{G}} - {\text{R}})_{{SHOT}} ({\text{G}} - {\text{R}})_{{1/f}} + F_{n} (t)} \right)} \\ {\frac{{\partial F_{{\text{o}}}^{k} }}{{\partial {\mu }_{{\text{h}}} }}\frac{{\partial {\mu }_{{\text{h}}} }}{{\partial {\tau }_{{{\text{rel}}}}^{{\text{h}}} }}\delta {\tau }_{{{\text{rel}}}}^{{\text{h}}} + \frac{{\partial F_{{\text{p}}}^{k} }}{{\partial ({\text{G}} - {\text{R}})}}\left( {\delta ({\text{G}} - {\text{R}})_{{SHOT}} ({\text{G}} - {\text{R}})_{{1/f}} + F_{p} (t)} \right)} \\ {{\mathbf{F}}_{{\mathbf{C}}} ({\mathbf{t}}) + {\mathbf{G}}_{{\mathbf{C}}} ({\mathbf{t}})} \\ \end{array} } \right] \hfill \\ \end{aligned}$$

(4)

The expressions (1)–(4) use standard conventions; the indexes n or e refer to electron, h or p refer to the holes, respectively, $\updelta$ denotes fluctuation, $\varvec{G}$ is the carrier generation rate, R is the carrier recombination rate. G–R processes are influenced by Auger 1 and Auger 7 inter-band mechanisms and enhanced additionally by SHR processes caused by metal vacancies and dislocations (Kopytko and Jóźwikowski 2015). Other symbols are explained in (Jóźwikowski et al. 2016). As the set of Eq. (4) is linear one can express all random variables by means of the Fourier series and separately consider all Fourier coefficients at any frequency. The random source terms, i.e. $\varvec{\delta}{\varvec{\uptau}}_{{{\mathbf{rel}}}}^{{\mathbf{e}}}$, $\varvec{\delta}{\varvec{\uptau}}_{{{\mathbf{rel}}}}^{{\mathbf{h}}}$, $\varvec{\delta}\left( {\varvec{G} - \varvec{R}} \right)_{{\varvec{SHOT}}} ,\varvec{ }$ $\varvec{\delta}\left( {\varvec{G} - \varvec{R}} \right)_{{1/\varvec{f}}}$, ${\mathbf{F}}_{{\mathbf{C}}} \left( {\mathbf{t}} \right)$, ${\mathbf{G}}_{{\mathbf{C}}} \left( {\mathbf{t}} \right)$, $\varvec{F}_{\varvec{n}} \left( \varvec{t} \right)$ and $\varvec{F}_{\varvec{p}} \left( \varvec{t} \right)$ are modeled and inserted into TEFF (set (4)) to determine the fluctuations of $\varPsi$, $\varPhi_{\text{n}}$, $\varPhi_{\text{n}}$ and T. Here $\varvec{\delta}{\varvec{\uptau}}_{{{\mathbf{rel}}}}^{{\mathbf{e}}}$ and $\varvec{\delta}{\varvec{\uptau}}_{{{\mathbf{rel}}}}^{{\mathbf{h}}}$ are the fluctuations of electron relaxation time and hole relaxation time, respectively. (Kousik et al. 1985), based on Handel’s theory of 1/f noise (Handel 1975, 1980) obtained theoretically spectral intensity of $\varvec{\delta}{\varvec{\uptau}}_{{{\mathbf{rel}}}}^{{\mathbf{e}}}$ for silicon. We have adopted their results for HgCdTe in some previous works (Jóźwikowski 2001, 2004, 2016). Handel’s theory of 1/f noise is based on the fact, that in accordance with the quantum electromagnetic field theory, electric charge carriers are accompanied by photons. Interactions leading to the change in carrier velocity are the sources of creation or annihilation of photons (Bremsstrahlung). They are called “soft photons” and are not energetic enough to be detected, however, the possibility of their absorption or emission must be taken into account in the calculation of the scattering amplitude. The number of these photons is inversely proportional to their energy, i.e. their frequency. This way both scattering processes determined by relaxation time and G–R processes determined by G–R terms are the potential sources of 1/f noise. In (Jóźwikowski et al. 2016) we have determined the Hooge coefficients (Hooge 1969) for 1/f noise caused by Auger1, Auger7, radiative and SHR G–R mechanisms in HgCdTe. The influence of dislocation on 1/f noise was determined as well by using our original model. In the presented paper, all those 1/f noise sources are included in TEFF in $\varvec{\delta}\left( {\varvec{G} - \varvec{R}} \right)_{{1/\varvec{f}}}$ terms. ${\mathbf{F}}_{{\mathbf{C}}} \left( {\mathbf{t}} \right)$ denotes the fluctuation of heat stream and ${\mathbf{G}}_{{\mathbf{C}}} \left( {\mathbf{t}} \right)$ denotes the fluctuation of heat generation rate (Jóźwikowski et al. 2004). $\varvec{F}_{\varvec{n}} \left( \varvec{t} \right)$ and $\varvec{F}_{\varvec{p}} \left( \varvec{t} \right)$ denote electron and hole diffusion noise, respectively (van der Ziel 1954, 1959). In the presented structures diffusion noise plays a marginal role and may be omitted. Knowing the SD of random sources (for example $S_{a} \left( f \right)$ of $\delta a\left( {\vec{r},t} \right)$), one may determine the complex amplitude $a_{f}$ of their Fourier coefficients defined as follows:

$$\delta a\left( {\vec{r},t} \right) = \mathop \int \limits_{0}^{\infty } \frac{1}{\sqrt 2 }c_{f} \exp \left( {i\varphi_{f} } \right)\exp \left( {i2\pi ft} \right)df;\quad a_{f} = \frac{1}{\sqrt 2 }c_{f} \exp \left( {i\varphi_{f} } \right);S_{a} \left( f \right)\Delta f = a_{f} a_{f}^{*}$$

(5)

Here $S_{a} \left( f \right)$ denotes the SD of fluctuation quantity, $\Delta f = 1Hz$ and $c_{f} exp\left( {i\varphi_{f} } \right)$ is the complex Fourier coefficient for frequency $f$ (van der Ziel 1976). The numerical method for solving TEFF equations is described in (Jóźwikowski 2001, 2004, 2016). Knowing the SD of fluctuation quantity being the random noise source we are able to determine $c_{f}$ only, which is the modulus of the complex coefficient $c_{f} exp\left( {i\varphi_{f} } \right).$ As we cannot determine the angle $\varphi_{f}$ being some number between 0 and $2\pi$, we generate it randomly using a computer. This procedure is applied independently for all random noise terms contained in TEFF. We usually generate about 100 trials to obtain a corvergent spatial distribution of mean values of the SD of fluctuations of intense parameters for arbitrarily chosen frequency. Having them we can calculate the fluctuation of all physical quantities contained in TEFF. The solver of TEFF has been implemented in Fortran Intel Compiler and complex numbers. To solve the set of Eq. (4) one has to know the SD of mobility fluctuations caused by fluctuations of relaxation times and the carrier concentration [this was shown in (Jóźwikowski et al. 2004)] as well as the SD of fluctuations of g–r processes generating both 1/f noise and the shot noise. Similar to (Jóźwikowski et al. 2016), the influence of dislocations on noise current was also taken into account in this paper. Current noise measured in electronic system connected with detector is caused by fluctuations of current density inside the detector. The idea to find it is based on the fact that the density of the Joule power, $\rho_{P}$ in heterostructure is the product of the current density and the gradients of quasi-Fermi energies, i.e.:

$$\mathop \int \limits_{V}^{{}} \left( { - \vec{j}_{n} \cdot \nabla \varPhi_{\text{n}} + \vec{j}_{p} \cdot \nabla \varPhi_{\text{p}} } \right)dV = \mathop \int \limits_{V}^{{}} \rho_{P} dV = UI$$

(6)

where $\vec{j}$ denotes the current density,$U$-the bias voltage, $I$-the total electric current, $V$-the volume of the detector.

$$\vec{j}_{n} = - n\mu_{n} \nabla \varPhi_{\text{n}} ,\quad \vec{j}_{p} = p\mu_{p} \nabla \varPhi_{\text{p}}$$

(7)

The noise power density is here treated as a result of the fluctuations of the quasi-Fermi levels as well as fluctuations of the current density, i.e.

$$\delta \rho_{P} = - \vec{j}_{n} \cdot \delta \left( {\nabla \varPhi_{n} } \right) - \nabla \varPhi_{n} \cdot \delta \vec{j}_{n} + \vec{j}_{p} \cdot \delta \left( {\nabla \varPhi_{p} } \right) + \nabla \varPhi_{p} \delta \vec{j}_{p}$$

(8)

The fluctuations of the total noise power density may be expressed by

$$\delta P_{N} = \int\limits_{V} {\delta \rho_{P} dV = \delta UI + U\delta I \approx U\delta I}$$

(9)

The fluctuation of the density of Joule’s heat power $\delta \rho_{P}$ is now considered as a noise power density. Taking into account the energy balance of Eq. (9), one may write an expression for the effective SD of the total noise current:

$$S_{I} = \frac{1}{{U^{2} }}S_{{P_{N} }} .$$

(10)

3 Numerical results

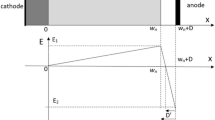
Below we present results of calculations of physical parameters of a cylindrical MESA Hg_1−xCd_xTe barrier detector with a radius of 76 μm (length of A′B line in Fig. 1) working at 300 K. Spatial distributions of mole fraction and donor and acceptor concentrations are shown along the axis of symmetry of the structure (line AA′ in Fig. 1) in Fig. 2. All the spatial distributions of physical parameters of the structure apply to distributions along AA′ line too. In the calculations we assume that the dislocation density in the whole structure equals 10⁶ cm⁻² except for areas where there is a gradient of molar composition. In these regions the density of dislocations is increased according to the relationship proposed by (Yoshikawa 1988). It is well seen in Fig. 3. Dislocations have an impact on the effective lifetime of carriers, calculated using the model proposed in (Jóźwikowski et al. 2012). The effective carrier lifetime is also affected by the supply voltage. The reason for this is the exclusion of carriers, which decreases the carrier concentration with the increasing of the supply voltage (mainly in the area of the absorber). This effect is illustrated in Fig. 4. The exclusion phenomenon has a strong influence on the current–voltage characteristics of the analyzed structure, as shown in Fig. 5. Calculations were carried out without considering the influence of series resistance, which affects shape of I(V) characteristic in real structures. The phenomenon of exclusion encountered in the non-cooled barrier structures has a significant impact on the spatial distribution of the spectral density of noise power density. Figure 6 shows this distribution in structure biased with voltage −100 mV (solid lines) and −1 V (dashed lines) for frequency of 1 Hz (blue line) and frequency of 10⁶ Hz (red line). One can see that for both, low frequency noise and high frequency noise, the greatest generation of noise power takes place in the interface between absorber and N⁺ layer. It’s seen that increasing the bias voltage reduces the generation of noise.

Fig. 1

The architecture of the half cross-section of cylindrical barrier mesa structures. Absorber with thickness 3.2 μm is located between two graded-gap layers

Fig. 2

Spatial distribution of mole fraction x donor concentration N_D and acceptor concentration N_A along AA′ line of half cross-section. Thickness is measured from point A on the border between the layer with mole fraction x = 0.4 and CdTe

Fig. 3

Calculated spatial distribution of effective carrier lifetime in structure biased with −100 mV an −1 V and distribution of dislocation density

Fig. 4

Calculated spatial distribution of electron and hole concentration in structure biased with −0.1 V (solid lines) and −1 V (dash lines). The exclusion effect is seen in the absorber area

Fig. 5

Calculated I(V) characteristic of device for reverse biased device

Fig. 6

Spatial distribution of SD of noise power density for 1 Hz of frequency (bold line) and 10⁶ Hz. Device is biased with −0.1 V (solid lines) and −1 V (dashed lines). Dotted lines show spatial distribution of the edge of the valence band (E_V) and conduction band (E_C) when the bias voltage is equal −1 V

Additionally, the dotted lines show the distribution of the edge of the valence band (E_V) and the conduction band (E_C) when the bias voltage is equal −1 V. The effect of the noise generation within the device is the noise current observed at the electronic circuit connected with the element. Figure 7 shows the noise current (in $AHz^{1/2}$) at $\Delta f = 1Hz$ as a function of frequency for bias voltage U = −1 V (blue line) and U = −100 mV (red line). In red line we can distinguish two generation–recombination Lorentzains compared to the two values of carrier lifetime. Black dashed lines mark these Lorentzians. The first is caused by g–r process determined by the carrier lifetime in absorber region ($\tau \sim5 \cdot 10^{ - 7}\,{\rm s}$) and the second by g–r process in the region near the upper electric contact determined by lifetime around $10^{ - 9}\,{\rm s}.$

Fig. 7

Calculated noise current at Δf = 1 Hz as a function of frequency for device biased with U = −100 mV and U = −1 V. Dashed lines mark two generation–recombination Lorentzians

These values of effective lifetime are shown in Fig. 3. Increasing of biasing voltage to −1 V leads to the exclusion of carrier from the region of absorber (see Fig. 4), increases the carrier lifetime in this region up to microseconds (see Fig. 3), and reduces the current (see Fig. 5). All this leads to the reduction of the noise current by almost an order of magnitude. Blue line in Fig. 7 is a result of 1/f noise caused mainly by fluctuation of carriers relaxation time and one Lorentzian corresponding to the lifetime equal around 10⁻⁹ s.

4 Conclusion

The set of TEFF is a useful tool for theoretical analysis of noise currents phenomena in devices. It may be solved by using the Langevin-like method which is based on the knowledge of the spectral density of different noise generators in the semiconductor structure. Theoretical analysis reported in this paper shows, that the noise current in a LWIR barrier non-cooled structure for frequencies higher than 10⁶ Hz is mainly generated by shot g–r mechanisms connected with g–r processes. 1/f noise caused by the fluctuations of relaxation times, i.e. of mobility, have a significant impact for low frequencies. The way to reduce the current noise in the considered barrier devices is strong biasing. Noise is generated most strongly in the interface between absorber and N⁺ layer.