1 Introduction

Quantum cascade lasers (QCLs) are compact, powerful, and versatile sources of mid-infrared radiation. Double trench deep mesa is one of the basic configuration of QCL waveguides (Yang et al. 2014). It has been shown, that if the width of such waveguide is larger than the wavelength, either the lowest-order transversal mode or the higher-order mode can exite, depending on the QCL resonator length (Kinzer et al. 2012). Generally higher-order modes are undesirable, mainly because of their large diffraction losses. There have been attempts to increase discrimination between the transverse modes (Bouzi et al. 2013), but according to our knowledge, there has been no analysis of causes of the weak mode discrimination in typical QCLs.

Mode losses and confinement factors of modes in the active region are the crucial parameters that determine mode selection and the discrimination between modes. Therefore, we determined these parameters based on numerical simulations. For verification, we compared the results of the simulations with results of measurements of QCL beam.

2 Methods

2.1 Laser design

In this paper we consider a waveguide of a QCL, which cross section is shown in Fig. 1. The active region of the laser consists 50 segments. The layer sequence of one segment, in nanometers, is: 2.75, 1.72, 2.46, 1.82, 2.15, 1.93, 2.07, 2.13, 1.97, 2.13, 1.77, 2.74, 1.77, 3.86, 1.18, 1.32, 4.23, 1.32, 3.73, 1.42, 3.54, 2.23. The bold numbers refer to \(\hbox {In}_{0.3634}\hbox {Al}_{0.6366}\hbox {As}\) and the plain numbers refer to \(\hbox {In}_{0.6663}\hbox {Ga}_{0.3337}\hbox {As}\). The underlined layers are Si-doped with a concentration of \(2\times 10^{17}\,\mathrm {cm}^{-3}\). The active region is sandwiched between two 500-nm low-doped (\(n=4\times 10^{16}\,\mathrm {cm}^{-3}\)) \(\hbox {In}_{0.5273}\hbox {Ga}_{0.4727}\hbox {As}\) layers. The remaining waveguide layers are InP substrate on the bottom and 2.5-\({\upmu } \hbox {m}\) low-doped (\(n=1\times 10^{17}\,\mathrm {cm}^{-3}\)) \(\hbox {In}_{0.5226}\hbox {Al}_{0.4774}\hbox {As}\) and 500-nm high-doped (\(n=8\times 10^{18}\,\mathrm {cm}^{-3}\)) \(\hbox {In}_{0.5273}\hbox {Ga}_{0.4727}\hbox {As}\) on the top.

Fig. 1
figure 1

Waveguide cross section

Full size image

The epitaxial structure of the quantum cascade laser was grown by solid-source molecular beam epitaxy. The double trench deep mesa was fabricated using wet etching and \(\hbox {Si}_3\hbox {N}_4\) for electrical insulation. Detailed information about the laser fabrication technology can be found in Bugajski et al. (2014) and Karbownik et al. (2015).

The above listed thicknesses of the active region layers and the compositions of all layers were determined on the basis of high resolution X-ray diffraction of the real structure. The thicknesses of the waveguide layers were determined on the basis of their growth time. The width of the top contact layers is \(9.46\,{\upmu } \hbox {m}\) and the width of the active region varies from \(10.14\,{\upmu } \hbox {m}\) on the top to \(13.51\,{\upmu } \hbox {m}\) on the bottom, which were determined on the basis of the laser mirror images taken by an optical microscope. The resonator length is \(2\,\mathrm {mm}\) and the mirrors are uncoated. The wavelength \(\lambda\) emitted by the laser is about \(4.4\,{\upmu } \hbox {m}\).

2.2 Numerical simulations

The calculations of the field distributions in the laser waveguide were performed with the finite element method using Photon Design Fimmwave software (http://www.photond.com). We were looking for transversal modes with the highest confinement factor with the active region \({\varGamma }\) and the lowest mode loss \(\alpha\). The confinement factor is defined as

$$\varGamma \equiv \frac{\int ^{AR}{\left| \left\langle\mathbf {S}(r)\right\rangle\right| dr} }{\int ^{\infty }{\left| \left\langle\mathbf {S}(r)\right\rangle\right| dr} },$$
(1)

where \(\langle\mathbf {S}(r)\rangle\) is the time-averaged Poynting vector, the numerator is the integral over the active region and the denominator is the integral over the whole structure. The mode loss were calculated with the assumption of zero gain in the active region as

$$\begin{aligned} \alpha =2{\text {Im}}(\beta ), \end{aligned}$$
(2)

where \({\text {Im}}(\beta )\) is the imaginary part of the propagation constant \(\beta\).

Threshold gain \(g_{th}\) was calculated as

$$\begin{aligned} g_{th}=\frac{1}{{\varGamma }}\left( \alpha +\frac{1}{L}\log \left( \frac{1}{R}\right) \right) , \end{aligned}$$
(3)

where L is the resonator length and R is the mirrors reflectivity. We considered uncovered, identical laser mirrors with reflectivity \(R=0.2858\).

Input material data (refractive indices \(n_r\) and absorption coefficients \(\alpha _r\)) for the simulations are listed in Table 1. These parameters for the semiconductors were calculated according to Drude–Lorentz model (Evans et al. 2012) with the following formula:

$$\begin{aligned} n_r+\iota \frac{\lambda }{4\pi } \alpha _r =\sqrt{\epsilon _{\infty }\left( 1 + \frac{\omega ^2_{LO}-\omega ^2_{TO}}{\omega ^2_{TO}-\frac{c}{\lambda }\left( \frac{c}{\lambda }+\iota \gamma _{phon}\right) } -\frac{{N_f q_e^2}}{\frac{c}{\lambda }\left( \frac{c}{\lambda }+\iota \frac{q_e}{m^{*}m\mu _e}\right) {\epsilon _0 \epsilon _{\infty }m^{*}m}} \right) }, \end{aligned}$$
(4)

where \(N_f\) is the free-carrier concentration, \(q_e\) is the electronic charge, m is the electron rest mass, c is the speed of light, and \(\epsilon _0\) is the permittivity of free-space. For the binary materials (InAs, GaAs, AlAs and InP) the remaining parameters, i.e. high-frequency dielectric constant \(\epsilon _\infty\), longitudinal optical phonon frequency \(\omega _{LO}\), transversal optical phonon frequency \(\omega _{TO}\), phonon damping frequency \(\gamma _{phon}\) come from Evans et al. (2012), electron effective mass \(m^{*}\) comes from Vurgaftman et al. (2001), and electron low-field mobility \(\mu _e\) comes from Sotoodeh et al. (2000). Parameters for the ternary materials were assumed as linear interpolation between the corresponding binary materials. The active region is considered as one bulk layer with zero absorption and with refractive index being weighted average of the refractive indices of the constituent materials with weights proportional to the thicknesses of the layers.

Table 1 Material parameters of the waveguide layers
Full size table

2.3 Experiment

The power distribution of the laser beam in the far field was measured in room temperature by using a goniometric profiler (Pruszyńska-Karbownik et al. 2013, 2015). The laser was supplied with \(100\,\mathrm {ns}\) pulses, frequency of \(500\,\mathrm {Hz}\), and current of 1.2 times threshold.

On the basis of experimental two-dimensional power distribution, we calculated one-dimensional distributions in one direction (slow axis or fast axis) by summation over the second direction (fast axis or slow axis). This gives a result identical with that measured by using a moving slit. Based on the slow axis distribution we estimated the near field distribution and the structure of the transversal modes by using reverse analysis method described in Pruszyńska-Karbownik et al. (2016).

3 Results

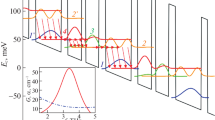
We have found numerically four transversal modes: TM00, TM10, TM20 and TM01. Figure 2 shows their calculated near-field power distributions in the laser waveguide. The confinement factor \({\varGamma }\) of the TM00, TM10, TM20, and TM01 modes is 0.702, 0.715, 0.729, and 0.399, respectively. The mode loss \(\alpha\) is 11.2, 10.7, 10.4, and \(33.9\,\mathrm {cm}^{-1}\), respectively. The optical parameters of the TM01 mode are significantly worse than the one of the others. Therefore, we did not take this mode and the higher-order modes into account in further analyses. Figure 3 shows the calculated far-field power distribution in slow axis (i.e. horizontally) for the remaining modes (TM00, TM10, and TM20). The calculated threshold gain \(g_{th}\) in 2-mm-long resonator for these modes is 33.8, 32.5, and \(31.4\,\mathrm {cm}^{-1}\), respectively.

Fig. 2
figure 2

Calculated near-field power distributions of first four lowest-order transversal modes: TM00 (upper left), TM10 (upper right), TM20 (bottom left) and TM01 (bottom right). The thin white lines indicate the interfaces between the layers of the waveguide

Full size image
Fig. 3
figure 3

Calculated far-field power distributions in slow axis direction of three lowest-order transversal modes: TM00 (left), TM10 (middle) and TM20 (right)

Full size image

The measured power distribution in the far field is shown in solid red lines in Fig. 4. The distribution in the slow axis is asymmetrical and has two lobes. The electric field distribution in the near field E(x), calculated by using the reverse beam analysis method, is

$$\begin{aligned} E(x)=471\cdot E_{TM00}(x)+1292\cdot E_{TM10}(x)\cdot \exp {i0.87\pi }+38\cdot E_{TM10}(x)\cdot \exp {i037\pi }, \end{aligned}$$
(5)

where \(E_{TM00}(x)\), \(E_{TM10}(x)\), and \(E_{TM20}(x)\) are near-field distributions for TM00, TM10, and TM20 modes, respectively. Black dotted lines in Fig. 4 shows calculated far-field power distributions with the assumption of the near-field distribution described by Eq. 5 and TM00, TM10, and TM20 modes distributions shown in Fig. 2. Full width at half maximum in fast axis for the calculated and measured distributions is \(44.2^{\circ }\) and \(45.8^{\circ }\), respectively.

Fig. 4
figure 4

Calculated and measured far-field power distributions in slow axis (left) and fast axis (right) direction

Full size image

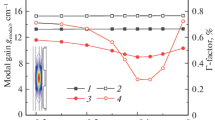
Because both the calculations and the measurement show that in the considered waveguide the TM00 mode has worse optical parameters than the TM10 mode, we were looking for the minimal laser width, for which the TM00 has better parameters than TM10. Thus, we have calculated how the confinement factor and the mode loss changes with the top layer (n+ InGaAs) width, assuming fixed curvature of the trenches. Figure 5 shows the results of the calculations: confinement factor and mode loss in function of the width. For considered previously resonator length (\(L=2\,\mathrm {mm}\)) the threshold gain, calculated by the formula 3, is better for TM00 than for TM10, if the width is smaller than \(3.27\,{\upmu } \hbox {m}\). If the resonator is short (\(L=0.5\,\mathrm {mm}\)), this minimal width is \(3.16\,{\upmu } \hbox {m}\) and if it is long (\(L=5\,\mathrm {mm}\)), the minimal width is \(3.31\,{\upmu } \hbox {m}\).

Fig. 5
figure 5

Calculated confinement factor (left) and mode loss (right) in function of the laser width for TM00 and TM10 modes

Full size image

4 Discussion

We have shown that the small discrimination between the transverse modes results from the similar values of confinement factor and mode loss for first three lowest-order transverse modes.

The experimental and numerical power far-field distributions agree well in terms of beam width and of spatial positions of the peaks. However, there is a difference between the experiment and the simulation in ratio of heights of the peaks. The difference is probably due to inconsistency between near-field distribution numerically calculated and sine near-field distributions assumed in the reverse analysis method. This does not affect the finding of the dominant mode—if other mode were the dominant one, the spatial positions of the peaks would be different—but it affect the results of the phase differences.

We found that three lowest-order transverse modes (TM00, TM10, and TM20) can excite in considered QCL waveguide. The results of the simulations show TM20 mode having the best parameters: both the confinement factor and the mode loss. The second best mode is TM10 and the third—TM00. However, the results of the measurements show TM10 mode being the dominant one. Most likely in the real structure there are losses at the interfaces between the mesa and \(\hbox {Si}_3\hbox {N}_4\), which is not taken into account in the simulations.

To achieve operation on the lowest-order transverse mode (TM00), the mesa should be much narrower than the wavelength. For the mesa wider than the wavelength the disctrimination between the modes decreases with its width, which leads to multi-transverse-mode operation. The maximal mesa width and the mode disctrimination depend only slightly on the resonator length.