Analytical method for the analysis of thin SiGe/Si solar cells with front surface field

Abstract

The present paper reports on a simulation study carried out to determine and optimize the effect of the high-low junction emitter (n⁺/n) of thin film SiGe/Si solar cell. The model is based on a simple analytical approach that draws on relevant device physics, including effective surface recombination velocity at the high-low junction and band discontinuities associated with heterojunctions. The collection of the light absorbed by the front surface field is discussed and an analytical solution is derived for the light-generated current in this layer. The photovoltaic parameters of SiGe/Si solar cells and those of the conventional cell Si/Si are compared. The findings revealed that the addition of Ge ~15 % to crystal Si highly enhances short-circuit current density and cell efficiency, whereas the SiGe band-gap degrades particularly the open-circuit voltage. The results also indicate that the solar cell maximum efficiency increase by about 1.7 % when the interface state density is lower than 10¹¹ cm⁻².

1 Introduction

Single-crystal silicon (Si) is widely used in the contemporary semiconductor industry and solar cells due to its natural abundance, thermal stability, and nontoxic properties (Timans 1996; Chen et al. 2007; International Technology Roadmap for Semiconductors 2011; Green 2003; Atwater and Polman 2010). More recently, studies of nanostructured Si have become a rich area in searching for high-efficiency and low-cost solar cell solutions (Atwater and Polman 2010; Hu and Chen 2007; Garnett and Yang 2010; Zhang and Ye 2013; Wang et al. 2013). In fact, Si and SiGe semiconductors materials with an indirect band gap energy, which has been regarded as a potential application in solar cells, because of its high absorption coefficient in the visible and infrared region (Chang et al. 2011).

In this context, recent research indicates that, owing to their compatibility with the mature Si-based cell process, silicon germanium can be applied in the active base region of the cell, thus offering a promising approach for the optimization of solar cell performance and improvement of cell efficiency (Larry Lee et al. 2010; Liou 1993; Usami et al. 2007; Hadi et al. 2014). In fact, the photocurrent in the small band-gap SiGe material is expected to undergo a substantial increase due to the increased absorption of photons. The open-circuit voltage would, on the other hand, undergo an inevitable decrease due to the decrease of the SiGe band-gap associated with the increase of the intrinsic carrier concentration (Hadi et al. 2014; Lang et al. 1985). Therefore, the optimal design for the high efficiency SiGe/Si hetero-junction solar cell still remains an open question.

The performance of solar cells is limited by various losses mechanisms, the most important losses is carrier recombination at the front surface (Berginski et al. 2008). A lot of studies were interesting to limit these losses. Zouari et al. have been demonstrate that front surface passivation of solar cells can minimize the carriers surface recombination (Zouari and Arab 2011; Zouari et al. 2008).

In the other hand several studies indicate that reducing the cell thickness, would lead to an increased efficiency provided that the cell surfaces are very well passivated and that the optical absorption is enhanced (Jeong et al. 2008; Grozdanov 1994; Wang et al. 2011; Mittiga et al. 2006; Minami et al. 2006; Musa et al. 1998). Another advantage of thin film cells is the promising opportunities they can offer with regards to reducing the cost of the component and to meeting the current high demand for silicon feed stock, Cuprous oxide (Cu₂O) is metal oxide semiconductor material, which has attracted much attention since 1920 due to its good room temperature mobility (Li et al. 2009).

A one-dimensional model based on a complete set of analytical solutions for the semi-conductor current density equations is presented in light of the relevant theory on highly doped regions. Two effective surface recombination velocities (ESRV) markers, namely $S_{{e,n^{ + } n}}$ and $S_{{e,nn^{ + }}}$, are defined, one in each side of the space charge layer of the high-low junction. Both ESRV markers are expressed as a function of the difference between the band-gap of c-Si and SiGe. The light-generated current density in the n⁺-layer is derived. The notion of a high-low junction factor F _h–l , which measures the collection effectiveness of the high-low junction, is then introduced. The study demonstrates that the high-low junction may be highly efficient in light current collection with F _h–l close to unity, a property that increases the short wavelength quantum efficiency in FSF rear junction solar cells.

The present study is a further step in this persistent search for the optimization of photovoltaic n⁺(Si)/n(SiGe)/p(c-Si) heterojunction solar cell efficiencies. The model presented in this work takes into consideration the currently available theories pertaining to Shockley–Read–Hall, Auger recombination’s processes and recombination rate to the interface of SiGe/Si and band-gap narrowing. The mobility and lifetime model of minority carriers used in this study are well established and described in the literature (Manasevit et al. 1982; Trabelsi 2013; Slotboom and Graaff 1976; Gatz et al. 2012). The impacts of the Ge concentration on the internal quantum efficiency (IQE) and the photovoltaic parameters are investigated, and the effects of the interface states on the current–voltage characteristic and cell efficiency are discussed, compared to the conventional n⁺(Si)/n(Si)/p(Si) solar cell, an optimized the Ge fraction can lead to a higher IQE consequently the enhancement of the conversion efficiency.

2 Theoretical development

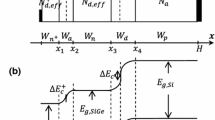
The SiGe/Si heterojunction solar cell used in the simulation is shown in Fig. 1a. The structure consists of high-low junction n⁺–n at the front and a rear n–p junction. The thickness values of the quasi-neutral layers are considered to be W ⁺ _n , W _n and W _p for the n⁺-region, n-region and p-region, respectively. The space charge region W _d of the n–p rear junction is determined using the fully depleted layer model of an n–p heterojunction (Banerjee et al. 2005). The physical parameter symbols used in the text are also given in Fig. 1a.

Fig. 1

a Schematic illustration of an n⁺/n/p/p⁺ solar cell. b Energy band diagram of n⁺/n/p double hetero-junction illustrating the band discontinuities ΔE _vi and ΔE _ci . Note that the bandgap of the c-Si is larger than that of the SiGe

Figure 1b shows the energy band diagram of an n⁺(c-Si)/n(SiGe)/p(c-Si) heterojuncion illustrating the conduction band discontinuity ΔE _c and valence band discontinuity ΔE _v . E _g,Si and E _g,SiGe are the band-gap of c-Si and SiGe, respectively. At 300 K, the band gap of SiGe is given by Lang et al. (1985):

$$ E_{g,SiGe} (y) = E_{g,Si} - 0.74y $$

(1)

The surface recombination velocities for the front and rear contacts are S _p and S _n , respectively. Two effective recombination velocities are introduced, $S_{{e,n^{ + } n}}$ and $S_{{e,nn^{ + } }}$. The physical meaning of $S_{{e,nn^{ + } }}$ (or $S_{{e,n^{ + } n}}$) is that it accounts for the effect of the n⁺-region (or the n-region) on the minority carriers from the n-region (or the n⁺-region).

The effective recombination velocity $S_{{e,nn^{ + } }}$ at the low-doped region of the high-low heterojunction (at x ₂) can be modeled as (Appendix):

$$ S_{{e,nn^{ + } }} = \frac{{N_{d,ef} D_{p,ef}^{ + } }}{{N_{d,ef}^{ + } L_{p,ef}^{ + } }} \cdot \frac{{\frac{{S_{p} L_{p,ef}^{ + } }}{{D_{p,ef}^{ + } }}cosh\left( {\frac{{W_{{n^{ + } }} }}{{L_{p,ef}^{ + } }}} \right) + sinh\left( {\frac{{W_{{n^{ + } }} }}{{L_{p,ef}^{ + } }}} \right)}}{{cosh\left( {\frac{{W_{{n^{ + } }} }}{{L_{p,ef}^{ + } }}} \right) + \frac{{S_{p} L_{p,ef}^{ + } }}{{D_{p,ef}^{ + } }} + sinh\left( {\frac{{W_{{n^{ + } }} }}{{L_{p,ef}^{ + } }}} \right)}} \times F_{{nn^{ + } }} $$

(2)

where,

$$ F_{{nn^{ + } }} = \frac{{N_{c,Si} N_{v,Si} }}{{N_{c,SiGe} N_{v,SiGe} }}exp\left( { - \frac{{E_{g,Si} - E_{g,SiGe} }}{{k_{B} T}}} \right) $$

(3)

For the heavily doped n⁺-region (or n-region) the donor density is replaced by an effective concentration given by $N_{d,ef}^{ + } = N_{d}^{ + } \left( {n_{i,Si} /n_{ie,Si} } \right)^{2}$, where n _i,Si is the intrinsic carrier concentration while n _ie,Si is the effective intrinsic carrier concentration which illustrates the heavy doping effects in crystalline silicon, degenerate statistics and band-gap narrowing (Liou et al. 1988). The effective intrinsic carrier concentration is given by: $n_{{ie,Si^{2} }} = n_{{i,Si^{2} }} exp\left( {\frac{\Delta Eg}{{k_{B} T}}} \right)$

The second effective recombination velocity, at x ₁, is taking the recombination velocity at the limit of the n–p junction space charge layer as infinite, then:

$$ S_{{e,n^{ + } n}} = \frac{{N_{d,ef}^{ + } D_{p,ef} }}{{N_{d,ef} L_{p,ef} }}coth\left( {\frac{{W_{n} }}{{L_{p,ef} }}} \right) \times \left( {F_{{nn^{ + } }} } \right)^{ - 1} $$

(4)

2.1 Photocurrent density contribution

The total photocurrent density J _ph,T (λ) at a wavelength of solar cell under illumination can be written as follows:

$$ J_{ph,T} (\lambda ) = J_{ph,E} (\lambda ) + J_{ph,D} (\lambda ) + J_{ph,B} (\lambda ) $$

(5)

where J _ph,E , J _ph,D and J _ph,B are the light-generated current density from the emitter layer, from the junction space-charge region (n–p), and from the p-type base region.

The light-generated hole current density, J _ph,E (λ), in the emitter consists of three contributions from the n⁺-region $J_{{ph,n^{ + } }} (\lambda )$, high-low junction space charge n ⁺–n J _ph,d (λ) and the n-region J _ph,n (λ). The photocurrent density J _ph,E (λ) (at x ₃) can be written as:

$$ J_{ph,E} (\lambda ) = J_{{ph,n^{ + } }} (\lambda ) + J_{ph,d} (\lambda ) + J_{ph,n} (\lambda ) $$

(6)

Under illumination, the current continuity equation for minority carriers, generated by a monochromatic light in the n-emitter region is given as follows:

$$ \frac{{d^{2} \left( {\Delta p_{L} } \right)}}{{dx^{2} }} - \frac{{\Delta p_{L} }}{{L_{p,ef}^{2} }} = - \frac{1}{{D_{p,ef} }}g_{SiGe} (x,\lambda ) $$

(7)

where Δp _L represents the hole concentration in the n-emitter region. The term g _SiGe (x, λ) refers to the generation rate of minority carriers. It is given by:

$$ g_{SiGe} (x,\lambda ) = \left( {1 - R} \right)\phi (\lambda )\alpha_{SiGe} (\lambda )e^{{ - \alpha_{Si} x_{2} }} e^{{ - \alpha_{SiGe} (x - x_{2} )}} $$

(8)

where R is the fraction of photon reflected from the front surface, α _Si and α _SiGe are the absorption coefficients of the c-Si and SiGe, respectively.

Using the following boundary conditions:

$$ \left. {\frac{{d\Delta p_{L} }}{dx}} \right|_{{x_{1} x_{2} }} = \frac{{S_{{e,nn^{ + } }} }}{{D_{p,ef} }}\Delta p_{L} (x = x_{2} ) $$

(9)

$$ \Delta p_{L} (x = x_{3} ) = 0 $$

(10)

The solution of the current continuity equation [Eq. (7)] is given by:

$$ \begin{aligned} J_{ph,n} (\lambda ) \hfill \\ = \frac{{q(1 - R)\alpha_{SiGe} \phi L_{p,ef} }}{{(\alpha_{SiGe}^{2} L_{p,ef}^{2} - 1)}}e^{{ - \alpha_{Si} x_{2} }} e^{{ - \alpha_{SiGe} W_{n} }} \hfill \\ \; \times \left\{ {\frac{{\left( {\frac{{S_{{e,nn^{ + } }} L_{p,ef} }}{{D_{p,ef} }} + \alpha_{SiGe} L_{p,ef} } \right)e^{{\alpha_{SiGe} W_{n} }} - \left[ {\frac{{S_{{e,nn^{ + } }} }}{{D_{p,ef} }}cosh\left( {\frac{{W_{n} }}{{L_{p,ef} }}} \right) + sinh\left( {\frac{{W_{n} }}{{L_{p,ef} }}} \right)} \right]}}{{\frac{{S_{{e,nn^{ + } }} L_{p,ef} }}{{D_{p,ef} }}sinh\left( {\frac{{W_{n} }}{{L_{p,ef} }}} \right) + cosh\left( {\frac{{W_{n} }}{{L_{p,ef} }}} \right)}} - \alpha_{SiGe} L_{p,ef} } \right\} \hfill \\ \end{aligned} $$

(11)

D _p,ef and L _p,ef are the minority hole diffusion coefficient and hole diffusion-length in the n-region, respectively.

The photo-generated excess holes in the front n⁺-region are collected by the high-low junction at x ₁ (Fig. 1a). Recombination in the high-low junction space charge region is assumed to be negligible. However, the photo-generated holes collected from the n⁺-region diffuse across the entire n-emitter region to be collected at x ₃, the n–p junction.

Under illumination, the photocurrent generated from the n⁺-region is the solution of the continuity equation (identical to the one given by Eq. (7) for the n-region) using special boundary conditions. The boundary conditions of the n⁺-region can be written as follows:

$$ \left. {\frac{{d\Delta p_{L}^{ + } }}{dx}} \right|_{x = 0} = \frac{{S_{p} }}{{D_{p,ef}^{ + } }}\Delta p_{L}^{ + } (x = 0) $$

(12)

$$ \Delta p_{L}^{ + } (x = x_{1} ) = \Delta p_{L,0}^{ + } $$

(13)

where represents the light-generated excess hole concentration at x = x ₁.

The light-generated current density in the n⁺-region, collected at x ₁ under the boundary conditions mentioned above, is given by:

$$ \begin{aligned} &J_{{ph,n^{ + } }} (at\,x_{1} )(\lambda ) \hfill \\ &= \frac{{q(1 - R)\alpha_{Si} \phi L_{p,ef}^{ + } }}{{(\alpha_{{Si^{2} }}^{2} L_{{p,ef^{2} }}^{ + } - 1)}} \hfill \\ &\quad \times \left\{ { - \alpha_{Si} L_{p,ef}^{ + } e^{{ - \alpha_{Si} W_{{n^{ + } }} }} + \frac{{\left( {\frac{{S_{p,} L_{p,ef}^{ + } }}{{D_{p,ef}^{ + } }} + \alpha_{Si} L_{p,ef}^{ + } } \right) - \left( {\frac{{\Delta p_{L,o}^{ + } }}{{P_{ph} }} + e^{{ - \alpha_{Si} W_{{n^{ + } }} }} } \right)\left[ {\frac{{S_{p} L_{p,ef}^{ + } }}{{D_{p,ef}^{ + } }}cosh\left( {\frac{{W_{{n^{ + } }} }}{{L_{p,ef}^{ + } }}} \right) + sinh\left( {\frac{{W_{{n^{ + } }} }}{{L_{p,ef}^{ + } }}} \right)} \right]}}{{\frac{{S_{p} L_{p,ef}^{ + } }}{{D_{p,ef}^{ + } }}sinh\left( {\frac{{W_{{n^{ + } }} }}{{L_{p,ef}^{ + } }}} \right) + cosh\left( {\frac{{W_{{n^{ + } }} }}{{L_{p,ef}^{ + } }}} \right)}}} \right\} \hfill \\ \end{aligned} $$

(14)

where,

$$ P_{ph} = \frac{{\left( {1 - R} \right)\phi \alpha_{Si} L_{{p,ef^{2} }}^{ + } }}{{D_{p,ef}^{ + } \left( {\alpha_{{Si^{2} }} L_{{p,ef^{2} }}^{ + } - 1} \right)}} $$

(15)

The expression (14) is quite similar to Eq. (11) due to the apparently similar boundary conditions, when the excess hole concentration $\Delta p_{L,0}^{ + } = 0$. The value of $J_{{ph,n^{ + } \left( {at \,x_{1} } \right)}} \left( \lambda \right)$ can be obtained if the concentration $\Delta p_{L,0}^{ + }$ is known. However, another boundary condition at x = x ₁ has to be introduced to account for the ESRV, then:

$$ J_{{ph,n^{ + } \left( {at \,x_{1} } \right)}} \left( \lambda \right) = qS_{{e,n^{ + } n}} \Delta p_{L,0}^{ + } $$

(16)

The expression (14) can be written as follows:

$$ J_{{ph,n^{ + } \left( {at \,x_{1} } \right)}} \left( \lambda \right) = J_{{ph,n^{ + } \left( {at \,x_{1} } \right)}}^{0} \left( \lambda \right) - q\Delta p_{L,0}^{ + } \left( {\frac{{N_{d,ef}^{ + } }}{{N_{d,ef} }}} \right)S_{{e,nn^{ + } }} $$

(17)

where $J_{{ph,n^{ + } \left( {at \,x_{1} } \right)}}^{0} \left( \lambda \right)$ is the collected photocurrent in the n⁺-region at x ₁ when Δp ⁺ _L,0  = 0.

The substitution of Eq. (16) into (17) gives the following:

$$ \Delta p_{L,0}^{ + } = \frac{{J_{{ph,n^{ + } \left( {at \,x_{1} } \right)}}^{0} \left( \lambda \right)}}{{q\left( {\frac{{N_{d,ef}^{ + } }}{{N_{d,ef} }}S_{{e,nn^{ + } }} + S_{{e,n^{ + } n}} } \right)}} $$

(18)

By combining Eqs. (16) and (18), $J_{{ph,n^{ + } \left( {at \,x_{1} } \right)}} \left( \lambda \right)$ can be rewritten in a more explicit form as follows:

$$ J_{{ph,n^{ + } \left( {at \,x_{1} } \right)}} \left( \lambda \right) = \frac{{J_{{ph,n^{ + } \left( {at \,x_{1} } \right)}}^{0} \left( \lambda \right)}}{{1 + \frac{{N_{d,ef}^{ + } }}{{N_{d,ef} }}\frac{{S_{{e,nn^{ + } }} }}{{S_{{e,n^{ + } n}} }}}} $$

(19)

The latter can be written also in the following form:

$$ J_{{ph,n^{ + } \left( {at \,x_{1} } \right)}} \left( \lambda \right) = J_{{ph,n^{ + } \left( {at \,x_{1} } \right)}}^{0} \left( \lambda \right)F_{h - l} $$

(20)

where F _h–l is the high-low factor given by the following equation:

$$ F_{h - l} = \frac{1}{{1 + \frac{{N_{d,ef}^{ + } }}{{N_{d,ef} }}\frac{{S_{{e,nn^{ + } }} }}{{S_{{e,n^{ + } n}} }}}} $$

(21)

Assuming that a negligible recombination in the space charge region of the high-low junction (the light-generated hole current collected by the high-low junction flows without any loss to $x = x_{2}$, i.e., $J_{{ph,n^{ + } \left( {at \,x_{1} } \right)}} = J_{{ph,n^{ + } \left( {at \,x_{2} } \right)}}$), then the collected photocurrent has to diffuse across the entire n-layer to be collected by the n–p junction at x ₃. The final expression for the contribution of the light-generated hole current from the n⁺-region, taking both the high-low junction extraction and the recombination loss in the n-region into account, is given by the following equation:

$$ J_{{ph,n^{ + } }} \left( \lambda \right) = J_{{ph,n^{ + } \left( {at \,x_{3} } \right)}} \left( \lambda \right) = J_{{ph,n^{ + } \left( {at \,x_{1} } \right)}}^{0} F_{h - l} \times sech\left( {\frac{{W_{n} }}{{L_{p,ef} }}} \right) $$

(22)

The generated carriers in the space charge of high-low junction (n⁺–n) are accelerated out of this region by the established electric field. Similarly, the contribution of this region $\left( {J_{ph,d} \left( \lambda \right)} \right)$ has to reach the n–p junction space charge region to be collected; accordingly, the following equation is obtained:

$$ J_{ph,d} \left( \lambda \right) = q\left( {1 - R} \right)\phi \left( \lambda \right) e^{{ - \alpha_{Si} W_{{n^{ + } }} }} (1 - e^{{ - \alpha_{Si} W_{a} }} ) \times sech\left( {\frac{{W_{n} }}{{L_{p,ef} }}} \right) $$

(23)

From these data, the total IQE as a function of wavelength was determined according to:

$$ IQE_{T} \left( \lambda \right) = \frac{{J_{ph,T} \left( \lambda \right)}}{{q\left( {1 - R} \right)\phi }} $$

(24)

when

$$ IQE_{T} \left( \lambda \right) = IQE_{E} \left( \lambda \right) + IQE_{D} \left( \lambda \right) + IQE_{B} \left( \lambda \right) $$

(25)

where IQE _E , IQE _D and IQE _B are the IQE from the emitter layer, from the junction space-charge region (n–p), and from the p-type base region.

The simulation is carried out using a photon density $\phi \left( \lambda \right)$ under AM 1.5 global normal sun condition as proposed by Liou and Wong (1992). The absorption coefficient in c-Si and SiGe are approximated by empirical expressions (Braunstkin et al. 1958).

2.2 Photovoltaic parameters

The J(V) characteristics of solar cell in the real case are expressed by the following equation (Lun et al. 2014):

$$ J\left( V \right) = J_{ph,T} - J_{0D} \left\{ {exp\left( {\frac{{V + JR_{s} }}{{V_{T} }}} \right) - 1} \right\} - J_{0R} \left\{ {exp\left( {\frac{{V + JR_{s} }}{{2V_{T} }}} \right) - 1} \right\} - \frac{{V + JR_{s} }}{{R_{sh} }} $$

(26)

with

$$ J_{0D} = J_{0E} + J_{0B} $$

(27)

where, J _0E and J _0B are the conventional reverse dark saturation current density in the emitter (n) and the base region (p), respectively (Liou 1993; Rohatgi and Rai-Choudhury 1984). Similarly for silicon solar cell, $J_{0E}$ and $J_{0B}$ are given by:

$$ J_{0E} = \frac{{qD_{p,ef} }}{{L_{p,ef} }}\Delta p\left( {x_{1} } \right)\frac{{\frac{{S_{{e,nn^{ + } }} L_{p,ef} }}{{D_{p,ef} }}cosh\left( {\frac{{W_{n} }}{{L_{p,ef} }}} \right) + sinh\left( {\frac{{W_{n} }}{{L_{p,ef} }}} \right)}}{{cosh\left( {\frac{{W_{n} }}{{L_{p,ef} }}} \right) + \frac{{S_{{e,nn^{ + } }} L_{p,ef} }}{{D_{p,ef} }}sinh\left( {\frac{{W_{n} }}{{L_{p,ef} }}} \right)}} $$

(28)

and

$$ J_{0B} = \frac{{q D_{n} }}{{L_{n} }}\Delta n\left( {x_{2} } \right)\frac{{\frac{{S_{n} L_{n} }}{{D_{n} }}cosh\left( {\frac{{W_{p} }}{{L_{n} }}} \right) + sinh\left( {\frac{{W_{p} }}{{L_{n} }}} \right)}}{{cosh\left( {\frac{{W_{p} }}{{L_{n} }}} \right) + \frac{{S_{n} L_{n} }}{{D_{n} }}sinh\left( {\frac{{W_{p} }}{{L_{p} }}} \right)}} $$

(29)

The minority carrier holes Δp(x ₁) and electrons $\Delta n\left( {x_{2} } \right)$ are expressed as follows (Liou 1993):

$$ \Delta p\left( {x_{1} } \right) = N_{a} { \exp }\left[ { - \left( {V_{d} + \frac{{\Delta E_{v } }}{q}} \right)/V_{T} } \right] $$

(30)

$$ \Delta n\left( {x_{2} } \right) = N_{d} exp\left[ { - \left( {V_{d} - \frac{{\Delta E_{c } }}{q}} \right)/V_{T} } \right] $$

(31)

where $V_{d}$ refers to the potential of the junction barrier,$\Delta E_{c } = \chi_{SiGe} - \chi_{Si}$, and $\Delta E_{v} = E_{g,Si} - E_{g,SiGe} - \Delta E_{c }$.

The recombination current density in the heterojunction space-charge layer (n–p) consists of the recombination current density in the bulk (J _0R,b ) as well as the recombination current density at the heterojunction interface (J _0R,i ), which is negligible in homojunctions, but is important and needs to be accounted for in heterojunctions because of the substantial trapping centers at the interface due to lattice mismatch between the two different materials. Thus

$$ J_{0R} = J_{0R,b} + J_{0R,i} $$

(32)

where J _0R,b is similar to the n(c-Si)–p(c-Si) junction, while, the reverse saturation current density due to interfacial recombination (J _0R,i ) is given by (Liou 1993):

$$ J_{0R,i} = 0.5 q \sigma_{p} V_{th} D_{i} n_{i,Si} $$

(33)

σ _p and D _i are the capture coefficient and the interface state density, respectively.$n_{i,Si}$ is the intrinsic carrier concentration of c-Si.

3 Results and discussion

The high-low junction factor F _h–l of SiGe/Si structure is plotted against Ge concentration (Fig. 2). The lightly doped n-region thickness is 0.3 µm, with N _d  = 10¹⁹ cm⁻³ (Usami et al. 2007), and the thickness of the n⁺-layer of c-Si is 20 nm, with N ⁺ _d  = 2.10²⁰ cm⁻³ (Zouari and Arab 2011). It can be clearly noted that the high-low factor F _h–l increases with the Ge concentration (y) and that when $y \ge 0.1$, $F_{h - l}$ approximates unity, resulting in $J_{{ph,n^{ + } \left( {at \,x_{1} } \right)}} \left( \lambda \right) = J_{{ph,n^{ + } \left( {at \,x_{1} } \right)}}^{0} \left( \lambda \right)$. In this case and similar to the n⁺–p junction, the high-low junction is highly efficient for the collection of light-generated current. It can also be concluded that the effective surface recombination velocity $S_{{e,nn^{ + } }}$ (or $S_{{e,n^{ + } n}}$) is more efficient when the Ge concentration exceeds 0.1.

Fig. 2

High-low junction factor, F _h–l , versus Ge concentration

3.1 Effect of the Ge concentration on the IQE

Figure 3a plots the IQE calculated for different values of Ge concentration “y”. For the sake of comparison, the IQE calculated for the conventional solar cell (n⁺(Si)/n(Si)/p(Si)) is presented in Fig. 3a as a dotted line (curve 1). The thicknesses of the n⁺-region and the n-region are 20 nm and 0.3 µm, respectively. The curves clearly indicate that the total generated photocurrent, from the n⁺(Si)/n(SiGe)/p(Si) heterojunction solar cell, reached the saturation when the y value is about 0.15.

Fig. 3

a Internal quantum efficiency of SiGe solar cell with high-low junction emitter for different Ge concentration (S _p  = 3 × 10⁶ cm s⁻¹, H = 50 µm). b Internal quantum efficiency for different regions (1) IQE _E from the emitter layer, (2) IQE _D from the junction space-charge region n–p, (3) IQE _B from the base region, (4) IQE _T total of the solar cell

The comparison of the IQE values of the two solar cell structures revealed that the heterojunction solar cells exhibit short wavelength spectral responses that are better than those of the conventional solar cells though they displayed comparable values in terms of the other spectra. This improvement in light-generated current, at low wavelength, is attributed to two main reasons. The first reason relates to the increase of the Ge concentration which improves the absorption coefficient in the SiGe layer (Zouari and Arab 2011), consequently the density of the minority carriers in this region increases compared to the density of holes generated in the emitter region realized by crystalline silicon (i.e. conventional structure). The second reason attributes this improvement to the decrease of the ESRV $S_{{e,nn^{ + } }}$ at the font surface at $x = x_{2}$ (see Fig. 3a). At high wavelength, we noted that the photocurrent generated in the base region for two structures are comparable for the rest of the spectra since the active material for the two structures is based on crystalline silicon.

Figure 3b plots the calculated IQE as function of wavelength for different regions with two values of Ge concentration, y = 0 (conventional cell) and y = 0.15. It can be noted that the enhancement of IQE is carried out by the emitter layer as compared to the conventional cell (curves 1). For y values of about 0.15, the photo-generated holes in the n⁺-region are collected by the high-low junction. This is explained by the increase in the effective recombination velocity $S_{{e,n^{ + } n}}$, as compared to the front surface velocity S _p , which induces the collection of holes at the high-low junction n⁺–n rather than their return to the front surface and recombination with electrons. Moreover, the low effective recombination velocity $S_{{e,nn^{ + } }}$ at the n-region side of the high-low junction plays the role of an effective mirror, and then almost all the light-generated holes in this region diffuse to the n–p junction where they are collected.

These curves displayed in Fig. 3b revealed that, compared to the conventional silicon solar cell presented as a dotted line, the light absorbed in the SiGe layer decreases slowly the contribution of light-generated current in the space-charge region (curves 2) and the base region (curves 3). This result is attributed to the fact that the carriers-generated rate in the crystalline silicon decreases with the $\alpha_{SiGe}$, i.e. with y.

3.2 Effect of the Ge concentration on the photovoltaic parameters

This section discusses the effect of the Ge concentration on the photovoltaic parameters. The values of the transport parameters of minority carriers and of the other parameters used in this study are given in Table 1.

Table 1 Physical parameters using in calculations

Figure 4 shows the variation in the values computed for the short-circuit current density $J_{sc}$, as a function of Ge concentration “y”, of the emitter layer with two values of cell thickness, H = 10 and 50 µm. The results show that, compared to the conventional silicon solar cell (y = 0), the short-circuit current density of the SiGe solar cell increases by about 4 mA cm⁻². This enhancement in J _sc is attributed to the increase of the light-generated in n-region $\left( {J_{ph,n} } \right)$.

Fig. 4

Variation of the short-circuit current density for SiGe solar cell with a high-low junction emitter versus Ge concentration under AM 1.5

The open-circuit voltage is plotted against Ge concentration as shown in Fig. 5. The results indicate that the V _oc decreases with the Ge mole fraction. This decrease is related to the reverse dark saturation current density in the emitter layer J _0E (i.e. J _0D ) and the recombination current density in the space charge region (J _0R ) (see Fig. 6). However, the substitution of Si by Ge increases the intrinsic carrier concentration due to the smaller band-gap of SiGe as compared to that of c-Si. These results show that the front surface passivation would not have much influence on J _0D or $V_{oc}$.

Fig. 5

Variation of the open-circuit voltage for SiGe solar cell with a high-low junction emitter versus Ge concentration

Fig. 6

Effect of the Ge concentration on the reverse dark saturation current density J _0D and the recombination current density J _0R

Figure 7 plots the variation of the cell efficiency (η) versus the Ge mole fraction. The values of interface state density (D _i ) used in this section, is 10¹¹ cm⁻². It shows that the optimal Ge concentration in the SiGe thin film solar cell is about 15 %. The maximum increase in cell efficiency 1.7 %, as compared to the conventional silicon solar cell (y = 0), is due to the improvement of the light-generated current density in the emitter layer. It can be noted that the cell efficiency of the SiGe solar cell increases when the value of y ≤ 0.15, this enhancement is related to the photocurrent. Moreover, and as expected from the (Figs. 5, 6), the reduction in cell efficiency for y > 0.15 is related to the increase of the saturation current densities ($J_{0D }$ and J _0R ) in which the reduced the open-circuit voltage.

Fig. 7

Variation of the cell efficiency for SiGe solar cell with a high-low junction emitter versus Ge concentration

3.3 Effect of the density of interface states on the photovoltaic parameters

This section discusses the effect of interface states density (D _i ) on the photovoltaic parameters of thin Si_0.85Ge_0.15 solar cells. Figure 8a, b illustrate the effect of D _i on the characteristic current–voltage and cell efficiency, respectively. The different photovoltaic parameters found in this study are summarized in Table 2. Both figures reveal that the photovoltaic parameters decrease when the interface states density increase. It is clear from the curves 1–4 in Fig. 8a that the short-circuit current density decreases by increasing the interface states density D _i . This result is attributed to the increases of the lifetime due to recombination rate to the interface SiGe/c-Si. It can be also be noted that the open circuit-voltage decrease with D _i , which allows to increase the recombination current density J _0R (i.e. J _0R,i ).

Fig. 8

a Characteristic J(V) of SiGe solar cells for different values of interface state density D _i (H = 50 µm, R _s  = 0.1 Ω cm² and R _sh  = 10⁵ Ω cm²). b Cell efficiency versus voltage V of SiGe solar cell under 100 mW cm⁻² for different values of interface state density D _i (H = 50 µm, R _s  = 0.1 Ω cm² and R _sh  = 10⁵ Ω cm²)

Table 2 Effect of the density of interface states on the photovoltaic parameters

We notice that the cell efficiency (η) and fill factor (FF) obtained for different values of D _i reflects more or less the same nature as J _sc and V _oc . Our study show that the cell efficiency decrease from 18.4 to 14.6 % when the value of D _i increases from 10¹¹ to 10¹³ cm⁻². It is clear from Fig. 8b that the cell efficiency value recorded for the SiGe solar cell is inferior to the conventional cell (for y = 0, curve ‘5’) when the value of D _i exceeds 10¹² cm⁻².

4 Conclusion

This study presents an analytical model developed to simulate the performance of thin SiGe solar cells with high-low junction emitter. It provides an analytical solution to a complete set of equations required for determining the contribution of the photocurrent generated from the heavily doped region. The n⁺-layer is modeled by an effective recombination velocity at the front surface. The results indicate that, compared to the conventional silicon solar cell, the IQE of the SiGe solar cell improves when the value of Ge concentration is about 0.15. A theoretical simulation was performed to investigate the optimal Ge concentration in the SiGe solar cell. The results revealed that the appropriate addition of Ge to the multi-layer SiGe-based solar cell efficiently enhances the short-circuit current density by ~4 mA cm⁻² with the degradation of the open circuit voltage. The overall efficiency is also effectively improved by about 1.7 % as compared to the conventional cell. This enhancement in cell efficiency is attributed to the light-generated current density in the emitter layer. The values calculated in terms of short-circuit current density enhancement suggest that, compared to conventional silicon solar cells, cell efficiency is also important for low density interface of states. Taken together, the results indicate that the model proposed in this work may offer a constructive tool for future use in applications involving thin film SiGe solar cells.

Appendix

The FSF (n⁺-region) is modelled by an effective surface recombination velocity $S_{{e,nn^{ + } }}$ in the vicinity of the low–high junction (at x = x ₂). The ESRV is calculated by solving the continuity equation and the current transport in the n⁺-region at the dark. The minority-carrier continuity equation in this region is given by the following expression:

$$ \frac{{d^{2} \Delta p^{ + } }}{{dx^{2} }} - \frac{{\Delta p^{ + } }}{{L_{{p,ef^{2} }}^{ + } }} = 0 $$

(34)

Using the following boundary conditions:

$$ \left. {\frac{{d\Delta p^{ + } }}{dx}} \right|_{x = 0} = \frac{{S_{p} }}{{D_{p,ef}^{ + } }}\Delta p^{ + } \left( {x = 0} \right) $$

(35)

$$ \Delta p^{ + } \left( {x = x_{1} } \right) = \frac{{n_{i,Si}^{2} }}{{N_{d,ef}^{ + } }} \left( {e^{{\frac{qV}{{k_{B} T}}}} - 1} \right) $$

(36)

and the injected current density in the n⁺-region which is given by:

$$ \left. {J_{{0b,n^{ + } }} = - qD_{p,ef}^{ + } \frac{{d\Delta p^{ + } }}{dx}} \right|_{{x = x_{1} }} $$

(37)

The solution of the current continuity equation Eq. (34), subject to the above boundary condition is given by:

$$ J_{{0b,n^{ + } }} \left( {x = x_{1} } \right) = \frac{{qn_{{i,Si^{2} }} D_{p,ef}^{ + } }}{{N_{d,ef}^{ + } L_{p,ef}^{ + } }}\frac{{\frac{{S_{p} L_{p,ef}^{ + } }}{{D_{p,ef}^{ + } }}cosh\left( {\frac{{W_{{n^{ + } }} }}{{L_{p,ef}^{ + } }}} \right) + sinh\left( {\frac{{W_{{n^{ + } }} }}{{L_{p,ef}^{ + } }}} \right)}}{{cosh\left( {\frac{{W_{{n^{ + } }} }}{{L_{p,ef}^{ + } }}} \right) + \frac{{S_{p} L_{p,ef}^{ + } }}{{D_{p,ef}^{ + } }}sinh\left( {\frac{{W_{{n^{ + } }} }}{{L_{p,ef}^{ + } }}} \right)}} \times \left( {e^{{\frac{qV}{{k_{B} T}}}} - 1} \right) $$

(38)

The depletion region n⁺–n is neglected, so $J_{{0b,n^{ + } }}$ at $x = x_{2}$ can be also written as:

$$ J_{{0b,n^{ + } }} \left( {x = x_{2} } \right) = S_{{e,nn^{ + } }} \frac{{qn_{i,SiGe}^{2} }}{{N_{d,ef} }} \times \left( {e^{{\frac{qV}{{kB^{T} }}}} - 1} \right) $$

(39)

By combining Eqs. (38) and (39), the ESRV at x = x ₂ can be simply obtained as:

$$ S_{{e,nn^{ + } }} = \frac{{N_{d,ef} D_{p,ef}^{ + } }}{{N_{d,ef}^{ + } L_{p,ef}^{ + } }} \frac{{\frac{{S_{p} L_{p,ef}^{ + } }}{{D_{p,ef}^{ + } }}cosh\left( {\frac{{W_{{n^{ + } }} }}{{L_{p,ef}^{ + } }}} \right) + sinh\left( {\frac{{W_{{n^{ + } }} }}{{L_{p,ef}^{ + } }}} \right)}}{{cosh\left( {\frac{{W_{{n^{ + } }} }}{{L_{p,ef}^{ + } }}} \right) + \frac{{S_{p} L_{p,ef}^{ + } }}{{D_{p,ef}^{ + } }}sinh\left( {\frac{{W_{{n^{ + } }} }}{{L_{p,ef}^{ + } }}} \right)}} \times F_{{nn^{ + } }} $$

(40)

where,

$$ F_{{nn^{ + } }} = \frac{{N_{c,Si} N_{v,Si} }}{{N_{c,SiGe} N_{v,SiGe} }}exp\left( { - \frac{{E_{g,Si} - E_{g,SiGe} }}{{k_{B} T}}} \right) $$

(41)

The second effective recombination velocity, $S_{{e,n^{ + } n}}$ at $x = x_{1}$, is calculated taking the recombination velocity at the limit of the n–p junction space charge layer as infinite, then

$$ S_{{e,n^{ + } n}} = \frac{{N_{d,ef}^{ + } D_{p,ef} }}{{N_{d,ef} L_{p,ef} }} coth\left( {\frac{{W_{n} }}{{L_{p,ef} }}} \right) \times \left( {F_{{nn^{ + } }} } \right)^{ - 1} $$

(42)