1 Introduction

Superlattices are artificial structures with a wide range of applications. They offer possibilities to study and control transport (Wacker 2002) and optical (Pereira 1995) properties of semiconductors. This paper uses an accurate analytical approximation that can be easily programmed and includes the main many body effects required to describe steady state nonlinear absorption. The expressions delivered reduce exactly to Elliott’s formula in the low density linear limit. This leads to an efficient numerical tool to investigate new materials, starting e.g. from ab initio calculations and has potential for a major impact in the development of new materials with applications from the THz and Mid Infrared to the Visible ranges (Pereira 2015). The superlattices are described as anisotropic media characterized by effective masses parallel and perpendicular to the growth direction (Pereira 1995). That suggests that new materials being currently investigated for solar cells and which are strongly anisotropic (Steinmann et al. 2015), may also be very useful for nonlinear optics applications, e.g. the controllable anisotropy in the superlattice case might be useful for applications such as power limiting (Poirier et al. 2002; Wu et al. 2003). Here the anisotropy-induced nonlinearity in the nanostructure is controlled per design in contrast with recent studies in which it depends on nanoparticle shape (Hua et al. 2015). We show that the nonlinearities increase with the anisotropic character. This paper is organized as follows: we start summarizing the main equations used, next numerical applications for GaAs–AlGaAs superlattices are given and a short summary follows.

2 Mathematical approach and model equations

The optical response of semiconductor materials can be obtained by self-consistent evaluation of Many Body Nonequilibrium Green’s Functions (NEGF). Efficient numerical methods used here have been successfully applied to both inter-subband (Pereira and Faragai 2014; Pereira 2007; Pereira 2008; Pereira et al. 2007; Pereira and Tomić 2011; Pereira 2011) and inter-band transitions (Grempel et al. 1996; Pereira et al. 1994; Pereira and Henneberger 1997; Chow et al. 1992) in quantum wells and superlattices.

We start with the interband polarization that has been used to describe superlattices as an effective anisotropic 3D material (Pereira 1995),

$$ \left[ {\hbar \omega + i\Gamma - E_{g} \left( \gamma \right) - \frac{{\hbar^{2} k^{2} }}{{2\mu_{\parallel } }}\xi \left( {\theta ,\gamma } \right)} \right]P\left( {\vec{k},\omega } \right) = A\left( \omega \right)\left[ {\wp \cdot E\left( \omega \right) + \mathop \sum \limits_{{\vec{k}{'} \ne \vec{k}}} {\mathcal{W}}_{{\vec{k} - \vec{k}{'}}} P\left( {\vec{k}{'},\omega } \right)} \right], $$
(1)

where the meaning of the anisotropy dependent bandgap is explained below and \( \xi \left( {\theta ,\gamma } \right) = sin^{2} \theta + \gamma cos^{2} \theta \). The anisotropy parameter \( \gamma \) is given by the ratio between the in-plane \( \mu_{\parallel } \) and perpendicular \( \mu_{ \bot } \) reduced effective masses, \( \gamma = \mu_{\parallel } /\mu_{ \bot } \), with \( \frac{1}{{\mu_{\parallel } }} = \frac{1}{{m_{e\parallel } }} + \frac{1}{{m_{h\parallel } }} \) and \( \frac{1}{{\mu_{ \bot } }} = \frac{1}{{m_{e \bot } }} + \frac{1}{{m_{h \bot } }} \) which are calculated from the non-interacting superlattice Hamiltonian \( {\mathcal{H}}_{0} \), \( \frac{1}{{m_{i\parallel } }} = \hbar^{ - 2} \partial^{2} /\partial k_{i\parallel }^{2}\Psi \left| {{\mathcal{H}}_{0} } \right|\Psi \), \( \frac{1}{{m_{i \bot } }} = \hbar^{ - 2} \partial^{2} /\partial k_{i \bot }^{2} \varPsi \left| {{\mathcal{H}}_{0} } \right|\varPsi \), for i = e, h. More details are given in Pereira (1995). Here we use a simple phenomenological scattering rate \( \Gamma \) to simulate the average dephasing that stems from the electron–electron, electron–phonon and electron-impurity scattering (Schmielau and Pereira 2009a, b, c), in order to keep the approach as simple as possible without affecting the conclusions. We have neglected any k-dependence on the transition dipole moment \( \wp \) induced by the electric field \( {\text{E}}\left(\upomega \right). \) In a superlattices there is a preferred direction determined by the growth (z-direction). The problem has consequently a cylindrical symmetry. The next step is to perform an angle average, \( \xi \left( {\uptheta,\upgamma} \right) = { \sin }^{2}\uptheta +\upgamma{ \cos }^{2}\uptheta = \frac{1}{2}\left( {1 +\upgamma} \right) \), leading to

$$ \frac{{\hbar^{2} k^{2} }}{{2\mu_{\parallel } }}\xi \left( {\theta ,\gamma } \right) \to \frac{{\hbar^{2} k^{2} }}{{2M_{\parallel } }}, $$
(2)

where \( M_{\parallel } = 2\mu_{\parallel } /\left( {1 + \gamma } \right) \). This anisotropic mass directly leads to an exciton Bohr radius \( a_{0} \) and corresponding 1S binding energy \( E_{0} \), given by

$$ a_{0} = a_{0} \left( \gamma \right) = \hbar^{2} \epsilon_{0} /e^{2} M_{\parallel } ,\quad E_{0} = E_{0} \left( \gamma \right) = 2Ry/\left( {1 + \gamma } \right),\quad Ry = \frac{{\mu_{\parallel } e^{4} }}{{2\hbar^{2} \epsilon_{0}^{2} }}, $$
(3)

where \( \epsilon_{0} \) is the background dielectric constant and e is the electron charge. The resulting exciton binding energies in superlattcies are very good agreement with experiments, as demonstrated in Pereira (1995).

The typical Yukawa potential used to represent the screened Coulomb potential does not have simple analytical solutions. The choice of inversion factor \( A\left( \omega \right) = \tanh \left[ {\beta \left( {\hbar \omega - \mu } \right)/2} \right] \) guarantees that the cross-over from absorption to gain takes place exactly at the total chemical potential and allows the expansion of the polarisation function in terms of the eigenfunctions, since A is not k-dependent and allows a simple Fourier transformation to real space. At this point, we thus replace the usual Yukawa potential used to describe screening in 3D by the Hulthén potential \( {\mathcal{W}}\left( r \right) = - 2e^{2} \kappa \epsilon_{0}^{\prime - 1} /\left( {\left( {{ \exp }(2\kappa r} \right) - 1} \right)) \) (Pereira 1995; Bányai and Koch 1986; Flügge 1974), which has successfully reproduced bulk nonlinear optical spectra (Bányai and Koch 1986) and has well known analytical solutions.

The total chemical potential \( \mu = \mu_{e} + \mu_{h} \) and screening wavelength \( \kappa = \kappa_{e} + \kappa_{h} \) are given by

$$ \beta \mu_{\lambda } = ln\nu_{\lambda } + K_{1} \ln \left( {K_{2} \nu_{\lambda } + 1} \right) + K_{3} \mu_{\lambda } , $$
(4)
$$ \kappa_{\lambda } = \sqrt {\frac{{4\pi e^{2} }}{{\epsilon_{0} }}\frac{{\partial n_{\lambda } }}{{\partial \mu_{\lambda } }}} = \sqrt {\frac{{\beta \pi e^{2} n_{\lambda } /\epsilon_{0} }}{{\frac{1}{{\nu_{\lambda } }} + \frac{{K_{1} K_{2} }}{{K_{2} \nu_{\lambda } + 1}} + K_{3} }}} , $$
(5)

with \( K_{1} = 4.897 \), \( K_{2} = 0.045 \) and \( K_{3} = 0.133. \) Here \( \nu_{\lambda } \) is obtained from the particle density for electrons and holes, \( n = n_{e} = n_{h} \) by \( \nu_{\lambda } = 4n_{\lambda } /[ {( {2m_{\parallel ,\lambda } /\beta \pi \hbar^{2} } )( {2m_{ \bot ,\lambda } /\beta \pi \hbar^{2} } )^{1/2} }] \) and \( \beta = 1/K_{B} T \) (Pereira 1995).

It is beyond the scope of this paper to show the intermediate details that lead to the next equation. In words, we combine the partly phenomenological approach of Bányai and Koch (1986) with the material parameters calculated with the anisotropic medium approach (Pereira 1995; Pereira et al. 1990). However, from the many possible options to express the eigenstates of the Hulthén potential (Flügge 1974) we use hypergeometric functions instead of the Jost function approach of Pereira (1995) and Flügge 1974). The resulting absorption spectrum then reads

$$ \begin{aligned} \alpha \left( \omega \right) = & \,\alpha_{0} \left( \gamma \right)\frac{\hbar \omega }{{e_{0} }}\tanh \left[ {\beta \left( {\hbar \omega - \mu } \right)/2} \right]\left\{ {\mathop \sum \limits_{n = 1}^{\sqrt g } \frac{4\pi }{n}\left( {\frac{1}{{n^{2} }} - \frac{{n^{2} }}{{g^{2} }}} \right)\delta_{\varGamma } \left( {\Delta - e_{n} } \right)} \right. \\ & \left. {\quad + \,2\pi \mathop \int \limits_{0}^{\infty } \frac{{\sinh \left( {\pi g\sqrt x } \right)}}{{\cosh \left( {\pi g\sqrt x } \right) - \cos \left( {\sqrt {4g - g^{2} x} } \right)}}\delta_{\varGamma } \left( {\Delta \left( { - x} \right)} \right)dx} \right\}, \\ \end{aligned} $$
(6)

where \( \alpha_{0} \left( \gamma \right) = 2\wp^{2} /\left( {n_{b} \hbar ca_{0}^{3} \left( \gamma \right)} \right) \). The normalized detuning is \( \Delta = \left( {\hbar \omega - E_{g} \left( \gamma \right)} \right)/E_{0} \left( \gamma \right) \). \( n_{b} \) and c denote, respectively, the background refractive index and the speed of light in vacuum. In Eq. (6) above, the band gap renormalization stems from the Mott criterion. This choice of bandgap renormalization is usually in good agreement with the full Green’s function approach and the Single Plasmon Pole Approximation (SPPA) simplified under a quasi-static approximation (Pereira 1995).

$$ E_{g} \left( \gamma \right) = E_{gap} + E_{0} \left( \gamma \right)\left\{ {\begin{array}{*{20}l} { - 1 + \left( {1 - \frac{1}{g\left( \gamma \right)}} \right)^{2} ,} \hfill & { g\left( \gamma \right) \ge 1} \hfill \\ { - 1/g\left( \gamma \right),} \hfill & { g\left( \gamma \right) < 1 } \hfill \\ \end{array} } \right. $$
(7)

where \( g\left( \gamma \right) = 1/\kappa a_{0} \left( \gamma \right) \) and \( E_{gap} = E_{c} \left( 1 \right) + E_{HH} \left( 1 \right) + E_{gap,bulk} \) is the bulk (temperature dependent) isotropic bandgap found in semiconductor materials tables in the literature plus the confinement energies of the lowest conduction subband and the top heavy hole subband.

The broadened delta function is chosen as \( \delta_{\varGamma } \left( x \right) = 1/\pi\updelta\eta cosh(x/\upeta) \), where \( \upeta =\Gamma /E_{0} \left( \gamma \right) \) which reproduces the Urbach tail very efficiently. The sum in the exciton part runs through the available states within the largest integer value of \( \sqrt {g\left( \gamma \right)} \). In the low density limit, \( g\left( \gamma \right) \to \infty \) and we recover the Elliot formula for excitonic luminescence with the correct balance between bound and continuum states.

3 Numerical results and discussion

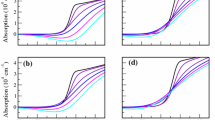
Figure 1 depicts the nonlinear optical absorption of GaAs–Al0.3Ga0.7As superlattices at T = 300 K. The scaled photon energy (x-axis) helps highlight the Coulomb correction effects that would otherwised be mixed with the changes due to carrier confinement, which are described by \( E_{gap} = E_{c} \left( 1 \right) + E_{HH} \left( 1 \right) + E_{gap,bulk} \) for different superlattices.

Fig. 1
figure 1

Nonlinear optical absorption of GaAs–Al0.3Ga0.7As superlattices at 300 K with increasing anisotropy characterized by decreasing γ = 0.62, 0.43, 0.16 and 5.52 × 10−2, respectively from a to d. This is obtained by fixing the well width at 10 nm and increasing the barrier width correspondingly by 1, 2, 4 and 6 nm. In each panel, from top to bottom the carrier density in both conduction and valence bands is N = 0, 0.1, 0.5, 1, 1.5 and 2 × 1018 cm−3. E 0,b  = 4.2 meV is the bulk GaAs exciton binding energy. From a to d, E gap  = 1.819, 1.827, 1.833 and 1.834 eV

Full size image

The increase in anisotropy (smaller γ) is obtained by increasing the barrier length. A larger barrier reduces the tunnelling from one well to the other and that is measured by a larger mass along the growth direction. The single quantum well case is obtained for a very large barrier, with \( \mu_{ \bot } \to \infty \) and correspondingly \( \gamma \to 0. \) In other words, smaller \( \gamma \) corresponds to larger anisotropy. From (a) to (d) we do see an increase in nonlinearity, i.e. a larger reduction in absorption with increasing carrier density. Note that even though Pereira (1995) also has analytical expressions for the nonlinear spectra of superlattices, to the best of that author’s knowledge numerical applications have never been given before as in the present paper. Figure 2 makes it more clear by showing the differential absorption \( \Delta \alpha \left( \omega \right) = \alpha \left( {\omega ,N} \right) - \alpha \left( {\omega ,N = 0} \right) \).

Fig. 2
figure 2

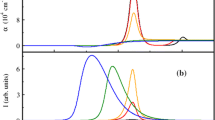
Differential absorption \( \varDelta \alpha \left( \omega \right) = \alpha \left( {\omega ,N} \right) - \alpha \left( {\omega ,N = 0} \right) \) for the structures in Fig. 1 with a carrier density N = 1×1017 cm−3 at 300 K. The solid, dashed, dot-dashed and dot-double dashed correspond to an increase in anisotropy, characterized respectively by γ = 0.62, 0.43, 0.16 and 5.52 × 10−2

Full size image

Figure 3 allows a better understanding of the excitonic bleaching and gain development as a function of anisotropy and carrier density.

Fig. 3
figure 3

Inverse screening length κ (a) and total chemical potential βμ (b) as a function of carrier density for the same structures in Figs. 1 and 2 at 300 K. The solid, dashed, dot-dashed and dot-double dashed correspond to an increase in anisotropy, characterized respectively by γ = 0.62, 0.43, 0.16 and 5.52 × 10−2

Full size image

The combined figures show that as the anisotropy increases, so does the inverse screening length \( \upkappa \) leading to a faster reduction of the screened Coulomb interaction and consequently larger optical nonlinearity, measured here directly by the differential absorption. This shows that an increase in nonlinearity is observed for all carrier densities, which are considered in the manuscript, and in the whole range of energies depicted in Fig. 1.

However, with increasing anisotropy, the z-direction electron and hole masses become to different, with a much larger increase in hole mass. When the upper and lower (average) curvatures or equivalently, the average effective masses are too different the total chemical potential is relatively smaller (see Fig. 3b) and so is the inversion factor \( \tanh \left[ {\upbeta\left( {\hbar\upomega -\upmu} \right)/2} \right] \) of Eq. (6), thus reducing the gain in Fig. 1. This influence of different electron and hole masses on the inversion is fully consistent with the detailed analysis for isolated quantum wells seen e.g. in Chow et al. (1992). Note that the method presented here can be used for a large number of other materials and superlattices as long as tunneling between adjacent periods allows a 3D-like spread of carriers wavefunctions—either electrons or holes so that movement along the z-direction is possible and an effective 3D medium can be considered with corresponding effective masses. Thus the model is better suited for absorption in superlattices far from the 2D limit. In the quasi-2D limit of quantum wells, the full numerical solution (Pereira et al. 1994; Pereira and Henneberger 1997; Chow et al. 1992) should be used. Thus, increase in nonlinearity is clearly demonstrated, which may be very important for truly 3D anisotropic new materials, but the high gain in quantum wells cannot be described by the method presented here.

In summary, the analytical expressions developed show a clear connection between an increase in optical nonlinearity with anisotropy by directly controlling the anisotropy and evaluating the resulting differential absorption and nonlinear spectra. This study shows the potential for other strongly anisotropic materials such as those used for solar cells and complex organic molecules for a role also as nonlinear optical materials and a possible recipe to improve their efficiency by controlling the anisotropy.