1 Introduction

Sensing is always a challenging, but indispensable task in the oil and gas sector. In recent years, oil and gas exploration and production has been moving into deeper and deeper zones in order to meet the growing demand. This results in harsh operating conditions, which is reflected by critical parameters like temperature, pressure, strain, etc. Therefore, reliable sensors which are able to continuously and accurately report current down-hole conditions has become very important in managing oil and gas reservoirs and wells (Algeroy et al. 2010). To support this need, multi-point distributed and multimodal simultaneous measurements will be required for drilling and oil and gas production monitoring. Hence, more sensors are required, with longer sensing range, for effective remote monitoring of down-hole. However, this results in higher signal attenuation, crosstalks and losses. In order to alleviate this situation, there is a need to enhance the sensing signals and reduce the fibre losses.

Optical fibre sensing technology have many advantages such as electrical isolation, immunity from electromagnetic interference (EMI), freedom from corrosion and ability to operate in harsh conditions (Lee 2003). They also offer the possibility of sensing different parameters at remote locations (Gholamzadeh and Nabovati 2008). Considering all these advantages, fibre-optic sensing technology offers an attractive alternative to conventional electronic sensing technology for permanent monitoring of oil and gas reservoirs. Current optical down-hole sensing approaches, based on fibre bragg gratings (FBGs) (Hill and Meltz 1997; Erdogan 1997) are capable of sensing almost all physical parameters like temperature, strain, pressure, vibration, etc. However, the FBG sensor responds to multiple sensing parameters, like temperature and strain, in a coupled fashion. In order to measure these physical parameters separately or to measure both simultaneously, the effects of strain and temperature need to be decoupled from each other. Therefore, multi-parameter measurement is very important, as it allows to reduce the size, cost and complexity of the sensing system, and also provides parameter discrimination in situations where cross-sensitivity is a critical issue (Frazao et al. 2005).

Even though intensive researches have been carried out on specialised fibres like photonic crystal fibres (PCFs) and FBGs for many years, to the best of our knowledge, no work has been reported exploiting their synergy in oil and gas sensing applications. PCF–FBG based sensor is capable of differentiating the effects of different parameters like temperature and strain (Martelli et al. 2005). Their combination can improve the overall performance of the sensor system in terms of power, energy scaling and discrimination of cross-sensitivities (Jollivet et al. 2014). The multi-resonant peaks from the PCF–FBG sensor helps to attain multi-parameter measurement simultaneously, offering good stability and wide range of broadband tuning (Zhao et al. 2013).

The main advantage of PCF (Knight et al. 1996; Knight 2003) is their high light confinement characteristics which is otherwise difficult to achieve in conventional fibres. Liquid crystal PCFs (LCPCFs) open new perspectives in sensing applications (Wolinski et al. 2006). With the addition of liquid crystals on to the PCF air holes, wavelength shifts results as the output signal with variation in physical parameters like temperature (Li et al. 2006) and also provides means of achieving active control over PCF propagation and polarization characteristics (Rajan 2015). The thermal and electrical tuning capabilities of LCPCFs along with their unique spectral and polarization properties opens up their possibilities for multi-parameter fibre-optic sensing (Wolinski et al. 2006).

Combination of LCPCF and FBG technologies enables effective control over the mode confinements and light characteristics. This is because, the liquid crystal infused in the cladding holes creates a PBG (Photonic Bandgap) effect, restricting the modes within the core region rather than leaking. However, LCPCF–FBG integration is quite challenging, mainly due to their difference in core sizes and mode field diameters (MFDs). Furthermore, this results in different forms of losses, which are dominated by confinement loss. Therefore, it is important to develop approaches to reduce losses occurring within the fibre core, so that signal power is enhanced and thereby transmission and sensing range of the fibre can also be increased. By optimizing geometrical parameters such as hole distribution, hole sizes, etc. of the PCF, confinement losses can be minimized. Furthermore, analyzing effective area and MFD gives a better insight of leakage loss, macro-bending loss and numerical aperture of the fibre sensor.

2 Theory

2.1 Losses in fibres

There are several sources of losses in fibres, such as structural imperfections, fibre bending, intrinsic material absorption, Rayleigh scattering, etc. Losses induced at the time of fabrication can be reduced by careful optimization and monitoring of the fabrication process. Confinement loss is another major type of loss that occurs mainly in fibres fabricated from raw material (Saitoh and Koshiba 2005). Confinement loss which is also known as leakage loss is the leakage of power from the core into the cladding and it occurs mainly in single mode fibres. The guided modes of PCFs are inherently leaky, as the refractive index of core is the same as that of outer cladding without air-holes (Pourmahyabadi and Nejad 2009). Theoretically, PCF with infinite number of air-holes in the cladding is expected to achieve lossless propagation. However, practically fabricated fibre experiences leaky modes due to finite number of air-holes in the photonic crystal cladding.

Confinement Loss (Tan et al. 2009) expressed in dB/Km is given by:

$$L = \frac{{\left( {\frac{{\mathop {20}\limits^\cdot }}{\ln 10}\left( {2\pi } \right)} \right)\;Im\left( {{n_{eff}}} \right)}}{\lambda }$$
(1)

where \(Im\left( {{n_{eff}}} \right)\) is the imaginary part of the effective refractive index and \(\lambda\) is the propagating wavelength.

2.2 LCPCF sensing principle

LCPCF sensors are based on the optical properties of the liquid crystal and have its index of refraction, \({n_{LC}}\) as the sensing magnitude. LCPCF temperature sensor takes advantage of the temperature dependence of the liquid crystal permittivity, which makes it less susceptible to other external influences and also a lambda shift is experienced at the output as a result of changes in temperature (Li et al. 2006).

Effective mode area (Agrawal 2007) of the PCF is given by the equation:

$${A_{eff}} = \frac{{{{\left[ {\iint \nolimits_{ - \infty }^\infty {{\left| {E\left( {x,y} \right)} \right|}^2}\;dxdy} \right]}^2}}}{{\iint \nolimits_{ - \infty }^\infty {{\left| {E\left( {x,y} \right)} \right|}^4}\;dxdy}}$$
(2)

where \(E\left( {x,y} \right)\) is the modal field distribution of fundamental fibre mode.

Also, effective area is related to MFD (Miyagi et al. 2010) by the equation:

$${A_{eff}} = {k_n}\;\left( {\frac{\pi }{4}} \right)\;MF{D^2}\; = \;{k_n}\;\pi \;{w^2}$$
(3)

Where \({k_n}\;\)is the correction factor and spot size, \(w = MFD/2\).

Mode Field diameter is approximated as,

$$MFD \approx \frac{2}{\sqrt \pi }\;\sqrt {{A_{eff}}}$$
(4)

2.3 FBG sensing principle

The basic principle of FBG sensor relies on the Bragg condition. Any changes in physical parameters like temperature, strain, polarization, etc. alters the refractive index or grating period of the fibre grating, which in turn change the Bragg wavelength correspondingly. The incident wave gets coupled to the same counter propagating wave and thus it gets reflected (Hill and Meltz 1997). The Bragg reflected wavelength (Hill and Meltz 1997; Kashyap 1999) is given by:

$${\lambda_b} = 2 \cdot {n_{eff}} \cdot \wedge$$
(5)

Where \({n_{eff}}\;\) is the effective refractive index and \(\wedge\) is the period of the grating.

3 Results and discussions

Confinement losses in the sensor are studied as a function of normalized wavelength (λ/Λ) by varying its different geometrical parameters such as hole diameter, inter-hole spacing and number of air hole rings around the core. Moreover, the MFD which is related to optical field distribution in the fibre gives a better idea of its loss characteristics. By optimizing the structural parameters of PCF, confinement losses can be minimized which improves the strength of the signal and thereby the transmission distance and range of the fibre sensor.

3.1 PCF design and simulation

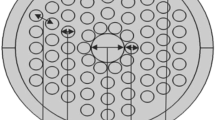
Figure 1 shows the cross section of the designed four ring LCPCF, where pitch (Λ) is the hole to hole spacing and d is the diameter of the air hole. Refractive index of the background material, silica is taken as 1.45 and the airhole is infiltrated with liquid crystal materials, cat. no. 1550 (refractive indices \({n_o} =1.461\), \({n_e} =1.522\) at 22 °C) and PCH-5 (refractive indices \({n_o} = 1.6049\), \({n_e} = 1.4863\) at 25 °C) (Yeh and Gu 2010). Considering oil and gas sensing environment, typical refractive index value of crude oil is 1.4785 and that of gasoline is in the range 1.42–1.44 (Jones 2010). For normal fuels, refractive index is a number bigger than one and normally lower than 1.7. However, for the fibre sensor configuration designed, oil and gas sensing medium has negligible effect on the strongly confined optical modes propagating through its core.

Fig. 1
figure 1

Cross section of LCPCF

Full size image

COMSOL MULTIPHYSICS software which is a finite element analysis software package, was used for the modelling and simulation of LCPCF. Figure 2 shows the 2D and 3D views respectively of a perfect Gaussian electric field pattern obtained in a four ring LCPCF. A Perfectly Matched Layer (PML) is introduced around the photonic crystal cladding, which acts as an additional domain to absorb incident radiations without producing back reflections. The PML is made of an artificial absorbing material which has anisotropic permeability and permittivity that matches with the physical medium outside. With the addition of liquid crystals, the fibre exhibits the common properties of photonic bandgap fibre (PBG) i.e. only certain frequencies of light propagate through the core and all other wavelengths tends to pass through the cladding which has a higher refractive index (Knight et al. 1998).

Fig. 2
figure 2

Electric field pattern 2D and 3D views for a four ring LCPCF

Full size image

Confinement loss decreases with increasing number of hole rings around the core. In our analysis, four ring structure showed minimum confinement loss which is due to the negligible field leakage. Figure 3 shows the variation in confinement loss (L) with respect to normalized wavelength (λ/Λ) for a LCPCF with d/Λ = 0.5, Λ = 2 µm, d = 1 µm for different number of air hole rings in the cladding. For small values of d/Λ, the resultant losses can be higher unless sufficiently larger number of holes are introduced on to the PCF core.

Fig. 3
figure 3

Confinement loss versus normalized wavelength for different number of hole rings

Full size image

Figure 4a depicts the variation of confinement loss (L) with respect to normalized wavelength (λ/Λ) for different values of diameter to spacing ratio (d/Λ). The hole spacing (Λ) is kept constant at 1.5 μm and the diameter (d) is increased. It can be observed that the confinement loss as expected increases with wavelength (λ) but it tends to decrease with increasing diameter to spacing ratio (d/Λ). Similarly Fig. 4b shows another plot of the confinement loss (L) with respect to normalized wavelength (λ/Λ) for a different spacing (Λ) 1.9 μm. Keeping the hole spacing constant, simulation is conducted for three structures (d/Λ = 0.4, 0.5, 0.6). It can be seen that confinement loss again increases with wavelength (λ) and also decreases with increase in d/Λ. Moreover, it is worth noting that confinement loss decreases with increasing spacing (Λ).

Fig. 4
figure 4

Confinement loss versus normalized wavelength for pitch: a Λ = 1.5 μm, b Λ = 1.9 μm

Full size image

Figure 5a, b shows the variation in confinement loss (in dB/Km) and MFD (in \(\upmu\hbox{m})\) with respect to wavelength (in nm) for the PCF filled-up with liquid crystalline mixture, Cat. No.1550 (\({n_{LC}} = 1.522\)) and PCH-5 (\({n_{LC}} = 1.6049\)). For LCPCF infused with Cat. No.1550, single mode operation was possible for wavelengths in the range 825–1100 nm. It was observed that, below the short cut-off wavelength (825 nm) and beyond the long cut-off wavelength (1100 nm), the electric field leaks into the cladding region. However, compared to single mode fibres, PCFs exhibit tighter mode confinement over a wide range of wavelength and hence lower mode area is achieved. In both Fig. 5a, b, it can be seen that the MFD decreases up to a particular wavelength and then it increases. At low wavelengths, the power density is high, intensity is low and therefore the area transversed by the fibre is less. But at higher wavelengths the power density is low, intensity is high, therefore the effective mode area is also high.

Fig. 5
figure 5

Confinement loss and MFD versus wavelength for LC refractive index: a n LC  = 1.522. b n LC  = 1.6049

Full size image

From Fig. 5 we can see that, by changing the liquid crystal material infiltrated into the holes (PCH-5, \({n_{LC}} = 1.6049\)), we can tune the confinement to wavelength range 1200–1650 nm. Through the simulation it was identified that the photonic bandgap (bands which can guide light), shifts to longer wavelength with increase in liquid crystal refractive index. Also, within the bandgap, leakage losses are smaller compared to outside of the bandgap. The shift in the photonic bandgap, finds numerous applications in fibre-optic sensing, tunable filters and switches. Further simulations carried out by increasing the hole sizes also resulted in reduced mode area and confinement loss, which is due to tighter mode confinement. However, changing the number of air hole rings around the core didn’t show any variation in the effective area of the LCPCF as observed for confinement loss. To sum up, judicious optimization of fibre geometrical parameters leads to improvement in light confinement and attenuation reduction which in turn enhance the spatial coverage and accuracy of the fibre sensor. The designed optical fibre sensor with the mentioned improved capabilities and with the potential to perform multiple parameter sensing can effectively solve the limitations of existing sensors down-hole.

4 Conclusion

From the current theoretical investigation, it was identified that, structural parameters have significant effects on fibre parameters such as confinement loss, effective mode area and MFD. It was found that confinement loss is a strong function of air-filling fraction (d/Λ) and the number of rings employed in the LCPCF cladding. Investigations carried out by varying the hole size and hole–hole distance also resulted in reduction of leakage losses and MFD. Low confinement loss automatically results in improved signal power, which in turn improves the accuracy and spatial range of the sensor. Besides this, the tunability of the photonic bandgap of the LCPCF by changing the liquid crystal material adds to its sensing capabilities. The present results shows promising future in the direction of PCF–FBG based long distance remote sensing system for oil and gas applications. Based on our investigation, the synergy of PCF and FBG develops an advanced fibre-optic sensing system with longer sensing range and enhanced accuracy for condition monitoring of oil and gas fields in deeper zones. Further analysis will be carried out on LCPCF–FBG based temperature sensing and simultaneous measurement of multiple parameters.