1 Introduction

Undesired mechanical vibration harms the running mechanical equipment’s. It could lead to material fatigue, deterioration of system performance, also increase the noise level. Particularly, the structure could be damaged due to the high amplitude vibration when the excitation just locates around structure eigenvalue frequencies. Several catastrophes such as bridge collapse, airplane crash have been ascribed to vibration caused problems. Thus, vibration control becomes to an urgent issue for the mechanical engineers. In the past decades, such techniques grew rapidly in kinds of industry domain. These approaches can be generally classified as three catalogs, which are passive control, active control and semi-active or semi-passive control.

Passive control is the earliest developed vibration control methods. These methods are easy to implement, sensor and power needless and unconditional stable. The main disadvantage of the passive control is that the control bandwidth is too narrow. Once the structure dynamic properties changes, the control system would need to be returned. In addition, the passive control need to add non negligible mass to the structure which could be unacceptable in aerospace field. Active control is developed based on the development of the computer science. The control system need sensors to monitor the displacement or velocity of the structure. The sensed signals then send to a controller in order to obtain a control signal by employing specific algorithms. The control signal would be amplified by power amplifier or directly exert on actuators to generate feedback force on the structure which usually has the opposite phase with the external excitation. Among kinds of semi-active and semi-passive vibration control methods, synchronized switch damping (SSD) techniques are proved to be an effective treatment. Compared with the passive methods, the system as the immunity against the structure dynamic properties shift due to the environmental change. They are also compact, lightweight which is convenient to apply to specific structure with weight or size restriction. Compared with the active control, SSD control system is very simple to implement and can easily be self-powered from the vibration itself. In these techniques, the switch in the circuit is intermittently switched leading to a non-linear voltage processing (Richard et al. 1999; Ji et al. 2014; Lefeuvre et al. 2006; Badel et al. 2006; Eddiai et al. 2012). The piezo-force induced by such voltage always shows an opposite sign with the structure velocity which leading the vibration suppression on the structure. Such behavior is similar with the well-known direct velocity feedback control.

The usual SSD technique performs well in mono-modal excitation; however, it hardly deals with the cases of the multimodal and complex vibrations. The limitation is due to the difficulty of defining the proper switching time in order to have optimal voltage magnification as well as proper phase according to the structure motion. To overcome this limitation, an alternative technique named Modal-SSDI was developed by Harari et al. (2009a, b). It consists of synchronizing the switch sequence on a given modal coordinate instead of the voltage. It therefore combines the simplicity, the robustness and low power operation of SSDI techniques, with the possibility of mode targeting and precision of active control strategies. Modal-SSDI takes advantage of a modal model of the structure to design a modal observer permitting the calculation of the modal coordinates characterizing the motional state of the structure. Based on the Modal-SSDI, SSDI-Max method (Chérif et al. 2012, 2015, 2013) was developed to deal with a multimodal control problem and to improve the damping performance by improving the piezoelectric element voltage amplitude. The principle of this method is developed with the objective of maximizing the self-generated voltage amplitude. Each time the chosen modal coordinate reaches an extremum, the device waits within a given limited time window for the next voltage extremum or for a significant voltage increase before to trigger the switch sequence. In this method, the extra voltage is gathered on the various non-controlled modes of the structure by the piezoelectric element itself.

In this article, based on SSDI-Max technique, a new global approach for improved vibration damping of smart structure, based on global energy redistribution by means of a network of piezoelectric elements. The objective of this work is to propose a new approach to increase the piezoelectric voltage in order to improve the damping performance. In this approach, the extra energy used to improve this voltage is gathered on the various modes of the structure using an interconnected piezoelectric element network. The network topologies developed in this paper is named SST-Max for “synchronized switch damping by energy transfer using SSDI-Max”. Performance evaluations and comparisons are performed on a model representative of a clamped plate equipped with piezoelectric elements in the case of multimodal motion. Compared to the SST developed by Wu et al. (2013), simulation results and a global theoretical model are proposed demonstrating the relationship between the achievable damping improvement and the ratio of transferred energy to the structure mechanical energy.

2 The semi-active Modal-SSDI-Max technique

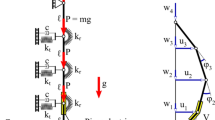
Damping performance is strongly dependent on the piezoelectric voltage amplitude. The Modal-SSDI-Max was developed (Chérif et al. 2012, 2015) with the objective of maximizing the self-generated voltage amplitude by a proper definition of the switch instants according to the chosen modal coordinate extremum. Compared with Modal-SSDI control method, the strategy of Modal-SSDI-Max consists in delaying the switch instant to the next voltage extremum immediately following the targeted modal coordinate extremum. It means that Modal-SSDI-Max also relies on a modal model and modal observer permitting the calculation of the modal coordinates to synchronize the switch with the targeted mode. In order to avoid a desynchronization with the target modal displacement, a time window is set up to limit the delay. Figure 1 illustrates the strategy of this technique in the various cases. The grey are a materializes the time window which is initiated for each extremum of the targeted modal coordinate. Points A, B, C and D illustrate the example of chosen switching time, which is indicated by the arrow.

  • Point A It is necessary to wait for the next positive maximum of the voltage to ensure the optimal voltage amplitude. Immediately switching would result in a wrong phase for the voltage of the piezoelectric actuator.

  • Point B Even if the voltage has the right sign, it is better to wait for the next voltage extremum to obtain a higher amplitude of the voltage.

  • Point C Voltage is decreasing at the beginning of the window, so it’s better to switch immediately.

  • Point D If no voltage extremum with the correct sign is located in the time window, the switch should be closed at the end of the time window, thus limiting the resulting voltage phase shift.

Fig. 1
figure 1

Strategy of Modal-SSDI-Max vibration control (Chérif et al. 2012)

Full size image

3 Smart structure definition

3.1 Smart structure modeling

The electromechanical behavior equations of a smart structure using usual assumption are as follows (Harari et al. 2009a, b):

$$ m\ddot{\delta } + c\dot{\delta } + \mathop k\nolimits^{E} \delta = - \alpha V + \beta F $$
(1)
$$ I = \,\mathop \alpha \nolimits^{t} \dot{\delta } - \mathop C\nolimits_{0} \dot{V} $$
(2)

with δ the nodal displacement vector, m, c, and k E are the mass, damping, and stiffness matrices, respectively, when the piezoelectric patches are in short circuit, α is the electromechanical coupling matrix, V is voltage vector of the i piezoelectric patches, I is the electric current vector, and C 0 is the diagonal capacitance matrix. F is the force applied to the system.

Using the following variable change where ϕ is the mode shape matrix limited to n modes and q the modal displacement vector:

$$ \delta = \phi q $$
(3)

The Eqs. (1) and (2) can be well represented by the projection in the modal basis by

$$ m\ddot{q} + c\dot{q} + \mathop k\nolimits^{E} q = - \theta V + \beta F $$
(4)
$$ I\, = \,\,\mathop \theta \nolimits^{t} \,\dot{q}\, - \,\mathop C\nolimits_{0} \,\dot{V} $$
(5)

where θ is the modal electromechanical coupling matrix with a [n, i] matrix size. Θ is defined as follows

$$ \theta = \phi^{t} \alpha $$
(6)

where M, C, and K E are the mass, damping, and stiffness modal matrices, respectively. The structure is assumed to be lightly damped, with proportional damping and decoupled modes. Equation (4) is normalized in order to have the modal mass matrix equal to identity. The modal matrices can therefore be written as a function of ξ the modal damping vector, ω E the short-circuit frequency vector, and ω D the open circuit frequency vector as follows

$$ M = I_{d} ;\quad C = 2 \,{\text{diag}}(\xi )\, {\text{diag}}\,(\omega^{D} );\quad K^{E} = {\text{diag((}}\omega^{E} )^{2} ) $$
(7)

The multi-modal model of the structure can be therefore expressed in matrix form as follows:

$$ \begin{aligned} & \left[ {\begin{array}{*{20}c} {m_{1} } & 0 & 0 \\ 0 & \ddots & 0 \\ 0 & 0 & {m_{n} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\ddot{q}_{1} } \\ \vdots \\ {\ddot{q}_{n} } \\ \end{array} } \right] + \left[ {\begin{array}{*{20}c} {c_{1} } & 0 & 0 \\ 0 & \ddots & 0 \\ 0 & 0 & {c_{n} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\dot{q}_{1} } \\ \vdots \\ {\dot{q}_{2} } \\ \end{array} } \right] + \left[ {\begin{array}{*{20}c} {k_{1}^{E} } & 0 & 0 \\ 0 & \ddots & 0 \\ 0 & 0 & {k_{n}^{E} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {q_{1} } \\ \vdots \\ {q_{n} } \\ \end{array} } \right] \\ & \quad = \left[ {\begin{array}{*{20}c} {\theta_{11} } & \ldots & {\theta_{1z} } \\ \vdots & \ddots & \vdots \\ {\theta_{n1} } & \ldots & {\theta_{nz} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {V_{1} } \\ \vdots \\ {V_{z} } \\ \end{array} } \right] + \left[ {\begin{array}{*{20}c} {\beta_{1} } \\ \vdots \\ {\beta_{n} } \\ \end{array} } \right]F \\ \end{aligned} $$
(8)
$$ \left[ {\begin{array}{*{20}c} {I_{1} } \\ \vdots \\ {I_{z} } \\ \end{array} } \right] = - \left[ {\begin{array}{*{20}c} {\theta_{11} } & \ldots & {\theta_{n1} } \\ \vdots & \ddots & \vdots \\ {\theta_{1z} } & \ldots & {\theta_{nz} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\dot{q}_{1} } \\ \vdots \\ {\dot{q}_{n} } \\ \end{array} } \right] - \left[ {\begin{array}{*{20}c} {C_{01} } & 0 & 0 \\ 0 & \ddots & 0 \\ 0 & 0 & {C_{0z} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\dot{V}_{1} } \\ \vdots \\ {\dot{V}_{z} } \\ \end{array} } \right] $$
(9)

For the sake of simplicity and in order to use powerful numerical tools, the smart structure is modeled by Eqs. (10) and (11), which are still presented by using a state space formulated equation (Eq. 12), respectively.

$$ \left[ {PP} \right]_{2n\times 2n} \left[ {\begin{array}{*{20}c} {\dot{q}_{1} } \\ \vdots \\ {\dot{q}_{n} } \\ {\ddot{q}_{1} } \\ \vdots \\ {\ddot{q}_{n} } \\ \end{array} } \right]_{2n \times 1} = - \left[ {QQ} \right]_{2n \times 2n} \left[ {\begin{array}{*{20}c} {{q}_{1} } \\ \vdots \\ {{q}_{n} } \\ {\dot{q}_{1} } \\ \vdots \\ {\dot{q}_{n} } \\ \end{array} } \right]_{2n \times 1} + \left[ {RR} \right]_{2n \times 2n} \left[ {\begin{array}{*{20}c} F \\ {V_{1} } \\ \vdots \\ {V_{z} } \\ \end{array} } \right]_{{\left( {z + 1} \right) \times 1}} $$
(10)

Here,

$$ \begin{aligned} \left[ {PP} \right]_{2n \times 2n} & = \left[ {\begin{array}{*{20}c} {\left[ {\begin{array}{*{20}c} 0 & \ldots & 0 \\ \vdots & \ddots & \vdots \\ 0 & \ldots & 0 \\ \end{array} } \right]_{n \times n} } & {\left[ {\begin{array}{*{20}c} {m_{1} } & 0 & 0 \\ 0 & \ddots & \vdots \\ 0 & 0 & {m_{n} } \\ \end{array} } \right]_{n \times n} } \\ {\left[ {\begin{array}{*{20}c} 1 & 0 & 0 \\ 0 & \ddots & 0 \\ 0 & 0 & 1 \\ \end{array} } \right]_{n \times n} } & {\left[ {\begin{array}{*{20}c} 0 & \ldots & 0 \\ \vdots & \ddots & \vdots \\ 0 & \ldots & 0 \\ \end{array} } \right]_{n \times n} } \\ \end{array} } \right]; \\ \left[ {QQ} \right]_{2n \times 2n} & = \left[ {\begin{array}{*{20}c} {\left[ {\begin{array}{*{20}c} {k_{1}^{E} } & \ldots & 0 \\ \vdots & \ddots & \vdots \\ 0 & \ldots & {k_{n}^{E} } \\ \end{array} } \right]_{n \times n} } & {\left[ {\begin{array}{*{20}c} {c_{1} } & 0 & 0 \\ 0 & \ddots & \vdots \\ 0 & 0 & {c_{n} } \\ \end{array} } \right]_{n \times n} } \\ {\left[ {\begin{array}{*{20}c} 0 & \ldots & 0 \\ \vdots & \ddots & \vdots \\ 0 & \ldots & 0 \\ \end{array} } \right]_{n \times n} } & {\left[ {\begin{array}{*{20}c} 1 & 0 & 0 \\ 0 & \ddots & 0 \\ 0 & 0 & 1 \\ \end{array} } \right]_{n \times n} } \\ \end{array} } \right] \\ \left[ {RR} \right]_{{2z \times \left( {z + 1} \right)}} & = \left[ {\begin{array}{*{20}c} {\left[ {\begin{array}{*{20}c} 1 \\ \vdots \\ 1 \\ \end{array} } \right]_{n \times 1} } & {\left[ {\begin{array}{*{20}c} {\theta_{11} } & \ldots & {\theta_{1z} } \\ \vdots & \ddots & \vdots \\ {\theta_{n1} } & \ldots & {\theta_{nz} } \\ \end{array} } \right]_{n \times z} } \\ {\left[ {\begin{array}{*{20}c} 0 \\ \vdots \\ 0 \\ \end{array} } \right]_{n \times 1} } & {\left[ {\begin{array}{*{20}c} 0 & \ldots & 0 \\ \vdots & \ddots & \vdots \\ 0 & \ldots & 0 \\ \end{array} } \right]_{n \times z} } \\ \end{array} } \right] \\ \end{aligned} $$
$$ \left[ R \right]^{ - 1} \left[ {\begin{array}{*{20}c} {V_{1} } \\ \vdots \\ {V_{z} } \\ \end{array} } \right]_{z \times 1} = - \left[ \theta \right]^{T}_{z \times n} \left[ {\begin{array}{*{20}c} {\dot{q}_{1} } \\ \vdots \\ {\dot{q}_{n} } \\ \end{array} } \right]_{n \times 1} - \left[ {C_{0} } \right]_{z \times z} \left[ {\begin{array}{*{20}c} {\dot{V}_{1} } \\ \vdots \\ {\dot{V}_{z} } \\ \end{array} } \right]_{z \times 1} $$
(11)

Here,

$$ \begin{aligned} \left[ R \right]_{z \times z}^{ - 1} & = \left[ {\begin{array}{*{20}c} {R_{1} } & 0 & 0 \\ 0 & \ddots & 0 \\ 0 & 0 & {R_{z} } \\ \end{array} } \right]_{z \times z}^{ - 1} ;\quad \left[ \theta \right]_{z \times n}^{T} = \left[ {\begin{array}{*{20}c} {\theta_{11} } & \ldots & {\theta_{n1} } \\ \vdots & \ddots & \vdots \\ {\theta_{1z} } & \ldots & {\theta_{nz} } \\ \end{array} } \right]_{z \times n} ; \\ \left[ {C_{0} } \right]_{z \times z} & = \left[ {\begin{array}{*{20}c} {C_{01} } & 0 & 0 \\ 0 & \ddots & 0 \\ 0 & 0 & {C_{0z} } \\ \end{array} } \right]_{z \times z} \\ \end{aligned} $$

Considering mechanical and electrical equations, the state vector x(t), control vector u(t) and the output vector y(t), which also correspond to the special state matrices term A, B, C and D:

$$ \dot{x}\left( t \right) = Ax\left( t \right) + Bu\left( t \right) $$
$$ y\left( t \right) = Cx\left( t \right) + D u\left( t \right) $$
(12)

3.2 Smart structure definition

Figure 2 illustrates the type of structure that is considered in the development of this work. It is a steel plate clamped on the four edges on a metallic frame. Four PZT patches (P189 hard PZT type) are attached on the lateral edges along the clamping frame. The four piezoelectric elements are globally coupled with the various mode of the structure. This structure has been fully characterized using usual techniques: resonance frequencies for the various open-circuited and short-circuited conditions for all the modes as well as voltage to modal displacement transfer function evaluation for all the piezoelements and all the modes. The dimensions, material properties of the steel plate and piezoelectric patches are gathered in Table 1. Details of the plate construction and characterization are given in Guyomar et al. (2008). Among the many low frequency modes that have been experimentally observed, only the four principal modes have been considered in the modal model, therefore n = 4. These modes are considered as principal in the sense that they do present the stronger electromechanical couplings. As a consequence, when the structure is excited, the voltage is a linear combination of the four considered frequencies, such as in the considered model. Table 2 lists the four considered mode frequencies and mechanical quality factors and piezoelectric element blocked capacitances.

Fig. 2
figure 2

The clamped steel plate with 4 with piezoelectric elements bonded at the lateral clamping edges

Full size image
Table 1 The material properties of the steel plate and piezoelectric patch
Full size table
Table 2 Resonance frequencies and mechanical quality factor of the four considered modes of the smart structure (a) and piezoelectric elements blocked capacitances (b)
Full size table

4 Energy transfer conception

4.1 Operative energy

The energy balance equation within the structure. It also can be given as in Eq. (13) for a given modal coordinate.

$$ \left[ {\frac{1}{2}m\dot{q}^{2} } \right]_{0}^{T} + \left[ {\frac{1}{2}k^{E} q^{2} } \right]_{0}^{T} + \int_{0}^{T} C \dot{q}^{2} dt - \int_{0}^{T} \theta V\dot{q}dt = \int_{0}^{T} F \dot{q}{\mkern 1mu} dt $$
(13)

The \( \int_{0}^{T} \theta V\dot{q}dt \) is also considered as the switching damping energy or extracted energy which is composed of electrostatic energy stored on the piezoelectric element capacitance and the energy absorbed by the electric circuit which is connected with the piezoelectric elements as shown in Eq. (14).

$$ \int_{0}^{T} \theta V\dot{q}dt = \left[ {\frac{1}{2}C_{0} V^{2} } \right]_{0}^{T} + \int_{0}^{T} V Idt $$
(14)

It is remarkable that the electrostatic energy, so-called operative energy is related to the damping performance. Generally, in SSD technique using piezoelectric element, the operative energy corresponding to the amplitude of piezoelectric voltage V plays an important role. It corresponds to the available energy to perform the control. Increased available operative energy or increased voltage results in better damping performance.

4.2 Energy transfer conception

The active control demonstrates high damping performance, but it usually requires a powerful external energy source to drive the control system. In some practical industrial applications, it is difficult to achieve supply of external energy to the system. Another method is the passive control. It consists of piezoelectric elements connected to an electrical network, which could degrade the mechanical energy of the structure. It does not require any operative energy for damping, but the damping performance would be much lower than active control. To increase the damping performance without external operative energy, several semi-active vibration control techniques have been proposed and developed. The SSD techniques are part of these methods. By using a very small amount of external energy to change its state, a simple switch can modify the dynamic property of a structure by changing the state of an embedded piezoelectric element, thus achieving stiffness change or damping. Only small amounts of energy are necessary to supply the electronic board used for monitoring the vibration and driving the switches.

5 Non-linear network configuration

It is seen that whatever the technique considered (SSD techniques or active control techniques); the damping performance is very dependent on the available operative energy related to the piezoelectric elements. This reactive energy, which corresponds to the electrostatic energy stored on the blocked capacitance, quantifies the intensity of the controlling action of the piezoelectric element. In the case of a structure with unwanted modes which are very weakly coupled to the controlling piezoelectric element, the voltage or energy requirement could be very high resulting in difficult control of these modes. This energy can be supplied with external sources, but more rationally is extracted from the structure itself in the case of semi-active switched technique. The optimization of this energy could result from a global management of the vibration energy of the structure.

The objective of this work is to propose a novel global approach based on Modal-SSDI and SSDI-Max for energy management and redistribution. In the case of an extended structure with many embedded piezoelectric elements, the proposed strategy consists of using a network implementing a low consumption energy transfer technique relying mainly on switches, diodes and passive elements. The operative energy is extracted from the structure vibration in a given area, on a give vibration mode, and converted into electrostatic energy by so-called source piezoelectric elements. Then this energy is transferred to another piezoelectric element considered as the target one in order to increase its overall charge, all this in a continuous and organized manner. The benefit of the energy transfer network is strongly related to the energy level of the source elements or modes, and more globally to the energy distribution in the smart structure. The objective is to show how the energy in the structure can be managed and redistributed, and to consider the suitable network arrangement.

5.1 SST and SST-Max configuration

The piezoelectric elements are arranged in two parts, the three source piezoelectric elements (PZ1, PZ2 and PZ3) and the target piezoelectric element PZ4 targeting by the vibration of the fourth mode of the structure. Each source piezoelectric element transfer its available energy using the left hand side switches. The switches are arranged in pair. One is for the positive voltage; the other is for the negative voltage. Each switch is triggered on the voltage extremum (or eventually on the source modal coordinate) to perform energy transfer toward CTP or CTN (Fig. 3).

Fig. 3
figure 3

The extended SST network reassembles the four piezoelectric elements of the smart structure

Full size image

The piezoelectric element PZ4, located on the right hand side of the schematic, is the target element of the energy transfer. The inversion of its voltage is triggered following the Modal-SSDI strategy (SST) and the Modal-SSDI-Max strategy (SST-Max) targeted on the q4 modal coordinate. The energy transfer from the storage capacitances is controlled in the same manner as in the basic circuit previously described.

6 Simulations results

The simulations are performed using the MATLAB/Simulink software environment.

6.1 Multimodal sinusoidal excitation

Figure 4a gives illustration of the benefit of proposed SST-Max network. It shows the operative energy, which is the electrostatic energy stored on the blocked capacitance of the target piezoelectric element PZ4. The considered excitation is a composite multimodal sinusoidal excitation in the centre of the plate. This energy in both case of SST. It appears that following the proposed approach, the peak energy for extended SST-Max is nearly twice, while the mean level is globally improved during the entire transient regime leading consequently to a better damping of the targeted mode displacement q4, as shown on Fig. 4b). It is interesting to note that different energy harvesting strategies can be implemented: switching on the source piezoelectric element side can be simply triggered on the voltage extreme (SECE harvesting), but the energy can be pumped voluntarily on specific modes of the structure by using the modal coordinates of the structure motion to trigger the harvesting switches. Finally, at it will be show further, the ability of the network for energy transfer can be quantified by the power flow that is established. This power flow is more convenient to quantify the performance of the network for steady state operation when the structure is excited by a 50 μs long, 5 mJ square force pulse.

Fig. 4
figure 4

a The operative energy or electrostatic energy stored on the target piezoelectric element PZ4 blocked capacitance in the case SST and SST-Max configurations of multimodal sinusoidal excitation and b corresponding q4 modal coordinate damping in the case of multimodal sinusoidal excitation

Full size image

6.2 Pulse excitation

The excitation is a wide frequency square force pulse, 50 μs long and corresponding to 5 mJ input energy, applied in the centre of the plate structure (Fig. 5).

Fig. 5
figure 5

Modal damping with a pulse excitation

Full size image

6.3 Influence of the time window on the performance of SST-Max

The time window, which is used to limit the possible time shift prior to switching, is a very important and critic parameter. If it is too small the voltage will not have the possibility to increase, and no significant enhancement will be observed. If it is too long, there is a risk of desynchronization of the actuator voltage with the targeted modal speed, thus resulting altered damping. In order to define an optimal time window (Fig. 6).

Fig. 6
figure 6

Influence of the time window for pulse excitation in the time domain

Full size image

7 Conclusion

In this paper, a novel synchronized switch damping by energy transfer (SST) network of piezoelectric elements is proposed for transferring the energy between source piezoelectric elements and target element. The objective of this work is to propose and evaluate the performance of a network of piezoelectric elements for improved semi-active damping of a smart structure. The basic idea is that semi-active damping is an interesting technique, but it relies on a good electromechanical coupling of the piezoelectric actuator. If the coupling is weak, it is possible to increase the damping by supplying this energy externally. Now the vibrating structure can be used as a source of energy if it is equipped with a network of piezoelectric elements and a low power energy redistribution technique allowing the transfer of operative energy toward the chosen piezoelectric actuator. SST and SST-Max techniques are proposed and will be compared on this basis using a clamped plate equipped with four piezoelectric elements as a benchmark. Modal SST-Max simulations results showed neatly improved damping performances compared to SST for the control of a single mode of the structure, in the case of sinusoidal excitation on the four modes of the plate, pulse, or sinus excitation. Remarkable gains in attenuation lying between 5 and 10 dB were obtained. Finally, the influence of the maximum time delay between the targeted modal coordinate extremum and the switch instant was evaluated, and the results emphasize the importance of the energy of the targeted mode compared to the other modes of the structure on the definition of the optimal time window.