Computationally-efficient FDTD modeling of supercontinuum generation in photonic crystal fibers

Abstract

It is shown in this paper that a finite-difference time-domain method can be successfully applied to rigorous electromagnetic analysis of supercontinuum generation in photonic crystal fibers. Large computational requirements of the method are alleviated by the use of a hybrid procedure where, at first, vector two-dimensional simulation is applied in order to determine mode properties of the fiber. Subsequently, one-dimensional simulation of a pulse propagating in a transmission line filled with effective material is performed. The parameters of the line take into account nonlinear characteristics of the filling material as well as the previously computed mode dispersion. It is depicted that the proposed novel hybrid approach opens the way for rigorous, yet, computationally-efficient modeling of third order nonlinear processes in optically long fibers. The example investigated in this paper shows very promising results as compared with experiments and approximate numerical simulations of a nonlinear Schrodinger equation performed with the aid of the split-step Fourier method.

Introduction

Supercontinuum (SC) generation in photonic crystal fibers (PCFs) has become one of promising ways to produce cost-effective broadband infrared radiation sources applicable in broadly-understood spectroscopy (Hult et al. 2007; Mandon et al. 2008). The process of SC generation relies on appropriate balance between dispersion and various third-order nonlinear effects, such as self-phase modulation, soliton generation/fission, and four-wave mixing (Agrawal 2007). However, PCFs are optically large structures, especially due to their length which extends well beyond a wavelength scale. Consequently, electromagnetic (EM) modeling of SC evolution is usually undertaken with the aid of approximate techniques, like the split-step-Fourier method (SSFM), which solves the one-dimensional nonlinear Schrodinger equation representing propagation along a fiber with a pre-defined mode characteristic (Travers et al. 2010). However, SSFM is an implicit method solving for the evolution of the pulse envelope in a one-dimensional EM transmission line. As a result, the method is not immune to spurious solutions (Bosco et al. 2000; Sinkin et al. 2003). In addition, the concept of slowly varying pulse envelope exploited in the nonlinear Schrodinger equation becomes questionable in the case of ultra-short pulses, the duration of which becomes comparable with an optical period (Agrawal 2007). As it will be shown later in this paper, the same issue occurs when the pulse break up into a noise-like signal, which leads to a rapid increase of spectral bandwidth.

The alternative is to apply a rigorous full-wave approach in order to solve such a nonlinear problem. One of prospective candidates is the finite-difference time-domain (FDTD) method as a versatile numerical tool naturally adapted to broadband EM analysis (Taflove and Hagness 2005). Although several valuable papers focused on FDTD modelling of third-order nonlinear effects, that stay behind SC generation, have been published (Fujii et al. 2004; Lubin et al. 2011), large computational effort and memory requirements involved in the full-wave EM analysis of centimeter-long PCFs make the method inapplicable (Hu et al. 2008). For that reason, a novel approach that takes the advantage of the accuracy of the FDTD method, while substantially alleviating its prohibitive computational requirements, is proposed in this paper.

The EM field in guiding structures, with geometry invariant along a propagation axis, can be represented as a product of a transverse vector function and a scalar longitudinal one:

$$\vec{E}\;\left( {x,y,z} \right) = \vec{E}_{t} \;\left( {x,y} \right)\;E_{f} \;\left( z \right),$$

(1)

As a result, the analysis can be split in two independent EM problems, namely, vector two-dimensional (V2D) one solving for E _t (x, y), and scalar one-dimensional (S1D) solving for E _f (z). The transverse field distribution, E _t (x, y), can be represented as a discrete set of well-defined functions (modes):

$$\vec{E}_{t} \;\left( {x,y} \right) = \sum\limits_{n} {\vec{E}_{t,n} \;\left( {x,y} \right)} ,$$

(2)

where n denotes the order of the mode with n = 1 indicating the fundamental mode with the lowest cut-off frequency.

If the transverse field distribution (mode) does not have its analytical representation, unlike homogeneously filled rectangular or circular metallic waveguides (Collin 1990), it has to be computed with the aid of a rigorous (full-wave) numerical technique, such as a finite element method (FEM) or FDTD. Consequently, the analysis reduced to the cross-section of a waveguide’s structure allows evaluating properties of the considered mode such as effective refractive index, group velocity dispersion, effective mode area, or confinement loss (Karpisz et al. 2014).

In the case of V2D-FDTD (Gwarek et al. 1993), the mode analysis can account for material dispersion represented as a multi-pole Lorentz model implemented with the aid of auxiliary differential equations (ADE) (Taflove and Hagness 2005). Recently, it has been shown that V2D-FDTD can also solve for third-order nonlinear Kerr-Raman effects, which allows studying the impact of pulse intensity on a dispersion characteristic of the mode propagating in a photonic crystal fiber (Salski et al. 2015).

However, electromagnetic study of SC generation in PCFs requires considering nonlinear effects occurring along the propagation. It is proposed in this paper to replace SSFM with S1D-FDTD in the analysis of longitudinal propagation of a given mode, as a direct consequence of (1). There are several advantages of such an approach. First of all, computational effort of S1D-FDTD simulation is several orders of magnitude smaller than complete 3D-FDTD computation. For instance, the model of a 1-cm-long PCF, discretized into 25-nm-long FDTD cells, consists of merely 4 × 10⁵ cells, while a complete 3D model would have required at least dozen of billions of FDTD cells, which is unsolvable at the moment. Second, FDTD as a rigorous numerical method can give a deep insight into the dynamics of SC generation, thus, contributing to a better understanding of the phenomena.

In Section II, the concept of the hybrid V2D-S1D FDTD modeling of SC generation in PCFs is discussed in details, while in Section III the elaborated technique is validated against experimental and numerical data available in literature.

Concept

Despite the ultimate choice of the method solving for nonlinear propagation of the pulse along the PCF (SSFM or FDTD), mode characteristics are usually computed with the aforementioned rigorous numerical techniques (FEM or FDTD). Subsequently, the obtained effective refractive index n _eff of a given mode can be treated as material dispersion. As a result, S1D-FDTD simulation of the pulse propagating in such artificial (equivalent) material can be undertaken.

Transverse properties

Transverse (mode) properties of the PCF can be computed with the V2D-FDTD method accounting for dispersion of the applied material (Salski et al. 2015). The real part of the refractive index of glass contained in the PCFs is usually represented with a Sellmeier equation, which has to be transformed into a Lorentz model with its representation in the FDTD method (Karpisz et al. 2014) given as:

$$\varepsilon = \varepsilon_{\infty } + \sum\limits_{n = 1}^{N} {\frac{{\left( {\varepsilon_{s,n} - \varepsilon_{\infty } } \right)\,\omega_{p,n}^{2} }}{{\omega_{p,n}^{2} - \omega^{2} + j\,\omega \,\omega_{c,n} }}} ,$$

(3)

where ε _∞ is optical permittivity, ε _S is static permittivity, ω _p,n stands for the nth pole frequency, and ω _c,n represents relaxation frequency of the nth pole.

Longitudinal properties

Once spectral properties of the considered mode, E _t,n (x, y), are determined, the next step is to represent it as material dispersion in a S1D-FDTD model. The most straightforward way to do that is to fit the aforementioned Lorentz model to the obtained effective refractive index n _eff of the mode. However, practical realization of that concept is not straightforward as it may look at first glance. First, SC generation is sensitive not only to n _eff , but even more to dispersion D, which is very vulnerable to fluctuations of n _eff . Consequently, as it will be shown later in this paper with specific examples, special attention must be paid to represent waveguide dispersion accurately up to its second order derivative with the wavelength.

Consider as an example a PCF fabricated from lead–bismuth–gallium-oxide glass (PBG-08) proposed in (Sobon et al. 2014), which is well-suited for SC generation (see Fig. 1). Solid lines in Figs. 2a and 3 show the characteristics of the corresponding effective refractive index n _eff and dispersion D, respectively, computed in (Sobon et al. 2014) in the range from 500 nm to 4000 nm. In the first attempt, a triple-pole Lorentz model will be fitted to the aforementioned curves using the Levenberg–Marquardt algorithm executed with no bounds imposed on the Lorentz parameters. According to (Sobon et al. 2014), SC evolves in the considered PCF in the 500–2400 nm range (see Fig. 5 therein), so the fitting has been limited to that range. The obtained Lorentz model (see the 2nd column in Table 1) provides the effective refractive index (dispersion) with a normalized root-mean-square deviation (NRMSD) of 0.047 % (0.777 %) in that spectrum. Due to negligibly small discrepancy, these curves are not plotted in Figs. 2 and 3.

Fig. 1

SEM images of a PCF made of PBG-08 glass (Sobon et al. 2014)

Fig. 2

a Real part of effective refractive index of the PCF computed in (Sobon et al. 2014) and b imaginary components of the corresponding Lorentz model obtained without imposing any restrictions (Lorentz fit 1) and assuming f _c,n  < 10⁻⁶ f _p,n (Lorentz fit 2)

Fig. 3

Dispersion of the PCF computed in (Sobon et al. 2014) (solid line) as compared to the Lorentz model obtained imposing f _c,n  < 10⁻⁶ f _p,n (Lorentz fit 2)

Table 1 Material representation of the PCF as in Fig. 1

It can be noticed that the lack of restrictions imposed on the Lorentz parameters results in a decent agreement with the properties of the fundamental mode computed rigorously. Practically, the third Lorentz pole with a very small resonant frequency f _p,3 = 0.0103 THz and large and negative relaxation frequency f _c,3 = −35.0282 THz can be approximated with a Drude model. Unfortunately, large relaxation frequencies f _c,n , that have been obtained (see the 2nd column in Table 1), contribute to prohibitively large propagation loss correlated with an imaginary part of (3). It is confirmed by the plot shown in Fig. 2b (Lorentz fit 1). Moreover, the condition ε _s,n  < ε _∞ makes the FDTD analysis numerically unstable. For that reason, it has been assumed in a subsequent step of curve fitting that f _c,n  < 10⁻⁶ f _p,n , thus, imposing substantially reduced losses (see the 3rd column in Table 1). As a result, the NRMSD of the effective refractive index (dispersion) has increased to 0.3363 % (0.7611 %) in the 500–2400 nm range, which is still within reasonable limits.

Several tests undertaken by the authors have shown that the multi-pole Lorentz model cannot accurately represent dispersion-flattened characteristics, which are decreasing with the wavelength at some spectral range. An example of such a scenario is shown in Fig. 3 (solid line) for λ > 2400 nm. Consequently, if that spectral range was essential for SC generation, other representation of mode dispersion should be applied instead. It should be noted, however, that the decrease of D with the wavelength usually coincides with the increase of confinement loss (Stepniewski et al. 2014), so that the evolution of spectrum does not extend beyond that limit.

The conclusion that can be derived from attempts to conveniently represent material properties undertaken so far is that suitable fitting of waveguide dispersion can be obtained only if no restrictions are imposed on an imaginary part of the Lorentz model. However, such an approach cannot be applied due to resulting erroneously large propagation loss leading to a rapid attenuation of the signal along the fiber. It seems that these losses may be suppressed if metamaterial representation is applied, where the effective refractive index is the square root of the product of complex permittivity as in (3), and complex permeability given in a similar Lorentz form:

$$\mu = \mu_{\infty } + \sum\limits_{n = 1}^{N} {\frac{{\left( {\mu_{s,n} - \mu_{\infty } } \right)\,\omega_{pp,n}^{2} }}{{\omega_{pp,n}^{2} - \omega^{2} + j\,\omega \,\omega_{cc,n} }}}$$

(4)

where μ _∞ is optical permeability, μ _S is static permeability, ω _pp,n stands for the n ^th magnetic pole frequency, and ω _cc,n represents the corresponding magnetic relaxation frequency.

If (3) and (4) are conjugates of each other (ε′ = μ′, ε″ = −μ″), the resulting effective refractive index of such single-negative metamaterial will be purely real:

$$n = \sqrt {\left( {\varepsilon^{{\prime }} - j\varepsilon^{{\prime \prime }} } \right)\;\left( {\varepsilon^{\prime} + j\varepsilon^{\prime\prime}} \right)} = \sqrt {\varepsilon^{{{\prime }2}} + \varepsilon^{{{\prime \prime }2}} } ,$$

(5)

The fourth column in Table 1 depicts the Lorentz parameters of the obtained metamaterial model, which resembles waveguide dispersion of the considered mode. The NRMSD of the effective refractive index (dispersion) is as low as 2.17 % (2.63 %) in the 500–2400 nm range, so there is no significant improvement when compared with the third column in Table 1. However, if the spectrum above the 2400 nm limit was also essential in the analysis, metamaterial representation would be a much better choice than the fitting done with the permittivity function only. Due to negligibly small discrepancy in the whole 500–4000 nm range, the plot of the corresponding metamaterial curves is omitted in Figs. 2a and 3. Unfortunately, tests undertaken by the authors have shown that the FDTD simulation is quickly becoming unstable if such metamaterial is computed. Apparently, instability is due to a large level of the positive imaginary part of (3) (loss), which is suppressed by the negative imaginary part of (4) (gain). It seems that the undertaken attempt at compensating the imaginary part of (5) improves the quality of the fit but it does not suppress numerical noise of the FDTD algorithm. Consequently, the noise is quickly amplified by the FDTD routines associated with the permeability model given by (4). Although that subject goes beyond the main scope of this paper, it can be expected that the presented technique with metamaterial representation of PCF waveguide dispersion may be useful in future studies if the aforementioned stability issues are resolved. In this paper, the fiber will be represented with the already discussed Lorentz permittivity model (see the third column in Table 1).

Nonlinear properties

Dispersive properties of the fiber will be supplemented in the S1D-FDTD model with a third-order nonlinear polarization model derived on the basis of the Born–Oppenheimer approximation (Fujii et al. 2004; Hellwarth 1977):

$$P^{\left( 3 \right)} \left( t \right) = \varepsilon_{0} \;\chi_{0}^{\left( 3 \right)} \;E\;\left( t \right)\;\left[ {g\,\left( t \right) \otimes E^{2} \left( t \right)} \right],$$

(6)

where ε ₀ is free-space permittivity, χ ⁽³⁾₀ is third-order susceptibility, and g(t) stands for a nonlinear response function consisting of both Kerr and Raman contributions. It is assumed that nonlinear properties of glass are not dispersive, which is quite common in EM modelling of SC generation (Agrawal 2007; Travers et al. 2010; Sobon et al. 2014).

The details of the corresponding FDTD model are discussed in (Salski et al. 2015), so only major features will be pointed out hereafter. Equation (3) can be implemented in FDTD with the aid of ADE [14]. However, an FDTD solution of (3) suffers from either low computational efficiency or substantially deteriorated accuracy (Maksymov et al. 2011). In (Salski et al. 2015), a new approach that combines the accuracy of a rigorous FDTD update scheme and the computational speed of an approximate solution has been proposed and successfully validated. In that approach, rigorous FDTD update equations are applied only in those nonlinear cells, where instantaneous amplitude of an electric field is relatively high, while all the remaining nonlinear FDTD cells are updated with approximate update equations. In the case of short femtosecond pulses propagating in a long transmission line, most of FDTD cells are populated with low electric field’s amplitude, and only a small fraction of FDTD cells requires more rigorous computation. As a result, FDTD simulation of nonlinear materials can be substantially speeded up with no deterioration of accuracy. As shown in (Salski et al. 2015) in selected cases the improvement can exceed 80 %.

Results

Once the material properties of the fiber are already represented with the Lorentz model (see previous Section) and the corresponding computationally efficient S1D-FDTD method is elaborated, as in (Salski et al. 2015), an FDTD model can be defined. In addition to the aforementioned time-efficient computation of the nonlinear FDTD cells, appropriate definition of the model allows further speeding up FDTD analysis of long transmission lines, like the one discussed in this paper. It can be achieved by taking advantage of the fact that a pulse spatial length is much shorter than a total length of the fiber, so that periodic boundary conditions (PBCs) with a zero phase shift (ψ _x  = 0 rad) can be applied at both ends of the model (see Fig. 4) (Salski et al. 2007). Consequently, pulse repetitively circulates in the model enabling the reduction of its length L from a few centimeters, which are typical for SC generation, down to a few multiples of the pulse spatial length.

Fig. 4

The S1D-FDTD model representing femtosecond pulse propagation in a photonic crystal fiber

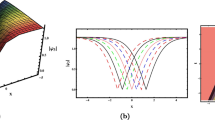
The length of the model with PBCs is L _p  = 500 μm, while an FDTD cell size is a = 30 nm and a time step is Δt = 0.05 fs. The pulse is excited with a total-field/scattered-field (TF/SF) soft source (Taflove and Hagness 2005; Salski et al. 2007) in an anomalous dispersion regime at λ = 1.56 μm (compare Fig. 3), and its duration is 400 fs (see Fig. 5a). An FDTD simulation has been carried out until the pulse reaches the end of a 5-cm-long fiber [compare Fig. 6 in Sobon et al. (2014)]. Figure 5 depicts the evolution of pulse shape along the fiber. At first, self-phase-modulation induced by large amplitude modifies the shape of the pulse, so that its front is stretched by long-wavelength components, while its rear part is compressed (see Fig. 5b). After some distance, a soliton is being created (see Fig. 5c) and, afterwards, modulation instability prevails (see Fig. 5d), finally leading to soliton fission.

Fig. 5

Pulse shape at consecutive distances along the fiber: a L = 0 cm, b L = 2.3 cm, c L = 3.3 cm and d L = 4.9 cm

Fig. 6

a Pulse train during the whole S1D-FDTD simulation and b evolution of supercontinuum spectrum along the fiber for the peak power of 30 kW assuming 6 % coupling efficiency into the fiber

For instance, if pulse duration is 400 fs, then its spatial length is about 60 μm, assuming n _eff  = 2. Consequently, the FDTD model can be as short as L _p  = 500 μm in order to avoid overlapping of the pulse circulating between the two PBC boundaries. The reduction of computational effort, which adds up to the previously mentioned speed-up factor due to the hybrid solution of the nonlinear FDTD cells, is at the level of L/L _p  = 100.

Figure 6a shows the results of the whole FDTD simulation in one plot, so that the evolution of the envelope can be observed, indicating that the amplitude is increasing with the distance. Consequently, nonlinear effects are being intensified so that the soliton is finally destroyed into a spectrally broadband signal. It is confirmed in Fig. 6b depicting the evolution of pulse spectrum, which is in good agreement with the corresponding plot shown in Fig. 6a (Sobon et al. 2014). Similarity of both plots obtained with completely different methods validates the approach proposed in this paper. However, the advantage of the FDTD method is that it rigorously treats the considered model of third-order nonlinearities assisted by mode dispersion. The proposed approach can, thus, be easily extended to additional effects, like multi-pole representation of Raman response, which may further enhance the capability and accuracy of the FDTD analysis. As in the case of SSFM, S1-FDTD does not take into account coupling efficiency to a given mode but, if needed, it can be computed with full-wave 3D EM methods. Although, coupling between the modes is not accounted for in the S1-FDTD method, there are no fundamental limitations that prevent extending the method in that direction.

The whole FDTD simulation executed on Intel Core i7-3930 K CPU took 10 h with the speed of 182 iterations per second, which is about 2 times faster than rigorous computation without a hybrid approach proposed in (Salski et al. 2015). What needs to be stressed out, the model elaborated without the use of PBCs would extend the S1D-FDTD analysis to about 15 days. There is still a lot of room for additional acceleration with such techniques as GPU computing or multi-threading (Rudnicki and Sypniewski 2012), but that subject goes beyond the main scope of this paper. In comparison, similar simulation undertaken with SSFM takes about 4 min. Nevertheless, it can be clearly seen that rigorous FDTD modeling of the whole supercontinuum evolution in microstructured optical fibers performed in reasonable time limits on a personal computer is well within reach.

Conclusion

A novel hybrid FDTD method applicable to a rigorous analysis of supercontinuum generation in photonic crystal fibers has been proposed in this paper. It takes the advantage of the separation of variables method. The analysis is split into vector-2D and scalar-1D electromagnetic problems accounting, respectively, for transverse and longitudinal properties of the photonic crystal fibers. It allows substantially speeding up the FDTD analysis of supercontinuum generation provided that the computational model and the FDTD algorithm are appropriately specified. First of all, it has been proposed to solve nonlinear FDTD cells in a hybrid manner, where cells with low electric field amplitude are updated with an approximate FDTD formula, while the remaining FDTD cells are computed rigorously. Secondly, it has been proposed to apply periodic boundary conditions to truncate the model from a centimeter scale down to a few multiples of a pulse spatial length.

Another novelty discussed in this paper is the representation of the effective refractive index of the mode with a dispersive model. It has been shown that a multi-pole Lorentz model represents fiber mode characteristics very well, provided that dispersion D is not flattened too much in the considered spectrum. The alternative is to apply metamaterial representation with gain of a permeability function compensated by loss of a permittivity function. The latter option is very promising, although it still requires thorough studies focused on the stability of an FDTD algorithm representing such model. Eventually, the obtained simulation results of supercontinuum generation in a 5-cm-long photonic crystal fiber are in good agreement with literature data. Future studies can be focused on such issues as hardware acceleration, multi-pole representation of Raman nonlinear response or vector 1D FDTD, which accounts for polarization effects in the analysis. In general, the proposed method opens room for rigorous studies of nonlinear effects occurring in optically-long transmission lines.