Abstract
We propose to use the blind deconvolution and its modification to extract the point spread function (PSF) of layered metamaterials from a SNOM measurement. The measurement results are processed using the blind deconvolution algorithm to reconstruct the real-valued non-coherent PSF, or using the modified blind deconvolution introduced in this paper to reconstruct the complex-valued coherent PSF. The two algorithms are tested in simulations with a layered metamaterial deposited on a thin metallic mask with test apertures. We show that the modified algorithm is capable of recovering the approximate shape of complex PSF with a sub-wavelength full width at half maximum from a measurement in which the apertures are larger than the wavelength.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Layered metamaterials consisting of metallic and dielectric layers (MDM) sandwiched in a periodic way find applications in imaging with sub-wavelength resolution (Fang et al. 2005), far-field imaging of sub-wavelength objects (Jacob et al. 2006), cloaking (Paul et al. 2012), or design of novel absorbers (Guclu et al. 2012; Pastuszczak et al. 2014). They can be designed to achieve such properties as an extreme anisotropy (Wood et al. 2006), effective-zero permittivity (Castaldi et al. 2012), or hyperbolic dispersion (Ni et al. 2011; Simovski et al. 2013), negative refraction (Scalora et al. 2007), superprism or supercollimation effects (Ceglia et al. 2008; Li et al. 2007), resonant tunneling (Liu and Behdad 2012), sub-wavelength focusing (Zapata-Rodríguez et al. 2012) etc.
MDM can be regarded as linear spatial filters (Schurig and Smith 2003) and the framework of shift invariant systems adapted from Fourier Optics (Goodman 2004) is useful for their characterization. The theory of three-dimensional point spread function (Zapata-Rodríguez et al. 2011) (PSF) as well as a vectorial PSF (Kotyński et al. 2011) have been recently developed for MDM. It is possible to measure the modulation transfer function (MTF) experimentally in a double exposure experiment (Moore and Blaikie 2012). However we are not aware of any attempts to measure the amplitude transfer function, or equivalently the complex PSF for coherent illumination.
In this paper we make an attempt to recover the PSF from the intensity measurement. Our method includes a phase retrieval algorithm, which can be seen as a modification of the blind deconvolution algorithm (Ayers and Dainty 1988; Yu and Paganin 2010). Additionally, we address the difficulty of obtaining a mask with aperture sizes of the same order or smaller than the size of measured PSF. Thanks to the use of the algorithm we propose, the apertures can be significantly larger than the size of PSF. On the other hand, the intensity measurement needs to be done with a high resolution. These assumptions agree well with typical SNOM measurement conditions.
2 Image formation models
We will refer to two different image formation models—a non-coherent model involving only real and positive functions, and a coherent model involving a complex-valued point spread function. In practice, the recovery of a complexed-valued PSF is by far more difficult than the recovery of real-valued PSF, and the complex-valued problem is more likely to have a non-unique solution. Only the non-coherent problem can be solved with the classical blind deconvolution algorithm.
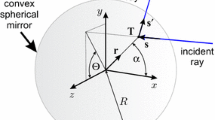
Let us consider a one-dimensional TM-polarized wavefront incident on a MDM through a mask consisting of a good conductor, such as Cr, which is thin and has a binary transmittance. Assuming that the layers within the MDM are optically linear and are infinite, the MDM defines a scalar linear shift-invariant optical system. In spite of the short coherence length of various sources used with SNOM, the sub-micrometer thickness of the MDM and layer thickness of the order of \(\lambda /10\) make it necessary to consider a coherent model for the measurement. A possible optical set-up is presented in Fig. 1.
2.1 Incoherent image formation model
In the case of incoherent illumination, the system is linear with respect to the intensity
where \(I(x)\) is the measured intensity, \(I_{in}(x)\) is the intensity right after the mask \(f(x)\), and \(|h(x)|^2\) is the incoherent point spread function, which is equal to the squared modulous of the coherent PSF \(h(x)\) and \(*\) denotes the convolution. For a binary mask \(f(x)\in \{0,1\}\), we may write approximately \(I_{in}(x)\approx const \cdot f(x)\). Now \(I\), \(f\), and \(|h|^2\) are real non-negative functions.
A direct application of the blind deconvolution iterative algorithm (Ayers and Dainty 1988) enables to determine the mask \(f\) and the PSF, \(|h|^2\), simultaneously from \(I\), provided that an initial estimate for the width of PSF is known, and that the decomposition (1) is unique. Importantly, the decomposition is not unique when the PSF is a Gaussian function, which is a common first-approach model for the PSF. The scheme of the classical blind deconvolution is shown in Fig. 2.
2.2 Coherent image formation model
In the case of coherent illumination, the system is linear with respect to the complex amplitude, for instance to the continuous out-of-plane component of the magnetic field \(H_z(x)\). The outgoing complex amplitude \(g(x)\) is then equal to
where \(f(x)\in \{0,1\}\) is the shape of the mask, and \(h(x)\) is the complex-valued PSF for a coherent system. The PSF is an unknown complex even function that combines the result of diffraction on the mask, transmission through MDM and measurement with a detector, such as a SNOM probe. The detector measures the intensity \(I(x)=|g(x)|^2\). We could write \(g(x)=\sqrt{I(x)}\cdot exp(i \phi (x))\), where \(\phi \) is some unknown phase distribution. Our intent is to determine \(h(x)\) from the measurement of \(I(x)\), with an a priori knowledge of \(f(x)\). This can be accomplished only with a sufficiently complicated design of apertures \(f(x)\) that results in a measurement \(I(x)\) rich in interference patterns. Moreover, it is not possible to resolve the sign of the phase of \(h(x)\), since both \(h(x)\) and \(h^{*}(x)\) produce the same distribution \(I(x)\).
In the simulations we assume first that \(f(x)\) is estimated from \(I(x)\), so that \(f(x)=\varTheta (\sqrt{I(x)}-0.5\cdot max(\sqrt{I(x)}))\), where \(\varTheta (\cdot )\) is the Heaviside step function. A more sophisticated procedure to determine \(f(x)\) can be used if necessary. In Ref. (Moore and Blaikie 2012), the MDM material was removed in order to make an AFM measurement of the developed photoresist.
2.3 Estimation of the PSF broadening due to diffraction on the apertures
Finally, let us determine the contribution to \(h(x)\) coming from the diffraction on the mask. This contribution may broaden the measured PSF, \(h(x)\), in a similar degree to the broadening due to the finite resolution of the SNOM probe. The resolution of SNOM is on the order of 50 nm, while the result of diffraction on the mask is estimated by us on 100 nm. The last result is based on finite difference time domain (FDTD) simulations presented in Fig. 3, where we have determined the size of the PSF corresponding to the transmission of light through the mask. We have calculated this contribution to PSF at the wavelength of 500 nm for a large range of aperture widths. Altogether, the PSF of MDM can be determined with the accuracy on the order of 150 nm. A further refinement of the measurement of PSF of MDM is possible based on the theoretical model for the PSF contributions due to diffraction on the mask and on the coupling to the SNOM probe.
a FDTD simulation of light transmission through an aperture in a perfect conductor (the aperture width \(w=100\) nm); b Full width at half maximum (FWHM) of the diffracted wavefront at the distance of 10 nm from the mask, and the FWHM of PSF due to diffraction on the aperture, calculated for a variety of aperture sizes. The wavelength is equal to 500 nm
3 Description of the algorithm
The schematic of the proposed modification of the blind deconvolution algorithm that we use for coherent illumination is presented in Fig. 4. It is assumed that a set of measurements \(\{I_n\}\) is processed simultaneously (here the index \(n\) is used to number the measurement samples. In the simulations we take \(n=1\ldots 20\), and every measurement includes an image measured through a mask with two apertures. The output wavefronts \(g_n(x)\) are initially assigned random phase distributions, while their amplitudes are fixed to \(\sqrt{I_n(x)}\) . The shape of each mask \(f_n(x)\) is estimated from the intensity \(I_n(x)\). In subsequent iterations, the transfer function \(H_p\) is being estimated as the median of the estimates \(\{H_{p,n}\}\) for all the apertures, where \(p\) numbers the iterations \(p=1 \ldots maxiter\) (in the simulations we take \(maxiter=50\)). Three comments on this step might be useful—(1) the purpose of using the median is to eliminate the values of \(H_{p,n}(k_x)=G_{p,n}(k_x)/F_{n}(k_x)\) for the spatial frequencies \(k_x\) at which \(F_{n}(k_x)\) has a small magnitude and may introduce noise; (2) the median of set of complex values is understood as if these values were ordered by their absolute values; (3) calculation of the median makes sense only after normalization of the phase (the functions \(\{H_{p,n}\}\) are assumed to be real and positive at \(k_x=0\)). Then we apodize \(H\) in every iteration by multiplying it by a Hamming window function of the width \(L\) (Hamming window is defined as \(w(u)=rect(x/L)\cdot (a+b\cdot cos(2\pi u/L))\) where \(a=0.5435, b=1-a\), and \(rect(.)\) is the rectangular function). In this way, the high spatial frequencies are slightly suppressed with respect to the low frequencies in every iteration. Subsequently, the complex PSF \(h_p(x)\) is calculated. We note, that in this work the capital letter always stands for the Fourier Transform of the corresponding function written with a lower case symbol. The PSF is apodized in a similar way as \(H_p\). In the simulations, the Hamming windows are rather broad (\(L=20 k_0\), and \(L=20 \lambda \)). Moreover \(h_p\) is forced to preserve an even symmetry in every iteration. The algorithm stops after iteration \(p=maxiter\).
4 Numerical results
In this section we demonstrate the recovery of PSF from a measurement which follows non-coherent, and coherent image formation models, given in Eqs. (1), (2), respectively. We also illustrate the problems with the recovery due to non-unique solution of the decompositions (1), (2). The measurement is one-dimensional and corresponds to one (for the non-coherent case) or more (for the coherent case) scans with a SNOM probe in the direction perpendicular to the rectangular apertures in the mask.
In the simulations we use a PSF obtained with the transfer matrix method for a layered metamaterial consisting of silver and \(TiO_2\). The operating wavelength is equal to the \(\lambda =404.7\) nm line of mercury lamp, the permittivities of both materials are equal to \(\varepsilon _{Ag}=-3.998+0.692i\) (Palik 1985) and \(\varepsilon _{TiO_2}=6.392\) (Devore 1951). The layered metamaterial consists of \(N=7\) elementary cells, each containing three layers–two external \(TiO_2\) layers with the thickness of \(d_{TiO_2}=22.5\) nm, and a middle silver layer with \(d_{Ag}=11\) nm. We have designed this metamaterial for superresolving imaging—the full width at half maximum (FWHM) of \(|h(x)|^2\) is subwavelength and is equal to \(0.2\lambda \). The amplitude transfer function \(H\), modulation transfer function MTF (normalised autocorrelation of \(H\)), coherent point spread function \(h\), and non-coherent point spread function \(|h|^2\) of the metamaterial are shown in Fig. 5.
Amplitude transfer function \(H\), modulation transfer function MTF, coherent point spread function \(h\), and non-coherent point spread function \(|h|^2\) of the metamaterial. The metamaterial consists of \(N=7\) elementary cells, each containing three layers–two external \({ TiO}_2\) layers with the thickness of \(d_{{ TiO}_2}=22.5\) nm, and a middle silver layer with \(d_{Ag}=11\) nm
Let us begin with the non-coherent measurement model expressed with Eq. (1). In this case we use the standard blind deconvolution algorithm (implemented as a standard routine in Matlab, see Fig. 2). Therefore, \(f(x)\) which is in non-coherent case the intensity right after the mask (\(I_{in}\)), is assumed to be unknown. As the initial guess for the algorithm we take Gaussian-like functions with various widths (called seed) for \(|h_0(x)|^2\). On the other hand, we impose an additional condition on \(|h(x)|^2\) which assures that the PSF is an even function. After blind deconvolution algorithm is completed MTF is reconstructed from the retrieved PSF profile. In Fig. 6 we present the simulation results of the a) mask, b) PSF and c) MTF recovery, calculated for the layered material. For a mask containing two apertures of different widths, and with the size of the seed function chosen in the right order, all the requested functions may be recovered very accurately. Otherwise, e.g. for the mask with only one slit (Fig. 7a) or for a too narrow seed function (Fig. 7b) the algorithm does not converge to the correct result.
Now, let us demonstrate the performance of the novel algorithm proposed in this paper. We apply the coherent image formation model from Eq. (2) and the algorithm presented in Fig. 4. The PSF recovery will be demonstrated for a set of 20 measurements, each of which is obtained using a pair of two apertures. The aperture widths and the distance between them vary randomly in the set of measurements assuring a rich information content of the interference patterns. The apertures and the distance between them are always larger than \(\lambda \). Therefore, the PSF is subwavelength in size, however the apertures are not.
The results of the algorithm are presented in Fig. 8. The figure includes one of the 20 aperture pairs with the corresponding intensity measurement, the original and reconstructed point spread function and transfer function, and the absolute reconstruction error of the measurement. As we can see, the algorithm is capable of retrieving an estimate for the PSF, although the result is not exact, and due to the problems with the uniqueness of the decomposition it should not be used in an automatic way. The recovered PSF visually differs from the original one, but the reconstruction error is not large. We are able to estimate the size of the PSF, and its phase near the origin. The convergence of the algorithm is characterised in Fig. 9.
Modified blind deconvolution used to determine coherent PSF; Top—intensity profile \(I(x)\) superimposed on a pair of two apertures and the corresponding reconstruction error obtained with the PSF recovered from the algorithm (an example chosen from 20 pairs of apertures used to determine the PSF). Center—original and recovered PSF of the metamaterial; Bottom—original and recovered transfer function of the metamaterial. Bold (red on-line) lines stand for the absolute value of the PSF and transfer function. Dashed lines correspond to the real and imaginay parts of the same functions. (Color figure online)
For layered metamaterials, the PSF, i.e. the response to a delta-shaped input signal, may be substantially different than the response to a sub-wavelength, still finite, Gaussian signal (Kotyński and Stefaniuk 2010). In fact, in this paper we address a problem which is often ill-posed i.e. there exist multiple PSF functions that give the same or almost the same interference pattern. Nontheless, the approximate resolution of the metamaterial can be estimated from the recovered PSF.
Altogether, thanks to the proposed algorithm, the resolution required for the fabrication of the mask can be relaxed significantly. In particular the mask may be produced with laser lithographic techniques, and still can be used to measure the PSF with a sub-wavelength resolution.
5 Conclusions
We have introduced an algorithm for improved measurement of complex PSF of layered metamaterials. The proposed algorithm is based on the blind deconvolution algorithm, however it operates on complex functions, and it is assumed that an estimate of the mask function is known first. Subsequently, the PSF is iteratively refined, including an apodization and symmetrization operation. The phase distribution of the output wavefront is also being estimated at the same time. Due to the problems with the uniqueness of the decomposition, the algorithm should be used with caution. Its main advantage is that it makes possible to determine the PSF in an experiment with the mask containing apertures significantly broader than the PSF, provided that the wavefront intensity is measured with a high resolution.
References
Ayers, G.R., Dainty, J.C.: An iterative blind deconvolution method and its applications. Opt. Lett. 13, 547–549 (1988)
Castaldi, G., Savoia, S., Galdi, V., Alu, A., Engheta, N.: Analytical study of subwavelength imaging by uniaxial epsilon-near-zero metamaterial slabs. Phys. Rev. B 86, 115–123 (2012)
de Ceglia, D., Vincenti, M.A., Cappeddu, M.G., Centini, M., Akozbek, N., D’Orazio, A., Haus, J., Bloemer, M.J., Scalora, M.: Tailoring metallodielectric structures for superresolution and superguiding applications in the visible and near-ir ranges. Phys. Rev. A 77, 033848 (2008)
Devore, J.R.: Refractive indices of rutile and sphalerite. J. Opt. Soc. Am. 9, 416–419 (1951)
Fang, N., Lee, H., Sun, C., Zhang, X.: Sub-diffraction-limited optical imaging with a silver superlens. Science 308(5721), 534–537 (2005). doi:10.1126/science.1110900
Goodman, J.: Introduction to Fourier Optics, 3rd edn. McGraw-Hill Companies Inc, New York (2004)
Guclu, C., Campione, S., Capolino, F.: Hyperbolic metamaterial as super absorber for scattered fields generated at its surface. Phys. Rev. B 86, 205130 (2012)
Jacob, Z., Alekseyev, L.V., Narimanov, E.: Optical hyperlens: far-field imaging beyond the diffraction limit. Opt. Express 14, 8247–8256 (2006)
Kotyński, R., Stefaniuk, T.: Multiscale analysis of subwavelength imaging with metal-dielectric multilayers. Opt. Lett. 35, 1133–1135 (2010)
Kotyński, R., Antosiewicz, T.J., Król, K., Panajotov, K.: Two-dimensional point spread matrix of layered metal-dielectric imaging elements. J. Opt. Soc. Am. A 28, 111–117 (2011)
Li, X., He, S., Jin, Y.: Subwavelength focusing with a multilayered Fabry-Perot structure at optical frequencies. Phys. Rev. B 75, 045103 (2007)
Liu, C.H., Behdad, N.: Tunneling and filtering characteristics of cascaded epsilon-negative metamaterial layers sandwiched by double-positive layers. J. Appl. Phys. 111, 014906 (2012)
Moore, C.P., Blaikie, R.J.: Experimental characterization of the transfer function for a silver-dielectric superlens. Opt. Express 20, 6412–6420 (2012)
Ni, X., Ishii, S., Thoreson, M.D., Shalaev, V.M., Han, S., Lee, S., Kildishev, A.V.: Loss-compensated and active hyperbolic metamaterials. Opt. Express 19, 25242–25254 (2011)
Palik, E.D. (ed.): Handbook of Optical Constants of Solids, vol. 1. Academic Press, New York (1985)
Pastuszczak, A., Stolarek, M., Antosiewicz, T.J., Kotynski, R.: Multilayer metamaterial absorbers inspired by perfectly matched layers. Opt. Quantum Electron. doi:10.1007/s11082-014-9986-z (2014)
Paul, O., Urzhumov, Y., Elsen, C., Smith, D., Rahm, M.: Construction of invisibility cloaks of arbitrary shape and size using planar layers of metamaterials. J. Appl. Phys. 111, 123106 (2012)
Scalora, M., D’Aguanno, G., Mattiucci, N., Bloemer, M.J., Ceglia, D., Centini, M., Mandatori, A., Sibilia, C., Akozbek, N., Cappeddu, M.G., Fowler, M., Haus, J.: Negative refraction and sub-wavelength focusing in the visible range using transparent metallo-dielectric stacks. Opt. Express 15, 508–523 (2007)
Schurig, D., Smith, D.R.: Spatial filtering using media with indefinite permittivity and permeability tensors. Appl. Phys. Lett. 82, 2215–2217 (2003)
Simovski, C., Maslovski, S., Nefedov, I., Tretyakov, S.: Optimization of radiative heat transfer in hyperbolic metamaterials for thermophotovoltaic applications. Opt. Express 21, 14988–15013 (2013)
Wood, B., Pendry, J.B., Tsai, D.P.: Directed subwavelength imaging using a layered metal-dielectric system. Phys. Rev. B 74, 115–116 (2006)
Yu, R.P., Paganin, D.M.: Blind phase retrieval for aberrated linear shift-invariant imaging systems. New J. Phys. 12, 073040 (2010)
Zapata-Rodríguez, C.J., Pastor, D., Camps, V., Caballero, T., Miret, J.J.: Three-dimensional point spread function of multilayered flat lenses and its application to extreme subwavelength resolution. J. Nanophotonics 5, 051807 (2011)
Zapata-Rodríguez, C.J., Pastor, D., Caballero, M.T., Miret, J.J.: Diffraction-managed superlensing using plasmonic lattices. Opt. Commun. 285, 3358–3362 (2012)
Author information
Authors and Affiliations
Corresponding author
Additional information
This work was supported by research project UMO-2011/01/B/ST3/02281 of the Polish National Science Center (TS, PW, RK), and project TEC2009-11635 from the from the Generalitat Valenciana (DP, CZR).
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution License which permits any use, distribution, and reproduction in any medium, provided the original author(s) and the source are credited.
About this article
Cite this article
Pastor, D., Stefaniuk, T., Wróbel, P. et al. Determination of the point spread function of layered metamaterials assisted with the blind deconvolution algorithm. Opt Quant Electron 47, 17–26 (2015). https://doi.org/10.1007/s11082-014-0010-4
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11082-014-0010-4