The window layers effect on the hardness improvement of space solar cells exposed to the 1 MeV electron irradiations

Abstract

Because of their state of art technology, GaAs solar cells are generally preferred for spatial applications. Exposure to proton and electron irradiations, solar cells suffer significant degradation in their performance such as short circuit current and open circuit voltage. Adding a window layer helps in effectively reducing the surface recombination at the emitter surface of the solar cell without absorbing the useful light required for the device. It remains to study the physics of the window-emitter hetero-interface in order to understand how the window layer presence increases the minority carrier lifetime of the solar cell exposed to particles irradiation. In this work Numerical simulation has been used to study the AlxGa1-xAs window composition effect on the current–voltage characteristics of a GaAs solar cell under AM0 illumination and exposed to 1 MeV electron irradiation. To predict the effect of window layers on solar cells degradation, the current voltage characteristic are evaluated for different electron irradiation fluences. The findings are supported by experimental data. They lead us to get to know how the window layer improves resistance to electron irradiation through its own parameters.

1 Introduction

Window layers help in effectively reducing the surface recombination at the emitter surface of the solar cells, without absorbing the useful light required for the device, resulting in significant improvement in energy conversion efficiency (Jain 2003). Various window layer materials have been investigated for III–V compound semiconductor based solar cells. To systematically reach this end, it will be important to understand the physics of the window-emitter hetero-interface as well as growth related issues (Lammasniemi et al. 1997).

In the case of $GaAs$ solar cell, it has been demonstrated with efficiency near to 25 % at one sun illumination and high efficiency $GaAs$ solar cells all use a wide band-gap window layer on the surface to reduce front surface recombination losses (Vernon et al. 1990). One of the more critical design areas in high efficiency $GaAs$ solar cell is $AlGaAs$ window layer and in order to minimize its optical absorption, high aluminium content alloys are favoured ones (Gee and Drummond 1990). In previous work, new approach, justified theoretically and experimentally is used, allowing to deduce the relationship between electron and hole minority-carrier lifetime then we have shown, by using this method, the effect of the device parameters, i.e. the thickness $X_p$ and $X_n$ respectively of emitter and base, and the level doping $N_A$ and $N_D$ on each side of the junction of the emitter and the base and the front surface recombination velocity, on how is the variation of characteristics and the electron irradiation resistance of solar cells (Idali Oumhand et al. 2008, 2009). In addition, the validity and accuracy of this approach has been justified by the fact that the degradation parameters, $\tau _{n0} , \tau _{p0} , K\sigma _n$ and $K\sigma _p$ which fit the experimental data are the same for both the short circuit current $J_{SC}$ and the open circuit voltage, $V_{OC}$ in the case of ${p^{+}}/n-InGaP$ and ${n^{+}}/p-InGaP$ solar cell (Idali Oumhand et al. 2008, 2009).

This paper is a suite of the study and prediction of solar cell device parameters. We rewrite the calculation principle of new approach by taking into account the physics of the window-emitter hetero- interface and we apply this approach to $p-AlGaAs {p^{+}}/n-GaAs$ solar cell under AM0 illumination and exposed to 1 MeV electron irradiation and then a comparison between both calculated and measured values would be studied (Friedman and Olson 2001). Moreover, we will show how the effect of window layer $p-AlGaAs$ on ${p^{+}}/n-GaAs$ through three parameters, absorption coefficient $\alpha _w (\lambda )$ at a given wavelength $\lambda$ and effective hetero-interface recombination velocity $S_{eff}^n$ and its thickness variation $X_w$ on variation of $J_{SC}$ and $V_{OC}$ versus the fluence of the irradiation, $\phi$ (Yoshikawa and Kasai 1981; Ueda et al. 1998 ; Nakayama et al. 2008). The comparison between $p-AlGaAs$ and $p-InGaP$ window-layers effects on degradation of $J_{SC}$ and $V_{OC}$ are investigated.

2 Experimental results and principle of degradation parameter calculation

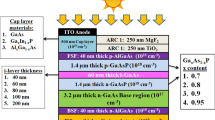
The $p-AlGaAs {p^{+}}/n-GaAs$ structure studied is MOCVD epitaxially grown and it has been irradiated with increasing fluences, in the range $10^{14}$–$10^{17}$ electrons $\hbox {cm}^{-2}$, at energy of 1 MeV. The irradiation was performed at room temperature with a scanned beam in order to ensure the uniformity of the fluence over the area of the cell (1–4$\,{\hbox {cm}}^{2}$). The intensity of the beam ($2\,\upmu {\hbox {A}}$) was chosen to keep negligible the temperature increase. The cell is placed in a Faraday cup allowing accurate measurement of the fluence with a current integrator. Current–voltage measurements were performed in situ in the accelerator under a 1 AM0 illumination provided by a Xe arc lamp (Bourgoin and Zazoui 2002). Defects induced by electron irradiation in n- and p-type materials have been extensively studied (for a review see Pons and Bourgoin 1985). These studies demonstrated that the defects introduced by room temperature irradiation are primary defects, resulting from the displacements of As in the As sub-lattice (Stievenard et al. 1986).

For simplicity it is assumed that the series resistance $R_{S}$ and shunt resistance $R_{Sh}$ have negligible effects and that there is no shadowing effect on the illuminated surface (Walters et al. 1998).

The calculated effective hetero-interface recombination velocity $S_{eff}^n$ assumes that the window layer effectively passive the solar cell front surface by reducing surface recombination at the emitter surface of the solar cells without absorbing the useful light required for the device and that the large band discontinuities at the hetero-interface provide a great potential barrier for the minority carriers, as it is illustrate in Fig. 1, and then well improving the performance of the solar cell (Jain and Landis 1991; Nelson 2003). When calculating the contribution of each side of the junction and the depletion region to current in presence of window layer, the incident flux, $\varphi (\lambda )$, and the electron recombination velocity, $S_n$, should be modified respectively to $\varphi (\lambda )e^{-\alpha _w (\lambda )X_w }$ and to $S_{eff}^n$ which is expressed as (Nelson 2003; Hovel 1979),

$$\begin{aligned} S_{eff}^n =S_n^w e^{({Eg-Eg^{w}}/{K_B T})}\frac{{D_n^w }/{S_n^w L_n^w }\tanh {(X_w }/{L_n^w })+1}{{S_n^w L_n^w }/{D_n^w }\tanh {(X_w }/{L_n^w })+1} \end{aligned}$$

$\hbox {E}_{\mathrm{g}}$ and $\hbox {E}_{\mathrm{g}}^{\mathrm{w}}$ are the energy gap in GaAs and in window respectively .

Fig. 1

Band structure diagram of p-AlGaAs-p/n-GaAs

3 Mechanism of degradation and parameters effects

3.1 Mechanism of degradation

The calculation of degradation parameters $\tau _{n0}, \tau _{p0} ,K\sigma _n$ and $K\sigma _p$ of $p-AlGaAs \quad {p^{+}}/n-GaAs$ solar cell will be possible, when the thickness of window layer and doping respectively of the emitter and base are given further information in (Idali Oumhand et al. 2009). The parameters of the studied cell are listed in Table 1 below (Makham et al. 2005).

Table 1 Physical parameter values of $\hbox {p}-\hbox {AlGaAs}-\hbox {p}^{+}/\hbox {n}-\hbox {GaAs}$ cell (Makham et al. 2005)

The knowledge of $J_{SC0}^{\exp }$ and $V_{OC0}^{\exp }$ under given illumination, prior irradiation is also necessary in order to derive the minority carrier lifetimes $\tau _{p0}$ and $\tau _{n0}$.

Once the initial values of the minority carrier lifetimes are determined, we inject them into calculation (Idali Oumhand et al. 2009).

The knowledge of $J_{SC_{\phi }}^{\exp }$ and $V_{OC_{\phi }}^{\exp }$ under given illumination and amount of irradiation $\phi$ allow it to deduce the values of $\tau _{n\phi }$ and $\tau _{p\phi }$ and hence $K\sigma _n , K\sigma _p$, for more detailed information see (Idali Oumhand et al. 2009).

Table 2 Calculated degradation parameters of $\hbox {p-AlGaAs-p}^{+}/\hbox {n-GaAs}$ cell (Makham et al. 2005)

Fig. 2

Calculated degradation (solid line), induced by 1 MeV electron irradiation, of the short circuit current (a), and open circuit voltage (b) in the p-AlGaAs-p+/n-GaAs cell under 1 AM0 illumination and comparison with measured data (open square) cited in Makham et al. (2005)

Then from the parameters $\tau _{n0}$ and $K\sigma _n$ in emitter, and $\tau _{p0}$ and $K\sigma _p$ in base, see Table 2, we derive the calculated values of $J_{SC\phi }$ and $V_{OC\phi }$ as shown in curve Fig. 2a , b respectively.

We add that these values extracted from our analysis are different from the values determined by other authors (Bourgoin and Angelis 2001; Angelis et al. 2001) because of the relationship between two carriers lifetime $\tau _{p0}$ and $\tau _{n0}$ (Idali Oumhand et al. 2009), and more the validity and accuracy of this approach was justified by the fact that the degradation parameters, $\tau _{n0} , \tau _{p0} , K\sigma _n$ and $K\sigma _p$ which fit the experimental data, $J_{SC}^{\exp } (\square )$ and $V_{OC}^{\exp } (\square )$, are the same for both the short circuit current, $J_{SC}^{cal}$ (solid line), and the open circuit voltage, $V_{OC}^{cal}$ (solid line) in case of $p-AlGaAs {p^{+}}/n-GaAs$.

3.2 The window-layer parameters effect

Now the degradation parameters,$\tau _{n0} , \tau _{p0} , K\sigma _n$ and $K\sigma _p$ of $p-AlGaAs-{p^{+}}/n-GaAs$ are calculated with the help of our calculation method, and we proceed to study the effects of parameters

For instance, thickness $X_w$ and effective hetero-interface recombination velocity $S_{eff}^n$ on the variation of $J_{SC}$ and $V_{OC}$ versus the fluence of the irradiation $\phi$, then a comparison between $p-AlGaAs-{p^{+}}/n-GaAs$ and $p-InGaP-{p^{+}}/n-GaAs$ is investigated by using variation of absorption coefficient $\alpha _w (\lambda )$.

The variations of the short-circuit currents and open circuit voltages versus fluence of this cell are given in Fig. 3a, b, under $1\hbox {AM0}$ illumination, versus the fluence of 1 MeV electron irradiation, calculated for different values of the thickness $x_w$. When we vary the thickness $x_w$ from 10 to 35 and to 70 nm the curve of the short-circuit current $J_{SC}$ versus the fluence of the irradiation $\phi$ leads to significant reduction in $J_{SC}$. Indeed, when the window layer thickness $x_w$ will be large, the attenuation becomes pronounced which causes a reduction of the spectral response and therefore a diminution of the value of $J_{SC}$. At high fluence of irradiation, we note a fast decrease of the curves representing the cells of which the thickness $x_w$ is large. On the contrary, the $V_{OC}$ curve exhibits no significant reduction at the time of the increase of $x_w$.

Fig. 3

Variation of the short circuit current Jsc (a) and the open circuit voltage Voc (b) under 1 AM0 illumination, versus the fluence of 1 MeV electron irradiation, calculated for different values $X_{w}$ such as: (solid line), $X_{w}=10 ^{-6}\hbox {cm}$, (dashed line), $X_{w}=3.5{\times }10 ^{-6}\hbox {cm}$ and (dotted line)  $X_{w}=7\times 10 ^{-6}\hbox {cm}$ of p-AlGaAs window-layer thickness

The Fig. 4a shows an important effect of variation of the effective hetero-interface recombination velocity on $J_{SC}$ while, this effect remains a little weak on the variation of the Voc parameter as is exhibited in Fig. 4b.

Fig. 4

Variation of the short circuit current Jsc (a) and the open circuit voltage Voc (b) under 1 AM0 illumination, versus the fluence of 1 MeV electron irradiation, calculated for both values of $S_{eff}^n ,\,2.5\times 10^{6} \hbox {cm/s}$ (dashed line) and $5\times 10^{6} \hbox {cm/s}$ (solid line) in p-AlGaAs window-layer

By comparing the degradation parameters of p/n- GaAs junction, as $\tau _p ,\tau _n , J_{SC}$ and $V_{OC}$ we find that the short circuit current $J_{SC}$ is sensitive to degradation. Moreover, the minority carrier lifetime $\tau _p$ in base is degraded faster than $\tau _n$, in emitter, as shown in Fig. 5.

Fig. 5

Normalized degradation parameters as: $\tau _{n0}$ (open square), $\tau _{p0}$ (asterisk), $J_{SC}$ (solid line) and $V_{OC}$ (dotted line) under 1 AM0 illumination, versus fluence of 1 MeV electron irradiation

Whereas, the degradation of $V_{OC}$ is less pronounced relatively to that of minority carrier lifetime. In addition, the study degradation of a series of solar cells technologically similar but differs in their effective front surface velocity was achieved. It can be seen from Table 3, that the degradation parameters $\tau _{n0} ,\tau _{p0} ,K\sigma _n$ and $K\sigma _p$ of solar are sensitive to variation of effective hetero-interface recombination velocity $S_{eff}^n$, when the value of this later is greater than a limit value of $5\times 10^{6} \hbox {cm}/\hbox {s}$.

Table 3 Variation of initial minority carrier lifetime versus effective hetero-interface recombination velocity $S_{eff}^n$

While these degradation parameters become non sensitive to this variation, if the values of $S_{eff}^n$ are smaller than a limit value. This explains why the optimum value of $S_{eff}^n$ must be smaller than a limit value of $5\times 10^{6} \hbox {cm}/\hbox {s}$.

Finally, the Fig. 6a, b exhibit the comparison between $p-AlGaAs-{p^{+}}/n-GaAs$ and $p-InGaP-{p^{+}}/n-GaAs$ solar cells, by using the absorption coefficient $\alpha _w (\lambda )$ and the effective hetero-interface recombination velocity $S_{eff}^n$. We note for both curves, Fig. 6a, b, that the variations of Jsc and Voc are clearly important in the case of p-AlGaAs than that of p InGaP and consequently $AlGaAs$ window layer structure is good candidate for solar cell.

Fig. 6

variation of the short circuit current Jsc, (a) and the open circuit voltage Voc (b) under 1 AM0 illumination, versus the fluence of 1 MeV electron irradiation, calculated in case of p-AlGaAs (solid line) and p-InGaP (dashed line) window-layer

4 Conclusion

In this paper we have investigated the effect of the window layer through three parameters, absorption coefficient $\alpha _w (\lambda )$, effective hetero-interface recombination velocity $S_{eff}^n$ and its thickness variation $x_w$, on the variation of $J_{SC}$ and $V_{OC}$ versus the fluence of the irradiation, $\phi$. We have demonstrated that the short circuit current $J_{SC}$ is sensitive to variations of the thickness of the window-layer, and the effective surface recombination velocity but the open voltage $V_{OC}$ remain little sensitive to these variations.