Triggering a variety of Nash-equilibria in oligopolistic electricity markets

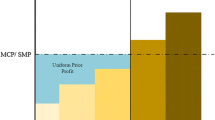
Abstract

Liberalized electricity markets promise a cost-efficient operation and expansion of power systems but may as well introduce opportunities for strategic gaming for price-making agents. Given the rapid transition of today’s energy systems, unconventional generation and consumption patterns are emerging, presenting new challenges for regulators and policymakers to prevent strategic behavior. The strategic offering of various price-making agents in oligopolistic electricity markets resembles a multi-leader-common-follower game. The decision problem of each agent can be modeled as a bi-level optimization problem, consisting of the strategic agent’s decision problem at the upper-level, and the market clearing at the lower-level. When modeling a multi-leader game, i.e., a set of bi-level optimization problems, the resulting equilibrium problem with equilibrium constraints poses several challenges. Real-life applicability or policy-oriented studies are challenged by the potential multiplicity of equilibria and the difficulty of exhaustively exploring this range of equilibria. In this paper, the range of equilibria is explored by using a novel simultaneous solution method. The proposed solution technique relies on applying Scholtes’ regularization before concatenating the strategic actor’s decision problems’ optimality conditions. Hence, the attained solutions are stationary points with high confidence. In a stylized example, different strategic agents, including an energy storage system, are modeled to capture the asymmetric opportunities they may face when exercising market power. Our analysis reveals that these models’ outcomes may span a broad range, impacting the derived economic metrics significantly.

Appendices

Appendix A: Single-level reformulation of ESS problem

We present the required steps to transform the bi-level formulation of the ESS owner problem (i) into the single-level (MPPDC) equivalent by the primal-dual optimality conditions, (ii) into a nonlinear complementarity problem by the KKT optimality conditions of the MPPDC form.

1.1 A.1 MPPDC ESS

The obtained single-level problem, after applying primal-dual reformulation on the LL Problem (7):

$$\begin{aligned}&\mathcal {F}_{ESS}^{l} = \max _{\Xi _{UL}^{ESS}} \sum _{t \in \mathcal {T}} \lambda _{t} \cdot (dch_{l,t} - ch_{l,t}) \end{aligned}$$

(A.1a)

$$\begin{aligned}&\text {subject to} \nonumber \\&p^{floor} \le c^{CH}_{l,t} \le p^{cap} : \quad (\underline{\kappa }_{l,t}^{ch}, \overline{\kappa }_{l,t}^{ch}) \quad \forall t \end{aligned}$$

(A.1b)

$$\begin{aligned}&p^{floor} \le c^{DCH}_{l,t} \le p^{cap} : \quad (\underline{\kappa }_{l,t}^{dch}, \overline{\kappa }_{l,t}^{dch}) \quad \forall t \end{aligned}$$

(A.1c)

$$\begin{aligned}&0 \le \overline{CH}_{l,t} \le P^{ESS,max}_l: \quad (\underline{\omega }_{l,t}^{ch}, \overline{\omega }_{l,t}^{ch}) \quad \forall t \end{aligned}$$

(A.1d)

$$\begin{aligned}&0 \le \overline{DCH}_{l,t} \le P^{ESS,max}_l: \quad (\underline{\omega }_{l,t}^{dch}, \overline{\omega }_{l,t}^{dch}) \quad \forall t \end{aligned}$$

(A.1e)

$$\begin{aligned}&0 \le SoC_{l,t} \le E^{ESS,max}_l: \quad (\underline{\omega }_{l,t}^{soc}, \overline{\omega }_{l,t}^{soc}) \quad \forall t \end{aligned}$$

(A.1f)

$$\begin{aligned}&SoC_{l,t} = SoC_{l,t-1} + \eta _l^{ch} ch_{l,t} - dch_{l,t}/\eta _l^{dch}: \quad (\mu _{l,t}^{soc}) \quad \forall t \end{aligned}$$

(A.1g)

$$\begin{aligned}&SoC_{l,T} = SoC_{0}: \quad (\mu _{0}^{soc}) \end{aligned}$$

(A.1h)

The resulting constraints from the LL reformulated via duality:

$$\begin{aligned}&d_{t} \! + \! \sum _{l \in \mathcal {L}}\! (ch_{l,t} \!- \! dch_{l,t}) \! - \!\sum _{k \in \mathcal {K}}\! w_{k,t} \! - \!\sum _{i \in \mathcal {I}} \! g_{i,t} \!= \! 0: \quad (\Pi _{j,t}) \quad \forall t \end{aligned}$$

(A.1i)

$$\begin{aligned}&0\le g_{i,t} \le \overline{G}_{i,t}: \quad (\underline{\nu }_{j,i,t}^{g}, \overline{\nu }_{j,i,t}^{g}) \quad \forall i, \forall t \end{aligned}$$

(A.1j)

$$\begin{aligned}&0\le w_{k,t} \le \overline{W}_{k,t}: \quad (\underline{\nu }_{j,k,t}^{w}, \overline{\nu }_{j,k,t}^{w}) \quad \forall k, \forall t\end{aligned}$$

(A.1k)

$$\begin{aligned}&0\le ch_{l,t} \le \overline{CH}_{l,t}: \quad (\underline{\nu }_{j,l,t}^{ch}, \overline{\nu }_{j,l,t}^{ch}) \quad \forall l, \forall t\end{aligned}$$

(A.1l)

$$\begin{aligned}&0\le dch_{l,t} \le \overline{DCH}_{l,t}: (\underline{\nu }_{j,l,t}^{dch}, \overline{\nu }_{j,l,t}^{dch}) \quad \forall l, \forall t\end{aligned}$$

(A.1m)

$$\begin{aligned}&0\le d_{t} \le \overline{D}_{t}: \quad (\underline{\nu }_{j,t}^{d}, \overline{\nu }_{j,t}^{d}) \quad \forall t \end{aligned}$$

(A.1n)

$$\begin{aligned}&c_{i,t}^{g} - \lambda _{t} - \underline{\beta }_{i,t}^{g} + \overline{\beta }_{i,t}^{g} = 0: \quad (\Psi _{j,i,t}^{g}) \quad \forall i, \forall t\end{aligned}$$

(A.1o)

$$\begin{aligned}&c_{k,t}^{w} - \lambda _{t} - \underline{\beta }_{k,t}^{w} + \overline{\beta }_{k,t}^{w} = 0: \quad (\Psi _{j,k,t}^{w}) \quad \forall k, \forall t \end{aligned}$$

(A.1p)

$$\begin{aligned}&c_{l,t}^{dch} - \lambda _{t} - \underline{\beta }_{l,t}^{dch} + \overline{\beta }_{l,t}^{dch} = 0: \quad (\Psi _{j,l,t}^{dch}) \quad \forall l, \forall t \end{aligned}$$

(A.1q)

$$\begin{aligned}&- c_{l,t}^{ch} + \lambda _{t} - \underline{\beta }_{l,t}^{ch} + \overline{\beta }_{l,t}^{ch} = 0: \quad (\Psi _{j,l,t}^{ch}) \quad \forall l, \forall t \end{aligned}$$

(A.1r)

$$\begin{aligned}&- c_{t}^{d} + \lambda _{t} - \underline{\beta }_{t}^{d} + \overline{\beta }_{t}^{d} = 0: \quad (\Psi _{j,t}^{d})\end{aligned}$$

(A.1s)

$$\begin{aligned}&\underline{\beta }_{i,t}^{g}, \ \overline{\beta }_{i,t}^{g}, \underline{\beta }_{k,t}^{w}, \ \overline{\beta }_{k,t}^{w}, \underline{\beta }_{l,t}^{dch}, \ \overline{\beta }_{l,t}^{dch}, \underline{\beta }_{l,t}^{ch}, \ \overline{\beta }_{l,t}^{ch}, \underline{\beta }_{t}^{d}, \ \overline{\beta }_{t}^{d} \ge 0: \quad \forall i, \forall k, \forall l, \forall t \nonumber \\&(\underline{\delta }_{j,i,t}^{g}, \overline{\delta }_{j,i,t}^{g}, \underline{\delta }_{j,k,t}^{w}, \overline{\delta }_{j,k,t}^{w}, \underline{\delta }_{j,l,t}^{dch}, \overline{\delta }_{j,l,t}^{dch}, \underline{\delta }_{j,l,t}^{ch}, \overline{\delta }_{j,l,t}^{ch}, \underline{\delta }_{j,t}^{d}, \overline{\delta }_{j,t}^{d}) \end{aligned}$$

(A.1t)

$$\begin{aligned}&s^{dch}_{l,t} - \overline{\beta }_{l,t}^{dch} \cdot \overline{DCH}_{l,t} \le \epsilon _{1}: \quad (\overline{\gamma }^{dch}_{j,l,t}) \end{aligned}$$

(A.1u)

$$\begin{aligned}&-s^{dch}_{l,t} + \overline{\beta }_{l,t}^{dch} \cdot \overline{DCH}_{l,t} \le \epsilon _{1}: \quad (\underline{\gamma }^{dch}_{j,l,t}) \end{aligned}$$

(A.1v)

$$\begin{aligned}&s^{ch}_{l,t} - \overline{\beta }_{l,t}^{ch} \cdot \overline{CH}_{l,t} \le \epsilon _{1}: \quad (\overline{\gamma }^{ch}_{j,l,t}) \end{aligned}$$

(A.1w)

$$\begin{aligned} -&s^{ch}_{l,t} + \overline{\beta }_{l,t}^{ch} \cdot \overline{CH}_{l,t} \le \epsilon _{1}: \quad (\underline{\gamma }^{ch}_{j,l,t}) \end{aligned}$$

(A.1x)

$$\begin{aligned}&- \sum _{t \in \mathcal {T}}(d_{t} \cdot c^{D}_{t}) \ + \sum _{i \in \mathcal {I},t \in \mathcal {T}}(g_{i,t} \cdot c^{G}_{i,t}) + \sum _{k \in \mathcal {K},t \in \mathcal {T}}(w_{k,t} \cdot c^{W}_{k,t}) \nonumber \\&\quad + \sum _{l \in \mathcal {L},t \in \mathcal {T}} (dch_{l,t} \cdot c^{DCH}_{l,t} - ch_{l,t} \cdot c^{CH}_{l,t}) \nonumber \\&\quad + \sum _{i \in \mathcal {I},t \in \mathcal {T}} (\overline{\beta }_{i,t}^{g} \cdot \overline{G}_{i,t})\nonumber \\&\quad + \sum _{k \in \mathcal {K}, t \in \mathcal {T}} (\overline{\beta }_{k,t}^{w} \cdot \overline{W}_{k,t}) + \sum _{l \in \mathcal {L},t \in \mathcal {T}}(s^{dch}_{l,t} + s^{ch}_{l,t}) + \sum _{t \in \mathcal {T}} (\overline{\beta }_{t}^{d} \cdot \overline{D}_{t}) = 0: \quad (\sigma _{j}^{PD}) \end{aligned}$$

(A.1y)

where $\epsilon _{1}$ is the first-stage regularization parameter for the nonlinear, non-convex strong duality constraint.

1.2 A.2 Linearization of the ESS’ objective

To linearize the initially bi-linear objective function following the method of Ruiz and Conejo (2009), we make use of the SDC equation (A.1y), the stationary conditions Eqs. A.1q–A.1r and the complementary slackness (CS) constraints of the LL. As the LL problem is convex, we know that the following CS conditions hold:

$$\begin{aligned}&\underline{\beta }_{l,t}^{dch} \cdot dch_{l,t} = 0 \end{aligned}$$

(A.2a)

$$\begin{aligned}&\overline{\beta }_{l,t}^{dch} \cdot dch_{l,t} = \overline{\beta }_{l,t}^{dch} \cdot \overline{DCH}_{l,t}\end{aligned}$$

(A.2b)

$$\begin{aligned}&\underline{\beta }_{l,t}^{ch} \cdot ch_{l,t} = 0 \end{aligned}$$

(A.2c)

$$\begin{aligned}&\overline{\beta }_{l,t}^{ch} \cdot ch_{l,t} = \overline{\beta }_{l,t}^{ch} \cdot \overline{CH}_{l,t} \end{aligned}$$

(A.2d)

Furthermore multiplying Eqs. A.1q–A.1r by $dch_{l,t}$ and $ch_{l,t}$ gives:

$$\begin{aligned} -&dch_{l,t} \cdot c_{l,t}^{dch} = -\lambda _{t} \cdot dch_{l,t} - \underline{\beta }_{l,t}^{dch} \cdot dch_{l,t} + \overline{\beta }_{l,t}^{dch} \cdot dch_{l,t} \end{aligned}$$

(A.3a)

$$\begin{aligned}&ch_{l,t} \cdot c_{l,t}^{ch} = \lambda _{t} \cdot ch_{l,t} - \underline{\beta }_{l,t}^{ch} \cdot ch_{l,t} + \overline{\beta }_{l,t}^{ch} \cdot ch_{l,t} \end{aligned}$$

(A.3b)

After substituting terms of Eq. A.2 in Eq. A.3:

$$\begin{aligned}&-dch_{l,t} \cdot c_{l,t}^{dch} = -\lambda _{t} \cdot dch_{l,t} + \overline{\beta }_{l,t}^{dch} \cdot \overline{DCH}_{l,t} \end{aligned}$$

(A.4a)

$$\begin{aligned}&ch_{l,t} \cdot c_{l,t}^{ch} = \lambda _{t} \cdot ch_{l,t} + \overline{\beta }_{l,t}^{ch} \cdot \overline{CH}_{l,t} \end{aligned}$$

(A.4b)

And lastly, to get the linearized equivalent of $\mathcal {F}_{ESS}^{l}$, we substitute Eq. A.4a in the SDC (Eq. A.1y):

$$\begin{aligned}&\lambda _{t} \cdot (dch_{l,t} - ch_{l,t}) = -\sum _{t \in \mathcal {T}}(d_{t} \cdot c^{D}_{t}) \ + \sum _{i \in \mathcal {I}, t \in \mathcal {T}}(g_{i,t} \cdot c^{G}_{i,t}) + \sum _{k \in \mathcal {K}, t \in \mathcal {T}}(w_{k,t} \cdot c^{W}_{k,t}) \nonumber \\&+ \sum _{i \in \mathcal {I}, t \in \mathcal {T}} (\overline{\beta }_{i,t}^{g} \cdot \overline{G}_{i,t}) + \sum _{k \in \mathcal {K}, t \in \mathcal {T}} (\overline{\beta }_{k,t}^{w} \cdot \overline{W}_{k,t}) + \sum _{t \in \mathcal {T}} (\overline{\beta }_{t}^{d} \cdot \overline{D}_{t}) \end{aligned}$$

(A.5)

We refer to the RHS of (A.5) as $\mathcal {D}_{ESS}^{l}$. Thus MPPDC-ESS with linearized objective function constitutes the objective function (A.5) and Constraints (A.1b–A.1y).

1.3 A.3 SCR-NCP, ESS

We recast MPPDC-ESS via its KKT conditions. This results in a nonlinear complementarity problem (NCP). After adding the regularization term $\epsilon _{2}$ as shown in Section (3.2), we obtain the SCR-NCP formulation: Primal feasibility:

$$\begin{aligned} \text {Eq. } A.1b-A.1y \end{aligned}$$

Dual feasibility:

All dual variables belonging to the inequality constraints of Eq. A.1b-A.1y are greater than or equal to 0.

$$\begin{aligned}&\text {Lagrangian stationarity:} \nonumber \\&\frac{\partial \mathcal {L}^{ESS}_{UL}}{\partial s^{DCH}_{l,t}} : - \underline{\gamma }^{dch}_{l,t} + \overline{\gamma }^{dch}_{l,t} +\sigma _{j}^{PD} = 0&\forall l, \forall t \end{aligned}$$

(A.6a)

$$\begin{aligned}&\frac{\partial \mathcal {L}^{ESS}_{UL}}{\partial s^{CH}_{l,t}} : - \underline{\gamma }^{ch}_{l,t} + \overline{\gamma }^{ch}_{l,t} +\sigma _{j}^{PD} = 0&\forall l, \forall t \end{aligned}$$

(A.6b)

$$\begin{aligned}&\frac{\partial \mathcal {L}^{ESS}_{UL}}{\partial c^{DCH}_{l,t}} : - \underline{\kappa }^{dch}_{l,t} + \overline{\kappa }^{dch}_{l,t} +\sigma _{j}^{PD} \cdot dch_{l,t} + \psi ^{dch}_{l,t} = 0&\forall l, \forall t \end{aligned}$$

(A.6c)

$$\begin{aligned}&\frac{\partial \mathcal {L}^{ESS}_{UL}}{\partial c^{CH}_{l,t}} : - \underline{\kappa }^{ch}_{l,t} + \overline{\kappa }^{ch}_{l,t} -\sigma _{j}^{PD} \cdot ch_{l,t} - \psi ^{ch}_{l,t} = 0&\forall l, \forall t \end{aligned}$$

(A.6d)

$$\begin{aligned}&\frac{\partial \mathcal {L}^{ESS}_{UL}}{\partial \overline{DCH}_{l,t}} : - \underline{\omega }^{dch}_{l,t} + \overline{\omega }^{dch}_{l,t} - \overline{\nu }^{dch}_{j,l,t} - \overline{\gamma }^{dch}_{j,l,t} \cdot \overline{\beta }^{dch}_{l,t} + \underline{\gamma }^{dch}_{j,l,t} \cdot \overline{\beta }^{dch}_{l,t} = 0&\forall l, \forall t \end{aligned}$$

(A.6e)

$$\begin{aligned}&\frac{\partial \mathcal {L}^{ESS}_{UL}}{\partial \overline{CH}_{l,t}} : - \underline{\omega }^{ch}_{l,t} + \overline{\omega }^{ch}_{l,t} - \overline{\nu }^{ch}_{j,l,t} - \overline{\gamma }^{ch}_{j,l,t} \cdot \overline{\beta }^{ch}_{l,t} + \underline{\gamma }^{ch}_{j,l,t} \cdot \overline{\beta }^{ch}_{l,t} = 0&\forall l, \forall t \end{aligned}$$

(A.6f)

$$\begin{aligned}&\frac{\partial \mathcal {L}^{ESS}_{UL}}{\partial dch_{l,t}} : - \frac{\mu ^{soc}_{l,t}}{\eta ^{dch}_{l}} -\Pi _{j,t} - \underline{\nu }^{dch}_{j,l,t} + \overline{\nu }^{dch}_{j,l,t} + \sigma _{j}^{PD} \cdot c^{DCH}_{l,t} = 0&\forall l, \forall t \end{aligned}$$

(A.6g)

$$\begin{aligned}&\frac{\partial \mathcal {L}^{ESS}_{UL}}{\partial ch_{l,t}} : \mu ^{soc}_{l,t} \cdot \eta ^{ch}_{l} + \Pi _{j,t} - \underline{\nu }^{ch}_{j,l,t} + \overline{\nu }^{ch}_{j,l,t} - \sigma _{j}^{PD} \cdot c^{CH}_{l,t} = 0&\forall l, \forall t \end{aligned}$$

(A.6h)

$$\begin{aligned}&\frac{\partial \mathcal {L}^{ESS}_{UL}}{\partial g_{i,t}} : c^{G}_{i,t} - \Pi _{j,t} - \underline{\nu }^{g}_{j,i,t} + \overline{\nu }^{g}_{j,i,t} + \sigma _{j}^{PD} \cdot c^{G}_{i,t} = 0&\forall i, \forall t \end{aligned}$$

(A.6i)

$$\begin{aligned}&\frac{\partial \mathcal {L}^{ESS}_{UL}}{\partial w_{k,t}} : c^{W}_{i,t} - \Pi _{j,t} - \underline{\nu }^{w}_{j,k,t} + \overline{\nu }^{w}_{j,k,t} + \sigma _{j}^{PD} \cdot c^{W}_{k,t} = 0&\forall k, \forall t \end{aligned}$$

(A.6j)

$$\begin{aligned}&\frac{\partial \mathcal {L}^{ESS}_{UL}}{\partial d_{t}} : - c^{D}_{t} + \Pi _{j,t} - \underline{\nu }^{d}_{j,t} + \overline{\nu }^{d}_{j,t} + \sigma _{j}^{PD} \cdot c^{D}_{t} = 0&\forall t \end{aligned}$$

(A.6k)

$$\begin{aligned}&\frac{\partial \mathcal {L}^{ESS}_{UL}}{\partial SoC_{l,t}} : \mu ^{soc}_{l,1} - \mu ^{soc}_{l,t} + \mu ^{soc}_{0} - \underline{\omega }_{l,t}^{soc} + \overline{\omega }_{l,t}^{soc} = 0&t = \mathcal {T} \end{aligned}$$

(A.6l)

$$\begin{aligned}&\frac{\partial \mathcal {L}^{ESS}_{UL}}{\partial SoC_{l,t}} : \mu ^{soc}_{l,t+1} - \mu ^{soc}_{l,t} - \underline{\omega }_{l,t}^{soc} + \overline{\omega }_{l,t}^{soc} = 0&\forall t \backslash \mathcal {T} \end{aligned}$$

(A.6m)

$$\begin{aligned}&\frac{\partial \mathcal {L}^{ESS}_{UL}}{\partial \lambda _{t}} : \Psi _{j,t}^{d} - \sum _{i \in \mathcal {I}}\Psi _{j,i,t}^{g} - \sum _{k \in \mathcal {K}}\Psi _{j,k,t}^{w} + \sum _{l \in \mathcal {L}}\Big (\Psi _{j,l,t}^{ch} -\Psi _{j,l,t}^{dch}\Big ) = 0 \end{aligned}$$

(A.6n)

$$\begin{aligned}&\frac{\partial \mathcal {L}^{ESS}_{UL}}{\partial \overline{\beta }_{l,t}^{dch}} : - \overline{\gamma }^{dch}_{j,l,t} \cdot \overline{DCH}_{l,t} + \underline{\gamma }^{dch}_{j,l,t} \cdot \overline{DCH}_{l,t} + \Psi _{j,l,t}^{dch} - \overline{\delta }_{j,l,t}^{dch} \end{aligned}$$

(A.6o)

$$\begin{aligned}&\frac{\partial \mathcal {L}^{ESS}_{UL}}{\partial \underline{\beta }_{l,t}^{dch}} : - \Psi _{j,l,t}^{dch} - \underline{\delta }_{j,l,t}^{dch} \end{aligned}$$

(A.6p)

$$\begin{aligned}&\frac{\partial \mathcal {L}^{ESS}_{UL}}{\partial \overline{\beta }_{l,t}^{ch}} : - \overline{\gamma }^{ch}_{j,l,t} \cdot \overline{CH}_{l,t} + \underline{\gamma }^{ch}_{j,l,t} \cdot \overline{CH}_{l,t} + \Psi _{j,l,t}^{ch} - \overline{\delta }_{j,l,t}^{ch} \end{aligned}$$

(A.6q)

$$\begin{aligned}&\frac{\partial \mathcal {L}^{ESS}_{UL}}{\partial \underline{\beta }_{l,t}^{ch}} : - \Psi _{j,l,t}^{ch} - \underline{\delta }_{j,l,t}^{ch} \end{aligned}$$

(A.6r)

$$\begin{aligned}&\frac{\partial \mathcal {L}^{ESS}_{UL}}{\partial \overline{\beta }_{i,t}^{g}} : \overline{G}_{i,t} + \sigma _{j}^{PD} \cdot \overline{G}_{i,t} + \Psi _{j,i,t}^{g} - \overline{\delta }_{j,i,t}^{g} \end{aligned}$$

(A.6s)

$$\begin{aligned}&\frac{\partial \mathcal {L}^{ESS}_{UL}}{\partial \underline{\beta }_{i,t}^{g}} : - \Psi _{j,i,t}^{g} - \underline{\delta }_{j,i,t}^{g} \end{aligned}$$

(A.6t)

$$\begin{aligned}&\frac{\partial \mathcal {L}^{ESS}_{UL}}{\partial \overline{\beta }_{k,t}^{w}} : \overline{W}_{k,t} + \sigma _{j}^{PD} \cdot \overline{W}_{k,t} + \Psi _{j,k,t}^{w} - \overline{\delta }_{j,k,t}^{w} \end{aligned}$$

(A.6u)

$$\begin{aligned}&\frac{\partial \mathcal {L}^{ESS}_{UL}}{\partial \underline{\beta }_{k,t}^{w}} : - \Psi _{j,k,t}^{w} - \underline{\delta }_{j,k,t}^{w} \end{aligned}$$

(A.6v)

$$\begin{aligned}&\frac{\partial \mathcal {L}^{ESS}_{UL}}{\partial \overline{\beta }_{t}^{d}} : \overline{D}_{t} + \sigma _{j}^{PD} \cdot \overline{D}_{t} + \Psi _{j,t}^{d} - \overline{\delta }_{j,t}^{d} \end{aligned}$$

(A.6w)

$$\begin{aligned}&\frac{\partial \mathcal {L}^{ESS}_{UL}}{\partial \underline{\beta }_{t}^{d}} : - \Psi _{j,t}^{d} - \underline{\delta }_{j,t}^{d} \end{aligned}$$

(A.6x)

Complementary slackness: Lower-level

Upper-level

$$\begin{aligned}&\overline{DCH} \cdot \underline{\omega }^{dch}_{l,t} \le \epsilon _{2} \end{aligned}$$

(A.8a)

$$\begin{aligned}&(P^{ESS,max}_{l} - \overline{DCH}) \cdot \overline{\omega }^{dch}_{l,t} \le \epsilon _{2} \end{aligned}$$

(A.8b)

$$\begin{aligned}&\overline{CH} \cdot \underline{\omega }^{ch}_{l,t} \le \epsilon _{2} \end{aligned}$$

(A.8c)

$$\begin{aligned}&(P^{ESS,max}_{l} - \overline{CH}) \cdot \overline{\omega }^{ch}_{l,t} \le \epsilon _{2} \end{aligned}$$

(A.8d)

$$\begin{aligned}&(c^{DCH} - p^{floor}_{l,t}) \cdot \underline{\kappa }^{dch}_{l,t} \le \epsilon _{2} \end{aligned}$$

(A.8e)

$$\begin{aligned}&(p^{cap}_{l,t} - c^{DCH}) \cdot \overline{\kappa }^{dch}_{l,t} \le \epsilon _{2} \end{aligned}$$

(A.8f)

$$\begin{aligned}&(c^{CH} - p^{floor}_{l,t}) \cdot \underline{\kappa }^{ch}_{l,t} \le \epsilon _{2} \end{aligned}$$

(A.8g)

$$\begin{aligned}&(p^{cap}_{l,t} - c^{CH}) \cdot \overline{\kappa }^{ch}_{l,t} \le \epsilon _{2} \end{aligned}$$

(A.8h)

$$\begin{aligned}&SoC_{l,t} \cdot \underline{\omega }^{soc}_{l,t} \le \epsilon _{2} \end{aligned}$$

(A.8i)

$$\begin{aligned}&(E^{ESS,max}_{l} - SoC_{l,t}) \cdot \overline{\omega }^{soc}_{l,t} \le \epsilon _{2} \end{aligned}$$

(A.8j)

Appendix B: Central planner objectives

The formulation of the three different CP objectives are listed below.

Competitive:

$$\begin{aligned}&max\sum _{t \in \mathcal {T}}(d_{t} \cdot p^{cap}) \ - \sum _{i \in \mathcal {L},t \in \mathcal {T}} \big ( g_{i,t} \cdot OPEX^{G}_{i} \big ) \end{aligned}$$

(B.1)

Collusive:

$$\begin{aligned}&max\sum _{t \in \mathcal {T}} \Bigg [ \lambda _{t} \cdot (dch_{t} - ch_{t} + g_{st,t} + w_{st,t}) \ - g_{st,t} \cdot OPEX^{G}_{st} \Bigg ] \end{aligned}$$

(B.2)

Favoring ESS:

$$\begin{aligned}&max\sum _{t \in \mathcal {T}} \lambda _{t} \cdot (dch_{t} - ch_{t}) \end{aligned}$$

(B.3)