Abstract
Ride comfort is a relevant performance for road vehicles. The suspension system can filter vibration caused by the uneven road to improve ride comfort. Optimization of the road vehicle suspension system has been extensively studied. As detailed models require significant computational effort, it becomes increasingly important to develop an efficient optimization framework. In this work, a multi-fidelity surrogate-based optimization framework based on the Approximate Normal Constraint method and Extended Kernel Regression surrogate modeling method is proposed and applied. An analytical model and a multi-body model of the suspension system are used as the low-fidelity and high-fidelity models, respectively. Compared with other well-known methods, the proposed method can provide good accuracy and high efficiency. In addition, the proposed method is applied to different types of vehicle suspension optimization problems and shows good robustness and efficiency.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The suspension system of road vehicles plays an important role in attenuating vibrations and shocks caused by road roughness. The suspension system is quite complex and difficult to be modeled accurately due to its high nonlinearity, such as damping nonlinearity, friction between components, geometric nonlinearity of the suspension, etc. Many analytical models have been introduced to describe the vibration response of the road vehicle, such as quarter-car models with 2 degrees of freedom (DOFs) (Ha 1985; Gobbi and Mastinu 2001; Alkhatib et al. 2004), 4-DOFs half-car models (Sun and Chen 2003; Yanfei and Xuan 2013), and 7-DOFs full vehicle models (Kim and Ro 2002; Sulaiman et al 2012), and even more DOFs models (Setiawan et al. 2009). These models can predict the vibration response at the center of mass by simplifying the full vehicle system to a rigid body system with springs and dampers. Among them, the 2-DOF model is widely used because of its simplicity and acceptable accuracy (Genta and Morello 2009).
With the development of computer aided engineering (CAE) technology, in order to accurately describe the behaviour of the suspension system, more detailed models (i.e., high-fidelity models) have been developed, such as finite element model (FEM), and multi-body models, which can consider the body as a flexible body and take into account more nonlinearities. However, in general, the simulation of a high-fidelity model requires a great deal of computational effort and time. To improve the computational efficiency, surrogate-based methods are adopted to generate ’black box’ models that can describe the behaviour of these computationally expensive models (Gobbi et al. 1999, 2014; Chen et al. 2015). Typical methods for generating surrogate models are artificial neural network (ANN) (Jain et al. 1996), support vector regression (SVR) (Drucker et al. 1996), kriging (Cressie 1990), and kernel regression (KR) (Wand and Jones 1994). Surrogate models can replace the original models to predict the response of the system with low computational effort. But, in order to obtain high prediction accuracy, a large amount of initial data is usually required to fit a surrogate model. Thus, for time-consuming high-fidelity models, this approach is still inefficient.
Multi-fidelity modeling methods take advantage from both low-fidelity and high-fidelity models. The core idea is to correct the low-fidelity data according to the high-fidelity data. Typically, low-fidelity data is used to capture general trends in system response, while high-fidelity data is used to provide accurate estimations and calculate the deviation of low-fidelity models (Peherstorfer et al. 2018). Some multi-fidelity methods have been proposed and applied in the engineering field. Among them, kriging methods based on gaussian process are the most used (Kennedy and O’Hagan 2000; Han et al. 2013; Han and Görtz 2012; Zhonghua et al. 2020; Zhao et al. 2021; Jesus et al. 2021). Co-Kriging (Kennedy and O’Hagan 2000) was proposed and applied to design an oil reservoir. Han et al. (2013) combined gradient-enhanced kriging (GEK) and generalized hybrid bridge function (GHBF) to significantly improve the efficiency and accuracy in aero-loads prediction. Zhao et al. (2021) employed adaptive multi-fidelity sparse polynomial chaos-kriging (AMF-PCK) to predict aerodynamic data, and conducted a comparison with some popular kriging-based methods to demonstrate efficiency and accuracy. In addition, artificial neural networks based methods have also been used for multi-fidelity modeling. Leary et al. (2003) applied knowledge-based artificial neural networks (KBNN) to beams optimization problems. Multi-fidelity deep neural network (MFDNN) was proposed to handle the complex high dimensional optimization problems (Meng and Karniadakis 2020) and adopted to optimize the aerodynamic shapes (Zhang et al. 2021). However, most of them require pre-definition of the weighting of low-fidelity models in different regions or only can take one low-fidelity model into account. In order to overcome this drawback, Lin et al. (2019) proposed the extended kernel regression (EKR) method which is able to consider multiple non-hierarchical low-fidelity models and choose proper low-fidelity models in different regions automatically.
The optimization algorithm also plays an important role in improving the efficiency. Evolutionary algorithms have been widely used in multi-objective optimization problems. For example, Deb et al. (2002) proposed the NSGA-II algorithm using fast non-dominated sorting and crowding distance strategy, which is very efficient and suitable for many optimization problems. The benefit of evolutionary algorithms is that the gradient computation is not required, but a large number of running parameters affect convergence and accuracy. In order to reduce the computational complexity, the multi-objective problem can be converted into a set of equivalent single-objective problems, by applying the \(\epsilon \)-constraint method (Mastinu et al. 2007), the normal constraint method (NC) (Messac et al. 2003), and the weighted sum method (Marler and Arora 2010). Zhang and Li (2007) proposed a multi-objective evolutionary approach based on decomposition (MOEA/D) to decompose a multi-objective problem into a set of single-objective problems, which combines a surrogate model to increase computational efficiency (Zhang et al. 2010). Normal constraint-based optimization methods, such as smart normal constraint (SNC) (Hancock and Mattson 2013; Munk et al. 2018), augmented normalized normal constraint (A-NNC) (Bagheri and Amjady 2019), and enhanced normalized normal constraint (ENNC) (Yazdaninejad et al. 2020), etc., have been widely used to obtain the Pareto frontier efficiently. Normal constraint based methods usually use a series of single-objective optimizations to obtain the anchor points and the Pareto points requiring a huge amount of simulations. In order to reduce the number of simulations, Gobbi et al. (2014) proposed a local approximation based on the normal constraint method, which is named approximate normal constraint (ANC), in which an artificial neural network was used to estimate the local response and updated iteratively to obtain the accurate Pareto frontier, and conducted a comparison with other popular optimization methods showing high efficiency and effectiveness.
In this paper, from the perspective of improving the optimization efficiency, a multi-fidelity based optimization method is proposed and applied on a road vehicle suspension optimization problem. The algorithm combines the approximate normal constraint method and the extended kernel regression method. In order to obtain a high fitting accuracy of the surrogate model, a complete factorial analysis is used to select the optimal parameters for the EKR method. The surrogate model is updated with the new data at each iteration until the convergence condition is met. The effectiveness and efficiency are verified by comparison with other methods selected from the literature. In addition, the generality of the used method power the way of the proposed combined approach to other problems or the same problem with more complicated low-fidelity or high-fidelity models.
This paper is organized as follows: Sect. 2 presents the description of the suspension optimization problem and the multi-fidelity models used. Section 3 introduces the proposed multi-fidelity based optimization method. The numerical results of the calibration of EKR parameters, a comparison with other algorithms, and generalization are shown and discussed in Sect. 4. Section 5 concludes the paper.
2 Problem description
In this section, the classical suspension system design problem is presented. A 2 DOFs linear analytical suspension system model and a 2 DOFs multi-body model including damping non-linearity and shock absorber friction are used as low and high fidelity models to describe the ride comfort performance of the road vehicle, respectively.
2.1 Ground vehicle suspension optimal design
The problem studied is a classical vehicle suspension system optimal design problem. When the car is driving on uneven road, the road unevenness causes vibration of the body through tires and suspension. Ride comfort is a metric of the vehicle’s effectiveness in shielding occupants from uneven road excitation (Genta and Morello 2009).
Let us to define the vertical displacements of the wheel and vehicle body as \(z_1\) and \(z_2\), respectively, and the contact force between the tires and the ground as \(F_z\). The ride comfort performance is expressed in terms of standard deviation of the body vertical acceleration \(\sigma _{\ddot{z}_{2}}\) (discomfort), tire-ground contact force \(\sigma _{F_z}\) (road holding), and the relative displacement between wheel and body \(\sigma _{(z_2-z_1)}\) (working space), which are conflicting performance indices related to the vehicle performance (Gobbi and Mastinu 2001). The suspension stiffness, named \(k_2\), and damping, named \(c_2\), which have a relevant impact on discomfort, road holding and working space, are used as design variables. Thus, the suspension optimal design problem is defined as follows
where \({\varvec{f}}\) is the vector of objective functions, \(k_2\) and \(c_2\) are the design variables. \(k_{2min}\), \(k_{2max}\), \(c_{2min}\), and \(c_{2max}\) are all positive numbers, which are the lower and upper bounds of suspension stiffness and damping, respectively.
2.2 Low-fidelity model
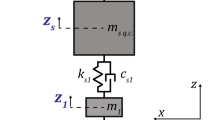
The low-fidelity model considered is the well-known quarter car linear model (shown in Fig. 1), which describes the vehicle as a 2 DOFs system. The masses \(m_2\) and \(m_1\) respectively represent the sprung mass, which is the vehicle body mass supported by the suspension, and the unsprung mass i.e. the part other than the sprung mass, which is approximately the sum of the mass of the wheel and the mass of the suspension. \(k_1\) is the radial stiffness of the tire. The stiffness \(k_2\) and damping \(c_2\) of the suspension system are considered linear. The wheel motion \({z}_{1}\) and the vehicle body motion \({z}_{2}\) with the road input r can be described as follows
The uneven road input can be described considering its power spectral density (Dodds and Robson 1973)
where \(A_{b}\) is the road irregularity parameter, v is the vehicle speed and \(\omega \) is the spatial frequency.
According to Gobbi and Mastinu (2001), when a vehicle runs on an uneven road, by converting the Eq. (2) to a Laplace transformation, discomfort (\(\sigma _{\ddot{z}_{2}}\)), road holding (\(\sigma _{F_z}\)), and working space (\(\sigma _{(z_2-z_1)}\)) can be derived as follows
2.3 High-fidelity model
High-fidelity models can accurately describe the real system working conditions. However, in general, the simulation of high-fidelity models is computationally expensive. In this study, the low-fidelity model describes the full vehicle system as a 2 DOFs linear system, whereas in reality, the damping characteristic of the damper is non-linear, and the relative sliding between the damper piston and the rod guide also generates coulomb friction forces (Yabuta et al. 1981; Lizarraga et al. 2008) not described by low-fidelity model. Thus, a multi-body model (shown in Fig. 2) that also considers the nonlinearity of damper and the friction in the shock absorber is used as a high-fidelity model to simulate the vehicle vibration response accurately while running an uneven road. The non-linear damping and friction are defined as follows
where \(F_{c_{2}}\) is the suspension damping force (N) and \(F_{\mu }\) is the friction (N). \(v_{c}\) is the damper velocity (m/s), \(c_2\) and \(A_{\mu }\) are damping coefficient (Ns/m) and friction coefficient, respectively, and are positive constants. The non-linear damping and friction characteristics are shown in Fig. 3.
The high-fidelity model is simulated on an uneven road that has the same parameters as the low-fidelity one for 40 s, while recording the vertical acceleration of the vehicle body, the contact force between the tire and the ground, and the relative displacement between wheel and body in time history. The standard deviations of the recorded data are computed to get the ride comfort performance indexes (i.e, discomfort, road holding, and working space).
3 Multi-fidelity surrogate-based optimization method
In this section, a local approximation multi-objective optimization algorithm combining multi-fidelity surrogate models is proposed for the road vehicle suspension design.
3.1 Main algorithm
Figure 4 shows the main structure of the proposed algorithm. In the first loop, the initial dataset which contains both low-fidelity and high-fidelity data is generated by design of experiments (DOE) and the surrogate model is created by the initial dataset based on EKR method introduced in Sect. 3.2. The Pareto set is then generated on the surrogate model using the ANC method described in Sect. 3.3. Within this phase, each Pareto solution is evaluated by the high-fidelity model, and a trust region is used to judge whether the results of the surrogate model and the high-fidelity model are consistent. The trust region is calculated using the following equation:
where the constant c describes the percentage of the trust region radius relative to the two-norm of the high-fidelity result \(f_{h}\). If the result of the surrogate model is within this trust region, this solution will be selected in the Pareto solutions sorting procedure. In subsequent loops, the surrogate model will be redesigned based on low-fidelity and high-fidelity responses of all optimal results generated by the ANC method in the current loop until the stopping condition is met, regardless of whether the trust region condition is satisfied.
3.2 Extended Kernel Regression (EKR) method
The extended kernel regression (EKR) is applied to generate surrogate models in this work. The EKR provides accurate predictions based on kernel regression (KR) by correcting the low-fidelity data according to the response of the high-fidelity model, and performing a local regression on the corrected data (Lin et al. 2019).
Two types of scaling function are considered to correct the response of low-fidelity models (Lin et al. 2019). The first one is the additive scaling function, which assumes that the difference between the high-fidelity model and the low-fidelity model is about the same at new design points. Thus, the output of low-fidelity can be corrected as follows
where \({\tilde{f}}_{i}^{l_{j}}\) is the corrected output of the jth low-fidelity model at the new design \({\varvec{x}}\) with the ith initial design point \({\varvec{x}}_{i}^{0}\). \(\left( f_{h}\left( {\varvec{x}}_{i}^{0}\right) -f_{l_{j}}\left( {\varvec{x}}_{i}^{0}\right) \right) \) is the difference between high-fidelity model and the jth low-fidelity model at the ith initial design points \({\varvec{x}}_{i}^{0}\). The multiplicative scaling function is another type of scaling function described as follows
where the corrected output is defined as the ratio of high-fidelity model output \(f_{h}\left( {\varvec{x}}_{i}^{0}\right) \) to low-fidelity model output \(f_{l}\left( {\varvec{x}}_{i}^{0}\right) \) at the ith initial design points \({\varvec{x}}_{i}^{0}\) multiplied by the low-fidelity model output \(f_{l_{j}}({\varvec{x}})\) at the new design \({\varvec{x}}\).
After correcting the low-fidelity data, a polynomial is fitted locally on the corrected j-th low-fidelity data \({\tilde{f}}_{i}^{l_{j}}({\varvec{x}})\) with distance-based weights through Kernel regression (Wand and Jones 1994). The system response can be estimated by using the j-th low-fidelity model as follows
where \({\varvec{x}}= \left[ x_1,\ldots ,x_d\right] ^{T}\) is the unobserved design point, d is the number of design variables, and
is an \(n \times (dp+1)\) matrix, n is the number of initial design points, p is the polynomial order, \({\varvec{e}}_{1}\) is a \((dp+1)\)-dimensional vector whose first element is 1 and the rest are 0, \(\tilde{{\varvec{F}}}_{l_{j}}=\left[ {\tilde{f}}_{1}^{l_{j}}({\varvec{x}}), \ldots , {\tilde{f}}_{n}^{l_{j}}({\varvec{x}})\right] ^{T}\) is the set of corrected low-fidelity data. \({\varvec{W}}_{{\varvec{x}}}={\text {diag}}\left\{ K_{1, \varvec{\varTheta }_{1}}\left( x_{1}^{0}-{\varvec{x}}\right) , \ldots , K_{1, \varvec{\varTheta }_{1}}\left( {\varvec{x}}_{n}^{0}-{\varvec{x}}\right) \right\} \) is an \(n\times n\) matrix, where \( K_{1, \varvec{\varTheta }_{1}}\left( x_{i}^{0}-{\varvec{x}}\right) \) is the Gaussian Kernel function, defined as follows
where \(\varvec{\varTheta }_{1}={\text {diag}}\left\{ \theta _{11}, \ldots , \theta _{1 d}\right\} \), and \(\theta _{1 k} \>0,\ k=1,\ldots ,d\) are parameters to be selected.
The final predictions are obtained by weighted averaging the estimates from different corrected low-fidelity surrogate models, as follows
where \(w_{l_{j}}\) is the weight representing the relative reliability of the j-th low-fidelity model, detailed in (Lin et al. 2019). A MATLAB toolbox developed by Lin et al. (2020) provides the EKR code and a manual.
3.3 Approximate Normal Constraint (ANC) method
The suspension optimal design problem is a classical multi-objective optimization problem, in which objectives are in conflict with each other. Let us consider a general multi-objective problem
where \({\varvec{f}}({\varvec{x}})\) is the vector of objective functions at design \({\varvec{x}}\), \(g({\varvec{x}})\) and \(h({\varvec{x}})\) are the inequality constraint and the equation constraint of the optimization problem, respectively.
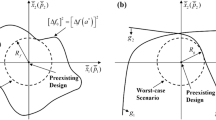
The ANC method is based on the normal constraint (NC) method (Messac et al. 2003) to approximate Pareto solutions by using surrogate models. In the NC method, also shown in Fig. 5, the anchor points, which are the minima of each objective function, are first obtained. Then, the utopia hyperplane containing all anchor points is constructed. The normal planes of a point P on the utopia hyperplane are used as constraints to divide the objective domain into feasible and infeasible regions, converting the multi-objective problem into a single-objective problem with non-linear constraints. By moving the position of point P, we can get the complete Pareto frontier. The optimization problem can be converted as follows
where \(f_{i}({\varvec{x}})\) is the response of the i-th objective function at design \({\varvec{x}}\); \({\varvec{v}}_{i j}\) is the vector connecting the i-th and the j-th anchor points; \({\varvec{F}}_{i}\) and \({\varvec{F}}_{j}\) are the minima of the ith and jth objective functions respectively.
In the ANC method, the surrogate model of objective functions (in this work, discomfort, road holding, and working space) is first obtained by fitting the initial data, and then using the utopia plane of the surrogate model instead of the one introduced in the NC method (Gobbi et al. 2014). The reason for this choice is that ANC has shown high efficiency on road vehicle suspension optimization problems with respect to widely used algorithms, and has a promising potential to further improve efficiency by including the multi-fidelity surrogate method (Gobbi et al. 2014). Algorithm 1 briefly shows how the ANC algorithm works in this optimization framework.

3.4 Stopping condition
The stopping condition is very important for a stochastic search problem. The stopping condition is usually defined by the distance between the true Pareto frontier and the approximated one (Rudolph and Agapie 2000). However, the true Pareto frontier is unknown in advance, and searching for the true Pareto frontier on a high-fidelity model is too computationally expensive. For multi-fidelity surrogate-based problem, the consistency between the corrected surrogate model and the high-fidelity model can ensure that the algorithm converges to the optimal solution (Peherstorfer et al. 2018; Jones 2001). In this work, the root mean squared error (RMSE) is adopted to describe the consistency between the high-fidelity model and the surrogate model. The RMSE is defined as follows
where N is the number of Pareto solutions. \( {\varvec{F}}_{s}\) is the Pareto frontier obtained from the surrogate model, \( {\varvec{F}}_{h}\) is the corresponding solution with the high-fidelity model. The fitting error of the surrogate model should be very tiny relative to the high-fidelity model, and the utopia solution is the minima of the surrogate model. The error condition can therefore be defined as the ratio of the fitting error to the two-norm of the utopia solution. It is also necessary to obtain a sufficient number of Pareto solutions. Thus, the stopping condition is defined as follows
where \( {\varvec{F}}_{utopia}\) is the utopia solution. Under condition (16), the algorithm is terminated and returns the last Pareto frontier. Otherwise, the surrogate model is updated with the new data.
4 Results and discussion
The proposed optimization algorithm is applied to a suspension optimal design problem for a small car. The parameters used in low-fidelity and high-fidelity models, as well as the optimization algorithm, are shown in Table 1. In this section, a factorial design based on sensitivity analysis is conducted to select the parameters of EKR method, see Sect. 4.1. In Sect. 4.2, the efficiency and effectiveness of the proposed algorithm for the road vehicle suspension optimization problem are demonstrated by comparing with state of art algorithms. Furthermore, the generality of the algorithm is demonstrated by applying it to other types of vehicle suspension optimization problems.
4.1 Calibration of EKR parameters
In order to obtain surrogate models with high accuracy, a full factorial design is performed to obtain the parameters of the surrogate model for each objective function. As described in Sect. 3.2, the selection of scaling functions, the regression polynomial order, and the initial DOE size are very important choices that influence the fitting accuracy of the EKR method. A sensitivity analysis is conducted in order to obtain an accurate surrogate model for each objective function. For the scaling function, 2 levels are considered: additive and multiplicative. The initial DOE size has 3 levels: 9, 16 and 25, and the polynomial order has 3 levels: 0, 1 and 2. Experiments are run 50 times with full parameter settings, and the initial DOE points are resampled using the Latin hypercube sampling method. A set of 400 checkpoints, which are the same for all experiments, are sampled uniformly in the feasible domain. Accuracy can be predicted in terms of mean absolute percentage error (MAPE), which is the average percentage of the error at unobserved points relative to the high-fidelity data.
where \(N_c\) is the number of the checkpoints, \(f\left( {\varvec{x}}_{j}\right) \) and \({\hat{f}}\left( {\varvec{x}}_{j}\right) \) are the high-fidelity output and the predicted result at the jth checkpoint \({\varvec{x}}_{j}\), respectively.
Figure 7 shows the mean MAPE of the 3 objective functions with different DOE sizes and different types of scaling functions. The DOE size has a relevant impact on the estimation accuracy. As expected, the fitted model has a higher degree of accuracy when the DOE size is larger. Furthermore, different types of scaling functions also affect the objective functions differently. In terms of discomfort, both additive and multiplicative scaling functions perform similarly. For the road holding, the multiplicative performs better. The surrogate model with additive scaling function performs better for working space. As a result, we use the additive scaling function for discomfort as well as for working space, and the multiplicative scaling function for road holding. 25 is selected as the DOE size for all the objective functions.
In addition, Fig. 8 illustrates the effect of the polynomial order on the prediction accuracy of the surrogate models with the optimal DOE size that is 25 and scaling functions mentioned previously. The result shows that all objective functions have a higher accuracy when the polynomial order is higher. Therefore, 2 is used as the polynomial order. Table 2 summarizes the parameters of EKR approach used in the remainder of the paper.
4.2 Effectiveness and efficiency analysis
A numerical comparison is carried out to demonstrate the effectiveness and efficiency of the proposed method. In order to demonstrate the benefit of the multi-fidelity surrogate-based method, a single-fidelity method named kernel regression method (Wand and Jones 1994), which only considers the high-fidelity model, is used to solve the suspension problem with ANC method.
Besides, a decomposition optimization algorithm with EKR method, proposed by Lin et al. (2021), is adopted to optimize the suspension. The decomposition with EKR method is used to solve the multi-objective optimization problem by applying a scalarization procedure i.e. we optimize the discomfort and constraint the road holding and the working space. Expected improvement (EI) criterion (Jones et al. 1998) of discomfort is applied as objective function. The EI is defined as
where \(f_{\min }\) is the best observation currently; \({\hat{f}}({\varvec{x}})\) is the predicted value at a new design \({\varvec{x}}\); \(s({\varvec{x}})\) is the standard deviation of the prediction at \({\varvec{x}}\); \(\varPhi (x)\) is the Gaussian cumulative distribution function and \(\phi (x)\) is the probability density function. The algorithm is stopped when \(\textrm{EI}\) is less than a positive number (Jones 2001), which is 0.5 in this study. Otherwise, the surrogate model is updated with the new solution at this iteration. 121 uniform sampling points in the feasible region of the Road holding and Working space have been used as constraints for the optimization problem. The optimization can be defined as follows
where \({\hat{f}}_{RH}({\varvec{x}})\) and \({\hat{f}}_{WS}({\varvec{x}})\) are the prediction of road holding and working space, respectively. \({y}^{i}_{RH}\) and \({y}^{i}_{WS}\) are the values of road holding and working space at the i-th sampling point in the feasible region of the road holding and working space respectively.
Another method that is commonly used for multi-fidelity optimization problems is to perform the optimization firstly on the low-fidelity model and then substitute the result to the high fidelity model (Peherstorfer et al. 2018). The Pareto frontier of the low-fidelity model has been obtained by using NSGA-II optimization algorithm.
Notation XXX-YYY is used: XXX represents the optimization algorithm used, (ANC represents the approximation normal constraint method, DEC represents the decomposition optimization method, LOW represents the approach based on the direct optimization of the low-fidelity model), YYY indicates the surrogate method used (EKR is the extended kernel regression method, KR is the kernel regression method, and NON means no surrogate method is used). Table 3 shows the algorithms used for this comparison. Except for LOW-NON optimization method, for all other algorithms, a DOE size of 25 has been considered, and 50 experiments have been completed.
For the ANC-EKR and the ANC-KR, the Pareto solutions are obtained by random sampling on the utopia hyperplane, so the solutions obtained in each experiment are at different positions on the Pareto front. Figure 9 shows the Pareto fronts obtained by the ANC-EKR and other methods in one of the 50 experiments. As we can see, the Pareto frontier obtained by the ANC-EKR is identical with the ANC-KR and the DEC-EKR. This is not the case for the LOW-NON method that is dominated by other methods. Moreover, as shown in Fig. 9c, the response of the high-fidelity model for the Pareto solutions obtained by using the low-fidelity model is significantly different from the actual Pareto solutions obtained directly from high-fidelity model. The introduction of nonlinearity increases the difference between the two models and decreases their correlation. Thus, the method of substituting the optimal solution of the low-fidelity model into the high-fidelity model is not applicable to this problem.
In addition, efficiency is an important criterion to measure the quality of an algorithm on the basis of its effectiveness. The computational effort can be defined as the sum of the number of model evaluations multiplied by weights, which can be set according to the duration of each model evaluation, as defined
where W represents the weight, N represents the number of simulations. Subscripts h, l, and s represent high-fidelity, low-fidelity, and surrogate models respectively.
For high-fidelity, low-fidelity, and surrogate models, 25 simulations of each model are executed, and the average evaluation time is calculated, and weights are defined as the ratio of the average time of each model to the low-fidelity model (shown in Table 4).
The efficiency can be described as the ratio of computational effort to Pareto set size (Gobbi et al. 2014). However, the average evaluation time of the high-fidelity model is far greater than others, so the efficiency can be roughly defined as the ratio of the number of the required high-fidelity simulations \({N_{h}}\) and the Pareto set size, as shown
The Pareto size obtained, the evaluations times of the analytical and surrogate model, the number of simulations of the multi-body model (high-fidelity model), and efficiency are recorded, as shown in Table 5. In terms of the comparison of the optimization algorithm, the result shows that DEC-EKR method requires more simulations than both ANC-EKR and ANC-KR. Therefore, it can be concluded that the ANC algorithm is more efficient than the DEC algorithm for the suspension optimization problem. Using surrogate models, the EKR algorithm requires less simulation times of the high-fidelity model than the KR algorithm, by comparing ANC-EKR with ANC-KR.
Figure 10a, b show the box plots of the efficiency and the fitting error between surrogate model and high-fidelity model. Similarly, the ANC-EKR is the most efficient algorithm for this problem. Besides, it is noteworthy that the EKR method can provide much more accurate prediction at the Pareto frontier than the KR method.
In summary, by comparing different optimization algorithms and surrogate algorithms, the proposed algorithm ANC-EKR shows good effectiveness and efficiency for the suspension optimization problem.
4.3 Application to other vehicles
The effectiveness and efficiency of the proposed method for a small car suspension optimization problem has been presented in the previous section. In order to determine the generality of the proposed method, the same test is performed on three other different types of vehicles (bus, truck, and off-road vehicle). The parameters for these systems are taken from the literature (Abdelkareem et al. 2018). Typically, the ride frequency (i.e. undamped natural frequency of the suspension) is between 1 and 2 Hz, and the relative damping ratio is between 0.2 and 1. The definition of the ride frequency and the damping ratio are shown as follows
where \(n_r\) and \(\psi \) are ride frequency and damping ratio respectively, \(k_2\) is the spring stiffness (N/m), \(c_2\) is the damping coefficient (Ns/m), and \(m_2\) is the sprung mass (kg). Based on the above, the design variable boundaries for the suspension are set. The used parameters are reported in Table 6.
Similarly, for each type of vehicle, the optimization experiment is performed 50 times, the Pareto set size obtained, the number of executions of high-fidelity, low-fidelity, and surrogate models, and efficiency are recorded, shown in Table 7. Figure 11 shows the efficiency distribution of the ANC-EKR algorithm applied to different vehicles.
The result shows that the bus experiment is less efficient. As can be seen from the Table 6, compared with other vehicles, the bus has a significantly greater sprung mass relative to the unsprung mass. The introduction of non-linearity may cause a significant difference in response between the low and high-fidelity models, or perhaps the parameters of the EKR method currently employed are not the optimal choice for the bus model, thus requiring more data (i.e., more simulations) to satisfy the termination conditions related to the fitting error. Moreover, the number of samples in the utopia hyperplane also affects efficiency. A fixed number of samples is taken into account in this optimization framework. During the iterative process, when the error condition is satisfied and only a few Pareto solutions are missing, an excessively large number of samples in the upcoming iteration will inevitably degrade the efficiency of the algorithm. However, a too small number of samples will conversely result in an increase in the number of iterations (i.e., an increase in the generation of surrogate models as well as in the number of optimizations with surrogate models).
In any case, for all four different types of vehicles, the mean efficiency values are less than 2, which means that on average less than two high-fidelity simulations are required to obtain a Pareto point. Therefore, it can be concluded that the ANC-EKR method shows good robustness and efficiency in the road vehicle suspension optimization problem.
5 Conclusion
In the presented study, an efficient multi-fidelity surrogate-based optimization method based on the approximate normal constraint method (ANC) and extended kernel regression (EKR) is proposed and tested on a road vehicle suspension optimization problem. A linear quarter car model and a multi-body model which considers the nonlinear dampering and the shock absorber friction are used to create surrogate models for discomfort, road holding, and working space. A full factorial design based on sensitivity analysis is used to select the suitable parameter for the EKR method. A comparison is conducted to verify the accuracy and efficiency of the ANC-EKR method. The result shows that less simulations of high-fidelity model are required by the ANC-EKR method with respect to other algorithms in the road vehicle suspension optimization problem. Furthermore, the proposed method also shows good robustness and efficiency in the optimization of suspension problems for other types of vehicles. Although in this work, the high-fidelity model is not the most detailed and there are some other nonlinear components that affect the suspension system behaviour, this method presents the possibility to improve efficiency while guaranteeing an adequate level of accuracy.
Future work will devote to considering more complexity in the high-fidelity models. In this work, only shock absorber friction and nonlinear damper behaviour are considered in the high-fidelity model. In order to have a better description of the vibrations received by the human body, the high-fidelity model could be enhanced by including more degrees of freedom for the full vehicle model that could provide not only the vertical vibration but the vibration on other axes as well, more complex tire models, bushings, flexible bodies, and other excitations other than the road (e.g. powertrain), etc. In addition, a strategy of varying the number of samples in the utopia hyperplane based on the results of the current iteration can be introduced to further enhance the efficiency of this optimization framework.
References
Abdelkareem MA, Xu L, Guo X, Ali MKA, Elagouz A, Hassan MA, Essa F, Zou J (2018) Energy harvesting sensitivity analysis and assessment of the potential power and full car dynamics for different road modes. Mech Syst Signal Process 110:307–332. https://doi.org/10.1016/j.ymssp.2018.03.009
Alkhatib R, Jazar GN, Golnaraghi MF (2004) Optimal design of passive linear suspension using genetic algorithm. J Sound Vib 275(3–5):665–691. https://doi.org/10.1016/j.jsv.2003.07.007
Bagheri B, Amjady N (2019) Stochastic multiobjective generation maintenance scheduling using augmented normalized normal constraint method and stochastic decision maker. Int Trans Electr Energy Syst 29(2):e2722, e2722 etep.2722. https://doi.org/10.1002/etep.2722
Chen S, Shi T, Wang D, Chen J (2015) Multi-objective optimization of the vehicle ride comfort based on Kriging approximate model and NSGA-II. J Mech Sci Technol 29(3):1007–1018. https://doi.org/10.1007/s12206-015-0215-x
Cressie N (1990) The origins of kriging. Math Geol 22(3):239–252. https://doi.org/10.1007/BF00889887
Deb K, Pratap A, Agarwal S, Meyarivan T (2002) A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans Evol Comput 6(2):182–197. https://doi.org/10.1109/4235.996017
Dodds C, Robson J (1973) The description of road surface roughness. J Sound Vib 31(2):175–183. https://doi.org/10.1016/S0022-460X(73)80373-6
Drucker H, Burges CJ, Kaufman L, Smola A, Vapnik V (1996) Support vector regression machines. Adv Neural Inf Process Syst 9
Genta G, Morello L (2009) The automotive chassis: vol 2: system design. Springer, New York
Gobbi M, Mastinu G (2001) Analytical description and optimization of the dynamic behaviour of passively suspended road vehicles. J Sound Vib 245(3):457–481. https://doi.org/10.1006/jsvi.2001.3591
Gobbi M, Mastinu G, Doniselli C (1999) Optimising a car chassis. Veh Syst Dyn 32(2–3):149–170. https://doi.org/10.1076/vesd.32.2.149.2085
Gobbi M, Guarneri P, Scala L, Scotti L (2014) A local approximation based multi-objective optimization algorithm with applications. Optim Eng 15(3):619–641. https://doi.org/10.1007/s11081-012-9211-5
Ha A (1985) Suspension optimization of a 2-DOF vehicle model using a stochastic optimal control technique. J Sound Vib 100(3):343–357. https://doi.org/10.1016/0022-460X(85)90291-3
Han ZH, Görtz S (2012) Hierarchical kriging model for variable-fidelity surrogate modeling. AIAA J 50(9):1885–1896. https://doi.org/10.2514/1.J051354
Han ZH, Görtz S, Zimmermann R (2013) Improving variable-fidelity surrogate modeling via gradient-enhanced kriging and a generalized hybrid bridge function. Aerosp Sci Technol 25(1):177–189. https://doi.org/10.1016/j.ast.2012.01.006
Hancock BJ, Mattson CA (2013) The smart normal constraint method for directly generating a smart Pareto set. Struct Multidiscip Optim 48(4):763–775. https://doi.org/10.1007/s00158-013-0925-6
Jain AK, Mao J, Mohiuddin KM (1996) Artificial neural networks: a tutorial. Computer 29(3):31–44. https://doi.org/10.1109/2.485891
Jesus T, Sohst M, do Vale JL, Suleman A (2021) Surrogate based MDO of a canard configuration aircraft. Struct Multidiscip Optim 64(6):3747–3771. https://doi.org/10.1007/s00158-021-03051-6
Jones DR (2001) A taxonomy of global optimization methods based on response surfaces. J Glob Optim 21(4):345–383. https://doi.org/10.1023/A:1012771025575
Jones DR, Schonlau M, Welch WJ (1998) Efficient global optimization of expensive black-box functions. J Glob Optim 13(4):455–492. https://doi.org/10.1023/A:1008306431147
Kennedy MC, O’Hagan A (2000) Predicting the output from a complex computer code when fast approximations are available. Biometrika 87(1):1–13. https://doi.org/10.1093/biomet/87.1.1
Kim C, Ro PI (2002) An accurate full car ride model using model reducing techniques. J Mech Des 124(4):697–705. https://doi.org/10.1115/1.1503065
Leary SJ, Bhaskar A, Keane AJ (2003) A knowledge-based approach to response surface modelling in multifidelity optimization. J Glob Optim 26(3):297–319. https://doi.org/10.1023/A:1023283917997
Lin Z, Matta A, Shanthikumar JG (2019) Combining simulation experiments and analytical models with area-based accuracy for performance evaluation of manufacturing systems. IISE Trans 51(3):266–283. https://doi.org/10.1080/24725854.2018.1490046
Lin Z, Frigerio N, Matta A, Du S (2021) Multi-fidelity surrogate-based optimization for decomposed buffer allocation problems. OR Spectr 43(1):223–253. https://doi.org/10.1007/s00291-020-00603-y
Lin Z, Matta A, Shanthikumar J (2020) A MATLAB extended kernel regression toolbox
Lizarraga J, Sala JA, Biera J (2008) Modelling of friction phenomena in sliding conditions in suspension shock absorbers. Veh Syst Dyn 46(S1):751–764. https://doi.org/10.1080/00423110802037024
Marler RT, Arora JS (2010) The weighted sum method for multi-objective optimization: New insights. Struct Multidiscip Optim 41(6):853–862. https://doi.org/10.1007/s00158-009-0460-7
Mastinu G, Gobbi M, Miano C (2007) Optimal design of complex mechanical systems: with applications to vehicle engineering. Springer, New York
Meng X, Karniadakis GE (2020) A composite neural network that learns from multi-fidelity data: application to function approximation and inverse PDE problems. J Comput Phys 401:109020. https://doi.org/10.1016/j.jcp.2019.109020
Messac A, Ismail-Yahaya A, Mattson CA (2003) The normalized normal constraint method for generating the Pareto frontier. Struct Multidiscip Optim 25(2):86–98. https://doi.org/10.1007/s00158-002-0276-1
Munk DJ, Kipouros T, Vio GA, Parks GT, Steven GP (2018) Multiobjective and multi-physics topology optimization using an updated smart normal constraint bi-directional evolutionary structural optimization method. Struct Multidiscip Optim 57(2):665–688. https://doi.org/10.1007/s00158-017-1781-6
Peherstorfer B, Willcox K, Gunzburger M (2018) Survey of multifidelity methods in uncertainty propagation, inference, and optimization. Siam Rev 60(3):550–591. https://doi.org/10.1137/16M1082469
Rudolph G, Agapie A (2000) Convergence properties of some multi-objective evolutionary algorithms. In: Proceedings of the 2000 Congress on Evolutionary Computation CEC00 Cat No 00TH8512, IEEE, vol 2, pp 1010–1016. https://doi.org/10.1109/CEC.2000.870756
Setiawan JD, Safarudin M, Singh A (2009) Modeling, simulation and validation of 14 DOF full vehicle model. Int Conf Instrum Commun Inf Technol Biomed Eng 2009:1–6. https://doi.org/10.1109/ICICI-BME.2009.5417285
Sulaiman S, Samin PM, Jamaluddin H, Rahman R, Burhaumudin MS (2012) Modeling and validation of 7-DOF ride model for heavy vehicle. In: Proceedings of the ICAMME
Sun PY, Chen H (2003) Multiobjective output-feedback suspension control on a half-car model. In: Proc. 2003 IEEE Conference Control Application 2003 CCA 2003, IEEE, vol 1, pp 290–295. https://doi.org/10.1109/CCA.2003.1223330
Wand MP, Jones MC (1994) Kernel smoothing. CRC Press, Boca Raton
Yabuta K, Hidaka K, Fukushima N (1981) Effects of suspension friction on vehicle riding comfort. Veh Syst Dyn 10(2–3):85–91. https://doi.org/10.1080/00423118108968641
Yanfei Jin, Xuan Luo (2013) Stochastic optimal active control of a half-car nonlinear suspension under random road excitation. Nonlinear Dyn 72(1–2):185–195. https://doi.org/10.1007/s11071-012-0702-x
Yazdaninejad M, Amjady N, Dehghan S (2020) VPP self-scheduling strategy using multi-horizon IGDT, enhanced normalized normal constraint, and bi-directional decision-making approach. IEEE Trans Smart Grid 11(4):3632–3645. https://doi.org/10.1109/TSG.2019.2962968
Zhang Q, Li H (2007) MOEA/D: a multiobjective evolutionary algorithm based on decomposition. IEEE Trans Evol Comput 11(6):712–731. https://doi.org/10.1109/TEVC.2007.892759
Zhang Q, Liu W, Tsang E, Virginas B (2010) Expensive multiobjective optimization by MOEA/D with gaussian process model. IEEE Trans Evol Comput 14(3):456–474. https://doi.org/10.1109/TEVC.2009.2033671
Zhang X, Xie F, Ji T, Zhu Z, Zheng Y (2021) Multi-fidelity deep neural network surrogate model for aerodynamic shape optimization. Comput Methods Appl Mech Eng 373:113485. https://doi.org/10.1016/j.cma.2020.113485
Zhao H, Gao Z, Xu F, Xia L (2021) Adaptive multi-fidelity sparse polynomial chaos-Kriging metamodeling for global approximation of aerodynamic data. Struct Multidiscip Optim 64(2):829–858. https://doi.org/10.1007/s00158-021-02895-2
Zhonghua H, Chenzhou X, Zhang L, Zhang Y, Zhang K, Wenping S (2020) Efficient aerodynamic shape optimization using variable-fidelity surrogate models and multilevel computational grids. Chin J Aeronaut 33(1):31–47. https://doi.org/10.1016/j.cja.2019.05.001
Funding
Open access funding provided by Politecnico di Milano within the CRUI-CARE Agreement.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Xue, H., Gobbi, M. & Matta, A. Multi-fidelity surrogate-based optimal design of road vehicle suspension systems. Optim Eng 24, 2773–2794 (2023). https://doi.org/10.1007/s11081-023-09793-0
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11081-023-09793-0