Abstract
In many real-world mixed-integer optimization problems from engineering, the side constraints can be subdivided into two categories: constraints which describe a certain logic to model a feasible allocation of resources (such as a maximal number of available assets, working time requirements, maintenance requirements, contractual obligations, etc.), and constraints which model physical processes and the related quantities (such as current, pressure, temperature, etc.). While the first type of constraints can often easily be stated in terms of a mixed-integer program (MIP), the second part may involve the incorporation of complex non-linearities, partial differential equations or even a black-box simulation of the involved physical process. In this work, we propose the integration of a trained tree-based classifier—a decision-tree or a random forest, into a mixed-integer optimization model as a possible remedy. We assume that the classifier has been trained on data points produced by a detailed simulation of a given complex process to represent the functional relationship between the involved physical quantities. We then derive MIP-representable reformulations of the trained classifier such that the resulting model can be solved using state-of-the-art solvers. At the hand of several use cases in terms of possible optimization goals, we show the broad applicability of our framework that is easily extendable to other tasks beyond engineering. In a detailed real-world computational study for the design of stable direct-current power networks, we demonstrate that our approach yields high-quality solutions in reasonable computation times.
Similar content being viewed by others
Explore related subjects
Find the latest articles, discoveries, and news in related topics.Avoid common mistakes on your manuscript.
1 Introduction
In recent years, mathematical optimization methods have been employed very successfully for the solution of many applied problems. One reason for this success is the enormous progress in algorithms for the global solution of mixed-integer non-linear programs (MIPs). Nowadays, more and more optimization problems of the form \( \min \{c^Tx \mid Ax \le b,\, x \in \mathbbm {Z}^{p - q} \times \mathbbm {R}^q\} \), with vectors c and b and a matrix A of appropriate dimensions, can routinely be solved with modern available software, even for large problem instances, see (Bixby and Rothberg 2007; Achterberg and Wunderling 2013). However, it is often difficult to develop accurate, efficiently tractable mixed-integer programming models for more general problem classes that, for example, incorporate physical processes. These processes often involve non-convex and non-linear relationships between the variables. For instance, this applies to the behaviour of electrical grids that are governed by partial differential equations (PDE). While the solution of PDEs is already complex in itself, the corresponding optimization problems are even more challenging. In addition, it might be that the exact laws or procedural rules underlying an optimization task are unknown or may only be given implicitly. On the other hand, typically, historical or simulated datasets are available from which approximations of these relationships can be derived. Such data can be analysed and prepared to train a machine learning classifier whose results may then be integrated into an optimization procedure. Training refers to the process by which a machine learning classifier autonomously recognises relationships between the given data in the dataset and extracts the rules needed to identify them. These rules are then used to categorise new, unseen input data. There are many types of classifiers and regression methodologies. An overview of many popular machine learning methods is provided e.g. by Bhavsar and Ganatra (2012), Hastie et al. (2009), Bishop (2006). Once a trained classifier is available, the task is to integrate its decision rules into the considered optimization model.
In this paper, we deal with tree-based classifiers, in particular random forests, which are ensemble classifiers consisting of multiple decision trees. Each of these decision trees classifies data points according to several hierarchically consecutive linear inequalities, which makes them very well suited for use in a mixed-integer linear optimization context. We exploit this to replace the implicitly given constraints in the optimization model by the decisions of trained decision trees.
Tree-based classifiers can make very accurate predictions in the scope of the training data, but are normally not suitable for extrapolation. Their prediction performances decrease with the distance from the training data, see (Shahriari et al. 2016). In order to be independent of the training data in the optimization model and at the same time to keep the prediction accuracy constantly high in the entire parameter range considered, we use data points with maximum distance to each other to train the classification model.
At the hand of a real-world case study, we evaluate the possibilities such a modelling approach offers, namely the design of stable direct-current (DC) electricity network, DC grids in brief, which comprise connected DC sources, consumers and storage systems. DC grids with system voltages below 1500 V, so-called low-voltage DC grids (LVDC grids or networks) are becoming increasingly important in the context of renewable energies, see (International Electrotechnical Commission 2016) for an introduction. For its safe and reliable operation, the stability of an LVDC grid must be maintained under all planned load scenarios. Network stability, in turn, is determined by the grid layout, device parameters and control methods. With increasing grid complexity, novel methods are necessary to enable continuous grid monitoring and automated adjustment in the case of grid instability. To assess the stability of a network for various configurations and setup parameters, we conduct the envisaged stability assessment by a small-signal analysis of the DC grid bus voltage and analyze the complex impedance of the source and load systems. The stability analysis can be realized in a simulation approach applying an electrical circuit model of a DC-network (cf. Kumar et al. 2020) or by a novel measurement system to investigate a physical DC-network. The applied stability criterion evaluates the retrieved impedance spectra, which can have complicated structures, and aims to simultaneously realize a sufficient attenuation of the impedance amplitude and a sufficient impedance phase distance to avoid an out-of-phase oscillation. Due to this two-step stability evaluation and its logically linked evaluation, a prediction is made by formulation as a classification problem to obtain the state of stability (stable or unstable) as the label for classification and there can be no continuous prediction in the formulation as a regression problem.
Incorporating multiple instead of only one decision tree is known to typically achieve a significant improvement of the prediction accuracy.
Thus, in many practical applications ensemble classifiers consisting of several smaller classifiers are used, for example the random-forest approach, see (Breiman 2001a). Multiple decision trees are trained using equally-sized subsets of the training data, and a joint classification is determined. Random forests have already been used in many contexts, e.g. statistics, medicine and fault detection, but according to our knowledge not yet for studying the stability of electricity networks. The combination of trained classifiers with optimization models has been used in similar applications. However, to the best of our knowledge, we are the first to use the structure of trained random forest classifiers in a MIP model to make (most) reliable inferences about input parameters, for the real use case of finding particularly stable regions in the electricity network.
1.1 Literature review
The combination of machine learning classifiers with optimization models is a very active research topic. The corresponding literature referred to in the following is divided into two categories: research articles where a classifier is trained in a globally optimal fashion using mixed-integer programming methods and works that exploit the decisions of already trained classifiers within optimization models.
The first topic is treated e.g. in Bonfietti et al. (2015) and Bertsimas and Dunn (2017) for random-forest classifiers and in Thorbjarnarson and Yorke-Smith (2020) for neural networks. In Kumar et al. (2019), optimization models are used to analyse trained deep neural networks with ReLU and Max Pooling Layers concerning their decision-making and to identify and visualise input data that are particularly well recognised.
In the second category, to which the present article also belongs, trained machine learning classifiers are used as input within optimization models of different kinds. A recent overview of methods to identify the feasible regions in optimization problems via trained machine learning classifiers can be found in Maragno et al. (2021), who present it as a more general framework for data-driven optimization. The works (Mistry et al. 2021; Thebelt et al. 2021, 2020; Ceccon et al. 2022; Thebelt et al. 2022) deal with the integration of trained gradient-boosted regression trees into optimization models stemming from different applications. There the distribution of the training data, that influences the prediction accuracy is integrated as a penalty term into the objective function to minimise risk. It is also described how it can be used to explore the search space. In contrast, in our work the training set is chosen such that it samples the whole relevant parameter space. As a consequence, such additional risk measures can be avoided. (Bertsimas et al. 2016) show how regression models, more precisely random forests and support vector machines predicting clinical trial outcomes, can be incorporated into MIP models in order to determine best possible chemotherapy treatments. In Ferreira et al. (2015), the development and implementation of a pricing decision support tool used to maximise sales of novel products are described, where the price-demand ratio was predicted using random forests. (Biggs et al. 2017) maximises over the predicted value of trained random forests to find the best possible input parameters. As possible applications, they consider maximising the profitability of estate investments and determining the most appropriate jury assignment in case studies. A similar approach was taken by Mišić (2020) for applications from the fields of drug development and customised pricing. Furthermore, the latter two works consider heuristic methods and Benders decomposition to handle random-forest classifiers with many decision trees, which are used to obtain a better prediction quality. Unlike the literature cited above, we deal with random forests for classification, where we are particularly interested in the practical implementation of models incorporating many decision trees. The work by Halilbašić et al. (2018) is motivated along similar lines. They use decision trees for classification in order to extract decision rules from data. These decision rules are incorporated into an optimization model to study redispatch measures performed by network transmission system operators in order to ensure network stability.
Our article discusses a closely related approach for larger and multiple decision trees. In addition, we investigate the possibilities our approach offers with respect to examining the areas predicted to be feasible by the classifier. This work is part of an approach to create tools and methods for designing and operating LVDC networks with the support of data analysis methods. In the design phase, different network configurations are calculated and the optimal configuration of network parameters to achieve grid stability are determined. During operation, LVDC networks are monitored continuously using a novel impedance measurement method and stabilised by optimizing feed-in characteristics or software parameters in the converter systems. For details, see (Roeder et al. 2021).
1.2 Contribution
Our main contributions are as follows. We summarise how complex or unknown constraints, implicitly given via a random forest, can be incorporated into a mathematical optimization problem. Using three exemplary use cases corresponding to different optimization goals, we demonstrate the versatility of a random-forest classifier for defining (part of) the feasible set of an MIP. In particular, we show how the closest feasible point and the largest feasible region represented by the classifier can be determined. In an extensive case study, we use MIP models to determine the best possible adjustment of network control or circuit parameters, e.g. capacitances, resistances and cable lengths of an LVDC network. Notably, the stability of the network is ensured by incorporating a random-forest classifier into the model. Within this case study, we find that the number of decision trees plays a significant role in the solution time of the resulting MIP model. For random forests above a certain size, we propose a modelling approach that has worked very well in this application: the sequential solution of slightly adjusted and and more and more restricted MIP models. We propose efficient algorithms to solve models incorporating random forests that were previously unsolvable or only solvable with great effort. They produce high-quality solutions for the design of stable LVDC networks.
1.3 Structure
This work is organised as follows. Section 2 introduces basic definitions and notation concerning decision tree and random-forest classifiers. Subsequently, Sect. 3 proposes algebraic reformulations of random-forest classifiers to integrate them into an MIP model. In Sect. 4, we discuss several practically relevant optimization-based approaches to examine the areas predicted to be feasible by a tree-based classifier. Section 5 explains the technical background on stability requirements in LVDC networks and describes the derivation of random-forest classifiers for stability prediction. The resulting classifiers are used in Sect. 6 as part of an integrated optimization approach to find the best possible stable designs of an LVDC network. We show that optimal solutions can be obtained within reasonable computation times for random-forest classifiers with more than 100 trees. We also describe a modelling trick for solving larger problem instances, which allows us to consider random-forest classifiers with up to 1000 decision trees and discuss the consequences for the application. We conclude in Sect. 7 with an outlook on possible extensions of our framework.
2 Preliminaries on tree-based classifiers
We consider a data set \( (X, Y) \in \mathbbm {R}^{n \times p} \times \mathbbm {R}^n \) consisting of n input-output data tuples \( (X_i, Y_i) \in \mathbbm {R}^p \times \mathbbm {R}\), \( i \in \{1, \ldots , n\} \). In each such data tuple, the input vector \( X_i \in \mathbbm {R}^p \), with p-many features, is assigned a binary label \( Y_i \in \{0, 1\}\). The data set (X, Y) can be used as training data to fit (“learn”) a classifier, i.e. a mapping function \( c:\mathbbm {R}^p \rightarrow \{0, 1\}\) to classify data points in \( \mathbbm {R}^p \) into either 0 or 1. This allows us to classify unseen data points as well. Estimates on the prediction certainty of the classification can be represented by a function \( f:\mathbbm {R}^p \rightarrow [0, 1]\). We start by considering a classifier widely used in practice, namely binary decision trees, and then describe their extension to random-forest classifiers.
2.1 Binary decision trees
Decision trees are among the most common data classifiers used in practice. Their advantages include that they can quickly be trained to satisfactory quality using heuristics, they allow for “human-interpretable” classification rules, which can be expressed in terms of the features of the input data and they can easily be visualised (cf. Breiman 2001b; Bertsimas et al. 2019). A review of tree-based classification and regression methods with discussion on their application in ensemble learning is given in Jena and Dehuri (2020), Loh (2011), Loh (2014), Sagi and Rokach (2018).
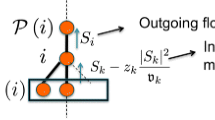
For a detailed introduction to decision trees, we refer the reader to Breiman et al. (1984). Here, we summarise the notation that is relevant here. A decision tree \( T = (V, E) \) is a connected arborescence, where V is the set of vertices and E the set of edges. It possesses exactly one node without an ancestor, the root. Nodes without outgoing edges, and thus without descendants, are called leaves, all others are intermediate nodes. For each vertex \( w \in V \) in a decision tree, there is a unique sequence of edges \( (v_1, v_2), (v_2, v_3), \ldots , (v_k, w) \in E \) from the root \(v_1\) to w, called the path to vertex w. The depth of the tree is the maximum number of edges in a path from the root to a leaf. The purpose of a decision tree is to classify data points in space by assigning each point to a leaf in the tree. It recursively subdivides the p-dimensional space into disjoint regions using logical rules. The node set V is thus partitioned into decision vertices \( V_{\text {Dec}} \), comprising the root and the intermediate nodes, and the class vertices \( V_{\text {Cl}} \) formed by the leaves of the tree.
In binary decision trees, intermediate nodes have exactly two outgoing edges and thus two descendants. Further, the logical split rule in a node \( v \in V \) takes the form of a linear constraint \( \tilde{a}_v^T x \le \tilde{b}_v \) with \( \tilde{a}_v \in \mathbbm {R}^p \) and \( \tilde{b}_v \in \mathbbm {R}\). The two descendants of v can be seen as the roots of two subtrees, where the “left-hand” subtree describes the subregion in space that satisfies the linear constraint, and the “right-hand” subtree the subregion that does not. In a univariate decision tree, \( \tilde{a}_v \) is a multiple of a standard unit vector, i.e. \( \tilde{a}_v = k \cdot e_i \) with \( k \in \mathbbm {R}\) and \( i \in \{1, \ldots , p\} \). As a result, each of the decision rules splits the data points at exactly one feature \( i \in \{1, \ldots , p\} \) in an axis-parallel fashion.
In this article, we focus on binary classifiers with labels representing two different categories. This is only done for ease of exposition and due to the fact that they are most relevant in the application. Our approach can, however, be extended to decision trees with more categories as they are considered in Breiman (1996), Breiman (2001a) as well as Bertsimas and Dunn (2017), for example. This can be done in a straight-forward way.
It could also be generalized to the prescriptive trees of Bertsimas et al. (2019) with the same accuracy of a random forest. For the application using real data studied here, we stick to random decision trees network. This is mainly due to the fact that the data spans over wide scales, where linear separation models of Bertsimas et al. (2019) seem not appropriate, but logarithmic separation was essentially necessary. For this setting, random forests are suited well, and also Bertsimas et al. (2019) notes that the quality of random trees can exceed their model.
Thus, in the following, each class vertex \( v \in V_{\text {Cl}} \) thus corresponds to one of the two categories 0 and 1, depending on the labels of the data points falling into the subregion in space, which fulfils all linear constraints in the decision vertices on the path from the root to v. If the majority of the points in that region have label 0, so does v, and 1 otherwise. In case of a tie, the class with the lowest label is predicted, i.e. class 0, as proposed in Breiman (1996).
2.2 Random-forest classifiers
One commonly-used type of ensemble classifiers are random forests, introduced in Breiman (2001a), which are based on Breiman’s bagging (bootstrap aggregation) idea. In this approach, multiple predictive classifiers are trained on a subset of the training data. Then, the predictions of all classifiers together are used to classify a given data point. The trained model does not necessarily retain interpretability, however as a result accuracy is received (cf. Breiman 2001b, a). Random-forest classifiers are implemented in many machine learning libraries, e.g. in scikit-learn (see Pedregosa et al. 2011). Detailed explanations can be found in Breiman (1996), Breiman (2001a), of which we give a short summary in the following.
The classification of a given data point produced by a random forest depends on the classifications of the individual decision trees. There are two main approaches in the literature for aggregating them into one decision: voting and averaging. The voting approach is the original version of the random-forest classifier used for categorical responses, and was introduced in Breiman (2001a). Here, each decision tree predicts a class, and the random-forest classifier “votes” for the most popular class. The averaging method was previously used in Breiman (1996), Breiman (2001a) to solve regression problems. Here, each decision tree predicts a class with a certain probability. The argmax of the average of these probability estimates determines the prediction of the random forest. In Biau et al. (2008), however, the authors prove that both types of random forests result in consistent classifiers for categorical responses. In this context, “consistent” means that the prediction becomes more accurate as the number of data points used in training increases. In the following, we will focus on averaging random forests, the type that is also implemented in scikit-learn, which we will use in the application studied in Sect. 6.
We consider a random forest \( \mathcal {T}{:=}\{T_t \mid T_t = (V_t, E_t),\, t \in \{1, \ldots , m\}\} \), represented as a set of m decision trees \( T_t \), the so-called base learners, where each of them is constructed as described in Sect. 2.1. The nodes \( V_t \) of each tree \( T_t \in \mathcal {T}\) are partitioned into decision vertices \( V_{t, \text {Dec}} \) and class vertices \( V_{t, \text {Cl}} \). In each decision vertex \( v \in V_{t, \text {Dec}} \), there is a split inequality of the form \( \tilde{a}_{t, v}^T x \le \tilde{b}_{t, v} \) to recursively subdivide the space \( \mathbbm {R}^p \) into disjoint regions. Let \( \gamma _{t,v} \in [0, 1]\) be the fraction of data points in v, which belong to class 1. The class predicted by the random forest for a given point \( x \in \mathbbm {R}^p \), then, results from the average over the fractions \( \gamma _{t, v_{t, x}} \in [0, 1]\) for class 1 of each base learner, where \( v_{t, x} \) represents the leaf belonging to the point x in each tree \( t \in \{1, \ldots , m\} \). If the value exceeds 0.5, class 1 is predicted, otherwise class 0:
The prediction certainty for the selected class results directly from the mean value of the average over the fractions \( \gamma _{t, v_{t, x}} \in [0, 1]\), i.e. from the expected value:
We remark that for \( m = 1 \), random forests naturally reduce to ordinary decision trees.
3 Using tree classifiers to define mixed-integer constraints
In this section, we model the input-output relation of tree-based classifiers algebraically. The subdivision of space into polyhedral feasible and infeasible regions inferred from a trained random forest is converted into mixed-integer linear constraints.
3.1 Problem setting
We consider a general mixed-integer and possibly non-linear program (MINLP) with decision variables \( x \in \mathbbm {Z}^{p - q} \times \mathbbm {R}^q \) of the following form:
where \( D \in \mathbbm {R}^{w \times p} \), \( d \in \mathbbm {R}^w \), \( c \in \mathbbm {R}^p \) and \( q \in \{0, \ldots , p\} \). The condition \( x \in \mathcal {F}\) represents partially unknown or “difficult-to-state” (i.e. algorithmically intractable) constraints. Without Constraint (2c), Model (2) is a classical mixed-integer linear problem (MIP), and thus NP-hard in general.
We now study the question of how it can be decided whether for a concrete variable assignment \( x \in \mathbbm {Z}^{p - q} \times \mathbbm {R}^q \) an implicitly given condition \( x \in \mathcal {F}\) holds or not, and how this condition can be formulated as mixed-integer linear constraints. To this end, we assume in our data-driven approach that we have n concrete realisations of data points \( X_i \in \mathbbm {Z}^{p - q} \times \mathbbm {R}^q, i \in \{1, \ldots , n\} \) for which it is known whether \( X_i \in \mathcal {F}\) is fulfilled or not, for example through a simulation or through explicit labelling by an expert. Each data point \( X_i \) can, thus, be assigned to a class \( Y_i \in \{0, 1\}\), where \( Y_i = 1 \) if \( X_i \in \mathcal {F}\) holds, and \( Y_i = 0 \) otherwise. This results in a training data set (X, Y) with \( X \in \mathbbm {Z}^{n \times (p - q)} \times \mathbbm {R}^{n \times q} \) and \( Y \in \{0, 1\}^n \), which can be used to train a classifier. The classifier can make a prediction for any \( x \in \mathbbm {Z}^{p - q} \times \mathbbm {R}^q \) whether \( x \in \mathcal {F}\) holds or not. In our exposition, we assume that the chosen trained classifier is accurate enough to trust its output.
3.2 Algebraic reformulation of a random-forest classifier
It is known that random forests can be modelled analytically by mixed-integer variables and linear constraints, see for example Maragno et al. (2021). We summarise the model we use next. Let a random forest
consist of m individual binary decision trees, each with a maximum depth of k, as defined in Sect. 2.2. In a random-forest classifier, the labelling of a point \( \tilde{x} \in \mathbbm {Z}^{p - q} \times \mathbbm {R}^q \) results from the individual predictions of the involved decision trees. In order to incorporate these predictions into a mixed-integer program, we have to model algebraically for each binary decision tree \( t \in \{1, \ldots , m\} \) the path
of length \( \tilde{k} \le k \) from the root \( v_{i_1} \in V_{t, \text {Dec}} \), along a sequence of intermediate decision nodes in \( V_{t, \text {Dec}} \) to one of the leaves in \( V_{t, \text {Cl}} \). This path depends on the results of the split inequalities along the \( \tilde{k} - 1 \) decision vertices from \( V_{t, \text {Dec}} \). At each decision vertex, if \( \tilde{x} \) satisfies \( \tilde{a}_v^T x \le \tilde{b}_v \), the left descendant is chosen, otherwise the path continues with the right descendant, until reaching one of the leaves in \( V_{t, \text {Cl}} \).
In order to formulate this classification with the help of mixed-integer constraints, we need to consider the two mutually exclusive linear inequalities
assigned to each decision vertex \( v \in V_{t, \text {Dec}} \) within each tree \( t \in \{1, \ldots , m\} \). Using a standard modelling approach, this disjunction can be incorporated into Model (2) by introducing, for each decision tree \( t \in \{1, \ldots , m\} \) and each decision vertex \( v \in V_{t, \text {Dec}} \), two binary auxiliary variables \( z^{(i)}_{t, v} \in \{0, 1\}\), \(i \in \{1, 2\} \). With these it is possible to activate (\( z^{(i)}_{t, v} = 1 \)) or to deactivate (\( z^{(i)}_{t, v} = 0 \)) such an inequality:
In this two constraints, the constants \( M^{(i)}_{t, v} \in \mathbbm {R}\), for \( v \in V_{t, \text {Dec}} \) and \( i \in \{1, 2\} \) have to be sufficiently large in order not to rule out otherwise feasible solutions:
As MIP solvers cannot work with strict inequalities, we introduce a small constant \( \varepsilon _{t, v} > 0 \) in Eq. (4). For numerical stability, \( \varepsilon _{t, v} \) should be chosen as small as necessary, but as large as possible. For example, in order to ensure, say, six valid digits in the left-hand side of the inequality, one can choose
Because of the mutually exclusive conditions, at most one auxiliary variable can be activated per decision node \( v \in V_{t, \text {Dec}} \):
After certifying, for each decision rule whether the given data point \(\tilde{x}\) satisfies it or not, we need to ensure that classification of the data point follows a connected path within each decision tree \( t \in \{1, \ldots , m\} \). For each node \( v \in V_{t, \text {Dec}} \), we thus introduce the shorthand notation l(v) for the first (left-hand) and r(v) for the second (right-hand) successor. Only if the first split rule of a vertex \( v \in V_{t, \text {Dec}} \) is activated, i.e. \( z^{(1)}_{t,v} = 1 \), the two inequalities given by Eqs. (3) and (4) of its left-hand successor l(v) can be activated, too. The same applies to the second split rule of such a node and its right-hand successor r(v) . Therefore, we add as additional constraints:
To avoid a case distinction in the statement of Eqs. (9) and (10) to cover the cases \( l(v) \in V_{t, \text {Cl}} \) and \( r(v) \in V_{t, \text {Cl}} \), we introduce the two binary variables \( z_{t, v}^{(1)} \) and \( z_{t, v}^{(2)} \) also for the class vertices \( v \in V_{t, \text {Cl}} \). For each leaf node, we thus require
In each of the decision trees belonging to the random forest \( \mathcal {T}\), at most one of the binary auxiliary variables belonging to a leaf must be active, i.e.
We call a tree with an active leaf an active tree. The inequalities along the associated path must then be satisfied by \( \tilde{x} \). To the contrary, a tree is inactive if all the inequalities in its nodes are deactivated via the corresponding z-variables, such that they are valid for any \( x \in \mathbbm {Z}^{p - q} \times \mathbbm {R}^q \). Consequently, if \( z^{(1)}_{t, \tilde{v}} = 1 \), the associated decision tree \( t \in \{1, \ldots , m\} \) is active and \( \tilde{x} \) is assigned to the leaf \( \tilde{v} \in V_{t, \text {Cl}} \), which is then the active leaf of the tree. Finally, to ensure feasibility in Eq. (2c), we can only allow solutions, which the random forest assigns to class 1. If the arithmetic mean of the predictions of the individual decision trees for \(\tilde{x}\) fulfil \( \frac{1}{m} \sum _{t = 1}^m \gamma _{t, v_{t,\tilde{x}}} > 0.5 \), the random forest assigns label 1, otherwise 0. To represent this averaging logic algebraically, we model the tree certainty of each individual decision tree \( t \in \{1, \ldots , m\} \) via a binary variable \( \Gamma _t \in [0, 1]\). Thanks to the auxiliary variables \( z^{(1)}_{t, v} \) we know which leaf is active in the respective tree. Thus, we can determine the tree certainty by multiplying the given constant fraction \( \gamma _{t, v} \in [0, 1]\) at leaf \( v \in V_{t, \text {Cl}} \) for class 1, described in Sect. 2.2, via the corresponding auxiliary variable \( z^{(1)}_{t, v} \):
For \( \tilde{x} \) to be assigned to class 1, the sum of tree probabilities must be at least half the number of decision trees:
In summary, the following MIP model emerges if we replace Eq. (2c) by our MIP representation of a trained random forest with averaging as the evaluation rule:
In particular, Inequalities (3)–(4) and (8)–(14) ensure that the random forest predicts label 1, i.e. feasible, for the chosen solution \( \tilde{x} \).
4 Optimization over random-forest classifiers
In order to demonstrate the modelling capabilities of random-forest classifiers within MIP formulations, we will now investigate three different use cases that are relevant in the real-world application studied later. They concern, in particular, the choice of optimization objective, as summarised in the following:
-
1.
Assume that we are given a point \( x \in \mathbbm {Z}^{p - q} \times \mathbbm {R}^q \), which is infeasible according to the trained classifier. This point may e.g. represent a solution candidate, which was “manually” found by some expert planner. An interesting question is now, which minimum adjustments need to be made to x in order to reach a solution \( \tilde{x} \in \mathbbm {Z}^{p - q} \times \mathbbm {R}^q \) that is feasible according to the classifier. This objective can be formulated straightforwardly, see Sect. 4.1.
-
2.
As a second setting, let us assume we want to ensure the “reliability” of a chosen solution \( x \in \mathbbm {Z}^{p - q} \times \mathbbm {R}^q \), i.e. the solution should not lie close to the split between two classes of points separated into feasible and infeasible. For this reason, we determine an optimal solution x so that a sphere of maximum possible radius around x is fully contained in a feasible class of the trained classifier, see Sect. 4.2.
-
3.
While we outline our modelling approach for multivariate decision trees, the case of univariate trees is very important in practice, and in particular for the application studied here. Focussing on this case, in Sect. 4.3 we show that for a random forest based on univariate decision trees we can also find the largest p-dimensional cuboid \( V_Q \) that is completely contained in a feasible class of the trained classifier.
In order to obtain meaningful results, we restrict x to the valid range of the classifier, i.e. the lower (\( l \in \mathbbm {R}^p \)) and upper (\( u \in \mathbbm {R}^p \)) bounds on the training data X. For the sake of simplicity, we assume that all parameter values are normalised to the interval \( [0, 1]\):
4.1 Smallest possible adjustment to make a solution candidate feasible
In the first setting, we assume that an initial solution candidate \( x^{\text {start}} \in \mathbbm {Z}^{p - q} \times \mathbbm {R}^q \) is given, which is not recognised as feasible by the classifier. We search for a solution \( x^{\text {opt}} \in \mathbbm {Z}^{p - q} \times \mathbbm {R}^q \), which is classified as feasible and which requires the minimum possible adjustment of the candidate \( x^{\text {start}} \). We will exemplarily show two possibilities for such an adjustment – first minimising the distance between \( x^{\text {start}} \) and \( x^{\text {opt}} \) and second minimising the number of differing coordinates between the two.
The initial situation for both problems is shown in Fig. 1a and b, respectively, for a random-forest classifier based on univariate decision trees. The plotted green points \( x_1 \), \( x_2 \) and \( x_3 \) are potential optimal solutions for the first problem. The continuous green lines in Fig. 1b represent equivalent optimal solutions for the second problem.
4.1.1 Finding the closest feasible point
To find the closest feasible point to \( x^{\text {start}} \), we minimise the distance
where \( \delta \) is the difference between x and \( x^{\text {start}} \), i.e. \( \delta = x - x^{\text {start}} \), and the r-norm is defined as \( \left\Vert \delta \right\Vert _r {:=}(\sum _{i = 1}^p {|\delta _i |^r})^{\frac{1}{r}} \). The most common norms are the norm \( \ell _1 \), the Euclidean norm \( \ell _2 \) and the infinity norm \( \ell _\infty \). For instance, to calculate the absolute value of \( \delta \) in the \( \ell _1 \)-norm, its entries are separated into their positive and negative parts, \( \delta ^+ \in \mathbbm {R}_+ \) and \( \delta ^+ \in \mathbbm {R}_- \) respectively:
Thus, to find the nearest point that is feasible according to the classifier, we can utilise the following MIP model:
where the constraints in (17c) represent the feasibility inside the random-forest classifier.
4.1.2 Minimum the number of coordinates to be adjusted
Suppose we are looking for the smallest number of coordinates to change in the solution candidate \( x^{\text {start}} \) in order to obtain a feasible solution \( x^{\text {opt}} \in \mathbbm {Z}^{p - q} \times \mathbbm {R}^q \). We introduce a binary variable \( \delta _i^{\text {on}} \) for each feature \( i \in \{1, \ldots , p\} \) that takes value 1 if \( x_i \ne x^{\text {start}}_i \), and 0 otherwise:
Here, \( M_{\delta _i}^- \) and \( M_{\delta _i}^+ \) are again sufficiently large constants, which in this case, for example, can be defined as the distances between the boundary values of x and the initial value:
In order to minimise the number of adjusted coordinates, we sum over the \( \delta _i^{\text {on}} \) in the objective function, which leads to the following optimization problem:
The constraints in (18c) again represent the trained random forest.
4.2 Finding reliable solutions
In many applications, a chosen solution \( x \in \mathbbm {Z}^{p - q} \times \mathbbm {R}^q \) is required to be feasible with a high degree of certainty. Thus, a solution on the boundary of a feasible class, as could be seen exemplarily in Fig. 1a, should be avoided as it may entail infeasibilities due to parameter fluctuations or uncertainties.
For a single decision tree, all its classification areas result from the paths leading from the root to the leaves. These areas are determined as the intersection of finitely many halfspaces and are thus polyhedra. In turn, all classification areas of a random forest result from intersections of the areas implied by the individual decision trees and are therefore also polyhedra. Because of the boundary condition in Eq. (16), they are actually polytopes. Thus, any solution \( x^{\text {opt}} \in \mathbbm {Z}^{p - q} \times \mathbbm {R}^q \) lies within a polytope that depends on the classifications of the active decision trees.
In order to determine a reliable solution that is as far as possible away from the boundaries, we calculate the Chebyshev center, see Boyd and Vandenberghe (2014) for a general reference. To this end, we introduce an optimisation variable \( r \in [0, 0.5] \). The optimum \(r^{\text {opt}}\) specifies the smallest distance of the point \( x^{\text {opt}} \) from any of the constraints of the feasible set. Geometrically, \(x^{\text {opt}}\) is thus the centre of a sphere within which all points are predicted to belong to the desired feasibility class. Algebraically, we shift all constraints of the original feasible set inwards. Because of the convexity of the feasible set, the resulting smaller feasible set contains only points that are also feasible in the original problem and has at least the distance \(r^{\text {opt}}\) from each constraint, as can be seen in Fig. 2:
where \( M^{(1)}_{t, v} \) and \( M^{(2)}_{t, v} \) are constants that have to be set in the spirit of Eqs. (5) and (6), but increased by \(0.5\Vert \tilde{a}_{t, v} \Vert \) so that they are sufficiently large and do not rule out feasible solutions. Figure 2b shows an exemplary result when maximising over r. We obtain a point \( x^{\text {opt}} \) that has the largest possible distance from all active constraints and is thus maximally reliable. A similar motivation to use the Chebyshev center for obtaining resilient solutions has been used for product design in Hendrix et al. (1996) and more generally for convex mixed-integer optimization in Kronqvist et al. (2017).
Altogether, we can find a reliable point \( x^{\text {opt}} \) with predicted class 1, i.e. with \( c^{RF}(x^{\text {opt}}) = 1 \), by solving the following MIP:
where the constraints in (20g) represent the feasibility inside the random-forest classifier.
4.3 Approximate largest area in univariate classifier
The solution of the previously considered problem (20) automatically leads to approximately the largest feasible area with the help of a largest feasible sphere centred at \( x^{\text {opt}} \), as can be seen in Fig. 3a. An interesting related task is searching for the largest connected feasible region \( \mathcal {U}^{\text {opt}} \) within the classifier. Besides the apparent motivation to identify a largest possible feasible range, we can also use this knowledge to analyse the trained classifier itself. For example, if that region turns out to be very large, it may be because only feasible data exist in it, but the reason could also be that this region is covered by too little training data. If, on the other hand, the largest feasible area is small, this is also true for all other feasible areas and could thus indicate difficulty in explaining the feasible areas.
Let us consider a general decision-tree-based classifier. To find the largest feasible region, we must first calculate the volumes of the polytopes implied by the random forest and compare them with each other. Computing the volume of a general polytope is a hard task. Until now, we have outlined the models for multivariate trees. In practical applications, on the other hand, usually univariate decision trees are very relevant, cf. the implementation of tree-based classifiers in scikit-learn (see Pedregosa et al. 2011). In the computational results, we will focus on univariate decision trees as they are most relevant for the considered application, and we focus on them in this subsection. For univariate decision trees, each decision rule refers to exactly one parameter. Thus, \( \tilde{a}_{t, v} = \tilde{k}_{t, v} e_i \) is the \( \tilde{k}_{t, v} \)-th multiple of a unit vector \( e_i \), \( i \in \{1, \ldots , p\} \). This simplifies the arising polytopes to p-dimensional cuboids, whose volumes can be calculated by multiplying their edge lengths. To find an approximately largest feasible cuboid within a univariate decision tree, its edge lengths can be determined by computing the centre \( x^{\text {opt}} \) using auxiliary variables \( r_i \in [0, 0.5] \) storing the distance to the edges for each parameter \( i \in \{1, \ldots , p\} \). Similar as in Sect. 4.2, any inequality within a decision tree that depends on parameter i is shifted inwards parallel to axis i. The resulting smaller feasible set contains only points that are also feasible in the original problem:
The purpose of the constants \( M^{(1)}_{t, v} \) and \( M^{(2)}_{t, v} \) is to deactivate the first two constraints if \( z^{(1)}_{t, v} = 0 \) or \( z^{(2)}_{t, v} = 0 \). Together with inequality (16), the constants in the univariate case simplify as follows:
Where \( i \in \{1, \ldots , p\} \) is the separating variable of the inequality and \( k_{t, v}^{\min } {:=}\min _{t, v} k_{t, v} \) and \( k_{t, v}^{\max } {:=}\max _{t, v} k_{t, v} \) the smallest and largest values, respectively.
Figure 3b shows an exemplary feasible point \( x^{\text {opt}} \) which is the centre of an axis-parallel cuboid. The minimum distance to each classifying inequality belonging to parameter \( i \in \{1, \ldots , p\} \) is given by \( r_i \). Each edge of the cuboid has length \( 2 r_i \), and its volume is calculated by multiplying the edge lengths. If we search for a feasible cuboid with largest possible volume, we can thus optimize with respect to the following objective function:
In order to linearise this objective, we rewrite it by using the logarithm and obtain
It remains to linearise the individual summands \( \log (r_i) \), or more generally the functions \( f_i:\mathbbm {R}_+ \setminus \{0\} \rightarrow \mathbbm {R}, r_i \mapsto \log (r_i) \), for all \( i \in \{1, \ldots , p\} \). For this purpose, we use the incremental method by Markowitz and Manne (1957), see e.g. Vielma (2015) for more recent results on this method. The reason is that the latter often leads to linearisations that can be solved practically efficient, see for example (Geißler et al. 2012) or (Kuchlbauer et al. 2021). First, we define \( s_i + 1 \) breakpoints \( (r_{i_k}, r^{\log }_{i_k}) \), \( i \in \{0, \ldots , p\} \), where the \( r_{i_k} \) have to be ascending and logarithmically distributed in the subset ]0, 0.5] of the domain of \( f_i \) and the \( r^{\log }_{i_k} = \log {r_{i_k}} \) represent the respective logarithmic value. At these breakpoints, we disjointly subdivide the domain of \( f_i \) into \( s_i \)-many subdomains. For each of these subdomains, indexed by \( k \in \{1, \ldots , s\} \), we further need a binary variable \( z_{i_k} \in \{0, 1\}\) that registers whether it is active or inactive and a continuous variable \( \delta _{i_k} \in [0, 1]\) that contains the exact proportional location of \( r_i \) in the k-th subdomain if it is active. The following mixed-integer linear inequalities can then be used to track the value of \( r_i \):
Overall, in the case of a univariate random forest with averaging, the following MIP model computes the approximate largest feasible cuboid:
where the constraints in (23c) represent the incremental method and the constraints in (23h) the feasibility inside the random-forest classifier.
5 Improving the stability of LVDC networks
We will now describe an indicative use case for the optimization models from Sect. 4, namely the design of stable direct-current (DC) networks. This application is very well suited to validate the derived MIP reformulation of tree-based classifiers, since it involves a large number of network parameters to be optimized, which come from a large range of possible values—from one to several orders of magnitude. Furthermore, different strategies for parameter adjustments are required here, according to the precise problem setting.
The overall approach for stability improvement with focus on the generation of the stability classes and the generation of the random-forest classifiers is described in Roeder et al. (2021). The remainder of this section summarises the approach and elaborates on some details concerning the input data, classifiers and optimization scenarios.
5.1 Stability of LVDC networks
Typically, electricity distribution networks operate with alternating current (ac). ac networks have been studied intensively in the literature, e.g. in Carpentier (1962), Mary et al. (2012), Aigner et al. (2021a), also in their linearised version as DC networks, see e.g. Aigner et al. (2021). Direct current networks with system voltages below 1500 V (so-called low-voltage direct-current (LVDC) grids, see Azaioud et al. (2021) for a detailed introduction and International Electrotechnical Commission (2016, Section 4.2, p. 19) for the definition of the technical standards) are of great importance for the realisation of an efficient, decentralised energy supply with an increasing share of renewable energy, as explained in Azaioud et al. (2021), Weiss et al. (2015), Gao et al. (2019). In short, the reason is that renewable energy generators, such as photovoltaic systems, storage systems such as batteries, and consumers, e.g. charging stations for e-mobility or computer systems, operate on a DC basis. The interconnection of these components in DC microgrids, which are typically operated as subsystems of AC grids, avoids unnecessary dc-ac and AC-DC conversion and enables a cost-efficient subgrid design as well as an increased self-consumption of renewable energies, see Azaioud et al. (2021). An essential element for the reliable design and operation of LVDC microgrids is the preservation of network stability. Switching operations may generate high-frequency ac currents and can cause the LVDC grid to oscillate, which may occur in particular when networks are reconfigured, e.g. when adding or removing loads and sources, see Ott et al. (2015a). Figure 4 shows a simplified model of a four-terminal DC microgrid network (4-TLN), as can be realised in an experimental laboratory setup. It serves as a development platform for real-world implementations, e.g. as operated at the Fraunhofer IISB. The LVDC circuit model comprises two unidirectional sources—a DC source, which mimics the input from the ac network after conversion and a photovoltaic source, as well as two unidirectional loads, respectively. In the following, we summarise the necessary details for understanding the application. For details on stability criteria for DC power distribution systems, we refer to Riccobono and Santi (2014).
The network is realised with a decentralised control structure, which exhibits inherent reliability in case of failures, see (Gao et al. 2019; Wunder et al. 2015). It comprises a current-mode droop control scheme as primary control, see (Gao et al. 2019; Wunder et al. 2015; Ott et al. 2015b), and a decentralised secondary control scheme for power-sharing as well as performance and voltage regulation, see (Wunder et al. 2015). The droop control scheme employs characteristic curves, which control the current input from the sources into the network and keep the bus voltage at 380 V. The voltage droop concept and the characteristic curves are further discussed in Ott et al. (2015b). The impedance measurement and the subsequent stability analysis, either by simulation or by measurement, is conducted by injecting a small-signal alternating current \( i_{\text {inj}} \) with varying frequency \( \omega \) at the bus. In the simulation, we calculate the impedance ratio \( T_{\text {bus}} \) from the source and load impedances \( Z_S \), \( Z_l \), see Riccobono and Santi (2014), according to the relationship
The impedances are calculated from the voltages \(V_S\), \(V_l\) and the currents \(I_S\), \(I_l\), which are determined at two measuring resistors next to the small-signal source feed. The measurement determines the complex impedance \( T_{\text {meas}} \) that contains equivalent information on stability as \( T_{\text {bus}} \), which is used for determining stability margins. The complex impedance spectrum is analysed, and the system stability is assessed by applying the gain margin and phase margin criterion, see Riccobono and Santi (2014). The gain margin and phase margin provide sufficient, but not necessary stability conditions and may be derived from the Nyquist plot, which represents the impedance ratio in the complex plane, or the Bode plot, which depicts the impedance spectrum as amplitude given in decibel and the phase angle given in degrees, see Riccobono and Santi (2014). According to Riccobono and Santi (2014), the total input-to-output transfer function of two cascaded individually stable subsystems, such as the source and load system, may be written as
with the minor loop gain \( T_{\text {MLG}} \) of the system depicted in Fig. 4 defined as
The interconnected system is stable if the Nyquist contour of \( T_{\text {MLG}} \) does not encircle the point \( (-1, 0) \) in the complex plane (Riccobono and Santi 2014). The gain margin and phase margin criterion allow that \( |Z_s | > |Z_l | \) in certain frequency ranges while ensuring respective margins such that the Nyquist criterion is satisfied (Riccobono and Santi 2014). Maintaining a gain margin ensures that the amplitude \( |T_{\text {bus}}(j \omega _{\text {pc}}) | \) at those phase cross-over frequencies \( \omega _{\text {pc}} \), where \( \textrm{Im}(T_{\text {bus}}(j \omega _{\text {pc}}))\), i.e. where the phase angle is \( -180^\circ \), is sufficiently distant from the point \( (-1, 0) \). The gain margin \( \text {GM}\) is defined as
see (Åström and Murray 2008). In the Bode plot, where the amplitude is depicted in decibels, the gain margin can be determined as
The phase margin at the gain frequency \( \omega _{\text {gc}} \) is defined as
where \( |T_{\text {bus}}(j \omega _{\text {gc}}) | = 1 \), and denotes the angle between the point \( (-1, 0) \) and the intersection of \( T_{\text {bus}}(j \omega _{\text {gc}}) \) with the unit circle, see Riccobono and Santi (2014). The choice of gain and phase margins depends on the application. Typical values for gain margin are \( \text {GM}= 2 \) to 6 dB and \( \text {PM}= 30^\circ - 60^\circ \), respectively (Åström and Murray 2008; Riccobono and Santi 2014). For further investigations, the network was labelled to be stable whenever the determined gain margins and phase margins both exceeded critical values according to
Otherwise, the network was labelled as unstable. With these parameters, the exciting amplitude must be damped by at least \( -6~\text {dB} \approx 0.5 \), and if this not the case, the phase angle must be at least \( 45^\circ \) distant to \( 180^\circ \), the range of the opposite-phase oscillation in resonance (Riccobono and Santi 2014). Figure 5 illustrates the identification of stable and unstable states in the Bode plot for the circuit model of Fig. 4, for a stable state at the default network parameter settings in Fig. 5a, and for parameter settings leading to instability in Fig. 5b. With the Bode plot, the phase margins are determined at \( \text {GM}= 0 \) and the gain margins are determined at \( \text {PM}= 180^\circ \). The margin exceeding the limits where the network is labelled as unstable according to Eq. (30) is indicated in red.
5.2 Parameter variation in the network
In a simulator, the small-signal DC network impedance was automatically calculated for multiple input parameter settings and the stability was analysed with the gain and phase margin limits given in Eq. (30), also providing the labels for the stability class. The grid input parameters are distributed by Latin hypercube sampling (LHS, see Lin and Tang 2015), autoscaling the data either on a linear or a logarithmic scale between the minimum and maximum values. The input parameters of the dc network, which are varied in the LHS design and their possible values are briefly described in Table 8 in the appendix.
For the development of the random-forest surrogate classifier and for testing the optimization models, simulations varying the parameter \( k_{\text {AC}} \), \( k_{\text {PV}} \) and \( P_{\text {load}1} \), \( P_{\text {load}2} \) as well as the input parameters depicted in Table 8 were conducted (Roeder et al. 2021). The summary as well as the imbalance ratio of stable and unstable states are depicted in Table 1.
By automated circuit modelling, 24,770 resp. 49,018 input parameter combinations and the resulting stability labels were calculated, which serve as predictors and labels in the random-forest classifiers, respectively. With the parameter combinations, different ratios of stable and unstable states, i.e. imbalance ratios were obtained. As the training of accurate and reliable classifiers requires balanced input data, specific measures were taken in the preparation of the random-forest classifiers as described in the next section.
5.3 Preparation of the random-forest classifiers
The random-forest classifiers were trained on the data as depicted in Table 1. The data sets were split into a training and an independent test data set with a split ratio of 70% down to 30%. Hyperparameter optimization (HPO) of the random-forest classifiers was conducted on the training data using a grid search strategy and a 10-fold stratified cross-validation to maximise the balanced accuracy and to minimise the false positives, i.e. the cases where an unstable state is predicted as stable (Roeder et al. 2021). For the investigation of the optimization models, two random-forest classifiers were prepared. For both classifiers, the parameters \( P_{\text {load}1} \), \( P_{\text {load}2} \) were excluded from the training to enable optimization within their complete parameter range. One classifier, further denoted as the 14-parameter classifier, was trained allowing all other input parameters to be varied. The second classifier, which is further denoted as the two-parameter classifier, was trained to allow the variation of \( k_{\text {AC}} \), \( k_{\text {PV}} \) as an example for droop control parameter adjustment. The HPO parameters were set differently to investigate the achievement of a preferably large leaf population and to limit the tree complexity while providing stable, balanced accuracy. The 14-parameter classifier was adjusted to have a minimum number of 11 samples per leaf, the number of estimators set to 1,000 trees, and the maximum depth of the trees was set to 20. The two-parameter classifier was adjusted to have a minimum number of 100 samples per leaf, the number of estimators was limited to 2,000 trees, and no limit was provided for the tree depth, i.e. the trees may be split until the minimum number of samples per leaf is obtained. The HPO was enabled to adjust the tree splitting criterion, the maximum number of features to be sampled and the adjustment of the class weights. The balanced accuracy, the parameters of the confusion matrix, and the selected hyperparameters are given in Table 2. The classifiers provide well-balanced accuracy on the training and test data and minimise the false-positive rate. During HPO, the class weights are adjusted to compensate for the imbalance in the data sets. Entropy was selected as the splitting criterion for both classifiers. All features were selected in the case of the two-parameter classifier, whereas the number of parameters remained at the default setting for the variation of all input parameters. The balanced accuracy, the parameters of the confusion matrix, the class weights of the input classes to compensate for their imbalance as well as the splitting criterion and the maximum number of sampled features are given in Table 2. The classifiers provide high balanced accuracy, which provides a corrected accuracy measure in the presence of imbalance, on the training and test data. Additionally, the classifiers specifically minimise the false-positive rate, i.e. the prediction of an unstable network as stable. Overall, accurate and reliable input parameters to the optimization are provided.
6 Case study for determining stable LVDC network settings
In this section, we use mixed-integer optimization models to find the best possible parameter setting for an LVDC network starting with an initial setting \( x^{\text {start}} \). The stability of the network is assessed exclusively from the prediction of the respective univariate random-forest classifiers presented in Sect. 5. As argued before, univariate decision trees were used as they can be interpreted easily by practitioners who work with them. We however note in passing that more generally also multivariate trees could be used for another application in the future.
From the input Table 8 we know the minimum value \( l_p \) and the maximum value \( u_p \) for each parameter p in the set of parameters P. To visualise and to describe the solutions from the different mixed-integer problems, we use the smaller two-parameter classifier trained on the two-dimensional data set with 25,000 instances of \( k_{\text {AC}} \) and \( k_{\text {PV}} \). For predicting the stability of the whole LVDC network, we use the large 14-parameter classifier trained on the dataset (X, Y) described in Sect. 5, which consists of 50,000 concrete network settings. A data point \( X_i \in \mathbbm {R}^{14} \), \( i \in \{1, \ldots , 50,000\} \), represents the value for each of the 14 parameters \( p \in P \), and the corresponding label \( Y_i \in \{0, 1\}\) describes the resulting network status “stable” (1) or “unstable” (0). Apart from the best found random-forest classifier with 1000 decision trees, each consisting of 920 to 1020 paths, and a maximum depth of 20, we will also use increasing subsets of the decision trees to demonstrate and discuss the performance of the MIP models.
Both random-forest classifiers have been trained with the Python machine learning library scikit-learn, see (Pedregosa et al. 2011), and consist of individual univariate decision trees, each trained with an improved CART algorithm; Scikit-Learn (nd) describes the specific implementation. The predictions of the random-forest classifiers are based on the averaging method. As MIP solver, we have used Gurobi, see (Gurobi Optimization LLC 2020), and all presented solution times have been obtained on Intel(R) Xeon(R) CPU E3-1240 v5 @ 3.50 GHz processors with 4 CPUs and 32 GB RAM.
6.1 The MIP models
We assume to be given an established LVDC network and a perfect random-forest classifier representing the relation of the network input parameter values to LVDC network stability. The latter means that the classifier predicts a stable state exactly when the LVDC network is stable. Furthermore, we are given the initial input parameter setting of the network. We now consider several different tasks with respect to choosing the network parameters in order to obtain a stable network.
6.1.1 Minimal adjustment of parameters to make a network stable (Adjust)
The first task, which henceforth will be called Adjust, is to bring the network into a stable state, using as few parameter changes as possible. Each parameter represents either a network component that needs to be replaced or a software parameter that needs to be adjusted. The fewer parameters have to be changed, the easier and less expensive the adaptation is. To solve this problem, we consider the MIP model described in Eqs. (18a)–(18g).
Before we examine the solution times of this task, we first want to ensure the suitability of the solution. For that purpose, we consider a two-dimensional problem where the distribution of the stable and unstable areas is easy to visualise and where the parameter decisions and the correctness of the solution are well comprehensible. For that purpose, we will use the small random-forest classifier trained only with the two control parameters \( k_{\text {AC}} \) and \( k_{\text {PV}} \) that were introduced in Sects. 5.1 and 5.3. After training the random-forest classifier with the given data set, it can be used to classify an arbitrary point \( x \in \mathbbm {R}^2 \) as stable or unstable within the given minimum (\( l_p = 0 \)) and maximum value (\( u_p = 2 \)) for \( p \in \{k_{\text {AC}}, k_{\text {PV}}\} \). The optimal assignment can be taken from the colour map in Section 6.1.1, which corresponds to the probability of the network being stable. The deeper the area is in the dark blue, the more confident the random-forest classifier is that it belongs to the stable class.
An optimal solution for Adjust changes as few parameters as possible, but the magnitude of the adjustment does not matter, which means that the objective is zero in case we start in a stable state; see Section 6.1.1. Starting in an unstable state, like in Section 6.1.1 , we are returned the number of parameters to be adjusted and receive the specific changes to make to reach a stable state. For Section 6.1.1, this means, for example, that all solutions with \( k_{\text {AC}} \ge k_{\text {AC}}^{\text {opt}} \) are equivalent to the point \( (k_{\text {AC}}^{\text {opt}}, k_{\text {PV}}^{\text {opt}}) \) found. The optimization model is only about achieving a stable network setting. The neighbourhood of the point is unimportant to the solution, as can be seen in Section Section 6.1.1, where it lies in a light blue area, close to unstable regions.
We will now consider the same task using the 14-dimensional data set and the larger 14-parameter classifier. As described in Sect. 5, we found that a good prediction requires a random-forest classifier with 1000 trees, each with 920 to 1020 paths and a maximum depth of 20. The number of trees provides a challenge for the MIP model. We verify that this is not due to incorrect modelling by comparing the solution times for differently sized subsets of the given decision trees with comparable objective values. With 100 decision trees, the MIP model finds a solution within 120 seconds, the classifier with 500 decision trees already needs 7550 seconds, and the model incorporating the full classifier with 1000 decision trees is not solvable within 4 hours.
The solution time of the MIP model can be reduced significantly by using the following iterative process. The integer objective value \( G = \sum _{i = 1}^{|P |} \delta _i^{\text {on}} \), which determines the number of parameters to be adjusted, is no longer to be chosen via the MIP model, but instead in an outer for-loop. The MIP models to be solved inside the loop are fixed to an objective value representing a certain number of parameters to be adjusted, \( G_k = \sum _{i = 1}^{|P |} \delta _i^{\text {on}} = k \), and are, thus, transformed to feasibility problems. We start with zero parameters to be adjusted and increase this number by one in each step. If the current MIP with the additional constraint \( G_k = k \), \( k \in \{0, \ldots , |P |\} \) is infeasible, then proceed with the fixation \( G_{k + 1} = k + 1 \). On the other hand, if the solver finds a solution for the current k, this value k is the optimal solution for the original MIP problem. The for-loop can then be terminated. It turns out in practical computations that this approach reduces the number of subproblems to be considered in the branch-and-bound tree. In our application, infeasibility can be determined more quickly in the simplified problem. The running time grows with the value of k which is why we use linear search with a linearly increasing value of k instead of another typical approach such as binary search.
As a result of this approach, even the model incorporating 1,000 decision trees could be solved within less than 3.5 hours of computation time, see Table 3. The table shows an overview of the optimization runs performed. Besides the number of decision trees, the required number of continuous and binary variables in the MIP model as well as the required computation time and the number of parameters to be changed (target of Adjust) are documented.
6.1.2 Most stable point possible within an already existing network (Reliable)
As a second objective, we study determining a network setting that is as stable as possible so that small fluctuations in the parameters do not affect stability. For this purpose, we determine a point in the centre of a stable region by using Eqs. (20a) to (20j). We call this task RELIABLE. Unlike in the simplified exposition of the optimization model (20), the considered parameters \( p \in P \) are defined on different intervals \( [l_p, u_p] \). In our application, \( r \in [0, 0.5] \) shall reflect the normalised safety margin. The conversion of the values is straightforward to incorporate by the linear scaling \( \bar{r} = (r_p - r_p^{\min }) / (r_p^{\max } - r_p^{\min }) \) for all parameters \( p \in P \). To understand the solution of the MIP model, we first consider the two-dimensional random-forest classifier in Fig. 7a. The model finds the largest possible intersection of more than 50% of the decision trees in the classifier such that the corresponding area is predicted to be “stable”. Since all decision trees are univariate, the intersection is a rectangle. For the objective function of RELIABLE, however, this is not necessary. The green centre of the optimal circle is the most reliable point w.r.t. the random-forest classifier. In both parameter dimensions, the coordinates of the center point can be changed additively by \( r_p = 0.36 \cdot (u_p - l_p) \) without becoming unstable. All points within the circle have at least 50.2% certainty and are, thus, predicted to be stable by the classifier. The actual certainty, which is the sum of all decision tree predictions of the specific position, exceeds this value. It is easy to see in Fig. 7a that the solution is not unique and that points \( (k_{\text {AC}}, k_{\text {PV}}) \), with \( k_{\text {PV}} = 1.31 \) and \( k_{\text {PV}} \in [0.89, 1.87] \) are equivalently reliable solutions for the MIP model.
Considering only the colour map, one could suppose that it is possible to move the centre slightly to the upper left and, thus, increase the circle radius. However, this solution cannot be found, because almost every decision tree restricts the stable sphere with the inequality \( k_{\text {AC}} \approx 0.5 \), as can be seen from the white dashed lines on the left-hand side. As a result, the total area cannot be found, even if the stable areas connect seamlessly.
Solving the Reliable problem with the large 14-parameter classifier requires significantly longer runtimes than Adjust. As a result, a model with a subset of only 250 decision trees still had a high optimality gap after 4 hours of computation, where we denote by optimality gap the relative difference between the best solution bs found and the best objective bound ob obtained from linear relaxations within the branch-and-bound tree: \( |ob - bs | / |bs | \).
The long runtime of this problem results from the high number of binary variables and constraints added to the model with each additional large decision tree. For each node in the path of a decision tree, one binary variable \( z_{t, v} \), the decision rule on the node associated with that path (Constraint (20c) or (20d)), the relationship between the two binary variables of the node (Constraint (8) or (11)) as well as the inequalities needed for the connected path (Constraint (9) or (10)) are added to the MIP. For a feasible solution, only one of these paths per decision tree is activated by the associated binary variables, rendering many of the inequalities non-binding. To reduce the number of variables and constraints in the MIP model, one can try to identify as many paths as possible that will not be activated in the optimal solution already before optimization. We again use an iterative approach to do this, taking advantage of the fact that the non-feasibility of an optimization model can usually be decided very quickly in practice. Let r be the normalised radius of the feasible sphere. We need to consider only those paths whose decision rules in the nodes together form a polyhedron which is large enough to accommodate a sphere with a normalised radius of size r. To decide whether the feasible polyhedron associated with a given path can enclose such a sphere, we compare whether the distance in each parameter between the lower and upper bounds given by the decision rules in its nodes is at least as large as twice the radius r of the sphere. When multiple paths are considered at once, the intersection of their associated feasible polyhedra needs to enclose the sphere. Now, in the first step of the iterative approach, we start with the largest possible sphere and, thus, with only a few paths that together yield a polyhedron which is large enough to accommodate it. With each iteration, we decrease the size of the sphere, so more and more paths and the feasible areas they describe can be taken into account. This is repeated until finally we consider enough paths to find a feasible region. To this end, the tree probabilities resulting exclusively from the active subset of the considered paths must sum to at least half the number of the decision trees such that Constraints (13) and (14) can be satisfied. More precisely, we introduce a lower bound \( {r}_k \in [0, 0.5] \) on the radius \( r \in [0, 0.5] \) as the objective of the current model. In each step k, we reduce this lower bound by a fixed amount as long as the MIP remains infeasible. Starting with the highest possible lower bound, \( {r}_0 = 0.5 \), we subtract a fixed value, here 0.05, from the lower bound in each iteration. In addition to the two constraints \( r \ge {r}_k \) and \( {r}_k = 0.5 - 0.05k \) in the k-th MIP model, we consider only those variables and constraints that belong to paths of the decision trees that form a polyhedron which is large enough to accommodate a normalised sphere with a normalised radius of size \( {r}_k \). If the k-th MIP is infeasible, we continue with the \( k + 1 \)-st problem; otherwise, we stop and return the solution found. It is, then, also the solution to the overall problem. By placing a lower bound on the normalised radius, we guarantee that the ignored paths in the optimal solution would have had to be deactivated anyway, since they do not yields a polyhedron which is large enough to accommodate a normalised sphere of radius \( r^{\text {opt}} \).
The benefit of the iterative optimization procedure can be seen in Table 5. We are now able to solve all instances optimally, including the largest one with 1000 trees, in just under an hour each. In particular, we also achieved much shorter solution times for the smaller instances.
6.1.3 Finding the largest stable cuboid (Volume)
Finally, we would like to find the largest possible region that contains only stable network settings w.r.t. the random-forest classifier. We call this optimization problem VOLUME. We take advantage of the point that only univariate decision trees are currently considered, and, thus, only axis-parallel cuboids can be regarded as a possible solution. We find the largest cuboid using the slightly adapted MIP model (23). As in the previous optimization problem in Sect. 6.1.2, the safety values \( r_p \) chosen individually per parameter must be normalised to \( \bar{r}_p \) in the objective function, such that each feature has equal weight. To describe the relationship between these parameters, we again use linear scaling.
The solution for the two-dimensional problem is shown in Fig. 7b. The largest possible rectangular area found is shaded in green. All points in the interior are, thus, predicted to be stable by the classifier. The centre of the rectangle is located such that it is as far away as possible from the active decision rules of the active decision trees, which are shown as dashed white lines. The safety margin in \( k_{\text {AC}} \) can increase independently of that in \( k_{\text {PV}} \), which is particularly interesting when parameters of different importance in the classifier are considered.
In Fig. 8, we see the frequency distribution of the 14-dimensional classifier, which results from the number of times each feature occurs across all decision nodes of the decision trees.
There are obviously more and less important parameters, which is also observable in Fig. 9. It shows the cuboid found for the 14-parameter classifier in sectional planes. The colours refer to starting from the centre of the cuboid. Within the limits of the cuboid found, all parameter combinations can be chosen without losing stability according to the classifier. The cuboid is of different size in each feature. For the rather important features \( l_{\text {load}1} \) and \( l_{\text {load}2} \), the cuboid is very small, while for all features with low importance almost the whole area is green.
In these plots, we demonstrate the solution to problem Volume we found using the 14-parameter classifier. The largest stable area found by the MIP solver, limited by 501 trees, is green striped. The normalised volume has a size of 0.015, which is 1.5% of the space. Within this area, there are 475 data points, of which 474 belong to a stable network setting, which is 1.36% of the training data. The area is, thus, relatively well represented. The artificial selection of data points on a grid has an important role in this
After the problem considered in Sect. 6.1.2 already required a very long optimization time, it is not surprising that the runtime is also a problem for Volume. Only up to 100 trees can be solved using the MIP model within 4 hours, as shown in Table 6.
In order to solve the problem also for the random-forest classifier with 1, 000 decision trees, we can again follow a step-by-step approach. Because of the non-linear objective function, we need two iterative procedures.
Analogously as in the previous problem, we want to consider only variables and constraints from a subset of the possible paths in an iterative approach to save computation time. For each path, we first determine the normalised volume of the axis-parallel cuboids resulting from the decision rules in the nodes. To this end, we consider all decision rules for each path and determine the largest lower bound and the smallest upper bound on each parameter. The bounds of a constraint \( k_i x_i \le b \) belonging to the parameter \( i \in \{1, \ldots p\} \) are obtained by dividing the right-hand side b by the multiplier \(k_i\). This is done equivalently for the constraint \( k_i x_k \ge b \). The distance between the upper and lower bound of a parameter is the length of the cuboid in that parameter. For calculating the normalised volume, we have to normalise this length to the interval [0, 1] at first. The normalised volume of the axis-parallel cuboid is, then, obtained by multiplying the normalised lengths.
We start the iterative approach with the largest possible minimum normalised volume of \( W_0 {:=}1 \). Only variables and constraints of paths whose decision rules form an axis-parallel cuboid with at least this normalised volume are considered. If we cannot form a feasible region with the current paths, the current MIP model is infeasible, and we decrease the volume and consider more paths. Specifically, we halve the minimum normalised volume \( W_k {:=}W_{k - 1} / 2 \) in each iteration \( k \in \mathbbm {N}\). As soon as we have found a feasible region (an axis-parallel sectional cuboid) in some iteration \( k^* \), we can calculate its normalised volume \( V^{\text {opt}}_{k^{*}} \). Now we have achieved a first goal: we know the lower bound \( V^{\text {opt}}_{k^{*}} \) and the upper bound \( W_{k^{*}} \) for the optimal axis-parallel sectional cuboid for the global problem.
Between the minimum normalised volume \( W_{k^{*}} \), which constrains the set of paths considered so far, and the normalised volume \( V^{\text {opt}}_{k^{*}} \), the optimal axis-parallel sectional cuboid found with these paths lies a (possibly very large) distance \( W_{k^{*}} \gg V^{\text {opt}}_{k^{*}} \). The largest possible axis-parallel sectional cuboid has a normalised volume of \( V^{\text {opt}} \) lying between this two values. Paths that form axis-parallel cuboids with their decision rules whose normalised volumes are smaller than \( V^{\text {opt}}_{k^{*}} \) can, thus, safely be ignored. The additional consideration of paths whose decision rules form an axis-parallel cuboid with a volume of at least \( V^{\text {opt}}_{k^{*}} \) can lead to a sectional cuboid with a larger normalised volume than \( V^{\text {opt}}_{k^{*}} \).
Because the distance between \( V^{\text {opt}}_{k^{*}} \) and \( W_{k^{*}} \) is possibly very large, we proceed with another, nested iterative procedure. We start again with the largest possible minimum normalised volume of the sectional cuboid \( \tilde{W}_0 {:=}V_{k^{*}} \). Only variables and constraints of paths whose decision rules form an axis-parallel cuboid with at least this normalised volume are considered in the MIP model. In this iterative process, we will always find a feasible optimal sectional cuboid. After optimization, we can calculate its normalised volume \( \tilde{V}^{\text {opt}}_{\tilde{k}} \). As long as the normalised volume of the found optimal sectional cuboid \( \tilde{V}^{\text {opt}}_{\tilde{k}} \) is smaller than the lower bound \( \tilde{W}_{\tilde{k}} \) on the axis-parallel cuboids of the considered paths, we will reduce it to \( \tilde{W}_{\tilde{k}} = \tilde{W}_{\tilde{k} - 1} \) and, thus, iteratively consider more paths. As soon as the volume of the optimal cuboid \( \tilde{V}^{\text {opt}}_{\tilde{k}^*} \) is at least as large as the lower bound \( \tilde{W}_{\tilde{k}^*} \) on the axis-parallel cuboids of the considered paths for the first time, we can stop the iterative process. The optimal volume of the global problem is that of the found intersection cuboid: \( V^{\text {opt}} = \tilde{V}^{\text {opt}}_{\tilde{k}^*} \). This is because adding more paths whose decision rules form an axis-parallel sectional cuboid whose normalised volume is smaller than the found normalised volume \( \tilde{V}^{\text {opt}}_{\tilde{k}^*} \) cannot lead to a larger sectional cuboid.
Using this iterative method, we were able to find a high-quality, though not optimal solution for the optimization problem corresponding to the large 14-parameter classifier within 4 hours. The computational results can be seen in Table 7.
After 4 hours, we have reached the following intermediate state for the problem with 1, 000 decision trees: using paths whose decision rules have an axis-parallel cuboid with a volume of at least \( \tilde{W}_{\tilde{k}} = 0.02 \), we find an optimal sectional cuboid whose normalised volume is \( \tilde{V}^{\text {opt}}_{\tilde{k}} = 0.014 \). The best solution found is already very close to the optimal solution.
6.2 Discussion of the optimization models and practical implications
Using various mixed-integer models, we developed three strategies to find best possible solutions to random-forest-based classification problems at the example of LVDC network stability.
As an advantage, the analysed data represents a real direct current network, and conclusions are drawn from real data, in contrast to the typical situation where at least certain parts of an instance have to be ’guessed’. However, this also means that the approach can only be tested for one network topology. In order still evaluate different settings, we have compared the quality of different optimization models and random forest sizes in our detailed computational study.
In the solution strategy Adjust, we provide a minimal adjustment of parameters to find the optimum solution. It is advantageous that for model Adjust we can determine solutions very quickly. For the application, Adjust enables a fast assessment of the stability situation in a given network. If the starting point is unstable, the extended parameter adjustments to reach a stable region can be estimated. Depending on the parametrisation of the optimization, i.e. which parameters are included, adjustments in different parameters, e.g. in software parameters \( k_{\text {AC}} \), \( k_{\text {PV}} \) may be compared to results where device parameters, e.g. \( c_{\text {AC}} \), \( c_{\text {PV}} \) are changed. As a potential drawback, the obtained solutions may be “at the border” of feasibility, such that perturbations in the data can potentially lead to infeasibilities.
The Reliable model initially requires more computation time than Adjust. Using the iterative procedure, we were able to match or outperform the times for the simple Adjust problem. For our instances, it could always produce a solution that is well contained inside a stable parameter region. As a result, solutions remain stable even under small input uncertainties. For the practical application, the strategy Reliable enables a reliable selection of the input parameters to obtain a stable network state. From the radius of the optimal sphere, the tolerance of the parameters to reach unstable states can be estimated. As possible future improvements, it might be worth integrating a way to rank the features. Furthermore, it is certainly interesting in the application to take certain parameters, such as the cable length, out of the optimization and assign them fixed realistic values. Depending on these, the other parameters can be chosen reliably enough with the help of the objective function Reliable.
A most reliable stable point is one that has the largest possible distance to all inequalities. Parameters with high feature importance typically constrain the feasible set more often and severely. Therefore, the position of the most reliable point usually depends on these parameters. Solutions with the same level of certainty in the parameters with high feature importance and a more reliable position for features with low feature importance could be given special consideration.
In contrast to Reliable, problem Volume determines large stable regions within which the network is stable. Here, the intervals of the parameters are considered individually and independently of their feature importance. However, due to the initially non-linear objective function and its linearisation, the optimization model typically requires significantly longer computation times. If a large number of random forests is to be considered, a stepwise approximation to the optimal solution is required. For the practical application, the strategy Volume is the most important setting for identifying reliable, stable regions. However, care needs to be taken in the generation of random-forest classifiers, since areas may differ in the density of calculated representations, especially when linear and logarithmic scaling points are overlaid. Thanks to the training data that has been generated to represent realistic problem settings, we were able to find a representative cuboid in our solution. Starting from a LVDC circuit model, where typically the device parameters are not fixed, e.g. when identifying a potential dimensioning of the grid parameters, and are varied within several orders of magnitude, e.g. as done for the parameters \( c_{\text {AC}} \), \( c_{\text {PV}} \), reliable, stable areas can be determined. To avoid unequal point densities as described above, the parameter ranges may be reduced until accurate random-forest classifiers can be obtained with linear scaling of the input parameters where the point density is nearly equivalent, and the largest stable region may be more precisely determined for the refined network setting.
In order to keep the model manageable, it is important to determine a relevant set of decision trees with limited size. Random-forest classifiers can be trained very easily and quickly with the help of software frameworks, even with many trees.
However, above a certain threshold, increasing the number of trees does not improve the accuracy further. The Grid_Search method of scikit-learn can be used to decide how many decision trees are needed for this purpose so that the effort can be estimated beforehand. For the network stability application, we have shown successfully that the optimization models can still be solved globally even with large classifier. We have simplified the optimization problem to an iterative solution of feasibility problems, as described for Adjust. Furthermore, we have strongly reduced the number of active inequalities in Reliable and Volume.
The work presented here concludes an initial study towards a new approach for optimizing stability in LVDC microgrids. The challenge here originates from the complexity of stability assessment including the selection of the stability criteria, their parametrisation and the capability for automated evaluation. Frequently, two parameters are evaluated independently for stability assessment as depicted in the presented examples – leading to a classification of the network as sufficiently stable or not. The new optimization approach presented here enables, for example, the design and parametrisation of new networks or the operation of existing networks targeting large stable operation regions or minimised adjustments in the latter case. In an ongoing experimental work to further validate the approach, an experimental setup was established, which mimics the network structure as depicted in Fig. 4. The modular structure of the approach allows for flexible modification of the input parameter settings in the digital twin. For the experimental setup, the individual parameters of the source components need to be characterised. Specifically, the capacitances and line inductances rather than the line lengths were measured to serve as input parameters to the digital twin and subsequent surrogate modelling and optimization. The runtime of the optimization and the performance of the optimization result will be further tested on the experimental setup. Concerning the computational effort, it is anticipated that for network design the computation time does not impose a restriction such that the approaches outlined here can be applied. Furthermore, in an existing setup less parameters need to be varied as several parameters are fixed, e.g. the capacitances or transmission line inductances, such that merely the factors \( k_{\text {AC}} \) and \( k_{\text {PV}} \) for changing the droop decline or the cut-off frequencies \( f_{\text {CAC}} \) and \( f_{\text {CPV}} \) of the output filter at the source converters need to be changed. Thus, the case study performed here is very relevant for our future work in network stability.
7 Conclusions
In this work, we have presented a practical optimization approach for integrating model- and data-based methods and showed its applicability in practice. For this purpose, we used a combined MIP- and machine-learning-based approach. Inequalities that can easily be formulated as linear mixed-integer inequalities are explicitly modelled in the optimization problem. To replace complex or unknown constraints, we performed two steps. First, using a representative data set, we trained a classifier, in our case a random-forest classifier, because it has several advantages to our considered settings. Then, we modelled the decisions algebraically and included them as additional constraints in the MIP model.
In our case study on the stability of DC networks, we showed that this approach leads to high-quality results in practical problems. The task was to find stable network settings for a DC grid with system voltages below 1500 V (low-voltage dc grids, LVDC grids) so that the safety and reliability of the model can be guaranteed. For this approach, a large dataset was used to train a random-forest classifier for which the resulting classifications were included in algebraic form in the MIP. As objective functions, we considered different relevant objectives, namely the closest and the most reliable stable network setting. Furthermore, we determined the largest possible stable area from the random-forest classifier.
Although modern MIP solvers can optimize large instances, the number of decision trees naturally plays a significant role in the performance of solving these optimization problems. In this work, we have shown how the solution of the MIPs can be enhanced by sequential execution of slightly adapted MIP models that are at first strongly constrained and thus typically infeasible. Then, the constraints are iteratively relaxed until the appropriate model is found from which the solution can be determined. This approach significantly reduces the runtime, because testing the infeasibility of a model is typically fast. As future work, it is interesting to analyse whether the runtime can be improved further, possibly by a better encoding of the random forests or by a potential extension to multivariate trees.
References
Achterberg T, Wunderling R (2013) Mixed integer programming: analyzing 12 years of progress, pages 449–481. Springer Berlin Heidelberg, Berlin, Heidelberg
Aigner K-M, Burlacu R, Liers F, Martin A (2021a) Solving AC optimal power flow with discrete decisions to global optimality. Preprint
Aigner K-M, Clarner J-P, Liers F, Martin A (2021) Robust approximation of chance constrained DC optimal power flow under decision-dependent uncertainty. Eur J Op Res 301(1):318–333
Azaioud H, Claeys R, Knockaert J, Vandevelde L, Desmet J (2021) A low-voltage DC backbone with aggregated res and bess: benefits compared to a traditional low-voltage AC system. Energies 14(5):1420
Bertsimas D, Dunn J (2017) Optimal classification trees. Mach Learn 106(7):1039–1082
Bertsimas D, Dunn J, Mundru N (2019) Optimal prescriptive trees. INFORMS J Optim 1(2):164–183
Bertsimas D, O’Hair A, Relyea S, Silberholz J (2016) An analytics approach to designing combination chemotherapy regimens for cancer. Manag Sci 62(5):1511–1531
Bhavsar H, Ganatra A (2012) A comparative study of training algorithms for supervised machine learning. Int J Soft Comput Eng 2:74–81
Biau G, Devroye L, Lugosi G (2008) Consistency of random forests and other averaging classifiers. J Mach Learn Res 9:2015–2033
Biggs M, Hariss R, Perakis G (2017) Optimizing objective functions determined from random forests. SSRN Electron J
Bishop CM (2006) Pattern recognition and machine learning. Springer, Berlin
Bixby R, Rothberg E (2007) Progress in computational mixed integer programming—a look back from the other side of the tipping point. Ann OR 149:37–41
Bonfietti A, Lombardi M, Milano M (2015) Embedding decision trees and random forests in constraint programming. In: Michel L (ed) Integration of AI and OR techniques in constraint programming. Springer, Cham, pp 74–90
Boyd SP, Vandenberghe L (2014) Convex optimization. Cambridge University Press, Cambridge
Breiman L (1996) Bagging predictors. Mach Learn 24(2):123–140
Breiman L (2001) Random forests. Mach Learn 45(1):5–32
Breiman L (2001) Statistical modeling: the two cultures (with comments and a rejoinder by the author). Stat Sci 16(3):199–231
Breiman L, Friedman JH, Olshen RA, Stone CJ (1984) Classification and regression trees. Wadsworth & Brooks, Monterey
Carpentier J (1962) Contribution a l’etude du dispatching economique. Bulletin de la Societe Francaise des Electriciens 3(1):431–447
Ceccon F, Jalving J, Haddad J, Thebelt A, Tsay C, Laird CD, Misener R (2022) Omlt: optimization & machine learning toolkit. J Mach Learn Res 23(349):1–8
Ferreira K, Lee B, Simchi-levi D (2015) Analytics for an online retailer: demand forecasting and price optimization. Manuf Serv Op Manag 18(1):69–88
Gao F, Kang R, Cao J, Yang T (2019) Primary and secondary control in DC microgrids: a review. J Modern Power Syst Clean Energy 7(2):227–242
Geißler B, Martin A, Morsi A, Schewe L (2012) Using piecewise linear functions for solving MINLPs. In: Lee J, Leyffer S (eds) Mixed integer nonlinear programming. Springer, New York, pp 287–314
Gurobi Optimization LLC (2020) Gurobi optimizer reference manual. https://www.gurobi.com/wp-content/plugins/hd_documentations/documentation/9.0/refman.pdf. Accessed on 14 Oct 2020
Halilbašić L, Thams F, Venzke A, Chatzivasileiadis S, Pinson P (2018) Data-driven security-constrained AC-OPF for operations and markets. In 2018 Power Systems Computation Conference (PSCC), pages 1–7
Hastie T, Tibshirani R, Friedman J (2009) The elements of statistical learning—data mining, inference, and prediction, 2nd edn. Springer, Berlin
Hendrix EM, Mecking CJ, Hendriks TH (1996) Finding robust solutions for product design problems. Eur J Op Res 92(1):28–36
International Electrotechnical Commission, editor (2016) Protection against electric shock – Common aspects for installations and equipment, volume IEC 61140:2016. VDE, Geneva, Switzerland, 4 edition
Jena M, Dehuri S (2020) Decisiontree for classification and regression: a state-of-the art review. Informatica, 44
Kronqvist J, Lundell A, Westerlund T (2017) A center-cut algorithm for solving convex mixed-integer nonlinear programming problems. In: EspuÃ\(\pm \)a A, Graells M, Puigjaner L (Eds), 27th European Symposium on Computer Aided Process Engineering, volume 40 of Computer Aided Chemical Engineering, pages 2131–2136. Elsevier
Kuchlbauer M, Liers F, Stingl M (2021) Outer approximation for mixed integer nonlinear robust optimization. Preprint
Kumar A, Serra T, Ramalingam S (2019) Equivalent and approximate transformations of deep neural networks. CoRR, arXiv:1905.11428
Kumar AL, Indragandhi V, Maheswari UY (2020) Software tools for the simulation of electrical systems, 1st edn. Academic Press, San Diego
Lin CD, Tang B (2015) Latin hypercubes and space-filling designs. CRC Press, Boca Taton, pp 593–625
Loh W-Y (2011) Classification and regression trees. WIREs Data Min Knowl Discov 1(1):14–23
Loh W-Y (2014) Fifty years of classification and regression trees. Int Stat Rev 82(3):329–348
Maragno D, Wiberg HM, Bertsimas D, Birbil SI, den Hertog D, Fajemisin AO (2021) Mixed-integer optimization with constraint learning. CoRR, arXiv:2111.04469
Markowitz HM, Manne AS (1957) On the solution of discrete programming problems. Econometrica 25(1):84
Mary A, Cain B, O’Neill R (2012) History of optimal power flow and formulations. Fed Energy Regul Comm 1:1–36
Mišić VV (2020) Optimization of tree ensembles. Oper Res 68(5):1605–1624
Mistry M, Letsios D, Krennrich G, Lee RM, Misener R (2021) Mixed-integer convex nonlinear optimization with gradient-boosted trees embedded. INFORMS J Comput 33(3):1103–1119
Ott L, Han Y, Stephani O, Kaiser J, Wunder B, März M, Rykov K (2015a) Modelling and measuring complex impedances of power electronic converters for stability assessment of low-voltage DC grids. In 2015 IEEE First International Conference on DC Microgrids (ICDCM), pages 51–56
Ott L, Han Y, Wunder B, Kaiser J, Fersterra F, Schulz M, März M (2015b) An advanced voltage droop control concept for grid-tied and autonomous dc microgrids. In 2015 IEEE International Telecommunications Energy Conference (INTELEC), pages 1–6
Pedregosa F, Varoquaux G, Gramfort A, Michel V, Thirion B, Grisel O, Blondel M, Prettenhofer P, Weiss R, Dubourg V, Vanderplas J, Passos A, Cournapeau D, Brucher M, Perrot M, Duchesnay E (2011) Scikit-learn: machine learning in Python. J Mach Learn Res 12:2825–2830
Riccobono A, Santi E (2014) Comprehensive review of stability criteria for dc power distribution systems. IEEE Trans Ind Appl 50(5):3525–3535
Roeder G, Ott L, Meier A, Wunder B, Wienzek P, Bärmann A, Liers F, Schellenberger M (2021) Analysis and improvement of LVDC-grid stability using circuit simulation and machine learning - a case study. NEIS 2021; Conference on Sustainable Energy Supply and Energy Storage Systems, pages 1–7
Sagi O, Rokach L (2018) Ensemble learning: a survey. WIREs Data Min Knowl Discov 8(4):e1249
Scikit-Learn (n.d.). Decision trees - scikit-learn 0.24.2 documentation. https://scikit-learn.org/stable/modules/tree.html. Accessed on 08 Mar 2021
Shahriari B, Swersky K, Wang Z, Adams RP, de Freitas N (2016) Taking the human out of the loop: a review of Bayesian optimization. Proc IEEE 104(1):148–175
Åström KJ, Murray RM (2008) Feedback systems—an introduction for scientists and engineers. Princeton University Press, New York, pp 278–282
Thebelt A, Kronqvist J, Lee RM, Sudermann-Merx N, Misener R (2020) Global optimization with ensemble machine learning models. In: Pierucci S, Manenti F, Bozzano GL, Manca D (eds) 30th European Symposium on Computer Aided Process Engineering, volume 48 of Computer Aided Chemical Engineering. Elsevier, pp 1981–1986
Thebelt A, Kronqvist J, Mistry M, Lee RM, Sudermann-Merx N, Misener R (2021) ENTMOOT: a framework for optimization over ensemble tree models. Comput Chem Eng 151:107343
Thebelt A, Tsay C, Lee RM, Sudermann-Merx N, Walz D, Tranter T, Misener R (2022) Multi-objective constrained optimization for energy applications via tree ensembles. Appl Energy 306:118061
Thorbjarnarson T, Yorke-Smith N (2020) On training neural networks with mixed integer programming. CoRR, arXiv:2009.03825
Vielma JP (2015) Mixed integer linear programming formulation techniques. SIAM Rev 57(1):3–57
Weiss R, Ott L, Boeke U (2015) Energy efficient low-voltage DC grids for commercial buildings. In 2015 IEEE First International Conference on DC Microgrids (ICDCM), pages 154–158
Wunder B, Ott L, Han Y, Kaiser J, Maerz M (2015) Voltage control and stabilization of distributed and centralized dc micro grids. In Proceedings of PCIM Europe 2015; International Exhibition and Conference for Power Electronics, Intelligent Motion, Renewable Energy and Energy Management, pages 1–8
Acknowledgements
We thank the DFG for their support within Projects B06 and Z01 in CRC TRR 154. Furthermore, we acknowledge financial support by the Bavarian Ministry of Economic Affairs, Regional Development and Energy through the Center for Analytics—Data—Applications (ADA-Center) within the framework of “BAYERN DIGITAL II” (20-3410-2-9-8). Last but not least, we thank the anonymous referees for their insightful comments, which led to a substantial improvement of the paper.
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
A list of network parameters
A list of network parameters
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Gutina, D., Bärmann, A., Roeder, G. et al. Optimization over decision trees: a case study for the design of stable direct-current electricity networks. Optim Eng 24, 2651–2691 (2023). https://doi.org/10.1007/s11081-023-09788-x
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11081-023-09788-x