1 Introduction

Distribution systems are large-scale systems consisting of many components and assets that need periodic maintenance to work properly and provide reliable electricity to consumers. Although the importance and severity of distribution system fault/failure are much greater than other parts of power systems (generation, transmission), there is a great number of fault/failures that happened in this section because of the numerous components it has. On the other hand, asset/equipment management has become a popular subject among large-scale companies like electrical distribution networks. Equipment management functions as a method that supplies and ensures continuous, reliable, and affordable energy to consumers. Maintenance management is a subdivision of facilities management. Maintenance is necessary for ensuring that assets such as equipment and components remain in operation status.

Maintenance does not follow a constant method and is not limited to component place and type. Maintenance cost is considered an economic burden and there is not enough willingness to pay more than necessary for ensuring that the system continues to operate. According to (Booty 2009), maintenance needs a lot of resources and takes up about three-quarters of the lifetime cost of a building. Deferring and neglecting maintenance is a non-economic strategy since it can be recovered in the form of a maintenance backlog which could be more expensive and disruptive (Hopland 2015). Thus, preventive maintenance (PM) is in priority over corrective maintenance (CM). Additionally, in performing preventive maintenance assets which are more expensive, more sensitive, or more effective on the reliable operation of the system are in preference (Chong et al. 2019; Schulze Spüntrup et al. 2021).

According to what is vividly explained, applying maintenance strategies should be done in a logical way that allocates limited maintenance budget to the most critical and sensible sections and manage maintenance backlogs. Asset managers should make adequate decisions about allocating the limited resources among most maintenance-needed components (prioritization). So that the prioritization is a complicated and comprehensive kind of decision-making process. Since proper maintenance prioritization requires a lot of consideration and detailed decision-making, a thorough understanding of various factors related to the components of the system prioritizations is needed (Moore and Starr 2006). Priorities are arranged based on subjective judgment and the immediate needs of the systems. Reliability, availability, affordability, security, etc., are some of the factors that distribution networks’ components prioritize by them (Canto 2011; Shen et al. 2010). Reliability-centered maintenance (RCM) is known as the most effective and accurate method of preventive maintenance scheduling in which the process of prioritization is considered the first and most important step.

Component prioritization of distribution systems for applying preventive maintenance has been the subject of many researches and decision-making techniques for maintenance action are very popular. For instance, in Dehghanian et al. (2011), an innovative approach based on an analytical hierarchical process (AHP) coupled with fuzzy sets is presented to prioritize the components of distribution power systems for maintenance scheduling. In Gupta and Mishra (2018), a hierarchical system based on an analytic network process is used to identify the critical components. In the decision-making environment, the most critical components for maintenance scheduling have been identified in Pintelon and Gelders (1992). In daily, seasonal and yearly scenarios, the load and availability of energy resources in the microgrid are forecasted in Reddy et al. (2012) by Artificial Neural Network (ANN) for maintenance management. Numerous approaches are established to improve the planning of PM, (Teera-achariyakul and Rerkpreedapong 2019) has been concentrated on component outage occurrence possibility and cost-based subsequences. (Arya 2016) presented a new factor named diagnostic factor that is based on the unavailability of components to set the prioritization.

On the other hand, (Afzali et al. 2019) introduced a new weighted importance (WI) reliability index model and presented a method to prioritize the components of the distribution system for reliability-centered maintenance (RCM) at two different levels. Two different models of passive PM (to minimize the maintenance costs) and active PM (to maximize the profit) for renewable energy resources systems are proposed in Mazidi and Sanz (2017).

Many studies have investigated the RCM in the distribution networks. For instance, the RCM model is presented in Yssaad et al. (2014) for maintenance management of equipment. In Yssaad and Abene (2015), a rational maintenance optimization is done by the experimental RCM approaches based on the analysis of the failure modes of inefficient systems. Reference (Sabouhi et al. 2016) has presented a risk-based method to identify critical components. A practical method involving three levels of prerequisites for analysis, identifying the critical components, and reporting technical and economical results is proposed in Dehghanian et al. (2013). Using the RCM process in distribution systems, a systematic method is proposed in Moradi et al. (2019) that exploits the fundamentals of multi-attribute decision making for evaluating the important features and failure attributes and identifying the micro-grid critical components with their failure rates evaluated at different time periods. A risk-based method to identify critical components has been proposed in Gorji et al. (2017).

Several research works are about the maintenance optimization of the distribution system components that consider the effects of optimal maintenance on the reliability of the system. In Piasson et al. (2016), a multi-objective model has been proposed to optimize the RCM scheduling of the distribution system. In Choobineh and Mohagheghi (2016), the maintenance-programming problem is modeled as a multi-objective non-linear mixed-integer optimization problem and is solved using the extended lexicographic goal programming method. Inspection-based maintenance results about the time and type of the maintenance tasks are recommended in Samadi et al. (2019) for annual transmission equipment maintenance management. The effect of main reliability indices and economic aspects is missing in previous works.

This study presents an innovative factor, namely the Weighted Cumulative Reliability-Based Diagnostic Importance Factor, as an appropriate new method of RCM prioritization for all components of the distribution system. As the nature of this factor is organized on reliability indexes, interruption cost reduction, and also using unique weighting system by covering size and kind of load points it is considered all technical and economic aspects of maintenance programming. Preparing a classified prioritized list of distribution systems’ components and determining the most critical one is the main result of this paper. Applying PM to the most critical section will decrease the maintenance cost significantly.

In this paper, MATLAB software is used for calculations and the maintenance prioritization of components has been carried out. Instead of using the reliability indexes, which were applied in many studies, a kind of sensitivity analysis of reliability indexes is used in this study named diagnostic factor. Two series of data to form sensitivity analysis are needed and indicated in two scenarios. The comprehensive weighting system is used to improve the validity of the prioritization method which involved size, importance and kind, and cost of interruption for each load point. To tie all these together, the main contributions and novelties of this article are as follows:

  1. (1)

    Bolding the role of prioritization in maintenance problems for two logical reasons:

    1. (a)

      Some parts of the system have more effect on improving the reliability level of the total system.

    2. (b)

      Considering all components of the system in maintenance problems makes it more difficult and complex.

  2. (2)

    Developing maintenance program efficiency by combining diagnostic importance idea with reliability indexes for making new factor used in Ranking distribution system components.

  3. (3)

    Applying the algorithm to sample radial distribution system with distributed generation units for checking the effect of distributed generations (DGs) on improving reliability level at load points that supply them.

The remaining part of this paper is organized as follows: Sect. 2 is about the basic concept of RCM and Sect. 3 introduced the framework and formulation of the proposed model. The model is implemented on a part of the radial distribution network and the results of effectiveness and practicality of this model in real‐world are shown in Sect. 4. Finally, the conclusion is given in Sect. 5.

2 Reliability centered maintenance requirements

Using RCM methods for electrical distribution networks needs to find the components that affect the system majorly. The criticality of each component is quantified with a designed factor. So this factor should be efficient enough in order to reach the target value of reliability after applying PM on the most critical component has been determined by that. Obviously, the appropriate prioritization method plays the main role in this manner. Then, identified critical components can lead the designers to perform a proper PM strategy for a distribution network. Therefore, in this study, developing maintenance program efficiency by combining diagnostic importance idea with reliability indexes for making new factor used in ranking distribution system components has been proposed.

3 Proposed framework

To prepare the effective and correct ranking list of components for applying maintenance activities on the distribution system we need to analyze the impact of each section's reliability and the interruption. In this section, the fundamental concepts are discussed, the developed algorithm is presented and the required mathematical formulations are introduced.

3.1 Data preparing

At the first level, all technical and economic data needed for our simulation including single line diagram (SLD), failure rate and repair rate of the feeder sections, load points power and number and type of each load point customer and cost of loss loads should be collected.

3.2 Reliability based diagnostic importance factors producing

Reliability-based diagnostic importance factor (RDIF) signifies the comparative importance of a component for maintenance activities in a system in relation with others. This factor expresses the contribution of each component to the overall system failure rate. Mathematically it is a conditional probability and defined as Eq. (1) (Xing 2004). Where n denotes desired component and SYS denotes the system.

$$ {\text{ d}}_{n} = {\text{P}}\left[ {\overline{n}/\overline{SYS} } \right] $$
(1)

According to probability rules, Eq. (1) could rewrite as follows:

$$ {\text{d}}_{n} = {\text{P}}\left[ {\overline{n} \cap \overline{SYS} } \right]/{\text{P}}\left( {\overline{SYS} } \right) $$
(2)
$$ {\text{d}}_{n} = {\text{ P}}\left[ {\overline{SYS} /\overline{n}} \right]{\text{P}}\left[ {\overline{n}} \right]/{\text{P}}\left( {\overline{SYS} } \right) $$
(3)

A new index for evaluating system and component failure can be created by using Eq. (3). This index considers not only components failure probability but also significance of their position in the system. For example, \({\text{P}}\left[ {\overline{n}} \right]\) may be high but if \({\text{P}}\left[ {\left( {\overline{SYS} } \right)/\overline{n}} \right] \) is insignificant then the RDIF measure will be small. The probability function which is used RDIF in Eq. (3) can appear in various forms and functions of the system’s reliability analysis. Some reliability functions that can apply in this form are unavailability, system average interruption frequency index (SAIFI), system average interruption duration index (SAIDI), and energy not supplied (ENS) or any other indexes which are considered by the systems maintenance manager.

The unavailability of the repairable section is calculated as Eq. (4). Where \(\lambda\) denotes the failure rate and r denotes the duration of failure.

$$ {\text{U}}_{n} = \lambda_{n} \times {\text{r}}_{n} $$
(4)

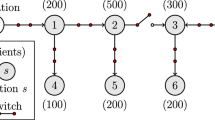
Depending on the system layout, parallel or series component composition is determined, and the total unavailability of each load is calculated. In series order Eq. (5) and in parallel mode the equivalent unavailability and failure rate is calculated as Eq. (6). Noted that if the system has distributed generation unit (DG) in any load point, it should be considered as a parallel component; adding DGs to the specific load point is leads to improving the reliability of it by decreasing the total failure rate and equivalent unavailability while considering DGs as serial component increase these parameters by arithmetic progression. The equivalent reliability network in load point with DG is shown in Fig. 1.

$$ U_{ser} = \mathop \sum \limits_{i = 1}^{NC} \lambda_{i} \times {\text{r}}_{i} $$
(5)
$$ U_{para} = \mathop \prod \limits_{i = 1}^{NC} \lambda_{i} \times {\text{r}}_{i} $$
(6)
Fig. 1
figure 1

Equivalent reliability network

Full size image

In Eq. 4, by replacing \({\text{P}}\left[ {\overline{n}} \right]\) with the unavailability of component (\({\text{U}}_{n}\)), \({\text{P}}\left[ {\overline{SYS} /\overline{n}} \right]\) with the unavailability of load point when the n-th component is not available (\({\text{U}}_{LP - k} \left( {\overline{n}} \right)\)) and \({\text{P}}\left( {\overline{SYS} } \right)\) with the unavailability of k-th load point (\({\text{U}}_{LP - k}\)), first part of RDIF for n-th component of k-th load is generated (7):

$$ {\text{d}}1_{n - k} = {\text{ U}}_{LP - k} \left( {\overline{n}} \right) \times {\text{U}}_{n} /{\text{U}}_{LP - k} $$
(7)

As described above, in process of unavailability-based RDIF of the system, two kinds of data are needed to form two scenarios. There are:

  1. 1.

    The average failure rate of every component including: DG’s, switches, cables, transformers, etc. These data are used to form the unavailability of each load point, average unavailability when all components are in their average failure rate.\( ({\text{U}}_{LP - k}\)).

  2. 2.

    The maximum amount of failure rate for components. This group of data uses for calculating the failure rate of load points when one of the components fails or in maximum failure rate and other components are working in under normal operation conditions and have an average failure rate. (\( {\text{U}}_{LP - k} \left( {\overline{n}} \right)\)).

By Eq. (8), the importance and effect of the n-th component in the unavailability of the k-th component are diagnosed. This importance will increase if the unavailability of the n-th component increases and the unavailability of a component will increase when the failure rate of that increases. From this view, we can dedicate that a component with a larger amount of diagnostic importance factor is prioritized for maintenance activity in relation to the other ones. On the other hand, each feeder component has a varying magnitude of \({\text{d}}1_{n - k}\) for various load points (that denotes as \(W_{1k}\) in Eq. (8).). So the total unavailability based diagnostic importance of a component will calculate:

$$ D1_{n - k} = \mathop \sum \limits_{k = 1}^{NLP} W_{1k} \times {\text{d}}1_{n - k} $$
(8)

For a more comprehensive study, other reliability indexes should be considered. Depending on the type of system and the manager’s reliability goals, various kinds of reliability indexes can sit in forming of the diagnostic importance factors. So exactly the same as what was done about unavailability, other forms of reliability-based diagnostic importance factors are produced:

$$ {\text{d}}2_{n - k} = {\text{ SAIFI}}_{LP - k} \left( {\overline{n}} \right){\text{U}}_{n} /{\text{SAIFI}}_{LP - k} $$
(9)
$$ {\text{d}}3_{n - k} = {\text{ SAIDI}}_{LP - k} \left( {\overline{n}} \right){\text{U}}_{n} /{\text{SAIDI}}_{LP - k} $$
(10)
$$ {\text{d}}4_{n - k} = {\text{ ENS}}_{LP - k} \left( {\overline{n}} \right){\text{U}}_{n} /{\text{ENS}}_{LP - k} $$
(11)

In which the reliability indices (SAIFI, SAIDI, and ENS) can be calculated using the hourly average failure rate of components as follows:

$$ {\text{SAIFI}} = \frac{{\mathop \sum \nolimits_{LP = 1}^{NLP} \lambda_{LP} \times N_{LP} }}{{\mathop \sum \nolimits_{LP = 1}^{NLP} N_{LP} }} $$
(12)
$$ {\text{SAIDI}} = \frac{{\mathop \sum \nolimits_{LP = 1}^{NLP} U_{LP} \times N_{LP} }}{{\mathop \sum \nolimits_{LP = 1}^{NLP} N_{LP} }} $$
(13)
$$ {\text{ENS}} = \mathop \sum \limits_{LP = 1}^{NLP} U_{LP} \times P_{LP} $$
(14)

3.3 Weighting coefficients designing for RDIFs

The differentiation between RDIF's is gained from the appropriate weighting coefficient. In this paper, the systematic framework of weighting coefficient production is constructed that contains three important aspects: the size of the load, the type of load, and also the financial view of each load point that is modeled with customer interruption cost (CIC). So \(W_{1i}\) is:

$$ W_{1i} = \frac{{CIC^{norm} }}{{{\text{d}}1_{n - k}^{norm} }} \times \frac{{P_{i} }}{{\mathop \sum \nolimits_{i = 1}^{NLP} P_{i} }} \times LT_{i} $$
(15)

Load type (LT) modeling: Generally, there are three types of loads: residential, commercial, industrial and according to this classification amount of LT is listed in the following Tables 1, 2. Equation (16) is the newly developed mathematical expression for practical and various types of load models (Bohre et al. 2016):

$$ LT = a_{1} \left( {\frac{{v_{i} }}{{v_{o} }}} \right)^{{\alpha_{0} }} + b_{1} \left( {\frac{{v_{i} }}{{v_{o} }}} \right)^{{\alpha_{i} }} + c_{1} \left( {\frac{{v_{i} }}{{v_{o} }}} \right)^{{\alpha_{r} }} + d_{1} \left( {\frac{{v_{i} }}{{v_{o} }}} \right)^{{\alpha_{c} }} $$
(16)

  • Load type-1: industrial load: \(a_{1}\) = 0, \(b_{1}\) = 1, \(c_{1}\) = 0,\(d_{1}\) = 0, and \(\frac{{v_{i} }}{{v_{o} }}\) = 1.05

  • Load type-2: residential load: \(a_{1}\) = 0, \(b_{1}\) = 0, \(c_{1}\) = 1,\(d_{1}\) = 0 and \(\frac{{v_{i} }}{{v_{o} }}\) = 1

  • Load type-3: commercial load: \(a_{1}\) = 0, \(b_{1}\) = 0, \(c_{1}\) = 0,\(d_{1}\) = 1 and \(\frac{{v_{i} }}{{v_{o} }}\) = 1.02

Table 1 Different load types
Full size table
Table 2 Average load at load points for radial distribution system
Full size table

Customer Interruption Cost (CIC) modeling: For modeling the financial importance aspect, the CIC equation which contains the failure rate of each load point (\(\lambda_{i}\)), the real power of them (\(P_{i}\)), fixed cost of load interruption (\(f_{i}\)), cost of energy not delivered (\(C_{i}\)) and also average repair time for a total component in the way of each load points. The CIC is calculated as follows:

$$ CIC_{i} = \lambda_{i} \times \left( {f_{i} \times P_{i} + C_{i} \times P_{i} \times r_{i} } \right) $$
(17)

Other weighting coefficient for these three RDIF’s will defined as bellow:

$$ W_{2i} = \frac{{CIC^{norm} }}{{{\text{d}}2_{n - k}^{norm} }} \times \frac{{P_{i} }}{{\mathop \sum \nolimits_{i = 1}^{NLP} P_{i} }} \times LT_{i} $$
(18)
$$ W_{3i} = \frac{{CIC^{norm} }}{{{\text{d}}3_{n - k}^{norm} }} \times \frac{{P_{i} }}{{\mathop \sum \nolimits_{i = 1}^{NLP} P_{i} }} \times LT_{i} $$
(19)
$$ W_{4i} = \frac{{CIC^{norm} }}{{{\text{d}}4_{n - k}^{norm} }} \times \frac{{P_{i} }}{{\mathop \sum \nolimits_{i = 1}^{NLP} P_{i} }} \times LT_{i} $$
(20)

Normalization processes in previous equations are done based on Eq. 21:

$$ X_{norm} = \frac{X}{{X_{max} }} $$
(21)

where \(X_{max}\) is the upper bound of X and \(X_{norm}\) is normalized X.

According to what is presented, SAIFI-based RDIF (\(D2_{n - k}\)), SAIDI-based RDIF (\(D3_{n - k}\)) and ENS-based RDIF (\(D4_{n - k}\)) respectively are:

$$ D2_{n - k} = \mathop \sum \limits_{k = 1}^{NLP} W_{2k} \times {\text{d}}2_{n - k} $$
(22)
$$ D3_{n - k} = \mathop \sum \limits_{k = 1}^{NLP} W_{3k} \times {\text{d}}3_{n - k} $$
(23)
$$ D4_{n - k} = \mathop \sum \limits_{k = 1}^{NLP} W_{4k} \times {\text{d}}4_{n - k} $$
(24)

For correct evaluation among all four RDIF’s, normalization in one common base is applied here. Each CIC’s is normalized in the same related RDIF’s. So that the weighting process of each RDIF is applied for four RDIF’s in the same base, and we should make a new cumulative factor with these Weighted Reliability-based Diagnostic Importance Factors (WRDIF). The proposed Weighted Cumulative RDIF model in this paper is defined as follows:

$$ {\text{WCRDIF}} = \mathop \sum \limits_{x = 1}^{4} Dx_{n - k} $$
(25)

Whatever the value of the WCRDIF index to be more, the reliability grade of the component is lower, the importance of it is more because its condition is critical, and its priority for maintenance action is higher. Any other reliability indexes can be inserted into this model. The important point is that all surveyed indexes here (Unavailability, SAIFI, SAIDI, ENS) have a negative effect on reliability (the less amount they have, the better reliability level system has), so they direct sum in WCRDIF. If there is a reliability index like ASAI (Average Service Availability Index) which has a positive aspect should inverse-sum in the weighing system of WCRDIF. According to obtained ranking list, the upper place in the ranking list, the more critical component is. The following flowchart shows the sequence of the proposed algorithm (Fig. 2).

Fig. 2
figure 2

Flowchart of the proposed algorithm

Full size image

4 Results and discussion

In this paper, the RCM prioritization process is analyzed by implementing the proposed framework on a sample distribution system. A single-line diagram of the proposed system is shown in Fig. 3 and consists of 33 load points and 34 sections. Randomly, three DGs have been considered at load points 3, 6, and 8. System data including the average and maximum rate of failure, average repair time of each component/DGs, and average load of each load point have been taken from Memarzadeh and Keynia (2020) in Tables 3, 4, 5.

Fig. 3
figure 3

Radial distribution system with distributed generation

Full size image
Table 3 The radial distribution network’s parameters
Full size table
Table 4 Failure rate and average down time for distributed generation units
Full size table
Table 5 Cost of interruption data for each load point
Full size table

The needed data for calculating CIC by Eq. 18 is interruption cost of each load point, the fixed cost for interruption per kWh(\(f_{i}\)), and the cost for energy not delivered (\(C_{i}\)) which have been taken from [14] and are collected in Table 5. In addition, the real power and total failure rate/failure time of each load point can be calculated from Tables 2 and 3.

As comprehensively described in the last sections, four RDIF’s are calculated using Eqs. 7, 9, 10, and 11 and the results are shown in Table 6. All of the RDIF’s have negative effects and aspects, which means that the higher the amount of them for one component, the more critical the component is. There should be a trade-off between these four factors to produce weighted cumulative factors which determine the criticality of the component from four different points of view.

Table 6 RDIF values of section
Full size table

The weighting coefficient results which are constructed from 3 important aspects of load points (load type, load size, and load interruption cost) using Eqs. 15, 18, 19, and 20 are shown in Table 7. All weighting coefficients and also RDIF’s should be normalized in their own base and then placed in the WCRDIF formula.

Table 7 The weighting coefficients
Full size table

The ranking list obtained from the proposed method is shown in Table 8. Section one is obviously in the first priority due to its critical role in supplying all feeders and its sub-busses, so it is put out of the ranking list calculation. According to the ranking list section, #25 is the most critical section of the system. Sections #24 and #34 are in second and third rank respectively. It means that the maintenance activities and budget should be focused on this part.

Table 8 Ranking list of components
Full size table

For a more thorough look results of ranking according to unavailability-based RDIF, SAIFI-based RDIF, SAIDI-based RDIF, and ENS-based RDIF are collected. If the SAIFI index is more important for the system, the SAIFI-based RDIF first ranked component is #2 (due to previous explanations, section one is omitted from the calculation). As mentioned before priority list organization completely depends on system manager goals and WCRDIF can support multi goals for the system. According to the WCRDIF ranking list interruption in Sect. 25 has more impact on cost than interruption/failure in other components. The following diagrams (Figs. 3, 4) show the ranking list based on criticality analysis for the 33-bus system. The effect of weighting coefficients is clearly observable in this Figure.

Fig. 4
figure 4

Component prioritization based on criticality analysis for the 33-bus system

Full size image

The proposed method has been compared to recent work (Afzali et al. 2019) that introduced a weighted importance (WI) reliability index model and presented a method to prioritize the components of the distribution system for RCM. In Table 9, the WI index and the WCRDIF index have been calculated for the radial distribution system in Fig. 3.

Table 9 Comparison between weighted importance and WCRDIF for components ranking
Full size table

From Table 9, obviously, the proposed WCRDIF index is more reasonable in components ranking results rather than other indexes.

5 Conclusion

There are a large number of equipment and components used in the distribution system and the frequency of their failure mode is too high. Therefore, the maintenance activity should be organized in a clear prioritized program that prevents wasting resources. In this paper, a novel index has been presented for the prioritization of all components of the distribution system from the view of diagnostic important factors. Covering four aspects of the reliability index (unavailability, SAIFI, SAIDI, and ENS) is the other innovative and effective concept of this article. MATLAB software has been used for simulating the proposed method. Customer interruption cost, size of each load point, and type of loads are considered in creating the weighting coefficient, these considerations didn’t apply in any previous works. The obtained results highlighted that WCRDIF is more important and useful than all other factors used in ranking, because of:

  • Idea of diagnostic importance factor is comparing the effect of each component on the system’s performance in two scenarios (average failure rate mode and maximum failure rate mode)

  • Considering four studied reliability indexes in one factor (these factors can be changed by the system manager’s opinion)

  • Using appropriate weighting coefficient which considers economic aspect beside other important aspects.

Without using any optimization, the critical components are identified and increased the reliability level of the system to the desired grade. The higher WCRDIF, the lower the reliability level and the more priority is to apply maintenance activity.