Abstract
Hydrological models are frequently used for water resources management. One of the most widely used is the Soil and Water Assessment Tool (SWAT). However, one weakness of SWAT is its simplicity in modeling groundwater, which might affect the representation of hydrological processes. Therefore, modeling strategies that are geared towards achieving more realistic simulations would increase the reliability and credibility of SWAT model predictions. In this study, the performance of a SWAT model in a geologically heterogeneous basin was optimized by incorporating geological properties through semi-automatic calibration strategies. Based on its geology, the basin was split into four regions, and a default calibration (Scheme I) was compared with three designed calibration schemes: a zonal calibration (Scheme II), obtaining a parameter set in each of the regions, a zonal calibration after introducing an impervious layer in an aquifuge region (Scheme III), and a final calibration scheme (Scheme IV) where an aquifer region was re-calibrated, changing a parameter controlling the required content of water in the aquifer for return flow to increase groundwater flow. The results from the four schemes were evaluated both statistically and by assessing their plausibility to determine which one resulted in the best model performance and the most realistic simulations. All schemes resulted in a satisfactory statistical model performance, but the sequential optimization in the final scheme realistically reproduced the heterogenous hydrological behavior of the geological regions within the basin. To the best of our knowledge, our work addresses this issue for the first time, providing new insights about how to simulate catchments including aquifuge substrates.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Hydrological models are frequently used for water resources management due to their capability to simulate scenarios and assess how they affect water resources (Fu et al. 2019). These tools are valuable in the context of global change, as they can predict the potential effects of mitigation measures and thus facilitate the adoption of the most appropriate and effective measures. Research in this field works towards making hydrological modeling useful for improving sustainable water resources management. This involves increasing the accuracy of the representation of the catchments´ characteristics and relevant processes and establishing guidelines for creating, calibrating, and evaluating hydrological models (Moriasi et al. 2012).
Basin-scale hydrological models are ideal tools for water resources management, since they allow estimating the basin water balance, which is highly relevant for sustainable river basin management. The Soil and Water Assessment Tool (SWAT) is the most widely used basin-scale hydrological model (Fu et al. 2019), mostly due to its computational efficiency and open access. SWAT is a physically-based, semi-distributed, and continuous-time model that simulates water quantity and quality at basin scale and can be used to predict eco-hydrological impacts of changes in land use, agricultural practices, or climate (Arnold et al. 1998). SWAT disaggregates watersheds into two levels: subbasins, creating a new subbasin when two reaches merge, and hydrologic response units (HRUs), portions of a subbasin with a unique combination of soil type, land use, and slope class, that are expected to have a common hydrological behavior. The HRUs represent the basic spatial units of the model.
The capability of hydrological models such as SWAT to carry out realistic simulations depends on the quality and detail of the input information provided and the values of the parameters used in the equations of the model (Baffaut et al. 2015). Different combinations of parameter values can provide similar model results, which is known as equifinality. Without critical observation of the obtained values, this can lead to a non-representative model and to incorrect results and conclusions, even if the model is statistically satisfactory (Moriasi et al. 2015a). The large number of parameters in this kind of models and their spatial variability, hinder using in-situ measured data for all of them. Therefore, it is necessary to identify the most realistic values for the parameters that have the strongest influence on model performance through a calibration process (Gharari et al. 2014; Moriasi et al. 2015b).
During calibration, the simulation of a variable (e.g., streamflow) is optimized by changing the parameter values with the aim of achieving the best possible fit of the simulated to the observed data. Once the best parameter values have been obtained, the model output is validated during a different time period (Arnold et al. 2012). Statistical guidelines (Moriasi et al. 2015a) are used in hydrological modeling to evaluate the performance of the models using metrics such as the Coefficient of determination (R²), the Nash-Sutcliffe efficiency (NSE) and the Percent bias (PBIAS). However, this evaluation should be complemented by visual comparison of the simulated and observed hydrograph and an evaluation of the water balance.
Although certain calibration methodologies are accepted by most hydrological modelers, there is no absolute consensus on the best way to perform calibration. For this reason, research comparing different calibration strategies is relevant. The calibration process can vary, among others, in time step (monthly calibration, daily calibration, etc.), in spatial scale (single point or multi-point calibration), or in the objective function used to optimize the variable of interest.
Calibration at catchment scale is often performed using the same parameters value for the entire basin (e.g., Pascual et al. 2015; Joorabian et al. 2017; López-Ballesteros et al. 2019). However, this is problematic in heterogeneous river basins, where parameter values can vary between different parts of the basin, but this variation is not considered by the model (Shrestha et al. 2016). This can lead to a loss of model accuracy, as the components of the water balance can vary greatly from one region to another within the same basin depending on its characteristics (Balin 2004). To overcome this lack of representativeness and accuracy, it is common to carry out a multi-spatial calibration. By means of this strategy, it is possible to calibrate a basin by drainage regions, using data from several gauging stations located across the basin (e.g., Qi and Grunwald 2005; Cao et al. 2006; Franco et al. 2020). This method might make a model more representative, as different parameter values are obtained for different parts of the basin (Zhang et al. 2008). However, this strategy still does not take into account the heterogeneity of some factors with strong influence on hydrological processes, as their spatial distribution might not be coextensive with the drainage areas of the gauging stations used for calibration (e.g., two types of soils or lithologies with different hydrological behavior might occur in one of the drainage areas in which the model has been divided for multi-calibration purposes). Therefore, the problem of representativeness could be minimized but not fully solved, and furthermore the need for gauging data limits the application of this strategy.
Another method to increase the model representativeness is to carry out a zonal parameter calibration, i.e., grouping those subbasins or HRUs that have similar properties, and calibrating them jointly. Although it would be optimal to carry out this method with several gauging stations, it is also possible to do it with a single gauging point. A zonal parameter calibration provides different parameter values for each zone (group of similar subbasins or HRUs), allowing the model to represent the heterogeneity of the basin even though it only has one calibration point. However, this strategy is rarely done, so there is a lack of studies showing the benefits of this technique.
One weakness of the SWAT model is its lack of accuracy when modeling groundwater systems (Kim et al. 2008; Nguyen and Dietrich 2018; Senent-Aparicio et al. 2020; Molina-Navarro et al. 2019), partly because geological information is not considered during model setup. Other models, such as PRMS or SUPERFLEX, have an advantage over SWAT in this respect, since they consider this factor when defining HRUs, which might result in more robust models (Fenicia et al. 2016; Dal Molin et al. 2020). By default, SWAT sets up a single-layer, shallow, unconfined aquifer for every HRU in the model, which can be unrealistic under some circumstances such as the presence of impervious areas. Geological substrate is a key factor influencing relevant components of the water balance (infiltration, groundwater flow, storage, and runoff, among others) and thereby also impacts other aspects such as water quality (Balin 2004). Therefore, realistic groundwater modeling would significantly increase the credibility of the SWAT model, and efforts are being made to address this weakness.
Expert knowledge of the study basin should guide these efforts, ensuring that the values adopted by the parameters and the model results are adequate. The knowledge of basin processes can be directly used to determine initial ranges for the parameter values or to calibrate ungauged basins, which is known as soft calibration (Arnold et al. 2015, Seibert and McDonell 2015). Basin knowledge includes the distribution of water balance and streamflow components, which are useful to determine if the model is simulating the hydrogeological behavior of the basin accurately. These components can be divided into direct runoff or quickflow (surface flow and lateral flow) and baseflow (Volk et al. 2007), which in this case is essentially the groundwater contribution to streamflow (henceforth groundwater flow). However, the assessment of the streamflow components is not carried out in most hydrological modeling works, with only few studies separating these three components (e.g., Samper et al. 2011; Marques et al. 2013; Bannwarth et al. 2015; Malagò et al. 2016; Pisani et al. 2017), and some studies separating between direct flow and baseflow (e.g., Molina-Navarro et al. 2016; Yan et al. 2018; Eini et al. 2020; Aboelnour et al. 2020).
In this work, the main objective was to find an optimized calibration method of a SWAT model in a geologically heterogeneous basin incorporating geological information through calibration strategies. Four calibration schemes were explored and compared, assessing their statistical performances and their ability to produce realistic simulations. The schemes represent a sequential optimization of the model through the introduction of geological properties of the catchment: Scheme I consisted in a default calibration for the entire catchment; in Scheme II the basin was split into four geological regions, which were calibrated independently; in Scheme III, the previous scheme was further improved adding an impervious layer in an aquifuge region before carrying out the calibration in the four regions; and in Scheme IV, a carbonate aquifer region was re-calibrated, changing the initial range for one parameter to increase groundwater flow. The influence of the time step (daily vs. monthly) and spatial scale (basin vs. geological regions) on calibration results was also assessed, aiming to increase the knowledge on this topic. This comparison will determine whether the proposed calibration schemes are able to provide a more robust model and whether these improvements are advisable to be applied in further studies.
This work aims to shed light on the importance of taking geology into account in catchment-scale modeling, highlighting the great influence that this factor has on the water balance and streamflow components. Particularly, to the best of our knowledge, this work satisfactorily uses for the first-time zonal calibration strategies to isolate impervious regions in a SWAT model application.
2 Materials and methods
This section describes the most relevant aspects of the study area and the methodology used in this work.
2.1 Study area
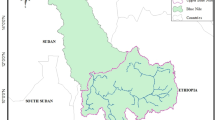
The Henares River basin is located in the provinces of Guadalajara and Madrid, in the center of the Iberian Peninsula (Fig. 1). This river, which has a length of 160 km, originates in Sierra Ministra, in the Castilian branch of the Iberian System, and flows into the Jarama River, one of the most important tributaries of the Tagus River. The Henares River basin has an area of 4070 km2, and its most important tributaries are the Sorbe, the Torote, the Dulce, and the Salado Rivers (Fig. 1).
The basin has an irregular topography, which can be divided into three regions: the Guadalajara mountain ranges, the Henares River terraces and the Alcarria plateau (Fig. 1). The altitude ranges from 2049 m.a.s.l. at the Ocejón Peak to 550 m.a.s.l. at the outlet of the basin.
According to the Köppen-Geiger Classification, the basin has a temperate climate with hot and dry summers (Csa). The extent of the watershed and its irregular topography generate a climate gradient from north to south, with the southern part located on the boundary with the cold steppe (Bsk) climate region (Chazarra et al. 2018). This gradient leads to noticeable climate differences across the basin: according to the normal climatologic values (1981 to 2010) of the Spanish Meteorological Agency (AEMET), the mean temperature from the northwest, northeast, and south are 9 °C, 12 °C, and 14 °C, respectively, and the annual precipitation values are 1000, 600, and 400 mm, with a catchment average around 530 mm (Chazarra et al. 2018).
Two mountain systems can be found in the Guadalajara mountain ranges: the Central System with a predominant metamorphic geology (i.e., slates, gneisses) in the west and the Iberian System with a predominant sedimentary carbonate geology (i.e., dolomites, limestones and marls) in the east. The area south of the Guadalajara mountain ranges is made up of Tertiary and Quaternary sedimentary materials resulting from the erosion of the fluvial network (gravels, conglomerates, sands, sandstones). Evaporitic and volcanic rocks outcrop in small areas in the center of the basin (IGME 2003).
This geological diversity, which is representative of the geological heterogeneity of the Iberian Peninsula, also generates a contrast in the hydrological behavior of the basin, and therefore this factor must be considered for its modeling. For this purpose, four geological regions were defined in this study (Fig. 2). There is an aquifuge in the metamorphic region, while the other three regions contain relevant aquifers. Among the aquifer regions, the carbonate materials of the Mesozoic sedimentary region are the most relevant aquifers of the basin due to their high permeability and depth, even though detrital materials with medium permeability occur in this region too. The Tertiary sedimentary rocks region is composed by detrital and calcareous materials with low and medium permeability. The Quaternary alluvial sediments region also has a high permeability, but the aquifers are shallow (Confederación Hidrográfica del Tajo 2022). Three soil types are predominant in the Henares River basin: cambisols (56%), regosols (30%), and fluvisols (10%), being all of them generally of calcareous type. As a minority, other types of soils such as acrisols and luvisols can be also found (FAO 2012).
Land use in the basin is dominated by agriculture (41%) and non-irrigated cereals are the most common crop type. A large area is dominated by different types of natural vegetation: 17% is forest, 16% grassland, and 10% scrubland. With a population of approximately 600.000, urban use is minor (3%) and mainly located in the southern sector (Ministerio de Fomento 2018a).
2.2 Model setup
The QGIS interfaces for SWAT 2012 (QSWAT v.1.9 and SWAT Editor 2012.10.23) (Dile et al. 2019) were used to set up the hydrological model of the Henares River basin. For watershed delineation, a digital elevation model (DEM) with a resolution of 25 × 25 meters of resolution (Ministerio de Fomento 2018b) and a 10 km² minimum threshold area for creating reaches were used. The main outlet of the basin is located at the confluence of the Henares and Jarama Rivers, and a calibration point was introduced at the streamflow gauging station of Espinillos (Fig. 1). The subbasins with an area less than the 10 percent of the average subbasin area were merged with the subbasin downstream, obtaining a model with 194 subbasins (Fig. 3).
Land use and soils information was introduced in raster format for the creation of HRUs. Three slope bands were defined (Fig. 3) following FAO recommendations (< 8 %, 8–30 %, > 30 %) (FAO 1980) and created from the DEM. The land use information was obtained from the Spanish Land Occupation Information System (SIOSE) (Ministerio de Fomento 2018a) in vector format, and it was rasterized to a resolution of 250 × 250 meters. The soils information was obtained from the Harmonized World Soil Database (HWSD) (FAO 2012), with a resolution of 1 × 1 km², and was resampled to 250 × 250 meters. A table that adapts the soil properties in the HWSD to those required by SWAT was provided by the Water Resources Planning and Management group of the San Antonio Catholic University of Murcia (UCAM). It has successfully been used it in previous works (Pérez-Sánchez et al. 2020).
Based on these input data, 19 different land uses and 13 soil types (which can be assigned to 7 soil groups) were identified. The model was simplified within each subbasin by eliminating land uses covering less than 10% of the subbasin area, soil types covering less than 10% of the area of the remaining land uses, and slope bands covering less than 10% of the area of each remaining land use and soil type combination. The areas of land uses, soils, and slope bands remaining in each subbasin were increased proportionally to make sure that 100% of the subbasin area was modelled. As a final result, a model with 2216 HRUs was obtained.
Meteorological data (daily precipitation and maximum and minimum temperature) were obtained from gridded climate data created by the AEMET (Herrera et al. 2016) with a resolution of 5 × 5 km for precipitation and a resolution of 20 × 20 km for temperature. This grid interpolates the meteorological data measured at weather stations across the country. A weather generator elaborated by SWAT developers (Dile and Srinivasan 2014) with the information of the Climate Forecast System Reanalysis (CSFR) (Saha et al. 2014) was used to simulate the three other climate variables required by SWAT (wind speed, relative humidity, and solar radiation).
2.3 Model calibration and validation
The calibration process was carried out using SWAT-CUP 2012 (v 5.1.6.2) (Abbaspour 2013), a widely used software for calibrating SWAT models. The Sequential Uncertainty Fitting routine (SUFI2) was used with the NSE as objective function, which has been reported as an adequate objective function to calibrate SWAT models (Molina-Navarro et al. 2017).
The model was calibrated against daily and monthly average streamflow at the Espinillos gauging station (MITECO 2019). Although SWAT is a daily scale continuous model, a monthly calibration is often carried out, which is not recommended if daily results are desired (Sudheer et al. 2007; Adla et al. 2019; Franco et al. 2020). Five iterations of 500 simulations were carried out for each calibration scheme, adapting the parameter ranges as suggested by the software, but modifying them in case of deviations from the initial ranges that were considered realistic based on expert knowledge. The model calibration period was 2006–2010 with a warm-up period of five years (2001–2005). After calibration, a split-sample validation was done for the period 2011–2016.
2.3.1 Calibration schemes
Four schemes following different zonal parameter calibration strategies were carried out to compare how each of them affect model performance and their capability to reproduce the basin water balance.
A total of 18 parameters (Table 1) were calibrated, all reported in previous successful SWAT applications in similar areas (Molina-Navarro et al. 2014, Molina-Navarro et al. 2021). A brief description of the parameters (Table 1) and of each scheme follows.
2.3.1.1 Calibration scheme I: default calibration
In the default calibration 18 parameters were included (Arnold et al. 2013) (Table 1) and calibrated for the entire basin, without taking the geological heterogeneity into account. This is the most common way to carry out SWAT model calibration.
2.3.1.2 Calibration scheme II: zonal calibration
To incorporate the geological heterogeneity, the watershed was split into four regions based on the dominant substrate of each subbasin: a Mesozoic sedimentary carbonate in the northeast, a Paleozoic metamorphic impervious region in the northwest, and two detrital aquifer regions in the south, one with Tertiary sedimentary rocks and the other with Quaternary alluvial sediments (Fig. 2). Subsequently, the four geologic zones were calibrated separately using all the parameters calibrated in Scheme I except for the surface runoff lag coefficient parameter (SURLAG) (Arnold et al. 2013), which is defined in SWAT as a basin-wide parameter, so the same value is assigned to the entire basin.
2.3.1.3 Calibration scheme III: zonal calibration with impervious region
As reported in the results section (3.3), after the application of Scheme II, SWAT was simulating noticeable groundwater recharge and contribution to streamflow in the metamorphic impervious region, which is not realistic considering its aquifuge character. For this reason, an impervious layer was introduced in this region below the maximum soil depth using the depth to impervious layer parameter (DEP_IMP) (Arnold et al. 2013), thus avoiding percolation of water from the soil into the groundwater. The zonal calibration was repeated after this adjustment.
2.3.1.4 Calibration scheme IV: III + targeting the Mesozoic carbonate region
There was still room for improvement after Scheme III, which resulted in an unrealistic simulation of the Mesozoic sedimentary region. In this case, the groundwater contribution to streamflow was very low, even though it is a region with carbonate aquifers. To solve this problem, the required content of water in the aquifer for return flow to occur parameter (GWQMN) (Arnold et al. 2013) in this region was lowered, thereby forcing a larger groundwater contribution. The initial range of GWQMN was narrowed from 0–5,000 to 0–2,000 mm, and the 17 regional parameters were calibrated again only for the Mesozoic carbonate region. In the other regions the best parameter values obtained after calibration scheme III were retained.
2.4 Model evaluation
The calibration schemes were evaluated statistically using three performance metrics. In addition, the plausibility of model results in each calibration scheme was assessed, since a model can be statistically correct despite a wrong representation of hydrological processes, as reported in several studies (Muleta et al. 2012; Pfannerstill et al. 2017; Triana et al. 2019), and as this work aims to proof.
The three metrics, R2 (1), NSE (2) and PBIAS (3), belong to different categories (regression, dimensionless and error indices). Achieving a good value for all of them would indicate robustness of the model, covering all aspects of the hydrograph (time pattern, extreme values, and mean value, respectively) (Moriasi et al. 2007). Final metric values were compared with the guidelines reported in the literature (Moriasi et al. 2015a), according to which satisfactory results are obtained when the values are higher than 0.60 and 0.50 for R2 and NSE, respectively, and when PBIAS is within ± 15 %. The metrics values were compared among schemes and between the calibration time steps (daily and monthly). Monthly metrics were also calculated for the results of the calibration at daily time step to complete the comparison among different schemes with statistics based on the same time step. The best parameter values for each scheme in the daily calibration were also assessed (Appendix 1).
where Q is the streamflow, m and s stand for measured and simulated, respectively, and i is the ith measured or simulated data.
The observed vs. simulated daily hydrograph and average contribution of the streamflow components (surface, lateral, and groundwater flow) during the entire simulation were analyzed to evaluate the capability of the model to simulate a realistic hydrological behavior in each region of the basin. The spatial distribution of the water balance and streamflow components was extracted and mapped at subbasin level to strengthen the results discussion and assess how each scheme simulates hydrological processes in the basin (Appendix 2).
3 Results and discussion
This section presents the results for the simulated schemes and their comparison, both from a statistical point of view and in terms of the plausibility of the model outputs.
3.1 Analysis of calibration and validation results
The changes of the statistical indices differed among metrics, time steps, and calibration schemes (Fig. 4). The behavior of R2 and NSE during calibration was similar, and therefore these metrics were assessed together, while PBIAS was assessed separately.
In the monthly calibration the largest improvement of the metrics happened after the first iterations (Fig. 4). In the daily calibration this improvement was achieved later, but the final values at monthly time step were similar. This suggests that if the daily calibration is not extended enough, it might not seem worthwhile, but it finally achieves a performance similar to that of the monthly calibration. A higher time resolution implies a higher variability, which justifies that the calibration process requires more time on daily time step (Baffaut et al. 2015).
The metrics improved less in the default scheme (Scheme I, Fig. 4) than in Schemes II and III, which suggests that more complex calibration strategies have greater room for improvement and need more extensive calibration processes. PBIAS had a random behavior for most of the schemes, but in Scheme III it improved progressively both at the daily and the monthly time steps. Calibration scheme IV hardly showed improvements during calibration, which was expected since it starts from the final configuration of Scheme III—already calibrated- and only the Mesozoic carbonate region parameters were modified, so just a slight improvement of PBIAS was obtained compared to final metrics in Scheme III (Fig. 4, Table 2).
Comparing the two calibration time steps (daily and monthly), the values of the calibration metrics achieved for the daily time step were worse for R2 and NSE than for the monthly time step (Table 2). This was expected since it is always more difficult to fit a daily hydrograph to simulated values than a monthly one (Molina-Navarro et al. 2017). Monthly metrics were also calculated from the daily-calibrated schemes to be able to compare both calibration procedures (daily and monthly). Although the values for NSE and R2 were better when calculating the monthly metrics from the daily-calibrated schemes, the monthly calibration yielded slightly better values, which was also reported in other studies (Xu et al. 2009; Franco et al. 2020). Regarding PBIAS, the best values were obtained during monthly calibration as in other works (Lerat et al. 2020), but they were also satisfactory for the daily calibration, especially in schemes III and IV (Table 2).
Daily and monthly split-sample validations were performed with the best parameter set obtained after each calibration scheme (Appendix 1). Table 2 shows the calibration and validation results obtained for monthly and daily time steps. Validation performance was slightly better at monthly time step for Schemes I, III and IV and significantly better for Scheme II.
Schemes I and II resulted in better values for R2 and NSE during calibration than Schemes III and IV (Table 2). However, during validation, the performance of these metrics worsened for Schemes I and II, while it improved for Schemes III and IV. This behavior occurred in both calibration time steps. Validation works as an indicator of the model’s robustness (Brulebois et al. 2018), and in this comparison proved that more complex calibration schemes are more robust.
The PBIAS performance was significantly better during calibration than during validation in all the schemes at monthly time step. At daily time step, during validation, PBIAS was considerably worse for Schemes III and IV, considerably better for Scheme I and slightly better for Scheme II. Scheme I performed best during validation based on PBIAS. However, it yielded unsatisfactory values for R2 and NSE, and as shown in the following section (3.2), the overestimation of baseflow and the underestimation of flood peaks drive this metric towards a “very good” value, without realistically simulating the hydrograph. This is one of the limitations of PBIAS that must be considered when using this metric to assess model performance (Moriasi et al. 2015a). Higher simulated flows during flood events worsened the model performance for the other schemes according to the metrics, but contributed to more realistic simulations.
Based on this analysis, the zonal calibration (Scheme II) showed the best statistical performance at the monthly time step, and Scheme III was the best for daily calibration. However, as discussed below, better metrics do not necessarily guarantee a better model. Therefore, the plausibility of the model outputs should be assessed. Since daily calibration is more exhaustive and demanding and metrics yielded similar statistics, the following analysis focuses on the models calibrated and validated at a daily time step for all the calibration schemes.
3.2 Graphical model evaluation
The statistical analysis should be complemented by a visual comparison of the observed and simulated hydrographs (Fig. 5) to determine if a hydrological model is simulating the streamflow accurately (Molina-Navarro et al. 2014, 2017).
The model underestimated streamflow during peak flows for all calibration schemes (Fig. 5), as observed in other works (Van Liew et al. 2007; Molina-Navarro et al. 2014; Bieger et al. 2014). However, as reported in Fohrer et al. (2014) and Franco et al. (2020), baseflow was slightly overestimated, and the streamflow recession was slower than in the observed data for most of the cases, but especially for Schemes I and II during validation.
This lack of accuracy was more noticeable in Schemes I and II. Scheme III resulted in larger peak flows and a faster recession, obtaining a more realistic hydrograph (Fig. 5). These effects are a consequence of the introduction of the impervious layer in the metamorphic region, since an aquifuge substrate favors direct runoff and a faster recession (Custodio and Llamas 1976). Nevertheless, this scheme also produced some peaks that were higher than the observed ones, due to the unrealistic simulation of the Mesozoic carbonate aquifer region. Generally, Scheme IV simulated peak flows similarly to Scheme III, but the magnitude of some peaks that were overestimated in Scheme III was smaller (Fig. 5). As this scheme decreased the threshold for groundwater flow in the Mesozoic carbonate region, its groundwater contribution increased, reducing the direct runoff and, therefore, the magnitude of peak flows (Balin 2004). Discussion of the flow components will be expanded in the following section (3.3). Weaknesses of SWAT when simulating the falling limb and groundwater storage depletion have also been reported by other authors (Gassman et al. 2014), but incorporating geological information through calibration strategies improved their representation, and the magnitude of peak flows (Fig. 5). Nevertheless, the simulation of baseflow during periods with the lowest streamflow levels continued to be slightly imprecise in all the schemes designed for this work.
Comparing calibration and validation periods (Fig. 5), Scheme I and especially Scheme II simulated the hydrograph in a less realistic way during the validation period, which was particularly noticeable for the falling limb. However, Schemes III and IV continued simulating the streamflow properly during validation, which confirmed the higher robustness of these schemes already discussed after statistical evaluation.
This assessment suggests that the most complex scheme (Scheme IV), which simulates the heterogeneous hydrological behavior of the basin due to incorporating geological constraints, allows reproducing the hydrograph in a more realistic way even though it had a slightly worse statistical performance than Scheme III, which yielded the best values for the daily metrics. As suggested by Pfannerstill et al. (2017), sometimes it is necessary to accept a slightly lower accuracy in simulating discharge to improve other objectives such as the correct simulation of the water balance components.
3.3 Streamflow components assessment
The objective of this work was to assess how introducing the geological heterogeneity of a basin can improve the model´s performance, both statistically and regarding the plausibility of the simulation. Therefore, an assessment of the hydrological behavior of the basin and of the most relevant regions (the metamorphic impervious and the carbonate aquifer regions) has been carried out, analyzing the streamflow components for the different calibration schemes. The metamorphic and carbonate regions have been considered the most relevant for several reasons: firstly, they are both located in the north of the basin, where precipitation is higher, so they have a large impact on the overall water balance of the basin. Secondly, their hydrogeological behavior is opposite, allowing the results obtained with the different schemes to be highlighted. Thirdly, the carbonate region contains the most relevant aquifers in the basin, as explained before (2.1).
In this geologically heterogeneous basin, regions with contrasting geology should show different contributions of the streamflow components: a predominance of the groundwater contribution in the aquifer regions and a noticeable predominance of direct runoff in the impervious region (Custodio and Llamas 1976, Balin 2004). In the Henares River basin, the impervious region is highly relevant, since it covers more than a quarter of the total area of the basin (Fig. 2) and the precipitation in this area is higher than in the rest of the basin (Fig. 7, Appendix 2) due to higher altitudes (Fig. 1).
Figure 6 shows the streamflow components in the most relevant regions and in the entire basin for each calibration scheme: Default (I), Zonal (II), Impervious (III) and Carbonate (IV).
The default scheme (Scheme I) did not consider the geological heterogeneity in the basin, so it yielded a similar hydrological behavior for the entire basin and for the two analyzed regions (Fig. 6), despite their contrasting hydrological behavior: groundwater flow is the major component, and lateral flow dominates direct runoff. This simulation is not realistic: in the metamorphic impervious region there are no relevant aquifers, so there should be hardly any groundwater contribution to the streamflow (Custodio and Llamas 1976). The other regions were also not realistically simulated, due to obtaining unrealistic parameter values. The Quaternary alluvial region might serve as example for comparing the schemes: the GWQMN parameter, the threshold of water in the shallow aquifer for movement of water to the unsaturated zone occur parameter (REVAPMN), and the fraction of percolation that reaches the deepest layer of the aquifer parameter (RCHRG_DP) (Arnold et al. 2013) were expected to be low since the alluvial aquifer is the shallowest in the catchment. However, in Scheme I, their values were higher than the values estimated for this region in Schemes II, III and IV (Appendix 1). Thus, the water balance for the entire basin is not reliable. Although this work assumes that geological heterogeneity must be considered when modeling watersheds, many studies do not consider this factor and obtain models with satisfactory metrics that do not represent the environment in a realistic way (Molina-Navarro et al. 2017; Triana et al. 2019).
The zonal calibration (Scheme II) yielded different balances in each region, as they were calibrated independently. However, these variations were not in accordance with the real behavior of the basin. In the metamorphic region, the groundwater storage increased (Figs. 9 and 13, Appendix 2), which reduced the total streamflow of this region (still dominated by groundwater contribution, Fig. 6). This was unrealistic, as this region is impervious. In the Mesozoic carbonate region, groundwater flow decreased and direct runoff increased significantly, especially lateral flow, resulting in an overall increase in streamflow. This hydrological representation is also unrealistic in a region where groundwater contribution is expected to be around 50% (Sastre-Merlín et al. 2020, Molina-Navarro et al. 2021). Regarding the parameter values in the Quaternary alluvial region, GWQMN and RCHRG_DP values were still relatively high, while REVAPMN decreased towards the minimum value (1,018 mm). Thus, Scheme II also produced an unrealistic model despite defining regions considering the geological heterogeneity and achieving favorable statistics in the calibration. This is because the final parameter values were not necessarily realistic, but rather the product of a random selection to optimize the objective function. Therefore, using expert knowledge to introduce some geological factors controlling the hydrogeological behavior during the model set-up or during its calibration, as done in Schemes III and IV, would allow to configure the model in a more plausible way and to start the calibration from a more advanced point.
In Scheme III, the parameter DEP_IMP was introduced in the metamorphic impervious region to simulate its aquifuge substrate. As a consequence, recharge in this region was inhibited (Fig. 6) and direct runoff and total streamflow increased (Custodio and Llamas 1976). Lateral flow became the main streamflow component and surface runoff also increased considerably. Given the importance of this region, the modification of its hydrological behavior affected the overall balance of the basin, increasing the contribution of direct runoff over groundwater flow. With this scheme, all the regions were calibrated again so parameter values in each region could vary considering the new expected behavior in the metamorphic region, since calibration was only performed at the outlet of the catchment. The representation of the Quaternary alluvial region also improved, in response to lower values for both GWQMN and RCHRG_DP. However, this strategy led to a set of parameter values in the Mesozoic carbonate region that produced a completely unrealistic simulation, reducing the groundwater contribution to almost zero. Accordingly, the simulation of the basin as a whole after application of Scheme III was not plausible: the metamorphic impervious region was represented more realistically than in the previous schemes, but the effect on the Mesozoic carbonate region still needed to be improved.
The last calibration scheme (Scheme IV) only affected the Mesozoic carbonate region, since the simulation of the other regions achieved with Scheme III was accurate. Therefore, its effect on the balance of the entire basin was limited. This scheme aimed to increase the groundwater contribution in the carbonate region, by changing the initial values of the GWQMN parameter. Groundwater flow increased in the Mesozoic carbonate aquifer region compared to the other calibration schemes, especially Schemes II and III, becoming the predominant component, which is expected in this region (Custodio and Llamas 1976, Molina-Navarro et al. 2021), similar to other Mediterranean catchments with relevant aquifers (Malagò et al. 2016; Senent-Aparicio et al. 2020). Groundwater contribution for the entire basin also increased compared to the Scheme III. Therefore, this scheme, despite not yielding the best statistical performance, was the best for simulating the hydrological behavior of the Henares River basin.
Scheme IV results indicate that the relative contribution of the surface, lateral and groundwater flow components at basin level are around 22%, 60%, and 18%, respectively. Considering the impervious character of the metamorphic region, its extension and relief with steep slopes, and the high precipitation in this region compared to the rest of the basin, the predominance of direct runoff at the basin scale would be expected. Although the other geological regions had a different distribution of streamflow components (i.e., a larger groundwater flow contribution), the impact of the metamorphic region on the global basin water balance was larger (Fig. 7, Appendix 2). Nevertheless, groundwater flow is highly relevant in the Henares River basin, since it is of great importance during the dry season, when rainfall is scarce and therefore, direct runoff becomes negligible.
The contribution of streamflow components depends on the properties of each basin (geology, climate, land use, etc.), so discussing the results obtained with studies of other basins is only of limited use. In the Henares River basin, with the calibration Scheme IV, lateral flow represents more than 70% of direct runoff, which could be explained by the importance of the metamorphic region, since some studies indicate that this component is predominant in watersheds with steep slopes and impermeable substrates (Samper et al. 2011; Marques et al. 2013; Pisani et al. 2017). Studies in Mediterranean regions dominated by karst processes suggested that groundwater is the main component, while lateral flow could contribute as little as 2% of the total streamflow (Malagò et al. 2016). The carbonate region of the Henares River basin contains varied geological substrates. Besides the carbonate materials above mentioned, there are also claystones, sandstones and conglomerates (IGME 2003), so as opposed to the basins studied by Malagò et al. (2016), it is not fully dominated by karst processes. Nevertheless, lateral flow in this region was lower than in the rest of the basin, indicating that its contribution should be lower in catchments with an important groundwater recharge capacity.
Some studies used other methodologies and methods to incorporate geological information within SWAT models. For example, Malagò et al. (2016) used a specific karst module incorporated into SWAT in order to improve the simulation of karstified watersheds, and Senent-Aparicio et al. (2020) modified the simulated baseflow by adding interbasin groundwater flow in a karstified basin. They obtained a baseflow contribution around and larger than 50% in their respective study areas, a reasonable value for Mediterranean Karst aquifer catchments. Nevertheless, the approached by Malagó et al. (2016) and Senent-Aparicio et al. (2020) focused on aquifer substrates, thus not resolving the issue of simulating impervious areas. A study carried out in the southern USA managed to reduce the contribution of groundwater flow and simulate surface runoff as the major streamflow component, albeit using information about the soil characteristics (rocky and clayey soils) of the study area, and not on the hydrogeological properties (Aboelnour et al. 2020).
In some studies that partitioned direct runoff into surface runoff and lateral flow, surface runoff was less important than lateral flow (Samper et al. 2011; Marques et al. 2013; Bannwarth et al. 2015), or even zero (Pisani et al. 2017). Malagò et al. (2016) found in a karstified basin that its contribution was larger than the contribution of lateral runoff and in wet years even larger than that of groundwater flow. Surface runoff occurs mostly during wet periods, when soils are saturated (Custodio and Llamas 1976). Therefore, except in situations of torrential or prolonged rain events, a relatively small contribution is expected in Mediterranean watersheds such as the Henares River basin (Fig. 6). The contribution of surface runoff component increases notably in the southern part of the basin. This is due to the predominance of urban land use, with large impervious areas (Fig. 3, Fig. 11, Appendix 2). This land cover inhibits infiltration of water into the soil, and thus also the generation of lateral flow, so the hydrological behavior of this area is different than that of the impervious area in the northwest of the basin (Fig. 12, Appendix 2).
4 Conclusions
This study explored a new calibration strategy for a SWAT model, incorporating information on the hydrogeological properties of different regions in a geologically heterogeneous basin. The catchment was split into four regions considering their expected hydrogeological behavior, and a default calibration scheme (Scheme I) was compared with three designed calibration schemes: a zonal calibration (Scheme II), obtaining a unique parameter set for each of the regions, a zonal calibration after introducing an impervious layer in an aquifuge region (Scheme III), and a final calibration scheme (Scheme IV) where a region with relevant aquifers was recalibrated to obtain a larger contribution of groundwater flow to streamflow. The improvement in the representation of the hydrological behavior of the basin based on expert knowledge led to a more realistic and robust model, and therefore, we recommend following a similar strategy in basins with noticeable geological heterogeneity.
The sequential optimization followed for the final calibration scheme (IV) addressed the unrealistic simulation of the different regions found in the other schemes. Although this optimization requires an additional effort in terms of number of parameters calibrated and iterations, this study indicates that it leads to more realistic models with higher performance. This work set an example for similar studies, particularly in geologically heterogeneous regions, encouraging modelers to avoid basin-level calibrations in such areas and thus favoring more realistic hydrological simulations.
Furthermore, this work demonstrates the importance of evaluating the results of hydrological models after optimization of model evaluation metrics, since a model can be statistically satisfactory while producing an inaccurate representation of reality. Assessing the parameter values, the observed vs. simulated hydrograph, and the contribution of streamflow components allows detection of inconsistencies in the simulation, which can be improved through adjustments such as those proposed in this work.
Despite the improvements achieved in this study and considering the relevance of geological properties in hydrological behavior, we can also highlight that it would be very beneficial having the possibility of introducing geological constrains during the SWAT model set-up process. This could involve the development of a more comprehensive groundwater module, considering the different hydrological behavior of the different materials, and the incorporation of the geology during the HRU definition. The correct representation of the geological substrate would result in more realistic and robust models, which would increase the confidence in hydrological modeling and especially in the SWAT model.
Abbreviations
- AEMET:
-
Spanish meteorological agency
- Bsk:
-
Cold steppe climate
- Csa:
-
Temperate climate with hot and dry summer
- CSFR:
-
Climate forecast system reanalysis
- DEM:
-
Digital elevation model
- DEP_IMP:
-
Depth to impervious layer parameter
- GWQMN:
-
Content of water in the aquifer for return flow to occur parameter
- HRUs:
-
Hydrologic response units
- HWSD:
-
Harmonized world soil database
- NSE:
-
Nash–Sutcliffe efficiency
- PBIAS:
-
Percent bias
- R2 :
-
Coefficient of determination
- RCHRG_DP:
-
Fraction of percolation that reaches the deepest layer of the aquifer parameter
- REVAPMN:
-
Threshold of water in the shallow aquifer for the movement of water to the unsaturated zone to occur parameter
- SIOSE:
-
Spanish land occupation information system
- SUFI 2:
-
Sequential uncertainty fitting routine
- SURLAG:
-
Surface runoff lag coefficient parameter
- SWAT:
-
Soil and water assessment tool
- UCAM:
-
San Antonio catholic university of murcia
References
Abbaspour, K. C. (2013). Swat-cup 2012. SWAT Calibration and uncertainty program—a user manual. Swiss Federal Institute of Aquatic Science and Technology. https://www.2w2e.com/. Accessed 10 July 2021.
Aboelnour M, Gitau MW, Engel BA (2020) A comparison of streamflow and baseflow responses to land-use change and the variation in climate parameters using SWAT. Water 12(1):191
Adla S, Tripathi S, Disse M (2019) Can we calibrate a daily time-step hydrological model using monthly time-step discharge data? Water 11(9):1750
Arnold JG, Srinivasan R, Muttiah RS, Williams JR (1998) Large area hydrologic modeling and assessment part I: model development 1. J Am Water Resour Assoc 34(1):73–89
Arnold JG, Moriasi DN, Gassman PW, Abbaspour KC, White MJ, Srinivasan R, Jha MK (2012) SWAT: Model use, calibration, and validation. Trans ASABE 55(4):1491–1508
Arnold JG, Kiniry JR, Srinivasan R, Williams JR, Haney EB, Neitsch SL (2013) SWAT 2012 input/output documentation. Texas Water Resources Institute. https://hdl.handle.net/1969.1/149194. Accessed 14 March 2021.
Arnold JG, Youssef MA, Yen H, White MJ, Sheshukov AY, Sadeghi AM, Gowda PH (2015) Hydrological processes and model representation: impact of soft data on calibration. Trans ASABE 58(6):1637–1660
Baffaut C, Dabney SM, Smolen MD, Youssef MA, Bonta JV, Chu ML, Arnold JG (2015) Hydrologic and water quality modeling: spatial and temporal considerations. Trans ASABE 58(6):1661–1680
Balin D (2004) Hydrological behaviour through experimental and modelling approaches (No. THESIS). École Polytechnique Fédérale de Lausanne (EPFL).
Bannwarth MA, Hugenschmidt C, Sangchan W, Lamers M, Ingwersen J, Ziegler AD, Streck T (2015) Simulation of stream flow components in a mountainous catchment in northern Thailand with SWAT, using the ANSELM calibration approach. Hydrol Process 29(6):1340–1352
Bieger K, Hörmann G, Fohrer N (2014) Simulation of streamflow and sediment with the soil and water assessment tool in a data scarce catchment in the three Gorges region. China J Environ Qual 43(1):37–45
Brulebois E, Ubertosi M, Castel T, Richard Y, Sauvage S, Sanchez-Perez JM, Amiotte-Suchet P (2018) Robustness and performance of semi-distributed (SWAT) and global (GR4J) hydrological models throughout an observed climatic shift over contrasted French watersheds. Open Water J 5(1):41–56
Cao W, Bowden WB, Davie T, Fenemor A (2006) Multi-variable and multi-site calibration and validation of SWAT in a large mountainous catchment with high spatial variability. Hydrol Process Int J 20(5):1057–1073
Chazarra A, Flórez García E, Peraza B, ToháRebull T, LorenzoMariño B, Criado E, Botey MR (2018) Mapas climáticos de España (1981–2010) y ETo (1996–2016). Agencia Estatal de Meteorología (AEMET), Ministerio para la Transición Ecológica y el Reto Demográfico (MITECO). Madrid, Spain.
Custodio E, Llamas MR (1976) Hidrología subterránea (Vol. 2). Omega, Barcelona
Dal Molin M, Schirmer M, Zappa M, Fenicia F (2020) Understanding dominant controls on streamflow spatial variability to set up a semi-distributed hydrological model: the case study of the Thur catchment. Hydrol Earth Syst Sci 24(3):1319–1345
Dile YT, Srinivasan R (2014) Evaluation of CFSR climate data for hydrologic prediction in data-scarce watersheds: an application in the Blue Nile River Basin. J Am Water Resour Assoc. https://doi.org/10.1111/jawr.12182
Dile Y, Srinivasan R, George C (2019) QGIS Interface for SWAT (QSWAT) version 1.9. College Station, Texas, EEUU. https://swat.tamu.edu/media/116371/qswat-manual_v19.pdf. Accessed 3 March 2021.
Eini MR, Javadi S, Delavar M, Gassman PW, Jarihani B (2020) Development of alternative SWAT-based models for simulating water budget components and streamflow for a karstic-influenced watershed. CATENA 195:104801
FAO (1980) Land evaluation for development. Food and Agriculture Organization of the United Nations, Rome
FAO/IIASA/ISRIC/ISSCAS/JRC, (2012) Harmonized world soil database (version 1.2). FAO, Rome, Italy and IIASA, Laxenburg, Austria. https://www.fao.org/soils-portal/soil-survey/soil-maps-and-databases/harmonized-world-soil-database-v12/ru/. Accessed 20 February 2021.
Fenicia F, Kavetski D, Savenije HH, Pfister L (2016) From spatially variable streamflow to distributed hydrological models: Analysis of key modeling decisions. Water Resour Res 52(2):954–989
Fohrer N, Dietrich A, Kolychalow O, Ulrich U (2014) Assessment of the environmental fate of the herbicides flufenacet and metazachlor with the SWAT model. J Environ Qual 43(1):75–85
Franco ACL, Oliveira DYD, Bonumá NB (2020) Comparison of single-site, multi-site and multi-variable SWAT calibration strategies. Hydrol Sci J 65(14):2376–2389
Fu B, Merritt WS, Croke BF, Weber TR, Jakeman AJ (2019) A review of catchment-scale water quality and erosion models and a synthesis of future prospects. Environ Model Softw 114:75–97
Gassman PW, Sadeghi AM, Srinivasan R (2014) Applications of the SWAT model special section: overview and insights. J Environ Qual 43(1):1–8
Gharari S, Hrachowitz M, Fenicia F, Gao H, Savenije HHG (2014) Using expert knowledge to increase realism in environmental system models can dramatically reduce the need for calibration. Hydrol Earth Syst Sci 18(12):4839–4859
Herrera S, Fernández J, Gutiérrez JM (2016) Update of the Spain02 gridded observational dataset for EURO-CORDEX evaluation: assessing the effect of the interpolation methodology. Int J Climatol 36(2):900–908
IGME (2003) Mapa geológico de España (MAGNA) E. 1:50.000. Madrid. http://info.igme.es/cartografiadigital/geologica/Magna50.aspx. Accessed 7 May 2021.
Joorabian Shooshtari S, Shayesteh K, Gholamalifard M, Azari M, Serrano-Notivoli R, López-Moreno JI (2017) Impacts of future land cover and climate change on the water balance in northern Iran. Hydrol Sci J 62(16):2655–2673
Kim NW, Chung IM, Won YS, Arnold JG (2008) Development and application of the integrated SWAT–MODFLOW model. J Hydrol 356(1–2):1–16
Lerat J, Thyer M, McInerney D, Kavetski D, Woldemeskel F, Pickett-Heaps C, Feikema P (2020) A robust approach for calibrating a daily rainfall-runoff model to monthly streamflow data. J Hydrol 591:125129
López-Ballesteros A, Senent-Aparicio J, Srinivasan R, Pérez-Sánchez J (2019) Assessing the impact of best management practices in a highly anthropogenic and ungauged watershed using the SWAT model: a case study in the El Beal Watershed (Southeast Spain). Agronomy 9(10):576
Malagò A, Efstathiou D, Bouraoui F, Nikolaidis NP, Franchini M, Bidoglio G, Kritsotakis M (2016) Regional scale hydrologic modeling of a karst-dominant geomorphology: the case study of the Island of Crete. J Hydrol 540:64–81
Marques JE, Marques JM, Chaminé HI, Carreira PM, Fonseca PE, Santos FAM, Borges FS (2013) Conceptualizing a mountain hydrogeologic system by using an integrated groundwater assessment (Serra da Estrela, Central Portugal): a review. Geosci J 17(3):371–386
Ministerio de Fomento (2018a) Documento Técnico SIOSE 2014. Versión 1. Equipo Técnico Nacional SIOSE. Dirección General del Instituto Geográfico Nacional, Madrid. 16 pp
Ministerio de Fomento (2018b) Modelos Digitales de Elevaciones. Modelo Digital de Terreno – MDT25. Centro de Descargas del Centro Nacional de Información Geográfica (CNIG). http://centrodedescargas.cnig.es/CentroDescargas/catalogo.do?Serie=LIDAR. Accessed 5 March 2021.
Ministerio para la Transición Ecológica y el Reto Demográfico (MITECO) (2019) Anuario de Aforos 2016–2017. Dirección General del Agua. Centro de Estudios y Experimentación de Obras Públicas (CEDEX). https://ceh.cedex.es/anuarioaforos/default.asp. Accessed 2 April 2021.
Molina-Navarro E, Martínez-Pérez S, Sastre-Merlín A, Bienes-Allas R (2014) Hydrological modelling in in a small Mediterranean basin as a tool to assess the feasibility of a limno-reservoir. J Environ Qual 43(1):121–131
Molina-Navarro E, Hallack-Alegría M, Martínez-Pérez S, Ramírez-Hernández J, Mungaray-Moctezuma A, Sastre-Merlín A (2016) Hydrological modeling and climate change impacts in an agricultural semiarid region. Case study: Guadalupe River basin. Mexico Agric Water Manag 175:29–42
Molina-Navarro E, Andersen HE, Nielsen A, Thodsen H, Trolle D (2017) The impact of the objective function in multi-site and multi-variable calibration of the SWAT model. Environ Model Softw 93:255–267
Molina-Navarro E, Bailey RT, Andersen HE, Thodsen H, Nielsen A, Park S, Trolle D (2019) Comparison of abstraction scenarios simulated by SWAT and SWAT-MODFLOW. Hydrol Sci J 64(4):434–454
Molina Navarro E, Sastre Merlín A, Martín-Loeches Garrido M, Vicente R, Sánchez Gómez A, Martínez Pérez S (2021) Impacto del cambio climático en la España rural: Modelizando la afección a los recursos hídricos en una cuenca del centro peninsular. En: Congreso Nacional de Medio Ambiente 2020. Comunicaciones Científico Técnicas, 4.12. Madrid
Moriasi DN, Arnold JG, Van Liew MW, Bingner RL, Harmel RD, Veith TL (2007) Model evaluation guidelines for systematic quantification of accuracy in watershed simulations. Trans ASABE 50(3):885–900
Moriasi DN, Wilson BN, Douglas-Mankin KR, Arnold JG, Gowda PH (2012) Hydrologic and water quality models: Use, calibration, and validation. Trans ASABE 55(4):1241–1247
Moriasi DN, Gitau MW, Pai N, Daggupati P (2015a) Hydrologic and water quality models: Performance measures and evaluation criteria. Trans ASABE 58(6):1763–1785
Moriasi DN, Zeckoski RW, Arnold JG, Baffaut C, Malone RW, Daggupati P, Douglas-Mankin KR (2015b) Hydrologic and water quality models: Key calibration and validation topics. Trans ASABE 58(6):1609–1618
Muleta MK (2012) Model performance sensitivity to objective function during automated calibrations. J Hydrol Eng 17(6):756–767
Nguyen VT, Dietrich J (2018) Modification of the SWAT model to simulate regional groundwater flow using a multicell aquifer. Hydrol Process 32(7):939–953
Pascual D, Pla E, Lopez-Bustins JA, Retana J, Terradas J (2015) Impacts of climate change on water resources in the Mediterranean Basin: a case study in Catalonia. Spain Hydrological Sciences Journal 60(12):2132–2147
Pérez-Sánchez J, Senent-Aparicio J, Martínez Santa-María C, López-Ballesteros A (2020) Assessment of ecological and hydro-geomorphological alterations under climate change using SWAT and IAHRIS in the Eo River in Northern Spain. Water 12(6):1745
Pfannerstill M, Bieger K, Guse B, Bosch DD, Fohrer N, Arnold JG (2017) How to constrain multi-objective calibrations of the SWAT model using water balance components. J Am Water Resour Assoc 53(3):532–546
Pisani B, Samper J, Paz A (2017) Modelos hidrológicos de balance de agua y evaluación de los impactos del cambio climático en zonas rurales de Galicia con eucaliptos. Estudios De La Zona No Saturada 13:565–576
Qi C, Grunwald S (2005) GIS-based hydrologic modeling in the Sandusky watershed using SWAT. Transactions of the ASAE 48(1):169–180
Saha S, Moorthi S, Wu X, Wang J, Nadiga S, Tripp P, Becker E (2014) The NCEP climate forecast system version 2. J Clim 27(6):2185–2208
Samper J, Pisani B, Marques JE, Fernández JM, Martín NS (2011) Estudio del flujo hipodérmico en zonas de montaña. Estudios En La Zona No Saturada Del Suelo 10:365–370
Seibert J, McDonnell JJ (2015) Gauging the ungauged basin: relative value of soft and hard data. J Hydrol Eng 20(1):A4014004
Senent-Aparicio J, Alcalá FJ, Liu S, Jimeno-Sáez P (2020) Coupling SWAT Model and CMB Method for modeling of high-permeability bedrock basins receiving interbasin groundwater flow. Water 12(3):657
Shrestha MK, Recknagel F, Frizenschaf J, Meyer W (2016) Assessing SWAT models based on single and multi-site calibration for the simulation of flow and nutrient loads in the semi-arid Onkaparinga catchment in South Australia. Agric Water Manag 175:61–71
Sudheer KP, Chaubey I, Garg V, Migliaccio KW (2007) Impact of time-scale of the calibration objective function on the performance of watershed models. Hydrol Process Int J 21(25):3409–3419
Triana JSA, Chu ML, Guzman JA, Moriasi DN, Steiner JL (2019) Beyond model metrics: the perils of calibrating hydrologic models. J Hydrol 578:124032
Van Liew MW, Veith TL, Bosch DD, Arnold JG (2007) Suitability of SWAT for the conservation effects assessment project: comparison on USDA agricultural research service watersheds. J Hydrol Eng 12(2):173–189
Volk M, Arnold JG, Bosch DD, Allen PM, Green CH (2007) Watershed configuration and simulation of landscape processes with the SWAT model. In: MODSIM 2007 international congress on modelling and simulation. Modelling and simulation society of Australia and New Zealand, Canberra, Australia, pp. 74–80
Xu ZX, Pang JP, Liu CM, Li JY (2009) Assessment of runoff and sediment yield in the Miyun Reservoir catchment by using SWAT model. Hydrol Process Int J 23(25):3619–3630
Yan T, Bai J, Yi LZ, A., & Shen, Z. (2018) SWAT-simulated streamflow responses to climate variability and human activities in the Miyun Reservoir Basin by considering streamflow components. Sustainability 10(4):941
Zhang X, Srinivasan R, Van Liew M (2008) Multi-site calibration of the SWAT model for hydrologic modeling. Trans ASABE 51(6):2039–2049
Acknowledgements
This work was funded by the Madrid Region Government Program for supporting Young Researchers, in agreement with the University of Alcalá (SIMTA project, reference CM/JIN/2019-035). Alejandro Sánchez-Gómez received additional support from the University of Alcalá PhD Fellowships Program. Authors want to thank the Water Resources Management and Planning Research Group (and particularly Dr. Javier Senent Aparicio) from the Catholic University of Murcia for providing soil and climate data for this project. Authors also want to thank the Organizers and Scientific Committee of the SDEWES Conference 2021 for the invitation to submit the work presented to this Special Issue.
Funding
Open Access funding provided thanks to the CRUE-CSIC agreement with Springer Nature.
Author information
Authors and Affiliations
Contributions
Alejandro Sánchez-Gómez, Eugenio Molina-Navarro and Silvia Martínez-Pérez contributed to the study conception and design. Francisco M. Pérez-Chavero set up the initial model. ASG and EMN designed the calibration schemes. ASG dealt with literature review, data production, analysis and interpretation, figures, tables, and maps and wrote the first draft of the manuscript. EMN commented on previous versions of the manuscript and contributed to data interpretation. SMP and FMPC commented on advanced versions of the manuscript. EMN and SMP supervised ASG work, revised the final manuscript and approved it.
Corresponding author
Ethics declarations
Conflict of interest
The authors have no relevant financial or non-financial interests to disclose.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Appendix 1: Best parameters
The following pages includes the best parameter set obtained in each calibration scheme for the entire basin (Scheme I) and for the calibrated regions (Schemes II, III and IV).




Appendix 2: Hydrological balance components spatial distribution
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Sánchez-Gómez, A., Martínez-Pérez, S., Pérez-Chavero, F.M. et al. Optimization of a SWAT model by incorporating geological information through calibration strategies. Optim Eng 23, 2203–2233 (2022). https://doi.org/10.1007/s11081-022-09744-1
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11081-022-09744-1