Abstract
We consider the optimistic bilevel optimization problem, known to have a wide range of applications in engineering, that we transform into a single-level optimization problem by means of the lower-level optimal value function reformulation. Subsequently, based on the partial calmness concept, we build an equation system, which is parameterized by the corresponding partial exact penalization parameter. We then design and analyze a Levenberg–Marquardt method to solve this parametric system of equations. Considering the fact that the selection of the partial exact penalization parameter is a critical issue when numerically solving a bilevel optimization problem by means of the value function reformulation, we conduct a careful experimental study to this effect, in the context of the Levenberg–Marquardt method, while using the Bilevel Optimization LIBrary (BOLIB) series of test problems. This study enables the construction of some safeguarding mechanisms for practical robust convergence of the method and can also serve as base for the selection of the penalty parameter for other bilevel optimization algorithms. We also compare the Levenberg–Marquardt method introduced in this paper to other existing algorithms of similar nature.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
We consider the optimistic bilevel optimization problem
where \(F:\mathbb {R}^n \times \mathbb {R}^m \rightarrow \mathbb {R}\), \(f:\mathbb {R}^n \times \mathbb {R}^m \rightarrow \mathbb {R}\), \(G:\mathbb {R}^n \times \mathbb {R}^m \rightarrow \mathbb {R}^q\), and \(g:\mathbb {R}^n \times \mathbb {R}^m \rightarrow \mathbb {R}^p\). As usual, we refer to F (resp. f) as the upper-level (resp. lower-level) objective function and G (resp. g) stands for the upper-level (resp. lower-level) constraint function. Solving problem (1) is very difficult, partly because of the implicit nature of the lower-level optimal solution set-valued mapping \(S : \mathbb {R}^n \rightrightarrows \mathbb {R}^m\) that partly describes the feasible set of the problem in (1).
Optimization problems in the form (1) have a wide range of applications in engineering. For example, in chemical engineering, we can mention the identification of optimal mixture of chemical substance (Oeder et al. 1988) and chemical equilibrium (William 1982), bioengineering and biotechnology (Burgard et al. 2003; Pharkya et al. 2003), the design of optimal chemical processes (Clarke and Westerberg 1990a, b) and parameter estimation in chemical engineering (Bollas et al. 2009; Mitsos et al. 2009). In civil engineering, bilevel optimization has been used for optimal shape design (Outrata et al. 1998), optimal pipe network design (Zhang and Zhu 1996), trust topology optimization (Friedlander and Gomes 2011), aircraft structural design (Hansen and Horst 2008), and optimal real-time path planning for unmanned aerial vehicles (Liu et al. 2013). In computer-aided engineering, note that classes of problem (1) can be applied for autonomous vehicles control and trajectory planning (Zhao et al. 2019), imaging science [e.g., image segmentation (Ranftl and Pock 2014), image reconstruction (Diamond et al. 2021), parameter learning in image applications (Ochs et al. 2016)] and well as machine learning and related applications [see the related survey paper (Liu et al. 2021)]. For applications of bilevel optimization in mechanics, interested readers are referred to Panagiotopoulos et al. (1998). Further applications of bilevel optimization in engineering and in many other fields such as economics and operations research can be found the recent collection of surveys (Dempe and Zemkoho 2020).
Our primary goal in this paper is to propose a tractable framework to solve problem (1). In the process of solving the problem, one of its most common single-level transformation is the Karush-Kuhn-Tucker (KKT) reformulation, which consists of replacing inclusion \(y\in S(x)\) with the equivalent KKT conditions of the lower-level problem, under appropriate assumptions; see, e.g., Allende and Still (2012, Dempe and Zemkoho (2013), Dempe and Dutta (2012), Herskovits et al. (2013), Pineda et al. (2018). As shown in Dempe and Dutta (2012), the first drawback of the KKT reformulation is that it is not necessarily equivalent to the original problem (1). Secondly, from the numerical perspective, the KKT reformulation involves derivatives from the lower-level problem that can require the calculation of second (resp. third) order derivatives for first (resp. second) order optimization methods. Thirdly, it is shown in the new paper Zemkoho and Zhou (2021) that the lower-level value function (LLVF) reformulation
where the LLVF \(\varphi\) is defined by
can lead to a better numerical performance than the KKT reformulation for certain problem classes; in particular for the Bilevel Optimization LIBrary (BOLIB) examples (Zhou et al. 2020). It is also important to note that problem (2)–(3) is equivalent to the original problem (1) without any assumption.
There is a number of recent studies on solution methods for bilevel programs that are based on the LLVF reformulation. For example, Mitsos et al. (2008), Paulavicius et al. (2020), Wiesemann et al. (2013) develop global optimization techniques for (2)–(3). Lin et al. (2014), Xu and Ye (2014) propose algorithms computing stationary points for (2)–(3) in the special case where G (resp. g) is independent from y (resp. x). But, the value function in the latter works is approximated by an entropy function, which is difficult to compute for problems with a big number of lower-level variables, as the corresponding approximation relies on integral calculations.
More recently, Fischer et al. (2021) and Zemkoho and Zhou (2021) have proposed Newton-type methods for problem (2)–(3) based on a special transformation that enables the optimality conditions of this problem to be squared. Naturally, detailed optimality conditions for (2)–(3) are non-square and are directly dealt with in Fliege et al. (2021) using Gauss-Newton-type methods. But these methods require inverse calculations at each iteration for matrices which are not necessarily nonsingular. Hence, to expand the applicability of the latter class of methods to a larger set of problems, the primary aim of this paper is to introduce and study the regularized version of the Gauss-Newton method (commonly known as the Levenberg–Marquardt method) tailored to the bilevel optimization problem in (2)–(3).
Recall that the standard approach to derive optimality conditions for problem (2)–(3), necessary to build this Levenberg–Marquardt method, is based on the concept of partial calmness (to be defined in the next section). This concept requires the provision of a penalty parameter, associated to the value function constraint \(f(x,y) - \varphi (x) \le 0\), to solve the surrogate problem. The consequence of this is that all the methods studied in the papers Fliege et al. (2021), Fischer et al. (2021), Zemkoho and Zhou (2021), Lin et al. (2014), Xu and Ye (2014) are based on a partial exact penalization parameter, which needs a special care to be selected. However, none of these papers pays a special attention on how to select this parameter. One of the goals of the current paper is to conduct a numerical study on the best way to select this parameter in the context of the BOLIB test set (Zhou et al. 2020) and the aforementioned Levenberg–Marquardt method to be introduced in the next section. This study will certainly enlighten the process of selecting the partial exact penalization parameter in the broader context of the LLVF reformulation in optimistic bilevel optimization.
We start the next section by introducing the necessary optimality for problem (2)–(3), which are solved in this paper. Due to the partial calmness requirement, these conditions depend on the partial exact penalization parameter (\(\lambda\)). The conditions are subsequently transformed into a system of equations by means of the well-known Fischer–Burmeister function (Fischer 1992) that we then perturb to build a smooth system. We also state the convergence of the Levenberg–Marquardt method and discuss the selection of the corresponding regularization parameter.
Section 3 is dedicated to the selection of the penalty parameter \(\lambda\). Recall that it is standard in the practical implementation of penalty methods to pick a large number to proceed with. Considering that the threshold value of \(\lambda\) is not known, it is unclear how small this value could be. Given that the true optimal solutions for almost all of our test problems are known, our numerical experiments show that very small values, possibly with \(\lambda \ll 1\), could be valid exact partial penalty parameters, as further confirmed by the analysis in Sect. 5. Considering the safeguard mechanisms that resulted from this analysis, the obtained ranges of possible choices for lambda could serve as base for the implementation of the partial exact penalization parameter in the context of other bilevel optimization solution algorithms tailored to the LLVF reformulation (2)–(3).
In Sect. 4, we assess the possibility of automatically selecting the parameter \(\lambda\); this is done by setting \(\lambda\) as an increasing sequence to evaluate how large the parameter can be while preserving the efficiency of the Levenberg–Marquardt method. The approach of varying \(\lambda\) is compared with a selection of different fixed values, which are powers of 10. The performance measures used for this comparison are accuracy of the upper-level objective function value, the feasibility of the computed point and the experimental order of convergence. A key outcome of this comparison is that both approaches can be equally good, but the varying sequence generally leads to an ill-behaviour as the values of the sequence grow. Nevertheless, the critical role of the varying sequence cannot be underestimated in the identification of the aforementioned safeguards, which are built in our Levenberg–Marquardt method to promote its robust convergence.
On the behaviour of the Levenberg–Marquardt method itself, as this is the first time that it is applied in the context of bilevel optimization, to the best of our knowledge, it is important to compare its performance with methods of similar characteristics. Hence, in Sect. 5, we compare the performance of our Levenberg–Marquardt method (see Sect. 2) to that of the Gauss–Newton-type method [developed in Fliege et al. 2021) and semismooth Newton-type method (introduced and studied in Fischer et al. (2021), Zemkoho and Zhou (2021)], as well as the MATLAB fsolve solver (Optimization 1990). As it will be clear in this section, the Levenberg–Marquardt method shows the best performance on the accuracy and feasibility measures, while having some limitations in comparison to the other methods. These limitations are largely explained by the structural differences (clearly highlighted in Sect. 5) between the methods.
The paper is concluded in Sect. 6 with some final observations and remarks.
2 The algorithm and convergence analysis
We start this section with some definitions necessary to state optimality conditions for the bilevel program (2)–(3), which will be used to construct the algorithm. The lower-level problem is fully convex if the functions f and \(g_i\), \(i=1, \ldots , p\) are convex in (x, y). A point \((\bar{x},\bar{y})\) is said to be lower-level regular if there exists a vector \(d\in \mathbb {R}^m\) such that we have
Obviously, this is the Mangasarian–Fromovitz constraint qualification (MFCQ) for the lower-level problem in (1). Similarly, a point \((\bar{x},\bar{y})\) is upper-level regular if there exists \(d\in \mathbb {R}^n\times \mathbb {R}^m\) such that
Finally, to write the necessary optimality conditions for problem (2)–(3), it is standard to use the following partial calmness concept (Ye and Zhu 1995):
Definition 2.1
Let \((\bar{x},\bar{y})\) be a local optimal solution of problem (2)–(3). The problem is partially calm at \((\bar{x},\bar{y})\) if there exists \(\lambda >0\) and a neighbourhood U of \((\bar{x},\bar{y},0)\) such that
The following relationship shows that the partial calmness concept enables the penalization of the optimal value function constraint \(f(x,y)-\varphi (x)\le 0\), to generate a tractable optimization problem, as it is well-known that standard constraint qualifications (including the MFCQ, for example) fail for problem (2)–(3); see Dempe and Zemkoho (2011) and Ye and Zhu (1995).
Theorem 2.2
(Ye and Zhu 1995) Let \(({\bar{x}}, {\bar{y}})\) be a local minimizer of (2)–(3). Then, this problem is partially calm at \(({\bar{x}}, {\bar{y}})\) if and only if there is some \({\bar{\lambda }} >0\) such that for any \(\lambda \ge \bar{\lambda }\), the point \(({\bar{x}}, {\bar{y}})\) is also a local minimizer of
Problem (6) is known as the partial exact penalization problem of (2)–(3), as only the optimal value constraint is penalized. Next, we state the necessary optimality conditions for problem (2)–(3) based on the aforementioned penalization, while using the upper- and lower-level regularity conditions and an estimate of the subdifferential of \(\varphi\) (3); see, e.g., Dempe and Zemkoho (2011), Dempe et al. (2007), Dempe and Zemkoho (2013), Ye and Zhu (1995), for the details.
Theorem 2.3
Let \((\bar{x},\bar{y})\) be a local optimal solution of problem (2), where all involved functions are assumed to be continuously differentiable, \(\varphi\) is finite around \(\bar{x}\), and the lower-level problem is fully convex. Furthermore, suppose that the problem is partially calm at \((\bar{x},\bar{y})\), and the lower- and upper-level regularity conditions are both satisfied at \((\bar{x},\bar{y})\). Then, there exist \(\lambda > 0\), as well as \(u, w\in \mathbb {R}^p\) and \(v\in \mathbb {R}^q\) such that
In this result, partial calmness and full convexity are essential and fundamentally related to the nature of the bilevel optimization. Hence, it is important to highlight a few classes of problems satisfying these assumptions. Partial calmness has been the main tool to derive optimality conditions for (1) from the perspective of the optimal value function; see, e.g., Dempe et al. (2007), Dempe and Zemkoho (2011, 2013), Ye and Zhu (1995). It automatically holds if G is independent from y and the lower-level problem is defined by
where \(A: \mathbb {R}^n \rightarrow \mathbb {R}^p\), \(c\in \mathbb {R}^m\), and \(B\in \mathbb {R}^{p\times m}\). More generally, various sufficient conditions ensuring that partial calmness holds have been studied in the literature; see (Ye and Zhu 1995) for the seminal work on the subject. More recently, the paper Mehlitz et al. (2021) has revisited the condition, proposed a fresh perspective, and established new sufficient conditions for it to be satisfied.
As for full convexity, it will automatically hold for the class of problem defined in (12), provided that each component of the function A is convex. Another class of nonlinear fully convex lower-level problem is given in Lampariello and Sagratella (2020). Note however that when it is not possible to guarantee that this assumption is satisfied, there are at least two alternative scenarios to obtain the same optimality conditions as in Theorem 2.3. The first is to replace the full convexity assumption by the inner semicontinuity of the optimal solution set-valued mapping S (1). Secondly, note that a much weaker qualification condition known as inner semicompactness can also be used here. However, under the latter assumption, it will additionally be required to have \(S({\bar{x}})=\{{\bar{y}}\}\) in order to get the optimality conditions in (7)–(11). The concept of inner semicontinuity (resp. semicompactness) of S is closely related to the lower semicontinuity (resp. upper semicontinuity) of set-valued mappings; for more details on these notions and their ramifications on bilevel programs, see, e.g., Dempe et al. (2007), Dempe and Zemkoho (2011, 2013).
It is important to mention that various other necessary optimality conditions, different from the above ones, can be obtained, depending on the assumptions made. Details of different stationarity concepts for (2) can be found in the latter references, as well as in Zemkoho (2012).
To reformulate the complementarity conditions (9)–(11) into a system of equations, we use the well-known Fischer-Burmeister function (Fischer 1992) \(\phi (a,b) := \sqrt{a^2+b^2}-a-b\), which ensures that
This leads to the reformulation of the optimality conditions (7)–(11) into the system of equations:
where we have \(z:=(x, y, u, v, w)\) and
\(\sqrt{v^2+G(x,y)^2 } - v+G(x,y)\) and \(\sqrt{w^2+g(x, y)^2 } - w+g(x, y)\) are defined as in (14). The superscript \(\lambda\) is used to emphasize the fact that this number is a parameter and not a variable for Eq. (13). One can easily check that this system is made of \(n+2m+p+q+ p\) real-valued equations and \(n+m+p+q+p\) variables. Clearly, this means that (13) is an overdetermined system and the Jacobian of \(\Upsilon ^\lambda (z)\), when it exists, is a non-square matrix.
To focus our attention on the main ideas of this paper, we smoothen the function \(\Upsilon ^\lambda\) (13) using the smoothed Fischer-Burmeister function [see Kanzow (1996)] defined by
where the perturbation \(\mu >0\) helps to guarantee its differentiability at points (x, y, u), where \(u_j = g_j(x,y)=0\) for \(j=1, \ldots , p\). It is well-known (see latter reference) that for \(j=1, \ldots , p\),
The smoothed version of system (13) then becomes
following the convention in (14), where \(\mu\) is a vector of appropriate dimensions with sufficiently small positive elements. Under the assumption that all the functions involved in problem (1) are continuously differentiable, \(\Upsilon ^{\lambda }_\mu\) is also a continuously differentiable function for any \(\lambda > 0\) and \(\mu >0\). We can easily check that for a fixed value of \(\lambda > 0\),
Hence, based on this scheme, our aim is to consider a sequence \(\{\mu _k\}\) decreasing to 0 such that Eq. (13) is approximately solved while leading to
for a fixed value of \(\lambda >0\). In order to proceed, let us define the least squares problem
Before we introduce the smoothed Levenberg–Marquardt method that will be one of the main focus points of this paper, note that for fixed \(\lambda >0\) and \(\mu >0\),
with the pair \(\left( \mathcal {T}^\mu , \Gamma ^\mu \right)\) defined by \(\mathcal {T}^\mu := diag~\{\tau _1^\mu ,\ldots ,\tau _p^\mu \}\) and \(\Gamma ^\mu := diag~\{\gamma _1^\mu ,\ldots ,\gamma _p^\mu \}\), where
The pairs \(\left( \mathcal {A}^{\mu },\, \mathcal {B}^{\mu }\right)\) and \(\left( \Theta ^{\mu }, \mathcal {K}^{\mu }\right)\) are defined in a similar way, based on \((v_j , G_j(x,y))\), \(j=1,\ldots ,q\) and \((w_j,g_j(x,y))\), \(j=1,\ldots ,p\), respectively.
We now move on to present some definitions that will help us state the algorithm with line search. It is well-known that line search helps to choose the optimal step length to avoid over-going an optimal solution in the direction \(d^k\) and also to globalize the convergence of the method, i.e., have more flexibility on the starting point \(z^0\). The optimal step length \(\gamma _k\) can be calculated through minimizing \(\Phi ^\lambda (z^k + \gamma _k d^k)\), with respect to \(\gamma _k\), such that
That is, we are looking for \(\gamma _k = arg \min _{\gamma \in \mathbb {R}} ||\Upsilon ^\lambda (z^k + \gamma d^k)||^2\). To implement line search, it is standard to use Armijo condition that guarantees a decrease at the next iterate.
Definition 2.4
Fixing d and z, consider the function \(\phi _\lambda (\gamma ) := \Phi ^\lambda (z+\gamma d)\). Then, the Armijo condition will be said to hold if \(\phi _\lambda (\gamma )\le \phi (0) + \gamma \sigma \phi '_\lambda (\gamma )\) for some \(0<\sigma <1\).
The practical implementation of the Armijo condition is based on backtracking.
Definition 2.5
Let \(\rho \in (0,1)\) and \(\bar{\gamma } >0\). Backtracking is the process of checking over a sequence \(\bar{\gamma }\), \(\rho \bar{\gamma }\), \(\rho ^2 \bar{\gamma }\), ..., until a number \(\gamma\) is found satisfying the Armijo condition.
Line search is widely used in continuous optimization; see, e.g., Nocedal and Wright (1999) for more details. For the implementation in this paper, we start with stepsize \(\gamma _0:=1\); then, if the condition
is not satisfied, we set \(\gamma _k = \gamma _k/2\) and check again until the condition above is satisfied. More generally, the algorithm proceeds as follows:
Algorithm 2.6
Smoothed Levenberg–Marquardt Method for Bilevel Optimization
- Step 0::
-
Choose \((\lambda , \mu , K, \epsilon , \alpha _0)\in \left( \mathbb {R}^*_+\right) ^5\), \((\rho , \sigma , \gamma _0) \in (0,1)^3\), \(z^0:=(x^0, y^0, u^0, v^0, w^0)\), and set \(k:=0\).
- Step 1::
-
If \(\left\Vert \Upsilon ^{\lambda }_\mu (z^k)\right\Vert <\epsilon\) or \(k\ge K\), then stop.
- Step 2::
-
Calculate the Jacobian \(\nabla \Upsilon _\mu ^\lambda (z^k)\) and subsequently find a vector \(d^k\) satisfying
$$\begin{aligned} \left( \nabla \Upsilon _\mu ^\lambda (z^k)^\top \nabla \Upsilon _\mu ^\lambda (z^k) + \alpha _k I\right) d^k = - \nabla \Upsilon _\mu ^\lambda (z^k)^\top \Upsilon ^\lambda _\mu (z^k), \end{aligned}$$(22)where I denotes the identity matrix of appropriate size.
- Step 3::
-
While \(\left\Vert \Upsilon ^\lambda _\mu (z^k+\gamma _k d^k)\right\Vert ^2 \ge \left\Vert \Upsilon ^{\lambda }_\mu (z^k)\right\Vert ^2 + \sigma \gamma _k \nabla \Upsilon _\mu ^\lambda (z^k)^T \Upsilon ^\lambda _\mu (z^k) d^k\), do \(\gamma _k \leftarrow \rho \gamma _k\) end.
- Step 4::
-
Set \(z^{k+1}:=z^k + \gamma _k d^k\), \(k:=k+1\), and go to Step 1.
Note that in Step 0, \(\mathbb {R}^*_+:=(0, \, \infty )\). Before we move on to focus our attention on the practical implementation details of this algorithm, we present its convergence result, which is based on the following selection of the Levenberg–Marquardt (LM) parameter \(\alpha _k\):
Theorem 2.7
(Fan and Yuan 2005) Consider Algorithm 2.6 with fixed values for the parameters \(\lambda >0\) and \(\mu >0\) and let \(\alpha _k\) be defined as in (23). Then, the sequence \(\{z^k\}\) generated by the algorithm converges quadratically to \(\bar{z}\) satisfying \(\Upsilon _\mu ^\lambda ({\bar{z}})=0\), under the following assumptions:
-
1.
\(\Upsilon _\mu ^\lambda : \mathbb {R}^{N} \rightarrow \mathbb {R}^{N+m}\) is continuously differentiable and \(\nabla \Upsilon _\mu ^\lambda : \mathbb {R}^{N} \rightarrow \mathbb {R}^{(N+m)\times (N)}\) is locally Lipschitz continuous in a neighbourhood of \({\bar{z}}\).
-
2.
There exists some \(C>0\) and \(\delta >0\) such that
$$\begin{aligned} C dist(z,Z^\lambda _\mu ) \le \left\Vert \Upsilon _\mu ^\lambda (z)\right\Vert \text {for all }\;\, z\in \mathcal {B} (\bar{z}, \delta ), \end{aligned}$$where dist denotes the distance function and \(Z^\lambda _\mu\) corresponds to the solution set of equation (17).
For fixed values of \(\lambda >0\) and \(\mu >0\), assumption 1 in this theorem is automatically satisfied if all the functions involved in problem (1) are twice continuously differentiable. According to Yamashita and Fukushima (2001), assumption 2 of Theorem 2.7 is fulfilled if the matrix \(\nabla \Upsilon _\mu ^\lambda\) has a full column rank. Various conditions guaranteeing that \(\nabla \Upsilon _\mu ^\lambda\) has a full rank have been developed in Fliege et al. (2021). Below, we present an example of bilevel program satisfying the first and second assumptions of Theorem 2.7.
Example 2.8
Consider the following instance of problem (1) from the BOLIB library (Zhou et al. 2020, LamprielloSagratelli2017Ex33):
Obviously, assumption 1 holds. According to Fliege et al. (2021), for this example, the columns of \(\nabla \Upsilon _\mu ^\lambda\) are linearly independent at the solution point
with the parameters chosen as \(\mu =2\times 10^{-2}\) and \(\lambda =10^{-2}\). \(\square\)
On the selection of the LM parameter \(\alpha _k\), we conducted a preliminary analysis based on the BOLIB library test set (Zhou et al. 2020). It was observed that for almost all the corresponding examples, the choice \(\alpha _k := \left\| \Upsilon _\mu ^\lambda (z^k)\right\| ^\eta\) with \(\eta \in (1, 2]\) leads to a very poor performance of Algorithm 2.6. The typical behaviour of the algorithm for \(\eta \in (1, 2]\) is shown in the following example.
Example 2.9
Consider the following scenario of problem (1) from Zhou et al. (2020, AllendeStill2013):
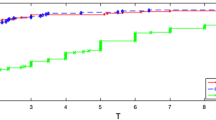
Figure 1 shows the progression of \(\left\Vert \Upsilon ^{\lambda }(z^k)\right\Vert\) generated from Algorithm 2.6 with \(\alpha _k\) selected as in (23) while setting \(\eta =1\) and \(\eta =2\), respectively. Clearly, after about 100 iterations \(\left\Vert \Upsilon ^{\lambda }(z^k)\right\Vert\) blows up relatively quickly when \(\eta =2\), while it falls and stabilizes within a certain tolerance for \(\eta =1\).
Typical behaviour of Algorithm 2.6 for two scenarios of the LM parameter
It is worth noting that the scale on the y-axis of Fig. 1b is quite large. Hence, it might not be apparent that solutions at the early iterations of the algorithm are much better for \(\eta =1\) compared to the ones obtained in the case where \(\eta =2\). \(\square\)
Note that for almost all of the examples in the BOLIB test set (Zhou et al. 2020), we have a behaviour of Algorithm 2.6 similar to that of Fig. 1b when \(\alpha _k=\left\Vert \Upsilon ^{\lambda }(z^k)\right\Vert ^\eta\) for many different choices of \(\eta \in (1,2]\). It is important to mention that the behaviour of the algorithm is not surprising, as it is well-known in the literature that with the sequence \(\alpha _k:=\left\Vert \Upsilon _\mu ^\lambda (z^k)\right\Vert ^2\), for example, the Levenberg–Marquardt method often faces some issues. Namely, when the sequence \(z^k\) is close to the solution set, \(\alpha _k:=\left\Vert \Upsilon _\mu ^\lambda (z^k)\right\Vert ^2\) could become smaller than the machine precision and hence lose its role as a result of this. On the other hand, when the sequence is far away from the solution set, \(\left\Vert \Upsilon ^\lambda _\mu (z^k)\right\Vert ^2\) may be very large; making a movement towards the solution set to be very slow. Hence, from now on, we use \(\alpha _k:=\left\Vert \Upsilon ^{\lambda }(z^k)\right\Vert\), with \(k=0, \, 1, \ldots\), for all the analysis of Algorithm 2.6 conducted in this paper. Note however that there are various other approaches to select the LM parameter \(\alpha _k\) in the literature; see, e.g., Behling et al. (2016), Fan and Yuan (2005), Yamashita and Fukushima (2001).
To conclude this section, it is important to recall that from the perspective of bilevel optimization, the partial exact penalization parameter \(\lambda\) is a key element of Algorithm 2.6, as it originates from the penalization of the value function constraint \(f(x,y)\le \varphi (x)\). Additionally, unlike the other parameters involved in the algorithm, which have benefited from many years of research, as it will be clear in Sect. 4, it remains unknown what is the best way to select \(\lambda\) while solving problem (1) via the value function reformulation (2)–(3). Hence, the focus of the remaining parts of this paper will be on the selection of \(\lambda\) and assessing its impact on the efficiency of Algorithm 2.6.
3 Partial exact penalty parameter selection
The aim of this section is to explore the best way to select the penalization parameter \(\lambda\). Based on Theorem 2.2, we should be getting the solution for some threshold value \({\bar{\lambda }}\) of the penalty parameter and the algorithm should be returning the value of the solution for any \(\lambda \ge {\bar{\lambda }}\). Hence, increasing \(\lambda\) at every iteration seems to be the ideal approach to follow this logic to obtain and retain the solution. Hence, to proceed, we use the increasing sequence \(\lambda _k := 0.5*(1.05)^k\), where k is the number of iterations of the algorithm. The main reason of this choice is that the final value of \(\lambda\) need not to be too small to recover solutions and not too large to avoid ill-conditioning. It was observed that going too aggressive with the sequence (e.g., with \(\lambda _k:=2^k\)) forces the algorithm to diverge. Also, it was observed that for fixed and small values of \(\lambda\) (i.e., \(\lambda <1\)), Algorithm 2.6 performs well for many examples. This justifies choosing the starting value for varying parameter less than 1. Overall, the aim here is to vary \(\lambda\) as mentioned above and assess what could be the potential best ranges for selection of the parameter based on our test set from BOLIB (Zhou et al. 2020).
3.1 How far can we go with the value of \(\lambda\)?
We start here by acknowledging that it is very difficult to check that partial calmness (cf. Definition 2.1) holds in practice. Nevertheless, we would like to consider Theorem 2.2 as the base of our experimental analysis, and ask ourselves how large \(\lambda\) needs to be for Algorithm 2.6 to converge. Intuitively, one would think that taking \(\lambda\) as whatever large number should be fine. However, this is usually not the case in practice. One of the main reasons for this is that for too large values of \(\lambda\), Algorithm 2.6 does not behave well. In particular, if we run Algorithm 2.6 with varying \(\lambda\) for a very large number of iterations, the value of the Error blows up at some point and the values \(\left\Vert \Upsilon ^{\lambda }_\mu (z^k)\right\Vert\) stop decreasing. Recall that ill-conditioning (and possibly the ill-behaviour) refers to the fact that one eigenvalue of the Hessian involved in \(\nabla \Upsilon _\mu ^\lambda (z^k)\) being much larger than the other eigenvalues, which affects the curvature in the negative way for gradient methods (Press et al. 1992). To analyze this ill-behaviour in this section, we are going to run our algorithm for 1, 000 iterations with no stopping criteria and let \(\lambda\) vary indefinitely. We will subsequently look at which iteration the algorithm blows up and record the value of \(\lambda\) there. To proceed, we denote by \(\lambda _{ill}\) the first value of \(\lambda\) for which the ill-behaviour is observed for each example. The table below presents the number of BOLIB examples that are approximately within certain intervals of \(\lambda _{ill}\) (Table 1).
On average, the ill-behaviour seems to typically occur after about 500 iterations (where \(\lambda _{ill}\approx 10^{10}\)), as it can be seen in the table above. For 34 problems ill-behaviour was not observed under the scope of 1000 iterations. We also see that for most of the problems (72/124), the starting point for the ill-behaviour happens when \(10^9<\lambda <10^{11}\). We further observe that algorithm has shown to behave well for the values of penalty parameter \(\lambda <10^9\) with only 7/124 examples demonstrating ill-behaviour for such \(\lambda\). This makes the choice of very large values of \(\lambda\) not attractive at all, as the algorithm would diverge for a large majority of our examples. For instance, taking \(\lambda =10^{20}\), we observed that the ill-behaviour would occur for 90/124 tested examples. Mainly, the analysis shows that choosing \(\lambda >10^9\) could cause the algorithm to diverge. Hence, based on our method, selecting \(\lambda \le 10^7\) seems to be a very safe choice for our BOLIB test set. This is useful for the choice of fixed \(\lambda\) as we can choose values smaller than \(10^7\). For the case of varying \(\lambda\) the values are controlled by the stopping criteria proposed in the next section. The complete results on the values of \(\lambda _{ill}\) for each example will be presented in Table 2 below.
Interestingly, 34 out of the 124 test problems do not demonstrate any ill behaviour signs even if we run the algorithm for 1000 iterations with \(\lambda =0.5*1.05^{iter}\). A potential reason for this could just be that the parameter \(\lambda\) does not get sufficiently large after 1, 000 iterations to cause problems for these problems. It could also be that the eigenvalues of the Hessian are not affected by large values of \(\lambda\) for these examples. Also, there is a possibility that elements of the Hessian involved in (22) do not depend on \(\lambda\) at all, as for 20/34 problems where the function g is linear in (x, y) or not present in these problems. Next, we focus our attention on assessing what magnitudes of the penalty parameter \(\lambda\) to better evaluate the performance of our method.
3.2 Do the values of \(\lambda\) really need to be large?
It is clear from the previous subsection that to reduce the chances for Algorithm 2.6 to diverge or exhibit some ill-behaviour, we should approximately select \(\lambda < 10^7\). However, it is still unclear whether only large values of \(\lambda\) would be sensible to ensure a good behaviour of the algorithm. In other words, it is important to know whether relatively small values of \(\lambda\) can lead to a good behaviour for Algorithm 2.6. To assess this, we attempt here to identify inflection points, i.e., values of k where we have \(\left\Vert \Upsilon ^{\lambda _k}_\mu (z^k)\right\Vert <\epsilon\) as \(\lambda _k\) varies increasingly as described in the introduction of this section. We would then record the value of \(\lambda _k\) at these points.
Ideally, we want to get the threshold \(\bar{\lambda }\) such that solution is retained for all \(\lambda >{\bar{\lambda }}\) in the sense of Theorem 2.2. To proceed, we extract the information on the final \(Error^*:=\left\Vert \Upsilon ^\lambda (z^*)\right\Vert\) for each example from Tin and Zemkoho (2020) and then rerun the algorithm with varying penalty parameter \(\lambda _k:=0.5*1.05^k\) with new stopping criterion (i.e., \(Error \le 1.1 Error^*\)) while relaxing all of the stopping criteria (see details in Sect. 4). This way, we stop once we observe \(Error_k:=\left\Vert \Upsilon ^{\lambda _k}(z)\right\Vert\) close to the \(Error^*\) that we obtained in our experiments (Tin and Zemkoho 2020). It is worth noting that it would make sense to test only 72/117 (\(61.54\%\)) of examples, for which algorithm performed well and produced a good solution. This approach can be thought of as finding the inflection point. For instance, if we have an algorithm running as below, we want to stop at the inflection point after 125–130 iterations. The illustration of how we aim to stop at the inflection point is presented in Fig. 2a–b below, where we have \(\left\Vert \Upsilon ^\lambda (z)\right\Vert\) on the y-axis and iterations on the x-axis.
For some of the examples, we obtained a better Error than initial \(Error^*\). For these cases, we stopped very early as \(Error_k \le 1.1Error^*\) was typically met at an early iteration k (where \(\lambda\) was still small), as demonstrated in Fig. 2c–d above. This demonstrates the disadvantage of \(\lambda\) being an increasing sequence. If the algorithm makes many iterations, the parameter \(\lambda\) keeps increasing without possibility to go back to the smaller values. It turns out that for some examples the smaller value of \(\lambda\) was as good as large values, or even better to recover a solution. This further justifies the choice to start from the small value of \(\lambda\), that is \(\lambda _0<1\) and increase it slowly.
(a) and (b) illustrate the inflection point identification for Example AllendeStill2013 and similarly (c) and (d) correspond to Example Anetal2009; the examples are taken from BOLIB (Zhou et al. 2020)
With the setting to stop whenever \(Error_k \le 1.1 Error^*\), we often stop very early. Hence, we do not always get \({\bar{\lambda }}\) that represents the inflection point, which we aimed to get; cf. Fig. 2c–d, where (c) has a scale of \(10^4\) on the y-axis. Although, we can clearly see from Fig. 2c that inflection point lies around 190–200 iterations, where the value of \(\lambda\) is much bigger. It is clear that we stopped earlier due to having small value of Error after 12–45 iterations. It was observed that such scenario is typical for the examples in the considered test set. For this reason, we want to introduce \(\lambda ^*\) as the large threshold of \(\lambda\). This value will be used to represent the value of the penalty parameter at the inflection point, where solution starts to be recovered for large values of \(\lambda\) (\(\lambda >6.02\)), while we also record \({\bar{\lambda }}\) as the first (smallest) value of \(\lambda\) for which good solution was obtained. For instance, with \(\lambda\) defined as \(\lambda := 0.5\times 1.05^k\) in Fig. 2c we have \({\bar{\lambda }} = 0.5\times 1.05^{12}\) and \(\lambda ^*=0.5\times 1.05^{190}\) as we obtain good solution for small \(\lambda\) after 12 iterations and for large \(\lambda\) after 190 iterations. We shall note that the value \(\lambda >6.02\) is the value of the penalty parameter after we make at least 50 iterations as for the case with varying \(\lambda\) we have \(\lambda = 0.5\times 1.05^{51}=6.02\).
The complete results of detecting \({\bar{\lambda }}\) and \(\lambda ^*\) is presented in Table 2 below. It was observed that the behaviour of the method follows the same pattern for the majority of the examples. Typically, we get a good solution, which is retained for some small values of \(\lambda\), and subsequently, the value of the Error blows up and takes some iterations to start decreasing, coming back to obtaining and retaining a good solution for large values of \(\lambda\). Such pattern is clearly demonstrated in Fig. 2c. Such a behaviour is interesting as usually, only large values of penalty parameters are used in practice (Burke 1991; Di Pillo and Grippo 1989), as intuitively suggested by Theorem 2.2. As mentioned in Fletcher (1975), some methods require penalty parameters to increase to infinity to obtain convergence.
We are now going to proceed with finding the threshold of \(\lambda\) for which we start getting a solution and retain the value for larger values of \(\lambda\). We are going to proceed with the technique of finding small threshold \({\bar{\lambda }}\) and large threshold \(\lambda ^*\), which was briefly discussed earlier. To find the threshold we first extract the value of the final \(Error^*\) for each example from Tin and Zemkoho (2020). To find \({\bar{\lambda }}\) we run the algorithm with \(\lambda\) being defined as \(\lambda :=0.5\times 1.05^k\), with the new stopping criteria:
Of course, we also relax all of the aforementioned stopping criteria, as Error is the main measure here and we know that desired value of Error exists. We then define \({\bar{\lambda }} := 0.5 \times 1.05^{{\bar{k}}}\), where \({\bar{k}}\) is the number of iterations after stopping whenever we get \(Error<1.1Error^*\). For most of the cases we detect \({\bar{\lambda }}\) early due to a good solution after the first few iterations in the same manner as shown in Fig. 2c. Since for many examples we satisfy condition \(Error\le 1.1 Error^*\) for early iterations (before the inflection point is achieved), we further introduce \(\lambda ^*\), the large threshold \(\lambda\). The value of \(\lambda ^*\) will be used to represent the value of the penalty parameter at the inflection point, where solution starts to be recovered for large values of \(\lambda\). This will be obtained in the same way as \({\bar{\lambda }}\) with the only difference that we additionally impose the condition to stop after at least 50 iterations. To obtain \(\lambda ^*\) we run the algorithm with \(\lambda :=0.5\times 1.05^k\) and the following stopping criteria:
Then the large threshold is defined as \(\lambda ^* := 0.5\times 1.05^{k^*}\), where \(k^*\) is the number of iterations after stopping whenever we get \(Error<1.1Error^*\) and \(k>50\). This way \(\bar{\lambda }\) represents the first (smallest) value of \(\lambda\) for which good solution was obtained, while \(\lambda ^*\) represent the actual threshold after which solution is retained for large values of \(\lambda\). The demonstration of stopping at the inflection point for large threshold \(\lambda ^*\) was shown in Fig. 2b and for small threshold \({\bar{\lambda }}\) in Fig. 2d.
It makes sense to test only the examples where algorithm performed well and produced a good solution. For the rest of the examples, the value of \(Error^*\) would not make sense as the measure to stop, and we do not obtain good solutions for these examples by the algorithm anyway. From the optimistic perspective we could consider recovered solutions to be the solutions for which the optimal value of upper-level objective was recovered with some prescribed tolerance. Taking the tolerance of \(20\%\), the total amount of recovered solutions by the method with varying \(\lambda\) is 72/117 (\(61.54\%\)) for the cases where solution was reported in BOLIB (Zhou et al. 2020). This result will be shown in more details in Sect. 4.2. Let us look at the thresholds \({\bar{\lambda }}\) and \(\lambda ^*\) for these examples in the figure below, where the value of \(\lambda\) is shown on \(y-axis\) and the example numbers on the \(x-axis\).
For 68/72 problems, we observe that large threshold of the penalty parameter has the value \(\lambda ^* \le 10^4\), which shows that we usually can obtain a good solution before 205 iterations. This further justifies stopping algorithm after 200 iterations (see next section) if there is no significant step to step improvement. As for the main outcome of Fig. 3, we observe that small threshold is smaller than large threshold (\({\bar{\lambda }} < \lambda ^*\)) for 59/72 (\(82 \%\)) problems. This clearly shows that for majority of the problems, for which we recover solution with \(\lambda :=0.5\times 1.05^k\), we obtain a good solution for small \(\lambda\) as well as for large \(\lambda\). This demonstrates that small \(\lambda\) could in principle be good for the method. For the rest \(18\%\) of the problems we have \({\bar{\lambda }} = \lambda ^*\), meaning that good solution was not obtained for \(\lambda <6\) for these examples. This also means that we typically obtain good solution for small values of \(\lambda\) and for large values of \(\lambda\), but not for the medium values (\(\bar{\lambda }<\lambda <\lambda ^*\)).
As for the general observations of Fig. 3, for 42/72 (\(58.33\%\)) examples we observed that the large threshold \(\lambda ^*\) is located somewhere in between \(90-176\) iterations with \(40<\lambda ^*<2680\). For 7/72 problems threshold is in the range \(6.02<\lambda ^* \le 40\), and for only 4/72 problems \(\lambda ^*>1.1\times 10^4\). Once again, this justifies that typically \(\lambda\) does not need to be large. It also suggests the optimal values of \(\lambda\) for the tested examples, at least for our solution method. We observe that for 19/72 problems we get \(\lambda ^*=51\), which should be treated carefully as this could mean that the inflection point could possibly be achieved before 50 for these examples. Nevertheless, \(\lambda ^*=6.02\) is still a good value of penalty parameter for these examples as solutions are retained for \(\lambda >\lambda ^*\).
As going to be observed in Sect. 4 we could actually argue that smaller values of \(\lambda\) work better for our method not only for varying \(\lambda\) but also for fixed \(\lambda\). Together with the fact that we often have the behaviour as demonstrated in Fig. 2c, it follows that small \(\lambda\) could be more attractive for the method we implement. We even get better values of Error and better solutions for small values of \(\lambda\) for some examples. Hence we draw the conclusion that small values of \(\lambda\) can generate good solutions. Since it is typical to use large values of \(\lambda\) for other penalization methods [e.g. in Bertsekas (1982), Burke (1991), Di Pillo and Grippo (1989)], it is interesting what could be the reasons that small \(\lambda\) worked better for our case. This could be due to the specific nature of the method, or due to the fact that we do not do full penalization in the usual sense. Other reason could come from the structure of the problems in the test set. The exact reason of why such behaviour was observed remains an open question. What is important is that this could possibly be the case that small values of \(\lambda\) would be good for some other penalty methods and optimization problems of different nature. This result contradicts typical choice of large penalty parameter for general penalization methods for optimization problems. As the conclusion for our framework, we can claim that for our method \(\lambda\) needs not to be large.
3.3 Partially calm examples
Intuitively, one would think that for partially calm examples, Algorithm 2.6 would behave well, in the sense that varying \(\lambda\) increasingly would lead to a good convergence behaviour. To show that it is not necessarily the case, we start by considering the following result identifying a class of bilevel program of the form (1) that is automatically partially calm.
Theorem 3.1
(Mehlitz et al. 2021) Consider a bilevel program (1), where G is independent of y and the lower-level optimal solution map is defined as follows, with \(c\in \mathbb {R}^m\), \(d\in \mathbb {R}^p\), \(B\in \mathbb {R}^{p\times m}\), and \(A :\mathbb {R}^n \rightarrow \mathbb {R}^p\):
In this case, problem (1) is partially calm at any of its local optimal solutions.
Examples 8, 40, 43, 45, 46, 188, and 123 in the BOLIB library (see Table 2) are of the form described in this result. The expectation is that these examples will follow the pattern of retaining solution after some threshold, that is for \(\lambda >\lambda ^*\), as they fit the theoretical structure behind the penalty approach as described in Theorem 2.2. Note that all of these examples follow the pattern shown in Fig. 1a. However, if we relax the stopping criteria used to mitigate the effects of ill-conditioning, as discussed in the previous two subsections, varying \(\lambda\) for 1000 iterations for these seven partially calm examples leads to the 3 typical scenarios demonstrated in Fig. 4.
In the first case of Fig. 4, we can clearly see the algorithm is performing well, retaining the solution for the number of iterations, but then blows up at one point (after 500 iterations) and never goes back to reasonable solution values. Examples 40 and 46 also follow this pattern. Example 123 (second picture in Fig. 4) shows a slightly different picture, where the zig-zagging pattern is observed. Algorithm 2.6 blows up at some point and starts zig-zagging away from the solution after obtaining it for a smaller value of \(\lambda\). Zig-zagging is very common issue in penalty methods and often caused by ill-conditioning (Nocedal and Wright 1999). Note that Example 118 exhibits a similar behaviour. This is somewhat similar to scenario 1. However, we put this separately as zig-zagging issue is often referred to as the danger that could be caused by ill-conditioning of a penalty function. The last picture of Fig. 4 shows a case where Algorithm 2.6 runs very well without any ill-behaviour observed for all the 1000 iterations. It could be possible that the algorithm could blow up after more iterations if we keep increasing \(\lambda\). It could also be possible that ill-conditioning does not occur for this example at all, as the Hessian of \(\Upsilon ^\lambda\) (13) is not affected by \(\lambda\). Out of the seven BOLIB problems considered here, only examples 43 and 45 follows this pattern.
4 Performance comparison under fixed and varying partial penalty parameter
Following the discussion from the previous section, two approaches for selecting the penalty parameter \(\lambda\) are tested and compared on the Levenberg–Marquardt method. Recall that for the varying \(\lambda\) case, we define the penalty parameter sequence as \(\lambda _k := 0.5\times 1.05^k\), where k is the iteration number. When fixed values of penalty parameter are considered, ten different values of \(\lambda\) are used for the experiments; i.e., \(\lambda \in \{10^6, 10^5, \ldots , 10^{-3}\}\). For the fixed values of \(\lambda\) one could choose best \(\lambda\) for each example to see if at least one of the selected values worked well to recover the solution. As in the previous section, the examples used for the experiments are from the Bilevel Optimization LIBrary of Test Problems (BOLIB) (Zhou et al. 2020), which contains 124 nonlinear examples. The experiments are run in MATLAB, version R2016b, on MACI64. Here, we present a summary of the results obtained; more details for each example are reported in the supplementary material (Tin and Zemkoho 2020). It is important to mention that algorithm always converges, unlike its Gauss-Newton counterpart studied in Fliege et al. (2021), where the corresponding algorithm diverges for some values of \(\lambda\).
4.1 Practical implementation details
For Step 0 of Algorithm 2.6 we set the tolerance to \(\epsilon :=10^{-5}\) and the maximum number of iterations to be \(K:=1000\). We also choose \(\alpha _0 := \left\Vert \Upsilon ^\lambda (z^0)\right\Vert\) (if \(\lambda\) is varying, we set \(\lambda :=\lambda _0\) here), \(\gamma _0:= 1\), \(\rho =0.5\), and \(\sigma =10^{-2}\). The selection of \(\sigma\) is based on the overall performance of the algorithm while the other parameters are standard in the literature.
4.1.1 Starting point
The experiments have shown that the algorithm performs much better if the starting point \((x^0,y^0)\) is feasible. As a default setup, we start with \(x^0=1_n\) and \(y^0=1_m\). If the default starting point does not satisfy at least one constraint and algorithm diverges, we choose a feasible starting point; see (Tin and Zemkoho 2020) for such choices. To be more precise, if for some i, \(G_i(x^0,y^0)>0\) or for some j we have \(g_j(x^0,y^0)>0\) and the algorithm does not converge to a reasonable solution, we generate a starting point such that \(G_i(x^0,y^0)=0\) or \(g_j (x^0,y^0) =0\). Subsequently, the Lagrange multipliers are initialised at \(u^0 = \max \,\left\{ 0.01,\;-g(x^0,y^0)\right\}\), \(v^0=\max \,\left\{ 0.01,\;-G(x,y)\right\}\), and \(u^0 = w^0\).
4.1.2 Smoothing parameter \(\mu\)
The smoothing process, i.e., the use of the parameter \(\mu\), is only applied when necessary (Step 2 and Step 3), where the derivative evaluation for \(\Upsilon ^\lambda _\mu\) is required. We tried both the case where \(\mu\) is fixed to be a small constant for all iterations, and the situation where the smoothing parameter is sequence \(\mu _k \downarrow 0\). Setting the decreasing sequence to \(\mu _k :=0.001/(1.5^k)\), and testing its behaviour and comparing it with a fixed small value (\(\mu :=10^{-11}\)), in the context of Algorithm 2.6, we observed that both options lead to almost the same results. Hence, we stick to what is theoretically more suitable, that is the smoothing decreasing sequence ; i.e., \(\mu _k:=0.001/(1.5^k)\).
4.1.3 Descent direction check and update
For the sake of efficiency, we calculate the direction \(d^k\) by solving (22) with the Gaussian elimination. Considering the line search in Step 3, if we have \(\left\Vert \Upsilon ^{\lambda }(z^k+\gamma _k d^k)\right\Vert ^2 < \left\Vert \Upsilon ^{\lambda }(z^k)\right\Vert ^2 + \sigma \gamma _k \nabla \Upsilon ^\lambda (z^k)^T \Upsilon ^\lambda (z^k) d^k\), we redefine \(\gamma _k = \gamma _k / 2\) and check again. Recall that the Levenberg–Marquardt direction can be interpreted as a combination of Gauss–Newton and steepest descent directions. In fact, if \(\alpha _k = 0\) this direction is a Gauss-Newton direction one and when as \(\alpha _k \rightarrow \infty\) the direction \(d^k\) from (22) tends to a steepest descent direction. Hence, if the Levenberg–Marquardt direction is not a descending at some iteration, we give more weight to the steepest descent direction. Hence, when \(\left\Vert \Upsilon ^\lambda (z^k)\right\Vert >\left\Vert \Upsilon ^\lambda (z^{k-1})\right\Vert\) setting \(\alpha _{k+1} := 10000 \left\Vert \Upsilon ^\lambda (z^k)\right\Vert\) has led to an overall good performance of Algorithm 2.6 for test set used in this paper.
4.1.4 Stopping criteria
The primary stopping criterion for Algorithm 2.6 is \(\left\Vert \Upsilon ^{\lambda }_\mu (z^k)\right\Vert <\epsilon\), as requested in Step 1. However, robust safeguards are needed to deal with ill-behaviours typically due to the size of the penalty parameter \(\lambda\). Hence, for the practical implementation of the method, we set \(\epsilon =10^{-5}\) and stop if one of the following six conditions is satisfied:
-
1.
\(\left\Vert \Upsilon ^\lambda (z^k)\right\Vert <\epsilon\),
-
2.
\(\big | \left\Vert \Upsilon ^\lambda (z^{k-1})\right\Vert - \left\Vert \Upsilon ^\lambda (z^{k})\right\Vert \big |<10^{-9}\),
-
3.
\(\big | \left\Vert \Upsilon ^\lambda (z^{k-1})\right\Vert - \left\Vert \Upsilon ^\lambda (z^{k})\right\Vert \big |<10^{-4}\) and \(iter>200\),
-
4.
\(\left\Vert \Upsilon ^\lambda (z^{k-1})\right\Vert - \left\Vert \Upsilon ^\lambda (z^{k})\right\Vert <0\) and \(\left\Vert \Upsilon ^\lambda (z^k)\right\Vert < 10\) and \(iter>175\),
-
5.
\(\left\Vert \Upsilon ^\lambda (z^k)\right\Vert <10^{-2}\) and \(iter>500\),
-
6.
\(\left\Vert \Upsilon ^\lambda (z^k)\right\Vert >10^2\) and \(iter>200\).
The additional stopping criteria are important to ensure that the algorithm is not running for too long. The danger of running algorithm for too long is that ill-conditioning could occur. A typical pattern that is clear is that we recover the solution earlier before the algorithm gets to stop running. This appears due to the nature of the overdetermined system. We do not know beforehand the tolerance with which we can solve for \(\left\Vert \Upsilon ^\lambda (z)\right\Vert\) as \(\Upsilon ^\lambda\) is overdetermined system. Hence, it is hard to select \(\epsilon\) that would fit all examples and allow to solve examples with efficient tolerance. With the stopping criteria defined above we avoid running unnecessary iterations, retaining the obtained solution. To avoid algorithm running for too long and to prevent \(\lambda\) to become too large, we impose additional stopping criterion 3, 5 or 6 above. These criteria are motivated by the behaviour of the algorithm.
For almost all of the examples we observe that after 100–150 iterations we obtain the value reasonably close to the solution but we cannot know beforehand what would be the tolerance of \(\left\Vert \Upsilon ^\lambda (z^k)\right\Vert\) to stop. Choosing small \(\epsilon\) would not always work due to the overdetermined nature of the system being solved. Choosing \(\epsilon\) too big would lead to worse solutions and possibly not recover some of the solutions. Further, a quick check has shown that ill-conditioning issue typically takes place after 500 iterations for majority of the problems. For these reasons we stop if the improve of the Error value from step to step becomes too small, \(\big | \left\Vert \Upsilon ^\lambda (z^{k-1})\right\Vert - \left\Vert \Upsilon ^\lambda (z^{k})\right\Vert \big |<10^{-4}\), after the algorithm has performed 200 iterations. Since ill-conditioning is likely to happen after 500 iterations we stop if by that time we obtain a reasonably small Error, \(\left\Vert \Upsilon ^\lambda (z^k)\right\Vert <10^{-2}\). Finally, if it turns out that system cannot be solved with a good tolerance, such that we would obtain a reasonably small value of the Error, we stop if the Error after 200 iterations is big, \(\left\Vert \Upsilon ^\lambda (z^k)\right\Vert >10^2\). This way additional stopping criteria plays the role of safeguard to prevent ill-conditioning and also does not allow the algorithm to keep running for too long once a good solution is obtained.
4.2 Accuracy of the upper-level objective function
Here, we compare the values of the upper-level objective functions at points computed by the Levenberg–Marquardt algorithm with fixed \(\lambda\) and varying \(\lambda\). For the comparison purpose, we focus our attention only on 117 BOLIB examples (Zhou et al. 2020), as solutions are not known for the other seven problems. To proceed, let \(\bar{F}_A\) be the value of upper-level objective function at the point \((\bar{x},\bar{y})\) obtained by the algorithm and \(\bar{F}_K\) the value of this function at the known best solution point reported in the literature (see corresponding references in Zhou et al. 2020). We consider all fixed \(\lambda \in \{10^6,10^5,\ldots ,10^{-3}\}\) and varying \(\lambda\) in one graph and present the results in Figure 5 below, where we have the relative error \((\bar{F}_A - \bar{F}_K) / (1+|\bar{F}_K|)\) on the \(y-axis\) and number of examples on the x-axis, starting from 30th example. We further plot the results for the best fixed value of \(\lambda\). The graph is plotted in the order of increasing error. From Fig. 5 we can clearly see that many more solutions were recovered for the small values of fixed \(\lambda\) than for large ones. For instance with the allowable accuracy error of \(\le 20\%\) we recover solutions for \(78.63\%\) for fixed \(\lambda \in \{10^{-2},10^{-3}\}\), while for \(\lambda \in \{10^6,10^{5},10^4,10^3,10^2\}\) we recover at most \(40.17\%\) solutions. Interestingly, the worst performance is observed for fixed \(\lambda =100\). With the varying \(\lambda\), we observe that the algorithm performed averagely in comparisons made on the use of large and small fixed values of \(\lambda\), recovering \(59.83\%\) of the solutions with the accuracy error of \(\le 20\%\). It is worth saying that implementing Algorithm 2.6 with \(\lambda :=0.5\times 1.05^k\) still recovers over half of the solutions, which is not too bad. However, fixing \(\lambda\) to be small recovers way more solutions, which shows that varying \(\lambda\) is not the most efficient option for our case.
It was further observed that for some examples only \(\lambda \ge 10^3\) performed well, while for others small values (\(\lambda <1\)) showed good performance. If we were able to pick best fixed \(\lambda\) for each example, we would obtain negligible (less than \(10\%\)) error for upper-level objective function for \(85.47\%\) of the tested problems. With the accuracy error of \(\le 25\%\) our algorithm recovered solutions for \(88.9\%\) of the problems for the best fixed \(\lambda\) and for \(61.54\%\) with varying \(\lambda\). This means that if one can choose the best fixed \(\lambda\) from the set of different values, fixing \(\lambda\) is much more attractive for the algorithm. However, if one does not have a way to choose the best value or a set of potential values cannot be constructed efficiently for certain problems, varying \(\lambda\) could be a better option to choose. Nevertheless, for the test set of small problems from BOLIB (Zhou et al. 2020), fixing \(\lambda\) to be small performed much better than varying \(\lambda\) as increasing sequence. Further, if one could run the algorithm for all fixed \(\lambda\) and was able to choose the best one, the algorithm with fixed \(\lambda\) performs extremely well compared to varying \(\lambda\). In other words, algorithm almost always finds a good solution for at least one value of fixed \(\lambda \in \{10^6, 10^5, \ldots , 10^{-3}\}\).
4.3 Feasibility check
Considering the structure of the feasible set of problem (2), it is critical to check whether the points computed by our algorithms satisfy the value function constraint \(f(x,y)\le \varphi (x)\), as it is not explicitly included in the expression of \(\Upsilon ^\lambda\) (13). If the lower-level problem is convex in y and a solution generated by our algorithms satisfies (8) and (11), then it will verify the value function constraint. Conversely, to guarantee that a point (x, y) such that \(y\in S(x)\) satisfies (8) and (11), a constraint qualification (CQ) is necessary. Note that conditions (8) and (11) are incorporated in the stopping criterion of Algorithm 2.6. To check whether the points obtained are feasible, we first identify the BOLIB examples, where the lower-level problem is convex w.r.t. y. As shown in Fliege et al. (2021) it turns out that a significant number of test examples have linear lower-level constraints. For these examples, the lower-level convexity is automatically satisfied. We detect 49 examples for which some of these assumptions are not satisfied, that is the problems having non-convex lower-level objective or some of the lower-level constraints being nonconvex. For these examples, we compare the obtained solutions with the known ones from the literature. Let \(f_A\) stand for \(f(\bar{x},\bar{y})\) obtained by one of the tested algorithms and \(f_K\) to be the known optimal value of lower-level objective function. In the graph below we have the lower-level relative error, \((f_A - f_K) / (1+|f_K|)\), on the y-axis, where the error is plotted in increasing order. In Fig. 6 below we present results for all fixed \(\lambda \in \{10^6,10^5,\ldots ,10^{-3}\}\) as well as varying \(\lambda\) defined as \(\lambda :=0.5\times 1.05^k\).
From the Fig. 6 below we can see that for 20 problems the relative error of lower-level objective is negligible (\(<5\%)\) for all values of fixed \(\lambda\) and varying \(\lambda\). We have seen that convexity and a CQ hold for the lower-level hold for 74 test examples. We consider solutions for these problems to be feasible for the lower-level problem. Taking satisfying feasibility error to be \(<20 \%\) and using information from the graph above, we claim that feasibility is satisfied for at most 100 (\(80.65\%\)) problems for fixed \(\lambda \in \{10^6,10^5,10^4,10^3\}\), for \(101-104\) (\(81.45-83.87\%\)) problems for \(\lambda \in \{10^3,10^2,10^1,10^0,10^{-1}\}\) and for 106 (\(85.48\%\)) problems for \(\lambda \in \{10^{-2},10^{-3}\}\). We further observe that feasibility is satisfied for 101 (81.4%) problems for varying \(\lambda\). Considering we could choose best fixed \(\lambda\) for each of the examples, we could also claim that feasibility is satisfied for 108 (87.1%) problems for best fixed \(\lambda\). From Fig. 6 we note that slightly better feasibility was observed for smaller values of fixed \(\lambda\) than for the big ones and that varying \(\lambda\) has shown average performance between these magnitudes in terms of the feasibility.
4.4 Experimental order of convergence
Recall that the experimental order of convergence (EOC) is defined by
where K is the number of the last iteration (Fischer et al. 2021). If \(K=1\), no EOC will be calculated (EOC\(=\infty\)). EOC is important to estimate the local behaviour of the algorithm and to show whether this practical convergence reflects the theoretical convergence result stated earlier. Let us consider EOC for fixed \(\lambda \in \{10^6,\ldots ,10^{-3}\}\) and for varying \(\lambda\) (\(\lambda =0.5\times 1.05^k\)) in Fig. 7 below.
It is clear from this picture that for most of the examples our method has shown linear experimental convergence. This is slightly below the quadratic convergence established by Theorem 2.7. It is however important to note that the method always converges to a number, although sometimes the output might not be the optimal point for the problem. There are a few examples that shown better convergence for each value of \(\lambda\), with the best ones being \(\lambda \in \{10^{-3},10^{-2},10^{-1},10^6\}\) as seen in the figure above. These fixed values have shown slightly better EOC performance than varying \(\lambda\). Varying \(\lambda\) showed slightly better convergence than fixed \(\lambda \in \{10^0,10^1,10^2,10^3,10^4,10^5\}\). EOC bigger than 1.2 has been obtained for less than 5 (4.03 %) examples for fixed \(\lambda \in \{10^0,10^1,10^2,10^3,10^4,10^5\}\), while varying \(\lambda\) showed such EOC for 11 (8.87%) examples. Fixed \(\lambda =10^6\) has shown almost the same result as varying \(\lambda\) with rate of convergence greater than 1.2 for 12 (9.67%) examples, while \(\lambda =10^{-1}\) has demonstrated such EOC for 14 (11.29%) examples and \(\lambda \in \{10^{-2},10^{-3}\}\) for 17 (13.71 %) examples. Finally, in the graph above, we can see that for all values of \(\lambda\) only a few (\(\le 4/124\)) examples have worse than linear convergence.
4.5 Line search stepsize
Let us now look at the line search stepsize, \(\gamma _k\), at the last step of the algorithm for each example. Consider all fixed \(\lambda\) and varying \(\lambda\) in Fig. 8 below. This is quite important to know two things. Firstly, how often line search was used at the last iteration, that is how often implementation of line search was clearly important. Secondly, as main convergence results are for the pure method this would be demonstrative to note how often the pure (full) step was made at the last iteration. This can then be compared with the experimental convergence results in the previous subsection, namely with Fig. 7. In the figure above whenever stepsize on the y-axis is equal to 1 it means the full step was made at the last iteration. For these cases the convergence results shown in Theorem 2.7 could be considered valid. From the graphs above we observe that stepsize at the last iteration was rather \(\gamma _k=1\) or \(\gamma _k<0.05\). We observe that for varying \(\lambda\) algorithm would typically do a small step at the last iteration. It seems that algorithm with varying \(\lambda\) benefits more from line search technique than the algorithm with fixed \(\lambda\). Possibly, pure Levenberg–Marquardt method with varying \(\lambda\) would not converge for most of the problems. Interestingly, for fixed values of \(\lambda\) stepsize was \(\gamma _k<0.05\) at the last iteration much more often for the values of \(\lambda\) that showed worse performance in terms of recovering solutions (i.e. \(\lambda \in \{10^1, 10^2\}\)).
We also observe that for medium values of \(\lambda\) (\(\lambda \in \{10^4,10^3,10^2,10^1,10^0\}\)) full stepsize was made for less than half of the examples. For large values \(\lambda \in \{10^6,10^5\}\) full step was made for \(63.71\%\) and \(70.16\%\) of the problems respectively. Further on, small values of \(\lambda\) for which more solutions were recovered would do the full step at the last iteration for most of the examples. For instance, with \(\lambda =10^{-3}\) and \(\lambda =10^{-2}\) full step was made at the last iteration for \(73.39\%\) of the problems, while for \(\lambda =10^{-1}\) full step was made for \(75.81\%\) of the problems. In terms of the fixed \(\lambda _{best}\) it is interesting to observe that full step was used only for 82/124 (\(66.13 \%\)) of the problems, meaning that for a third of the problems linesearch was implemented in the last step for the best tested value of \(\lambda\). This also coincides with the results of Fig. 7 where with smaller values of \(\lambda\) the algorithm has shown faster than linear convergence for more examples than for big values of \(\lambda\). This is likely to be the case that small steps were made in the other instances due to the non-efficient direction of the method at the last iteration.
5 Performance comparison with other algorithms
We focus here on numerical comparison of Algorithm 2.6 with the bilevel optimization algorithms recently introduced in the papers (Fischer et al. 2021; Fliege et al. 2021) and evaluated on the same set of test problems used so far in this paper; i.e., the 124 nonlinear examples from BOLIB Zhou et al. (2020). Our comparisons also consider the MATLAB built-in solver fsolve (Optimization 1990). Clearly, the framework of the experiments will be the same as introduced in Sect. 4. We present the results from the implementation of the aforementioned four methods to solve problems from BOLIB test set. To be more specific, note that the tested methods are Algorithm 2.6 to solve optimality conditions based on LLVF reformulation, the pseudo-Newton method based on LLVF reformulation presented in Fliege et al. (2021), the semismooth Newton method based on LLVF reformulation developed in Fischer et al. (2021), and the Matlab fsolve solver Optimization (1990).
Let us start by noting that the semismooth Newton method from Fischer et al. (2021) uses a slightly different reformulation, although it is also based on LLVF reformulation. The system there is forced to be square with a trick consisting of introducing a new variable z. However, the Levenberg–Marquardt method introduced in this paper solves our optimality conditions directly. Algorithm 2.6 does not require the system to be square and hence has no need to check the condition \(y=z\) due to the aforementioned new variable (Fischer et al. 2021). As we perform a comparison based on Algorithm 2.6, we select parameters in the same fashion as chosen in the actual experiments [see Supplementary materials for this paper Tin and Zemkoho (2020)]. Such parameter choices might lead to other methods not performing at their best and possibly produce worse results than presented in Fischer et al. (2021) and Fliege et al. (2021).
From the results that we show below, Algorithm 2.6 generally has the best performance. One of the other benefits of our method is that it does need any of the matrices to be non-singular for the direction of the method to be well-defined. Other methods lack such property. Making comparison with the varying parameters \(\mu\) and \(\lambda\) could put these invertibilities at high risk, as varying these parameters creates some instability of the matrices. Hence, we believe it is more fair to use only fixed values of parameters \(\mu\) and \(\lambda\). Nevertheless, these points clearly show that we do not claim that results of this comparison demonstrate full potential of the methods from Fischer et al. (2021) and Fliege et al. (2021), as these methods might not show their best performance under the specific setup used here. However, we believe that comparison is fair as all parameters make sense in the context of all of the methods and they would show which method performs better and, moreover, which method is more robust in the given setup. We can summarize the parameters required for our comparisons as follows:
-
Initialization At the start we set the tolerance to \(\epsilon :=10^{-5}\) and the maximum number of iterations to be \(K:=1000\). We also choose \(\alpha _0 := \left\Vert \Upsilon ^\lambda (z^0)\right\Vert\), \(\gamma _0:= 1\), \(\rho =0.5\) and \(\sigma =10^{-2}\).
-
Starting Point We take the starting point as defined in the actual experiments for Algorithm 2.6. The Lagrange multipliers are then initialised as \(u^0 = \max \,\left\{ 0.01,\;-g(x^0,y^0)\right\}\), \(v^0=\max \,\left\{ 0.01,\;-G(x,y)\right\}\), and \(u^0 = w^0\).
-
Smoothing fixed Set \(\mu =10^{-11}\) for all iterations.
-
Penalizing fixed Run algorithms with fixed \(\lambda \in \{10^6, 10^5, 10^4, 10^3, 10^2,10^1,10^0,10^{-1},10^{-2}, 10^{-3}\}\).
-
Stopping Criteria The primary stopping criterion for all of the compared algorithms is set to \(\left\Vert \Upsilon ^{\lambda }_\mu (z^k)\right\Vert <\epsilon\), as imposed in Step 1. However, robust safeguards (specific for each method) are still used by all of the methods.
In the following subsections, we compare the aforementioned four algorithms based on several characteristics in the context of solving 124 nonlinear test problems from the BOLIB library (Zhou et al. 2020). For the rest of this section the graphs will have the following notation: LM for Levenberg-Marquardt method, PN for Pseudo-Newton method, and SN for the Semismooth Newton method.
5.1 Accuracy of the upper-level objective function
Let us firstly look at the level of accuracy of the algorithms in terms of recovering known optimal values of upper-level objective function for each example. We only consider 117 examples here, as these are the examples for which solutions were reported in Zhou et al. (2020). Let us combine two values of \(\lambda\) for each plot in Fig. 9 below. As in Fig. 5, the accuracy error is presented in increasing order from 0 to 1 over y-axis, while the x-axis represents the number of examples for which accuracy was smaller than given value on the y-axis. As can be seen from (a) and (b) in Fig. 9, all algorithms are not performing very well for large values of \(\lambda\). For \(\lambda \in \{10^6,10^5\}\), the best results are obtained by the Levenberg–Marquardt and semismooth Newton methods, having \(Accuracy\le 40\%\) for 57/117 examples. In terms of \(40\% \le Accuracy \le 100\%\), the Levenberg–Marquardt shows a better performance, obtaining \(Accuracy \le 90\%\) for 85/117 examples, while the other algorithms show this level of accuracy only for 65/117 examples.
The situation with \(\lambda \in \{10^4,10^3\}\) is very similar. Not that many solutions are recovered with high level of accuracy. Once again, the best results were shown by the Levenberg–Marquardt method here with \(Accuracy \le 90\%\) for 90/117 examples for \(\lambda =10^4\). It is further interesting that overall, the performance of fsolve is clearly worse than that of all the other three algorithms, with the line graphs being completely to the left of the line graphs representing the other algorithms throughout both (a) and (b) graphs. This demonstrates that algorithms specifically developed for bilevel framework perform better than standard solvers.
Looking at Fig. 9c, the situation is slightly different. We can clearly see that for \(\lambda \in \{ 10^2, 10^1 \}\), the semismooth Newton method outperformed the other algorithms. That said, it still does not recover very many solutions with a high level of accuracy. The \(Accuracy \le 30 \%\) is obtained by semismooth Newton method just for 80/117 examples for \(\lambda =10^1\), and only for 68/117 examples for \(\lambda =10^2\), which is on the same level with the other algorithms. We do not consider this level of accuracy to be high, but it is still interesting to see that some algorithms are better for some values of \(\lambda\) and worse for the other ones. Based on the performance of all tested algorithms, it seems that \(\lambda \in \{ 10^2, 10^1 \}\) is not the best choice of the penalty parameter for the given framework. Hence, the difference in performance for these values of \(\lambda\) is not so critical.
From Fig. 9d, we see that for \(\lambda \in \{10^0,10^{-1}\}\) Levenberg–Marquardt and Pseudo-Newton performed really well, having \(Accuracy\le 30\%\) for 99/117 examples, compared to only 89 examples for Semismooth Newton and fsolve. Further \(Accuracy \le 80\%\) is obtained by the Levenberg–Marquardt method for 110/117 examples, showing that Levenberg–Marquardt can almost always produce somewhat reasonable solutions for these values of \(\lambda\). Finally, in Fig. 9e we observe that for small values of \(\lambda\) Levenberg–Marquardt method performs the best and recovers many solutions, which is the critical point of the comparison. The level of accuracy for \(\lambda \in \{10^{-2},10^{-3}\}\) is similar to the one for \(\lambda \in \{10^0,10^{-1}\}\). Levenberg–Marquardt managed to have \(Accuracy\le 30\%\) for 98/117 examples and \(Accuracy\le 90\%\) for 111/117 examples for \(\lambda \in \{10^{-2},10^{-3}\}\). The pseudo-Newton method and fsolve show slightly worse performance here, while the semismooth Newton shows much worse performance for \(\lambda \in \{10^{-2},10^{-3}\}\) with \(Accuracy\le 90\%\) for only 80/117 examples. Summarizing, Fig. 9 clearly demonstrates that Levenberg–Marquardt algorithm for small values of \(\lambda\) was the most effective combination to solve the test set of bilevel problems from Zhou et al. (2020), in the sense of recovering optimal values of upper-level objective function.
5.2 Feasibility comparison
In this section, we compare values of the lower-level objective functions obtained by the algorithms, in the case the true/known optimal values are reported in Zhou et al. (2020). Unlike Fig. 6, let us conduct comparison for all examples with true/known optimal solutions. The reason for this is that the system in Fischer et al. (2021) uses slightly different assumptions, required for feasibility of the system. Let us look at the values of \({\hat{f}}\) compared to known lower-level optimal values at the solution stated in Zhou et al. (2020). As before, we combine results for two values of \(\lambda\) for each plot. The plots are presented with the increasing order of the feasibility error. From Fig. 10a, we observe that for \(\lambda \in \{10^6,10^5\}\), the semismooth Newton method has smaller feasibility errors (\(\le 20\%\)) for a few more examples than the other algorithms. However, the Levenberg–Marquardt method was the best for \(20\% < Error \le 90\%\). In fact, this method has \(Error \le 90\%\) for 110/117 examples, while the next best result for the other algorithms is only 98/117 examples. Furthermore, the Levenberg–Marquardt method has \(Error \le 60\%\) for 101/117 examples, while the next best result for the other algorithms is only 82 examples. In other words, the other algorithms have very high feasibility errors for many examples in the cases where we have \(\lambda \in \{10^6,10^5\}\).
Looking at Fig. 10b, the Levenberg–Marquardt is even a clearer winner for \(\lambda \in \{10^4,10^3\}\). Once again, the semismooth Newton method has a negligible error (\(Error \le 20\%\)) for slightly more examples. However, the Levenberg–Marquardt feasibility error is much smaller on average with the line graph lying almost completely to the right of the other algorithms. Once again, the Levenberg–Marquardt error almost never goes beyond \(90\%\), and stays below \(60\%\) for majority of the examples, which cannot be said about the other algorithms.
Figure 10c demonstrates that the Levenberg–Marquardt is the clear leader for \(\lambda \in \{10^2,10^1\}\) in terms of recovering optimal values of the lower-level objective function (with the line graphs for LM being completely to the right). The semismooth Newton method was clearly second best out of the four tested algorithms. Surprisingly, Fig. 10d shows that for \(\lambda \in \{10^0,10^{-1}\}\) the semismooth Newton produces small error for more examples than the other algorithms. However, this is only true for \(Error \le 40\%\) for \(\lambda =10^0\). The gap between the Levenberg–Marquardt and semismooth Newton methods in this case remains small.
Finally, from Fig. 10e, we see that for small values of \(\lambda\), the Levenberg–Marquardt method performs slightly better than the other algorithms, having low feasibility error for more examples than other algorithms. It is interesting to see that fsolve is the only algorithm that performs bad for \(\lambda \in \{10^{-2},10^{-1}\}\). Since the Levenberg–Marquardt algorithm for small values of \(\lambda\) is the most effective to recover optimal values of upper-level objective function, this strengthens the view that it performs better than the other considered algorithms.
5.3 Final observations
Now let us quickly look at the other parameters of the performance of the algorithms compared in this section. All tested algorithms have shown great computing time with less than 0.5 second to solve an example for a fixed value of \(\lambda\), which means that the difference in the CPU time is not significant. In terms of the Error (norm of the system being solved) at the last iteration, the semismooth Newton shows much better results than other algorithms, as one would expect. The reason for this is that it solves a different system, which is indeed square. Clearly, it is possible to solve a square system of equations more accurately in comparison to the case of an overdetermined system, which is much more challenging to solve to high accuracy. This is why for \(\lambda \in \{10^6,10^5,10^4,10^3,10^2,10^1\}\), the semismooth Newton method produces \(\left\Vert \Phi ^\lambda \right\Vert <10^0\) for 110-115 examples, while the other three tested methods perform worse, producing \(\left\Vert \Upsilon ^\lambda \right\Vert <10^0\) for only 70-80 examples. For \(\lambda \in \{10^0,10^{-1},10^{-2},10^{-3}\}\), the semismooth Newton produces \(Error<10^0\) for 122 examples, while the other methods show \(Error<10^0\) for only 100 examples. However, it is clearly not sensible to compare the methods on the measure of the Error as the two classes of method do not solve the same system of equations as indicated at the introduction of this section.
The advantage of the Levenberg–Marquardt method (Algorithm 2.6) is that it solves the optimality conditions (7)–(11) directly, while the semismooth Newton method solves a somewhat approximation of these optimality conditions, where the trick of introducing artificial variable z makes the system square. The main disadvantage here is that this trick requires condition \(y=z\) to recover points satisfying (7)–(11). The following table shows how often this condition is approximately satisfied for \(\Phi ^\lambda\) at the last iteration of semismooth Newton method in the context of solving the 124 test examples for a given value of the partial exact penalty \(\lambda\).
We can see that the condition \(y \approx z\) is not satisfied for a significant portion of the examples, especially for \(\lambda \in \{10^4, 10^3, 10^2, 10^1\}\) for which it is not satisfied for more than half of the problems. Interestingly, the condition was satisfied for majority of the examples for \(\lambda \in \{10^{-1}, 10^{-2}\}\). This is counter-intuitive as for these values of \(\lambda\), where the semismooth Newton shows worse performance in comparison to the other methods in terms of recovering optimal values of upper-level and lower-level objective functions. Nevertheless, we see that despite the fact that the Error parameter for semismooth Newton algorithm seems to be much better than for the other methods; this parameter is not very reliable as the crucial condition \(y^k \approx z^k\) is not satisfied in many cases.
Lastly, let us look at the experimental order of convergence (EOC) of the algorithms. The EOC is defined as in Sect. 4.4, with \(\Phi ^\lambda\) instead of \(\Upsilon ^\lambda\) for the semismooth Newton method (see Fischer et al. 2021 for the precise definition of \(\Phi ^\lambda\)). For all values of \(\lambda\), the semismooth Newton is the clear winner when talking about the EOC, as well as the Error. These results are expected, given that the reason for this is that the SN method is solving a square system, as already discussed above. As it can be seen in Fig. 11, the condition \(EOC>1.5\) is obtained when solving the square system for the majority of the tested examples, while the other methods demonstrate linear rate (\(EOC<1.1\)) for the majority of the examples for all values of \(\lambda\). This is easily explained by the fact that the latter methods try to solve the non-square system of optimality conditions (7)–(11), where it is often not possible to compute highly accurate solution. In fact, for most of the cases, we would expect that highly accurate solution does not exist even with some tolerance \(\Upsilon ^\lambda < \epsilon\) for some small \(\epsilon\). Furthermore, even the pseudo-Newton method has shown slightly better EOC for all values of \(\lambda\), which shows that Algorithm 2.6 generally has a linear convergence rate in the current framework.
As we have seen from Figs. 9 and 10, the Levenberg–Marquardt algorithm seems to be more attractive than the other tested algorithms based on the rate of recovering optimal values of upper-level and lower-level objective functions. All algorithms have shown similar speed, so there is no clear winner along this parameter. In terms of Error of the system at the last iteration and EOC, the semismooth Newton has shown the best performance. However, we have discussed that it would not be very accurate to compare these characteristics due to different systems being solved by the algorithms. Further, as we have seen from Table 3, there is some disadvantage of solving the system artificially constructed square system solved in Fischer et al. (2021) by means of a semismooth Newton method. Hence, despite the EOC measure, we believe that Algorithm 2.6 has shown the best performance along the main points of the comparison, namely accuracy and feasibility.
6 Conclusions and final comments
We introduce a smoothing Levenberg–Marquardt method to solve LLVF-based optimality conditions for optimistic bilevel programs. Since these optimality conditions are parameterized by a certain \(\lambda\), its selection is carefully studied in light of the BOLIB library test set. Surprisingly, small values of this partial exact penalty parameter showed a good behaviour for our method, as they generally performed very well, although classical literature on exact penalization usually suggests large values. However, relatively medium values of \(\lambda\) did not perform as well. Furthermore, as both the varying and fixed scenarios were considered for \(\lambda\), it was observed that both approaches showed a linear experimental order of convergence for most of the examples. Average CPU time for all fixed \(\lambda\) is 0.243 s, while it is 0.193 s for \(\lambda _{best}\) and 0.525 s for varying \(\lambda\). The algorithm with varying \(\lambda\) turns out to be more than twice slower than for fixed \(\lambda\). However, running it for all fixed values of \(\lambda\) can take way more time than the case where the value of \(\lambda\) is varying. In terms of the comparison with other existing algorithms, the Levenberg–Marquardt method has shown strong performance in the context of using fixed \(\lambda\), especially for \(\lambda \in \{10^{-2},10^{-3}\}\). This further justifies the observation that small values of penalty parameter could be good for certain frameworks.
References
Allende GB, Still G (2012) Solving bi-level programs with the KKT-approach. Math Program 131:37–48
Behling R, Fischer A, Haeser G, Ramos A, Schönefeld K (2016) On the constrained error bound condition and the projected Levenberg–Marquardt method. Optimization 66(8):1397–1411
Bertsekas DP (1982) Constrained optimization and Lagrange multiplier methods. Academic Press, London
Bollas GM, Barton PI, Mitsos A (2009) Bilevel optimization formulation for parameter estimation in vapor–liquid (-liquid) phase equilibrium problems. Chem Eng Sci 64(8):1768–1783
Burgard AP, Pharkya P, Maranas CD (2003) Optknock: a bilevel programming framework for identifying gene knockout strategies for microbial strain optimization. Biotechnol Bioeng 84(6):647–657
Burke JV (1991) An exact penalization viewpoint of constrained optimization. SIAM J Control Optim 29(4):968–998
Clarke P, Westerberg A (1990) Bilevel programming for steady-state chemical process design-I. Fundamentals and algorithms. Comput Chem Eng 14:87–98
Clarke P, Westerberg A (1990) Bilevel programming for steady-state chemical process design-II. Performance study for nondegenerate problems. Comput Chem Eng 14:99–110
Dempe S, Dutta J (2012) Is bilevel programming a special case of mathematical programming with equilibrium constraints? Math Program 131:37–48
Dempe S, Zemkoho AB (2011) The generalized Mangasarian–Fromowitz constraint qualification and optimality conditions for bilevel programs. J Optim Theory Appl 148(1):46–68
Dempe S, Zemkoho AB (2013) The bilevel programming problem: reformulations, constraint qualification and optimality conditions. Math Program 138:447–473
Dempe S, Zemkoho AB (eds) (2020) Bilevel optimization: advances and next challenges. Springer, Cham
Dempe S, Dutta J, Mordukhovich BS (2007) New necessary optimality conditions in optimistic bilevel programming. Optimization 56(5–6):577–604
Di Pillo G, Grippo L (1989) Exact penalty functions in constrained optimization. SIAM J Control Optim 27(6):1333–1360
Diamond S, Sitzmann V, Julca-Aguilar F, Boyd S, Wetzstein G, Heide F (2021) Dirty pixels: towards end-to-end image processing and perception. ACM Trans Graphics (TOG) 40(3):1–15
Fan JY, Yuan YX (2005) On the quadratic convergence of the Levenberg–Marquardt method without nonsingularity assumption. Computing 74:23–39
Fischer A (1992) A special Newton-type optimization method. Optimization 24(3):269–284
Fischer A, Zemkoho AB, Zhou S (2021) Semismooth Newton-type method for bilevel optimization: global convergence and extensive numerical experiments. Optim Methods Softw. https://doi.org/10.1080/10556788.2021.1977810
Fletcher R (1975) An ideal penalty function for constrained optimization. IMA J Appl Math 15:319–342
Fliege J, Tin A, Zemkoho AB (2021) Gauss-Newton-type methods for bilevel optimization. Comput Optim Appl 78(3):793–824
Friedlander A, Gomes FAM (2011) Solution of a truss topology bilevel programming problem by means of an inexact restoration method. J Comput Appl Math 30(1):109–125
Hansen LU, Horst P (2008) Multilevel optimization in aircraft structural design evaluation. Comput Struct 86(1):104–118
Herskovits J, Filho MT, Leontiev A (2013) An interior point technique for solving bilevel programming problems. Optim Eng 14(3):381–394
Kanzow C (1996) Some noninterior continuation methods for linear complementarity problems. SIAM J Matrix Anal Appl 17(4):851–868
Lampariello L, Sagratella S (2020) Numerically tractable optimistic bilevel problems. Comput Optim Appl 76(2):277–303
Lin G-H, Xu M, Ye JJ (2014) On solving simple bilevel programs with a nonconvex lower level program. Math Program 144(1–2):277–305
Liu W, Zheng K-Y, Cai Z (2013) Bi-level programming based real-time path planning for unmanned aerial vehicles. Knowl-Based Syst 44:34–47
Liu R, Gao J, Zhang J, Meng D, Lin Z (2021) Investigating bi-level optimization for learning and vision from a unified perspective: a survey and beyond. arXiv:2101.11517
MATLAB Optimization Tool Box User’s Guide Version 3 (1990). http://cda.psych.uiuc.edu/matlab_pdf/optim_tb.pdf, https://www.mathworks.com accessed 30 Jan 2022
Mehlitz P, Minchenko LI, Zemkoho AB (2021) A note on partial calmness for bilevel optimization problems with linear structures at the lower level. Optim Lett 15(4):1277–1291
Mitsos A, Lemonidis P, Barton PI (2008) Global solution of bilevel programs with a nonconvex inner program. J Global Optim 42(4):475–513
Mitsos A, Bollas GM, Barton PI (2009) Bilevel optimization formulation for parameter estimation in liquid-liquid phase equilibrium problems. Chem Eng Sci 64(3):548–559
Nocedal J, Wright SJ (1999) Numerical optimization. Springer, New York
Ochs P, Ranftl R, Brox T, Pock T (2016) Techniques for gradient-based bilevel optimization with non-smooth lower level problems. J Math Imaging Vision 56(2):175–194
Oeder W (1988) Ein Verfahren zur Lösung von Zwei-Ebenen Optimierungsaufgaben in Verbindung mit der Untersuchung von chemischen Gleichgewichten. PhD thesis, Technische Universität Karl-Marx-Stadt
Outrata J, Kočvara M, Zowe J (1998) Nonsmooth approach to optimization problems with equilibrium constraints. Kluwer Academic Publishers, Dordrecht
Panagiotopoulos PD, Mistakidis ES, Stavroulakis GE, Panagouli OK (1998) Multilevel optimization methods in mechanics. In: Migdalas A, Pardalos PM, Varbrand P (eds) Multilevel optimization: algorithms and applications. Springer, Boston, pp 51–90
Paulavicius R, Gao J, Kleniati P, Adjiman CS (2020) BASBL: branch-and-sandwich bilevel solver. Implementation and computational study with the BASBLib test sets. Comput Chem Eng 132:18
Pharkya P, Burgard AP, Maranas CD (2003) Exploring the overproduction of amino acids using the bilevel optimization framework OptKnock. Biotechnol Bioeng 84(7):887–99
Pineda S, Bylling H, Morales JM (2018) Efficiently solving linear bilevel programming problems using off-the-shelf optimization software. Optim Eng 19(1):187–211
Press WH, Teukolsky SA, Vetterling WT, Flannery BP (1992) Numerical recipes in C: the art of scientific computing, 2nd edn. Cambridge University Press, Cambridge
Ranftl R, Pock T (2014) A deep variational model for image segmentation. Springer, Berlin, pp 107–118
Tin A, Zemkoho AB (2020) Supplementary material for “Levenberg–Marquardt method for bilevel optimization’’. University of Southampton, School of Mathematical Sciences, Southampton
Wiesemann W, Tsoukalas A, Kleniati P, Rustem B (2013) Pessimistic bilevel optimization. SIAM J Optim 23(1):353–380
William R (1982) Theory and algorithms, chemical reaction equilibrium analysis. Wiley, Hoboken
Xu M, Ye JJ (2014) A smoothing augmented Lagrangian method for solving simple bilevel programs. Comput Optim Appl 59(1–2):353–377
Yamashita N, Fukushima M (2001) On the rate of convergence of the Levenberg–Marquardt method. Computing 15:237–249
Ye JJ, Zhu DL (1995) Optimality conditions for bilevel programming problems. Optimization 33:9–27
Zemkoho AB (2012) Bilevel programming: reformulations, regularity and stationarity, PhD thesis, Department of Mathematics and Computer Science, TU Bergakademie Freiberg, Freiberg, Germany
Zemkoho AB, Zhou S (2021) Theoretical and numerical comparison of the Karush–Kuhn–Tucker and value function reformulations in bilevel optimization. Comput Optim Appl 78(2):625–74
Zhang J, Zhu D (1996) A bilevel programming method for pipe network optimization. SIAM J Optim 6(3):838–857
Zhao W, Liu R, Ngoduy D (2019) A bilevel programming model for autonomous intersection control and trajectory planning. Transportmetrica A 17(1):34–58
Zhou S, Zemkoho AB, Tin A (2020) BOLIB: bilevel optimization LIBrary of test problems. In: Dempe S, Zemkoho AB (eds) Bilevel optimization: advances and next challenges. Springer, Berlin
Funding
AT was supported by a University of Southampton Vice Chancellor Scholarship, while ABZ was supported by the EPSRC Grant EP/V049038/1 and the Alan Turing Institute under the EPSRC Grant EP/N510129/1.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Tin, A., Zemkoho, A.B. Levenberg–Marquardt method and partial exact penalty parameter selection in bilevel optimization. Optim Eng 24, 1343–1385 (2023). https://doi.org/10.1007/s11081-022-09736-1
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11081-022-09736-1