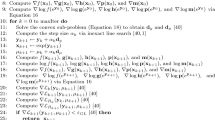1 Motivation

Geometric Programming (GP) and Signomial Programming (SP) are two related classes of non-linear optimization that have recently been applied with great success to the field of aircraft design (Hoburg and Abbeel 2014; Torenbeek 2013; Hoburg and Abbeel 2013; Kirschen et al. 2016; Brown and Harris 2018; York et al. 2018; Burton and Hoburg 2018; Lin et al. 2020; Kirschen et al. 2018; York et al. 2018; Saab et al. 2018; Hall et al. 2018). Despite these developments, the GP and SP formulations do not allow the use of black box analysis tools that are common in practical design problems (Hall et al. 2018; Martins and Lambe 2013). One method proposed by Hoburg et al. (2016) to overcome this limitation is to fit a GP compatible function to a set of training data that represents the black-box relationship, and then to impose this fitted function as a constraint in the GP formulation. In cases where the black-box relationship is log–log convexFootnote 1, the three functions proposed in Hoburg et al. are capable of capturing the true relationship with a high degree of accuracy (Hoburg et al. 2016). But when black-box relationships between inputs and outputs are not log–log convex, as might be the case with high fidelity CFD or FEA, then GP compatible functions lack the ability to model the relationship with sufficient accuracy. Unlike Geometric Programming, Signomial Programming is not limited to log–log convex relationships, but no SP compatible functions exist for the purpose of data fitting. This work fills this gap by developing a SP compatible function capable of capturing black-box relationships that are not log–log convex.

2 Geometric programming and signomial programming

2.1 Geometric programming

Geometric Programs (GPs) are built upon two fundamental building blocks: monomial and posynomial functions. A monomial function is defined as the product of a leading constant with each variable raised to a real power (Boyd et al. 2007):

$$\begin{aligned} m(\mathbf{x} ) = c{x_1}^{a_1}{x_2}^{a_2}...\;{x_n}^{a_n} = c \prod _{i=1}^{N} x_i^{a_i} \end{aligned}$$
(1)

A posynomial is the sum of monomials (Boyd et al. 2007), which can be defined in notation as:

$$\begin{aligned} p(\mathbf{x} ) = m_1(\mathbf{x} ) + m_2(\mathbf{x} ) + \cdots + m_n(\mathbf{x} ) = \sum _{k=1}^{K} c_k \prod _{i=1}^{N} x_i^{a_{ik}} \end{aligned}$$
(2)

From these two building blocks, it is possible to construct the definition of a GP in standard form (Boyd et al. 2007):

$$\begin{array}{*{20}l} {\mathop {{\text{minimize}}}\limits_{{\mathbf{x}}} } & {p_{0} ({\mathbf{x}})} \\ {{\text{subject to}}} & {m_{i} ({\mathbf{x}}) = 1,\;i = 1, \ldots ,N} \\ {} & {p_{j} ({\mathbf{x}}) \le 1,\;j = 1, \ldots ,M} \\ \end{array}$$
(3)

When constraints and objectives can be written in the form specified in Eq. 3 it is said that the problem is GP compatible.

2.2 Signomial programming

Signomal Programs (SPs) are a logical extension of Geometric Programs that allow the inclusion of negative leading constants and a broader set of equality constraints. The key building blocks of Signomial Programing are signomials, defined as the difference between two posynomials \(p(\mathbf{x} )\) and \(n(\mathbf{x} )\):

$$\begin{aligned} s(\mathbf{x} ) = p(\mathbf{x} ) - n(\mathbf{x} ) = \sum _{k=1}^{K} c_k \prod _{i=1}^{N} x_i^{a_{ik}} - \sum _{p=1}^{P} d_p \prod _{i=1}^{N} x_i^{g_{ik}} \end{aligned}$$
(4)

The posynomial \(n(\mathbf{x} )\) is often referred to as a ‘neginomial’ because it is made up of all of the terms with negative leading coefficients. From this definition, it is now possible to write the standard form for a Signomial Program (Kirschen et al. 2016):

$$\begin{array}{*{20}l} {\mathop {{\text{minimize}}}\limits_{{\mathbf{x}}} } & {\frac{{p_{0} ({\mathbf{x}})}}{{n_{0} ({\mathbf{x}})}}} \\ {{\text{subject to}}} & {s_{i} ({\mathbf{x}}) = 0,\;i = 1, \ldots ,N} \\ {} & {s_{j} ({\mathbf{x}}) \le 0,\;j = 1, \ldots ,M} \\ \end{array}$$
(5)

however, another useful form is:

$$\begin{array}{*{20}l} {\mathop {{\text{minimize}}}\limits_{{\mathbf{x}}} } & {\frac{{p_{0} ({\mathbf{x}})}}{{n_{0} ({\mathbf{x}})}}} \\ {{\text{subject to}}} & {\frac{{p_{i} ({\mathbf{x}})}}{{n_{i} ({\mathbf{x}})}} = 1,i = 1, \ldots ,N} \\ {} & {\frac{{p_{j} ({\mathbf{x}})}}{{n_{j} ({\mathbf{x}})}} \le 1,j = 1, \ldots ,M} \\ \end{array}$$
(6)

In this alternative form, the neginomial is added to both sides, and then used as a divisor to construct an expression either equal to or constrained by a value of one.

SPs are not convex upon transformation to log–log space, unlike their GP counterparts, and therefore must be solved using general non-linear methods. However many signomial programs of interest still exhibit an underlying structure which is well approximated by a log–log convex formulation, and as a result can be efficiently solved by a series of GP approximations via the Difference of Convex Algorithm (DCA). In this process the various neginomials \(n(\mathbf{x} )\) are replaced with local monomial approximations, yielding substantial benefits over other non-linear solution methods (see Kirschen et al. 2018 and York et al. 2018 for discussion).

3 Difference of convex functions for data fitting

3.1 Difference of convex (DC) functions

Most continuous functionsFootnote 2 (\(f(\mathbf {x})\)) can be written as the difference of two convex functions (\(g(\mathbf {x})\) and \(h(\mathbf {x})\)) (Hartman 1959):

$$\begin{aligned} f(\mathbf {x}) = g(\mathbf {x}) - h(\mathbf {x}) \end{aligned}$$
(7)

Functions of the form in Eq. 7 are said to be Difference of Convex (DC) functions.

By extension, it follows that most datasets that can be well approximated by a continuous function should also be well approximated by the difference between two convex functions. In other words, if there is some continuous function (or more precisely some function of bounded variation) \(f(\mathbf {x})\) that fits some data set sampled from a mapping from \(\mathbb {R}^N \rightarrow \mathbb {R}\), then there also exist functions \(g(\mathbf {x})\) and \(h(\mathbf {x})\) such that \(g(\mathbf {x})\) and \(h(\mathbf {x})\) are both convex and \(g(\mathbf {x}) - h(\mathbf {x})\) is an equally good fit to the mapping as the original function \(f(\mathbf {x})\). Taking functions \(g(\mathbf {x})\) and \(h(\mathbf {x})\) to be log–log convex functions such as those proposed in Hoburg et. al. (2016), it is possible to fit approximations for these functions \(g(\mathbf {x})\) and \(h(\mathbf {x})\) to data sets from mappings which are not log–log convex.

3.2 Function definitions

3.2.1 Notation

Consider a data set sampled from a black box mapping from \(\mathbb {R}^N \rightarrow \mathbb {R}\). Consistent with the notation in Hoburg et al. (2016) let the vector \(\mathbf {u}_j\) represent the independent variables in \(\mathbb {R}^N\) for data point j and the scalar \(w_j\) represent the output in \(\mathbb {R}\) for data point j. The log–log space variables are then represented as \(\mathbf {x}_j = \log \mathbf {u}_j\) and \(y_j = \log w_j\).

3.2.2 Difference of max affine (DMA) functions

The first function proposed by Hoburg et al. (2016) is the Max Affine (MA) function:

$$\begin{aligned} f_{\text {MA}}(\mathbf{x} ) = \max _{k=1\ldots K} \left[ b_k + \mathbf{a} _k^{\text {T}} \mathbf{x} \right] \end{aligned}$$
(8)

This function class is known to create a convex epigraph. In fact, any convex function can be reasonably approximated as a Max Affine function given a sufficient number of affine functions, K (Bertsimas 2009). Upon transformation back to variables \(\mathbf {u}_j\) and \(w_j\), the Max Affine function becomes Max Monomial, which can be implemented as a set of monomial constraints in the Geometric Program.

Now consider the difference between two of these max affine functions (Eq. 8), which henceforth will be called the Difference of Max Affine (DMA) function:

$$\begin{aligned} f_{\text {DMA}}(\mathbf{x} ) = \max _{k=1\ldots K} \left[ b_k + \mathbf{a} _k^{\text {T}} \mathbf{x} \right] - \max _{m=1\ldots M} \left[ h_m + \mathbf{g} _m^{\text {T}} \mathbf{x} \right] , \end{aligned}$$
(9)

The subtracted term is represented by an entirely separable Max Affine function defined by fitting parameters M, h, and \(\mathbf {g}\). Based on an understanding of DC functions, and the fact that convex functions can be well approximated as Max Affine for large K or M, this DMA function should be highly versatile as a fitting function.

While the Max Affine function has a realizable transformation back from log–log space, the Difference of Max Affine function has no such transformation due to the inability to readily construct a meaningful epigraph or subgraph using a set of separable inequalities, making it somewhat impractical for use in optimization. Despite this, the DMA function is quite rapid to fit, and could be of application in other areas where a cheap surrogate is desired for non-convex fitting. Here, the DMA function is a used as an intellectual building block to the next function class, and as a seed function for the fitting process.

3.2.3 Difference of softmax affine (DSMA) functions

The second function proposed by Hoburg et al. (2016) is the Softmax Affine (SMA) function:

$$\begin{aligned} f_{\text {SMA}}(\mathbf{x} ) = \frac{1}{\alpha } \log \sum _{k=1}^{K} \exp \left( \alpha (b_k + \mathbf {a}_k^{\text {T}} \mathbf {x}) \right) \end{aligned}$$
(10)

The SMA function uses a global softening parameter (\(\alpha\)) to ‘smooth’ the sharp corners of the Max Affine function and has the benefit of requiring far fewer affine terms K to capture smooth convex functions with reasonable accuracy (Hoburg et al. 2016). However, the global softening parameter results in a poor representation in regions where the curvature deviates substantially from the global average (Hoburg et al. 2016).

Consider the following function which is the difference between two Softmax Affine functions (Eq. 10):

$$\begin{aligned} f_{\text {DSMA}}(\mathbf{x} ) = \frac{1}{\alpha } \log \sum _{k=1}^{K} \exp \left( \alpha (b_k + \mathbf {a}_k^{\text {T}} \mathbf {x}) \right) - \frac{1}{\beta } \log \sum _{m=1}^{M} \exp \left( \beta (h_m + \mathbf {g}_m^{\text {T}} \mathbf {x}) \right) \end{aligned}$$
(11)

In the same way that an individual SMA function requires fewer terms K than the Max Affine function, the two SMA functions of DSMA require fewer terms K and M to fit smooth convex functions Hoburg et al. (2016). Thus, the DSMA function will generally require fewer terms \(K+M\) than the DMA function to obtain an accurate fit to DC functions.

Transforming the DSMA function back to the optimization variables \(\mathbf {u}_j\) and \(w_j\) proceeds as follows:

$$\begin{aligned} \begin{aligned} y&= \frac{1}{\alpha } \log \sum _{k=1}^{K} \exp \left( \alpha (b_k + \mathbf {a}_k^{\text {T}} \mathbf {x}) \right) - \frac{1}{\beta } \log \sum _{m=1}^{M} \exp \left( \beta (h_m + \mathbf {g}_m^{\text {T}} \mathbf {x}) \right) \\ \exp (y)&= \exp \left( \frac{1}{\alpha } \log \sum _{k=1}^{K} \exp \left( \alpha (b_k + \mathbf {a}_k^{\text {T}} \mathbf {x}) \right) - \frac{1}{\beta } \log \sum _{m=1}^{M} \exp \left( \beta (h_m + \mathbf {g}_m^{\text {T}} \mathbf {x}) \right) \right) \\ w&= \frac{\exp \left( \frac{1}{\alpha } \log \sum _{k=1}^{K} \exp \left( \alpha (b_k + \mathbf {a}_k^{\text {T}} \mathbf {x}) \right) \right) }{\exp \left( \frac{1}{\beta } \log \sum _{m=1}^{M} \exp \left( \beta (h_m + \mathbf {g}_m^{\text {T}} \mathbf {x}) \right) \right) } \\ w&= \frac{\exp \left( \log \left( \left( \sum _{k=1}^{K} \exp \left( \alpha (b_k + \mathbf {a}_k^{\text {T}} \mathbf {x}) \right) \right) ^{\frac{1}{\alpha }} \right) \right) }{\exp \left( \log \left( \left( \sum _{m=1}^{M} \exp \left( \beta (h_m + \mathbf {g}_m^{\text {T}} \mathbf {x}) \right) \right) ^{\frac{1}{\beta } } \right) \right) } \end{aligned} \end{aligned}$$
(12)

At this point it is obvious from the definition of a posynomial function that the form will reduce to:

$$\begin{aligned} w = \frac{ \left( \sum _{k=1}^{K} e^{\alpha b_k} \prod _{i=1}^N u_i^{\alpha a_{ik}} \right) ^{1/\alpha } }{ \left( \sum _{m=1}^{M} e^{\beta h_m} \prod _{i=1}^N u_i^{\beta g_{im}} \right) ^{1/\beta } } \end{aligned}$$
(13)

Though Eq. 13 is not compatible with the SP formulation, consider the following substitutions:

$$\begin{aligned} p_{\text {convex}}&= \sum _{k=1}^{K} e^{\alpha b_k} \prod _{i=1}^N u_i^{\alpha a_{ik}} \end{aligned}$$
(14)
$$\begin{aligned} p_{\text {concave}}&= \sum _{m=1}^{M} e^{\beta h_m} \prod _{i=1}^N u_i^{\beta g_{im}} \end{aligned}$$
(15)

which then reduces Eq. 13 to:

$$\begin{aligned} w = \frac{(p_{\text {convex}})^{1/\alpha } }{(p_{\text {concave}})^{1/\beta } } \end{aligned}$$
(16)

Thus, taking the three constraints Eqs. 14, 15, 16 as a set does result in an SP compatible scheme. This method of substitution is consistent with other approaches to constructing GP and SP compatible constraints (Boyd et al. 2007).

3.2.4 Consideration of implicit difference of softmax affine (IDSMA) functions

Hoburg et al. (2016) proposes a third function class called Implicit Softmax Affine (ISMA). Unlike MA and SMA, the ISMA function class is an implicit function of y:

$$\begin{aligned} \tilde{f}_{\text {ISMA}}(\mathbf {x}, y)&= \log \sum _{k=1}^{K} \alpha _k \exp \left( \alpha _k(b_k + \mathbf {a}_k^{\text {T}}\mathbf {x} - y) \right) \end{aligned}$$
(17)

Since the ISMA function proved superior to the SMA function, particularly for functions with corners, cusps, and highly varying curvature, it is tempting to write an Implicit Difference of Softmax Affine function as follows:

$$\begin{aligned} \tilde{f}_{\text {IDSMA}}(\mathbf {x}, y)&= \log \sum _{k=1}^{K} \alpha _k \exp \left( \alpha _k(b_k + \mathbf {a}_k^{\text {T}}\mathbf {x} - y) \right) - \log \sum _{m=1}^{M} \beta _m \exp \left( \beta _m (h_m + \mathbf {g}_m^{\text {T}}\mathbf {x} - y) \right) \end{aligned}$$
(18)

However, this function is not a one to one mapping in that there are multiple possible values y for each vector \(\mathbf {x}\). To demonstrate this, consider the case where \(K = M = 1\), \(\alpha _k = \beta _m = 1\), and all other constants are zero. Substituting these values into Eq. 18 yields the expression \(y-y = 0\), which holds true for all values of y. It is therefore not generally possible to solve for a unique y for any given \(\mathbf {x}\). Fortunately, in practice the DSMA function performs well in regions that proved challenging to SMA functions due to the DC construction, somewhat negating the desire for IDSMA functions in the first place.

4 Process for using the DSMA function in an optimization formulation

Consider a constraint that might be posed in an optimization problem:

$$\begin{aligned} w \ge g(\mathbf {u}) \end{aligned}$$
(19)

where function \(g(\mathbf {u})\) represents the black box mapping from \(\mathbb {R}^N \rightarrow \mathbb {R}\) discussed above in Sect. 3.2.1. The steps to model this constraint in a Signomial Programming compatible form are as follows:

  1. 1.

    Select a set of trial points \(\{\mathbf {u}_j\) | \(j\in J\}\)

  2. 2.

    Generate dataset \(\{\mathbf {u}_j, w_j\) | \(j \in J, w_j = g(\mathbf {u}_j)\}\) by evaluating each \(\mathbf {u}_j\) using the black box function

  3. 3.

    Apply the log transformation \(\{\mathbf {x}_j, y_j\} = \{\log \mathbf {u}_j, \log w_j\}\)

  4. 4.

    Fit a DSMA function f to the transformed data such that \(y_j \approx f(\mathbf {x}_j)\)

  5. 5.

    Use the fit parameters from the DSMA function f to construct Eqs. 14, 15, and 16

  6. 6.

    Relax the equalities in Eqs. 14, 15, and 16 as appropriate to construct the desired constraint (See Table 1)

The first three steps are trivial, so discussion here will focus on fitting and constraint construction.

4.1 Fitting method

For a set of m number of data points (ie, if there are m number of data points in set J), the fitting problem can be written as an unconstrained least squares optimization problem with objective function:

$$\begin{aligned} \underset{\gamma }{\text {minimize}} \sum _{j = 1}^m \left( f(\mathbf {x}_j; \mathbf {\gamma }) - y_j \right) ^2 \end{aligned}$$
(20)

where the fitting parameters are stacked in the vector \(\gamma\) (Hoburg et al. 2016).

This problem is solved using the Levenberg–Marquardt (LM) algorithm presented by Hoburg et al. (2016). The LM algorithm computes a step size at each iteration but requires a Jacobian to be computed at each step, and so relevant analytical derivatives are presented in the following Sects. 4.3 and 4.4. The gradient based nature of the LM algorithm requires a number of random restarts to be performed from varying initial guesses. The cases presented below utilize between 30 and 100 random restarts, though the required number will be problem dependent.

When fitting a DSMA function, a DMA function is first fit in order to provide an initial guess for the DSMA fitting algorithm when combined with a relatively large softening parameter. The ability to quickly achieve a DMA initial guess is critical to the success of fitting DSMA functions, as starting from random starting conditions does not typically yield a satisfactory result.

4.2 Constraint construction

Equations 14, 15, and 16 combine to represent the function \(g(\mathbf {u})\) in a form that is compatible with Signomial Programming, but a constraint in an optimization problem (Eq. 19) is defined by both the function \(g(\mathbf {u})\) and the relationship between \(g(\mathbf {u})\) and w as defined by a relational operator (\(=,\ge ,\le\)). Eqs. 14, 15, and 16 must therefore be modified to contain this relational information.

For example, if as presented in Eq. 19, w is lower bounded by the function \(g(\mathbf {u})\), then Eq. 16 must similarly present a lower bound on w. Since softening parameters are strictly positive by definition (Hoburg et al. 2016), intermediate variable \(p_{\text {convex}}\) must also be lower bounded in Eq. 14 since it appears in the numerator of Eq. 16. However, intermediate variable \(p_{\text {concave}}\) must be upper bounded to prevent the denominator of Eq. 16 from growing too large. This case corresponds to the second column of Table 1. Similar cases are presented for all three possible relational operators of the original constraintFootnote 3.

Table 1 Lookup table for the relational operators of Eqs. 14, 15, and 16 given the relational operator of the original constraint being replaced with an SP compatible model
Full size table

4.3 Derivatives for the DMA function

$$\frac{{\partial f_{{{\text{DMA}}}} }}{{\partial b_{i} }} = \left\{ {\begin{array}{*{20}l} {1,} & {{\text{if}}\;i = {\text{argmax}}_{k} b_{k} + {\mathbf{a}}_{k}^{{\text{T}}} {\mathbf{x}}} \\ {0,} & {otherwise} \\ \end{array} } \right.$$
(21)
$$\frac{{\partial f_{{{\text{DMA}}}} }}{{\partial {\mathbf{a}}_{i} }} = \left\{ {\begin{array}{*{20}l} {{\mathbf{x}}^{{\text{T}}} } & {{\text{if}}\;i = {\text{argmax}}_{k} b_{k} + {\mathbf{a}}_{k}^{{\text{T}}} {\mathbf{x}}} \\ {0,} & {otherwise} \\ \end{array} } \right.$$
(22)
$$\frac{{\partial f_{{{\text{DMA}}}} }}{{\partial h_{i} }} = \left\{ {\begin{array}{*{20}l} { - 1,} & {{\text{if}}\;i = {\text{argmax}}_{k} b_{k} + {\mathbf{a}}_{k}^{{\text{T}}} {\mathbf{x}}} \\ {0,} & {otherwise} \\ \end{array} } \right.$$
(23)
$$\frac{{\partial f_{{{\text{DMA}}}} }}{{\partial {\mathbf{g}}_{i} }} = \left\{ {\begin{array}{*{20}l} { - {\mathbf{x}}^{{\text{T}}} } & {{\text{if}}\;i = {\text{argmax}}_{k} b_{k} + {\mathbf{a}}_{k}^{{\text{T}}} {\mathbf{x}}} \\ {0,} & {otherwise} \\ \end{array} } \right.$$
(24)

4.4 Derivatives for the DSMA function

$$\begin{aligned} \frac{\partial f_{\text {DSMA}}}{\partial b_i}&= \frac{\exp ({\alpha (b_i + \mathbf {a}_i^{\text {T}}\mathbf {x}))}}{\sum _{k = 1}^K \exp (\alpha (b_k + \mathbf {a}_k^{\text {T}}\mathbf {x}))} \end{aligned}$$
(25)
$$\begin{aligned} \frac{\partial f_{\text {DSMA}}}{\partial \mathbf {a}_i}&= \frac{\mathbf {x}^{\text {T}} \cdot \exp (\alpha (b_i + \mathbf {a}_i^{\text {T}}\mathbf {x}))}{\sum _{k = 1}^K \exp (\alpha (b_k + \mathbf {a}_k^{\text {T}}\mathbf {x}))} \end{aligned}$$
(26)
$$\begin{aligned} \frac{\partial f_{\text {DSMA}}}{\partial \alpha }&= \frac{1}{\alpha } \frac{\sum _{k=1}^K(b_k + \mathbf {a}_k^{\text {T}} \mathbf {x}) \exp (\alpha (b_k + \mathbf {a}_k^{\text {T}}\mathbf {x}))}{\sum _{k = 1}^K \exp (\alpha (b_k + \mathbf {a}_k^{\text {T}}\mathbf {x}))} - \frac{1}{\alpha ^2} \log \sum _{k=1}^{K} \exp \left( \alpha (b_k + \mathbf {a}_k^{\text {T}} \mathbf {x}) \right) \end{aligned}$$
(27)
$$\begin{aligned} \frac{\partial f_{\text {DSMA}}}{\partial (\log \alpha )}&= \frac{\sum _{k=1}^K(b_k + \mathbf {a}_k^{\text {T}} \mathbf {x}) \exp (\alpha (b_k + \mathbf {a}_k^{\text {T}}\mathbf {x}))}{\sum _{k = 1}^K \exp (\alpha (b_k + \mathbf {a}_k^{\text {T}}\mathbf {x}))} - \frac{1}{\alpha } \log \sum _{k=1}^{K} \exp \left( \alpha (b_k + \mathbf {a}_k^{\text {T}} \mathbf {x}) \right) \end{aligned}$$
(28)
$$\begin{aligned} \frac{\partial f_{\text {DSMA}}}{\partial h_i}&= \frac{-\exp ({\beta (h_i + \mathbf {g}_i^{\text {T}}\mathbf {x}))}}{\sum _{m = 1}^M \exp (\beta (h_m + \mathbf {g}_m^{\text {T}}\mathbf {x}))} \end{aligned}$$
(29)
$$\begin{aligned} \frac{\partial f_{\text {DSMA}}}{\partial \mathbf {g}_i}&= \frac{-\mathbf {x}^{\text {T}} \cdot \exp (\beta (h_i + \mathbf {g}_i^{\text {T}}\mathbf {x}))}{\sum _{m = 1}^M \exp (\beta (h_m + \mathbf {g}_m^{\text {T}}\mathbf {x}))} \end{aligned}$$
(30)
$$\begin{aligned} \frac{\partial f_{\text {DSMA}}}{\partial \beta }&= -\frac{1}{\beta } \frac{\sum _{m=1}^M(h_m + \mathbf {g}_m^{\text {T}} \mathbf {x}) \exp (\beta (h_m + \mathbf {g}_m^{\text {T}}\mathbf {x}))}{\sum _{m = 1}^M \exp (\beta (h_m + \mathbf {g}_m^{\text {T}}\mathbf {x}))} + \frac{1}{\beta ^2} \log \sum _{m=1}^{M} \exp \left( \beta (h_m + \mathbf {g}_m^{\text {T}} \mathbf {x}) \right) \end{aligned}$$
(31)
$$\begin{aligned} \frac{\partial f_{\text {DSMA}}}{\partial (\log \beta )}&= -\frac{\sum _{m=1}^M(h_m + \mathbf {g}_m^{\text {T}} \mathbf {x}) \exp (\beta (h_m + \mathbf {g}_m^{\text {T}}\mathbf {x}))}{\sum _{m = 1}^M \exp (\beta (h_m + \mathbf {g}_m^{\text {T}}\mathbf {x}))} + \frac{1}{\beta } \log \sum _{m=1}^{M} \exp \left( \beta (h_m + \mathbf {g}_m^{\text {T}} \mathbf {x}) \right) \end{aligned}$$
(32)

5 Demonstrations of the fitting models

5.1 A 1D fitting problem

Consider the 1D function, which uses the log transformed variables \(\mathbf {x}\) and y:

$$\begin{aligned} y = \max \left[ -6x - 6, x^4-3x^2 \right] \end{aligned}$$
(33)

This function is used as a test case due to a non-differentiable corner along with significant variations of curvature. Log–log convex methods (MA, SMA, ISMA) are unable to capture the highly non-convex region of the data, essentially approximating this portion of the curve as a straight line (Fig. 1).

Fig. 1
figure 1

Fifth order fits to the simple 1D function. RMS Error is as follows: MA: 44.6%, SMA: 44.6%, ISMA: 44.8%, DSMA: 0.019%

Full size image

As a result, the convex fitting methods all converge to nearly identical representations with an RMS error of between 44–45%. In contrast, the DSMA function captures all of the major features of the function, including the non-differential corner. Unlike SMA functions, which can only capture a single curvature due to the single parameter \(\alpha\), the DSMA function can capture complex, multi-radius curvature as a direct result of the DC construction. Fitting this function with functions of increasing order substantially improves the RMS error, largely driven by the error at the non-differentiable corner point (Fig. 2).

Fig. 2
figure 2

The log of RMS error with increasing fit order

Full size image

5.2 A 2D fitting problem

Consider the 2D test case shown in Fig. 3, which is an eigenfunction of the wave equation with a clamped lower right quadrant.

Fig. 3
figure 3

An eigenfunction of the wave equation with clamped lower right quadrant

Full size image

This function features complex regions of both convex and concave curvature, an entirely flat quadrant, and a sharp non-differentiable cusp at the origin. Though this particular function has no explicit form, the Matlab ‘membrane’ function produces the necessary data.

Fitting this function with an DSMA function yields a reasonably accurate surrogate (See Fig. 4 for a 9th order fit). As might be expected, the fitting scheme struggles along the non-differentiable L-shaped curve, and at origin specifically. Error near the point (0,1) is due to an inflection in the data where curvature changes from concave to convex in a very small region, which proves a difficult feature to capture in the fit. As with the previous example, increasing the fit order improves the fit quality (Fig. 5).

Fig. 4
figure 4

The fitted 9th order function and associated absolute error

Full size image
Fig. 5
figure 5

The log of RMS error with increasing fit order

Full size image

5.3 Fitting XFOIL performance data of the NACA 24xx family of airfoils

Hoburg et al. (2016) fit performance data for NACA 24xx airfoils generated from XFOIL (Drela 1989), but only by considering curves of lift coefficient vs. drag coefficient. In many cases, it is more useful to have two separate curves of lift coefficient vs. angle of attack and drag coefficient vs. angle of attack, but the CL vs. \(\alpha\) curve is not compatible with log–log convex fitting techniques.

Consider the problem of fitting the following function:

$$\begin{aligned} C_L = f(\alpha ,Re,\tau ) \end{aligned}$$
(34)

where \(C_L\) is the airfoil lift coefficient, \(\alpha\) is the airfoil angle of attack, Re is the Reynolds number, and \(\tau\) is the airfoil thickness (ex, a \(\tau =0.12\) would be a NACA 2412 airfoil).

Sweeping with XFOIL over a grid from \(\alpha =[1,23]\), \(Re=[10^6,10^7]\), and \(\tau =[.09,.21]\) yields a training set of untransformed variables \(\mathbf {u}_j\) and \(w_j\). This data is then transformed, fit with a DSMA function, and then used to construct a SP compatible equation set as described in Sect. 4.2, with the results shown in Fig. 6. Once again, increasing fit order improves the overall quality of the fit (Fig. 7).

Fig. 6
figure 6

5th order DSMA fits representing Lift Coefficient vs. Angle of Attack for the NACA 24xx family of airfoils, plotted with the sampled data from XFOIL

Full size image
Fig. 7
figure 7

The log of RMS error with increasing fit order

Full size image

6 Conclusions

This work serves to develop and validate a Signomial Programming compatible method for fitting black-box data when the underlying mathematical relationships are not log–log convex. The Difference of Softmax Affine (DSMA) function is a key link in the chain from Geometric Programming, where analysis models are predominately limited to either simple explicit relationships or log–log convex data fits, to more traditional MDAO methods like Sequential Quadratic Programming, where the mathematical form of an analysis model has few limitations.