A sensitivity interpolation algorithm for the concurrent optimization of bodies sharing a common design space

Abstract

In this paper the problem of the concurrent topological optimization of two different bodies sharing a region of the design space is dealt with. This design problem focuses on the simultaneous optimization of two bodies (components) where not only the material distribution of each body has to be optimized but also the design space has to be divided among the two bodies. This novel optimization formulation represents a design problem in which more than one component have to be located inside a limited allowable room. Each component has its own function and load carrying requirements. In the paper a novel development solution algorithm is presented. With respect to previously published papers, the new algorithm comprises an interpolation of the density fields which allows a complete independence of the meshes of the two bodies. As the bodies can be meshed with any arbitrary mesh, this new algorithm can be applied to any real geometry. The developed algorithm is used to design a complex three dimensional system, namely a multi-component arm for a tube bending machine.

1 Introduction

In the literature many different engineering problems referring to the topological optimization of structural components can be found [see for instance Rozvany (2009), Guo and Cheng (2010), Eschenauer and Olhoff (2001), Bendsøe and Sigmund (2004), Zhu et al. (2016) and Zhang et al. (2016b)]. In most cases, only one component is considered. Recently, however, problems involving multi-domain optimization, such as the design of multi-phase or multi-material structures (Tavakoli and Mohseni 2014), have been considered.

Referring to the particular problem of the optimization of systems composed by two bodies sharing the same design domain, some applications can be found. In Lawry and Maute (2018) and Strömberg (2018), the level set method is used for the optimization of the interface between two, or more, phases (components) in order to obtain some prescribed interaction force. In Zhang et al. (2016a), a completely different approach, the Moving Morphable Components method, which seems to be adaptable to solve such problems, is discussed.

In Previati et al. (2018) and Ballo et al. (2019), the authors have presented a simple algorithm based on the SIMP approach (Rozvany 2009; Bendsøe and Sigmund 2004). The method is able to optimize the material distribution of two different bodies while, at the same time, allocate in an efficient way the space shared between the bodies. The algorithm has also proved to be easily implementable and can be used along with available optimization algorithms. The applicability of the algorithm is limited to bodies presenting the same mesh in the shared portion of the domain. Such limitation prevents the utilization of the algorithm on arbitrary shaped optimization domains.

This paper presents a newly developed algorithm. By considering a density field interpolation on the shared part of the domain, the limitation regarding the correspondence of the elements of the two meshes can be removed. By removing this limitation, the applicability of the method is extended to any design domain and any kind of finite element, as explained in Sects. 2 and 3 of the paper. In Sect. 4, the new algorithm will be tested by considering a two-dimensional example. Then, in Sect. 5, the application of the presented algorithm to the optimization of a multi-component arm for a tube bending machine will be shown.

2 Problem formulation and numerical solution

The formulation of the concurrent structural optimization of two bodies sharing the same design space has been given and discussed in Previati et al. (2018). In this section, it is briefly summarized.

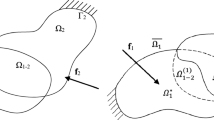
Figure 1 depicts the two bodies sharing (a portion of) the design space. The optimization process consists in finding the optimal material distribution for each body along with the optimal division of the shared part of the domain space among the two bodies. The two optimization problems are solved simultaneously and the allocation of the shared part of the domain changes accordingly to the actual structural configuration of the two bodies. The following nomenclature is considered.

• $\varOmega _1$ and $\varOmega _2$: bodies to be optimized.

• $\varOmega _{1-2}$: shared portion of the design space that can be occupied by any of the two bodies (or left void). Any given point of this region can be occupied by only one of the two bodies.

• $\varOmega _{1}^{*}$ and $\varOmega _{2}^{*}$: the two unshared parts of the domains $\varOmega _{1}$ and $\varOmega _{2}$ respectively (s.t. $\varOmega _{1}=\varOmega _{1}^{*}\cup \varOmega _{1-2}$ and $\varOmega _{1}=\varOmega _{1}^{*}\cup \varOmega _{1-2}$).

• $\varOmega _{1-2}^{\left( 1\right) }$ and $\varOmega _{1-2}^{\left( 2\right) }$: portion of the shared design space assigned to $\varOmega _1$ or $\varOmega _2$ respectively (s.t. $\varOmega _{1-2}^{\left( 1\right) }\cup \varOmega _{1-2}^{\left( 2\right) }=\varOmega _{1-2}$ and $\varOmega _{1-2}^{\left( 1\right) }\cap \varOmega _{1-2}^{\left( 2\right) }=\emptyset$).

• $\overline{\varOmega _{1}}$ and $\overline{\varOmega _{2}}$: actual design space of the two bodies, given by $\overline{\varOmega _{1}}=\varOmega _{1}^{*}\cup \varOmega _{1-2}^{\left( 1\right) }$ and $\overline{\varOmega _{2}}=\varOmega _{2}^{*}\cup \varOmega _{1-2}^{\left( 2\right) }$

• $\mathbf {f_1}$ and $\mathbf {f_2}$: applied load on $\varOmega _1$ and $\varOmega _2$ respectively.

• $\varGamma _1$ and $\varGamma _2$: boundary conditions on $\varOmega _1$ and $\varOmega _2$ respectively.

Fig. 1

Generalized geometries of the design domains ($\varOmega _1$ and $\varOmega _2$) of two bodies sharing a portion of the design space. Each body has its own system of applied forces ($\mathbf {f_1}$ and $\mathbf {f_2}$) and boundary constraints ($\varGamma _1$ and $\varGamma _2$). $\varOmega _{1-2}$ represents the shared portion of the design space. Left: initial definition of the domains. Right: division of the domains with assignment of the shared portion of the design space to each body

Obviously, for a physical meaningful solution of the problem, $\overline{\varOmega _{1}}$ and $\overline{\varOmega _{2}}$ must be connected.

It must be emphasized that the portion of the shared domain $\varOmega _{1-2}$ to be allocated to each body (i.e. $\varOmega _{1-2}^{\left( 1\right) }$ and $\varOmega _{1-2}^{\left( 2\right) }$) is not given a priori, but must be allocated during the optimization process and can change according to the evolution of the shapes of the two bodies themselves.

Under the hypotheses of

• linear elastic bodies with small deformations;

• the two bodies do not interact in the shared portion of the domain (i.e. no contact is considered between the two bodies in the shared portion of the domain, interactions between the two bodies outside this region is possible);

• each body is made by only one isotropic material;

• both materials have the same reference density, but they can have different elastic moduli;

• loads and boundary conditions can be applied at any location of the domains, even in the shared portion;

• the structural problem is formulated by the finite element theory;

the problem can be stated in the framework of finite elements as

$$\begin{aligned} \begin{array}{ll} Find&{}\min _{\mathbf {u_1},\mathbf {u_2},\rho }\left( \mathbf {f_{1}^{T}}\mathbf {u_1}+\mathbf {f_{2}^{T}}\mathbf {u_2}\right) \\ \\ s.t.:&{}{\mathbf {K}}\left( E_{e}^1\right) \mathbf {u_1}=\mathbf {f_1}\;\;and\;\;{\mathbf {K}}\left( E_{e}^2\right) \mathbf {u_2}=\mathbf {f_2}\\ &{} E^{1}_{e}=\rho \left( x_e\right) ^p E_{e}^{*1}, \qquad x_e\in \overline{\varOmega _{1}} \\ &{} E^2_{e}=\rho \left( x_e\right) ^p E_{e}^{*2}, \qquad x_e\in \overline{\varOmega _{2}} \\ &{}\varOmega _{1-2}^{\left( 1\right) }\cup \varOmega _{1-2}^{\left( 2\right) }=\varOmega _{1-2}\;\;and\;\;\varOmega _{1-2}^{\left( 1\right) }\cap \varOmega _{1-2}^{\left( 2\right) }=\emptyset \\ &{}\sum \limits _{e=1}^{N_1}\rho \left( x_e\right) +\sum \limits _{e=1}^{N_2}\rho \left( x_e\right) \le V\qquad 0<\rho _{min}\le \rho \le 1\\ &{}\\ where:\;&{} {\mathbf {K}}\left( E_{e}^1\right) =\sum _{e=1}^{N_1}\mathbf {K_e}\left( E_{e}^1\right) \;\; and\;\;{\mathbf {K}}\left( E_{e}^2\right) =\sum _{e=1}^{N_2}\mathbf {K_e}\left( E_{e}^2\right) \\ &{} \overline{\varOmega _{1}} \;\;and\;\; \overline{\varOmega _{2}} \;\;connected \end{array} \end{aligned}$$

(1)

where $\mathbf {u_1}$ and $\mathbf {u_2}$ are the displacement fields of the two bodies, $x_e$ are the coordinates of the centre of the considered element, ${\mathbf {K}}$ is the stiffness matrix of each body with $\mathbf {K_e}$ the element stiffness matrix, $E_{e}^{1}$ and $E_{e}^{2}$ are the elastic moduli of each element of the two bodies, with $E_{e}^{*1}$ and $E_{e}^{*2}$ reference elastic moduli, $N_1$ and $N_2$ are the number of elements of each body and $\rho$ is the pseudodensity, with p the penalty term.

Fig. 2

Diagram of the algorithm for the concurrent topological optimization. Symbols refer to Fig. 1

In Previati et al. (2018); Ballo et al. (2019), the authors have presented a solution algorithm able to solve the problem stated in Eq. 1 under the condition that the two bodies present the same mesh in the shared part of the domain, i.e. in this region there is a one-to-one correspondence of each element of the two bodies. This condition introduces strong limitations to the applicability of the method to actual engineering problems, as the designer is forced to choose the same mesh for the two bodies in the shared portion of the design domain, regardless of the actual shape of the bodies themselves. In the following, this condition is removed, thus leaving the designer total freedom in selecting the finite element mesh that best copes with the geometry of each single body.

The new solution algorithm is described in the diagram reported in Fig. 2. The algorithm is basically divided in two parts, namely sub-algorithm (a) and sub-algorithm (b). The two parts are highlighted by the two dashed rectangles of Fig. 2. Sub-algorithm (a) is based on the standard structural optimization algorithm derived in Sigmund (2001). The innovative part of the algorithm is mostly in the sub-algorithm (b) and is related to the subdivision of the shared part of the domain.

Referring to the diagram of Fig. 2, the algorithm starts from Block 1 with the solution of the FEM model on the two domains $\varOmega _{1}$ and $\varOmega _{2}$. The solution of the FEM model can be done in a single analysis, if interaction is present between the two bodies, or in two separate analyses, if no interaction is present. Nonlinear FE analysis can be employed.

After the FEM models have been solved, in Block A1, the sensitivities of the total compliance of each element with respect to the pseudo-density are computed as

$$\begin{aligned} \frac{\partial c}{\partial x_e}=-p\rho \left( x_e\right) ^{p-1}\mathbf {u_{e}^{T}}\mathbf {K_{e}^{*}}\mathbf {u_{e}} \end{aligned}$$

(2)

It must be emphasized that sensitivities are computed for all the elements of $\varOmega _{1}$ and $\varOmega _{2}$. In particular, the shared part of the domain $\varOmega _{1-2}$ is described by two sensitivity fields, one with respect to the elements of the first body on $\varOmega _{1-2}$ and one with respect to the elements of the second body on $\varOmega _{1-2}$.

The two sensitivity fields computed on the shared part of the domain $\varOmega _{1-2}$ have now to be compared in order to divide the domain between the two bodies in the most effective way. In the original version of the algorithm (Previati et al. 2018), this comparison was done elementwise. The common part of the domain was meshed in the same way with respect to the two bodies and each element was assigned to the body that exhibits the highest sensitivity. This, of course, was a quite strong limitation to the actual applicability of the method to real world problems with complex geometry. In this new version, the comparison is done pointwise and independently of the meshes of the two bodies. The procedure is done in Block B1 and Block B2. Firstly, in Block B1, the two sensitivity fields on $\varOmega _{1-2}$ are interpolated on a given grid of points, which is common for the two bodies. Then, in Block B2, the sensitivities are compared pointwise. On the basis of this comparison, each point is attributed either to $\varOmega _{1-2}^{\left( 1\right) }$ or to $\varOmega _{1-2}^{\left( 2\right) }$.

Connectivity among the assigned points is then enforced in Block B3.

The obtained division of the domain is finally mapped back on the elements of the two bodies in Block B4.

For clarity, the algorithm for the interpolation of the sensitivities and for the assignment of the shared part of the domain (i.e. from Block B1 to Block B4) is described in Sect. 3.

The sensitivities on $\varOmega _{1}$ and $\varOmega _{2}$ are filtered separately on the two domains in Block A2 by the filter proposed in Sigmund (2001)

$$\begin{aligned} \widehat{\frac{\partial c}{\partial \rho _e}}=\frac{1}{\rho _e\sum _{f=1}^{N}{\hat{H}}_f}\sum _{f=1}^{N}{\hat{H}}_f \rho _f\frac{\partial c}{\partial \rho _f} \end{aligned}$$

(3)

The weighting factor ${\hat{H}}_f$ is written as

$$\begin{aligned} \begin{aligned} {\hat{H}}_f=r_{min}-\mathtt {dist}\left( e,f\right) , \;\;with\;\;&\left\{ f\in N\vert \mathtt {dist}\left( e,f\right) \le r_{min} \right\} ,\\ {}&e=1,\ldots ,N \end{aligned} \end{aligned}$$

(4)

where the distance is computed between the centre of the elements e and f.

Once the elements describing $\varOmega _{1}$ and $\varOmega _{2}$ have been identified, the new pseudo-densities are computed in Block A3. The new density field is computed as (Sigmund 2001; Bendsøe and Sigmund 2004)

$$\begin{aligned} \rho _{e}^{new}=\left\{ \begin{array}{ll} \max \left( \rho _{min},\rho _{e}-m\right) , \;\;if\;\;\rho _{e}B_{e}^{\eta }\le \max \left( \rho _{min},\rho _{e}-m\right) \\ \rho _{e}B_{e}^{\eta },\;\;if\;\;\max \left( \rho _{min},\rho _{e}-m\right)<\rho _{e}B_{e}^{\eta }<\min \left( 1,\rho _{e}+m\right) \\ \min \left( 1,\rho _{e}+m\right) \;\;if\;\;\min \left( 1,\rho _{e}+m\right) \le \rho _{e}B_{e}^{\eta } \end{array}\right. \end{aligned}$$

(5)

where m is a positive move limit and $B_{e}$ represents the optimality condition

$$\begin{aligned} B_{e}=\frac{-\frac{\partial c}{\partial \rho _e}}{\lambda \frac{\partial V}{\partial \rho _{e}}},\quad \quad \frac{\partial V}{\partial \rho _{e}}=v_{e} \end{aligned}$$

(6)

The Lagrange multiplier $\lambda$ is computed by a Trust-Region Dogleg algorithm. The computation of the new pseudo-density field is performed on the whole domain $\varOmega _{1}\cup \varOmega _{2}$. In this way, the total mass is not assigned a priori, but is divided among the two bodies according to the computed sensitivities. To guarantee that the total mass on the two physical domains $\overline{\varOmega _{1}}$ and $\overline{\varOmega _{2}}$ matches the target on the design volume fraction, the Lagrange multiplier $\lambda$ is computed over $\overline{\varOmega _{1}}\cup \overline{\varOmega _{2}}$ and not $\varOmega _{1}\cup \varOmega _{2}$.

The pseudo-density of the non-active elements of $\varOmega _{1}$ and $\varOmega _{2}$ is set equal to $\rho _{min}$ in Block B5.

3 Sensitivity interpolation and assignment of the shared part of the domain

In this section, the algorithm for the interpolation of the sensitivities and the assignment of the shared part of the domain is described. The aim of such algorithm is to divide the shared part of the domain when there is no correspondence between the mesh of the two bodies. To illustrate this situation, let us consider the example of Fig. 3. The example is based on the well-known problem of a cantilever loaded at the free end [see Bendsøe and Sigmund (2004) p. 49]. In the proposed example, two cantilevers are considered and are positioned to have an overlap in the respective design domains.

Figure 4a shows the two different meshes for the two bodies. The meshes are very different, on $\varOmega _{1}$ a four node bilinear mesh is considered, while on $\varOmega _{2}$ a three node linear mesh. The two meshes are coarse, with a mean size of 2 mm, for representation reasons.

Fig. 3

Two beams under bending numerical example definition

Fig. 4

Two beams under bending. a Mesh of the two domains. b Detail of the grid of interpolating points on the shared part of the design domains

Firstly, a grid of uniformly spaced points is set in the shared domain. This grid, denoted as interpolation grid in the following, is the same for the two bodies. The sensitivities will be interpolated at each point of the interpolation grid and used to assign the domain to either body 1 or body 2. In Fig. 4b a detail of the shared part of the domain is reported, where the black dots represent the points of the interpolation grid.

The interpolation scheme is shown in Fig. 5. For each of the two body meshes, the centre of the elements (i.e. the centroids) are used as nodes to create an auxiliary linear triangular mesh. The centres of the elements are where the sensitivities have been computed, so are a natural choice as nodes of the auxiliary mesh used for the interpolation. The element containing each of the points of the interpolation grid is identified. The sensitivity at each point of the interpolating grid is then computed by applying the usual finite elements interpolation as

$$\begin{aligned} \left( \frac{\partial c}{\partial \rho }\right) _p=\sum _{i=1}^{3}{N_i\left( \frac{\partial c}{\partial \rho _{e}}\right) _i} \end{aligned}$$

(7)

where $\left( \frac{\partial c}{\partial \rho }\right) _p$ is the sensitivity at each point p of the grid and $\left( \frac{\partial c}{\partial \rho _{e}}\right) _i$ is the sensitivity at the i-th node of the element containing p, which has been computed at the centre of the corresponding element of the mesh of the body (Eq. 2). $N_i$ are the three standard shape functions of the linear triangle element. It has to be observed that, being the sensitivity computed on elements of different size, each value computed by Eq. 2 has to be divided by the area of the corresponding element.

Fig. 5

Construction of the triangular mesh for the interpolation of the grid points. Left: body 1. Right: body 2

Once the sensitivity has been interpolated on the shared part of the domain for the two bodies, the interpolated fields are compared at each point of the interpolation grid. Each point is then attributed to the first body ($\varOmega _{1-2}^{\left( 1\right) }$) if the sensitivity interpolated from the solution on $\varOmega _{1}$ is greater than the sensitivity interpolated from $\varOmega _{2}$, or to the second body ($\varOmega _{1-2}^{\left( 2\right) }$) otherwise.

The connectivity of the two sets $\varOmega _{1-2}^{\left( 1\right) }$ and $\varOmega _{1-2}^{\left( 2\right) }$ is enforced as described in the following. The points assigned to the two sets $\varOmega _{1-2}^{\left( 1\right) }$ and $\varOmega _{1-2}^{\left( 2\right) }$ are clustered according to their connectivity to the points of the same set. If a point (or a group of points) is insulated with respect to the main part of its set, it is assigned to the other set. This analysis is performed simultaneously on the two sets, in this way neither set has the priority on the other.

Finally, the regions $\varOmega _{1-2}^{\left( 1\right) }$ and $\varOmega _{1-2}^{\left( 2\right) }$ have to be mapped back from the interpolation grid to the two meshes of the bodies. In other words, the elements of $\varOmega _{1}$ that belong also to $\overline{\varOmega _{1}}$ and the elements of $\varOmega _{2}$ that belong also to $\overline{\varOmega _{2}}$ are considered active, while the other elements are considered not active. In this operation, three situations can arise. An element can be entirely inside the active domain, entirely outside the active domain or partially inside and partially outside the active domain. In the latter case, the element has to be marked as partially active. To take into consideration these cases, the activity of each element is evaluated as shown in Fig. 6. Each point of the interpolation grid has been marked as active (red circle, value 1) or inactive (black circle, value 0). To compute the activation level of the elements of the body mesh, for each element a certain number of control points is used. As control points, a very simple and convenient choice are the Gauss points of the element (Liu et al. 2005; Li et al. 2018; Kang and Wang 2011; Wang et al. 2013), represented as squares in Fig. 6. There is no restriction on the number of Gauss points to be used for the interpolation. In the following examples, the same number of Gauss points used for the element integration is adopted to maintain the same formulation of the finite element solver. The activation value of each Gauss point is computed by considering a linear triangular grid on the interpolation points as done for the interpolation of the sensitivity field. Once the activation level has been interpolated at each Gauss point, the activation level of the entire element is computed by applying the quadrature rule on the values at the Gauss points and associated to the centre of the element itself as

$$\begin{aligned} a_e=\sum _{i=1}^{n_{GP}}{w_i a_{GP,i}} \end{aligned}$$

(8)

where $a_e$ and $a_{GP,i}$ are the activation level of the element and of each Gauss point respectively, $n_{GP}$ is the number of Gauss points and $w_i$ are the Gauss point weights. In Fig. 6, the activation level of each Gauss point is in black and the resulting activation level of the element is in blue.

In Fig. 6, the bilinear quadrilateral mesh of $\varOmega _{1}$ has been considered. The same approach can be applied to the linear triangles of the mesh of $\varOmega _{2}$, or to any other mesh. For this example, the same number of Gauss points of the base elements has been considered. However, this is not required and any number of Gauss points can be used.

Fig. 6

Mapping of the activity field from the interpolation grid points to the centre of each element

The activation level $a_e$ of each element is then considered in the computation of its new pseudo-density by modifying Eq. 5 as

$$\begin{aligned} \rho _{e}^{new}=\left\{ \begin{array}{ll} \max \left( \rho _{min},\rho _{e}-m\right) , \;\;if\;\;a_e\rho _{e}B_{e}^{\eta }\le \max \left( \rho _{min},\rho _{e}-m\right) \\ a_e\rho _{e}B_{e}^{\eta },\;\;if\;\;\max \left( \rho _{min},\rho _{e}-m\right)<a_e\rho _{e}B_{e}^{\eta }<\min \left( 1,\rho _{e}+m\right) \\ \min \left( 1,\rho _{e}+m\right) \;\;if\;\;\min \left( 1,\rho _{e}+m\right) \le a_e\rho _{e}B_{e}^{\eta } \end{array}\right. \end{aligned}$$

(9)

The proposed interpolation approach has been presented by considering a two-dimensional example. The extension to the three-dimensional case is straightforward. A three-dimensional interpolation grid is created. The values of sensitivity are computed at each point of the grid by interpolating the sensitivities computed at the centres of the elements by considering an auxiliary mesh of linear tetrahedrons with vertices in the centres of the elements. The back mapping of the sensitivities is realized by considering the Gauss points of the elements and an auxiliary mesh of linear tetrahedrons with vertices in the interpolation points.

4 Two dimensional numerical example

In this section a simple two dimensional problem is reported. The problem is the one depicted in Fig. 3 and consists of two cantilevers with an end load sharing part of the domain. Each of the two cantilevers corresponds to the well-known problem of the cantilever with load end (Bendsøe and Sigmund 2004). The two cantilevers have the same geometry, material, load and boundary conditions. However, the two domains are meshed with very different meshes.

The proposed example is solved for different meshes conbination. Four mesh types are considered, namely linear triangular (T3), quadratic triangular (T6), bilinear quadrilateral (Q4) and quadratic quadrilateral (Q8). The properties of the finite element meshes are defined in Table 1. The mean element size is 0.5 mm for both triangular and quadrilateral elements, thus quadrilateral elements have approximately a double area with respect to the triangular elements. The volume fraction is set to 0.55 and the interpolation grid has a dimension of 0.5 mm. The obtained compliances and mass fractions of the two bodies are analysed and compared for the different mesh combinations.

Table 1 Meshes used for the solution of the example of Fig. 3

The results of the concurrent topological optimization of the two cantilevers are reported in In Fig. 7. At first, the results of the original algorithm presented in Previati et al. (2018) are shown for comparison. In this case, the two bodies are meshed with the same mesh of Q4 elements with corresponding positions of the nodes. Then, in Fig. 7b, c, the results for two mesh combinations obtained by using the algorithm proposed in this paper are shown. In particular, in Fig. 7b, the combination T3-Q8 is reported, while in Fig. 7c the combination T6-Q4. The subdivision of the common part of the design space and the two optimized structures are shown.

Referring to the two structures of Fig. 7b, c, the two optimized topological layouts are very similar, as one may expect as the two sub-problems are the same and the found topology is also similar to the theoretical solution of the problem of the cantilever with loaded end (Bendsøe and Sigmund 2004, p. 49). Also, the solution is very similar for the two different mesh combinations. When compared with the output of the original algorithm (Fig. 7a), it emerges that the results of the algorithm presented in this paper are very similar, showing that the interpolation process does not affect the final solution.

In Table 2, the resulting compliance and mass of the optimized cantilever are reported for all the mesh combinations. As reference, the compliance of the structures obtained by the original algorithm presented in Previati et al. (2018) is also reported. In all the considered mesh combinations, the compliance of the two bodies is very close and the mean compliance is similar for the different cases. Also, for all mesh combinations, the compliance is similar to the compliance of the two cantilevers obtained by using the original algorithm. A sightly higher compliance is obtained for the quadratic elements, which can be related to the less stiff mathematical formulation of these elements. In fact, at the first step, when all the domains are equal and the density is uniform, the compliances for the different elements read 45.52 J for T3, 47.14 J for T6, 46.28 J for Q4 and 47.24 J for Q8. Referring to the masses, for all the mesh combinations a mass division very close to 50% has been obtained for the two bodies. Slightly more mass is attributed to the body with more compliant mesh, in order to compensate for the different stiffness of the meshes.

Fig. 7

Solution of the two dimensional example of Fig. 3 with two different mesh types. a Original algorithm presented in Previati et al. (2018), linear quadrilateral elements. b Linear triangular elements and quadratic quadrilateral elements. c Quadratic triangular elements and linear quadrilateral elements

Table 2 Results of the two cantilevers example (Fig. 3). Mesh properties in Table 1

5 Concurrent topological optimization of a tool support swing arm

The described algorithm has been employed for the optimization of a tool support swing arm for a tube bending machine. This research activity has been completed in collaboration with BLM Group (BLM 2019). This example has been originally presented in Ballo et al. (2019, 2020). Due to the very high production rate of the machine, the swing arm is subjected to high accelerations and, as a consequence, an inertial torque arises. The optimization of the system is thus important to reduce energy consumption and increase the production rate.

Figure 8 shows a 3D model of the tool support swing arm, where all its main parts are highlighted. The figure shows only half of the model due to the symmetry in the geometry of the system. The two parts that are optimised are the support arm and the sledge, shown respectively in blue and red colour in Fig. 8. The support arm rotates around the vertical rotation axis of Fig. 8, while the sledge is allowed to slide on a guide rail on the support arm in the y direction of Fig. 8. The sledge sustains the tube clamp die and is set in motion through an electric motor and a ball screw drive.

Fig. 8

Half view of the 3D model of the tool support swing arm of a tube bending machine

Fig. 9

Tool support swing arm model (BLM 2019)

In Fig. 9, the finite element model of the tool support swing arm is depicted. In the model, symmetry has been exploited by considering only half of the system. The tool load due to the contact between the clamp die and the tube surface is applied to the sledge by a multi-point constraint. A contact interaction is imposed between the sledge and the support arm in correspondence of the guide rail. It is worth noting that, by including this contact condition, a non linear finite element analysis has to be run for each optimization step. The ball screw drive is modelled by a rigid connector between the sledge and the support arm as depicted in Fig. 9.

The system is subject to an angular acceleration around the rotation axis. Also, three different loads are considered. The loads are applied one at the time and for different positions of the sledge along the rail. Forces $F_2$ and $F_3$ act only in the y direction, while force $F_1$ has x and y components. Due to the angular acceleration and force $F_1$, the system undergoes a non symmetric deformation. To maintain the geometrical symmetry of the components, a symmetry constraint is applied in the optimization algorithm. The symmetry constraint is enforced as explained in Kosaka and Swan (1999). The components are manufactured by additive manufacturing, thus no manufacturability constraint is considered.

The optimization domains of the support arm and of the sledge are also reported in Fig. 9. In the figure, a relatively small region is highlited in green. This region is quite critical for the stiffness of both components and cannot be used by both as they would interfere when the sledge is in the most inner position. This region is considered as shared domain that can be assigned to either component during the optimization process. With respect to the algorithm of Fig. 2, in the optimization of the tool support swing arm, not only the connectness of the two design spaces is enforced, but an additional condition that the shape of the domains must allow the sliding of the sledge is considered. The two components to be optimized are meshed by four-nodes tetrahedrons with mean size of 1.5 mm. A total of about $1.65\times 10^6$ elements is present in the model. The total compliance of the system is minimised by enforcing an upper bound on the overall volume fraction.

The optimization problem is solved by using Abaqus™2016 for the solution of the non linear finite element model and a handwritten code to read the results, implement the optimization algorithm and write the new input file. The handwritten code is realized by using Python and Matlab™. At the beginning of the analysis, the same pseudodensity has been assigned to all the elements.

The results of the optimization process, with an overall target volume fraction of 0.55, are shown in Fig. 10. In Fig. 10a an overall view of the optimized system is reported. In Fig. 10b, c, details of the two optimized components can be seen. The shared domain, marked with two arrows in Fig. 10b, c, has been divided in a quite complex way, allowing an internal reinforcement for the sledge and a lower reinforcement for the support arm. Finally, Fig. 11 highlights a detail of the division of the shared domain between the two optimised structures.

Fig. 10

Optimization results—surfaces with pseudodensity greater than 0.3. a Complete system. b Detail of the optimized sledge. c Detail of the optimized support arm. The two arrows indicate the shared region

Fig. 11

Optimization results—detail of the division of the common part of the domain. Elements with pseudodensity less than 0.3 have been removed

6 Conclusion

In the paper, a novel algorithm has been presented for the concurrent topological optimization of two bodies sharing part of the design domain. The new algorithm allows for the utilization of any arbitrary mesh on the bodies. Also, the algorithm has been used with a commercial finite element software by considering a SIMP approach and a symmetry constraint in the solution, proving the applicability of the method with an existing optimization algorithm. In this way, the algorithm can be applied to real world optimization problems, enabling the designer to select topology and size of the mesh that best adapt to the shape of each single body.

The new algorithm has been tested on a simple two dimensional problem and then applied to the optimization of the arm of a tube bending machine designed in collaboration with BLM Group. The application has shown the ability of the algorithm to solve real problems and find non trivial efficient solutions for the assignment of the shared domain. Further developments of the method that consider the possibility to include contact interactions in the shared part of the domain will be investigated.