Abstract
In engineering applications one often has to trade-off among several objectives as, for example, the mechanical stability of a component, its efficiency, its weight and its cost. We consider a biobjective shape optimization problem maximizing the mechanical stability of a ceramic component under tensile load while minimizing its volume. Stability is thereby modeled using a Weibull-type formulation of the probability of failure under external loads. The PDE formulation of the mechanical state equation is discretized by a finite element method on a regular grid. To solve the discretized biobjective shape optimization problem we suggest a hypervolume scalarization, with which also unsupported efficient solutions can be determined without adding constraints to the problem formulation. FurthIn this section, general properties of the hypervolumeermore, maximizing the dominated hypervolume supports the decision maker in identifying compromise solutions. We investigate the relation of the hypervolume scalarization to the weighted sum scalarization and to direct multiobjective descent methods. Since gradient information can be efficiently obtained by solving the adjoint equation, the scalarized problem can be solved by a gradient ascent algorithm. We evaluate our approach on a 2 D test case representing a straight joint under tensile load.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
In engineering design one often follows multiple incompatible goals, for example, when maximizing reliability and efficiency while simultaneously minimizing cost. In practical applications, conflicting goals are often combined into one single objective function using a weighted sum of the criteria. The main advantage of this approach is its simplicity and its numerical stability. Particularly, in the context of multiobjective PDE-constrained optimization the weighted sum method has another essential advantage: it does not add constraints to the problem formulation, which can raise additional difficulties for the numerical solution of the PDE. On the downside, the selection of meaningful weights is generally difficult. Moreover, relevant compromise solutions may be missed when the problem is non-convex. In this paper, we consider a biobjective shape optimization problem with the two objectives reliability and cost. To carry over the main advantages of the weighted sum and simultaneously overcome its main drawbacks without adding constraints, we suggest to use parametric hypervolume scalarizations to efficiently generate compromise solutions. The scalarized subproblems are solved using a gradient ascent method that takes advantage of derivative information obtained from the numerical solution of the adjoint equation.
Shape optimization problems are typical examples of engineering problems where multiple conflicting objective functions have to be considered. In this paper, we focus on the maximization of the mechanical stability of a ceramic component under tensile load while simultaneously minimizing its volume (as a measure of cost and weight). We follow the modeling approach proposed in Doganay et al. (2019), where the mechanical stability is modeled using a Weibull formulation of the probability of failure. For a general introduction to shape optimization we refer to Haslinger and Mäkinen (2003).
The main advantage of using a probabilistic formulation for the mechanical stability is that in this way the probability of failure can be assessed with a differentiable objective function. This paves the way for the application of efficient optimization methods using gradient information. We adopt the formulation suggested in Bolten et al. (2015, 2019) that is based on the probabilistic model of Weibull (1939). In our numerical implementation we follow a ‘first discretize, then optimize’ paradigm as suggested in Doganay et al. (2019). In this approach, a finite dimensional optimization problem is solved on a finite element grid subject to a discretized PDE-constraint that is induced by the mechanical state equation.
The minimization of the probability of failure of a component usually leads to large and hence costly components. This unwanted effect can be avoided by setting an upper bound on the admissible volume, see, for example, Bolten et al. (2019). However, such a constrained formulation of the shape optimization problem does not provide information on the trade-off between reliability and cost. Indeed, interpreting the volume of the component as a second and independent objective function allows for the computation of alternative shapes, thus supporting the decision maker with the selection of a most preferred solution with respect to both criteria. Following the approach of Doganay et al. (2019), we complement the minimization of the probability of failure of a component by the minimization of its volume in a biobjective shape optimization model.
For a general introduction into the field of multiobjective optimization we refer to Miettinen (1998) and Ehrgott (2005). Problems of multiobjective shape optimization have mainly been approached with evolutionary multiobjective optimization (EMO) algorithms, see, for example, Deb and Goel (2002); Chirkov et al. (2018). However, recently multiobjective PDE constrained optimization problems have also been considered from an optimal control point of view in Iapichino et al. (2017).
In this paper, we employ a scalarization-based approach to approximate the Pareto front of the biobjective shape optimization problem. Due to its simplicity and its numerical stability, the weighted sum method is a widely used scalarization method in this context. It combines all objective functions into one weighted sum objective, hence yielding a single objective counterpart problem without adding any additional constraints. However, the weighted sum method is quite limited in the context of non-convex problems. Indeed, by varying the weights only supported efficient solutions can be computed, i.e., Pareto optimal shapes for which the corresponding outcome vectors lie on the convex hull of the set of all feasible outcomes. However, most other scalarization methods which are not restricted to supported solutions like, e.g., the \(\varepsilon\)-constrained method rely on the introduction of additional constraints which we seek to avoid. Reformulations of by means of Lagrangian relaxation do not overcome this problem since they correspond to weighted sum objectives and are therefore also limited to solutions on the convex hull. Since relevant compromise solutions may thus be missed, we suggest to use nonlinear scalarizing functions as, for example, the hypervolume scalarization. While sharing the property that it leads to single-objective counterpart problems without adding constraints to the problem formulation, it is not restricted to supported efficient solutions.
The hypervolume scalarization is based on the hypervolume indicator that was introduced in Zitzler and Thiele (1999) as a measure to compare the performance of EMO algorithms. The hypervolume indicator has since become an important measure in a large variety of applications, of which the fitness evaluation of solutions sets (particularly in the context of EMO algorithms) and of individual solutions are only two examples. Given a reference point in the objective space, the hypervolume indicator of a solution set measures the volume that is (a) Dominated by the solution set, and (b) Dominates the reference point, c.f. Fig. 1. A formal definition is given in Sect. 3 below.
We exemplarily refer to Auger et al. (2009); Yang et al. (2019) as two examples from this active research field. The hypervolume indicator also plays a prominent role as a quality indicator in the subset selection problem (see, for example, Guerreiro and Fonseca (2020)), i.e., when a subset of usually bounded cardinality is sought to represent the Pareto front. Theoretical properties as well as heuristic and exact solution approaches for subset selection problems were discussed, among many others, in Auger et al. (2009, 2012); Bringmann et al. (2014, 2017); Guerreiro et al. (2016); Kuhn et al. (2016). We particularly mention Emmerich et al. (2014) for a detailed analysis of hypervolume gradients in the context of subset selection problems, a special case of which is considered in this work.
When restricting the search to individual solutions rather than solution sets, then the hypervolume indicator can be interpreted as a nonlinear scalarizing function, see, for example, Hernandez et al. (2018); Touré et al. (2019); Schulze et al. (2020). In the biobjective case, the hypervolume scalarization yields a quadratic objective function that has an intuitive geometrical interpretation. We note that quadratic scalarizations are also considered in Fliege (2004) and in the context of reference point methods in Dandurand and Wiecek (2016), and that in the biobjective case the hypervolume scalarization can be interpreted as a special case of these approaches. Furthermore, hypervolume scalarizations can be easily integrated into interactive approaches that are based on the iterative selection of reference points (like, for example, the Nimbus method). See Miettinen and Mäkelä (2002) for a comparison of reference point methods illustrating how different methods elicitate the decision makers preferences.
The hypervolume scalarization shows some similarities with other reference point based methods like, e.g., compromise programming techniques which were introduced by Bowman (1976) and Yu (1973); Freimer and Yu (1976) in the context of group decisions. See also Büsing et al. (2017) for recent research on reference point methods in the context of approximations of discrete multiobjective optimization problems.While compromise programming models typically aim at the minimization of the distance of an outcome vector from a given (utopian) reference point, e.g., based on \(\ell _p\)-norms, the hypervolume scalarization aims at maximizing the volume dominated by an outcome vector w.r.t. a given reference point. Both approaches use nonlinear objective functions (except for compromise programming with \(\ell _1\)-distances) and do not require additional constraints.
In this paper, we provide a thorough theoretical analysis of the hypervolume scalarization and its relation to weighted sums scalarizations. By introducing the concept of Pareto front generating reference sets we investigate the impact of the choice of different sets of reference points on the potential for generating a representative range of solution alternatives. From an algorithmic point of view, we focus on (multiobjective) descent algorithms and analyse the impact of different scalarizations on the generated sequence of search directions and hence on the finally chosen solution. The paper is organized as follows. In Sect. 2 a biobjective shape optimization model is introduced together with some fundamental properties of multiobjective optimization in the context of shape optimization. In Sect. 3 the hypervolume indicator is formally defined and its properties as a scalarizing functions are discussed and compared to the weighted sum method and the multiobjective gradient descent approach. Section 4 is devoted to the details of the numerical implementation. In particular, a finite element discretization and an iterative accent algorithm using smoothed gradients are presented. Furthermore, the choice of the reference point for the hypervolume scalarization is discussed. In Sect. 5 we consider in a 2 D case study the optimal shape of a rod under tensile load. The article is concluded in Sect. 6.
2 Biobjective shape optimization
In this section, we first provide a general formulation of multiobjective shape optimization problems (Sect. 2.1) and then focus on a particular engineering application, namely the biobjective shape optimization of a ceramic component under tensile load w.r.t. the two objectives mechanical stability and volume (Section 2.2).
2.1 Multiobjective optimization
We consider multiobjective optimization problems occurring in engineering applications and particularly focus on multiobjective shape optimization problems. To keep the exposition general, we denote the set of all admissible shapes by \(\mathcal {O}^{\text {ad}}\) and refer to individual shapes as \(\varOmega \in \mathcal {O}^{\text {ad}}\). Let \(J : \mathcal {O}^{\text {ad}}\rightarrow \mathbb {R}^Q\) be a vector valued objective function comprising Q individual objective functions \(J_i: \mathcal {O}^{\text {ad}}\longrightarrow \mathbb {R}\), \(i=1,\ldots ,Q\) and let \(J(\varOmega )= (J_1(\varOmega ), \ldots , J_Q(\varOmega ))^\top\). Then the multiobjective shape optimization problem is given by
Note that in general there does not exist a solution \(\varOmega ^{*}\in \mathcal {O}^{\text {ad}}\) that minimizes all Q objective functions simultaneously (such a solution would be called ideal solution). Throughout the article we use the Pareto concept of optimality: A solution \(\bar{\varOmega } \in \mathcal {O}^{\text {ad}}\) is called efficient or Pareto optimal, if its objective function vector \(J(\bar{\varOmega })\) can not be improved in one component without deterioration in at least one other component. More precisely, \(\bar{\varOmega }\) is efficient if and only if there does not exist \(\varOmega ' \in \mathcal {O}^{\text {ad}}\) such that \(J(\varOmega ')\leqslant J(\bar{\varOmega })\), i.e., \(J_i(\varOmega ') \le J_i(\bar{\varOmega })\) for all \(i=1,\ldots ,Q\) and \(J(\varOmega ')\ne J(\bar{\varOmega })\). The objective vector \(J(\bar{\varOmega } ) = (J_1(\bar{\varOmega } ), \dots , J_Q(\bar{\varOmega } ))^\top\) of an efficient solution \(\bar{\varOmega }\) is called nondominated point or nondominated outcome vector. The set of all nondominated points is denoted as Pareto front \({\mathcal Y}_{\text {ND}}\subset \mathbb {R}^Q\). An efficient solution \(\bar{\varOmega }\) (respectively a nondominated point \(J(\bar{\varOmega })\)) is called supported efficient (or supported nondominated, respectively) if there is no point \(y\in {\text{conv}}\{J(\varOmega ) :\varOmega \in \mathcal {O}^{\text {ad}}\}\) dominating \(J(\bar{\varOmega })\).
Moreover, an efficient solution \(\bar{\varOmega }\) is called properly efficient in Geoffrion’s sense (Geoffrion 1968) if
A corresponding outcome vector \(J(\bar{\varOmega })\) is called properly nondominated. Let \({\mathcal Y}_{\text {PND}}\) denote the set of all properly nondominated outcome vectors (briefly speaking this is the set of all nondominated outcome vectors that have bounded trade-offs).
For an extensive introduction to multiobjective optimization see, e.g., Steuer (1986); Miettinen (1998); Ehrgott (2005).
2.2 Biobjective optimization of stability and cost
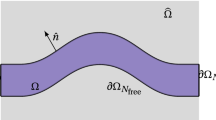
In the biobjective case study described in this paper we consider a ceramic component under tensile load. The component is represented by a two dimensional compact body with Lipschitz boundary, denoted by \(\varOmega \subset \mathbb {R}^2\) (in general, \(\varOmega \subset \mathbb {R}^d,\, d=2,3\)). We assume that the boundary of \(\varOmega\) is composed of three parts, i.e.,
Here, \(\partial \varOmega _D\) is the part where the boundary is fixed, i.e., where Dirichlet conditions are satisfied. The tensile load acts at \(\partial \varOmega _{N_{\text {fixed}}}\), which is also fixed and where Neumann conditions apply. The remaining parts of \(\partial \varOmega\) can be modified during the optimization and are denoted by \(\varOmega _{N_{\text {free}}}\). Furthermore, we assume that all reasonable shapes are contained in a (sufficiently large) bounded open set \(\hat{\varOmega }\subset \mathbb {R}^2\) that satisfies the cone property (see, e.g., Bolten et al. 2015; Doganay et al. 2019). Using this notation, the set of admissible shapes can be defined as
see Fig. 2 for an exemplary setting.
A ceramic component under tensile load behaves according to the linear elasticity theory, see, e.g., Braess (2007). Its deformation under tensile loads is described by the state equation which is an elliptic PDE given by
Here, \(f\in L^2(\varOmega ,\mathbb {R}^2)\) denotes the volume force density and \(g\in L^2(\partial \varOmega _{N_{\text {fixed}}},\mathbb {R}^2)\) denotes the surface loads. Moreover, \(u\in H^1(\varOmega ,\mathbb {R}^2)\) describes the displacement field as the reaction on the given loads, the stress tensor is denoted by \(\sigma \in L^2(\varOmega ,\mathbb {R}^{2\times 2})\), and n(x) is the outward pointing normal vector at \(x\in \partial \varOmega\) (which is defined almost everywhere on \(\partial \varOmega\)). We refer to Doganay et al. (2019) for further details.
Based on this formulation we consider the biobjective optimization of the mechanical stability and the cost of the component. Note that these two objective functions are usually conflicting since larger components tend to have a higher stability. We use the same formulation as Doganay et al. (2019) to assess the mechanical stability of the component via its probability of failure, that is to be minimized. Thus, our first objective function, \(J_1\), is based on a probabilistic Weibull-type model as suggested in Bolten et al. (2015):
Here, m denotes the Weibull module that typically assumes values between 5 and 25, Du denotes the Jacobian matrix of u and \(\sigma _0\) is a positive constant.
The second objective function, \(J_2\), models the material cost which is approximated by the volume of the component \(\varOmega \in \mathcal {O}^{\text {ad}}\), and which is also to be minimized:
All in all, we obtain a biobjective PDE constrained shape optimization problem w.r.t. reliability and cost which is given by
3 Hypervolume scalarization
In this section, general properties of the hypervolume scalarization are discussed. While most results are formulated and exemplified using the biobjective shape optimization problem introduced in Sect. 2, the results in this section on the hypervolume indicator hold for general biobjective optimization problems.
Given a biobjective optimization problem (2.5), the hypervolume indicator measures the hypervolume spanned by an outcome vector \(J(\varOmega )\in \mathbb {R}^2\) (or a set of outcome vectors J(S), respectively) and a predetermined reference point \(r\in \mathbb {R}^2\) (that should be selected such that it is dominated by all considered outcome vectors), see Fig. 1. The value of the hypervolume indicator for a set of solutions \(S\subset \mathcal {O}^{\text {ad}}\) and an appropriate reference point \(r\in \mathbb {R}^2\) can be written as
where \(\mathbb {R}^2_+=\{y\in \mathbb {R}^2 :y_i\ge 0,\, i=1,2\}\) denotes the positive orthant. Note that the hypervolume indicator is only meaningful when the reference point \(r\) is chosen such that \(r_i\ge J_i(\varOmega )\) for \(i=1,2\) and for all \(\varOmega \in S\).
In the case of a single solution \(\varOmega \in \mathcal {O}^{\text {ad}}\) the hypervolume indicator function simplifies to
which corresponds to the area of the hypervolume rectangle defined by the corner points \(J(\varOmega )\) and r.
While in EMO algorithms the hypervolume indicator is mainly used to evaluate the quality of already computed solutions (or solution sets, respectively), it can also be used as an objective function in a scalarization of (2.5) that aims at finding solutions that maximize the dominated hypervolume. For a given reference point \(r :=(r_1, r_2)^\top \in \mathbb {R}^2\), the hypervolume scalarization for (2.5) is formulated as
The constraints \(J_1(\varOmega ) \le r_1\) and \(J_2(\varOmega ) \le r_2\) ensure that \(H(\varOmega )\) is non-negative. They are redundant when all feasible outcome vectors lie below the reference point, i.e., when r is chosen such that \(J(\varOmega )\leqslant r\) for all \(\varOmega \in \mathcal {O}^{\text {ad}}\). If this is not the case, however, these two constraints can not be omitted in general, since also points that are strictly dominated by the reference point have positive hypervolume values and are thus potential candidates for maximizing \(H(\varOmega )\). Note that even in this case it is sufficient to include one of these constraints, since then the other will be automatically satisfied at optimality due to the maximization of the product \(H(\varOmega ) = (r_1 - J_1(\varOmega )) \cdot (r_2 - J_2(\varOmega ))\). Moreover, when problem (3.1) is solved with a steepest ascent algorithm (c.f. Sect. 4.2 below), starting with a shape \(\varOmega ^{(0)}\) such that \(J(\varOmega ^{(0)})< r\) (i.e., \(J_1(\varOmega ^{(0)})<r_1\) and \(J_2(\varOmega ^{(0)})<r_2\)), then the constraints \(J_1(\varOmega ) \le r_1\) and \(J_2(\varOmega ) \le r_2\) will always be satisfied during the course of the algorithm and can hence be omitted. We conclude that while some caution is necessary with regard to the choice of the reference point r, the constraints \(J_1(\varOmega ) \le r_1\) and \(J_2(\varOmega ) \le r_2\) can in most cases be omitted. If not stated otherwise, we will hence assume in the following that the scalarized problem shares the same feasible set as the original problem.
The following result shows that under the above assumptions the hypervolume scalarization (3.1) always generates an efficient solution. This result is not new, however, we include a proof for the sake of completeness.
Theorem 1
An optimal solution of the hypervolume scalarization (3.1) is an efficient solution of the corresponding biobjective optimization problem (2.5).
Proof
Suppose that \(\varOmega ^{*}\in \mathrm{arg max}_{\mathcal {O}^{\text {ad}}} H(\varOmega )\) is not efficient for (2.5). Then there exists a shape \(\varOmega ^{\prime }\in \mathcal {O}^{\text {ad}}\) such that \(J_1(\varOmega ^{\prime }) \le J_1(\varOmega ^{*})\) and \(J_2(\varOmega ^{\prime }) \le J_2(\varOmega ^{*})\), with at least one strict inequality. It follows that
contradicting the assumption that \(\varOmega ^{*}\in \mathrm{arg max}_{\mathcal {O}^{\text{ad}}} H(\varOmega )\). \(\square\)
Note that Theorem 1 also follows directly from the theory of achievement scalarizing functions of which the hypervolume indicator is a special case (see, e.g., Wierzbicki (1986a, 1986b); Miettinen (1998)). Indeed, since \(-H(\varOmega )\) is a strongly increasing function (i.e., \(J(\varOmega )\leqslant J(\varOmega '){\text{ implies that }}-H(\varOmega )< -H(\varOmega ')\)), an optimal solution of \(\max _{\varOmega \in \mathcal {O}^{\text {ad}}} H(\varOmega )=\min _{\varOmega \in \mathcal {O}^{\text {ad}}} -H(\varOmega )\) is efficient for (2.5).
Efficient numerical optimization procedures require gradient information to obtain fast convergence. In this situation, we can take advantage of the fact that the gradient of the hypervolume indicator can be determined from the gradients of the individual objective functions using the chain-rule of differentiation:
Observe that the gradient vector of the hypervolume indicator is a negative weighted sum of the gradients of the individual objective functions.
3.1 Hypervolume scalarization versus weighted sum scalarization
Let \(\lambda =(\lambda _1,\lambda _2)\in \mathbb {R}^2_{+}\) with \((\lambda _1,\lambda _2) \ne (0,0)^\top\) be a given weight vector. Then the weighted sum scalarization of problem (2.5) is given by
Note that the weights are usually normalized such that \(\lambda _1+\lambda _2=1\). We omit this normalization to simplify the notation in the following. Note that this does not affect the properties of the weighted sum scalarization. Note also that under the assumption that the set of feasible outcome vectors is bounded and the reference point in the hypervolume scalarization (3.1) is chosen sufficiently large the feasible sets of the hypervolume scalarization (3.1) and the weighted sum scalarization (3.3) (and the biobjective problem (2.5)) coincide. Thus, both scalarizations share the advantage that the feasible set of the original multiobjective optimization problem is not modified, i.e., no additional constraints have to be added to the problem formulation. However, since the level sets of the hypervolume indicator in the objective space are non-convex, non-supported efficient solutions can be determined using the hypervolume scalarization, which is not possible using the weighted sum scalarization. Formally, the level set of the hypervolume indicator in the objective space at level \(H(\bar{\varOmega })\) is given by
The non-convexity of the hypervolume indicator as a function of the outcome vector \(J(\varOmega )\) is easy to see when rewriting \(H(\varOmega )\) as a quadratic form
Since the quadratic form is negative semi-definite, \(H(\varOmega )\) is a concave function. Thus, the hypervolume scalarization is not limited to supported efficient solutions. Even more so, by interpreting the reference point as a scalarization parameter, every efficient solution can be obtained as an optimal solution of a hypervolume scalarization with an appropriately chosen reference point. Note that the concavity of the level-sets of the hypervolume indicator in the objective space is a direct consequence of a more general result in Beume et al. (2009).
Corollary 1
If \(\varOmega ^*\in \mathcal {O}^{\text {{ad}}}\) is an efficient solution of (2.5), then it is optimal for (3.1) with reference point \(r:=J(\varOmega ^*)\).
Note that this is of rather theoretical interest since this choice of the reference point assumes that the corresponding efficient solution is already known. Practical choices for reference points in the context of biobjective shape optimization are discussed in Sect. 4.3.
In the following, let \(r=(r_1,r_2)^\top\) be a fixed reference point and let \(\bar{\varOmega }\in \mathcal {O}^{\text {ad}}\) be a strictly feasible solution of (3.1), i.e., \(J(\bar{\varOmega })<r\). To interrelate hypervolume scalarizations with weighted sum scalarizations, we analyze the level sets and the gradient of the hypervolume indicator, cf. Emmerich et al. (2014). To simplify the notation in the biobjective case, we denote the two sides of the hypervolume rectangle spanned by \(J(\bar{\varOmega })=(J_1(\bar{\varOmega }), J_2(\bar{\varOmega }))^\top\) and r by \(a(\bar{\varOmega }):=r_1-J_1(\bar{\varOmega })\) and \(b(\bar{\varOmega }):=r_2-J_2(\bar{\varOmega })\), respectively, see Fig. 3. Now the hypervolume induced by \(J(\bar{\varOmega })\) can be rewritten as
Note that this corresponds to the area of the rectangle spanned by the point \(J(\bar{\varOmega })\) and the reference point \(r\) in the biobjective case. Using this notation, the contour line of the hypervolume indicator at the level \(H(\bar{\varOmega })\) can be described by the parameterization \(h_{\bar{\varOmega }}:\mathbb {R}\longrightarrow \mathbb {R}\) given by
see Figure 3 for an illustration. Denoting the contour line by
we can conclude that all points \((J_1, h_{\bar{\varOmega }}(J_1))^\top \in h_{\bar{\varOmega }}\) attain the same hypervolume indicator value as \(J(\bar{\varOmega })\). For example, the two highlighted rectangles in Fig. 3 have the same area, and hence the same hypervolume indicator value.
The derivative of \(h_{\bar{\varOmega }}(J_1)\) w.r.t. \(J_1\) can be computed as
Evaluating this derivative at \(J_1 = J_1(\bar{\varOmega })\) yields
which is the slope of the tangent to the level set of the hypervolume indicator at the point \(J(\bar{\varOmega })\), see again Fig. 3. Note that this slope corresponds to the ratio of the two sides of the hypervolume rectangle, and thus also corresponds to the slope of the diagonal passing through two opposite corners of the current hypervolume rectangle as illustrated in Fig. 3, given by the equation
As can be seen in Fig. 3, the tangent to the level set of the hypervolume indicator at the point \(J(\bar{\varOmega })\) also corresponds to the contour line of the weighted sum scalarization \(W(\varOmega )\) with weights \((\lambda _1,\lambda _2)=(b(\bar{\varOmega }), a(\bar{\varOmega }))\) at this point. This contour line can be described by a function of \(J_1\), similar to (3.6), as
where \(c:=b(\bar{\varOmega })\,J_1(\bar{\varOmega })+ a(\bar{\varOmega })\, J_2(\bar{\varOmega })\) is defined by the point \(J(\bar{\varOmega })\). The corresponding contour line is denoted by
As a consequence, the contour lines of both scalarizations, the hypervolume indicator and the weighted sum function, have the same slope at the point \(J(\bar{\varOmega })\), and hence both scalarizations share the same direction of largest improvement. Indeed, if we consider the gradient \(\nabla H(\bar{\varOmega })\) of the hypervolume indicator at the point \(J(\bar{\varOmega })\) (which is the steepest ascent direction, see (3.2)) we obtain
Similarly, the steepest descent direction for the weighted sum scalarization (3.3) with weights \((\lambda _1,\lambda _2)=(b(\bar{\varOmega }), a(\bar{\varOmega }))\) at the point \(J(\bar{\varOmega })\) can be computed as
Hence, in an iterative algorithm the direction of steepest ascent of the hypervolume indicator (which is to be maximized) corresponds to the direction of steepest descent w.r.t. the weighted sum scalarization (which is to be minimized) with weights \((\lambda _1,\lambda _2)=(b(\bar{\varOmega }), a(\bar{\varOmega }))\). Note that these associated weights are determined by the ratio of the sides of the hypervolume rectangle.
The above analysis implies that if an iterative ascent algorithm for the hypervolume scalarization (3.1) is initialized with a strictly feasible starting solution \(\varOmega ^{(0)}\in \mathcal {O}^{\text {ad}}\), i.e., \(J(\varOmega ^{(0)})<r\), then moving in the direction of steepest ascent ensures that the next iterate \(\varOmega ^{(1)}\) is also strictly feasible irrespective of the step length, i.e., \(J_1(\varOmega ^{(1)})<r_1\) and \(J_2(\varOmega ^{(1)})<r_2\). Hence, the constraints \(J_1(\varOmega ) \le r_1\) and \(J_2(\varOmega ) \le r_2\) can be omitted in (3.1) when starting with a strictly feasible starting solution. Note that, for any strictly feasible solution \(\bar{\varOmega }\in \mathcal {O}^{\text {ad}}\), the side lengths of the hypervolume rectangle \(a(\bar{\varOmega })\) and \(b(\bar{\varOmega })\) correspond to the slackness of the constraints \(J_1(\bar{\varOmega }) \le r_1\) and \(J_2(\bar{\varOmega }) \le r_2\). This is reflected in the gradient direction \(\nabla H(\bar{\varOmega })\) at \(J(\bar{\varOmega })\) that is composed of a weighted sum of the gradients of the individual objective functions \(\nabla J_1(\bar{\varOmega })\) and \(\nabla J_2(\bar{\varOmega })\). The ratio of the side lengths of the hypervolume rectangle defines the relative contribution of \(\nabla J_1(\bar{\varOmega })\) and \(\nabla J_2(\bar{\varOmega })\) to the ascent direction \(\nabla H(\bar{\varOmega })\). If this ratio is very large (very small, respectively), which is the case when one side of the hypervolume rectangle is considerably larger than the other, then the opposite objective function is emphasized in the computation of \(\nabla H(\bar{\varOmega })\).
3.2 Hypervolume scalarization versus MO descent algorithms
Multiobjective gradient descent algorithms were proposed in Fliege and Svaiter (2000); Désidéri (2012); Fliege et al. (2019). In the minimization case, they can be interpreted as iterative optimization processes with search direction
in iteration k with weights \(\omega _1^{(k)},\omega _2^{(k)}\ge 0\). The search direction \(d^{(k)}\) is thus induced by a positive linear combination of the gradients of the individual objective functions with weights \(\omega _1^{(k)},\omega _2^{(k)}\). These weights are chosen adaptively to achieve the steepest descent w.r.t. all objectives in each iteration. This is in contrast to applying a single-objective gradient descent algorithm to the weighted sum scalarization (3.3), in which the weights are predefined and thus fixed throughout all iterations of the optimization procedure. We argue that performing gradient ascent steps w.r.t. the hypervolume indicator is somewhat similar to applying a multiobjective gradient descent algorithm: The weights \(\omega _1^{(k)}=b(\varOmega ^{(k)})\) and \(\omega _2^{(k)}=a(\varOmega ^{(k)})\) of the gradients of the individual objective functions are chosen adaptively, depending on the side lengths of the hypervolume rectangle induced by the current iterate, c.f. (3.7).
While each iterate \(\varOmega ^{(k)}\) in a multiobjective gradient descent algorithm dominates all previous iterates \(\varOmega ^{(k-\ell )}\) for all \(\ell =1,\ldots ,k\), i.e., \(J(\varOmega ^{(k)})\leqslant J(\varOmega ^{(k-\ell )})\), this is in general not the case when applying a single-objective ascent algorithm to the hypervolume scalarization or a single-objective descent algorithm to the weighted sum scalarizazion, respectively. Indeed, only single-objective improvements can be guaranteed with respect to the hypervolume indicator and the weighted sum objective, i.e., \(H(\varOmega ^{(k)})\ge H(\varOmega ^{(k-\ell )})\) and \(\lambda ^\top J(\varOmega ^{(k)}) \le \lambda ^\top J(\varOmega ^{(k-\ell )})\), respectively. This can be seen in Fig. 3 when comparing the dominance cone \(J(\bar{\varOmega })-\mathbb {R}^2_+\) (which contains the image of the next iterate in a multiobjective descent algorithm), the set of improving points for the hypervolume indicator given by \(h_{\bar{\varOmega }}-\mathbb {R}^2_+ = \{y\in \mathbb {R}^2:(r_1-y_1)\cdot (r_2-y_2) \ge H(\bar{\varOmega })\}\), and the set of improving points for the weighted sum objective given by \(w_{\bar{\varOmega }}-\mathbb {R}^2_+ = \{y\in \mathbb {R}^2:\lambda ^\top y \le J(\bar{\varOmega })\}\) (with \(\lambda ^\top =(b(\bar{\varOmega }),a(\bar{\varOmega }))\)). Since the dominance cone \(J(\bar{\varOmega })-\mathbb {R}^2_+\) is a proper subset of the respective sets of improving points, multiobjective gradient descent algorithms are more restrictive regarding the choice of the next iterate. The weighted sum scalarization is in this regard the most flexible approach, allowing for the deterioration of individual objective functions as long as the weighted sum value improves. In this respect, we can say that the hypervolume indicator function compromises between the other two approaches.
3.3 Contour lines of the hypervolume indicator
The regions of the Pareto front which can be attained using a scalarization method are determined by the level sets and contour lines of the scalarizing function. Consider, for example, the contour lines of the weighted sum scalarization (hyperplanes) and the weighted Chebyshev scalarization (hyperboxes with weight-dependent aspect ratio), respectively. While the former is restricted to supported nondominted points, the latter has the potential to determine all nondominated points, including the non-supported ones. The contour lines of the hypervolume indicator for a given reference point \(r\in \mathbb {R}^2\) are illustrated in Fig. 4a. It can be seen that their shape strongly depends on their Hausdorff distance from the reference point. The closer the reference point is to a nondominated outcome vector in at least one component, the more the corresponding contour line resembles the contour line of a weighted \(l_\infty\) function, i.e., a weighted Chebyshev scalarization. On the other hand, the further the reference point is from a nondominated outcome vector (in all components), the more the contour line resembles that of an \(l_1\) function, that is, a weighted sum scalarization with equal weights. More formally, considering again the parameterization of the contour line of the hypervolume indicator w.r.t. \(J_1\), see (3.5), and assuming for now that \(J_1<J_1(\bar{\varOmega })<r_1\), we can see that
This implies that for \(r\rightarrow J(\bar{\varOmega })\) the contour line \(h_{\bar{\varOmega }}\) converges point-wise to a horizontal line passing through r when \(J_1<J_1(\bar{\varOmega })\). By using a parameterization of \(h_{\bar{\varOmega }}\) w.r.t. \(J_2\) it can be shown that the contour line \(h_{\bar{\varOmega }}\) converges point-wise to a vertical line passing through r when \(J_2<J_2(\bar{\varOmega })\).
Similarly, when \(r=(r_1,r_1)^\top\) (i.e., \(r_2=r_1\)) and \(r_1\rightarrow \infty\) we obtain for \(J_1\ne J_1(\bar{\varOmega })\) that
and hence \(h_{\bar{\varOmega }}\) converges point-wise to a line with slope \(-1\) and passing through \(J(\bar{\varOmega })\). The contour lines passing through a given point \(J(\bar{\varOmega })\), that are generated by different reference points, are illustrated in Fig. 4(b).
4 Numerical Implementation
The hypervolume scalarization (3.1) of the biobjective shape optimization problem (2.5) is solved using an iterative ascent algorithm in the framework of a ‘first discretize, then optimize’ approach.
The discretization of the shape optimization problem is based on a finite element approach (see, e.g., Braess (2007)). Consequently, the state Eq. (2.2) and the objective functions given in (2.3) and (2.4) are evaluated on a finite element grid. In this section details of the numerical implementation are presented including the discretization approach using structured finite element grids, the determination of ascent directions for the hypervolume scalarization, and the update scheme for the current shape. Finally, the choice of the reference point is discussed.
4.1 Finite element discretization
The component to be optimized (i.e., the current shape) is discretized via finite elements on a structured grid in the following way. Consider a rectangular domain \(\hat{\varOmega }\) with width \(\hat{\varOmega }_l\) and height \(\hat{\varOmega }_h\) that entirely covers the initial shape \(\varOmega ^{(0)}\) (see Fig. 2 for an illustration). The domain is discretized by a regular triangular grid denoted by \(\hat{T}\) with \(n_x\) and \(n_y\) grid points in x- and y-direction, respectively. The corresponding mesh sizes are given by \(m_x = \hat{\varOmega }_l/(n_x-1)\) and \(m_y = \hat{\varOmega }_h/(n_y-1)\). The mesh sizes should be chosen such that \(m_x\approx m_y\) in order to avoid distorted finite elements. In a next step, as visualized in Fig. 5, the boundary \(\partial \varOmega ^{(0)}\) of the initial shape is superimposed onto the grid and the closest grid points are moved onto the boundary in a controlled way, such that degenerate elements do not occur. More precisely, it is guaranteed that the maximum angle condition (Babuska and Aziz (1976)) is satisfied. The adapted grid is denoted by \(T_0^{\infty }\). The computations are performed only on that part of the grid that represents \(\varOmega ^{(0)}\) which is called the active grid and denoted by \(T_0\), see Fig. 5.
In the iterative optimization process (see Sect. 4.2 for more details) the active grid \(T_{k+1}\) of the next iteration, \(k=0,1,2,\dots\), representing the updated shape \(\varOmega ^{(k+1)}\), is generated by starting again from \(\hat{T}\). Consequently, the connectivity is maintained throughout all iterations. Rather than going through all elements (as required in the first iteration) we now incorporate the information from the previous mesh \(T_{k}^{\infty }\). In the ‘updating procedure’ it is only necessary to iterate over elements in a certain neighborhood of previous boundary elements, and adapt them if necessary.
Note that a complete re-meshing is necessary only when the next iterate \(\varOmega ^{(k+1)}\) differs too much from \(\varOmega ^{(k)}\), which is usually only the case when the update step exceeds the mesh size in at least one grid point. This property and the persistent connectivity lead to a significant speed up compared to standard re-meshing techniques. As stated above, in most iterations the majority of the elements inside the component remain unchanged. This leads to an additional advantage over both standard re-meshing and mesh morphing approaches. In regions where elements are not changed, the entries of the governing PDE are also not changed. Therefore, a full re-assembly of the system matrix and the right hand side is avoided and only entries corresponding to modified elements have to be updated.
In the following, we distinguish between the continuous shape \(\varOmega ^{(k)}\) and its (approximative) representation on the finite element grid. The discretized shape, induced by the active grid \(T_k\), is denoted by \(\varOmega ^{(k)}_{n_x \times n_y}\). This implicates that the gradient of the hypervolume indicator \(\nabla H\) is evaluated w.r.t. the discretized shape, i.e., \(\nabla H(\varOmega ^{(k)}_{n_x \times n_y})\) is defined on the grid points given by \(T_{k}\).
4.2 Iterative ascent algorithm
4.2.1 Ascent direction and update scheme
In the following we develop an iterative update scheme for the biobjective shape optimization problem (2.5). As stated above, the finite element discretization of the component is based on a regular grid, where only the grid points that are close to the boundary of the current shape \(\varOmega ^{(k)}\) are adapted to the boundary of the component. All finite elements that are not adjacent to the boundary of the current shape \(\varOmega ^{(k)}\) remain unchanged and form a subset of the regular grid. Whenever the component is updated, we thus want to modify the boundary points of the component without moving inner or outer grid points. For this purpose we consider the grid points lying on the boundary of the shape \(\varOmega ^{(k)}\), or rather of its finite element representation \(\varOmega ^{(k)}_{n_x \times n_y}\). Since these grid points are induced by the active grid \(T_k\), we call them boundary points and denote them by \(\partial T_k\).
The discretized shape \(\varOmega ^{(k)}_{n_x \times n_y}\) in iteration k is updated by determining a search direction and calculating a step length. For a given search direction \(d^{(k)}\) and step length \(t_k\), we define the update of the component by the expression
The operation \(\oplus\) is defined as follows: First, the boundary points are moved by \(t_k \cdot d^{(k)}\) resulting in
Then \(\partial T_k^{\prime }\) is fitted by cubic splines, resulting in the updated shape \(\varOmega ^{(k+1)}\). Finally, the new active grid \(T_{k+1}\) is generated based on \(\partial \varOmega ^{(k+1)}\) as detailed in Sect. 4.1. This defines \(\varOmega ^{(k+1)}_{n_x \times n_y}\) in (4.1). Note that the boundary points \(\partial T_{k+1}\) of iteration \((k+1)\) do not have to coincide with \(\partial T_k^{\prime }\) since \(T_{k+1}\) is generated based on \(\partial \varOmega ^{(k+1)}\), which is defined by cubic splines.
The search direction \(d^{(k)}\) is computed based on the gradient of the hypervolume indicator function \(\nabla H(\varOmega ^{(k)}_{n_x \times n_y})\). However, due to the discretization \(\nabla H(\varOmega ^{(k)}_{n_x \times n_y})\) is usually largely irregular and needs to be smoothed to avoid zigzagging boundaries and overfitted spline representations of the next iterate. To obtain a smooth deformation field for the boundary points, we follow the approach suggested in Schmidt and Schulz (2009) and use a Dirichlet-to-Neumann map to compute a smoothed gradient.
Let \(\tilde{\nabla } H(\varOmega ^{(k)}_{n_x \times n_y})\) denote the smoothed gradient. Then
denotes its values on the boundary points. See Fig. 6 for a visual comparison of the gradient \(\nabla H(\varOmega ^{(k)}_{n_x \times n_y})\) and the smoothed gradient \(\tilde{\nabla } H(\varOmega ^{(k)}_{n_x \times n_y})\) of an exemplary shape.
The step length \(t_k\) in direction \(d^{(k)}\) is determined according on the Armijo-rule (see, e.g., Geiger and Kanzow 1999; Bazaraa et al. 2006). For given parameters \(\sigma ,\beta \in (0,1)\) we set
The complete iterative ascent algorithm using smoothed gradients is summarized in Algorithm 1. As stopping conditions, an upper bound K on the number of iterations, an upper bound on the number of iterations \(\ell\) in the evaluation of the Armijo rule (4.3), and a lower bound \(\varepsilon\) on the Frobenius norm of the search direction are used.

4.2.2 Re-scaling the search direction
In order to avoid re-meshing operations whenever possible, it is often advantageous to re-scale the search direction such that the gird \(T_{k+1}^{\infty }\) can be computed by performing a simple grid adaption (c.f. Section 4.1). Indeed, when for example for a large gradient (e.g., resulting from large given loads) the step \(t_k = 1\) is not feasible, this leads to numerical problems when implementing Algorithm 1. To avoid such situations, the search direction \(d^{(k)}\) is re-scaled in the following way: First, the norm \(\Vert d^{(k)}_{ij} \Vert _2\) is calculated for all grid points (i, j), \(i=1,\dots ,n_x\) and \(j=1,\dots , n_y\), where \(d^{(k)}_{ij}\) is the entry of \(d^{(k)}\) for grid point (i, j). Since \(d^{(k)}\) is only defined at the boundary points, \(d^{(k)}_{ij}\) is set to zero for grid points (i, j) that are not related to the boundary points. When \(\max _{i,j}\Vert d_{ij} \Vert _2\) is larger than a predefined percentage \(p_{\max }\) of the minimum mesh size \(\min \{m_x, m_y\}\), with \(p_{\max }<1\), then the search direction is re-scaled by the factor \(s(p_{\max })\) given by
By computing a step length \(t_k \in (0,1]\) it is then guaranteed that the boundary points do not move more than the mesh size, and a grid apdation can be performed.
Furthermore, numerical tests have shown that near an efficient solution the search direction \(d^{(k)}\) becomes very small, thus slowing down the potential improvement while the unsmoothed gradient \(\nabla H(\varOmega ^{(k)}_{n_x\times n_y})\) may still be large. Then the search direction is re-scaled when \(\max _{i,j}\Vert d_{ij} \Vert _2\) is less than a given percentage \(p_{\min }\in (0,1)\) of the mesh size. In this case, the search direction is multiplied by \(s(p_{\min })\).
4.2.3 Grid refinement
In order to accelerate the convergence to the Pareto front, it may be useful to start the optimization on a coarse grid and later continue on a finer grid. Since for numerical reasons each update step is restricted to the mesh size, we expect that a coarse grid allows for larger steps in early stages of the optimization procedure. Moreover, the evaluation of objective function values and gradients on the coarse grid is generally faster. On the other hand, with a finer resolution of the grid the accuracy of the approximation of objective function values and gradients is improved. Thus, near an efficient solution large steps are not necessary and a finer grid may result in a better approximation of the shape.
4.3 Choice and variation of the reference point
For the iterative ascent algorithm (Algorithm 1) a feasible starting solution \(\varOmega ^{(0)}_{n_x \times n_y}\) and a reference point \(r\in \mathbb {R}^2\) with \(r>J(\varOmega ^{(0)}_{n_x \times n_y})\) are needed as input. Since in general neither the Pareto front nor efficient shapes are known beforehand, the reference point can only be chosen based on a known feasible shape \(\varOmega ^{(0)}_{n_x \times n_y}\) that may actually be far from the Pareto front. To ensure that the hypervolume scalarization (3.1) is well defined and that the constraints \(J_1(\varOmega ) \le r_1\) and \(J_2(\varOmega ) \le r_2\) are redundant throughout the execution of Algorithm 1 (c.f. Section 3 for a discussion of this issue,) we select the reference point r such that
with positive parameters \(\delta _1\), \(\delta _2 > 0\).
The impact of the reference point on the hypervolume indicator was already discussed in Auger et al. (2009). They derive properties of optimal \(\mu\) distributions depending on the choice of the reference point, i.e., of representative subsets of the Pareto front of cardinality \(\mu\) maximizing the joint hypervolume. Moreover, they derive an explicit lower bound for the reference point guaranteeing that, under appropriate conditions, the extreme solutions are contained in the representation.
In order to take advantage of the fact that, at least theoretically, the complete Pareto front can be generated by varying the reference point in the hypervolume scalarization (3.1) (see Corollary 1), we suggest a systematic approach to approximate the Pareto front of problem (2.5) by repeatedly solving problem (3.1) with different reference points. The ultimate goal is the determination of a Pareto front generating reference set (PFG reference set for short). Let \({\mathcal Y}_{\text {H}}(r)\) denote the optimal outcome vector obtained from solving problem (3.1), and let \({\mathcal Y}_{\text {H}}(R):=\bigcup _{r\in R}{\mathcal Y}_{\text {H}}(r)\) denote the set of all optimal outcome vectors obtained over all reference points in the set \(R\subseteq \mathbb {R}^2\), called reference set.
Definition 1
A set \(R\subseteq \mathbb {R}^2\) is called Pareto front generating (PFG) reference set if and only if \({\mathcal Y}_{\text {ND}}={\mathcal Y}_{\text {H}}(R)\). Moreover, we denote a reference set \(R\subseteq \mathbb {R}^2\) as pPFG reference set, if and only if it is generating the set of properly nondominated outcome vectors, i.e., \({\mathcal Y}_{\text {PND}}={\mathcal Y}_{\text {H}}(R)\).
Note that a PFG reference set always exists since, for example, \(R={\mathcal Y}_{\text {ND}}\) is a valid selection, c.f. Corollary 1. Note also that a PFG reference set may contain redundant reference points that can be omitted without loosing the PFG property.
From a practical point of view, we can not expect to solve the hypervolume scalarization (3.1) to global optimality and thus only aim at an approximation of the Pareto front \({\mathcal Y}_{\text {ND}}\). Towards this end, we suggest to choose the reference set R based on varying values of \(\delta =(\delta _1,\delta _2)>(0,0)\) in (4.5). More precisely, we suggest to set \((\delta _1, \delta _2) = (\xi , \frac{1}{\xi })\) with \(\xi >0\) in (4.5), i.e.,
and set \(R_{\text {H}}:=\{r(\xi )\in \mathbb {R}^2 :\xi >0\}\). This ensures that the starting solution \(\varOmega ^{(0)}_{n_x \times n_y}\) is strictly feasible for the hypervolume scalarization (3.1) for all choices of \(r(\xi )\in R_{\text{H}}\), i.e., \(J(\varOmega ^{(0)}_{n_x \times n_y})<r(\xi )\) for all \(\xi >0\). This implies that \(R_{\text {H}}\subset J(\varOmega ^{(0)}_{n_x \times n_y})+\mathbb {R}^2_>\) with \(\mathbb {R}^2_> = \{y\in \mathbb {R}^2 :y_i> 0,\, i=1,2\}\). Hence, \({\mathcal Y}_{\text {ND}}\cap R_{\text{H}}=\emptyset\), i.e., the Pareto front lies completely ‘below’ the reference set.
For reference points from the reference set \(R_{\text{H}}\) the result of Theorem 1 can be strengthened.
Lemma 1
An optimal solution of the hypervolume scalarization (3.1) w.r.t. a reference point from the set \(R_{\text{H}}\) is a properly efficient solution of the corresponding biobjective optimization problem (2.5).
Proof
Consider an optimal solution of the hypervolume scalarization (3.1) \(y=J(\bar{\varOmega })\in {\mathcal Y}_{\text{H}}(\bar{r})\) for an arbitrary reference point \(\bar{r}\in R_{\text{H}}\). Since \(J(\varOmega ^{(0)}_{n_x \times n_y})<\bar{r}\) we know that for this reference point \(H(\varOmega ^{(0)}_{n_x \times n_y})>0\), and hence also \(H(\bar{\varOmega })>0\). Therefore, the hypervolume rectangle induced by y and \(\bar{r}\) must have positive side lengths \(a(\bar{\varOmega })>0\) and \(b(\bar{\varOmega })>0\). This implies that y is locally optimal for a weighted sum scalarization with weights \(\lambda _1=b(\bar{\varOmega })>0\) and \(\lambda _2=a(\bar{\varOmega })>0\) since this has the same cone of improving directions as the hypervolume indicator in this point (see Sect. 3.1 for a detailed derivation). It follows that \(y\in {\mathcal Y}_{\text {PND}}\). \(\square\)
Note that Lemma 1 is in line with the results of Auger et al. (2009) who showed that, irrespective of the choice of the reference point, nondominated points with unbounded trade-off are not part of what they call ‘optimal \(\mu\) distributions’, that is, of subsets of points on the Pareto front that maximize the joint hypervolume.
Note also that by varying \(\xi >0\) different reference points are obtained that lie along a hyperbola in the objective space, see Fig. 7 for an illustration. Indeed, for two parameter values \(0<\xi _1<\xi _2\) we have that \(r_1(\xi _1)<r_1(\xi _2)\) and \(r_2(\xi _1)>r_2(\xi _2)\). Hence, the hypervolume rectangle spanned by \(J(\varOmega ^{(0)}_{n_x \times n_y})\) and \(r(\xi _1)\) cannot be contained in the hypervolume rectangle spanned by \(J(\varOmega ^{(0)}_{n_x \times n_y})\) and \(r(\xi _2)\) and vice versa. However, for all associated hypervolume rectangles it holds that \(a(\varOmega ^{(0)}_{n_x \times n_y}) \cdot b(\varOmega ^{(0)}_{n_x \times n_y}) = 1\).
While we can not guarantee that the set \(R_{\text{H}}\) is a PFG reference set in general, we argue that the chances are high that the reference set \(R_{\text{H}}\) induces solutions with varying objective values. This is validated by the numerical experiments described in Sect. 5 below. From a theoratical perspective, we argue that at least for convex problems the reference set \(R_{\text{H}}\) is pPFG, i.e., the properly efficient set can be generated by varying the reference points in \(R_{\text{H}}\).
Theorem 2
Suppose that the biobjective optimization problem (2.5) is convex, i.e., all efficient solutions of (2.5) are supported efficient solutions.
Then \({\mathcal Y}_{\text{PND}}={\mathcal Y}_{\text {H}}(R_{\text {H}})\), i.e., \(R_{\text{H}}\) is a pPFG reference set.
Proof
First, recall that Lemma 1 implies that \({\mathcal Y}_{\text{H}}(R_{\text {H}})\subseteq {\mathcal Y}_{\text {PND}}\). Thus, it remains to be shown that \({\mathcal Y}_{\text {PND}}\subseteq {\mathcal Y}_{\text {H}}(R_{\text {H}})\).
Now let \(y=J(\bar{\varOmega })\in {\mathcal Y}_{\text {PND}}\) be properly efficient. Then there exist weights \(\lambda _1,\lambda _2>0\) such that \(\bar{\varOmega }\) is optimal for the associated weighted sum scalarization (3.3), see, e.g., Ehrgott (2005); Geoffrion (1968). Now define a rectangle with sides \(a:=\lambda _2>0\) and \(b:=\lambda _1>0\) and let \(r':=J(\bar{\varOmega })+(a,b)^\top\). It is easy to see that the hypervolume rectangle spanned by \(J(\bar{\varOmega })\) and \(r'\) is precisely the rectangle with side lengths a and b. From the discussion in Sect. 3.1 we can conclude that \(\bar{\varOmega }\) is optimal for the hypervolume scalarization (3.1) with reference point \(r'\) since in this situation the set of improving points w.r.t. the hypervolume indicator is completely contained in that of the weighted sum (which is empty in this case). See Fig. 8 for an illustration of the respective contour lines. Moreover, \(J(\bar{\varOmega })\) is the unique optimal outcome vector of the hypervolume scalarization (3.1) in this case. Since this property only relies on the ratio \(\frac{b}{a}\) of the side lengths of the hypervolume rectangle, the reference point can be moved along the half-line starting at \(J(\bar{\varOmega })\) and passing through \(r'\) until it intersects the set \(R_{\text {H}}\). This intersection point exists and can be determined as the positive solution \(\xi\) of the system
which yields
We obtain two solutions for \(\xi\), namely
Since \(\frac{a}{b}>0\) we have that \((\frac{c^2}{4}+\frac{a}{b})^{\frac{1}{2}}>|\frac{c}{2}|\) and hence exactly one of the two solutions for \(\xi\) is positive, irrespective of the sign of c. This solution yields the sought reference point \(r(\xi )\in R_{\text {H}}\), and we can conclude that \({\mathcal Y}_{\text {PND}}\subseteq {\mathcal Y}_{\text {H}}(R_{\text {H}})\). \(\square\)
Note that even though Theorem 2 is restricted to convex problems, the set \(R_{\text {H}}\) may be pPFG also for non-convex problems. This depends on the degree of non-convexity on one hand, and on the distance of the reference set \(R_{\text {H}}\) from the Pareto front in the objective space on the other hand, where the latter is defined by the image of the starting solution \(J(\varOmega ^{(0)}_{n_x \times n_y})\).
5 Numerical tests
We consider a 2 D test case of a ceramic rod consisting of Beryllium oxide (BeO). The rod is \(0.6\,\text {m}\) long and has a height of \(0.1\,\text {m}\). It is fixed on one side while tensile load is applied on the other side, modeling a horizontal load transfer. On the fixed boundary \(\varOmega _D\) of the rod the displacement field \(u(x)\) is zero, i.e., here Dirichlet boundary conditions hold, c.f. (2.2). The part \(\varOmega _{N_{\text {fixed}}}\) denotes the boundary on which the surface loads \(g\) are applied, i.e., where Neumann boundary conditions hold. The remaining parts of the boundary, denoted by \(\varOmega _{N_{\text {free}}}\), can be modified according to the optimization objectives whereas the boundaries \(\varOmega _D\) and \(\varOmega _{N_{\text {fixed}}}\) are fixed during the optimization. In particular, the corner points cannot be moved. In Figure 2 the rod and the decomposition of its boundary into \(\varOmega _D\), \(\varOmega _{N_{\text {fixed}}}\) and \(\varOmega _{N_{\text {free}}}\) are illustrated.
As we consider the same ceramic material BeO as in Doganay et al. (2019), we use the same material parameter setting in order to evaluate the state Eq. (2.2) and the PoF objective (2.3). In particular, Young’s modulus is set to \(\text {E}=320\,\text {GPa}\), Poisson’s ratio to \(\nu =0.25\), the ultimate tensile strength to \(140\,\text {MPa}\) and the Weibull parameter to \(m=5\). The surface loads, acting on \(\varOmega _{N_{\text {fixed}}}\), are set to \(g=(10^8, 0)^\top \,\text {Pa}\) and the volume force density is set to \(f=(0,1000)^\top \,\text {Pa}\). To speed up the numerical evaluation of the state equation, an improved discretization approach based on regular grids is employed, see Sect. 4.1 for more details and Fig. 9 for an illustration of the considered shape. In contrast to Doganay et al. (2019), volume forces that model, e.g., gravity, are included in the numerical evaluation.
We choose a bent rod as shown in Fig. 2 as the initial shape (i.e., as the starting solution) for the optimization that is implemented using Algorithm 1. Note that this shape is clearly not efficient. Indeed, in this situation the efficient shapes are straight rods of different width, trading off between small probabilities of failure and high volumes on one hand, and high probabilities of failure and low volumes on the other hand. This simple setting has the advantage that the optimization results can be validated and compared with the ‘true’ Pareto front.
The rectangular domain \(\hat{\varOmega }\) that contains all admissible shapes \(\mathcal {O}^{\text {ad}}\) is given by a rectangle of width \(\hat{\varOmega }_l = 0.7\,\text {m}\) and height \(\hat{\varOmega }_h = 0.35\,\text {m}\). The initial shape is placed in the interior of this rectangle. Moreover, the whole setting is slightly rotated so that the boundaries of the initial shape can be represented by interpolating cubic splines. The domain \(\hat{\varOmega }\) is discretized by a triangular grid with \(n_x \times n_y\) grid points as described in Section 4.1. Hereby, we determine the number of grid points such that a prescribed mesh size of \(m_x=m_y \approx 0.02\,\text {m}\) is realized. In our setting, this results in a discretization with \(36\times 18\) grid points, see Figure 9. Note that this shape representation has more degrees of freedom than the B-spline representation in Doganay et al. (2019). This significantly increases the flexibility of our approach.
In the numerical tests reported below, we use the Armijo-rule (4.3) with parameters \(\beta = 0.5\) and \(\sigma = 0.1\). Moreover, the smoothed gradient \(d^{(k)}\) is adaptively scaled such that \(\max _{i,j}\Vert d_{ij}^{(k)}\Vert _2\) is within 10% to 90% of the mesh size, i.e., \(p_{\min }=0.1\) and \(p_{\max }=0.9\) as explained in Sect. 4.2. The optimization process is restricted to \(500\) iterations, i.e., \(K= 500\). To avoid tiny step sizes, the Armijo-rule is restricted to \(30\) iterations, i.e., \(\ell \in \{0,\ldots ,30\}\). Whenever the Armijo rule does not yield a sufficient improvement for reasonable step sizes, the algorithm stops. Moreover, the algorithm stops when the Frobenius norm of the unscaled search direction \(d^{(k)}\) is lower than \(\varepsilon =10^{-10}\).
Twelve exemplary reference points \(r(\xi )\) are selected from the pPFG reference set \(R_{\text {H}}\) (see (4.6)), with \(\xi \in \{ 0.0005, 0.001, 0.0015, \dots , 0.005, 0.006, 0.007\}\). Algorithm 1 is implemented in Python 3.6 and all tests are run under opensuse 15.0 on an IntelCore i7-8700 with 32 GB RAM.
5.1 Results
The twelve optimization runs with varying reference points yield 12 different mutually nondominated outcome vectors. The resulting approximation of the Pareto front is shown in Fig. 10. As was to be expected, the optimized shapes resemble a straight rod with varying thickness. The objective vector of the initial shape \(\varOmega ^{(0)}_{36\times 18}\) is \((18456.28 , 0.06)^\top\), which is actually far form the Pareto front.
Several exemplary shapes are shown in Fig. 10. In addition to the illustration of the respective shapes, the stresses in the direction of the tensile load acting on the finite elements are depicted as arrows at the respective center points. Note that the diagonal pattern of the arrows is due to the rotated (not axis-parallel) grid structure.
It turns out that the iterates evolve similarly for different optimization runs. For about \(50\) iterations the hump of the rod decreases quickly, and the Armijo rule often returns a sufficient improvement already for \(t_k=1\). Thus, the shape converges quickly to a nearly straight joint, however, usually with a wavy boundary, and its probability of failure improves considerably. In later iterations the changes are less visible and the shape converges slowly to a straight joint, the thickness of which depends on the chosen reference point. During the optimization process, the volume decreases only slowly as the wavy boundary gets smoother.
The optimization runs require between \(292\) and \(486\) iterations with one exception: for the reference point \(r(0.0005)\) the optimization process stops at the maximum of \(500\) iterations. In all other cases the algorithm terminated in the Armijo rule.
The solutions from the coarse \(36\times 18\) grid were used as starting solutions on a refined \(71\times 36\) grid with mesh size \(m=0.01\,\text {m}\). Exemplary results for the reference points \(r(0.001)\) and \(r(0.003)\) are shown by red crosses in Fig. 10. The respective starting solutions, which are now evaluated on a \(71\times 36\) grid, are illustrated by red circles in the same Figure. The results are smoother, see Fig. 11, but require significantly more computational time. Nevertheless, in this test case setting the coarse grid approximation obtained already considerably good results, which are not dominated by the corresponding results on the finer grid.
Moreover, numerical tests show that shapes representing very thin or thick straight rods, respectively, induce numerical difficulties due to the fixed boundary parts and, particularly, their corner points. Thick rods suffer from overfitted spline representations of their boundaries. Thin rods, on the other hand, lead to distorted finite elements at the spiky corner points.
6 Conclusion
The hypervolume indicator function is a well suited scalarization approach for multiobjective shape optimization problems, since it does not require an explicit handling of additional constraints. In contrast to the weighted sum approach which shares this advantage it is also capable of computing non-supported efficient solutions. The nonlinear dependency on the individual objective functions is not a critical issue in this context since the individual objective functions are already nonlinear. Furthermore, the gradient of the hypervolume can be easily computed based on the gradients of the objective functions.
We show that for convex problems, a non-trivial reference set generating the set of properly nondominated outcome vectors (pPFG reference set) can be determined without prior knowledge on the Pareto front. We validate the approach at a case study from engineering design where the shape of a horizontal bar under tensile load is to be optimized w.r.t. reliability and cost.
Clearly, there are other possibilities for defining pPFG reference sets. We will test and analyze different choices of reference sets in the future. Moreover, the question if and how non-trivial pPFG reference sets can be defined for non-convex problems – without knowing the Pareto front beforehand – will be analyzed. From an engineering point of view, 3 D shape optimization are still a challenge that needs further attention.
References
Auger A, Bader J, Brockhoff D, Zitzler E (2009) Theory of the hypervolume indicator: optimal \(\mu\)-distributions and the choice of the reference point. In: Proceedings of the 10th ACM SIGEVO workshop on Foundations of genetic algorithms, pages 87–102. ACM
Auger A, Bader J, Brockhoff D, Zitzler E (2012) Hypervolume-based multiobjective optimization: theoretical foundations and practical implications. Theor Comput Sci 425:75–103
Babuska I, Aziz A (1976) On the angle condition in the finite element method. SIAM J Numer Anal 13(2):214226
Bazaraa MS, Sherali HD, Shetty CM (2006) Nonlinear programming – theory and algorithms, 3rd edn. Wiley, NJ
Beume N, Naujoks B, Preuss M, Rudolph G, Wagner T (2009) Effects of 1-greedy \(\cal{S}\) -metric-selection on innumerably large pareto fronts. in lecture notes in computer science. Springer Berlin Heidelberg, Berlin, pp 21–35. https://doi.org/10.1007/978-3-642-01020-0_7
Bolten M, Gottschalk H, Schmitz S (2015) Minimal failure probability for ceramic design via shape control. J Optim Theory Appl 166:983–1001. https://doi.org/10.1007/s10957-014-0621-8
Bolten M, Gottschalk H, Hahn C, Saadi M (2019) Numerical shape optimization to decrease failure probability of ceramic structures. Comput Vis Sci 21:1–10. https://doi.org/10.1007/s00791-019-00315-z
Bowman VJ (1976) On the relationship of the tchebycheff norm and the efficient frontier of multiple826 criteria objectives. in lecture notes in economics and mathematical systems. Springer Berlin Heidelberg, Berlin
Braess D (2007) Finite elements: theory, fast solvers, and applications in solid mechanics. Cambridge University Press, Cambridge. https://doi.org/10.1017/CBO9780511618635
Bringmann K, Friedrich T, Klitzke P (2014) Two-dimensional subset selection for hypervolume and epsilon-indicator. In Proceedings of the 2014 conference on Genetic and evolutionary computation - GECCO’14. ACM Press, p 589–596 https://doi.org/10.1145/2576768.2598276
Bringmann K, Cabello S, Emmerich MTM (2017) Maximum volume subset selection for anchored boxes. https://doi.org/10.4230/LIPICS.SOCG.2017.22
Büsing C, Goetzmann K-S, Matuschke J, Stiller S (2017) Reference points and approximation algorithms in multicriteria discrete optimization. Eur J Op Res 260(3):829–840. https://doi.org/10.1016/j.ejor.2016.05.027
Chirkov DV, Ankudinova AS, Kryukov AE, Cherny SG, Skorospelov VA (2018) Multi-objective shape optimization of a hydraulic turbine runner using efficiency, strength and weight criteria. Struct Multidiscip Optim 58(2):627–640. https://doi.org/10.1007/s00158-018-1914-6
Dandurand B, Wiecek MM (2016) Quadratic scalarization for decomposed multiobjective optimization. OR Spectr 38(4):1071–1096. https://doi.org/10.1007/s00291-016-0453-z
Deb K, Goel T (2002) Multi-objective evolutionary algorithms for engineering shape design. Evolutionary Optimization, volume 48 of International Series in Operations Research and Management Science. Springer, Boston
Désidéri J-A (2012) Multiple-gradient descent algorithm (MGDA) for multiobjective optimization. Comptes Rendus Mathematique 350:313–318. https://doi.org/10.1016/j.crma.2012.03.014
Doganay OT, Hahn C, Gottschalk H, Klamroth K, Schultes J, Stiglmayr M (2019) Gradient based biobjective shape optimization to improve reliability and cost of ceramic components. Optim Eng. https://doi.org/10.1007/s11081-019-09478-7
Ehrgott M (2005) Multicriteria Optimization, 2nd edn. Springer, Berlin Heidelberg
Emmerich M, Deutz A (2014) Time complexity and zeros of the hypervolume indicator gradient field. In O. Schuetze, C. A. Coello Coello, A.-A. Tantar, E. Tantar, P. Bouvry, P. D. Moral, and P. Legrand, editors, EVOLVE - a bridge between probability, set oriented numerics, and evolutionary computation III Springer International Publishing, Heidelberg
Fliege J (2004) Gap-free computation of Pareto-points by quadratic scalarizations. Math Methods Op Res 59:69–89
Fliege J, Svaiter BF (2000) Steepest descent methods for multicriteria optimization. Math Methods Op Res 51(3):479–494. https://doi.org/10.1007/s001860000043
Fliege J, Vaz A, Vicente L (2019) Complexity of gradient descent for multiobjective optimization. Optim Methods Softw 34(5):949–959. https://doi.org/10.1080/10556788.2018.1510928
Freimer M, Yu PL (1976) Some new results on compromise solutions for group decision problems. Manag Sci 22(6):688–693. https://doi.org/10.1287/mnsc.22.6.688
Geiger C, Kanzow C (1999) Numerische Verfahren zur Lösung unrestringierter Optimierungsaufgaben. Springer, US
Geoffrion AM (1968) Proper efficiency and the theory of vector maximization. J Math Anal Appl 22(3):618–630
Guerreiro AP, Fonseca CM (2020) An analysis of the hypervolume sharpe-ratio indicator. Eur J Op Res 283(2):614–629. https://doi.org/10.1016/j.ejor.2019.11.023
Guerreiro AP, Fonseca CM, Paquete L (2016) Greedy hypervolume subset selection in low dimensions. Evolut Comput 24(3):521–544. https://doi.org/10.1162/EVCO_a_00188
Haslinger J, Mäkinen RAE (2003) Introduction to shape optimization. Society for Industrial and Applied Mathematics, US
Hernandez VAS, Schütze O, Wang H, Deutz A, Emmerich M (2018) The set-based hypervolume newton method for bi-objective optimization. IEEE Transactions on Cybernetics, pages 1–11, https://doi.org/10.1109/tcyb.2018.2885974
Iapichino L, Ulbrich S, Volkwein S (2017) Multiobjective PDE-constrained optimization using the reduced-basis method. Adv Comput Math 43(5):945–972. https://doi.org/10.1007/s10444-016-9512-x
Kuhn T, Fonseca CM, Paquete L, Ruzika S, Duarte MM, Figueira JR (2016) Hypervolume subset selection in two dimensions: formulations and algorithms. Evolut Comput 24(3):411–425. https://doi.org/10.1162/evco_a_00157
Miettinen K (1998) Nonlinear multiobjective optimization. Springer, US
Miettinen K, Mäkelä MM (2002) On scalarizing functions in multiobjective optimization. OR Spect 24:193–213
Schmidt S, Schulz V (2009) Impulse response approximations of discrete shape hessians with application in cfd. SIAM J Control Optim 48(4):2562–2580. https://doi.org/10.1137/080719844
Schulze B, Stiglmayr M, Willems D, Fonseca CM, Paquete L, Ruzika S (2020) On the biobjective cardinality constrained knapsack problem – approximating the hypervolume by quadratic scalarizations. Math Methods Op Res. https://doi.org/10.1007/s00186-020-00702-0
Steuer RE (1986) Multiple criteria optimization: theory computation and application. John Wiley, New York
Touré C, Hansen N, Auger A, Brockhoff D (2019) Uncrowded hypervolume improvement. In Proceedings of the Genetic and Evolutionary Computation Conference on - GECCO’19. ACM Press, NY. doi: https://doi.org/10.1145/3321707.3321852
Weibull W (1939) A statistical theory of the strength of materials, volume 151 of Ingeniörsvetenskapsakedemiens Handlingar. Generalstabens Litografiska Anst. Förlag, Sweden
Wierzbicki AP (1986a) On the completeness and constructiveness of parametric characterizations to vector optimization problems. OR-Spektrum 8(2):73–87. https://doi.org/10.1007/bf01719738
Wierzbicki AP (1986b) A methodological approach to comparing parametric characterizations of efficient solutions in Lecture Notes in Economics and Mathematical Systems. Springer, Berlin Heidelberg, Berlin DOI: https://doi.org/10.1007/978-3-662-02473-7_4
Yang K, Emmerich M, Deutz A, Bäck T (2019) Efficient computation of expected hypervolume improvement using box decomposition algorithms. J Global Optim 75(1):3–34. https://doi.org/10.1007/s10898-019-00798-7
Yu PL (1973) A class of solutions for group decision problems. Manag Sci 19(8):936–946. https://doi.org/10.1287/mnsc.19.8.936
Zitzler E, Thiele L (1999) Multiobjective evolutionary algorithms: a comparative case study and the strength Pareto approach. IEEE Transact Evolut Comput 3(4):257–271
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
This work was supported by the federal ministry of research and education (BMBF, Grant-No. 05M18PXA) as a part of the GiVEN consortium.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Schultes, J., Stiglmayr, M., Klamroth, K. et al. Hypervolume scalarization for shape optimization to improve reliability and cost of ceramic components. Optim Eng 22, 1203–1231 (2021). https://doi.org/10.1007/s11081-020-09586-9
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11081-020-09586-9