Nonlinear optimization of district heating networks

Abstract

We develop a complementarity-constrained nonlinear optimization model for the time-dependent control of district heating networks. The main physical aspects of water and heat flow in these networks are governed by nonlinear and hyperbolic 1d partial differential equations. In addition, a pooling-type mixing model is required at the nodes of the network to treat the mixing of different water temperatures. This mixing model can be recast using suitable complementarity constraints. The resulting problem is a mathematical program with complementarity constraints subject to nonlinear partial differential equations describing the physics. In order to obtain a tractable problem, we apply suitable discretizations in space and time, resulting in a finite-dimensional optimization problem with complementarity constraints for which we develop a suitable reformulation with improved constraint regularity. Moreover, we propose an instantaneous control approach for the discretized problem, discuss practically relevant penalty formulations, and present preprocessing techniques that are used to simplify the mixing model at the nodes of the network. Finally, we use all these techniques to solve realistic instances. Our numerical results show the applicability of our techniques in practice.

1 Introduction

Many countries in the world are striving to make a transition towards an energy system that is mainly based on using energy from renewable sources like wind and solar power, complemented by classical energy sources like gas, oil, coal, or waste incineration. The increasing use of highly fluctuating renewable energy sources leads to many challenging problems from the engineering, mathematical, and economic point of view. A key to the success of this energy transition is the efficient and intelligent coupling of the energy resources and the optimal operation of the energy networks and energy storage. In this direction, district heating networks play an important role, since they can be used as energy storage, e.g., to balance fluctuations at the electricity exchange. To this end, district heating networks need to be operated efficiently so that no unnecessary energy is used and, on the other hand, security of supply should not be compromised. This is a hard task since uncertainties of the heat demand of households need to be considered and because the physics-based time delays in these networks make it difficult to react to changes in short periods of time.

To make the described intelligent use of district heating networks possible, one needs (i) a proper mathematical model of the network as well as fast and stable (ii) simulation and (iii) optimization techniques. In this paper, we develop a continuous optimization model for the short-term optimal operation of a district heating network. To this end, we assume that the heat demand of the households is given and set up a nonlinear optimization model (NLP) for the control of the heat supply and the pressure control of the network. The building blocks of the entire model are nonlinear models of the households, where thermal energy is withdrawn, the network depot, in which the heat is supplied to the network and the pressure is controlled, and a model of the transport network itself.

The model of the transport network is governed by two main mathematical components; a system of one-dimensional (1d) nonlinear hyperbolic partial differential equations (PDEs) to model the relations of mass flows, water pressure, and temperature in a pipe over time, and a system of algebraic equations that is used at every node of the network to model mass conservation, pressure continuity, and the mixing of water temperatures. The last aspect is very challenging since these mixing models are genuinely nonsmooth due to their dependence on flow directions, which are part of the solution of the PDE and not known a priori. To avoid integer-valued variables, we develop a mixing model using complementarity constraints. In summary, we consider a PDE-constrained nonlinear mathematical program with complementarity constraints (MPCC), which is a highly challenging class of optimization problems; see, e.g., Luo et al. (1996).

Somehow surprisingly, there is not much literature about the mathematical optimization of district heating networks. A branch of applied publications focuses on specific case studies. For instance, in Pirouti et al. (2013), a case study for a simplified model of a district heating project in South Wales is carried out. The focus is more on an economic analysis than on mathematical and physical modeling or optimization techniques. The resulting problems are solved by a linear solver invoked in a sequential linear programming approach. A more general discussion about the technology and potentials of district heating networks is presented in Rezaie and Rosen (2012). In Schweiger et al. (2017), the authors discuss different discrete and continuous optimization problems. As in our contribution, the authors start with a PDE-constrained optimization problem and apply the first-discretize-then-optimize approach yielding a finite-dimensional problem that is then solved. Energy storage or storage tanks combined with district heating networks are discussed in Colella et al. (2011), Verda and Colella (2011) and the impact of load variations and the integration of solar energy is considered in Hassine and Eicker (2013). The design of district heating networks for stationary mathematical models is carried out in Roland and Schmidt (2020), Bordin et al. (2016), as well as Dorfner and Hamacher (2014). In contrast to the mid- to long-term planning problems addressed in these papers, in Sandou et al. (2005), the authors consider a model predictive control (MPC) approach for computing a good operational control of a network for a given design. The resulting models are continuous nonlinear problems that need to be solved in every iteration of the MPC loop. A related approach is discussed in Verrilli et al. (2017), where an MPC control is computed for a district heating system with thermal energy storage and flexible loads. Numerical simulation of district heating networks using a local time stepping method is studied in Borsche et al. (2018) and model order reduction techniques for the hyperbolic equations in district heating networks are discussed in Rein et al. (2019b) or Rein et al. (2018), Rein et al. (2019a). In the last two papers, however, no optimization tasks are considered.

As discussed above, a very important aspect of district heating network models is the mixing of different water temperatures at the nodes of the network. Since the models are similar, related literature can also be found in the field of optimization for gas transport networks; cf., e.g., van der Hoeven (2004), Schmidt et al. (2015), Geißler et al. (2018), Schmidt et al. (2016), Geißler et al. (2015), Hante and Schmidt (2019).

Our contribution is to consider the optimization of district heating networks at a great level of detail and physical accuracy; see Sect. 2 for our modeling approach that includes both 1d nonlinear PDEs and mixing models. In order to obtain tractable optimization problems, we present tailored discretizations of the PDEs in space and time in Sect. 3 and also provide different equivalent formulations for the nodal mixing conditions; see Sect. 4. In Sect. 5, we present problem-specific optimization techniques that enable us to solve instances on realistic networks with reasonable space and time discretizations. To be more specific, we set up an instantaneous control approach that can both be used stand-alone and as a procedure for computing initial values of good quality for the problem on the entire time horizon. Additionally, we derive suitable penalty formulations of the problem that render the instances numerically more tractable. Moreover, we present an easy-but-useful preprocessing technique to decide flow directions in advance so that the amount of nonsmoothness and the number of complementarity constraints for modeling the nodal mixing conditions is reduced. The described techniques are then used to solve realistic instances in Sect. 6. Finally, we close the paper with a conclusion and some comments on possible directions of future work in Sect. 7.

2 Modeling

We use a connected and directed graph ${G}= ({V}, {A})$ to model the district heating network. The network consists of

• a forward-flow part, which provides the consumers with hot water;

• consumers, that use the hot water for heating;

• a backward-flow part, which transports the cooled water back to the depot;

• and the depot, where the heating of the cooled water takes place.

See Fig. 1 for a schematic district heating network.

The nodes ${V}= {V}_{\text {ff}}\cup {V}_{\text {bf}}$ are the disjoint union of nodes ${V}_{\text {ff}}$ of the forward-flow part and nodes ${V}_{\text {bf}}$ of the backward-flow part of the network. The arcs ${A}$ are divided into forward-flow arcs ${A}_{\text {ff}}$, backward-flow arcs ${A}_{\text {bf}}$, consumer arcs ${A}_{\text {c}}$, and the depot arc $a_{\text {d}}$ of the district heating network provider. Therefore, ${A}= {A}_{\text {ff}}\cup {A}_{\text {bf}}\cup {A}_{\text {c}}\cup \{a_{\text {d}}\}$ and we have

$$\begin{aligned} a= (u, v) \in {A}_{\text {ff}}&\implies u\in {V}_{\text {ff}}, \ v\in {V}_{\text {ff}},\\ a= (u, v) \in {A}_{\text {bf}}&\implies u\in {V}_{\text {bf}}, \ v\in {V}_{\text {bf}},\\ a= (u, v) \in {A}_{\text {c}}&\implies u\in {V}_{\text {ff}}, \ v\in {V}_{\text {bf}},\\ a_{\text {d}}= (u, v)&\implies u\in {V}_{\text {bf}}, \ v\in {V}_{\text {ff}}. \end{aligned}$$

We optimize the district heating network in the time horizon $\mathcal {T}:=[0, T]$ with predefined final time $T> 0$. In what follows, we introduce mathematical models for the different parts of the network; namely pipes, nodes, consumers, and the depot of the network provider. After that, we introduce bounds for some of the quantities and state the objective function. To conclude this section, we summarize the parts to obtain a complete model of the entire district heating network.

Fig. 1

A schematic district heating network: forward-flow arcs are plotted in solid black, backward-flow arcs in dashed blue, consumers in dotted violet, and the depot in dashed-dotted red

2.1 Pipe modeling

We use the 1d Euler equations to model the physics of hot water flow in the pipe network (Borsche et al. 2018; Rein et al. 2018; Köcher 2000). In what follows, we use $x \in [0, L_a]$ to denote the spatial coordinate, with $L_a$ being the length of pipe $a\in {A}_{\text {ff}}\cup {A}_{\text {bf}}$. The continuity equation then is given by

$$\begin{aligned} \frac{\partial \rho _a}{\partial t}(x,t) + \frac{\partial (\rho _av_a)}{\partial x}(x,t) = 0, \quad a\in {A}_{\text {ff}}\cup {A}_{\text {bf}}. \end{aligned}$$

(1)

The 1d momentum equation for compressible fluids in cylindrical pipes has the form

$$\begin{aligned} \begin{aligned} \frac{\partial (\rho _av_a)}{\partial t}(x,t) &+& \frac{\partial p_a}{\partial x}(x,t) + \frac{\partial (\rho _av^2_a)}{\partial x}(x,t) \quad \\ &&+\, g\rho _a(x,t) h'_a+ \lambda _a\frac{|{v_a}| v_a\rho _a}{2D_a}(x,t)&= 0, \quad a\in {A}_{\text {ff}}\cup {A}_{\text {bf}}; \end{aligned} \end{aligned}$$

(2)

see, e.g., (Schmidt et al. 2015; Mehrmann et al. 2018).

Here and in what follows, $\rho _a$, $p_a$, and $v_a$ denote the density, pressure, and velocity of the water in pipe $a$. Furthermore, $D_a$ is the diameter and $h'_a$ is the slope of pipe $a$, which we assume to be constant. The gravitational acceleration is denoted by g. The friction factor $\lambda _a$ for turbulent flow is modeled by the flow-independent law of Nikuradse (see, e.g., Fügenschuh et al. 2015), i.e.,

$$\begin{aligned} \lambda _a= \left( 2 \log _{10} \left( \frac{D_a}{k_a} \right) + 1.138 \right) ^{-2}, \quad a\in {A}_{\text {ff}}\cup {A}_{\text {bf}}, \end{aligned}$$

where $k_a$ is the roughness of the inner pipe wall. We are aware that there are also other empirical models of the friction factor for the turbulent case, which might also render $\lambda$ being dependent on x and t. Moreover, there is Hagen–Poiseuille’s exact law for laminar flow; see, e.g., Fügenschuh et al. (2015) and the references therein. For the ease of presentation, we restrict ourselves to the law of Nikuradse, which only depends on the data of the pipe. However, other models can in principle also be incorporated. For a list of all parameters and variables of the model see Table 1, where we also distinguish between directly controllable variables at the depot and physical state variables in the network.

Table 1 Controllable variables at the depot (top), physical state variables in the network (mid), and given parameters (bottom) of the district heating network model

In the considered setting it is well-known that incompressibility leads to constant velocity in the pipe. We briefly give the derivation here for completeness. Since we assume that the water is incompressible, i.e.,

$$\begin{aligned} \frac{\partial \rho _a}{\partial t}(x,t) + v_a(x,t) \frac{\partial \rho _a}{\partial x}(x,t) = 0,\quad a\in {A}_{\text {ff}}\cup {A}_{\text {bf}}; \end{aligned}$$

(3)

see, e.g., Marsden and Chorin (1993) for details on fluid flow modeling, we can rewrite the continuity Eq. (1) as

$$\begin{aligned} 0&= \frac{\partial \rho _a}{\partial t}(x,t) + \frac{\partial (\rho _av_a)}{\partial x}(x,t)\\&= \frac{\partial \rho _a}{\partial t}(x,t) + \rho _a\frac{\partial v_a}{\partial x}(x,t) + v_a\frac{\partial \rho _a}{\partial x}(x,t)\\&= \rho _a\frac{\partial v_a}{\partial x}(x,t). \end{aligned}$$

Since the density $\rho _a(x, t)$ is always positive, we can divide by it and obtain

$$\begin{aligned} \frac{\partial v_a}{\partial x}(x,t) = 0. \end{aligned}$$

Using these consequences of incompressibility, the momentum Eq. (2) simplifies to

$$\begin{aligned}&\frac{\partial (\rho _av_a)}{\partial t}(x,t) + \frac{\partial (\rho _av^2_a)}{\partial x}(x,t)\\& = \rho _a\frac{\partial v_a}{\partial t}(x,t) + v_a\frac{\partial \rho _a}{\partial t}(x,t) + (\rho _av_a) \frac{\partial v_a}{\partial x}(x,t) + v_a\frac{\partial (\rho _av_a)}{\partial x}(x,t)\\&= \rho _a\frac{\partial v_a}{\partial t}(x,t) + v_a\left( \frac{\partial \rho _a}{\partial t}(x,t) + \frac{\partial (\rho _av_a)}{\partial x}(x,t)\right) \\&= \rho _a\frac{\partial v_a}{\partial t}(x,t) \end{aligned}$$

and we thus obtain the simplified 1d system of incompressible Euler equations

$$\begin{aligned}&\frac{\partial v_a}{\partial x}(x,t) = 0, \quad a\in {A}_{\text {ff}}\cup {A}_{\text {bf}}, \end{aligned}$$

(4a)

$$\begin{aligned}\rho _a(x,t) \frac{\partial v_a}{\partial t}(x,t) &+& \frac{\partial p_a}{\partial x}(x,t) + g\rho _a(x,t) h'_a\quad \nonumber \\\quad &+&\, \lambda _a\frac{|{v_a}| v_a\rho _a}{2D_a}(x,t) = 0, \quad a\in {A}_{\text {ff}}\cup {A}_{\text {bf}}, \end{aligned}$$

(4b)

that we use for setting up our optimization problem.

It should be noted that (4a) implies constant velocity in the pipe, i.e., $v_{a}(x,t) = v_{a}(t)$ for all $x \in [0, L_a]$.

The thermal energy equation for each pipe $a\in {A}_{\text {ff}}\cup {A}_{\text {bf}}$ is given by

$$\begin{aligned} \frac{\partial T_a}{\partial t}(x,t) + v_a(t) \frac{\partial T_a}{\partial x}(x,t) + \frac{4 U_a}{c_{\mathrm {p}}\rho _a(x,t) D_a}(T_a(x,t)-T_0) = 0, \quad a\in {A}_{\text {ff}}\cup {A}_{\text {bf}}; \end{aligned}$$

(5)

see Sandou et al. (2005); Borsche et al. (2018); Rein et al. (2018). In (5), $T_a$ describes the water temperature, $U_a$ is the heat transfer coefficient of the pipe’s wall, $c_{\mathrm {p}}$ is the specific heat capacity of water, and $T_0$ is the temperature in the environment surrounding the pipe.

To close the system, one finally needs initial and boundary conditions as well as an equation of state. In the literature one can find formulas for the density of water depending on the temperature; see, e.g., Köcher (2000). Since we make the incompressibility assumption (3), in the context of our optimization model, we assume as another simplification that the density of the water is constant, i.e., $\rho _a(x, t) = \rho$.

This assumption allows us to rewrite the momentum Eq. (4b) as follows:

$$\begin{aligned} \frac{\partial p_a}{\partial x}(x,t) = - \rho \frac{\partial v_a}{\partial t}(t) - g\rho h'_a- \lambda _a\frac{|{v_a}| v_a\rho }{2D_a}(t), \quad a\in {A}_{\text {ff}}\cup {A}_{\text {bf}}. \end{aligned}$$

Since the right-hand side does not depend on the spatial coordinate x, the pressure $p_a(x, t)$ is linear in x. Thus, it holds that

$$\begin{aligned} \frac{p_a(L_a,t) - p_a(0,t)}{L_a} = - \rho \frac{\partial v_a}{\partial t}(t) - g\rho h'_a- \lambda _a\frac{|{v_a}| v_a\rho }{2D_a}(t), \quad a\in {A}_{\text {ff}}\cup {A}_{\text {bf}}. \end{aligned}$$

(6)

In this subsection, we have presented a simplified model of the 1d compressible Euler equations for the description of the pipe flow. More sophisticated models, or even complete hierarchies of models for example those constructed in gas flow (Domschke et al. 2017), should be used for detailed simulation methods or the analysis of the flow. However, in the context of our optimization methods, already the discussed modeling level presents a mathematical and computational challenge.

2.2 Nodal coupling equations

In this subsection, we expand our network model by suitable coupling conditions on the nodes for mass flow, pressure, and temperature. These conditions are modeled by algebraic equations.

The mass balance equation for each node $u\in {V}$ is described by

$$\begin{aligned} \sum _{a\in \delta ^{\text {in}}(u)} q_a(t) = \sum _{a\in \delta ^{\text {out}}(u)} q_a(t), \quad u\in {V},\, t \in \mathcal {T}, \end{aligned}$$

(7)

where $q_a= A_a\rho v_a$ denotes the mass flow of pipe $a$ with cross-sectional area $A_a=\pi (D_a/ 2)^2$. Here and in what follows, we use the standard $\delta$-notation, i.e., we define

$$\begin{aligned} \delta ^{\text {out}}(u)&:=\{a\in {A}:\exists v\text { with } a= (u, v)\}, \\ \delta ^{\text {in}}(u)&:=\{a\in {A}:\exists v\text { with }a= (v, u)\}, \end{aligned}$$

and $\delta (u) :=\delta ^{\text {out}}(u) \cup \delta ^{\text {in}}(u)$. Note that (7) implies that we have no in- and outflow to or from the network.

The pressure continuity equations for each node are given by

$$\begin{aligned} p_u(t)&= p_a(0, t), \quad u\in {V}, \, a\in \delta ^{\text {out}}(u),\, t \in \mathcal {T}, \end{aligned}$$

(8a)

$$\begin{aligned} p_u(t)&= p_a(L_a, t), \quad u\in {V}, \, a\in \delta ^{\text {in}}(u),\, t \in \mathcal {T}, \end{aligned}$$

(8b)

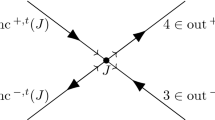
where $p_u(t)$ denotes the pressure at node $u$; see Fig. 2 for an illustration.

Fig. 2

Pressure continuity at node u

We also need to introduce temperature mixing equations to describe the behavior of the water temperature in the nodes, where water of different temperatures is mixed. Since the mixing model depends on the flow directions, we define the inflow and outflow arcs of a node $u$ at a given time $t \in \mathcal {T}$ as

$$\begin{aligned} \mathcal {I}(u, t)&:=\{a\in \delta ^{\text {in}}(u):v_a(t) \ge 0\} \cup \{a\in \delta ^{\text {out}}(u):v_a(t) \le 0\},&u\in {V},\, t \in \mathcal {T}, \\ \mathcal {O}(u, t)&:=\{a\in \delta ^{\text {in}}(u):v_a(t) < 0\} \cup \{a\in \delta ^{\text {out}}(u):v_a(t) > 0\},&u\in {V},\, t \in \mathcal {T}. \end{aligned}$$

The temperature mixing equations for each node are modeled as

$$\begin{aligned} T_u(t)&= \frac{\sum _{a\in \mathcal {I}(u, t)} |{q_a(t)}| c_{\mathrm {p}}T_{a:u}(t)}{\sum _{a\in \mathcal {I}(u, t)} |{q_a(t)}| c_{\mathrm {p}}},&u\in {V},\, t \in \mathcal {T}, \end{aligned}$$

(9a)

$$\begin{aligned} T_u(t)&= T_{a:u}(t),&u\in {V}, \ a\in \mathcal {O}(u, t),\, t \in \mathcal {T}, \end{aligned}$$

(9b)

where $T_u(t)$denotes the mixed water temperature at node $u$ and where we use the notation

$$\begin{aligned} T_{a:u}(t) :={\left\{ \begin{array}{ll} T_a(0, t), &{} u\in {V}, \ a\in \delta ^{\text {out}}(u),\, t \in \mathcal {T},\\ T_a(L_a, t), &{} u\in {V}, \ a\in \delta ^{\text {in}}(u),\, t \in \mathcal {T}; \end{array}\right. } \end{aligned}$$

see, e.g., Schmidt et al. (2015, 2016); Hante and Schmidt (2019), where a similar model is considered for mixing effects in natural gas transport networks.

Equation (9a) can be derived from the conservation of energy if the specific heat capacities in (9) are independent of the water temperature. Since we consider the mixing of water only, the additional assumption that all heat capacities are the same is appropriate. Using this, (9) can be simplified to

$$\begin{aligned} T_u(t)&= \frac{\sum _{a\in \mathcal {I}(u, t)} |{q_a(t)}| T_{a:u}(t)}{\sum _{a\in \mathcal {I}(u, t)} |{q_a(t)}|},&u\in {V},\, t \in \mathcal {T}, \end{aligned}$$

(10a)

$$\begin{aligned} T_u(t)&= T_{a:u}(t),&u\in {V}, \ a\in \mathcal {O}(u, t),\, t \in \mathcal {T}. \end{aligned}$$

(10b)

Obviously, the discussed mixing model is only defined at nodes $u$ with inflow, i.e., if

$$\begin{aligned} \sum _{a\in \mathcal {I}(u, t)} |{q_a(t)}| > 0. \end{aligned}$$

Although zero flows in district heating networks are rather unusual (which also legitimates the assumption above) in typical situations, they might appear in special situations such as during maintenance works.

Note further that the mixing model in (10) cannot be used directly in an optimization context because the sets $\mathcal {I}(u, t)$ and $\mathcal {O}(u, t)$ depend on the solution and are thus not known a priori. In Sects. 4.1 and 4.2, we present a reformulation of the mixing model that deals with this difficulty.

2.3 Consumer and depot models

Consumers at arcs $a= (u, v) \in {A}_{\text {c}}$ are modeled by

$$\begin{aligned} v_a(t)&\ge 0,&t \in \mathcal {T}, \end{aligned}$$

(11a)

$$\begin{aligned} P_a(t)&= q_a(t) c_{\mathrm {p}}\left( T_{a:u}(t) - T_{a:v}(t)\right) ,&t \in \mathcal {T}, \end{aligned}$$

(11b)

$$\begin{aligned} T_{a:v}(t)&= T^{\text {bf}},&t \in \mathcal {T}, \end{aligned}$$

(11c)

$$\begin{aligned} T_{a:u}(t)&\ge T^{\text {ff}}_a,&t \in \mathcal {T}, \end{aligned}$$

(11d)

$$\begin{aligned} p_{a:v}(t)&\le p_{a:u}(t),&t \in \mathcal {T}, \end{aligned}$$

(11e)

where $P_a(t)$ is the given power consumption of the consumer $a\in {A}_{\text {c}}$, $T^{\text {bf}}$ is the contractually agreed temperature of the water that flows into the backward-flow network, and $T^{\text {ff}}_a$ is the minimum inlet water temperature of the consumer $a\in {A}_{\text {c}}$. Later in our numerical experiments, we will relax the equality constraint (11c) to $T_{a:v}(t) \in [T^{\text {bf}}- \varepsilon , T^{\text {bf}}+ \varepsilon ]$ for a small $\varepsilon > 0$, since this leads to a significantly improved convergence behavior of the tested solvers in our numerical experiments.

The depot at arc $a= a_{\text {d}}= (u,v)$ is modeled by

$$\begin{aligned} v_{a}(t)&\ge 0,&t \in \mathcal {T}, \end{aligned}$$

(12a)

$$\begin{aligned} p_u(t)&= p_\mathrm {s},&t \in \mathcal {T}, \end{aligned}$$

(12b)

$$\begin{aligned} P_{\mathrm {p}}(t)&= \frac{q_a(t)}{\rho } \left( p_{a:v}(t) - p_{a:u}(t)\right) ,&t \in \mathcal {T}, \end{aligned}$$

(12c)

$$\begin{aligned} P_{\mathrm {w}}(t) + P_{\mathrm {g}}(t)&= q_a(t) c_{\mathrm {p}}\left( T_{a:v}(t) - T_{a:u}(t)\right) ,&t \in \mathcal {T}, \end{aligned}$$

(12d)

$$\begin{aligned} \left|\frac{\partial P_{\mathrm {w}}}{\partial t}(t)\right|&\le \xi _P,&t \in \mathcal {T}, \end{aligned}$$

(12e)

$$\begin{aligned} \left|\frac{\partial T_{a:v}}{\partial t}(t)\right|&\le \xi _T,&t \in \mathcal {T}, \end{aligned}$$

(12f)

where $p_\mathrm {s}$ is the so-called stagnation pressure of the network. Since all other physical and technical equations of the model are stated in pressure differences, the fixation of one pressure value leads to unique pressure values everywhere in the network, which is the reason for introducing the stagnation pressure. In our implementation, we however will allow a variation in an interval $p_u(t) \in [p_\mathrm {s}- \varepsilon , p_\mathrm {s}+ \varepsilon ]$ instead; cf. the relaxation of the backward-flow temperature constraint (11c) above. The power to run the pumps to realize a pressure increase in the depot of the district heating network provider is denoted by $P_{\mathrm {p}}(t)$. A temperature gain is obtained by thermal power production in the depot. The corresponding Eq. (12d) is similar to the power consumption Eq. (11b) for consumers, where $P_{\mathrm {w}}(t)$ and $P_{\mathrm {g}}(t)$ describe the thermal power produced by waste incineration and gas combustion, respectively. Finally, (12e) and (12f) bound the change over time of the power from waste incineration as well as the change over time of the depot’s outflow temperature.

2.4 Bounds, objective function, and model summary

The different variables of the network that are used in the model are subject to the following bounds for all $t \in \mathcal {T}$,

$$\begin{aligned} p_u(t)&\in [p_u^-,p_u^+], \quad T_u(t) \in [T_u^-,T_u^+], \quad u\in {V}, \end{aligned}$$

(13a)

$$\begin{aligned} P_{\mathrm {w}}(t)&\in [0,P_{\mathrm {w}}^+], \quad P_{\mathrm {g}}(t) \in [0,P_{\mathrm {g}}^+], \quad P_{\mathrm {p}}(t) \in [0,P_{\mathrm {p}}^+]. \end{aligned}$$

(13b)

The objective function to minimize is given by

$$\begin{aligned} \int _0^{T} \left( \omega _{\mathrm {w}}P_{\mathrm {w}}(\tau ) + \omega _{\mathrm {g}}P_{\mathrm {g}}(\tau ) + \omega _{\mathrm {p}}P_{\mathrm {p}}(\tau ) \right) \,\mathrm {d}\tau , \end{aligned}$$

(14)

where $\omega _{\mathrm {w}}$, $\omega _{\mathrm {g}}$, and $\omega _{\mathrm {p}}$ are cost coefficients of the waste incineration, the gas combustion, and the pumping power, respectively. Here, we assume that these cost coefficients are constant over time. However, time-dependent costs can also be considered in a similar manner. Note that, in principle, other methods of thermal power production, e.g., power-to-heat, can be modeled in an analogous way.

In summary, we obtain the following nonlinear optimization problem with PDE constraints

$$\begin{aligned} \begin{aligned} \min \quad&(14)\\ \text {s.t.}\quad&\text {Incompressible Euler equation: } (6),\\&\text {Thermal energy equation: } (5),\\&\text {Mass balance equation: } (7),\\&\text {Pressure continuity equations: } (8),\\&\text {Temperature mixing equations: } (10),\\&\text {Consumer constraints: } (11),\\&\text {Depot constraints: } (12),\\&\text {Bounds: } (13). \end{aligned} \end{aligned}$$

(15)

Note that (15) is a nonsmooth and infinite-dimensional nonlinear optimization problem subject to PDEs and algebraic constraints. While the separate parts of the model such as the incompressible Euler equations or the mixing models at nodes are known in the literature, the novelty of the modeling discussed here is the combination of these aspects that leads to a highly accurate representation of the physical behavior.

Since we want to solve the presented model as an NLP, we apply a first-discretize-then-optimize approach by using suitable finite difference discretizations of the differential equations. This will be discussed in the next section.

3 PDE discretization

In this section, we discuss the discretization in space and time via finite difference schemes.

3.1 Implicit Euler discretization in space and time

For the time discretization, we partition the time horizon $\mathcal {T}= [0, T]$ equidistantly in $N+1 \in \mathbb {N}$ time points

$$\begin{aligned} t_i :=\frac{i T}{N}, \quad i \in \{0,\dots ,N\}. \end{aligned}$$

Thus, the length of the discretization intervals is $\Delta t:=T/ N$.

For the discretization in space of pipe $a\in {A}_{\text {ff}}\cup {A}_{\text {bf}}$, we use $M_a+1 \in \mathbb {N}$ discretization points

$$\begin{aligned} x_{a,k} :=\frac{k L_a}{M_a},\quad k \in \{0,\dots ,M_a\}, \quad \text {and} \quad \Delta x_a:=\frac{L_a}{M_a}. \end{aligned}$$

To obtain a large stability region for the method, we use an implicit Euler discretization for the momentum Eq. (6), which leads to the difference equation

$$\begin{aligned} \begin{aligned} \rho \frac{v_a(t_{i+1}) - v_a(t_{i})}{\Delta t} &+& \frac{p_a(L_a, t_{i+1}) - p_a(0, t_{i+1})}{L_a} \quad \\ &+\, g\rho h'_a+ \lambda _a\frac{|{v_a(t_{i+1})}| v_a(t_{i+1}) \rho }{2D_a}&= 0 \end{aligned} \end{aligned}$$

(16)

for $a\in {A}_{\text {ff}}\cup {A}_{\text {bf}}$ and $i \in \{0,\dots ,N - 1\}$. Note that in the context of a forward simulation, to avoid the solution of (large) nonlinear systems, we could have also used an explicit integration scheme for the momentum equation. However, since we are using the discretization method within an optimization model, the implicit discretization does not lead to increased costs anyway.

For the spatial semi-discretization of the thermal energy Eq. (5) we use an implicit Euler discretization, yielding

$$\begin{aligned} \begin{aligned} \frac{\partial T_a}{\partial t}(x_{a, k + 1},t) &+& v_a(t) \frac{T_a(x_{a, k + 1}, t) - T_a(x_{a, k}, t)}{\Delta x_a} \quad \\ & \quad +\, \frac{4 U_a}{c_{\mathrm {p}}\rho D_a}(T_a(x_{a, k + 1},t)-T_0)&= 0 \end{aligned} \end{aligned}$$

for $a\in {A}_{\text {ff}}\cup {A}_{\text {bf}}$ and $k \in \{0,\dots ,M_a- 1\}$. Note that in the optimality conditions for the discretized optimization problem, which form a boundary value problem, there is no preferred space direction, so we will discuss an alternative approach based on central differences in the next section.

The time discretization of the space-discretized thermal energy equation is again done in an implicit way via

$$\begin{aligned} \begin{aligned}&\frac{T_a(x_{a, k + 1},t_{i+1}) - T_a(x_{a, k + 1},t_{i})}{\Delta t}\\&\quad +\, v_a(t_{i+1}) \frac{T_a(x_{a, k + 1}, t_{i+1}) - T_a(x_{a, k}, t_{i+1})}{\Delta x_a}\\&\quad +\, \frac{4 U_a}{c_{\mathrm {p}}\rho D_a}(T_a(x_{a, k + 1},t_{i+1})-T_0) = 0 \end{aligned} \end{aligned}$$

(17)

for $a\in {A}_{\text {ff}}\cup {A}_{\text {bf}}$, $k \in \{0,\dots ,M_a- 1\}$, and $i \in \{0,\dots ,N - 1\}$. The differential depot constraints (12e) and (12f) are discretized as

$$\begin{aligned} \frac{|{P_{\mathrm {w}}(t_{i+1}) - P_{\mathrm {w}}(t_{i})}|}{\Delta t} \le \xi _P, \quad \frac{|{T_{a:v}(t_{i+1}) - T_{a:v}(t_i)}|}{\Delta t} \le \xi _T, \quad i = 0, \dotsc , N-1. \end{aligned}$$

Discretizing the algebraic equations just means formulating them for each discretization point in time. For example, the discretized version of the mass balance Eq. (7) reads

$$\begin{aligned} \sum _{a\in \delta ^{\text {in}}(u)} q_a(t_i) = \sum _{a\in \delta ^{\text {out}}(u)} q_a(t_i),\quad u\in {V},\ i \in \{0,\dots ,N\}. \end{aligned}$$

Finally, discretizing the objective function (14) with the trapezoidal rule, which is the appropriate discretization of the costs associated with the space-time discretization that we have chosen, gives

$$\begin{aligned} \frac{\Delta t}{2} \sum _{i=0}^{N-1} \omega _{\mathrm {w}}(P_{\mathrm {w}}(t_i) + P_{\mathrm {w}}(t_{i+1})) + \omega _{\mathrm {g}}(P_{\mathrm {g}}(t_i) + P_{\mathrm {g}}(t_{i+1})) + \omega _{\mathrm {p}}(P_{\mathrm {p}}(t_i) + P_{\mathrm {p}}(t_{i+1})). \end{aligned}$$

(18)

3.2 A space discretization scheme based on central differences

Since in the discretized optimization problem there is no preferred space direction, in this section we present an alternative spatial discretization scheme using central differences. Later in our numerical results, we then compare this scheme with the implicit scheme of the last section.

Using the notation of Sect. 3.1, i.e., $t_i$, $i \in \{0, \dotsc , N\}$, for the discrete time points and $x_{a, k}$, $k \in \{0, \dotsc , M_a\}$, for the discrete points in space, we obtain the following discretized system for $i = 0, \dotsc , N-1$ and $k = 1, \dotsc , M_a-1$ that contains (16) and

$$\begin{aligned} \begin{aligned}&\frac{T_a(x_{a, k}, t_{i+1}) - T_a(x_{a, k}, t_i)}{\Delta t}\\&\quad +\, v_a(t_{i+1}) \frac{T_a(x_{a, k+1}, t_{i+1}) - T_a(x_{a, k-1}, t_{i+1})}{2 \Delta x} \\&\quad +\, \frac{4 U_a}{c_{\mathrm {p}}\rho D_a} \left( T_a(x_{a, k}, t_{i+1}) - T_0\right) = 0. \end{aligned} \end{aligned}$$

(19)

Because the central difference scheme in (19) takes two spatial steps at a time, we are missing one equation in every timestep. Therefore, an additional discretization step is needed at the beginning or the end of the pipe, where we arbitrarily choose the end of the pipe:

$$\begin{aligned} \begin{aligned}&\frac{T_a(x_{a, M_a},t_{i+1}) - T_a(x_{a, M_a},t_i)}{\Delta t}\\&\quad +\, v_a(t_{i+1}) \frac{T_a(x_{a, M_a}, t_{i+1}) - T_a(x_{a, M_a- 1}, t_{i+1})}{\Delta x_a} \\&\quad + \frac{4 U_a}{c_{\mathrm {p}}\rho D_a}(T_a(x_{a, M_a},t_{i+1})-T_0) = 0. \end{aligned} \end{aligned}$$

(20)

Note that we do not discretize the continuity equation since it simply states that velocities only depend on time and not on space. Finally, the algebraic constraints and the objective function are discretized as in the last section.

4 Mixing models

As already mentioned in Sect. 2, the mixing model originally is not well-posed since it is based on arc sets that are not known a priori. To handle this issue, we present two different reformulations that we later compare numerically in Sect. 6.

4.1 A complementarity-constrained temperature mixing model

The sets $\mathcal {I}(u, t)$ and $\mathcal {O}(u, t)$ used in the temperature mixing constraints (10) of Problem (15) are not known a priori, which makes it difficult to use them in an optimization model. We resolve this problem by replacing them with nonsmooth $\max$-constraints introduced in Hante and Schmidt (2019) for a similar setting in gas transport networks. The newly introduced variable

$$\begin{aligned} \beta _a(t) :=\max \{0, q_a(t)\}, \quad a\in {A}_{\text {ff}}\cup {A}_{\text {bf}}, \end{aligned}$$

(21)

models the positive part of the mass flow $q_a(t)$ of arc $a$. This is equivalent to

$$\begin{aligned} \beta _a(t) - q_a(t) = \max \{0, -q_a(t)\}, \quad a\in {A}_{\text {ff}}\cup {A}_{\text {bf}}. \end{aligned}$$

The variable $\gamma _a(t) :=\beta _a(t) - q_a(t)$ thus models the negative part of the mass flow $q_a(t)$. For each node $u\in {V}$ and all $t \in \mathcal {T}$, then the following implications are satisfied,

$$\begin{aligned} a\in \mathcal {I}(u, t) \cap \delta ^{\text {in}}(u) \implies&\beta _a(t) = q_a(t), \ \gamma _a(t) = 0,\\ a\in \mathcal {O}(u, t) \cap \delta ^{\text {in}}(u) \implies&\beta _a(t) = 0, \ \gamma _a(t) = -q_a(t),\\ a\in \mathcal {I}(u, t) \cap \delta ^{\text {out}}(u) \implies&\beta _a(t) = 0, \ \gamma _a(t) = -q_a(t),\\ a\in \mathcal {O}(u, t) \cap \delta ^{\text {out}}(u) \implies&\beta _a(t) = q_a(t), \ \gamma _a(t) = 0. \end{aligned}$$

We can thus reformulate the temperature mixing Eq. (10) at node $u\in {V}$ without explicitly using the sets $\mathcal {I}(u, t)$ and $\mathcal {O}(u, t)$ and obtain

$$\begin{aligned} T_u(t)&= \frac{\sum _{a\in \delta ^{\text {in}}(u)} \beta _a(t) T_{a:u}(t) + \sum _{a\in \delta ^{\text {out}}(u)} \gamma _a(t) T_{a:u}(t)}{\sum _{a\in \delta ^{\text {in}}(u)} \beta _a(t) + \sum _{a\in \delta ^{\text {out}}(u)} \gamma _a(t)}, \end{aligned}$$

(22a)

$$\begin{aligned} 0&= \beta _a(t)(T_{a:u}(t) - T_u(t)),&a\in \delta ^{\text {out}}(u), \end{aligned}$$

(22b)

$$\begin{aligned} 0&= \gamma _a(t)(T_{a:u}(t) - T_u(t)),&a\in \delta ^{\text {in}}(u), \end{aligned}$$

(22c)

for all $t \in \mathcal {T}$. In Lemma 1 of Hante and Schmidt (2019), it is shown that Condition (21) is equivalent to the complementarity-constrained model

$$\begin{aligned} q_a(t) = \beta _a(t) - \gamma _a(t), \quad \beta _a(t) \ge 0, \quad \gamma _a(t) \ge 0, \quad \beta _a(t) \gamma _a(t) = 0 \end{aligned}$$

(23)

for $u\in {V}$ and $a\in \delta (u)$. This is a classical mathematical program with complementarity constraints (MPCC) formulation, since for all $u\in {V}$, $a\in \delta (u)$, and $t \in \mathcal {T}$, the positive mass flow $\beta _a(t)$ or the negative mass flow $\gamma _a(t)$ is equal to zero. Thus, $\beta _a(t)$ and $\gamma _a(t)$ form a complementarity pair.

Using this constraint, we obtain the finite-dimensional MPCC model

$$\begin{aligned} \begin{aligned} \min \quad&(18)\\ \text {s.t.}\quad&\text {Discretized Euler equation: } (16), \\&\text {Discretized thermal energy equation: } (17) \text { or } (19) \text { and } (20),\\&\text {Discretized mass balance equation: } (7),\\&\text {Discretized pressure continuity equations: } (8),\\&\text {Discretized temperature mixing equations: } (22),\\&\text {Discretized MPCC max-reformulation: } (23),\\&\text {Discretized consumer constraints: } (11),\\&\text {Discretized depot constraints: } (12),\\&\text {Discretized bounds: } (13) \end{aligned} \end{aligned}$$

(24)

for optimizing the control of the district heating network, which is equivalent to a discretized version of the original problem (15).

In general, MPCCs are hard to solve, since they usually do not satisfy standard constraint qualifications of nonlinear optimization (Hoheisel et al. 2013). To see this, consider the complementarity constraints (23). If $\beta _a(t) = \gamma _a(t) = 0$ holds, i.e., if there is no flow, then the tangential cone of (24) restricted to the constraints (23) is nonconvex. In this case, the tangential cone cannot coincide with the linearized tangential cone, because the latter cone is always convex. Thus, the Abadie constraint qualification (ACQ) is not satisfied; see, e.g., Bonnans et al. (2006) for some details on constraint qualifications.

4.2 A nonlinear programming based temperature mixing model

Some of our preliminary numerical experiments showed that the MPCC-based formulation of the mixing model tends to be hard to solve for standard NLP solvers. For this reason, in this section we develop a reformulation for which we later demonstrate that it has better numerical properties.

The thermal energy balance equation in the nodes given by

$$\begin{aligned} \sum _{a\in \delta ^{\text {in}}(u)} q_a(t) T_{a:u}(t) c_{\mathrm {p}}= \sum _{a\in \delta ^{\text {out}}(u)} q_a(t) T_{a:u}(t) c_{\mathrm {p}}, \quad u\in {V},\, t \in \mathcal {T}\end{aligned}$$

ensures that no thermal energy is added or lost in the mixing process. Assuming that the specific heat capacity $c_{\mathrm {p}}$ of water is constant, we can rewrite these equations as

$$\begin{aligned} \sum _{a\in \delta ^{\text {in}}(u)} q_a(t) T_{a:u}(t) = \sum _{a\in \delta ^{\text {out}}(u)} q_a(t) T_{a:u}(t), \quad u\in {V},\, t \in \mathcal {T}. \end{aligned}$$

(25)

However, only formulating the thermal energy balance is not sufficient to get a complete mixing model, since multiple outflow arcs still could have different temperatures after mixing. To prevent this, we explicitly include the temperature propagation equations at the nodes, which equate the temperatures of all outflow arcs with the mixed node temperature,

$$\begin{aligned} v_{a}(t) |{T_{a:u}(t) - T_u(t)}|&\le 0,&u\in {V}, \ a\in \delta ^{\text {out}}(u),\ t \in \mathcal {T}, \end{aligned}$$

(26a)

$$\begin{aligned} v_{a}(t) |{T_{a:u}(t) - T_u(t)}|&\ge 0,&u\in {V}, \ a\in \delta ^{\text {in}}(u),\ t \in \mathcal {T}. \end{aligned}$$

(26b)

For $a\in \mathcal {I}(u, t)$, these inequalities are always fulfilled independent of the absolute value of the temperature difference $|{T_{a:u}(t) - T_u(t)}|$. For $a\in \mathcal {O}(u, t)$, the inequalities are only satisfied if $|{T_{a:u}(t) - T_u(t)}| = 0$ holds. See also Borsche et al. (2018), where a similar model is used in a simulation model with known flow directions. The following theorem shows that this reformulation is equivalent to the original one.

Theorem 1

Suppose that all nodes have a positive inflow, i.e.,

$$\begin{aligned} \sum _{a\in \mathcal {I}(u, t)} |{q_a(t)}| > 0, \quad u\in {V}. \end{aligned}$$

Then, the mixing model (25) and (26) is an equivalent reformulation of the mixing Eq.  (10).

Proof

Let $u\in {V}$. We rewrite the mass balance Eq. (7) using inflow- and outflow-arcs and obtain

$$\begin{aligned} \begin{aligned} 0 =&\sum _{a\in \delta ^{\text {in}}(u)} q_a(t) - \sum _{a\in \delta ^{\text {out}}(u)} q_a(t)\\ =&\left( \sum _{a\in \delta ^{\text {in}}(u) \cap \mathcal {I}(u, t)} q_a(t) - \sum _{a\in \delta ^{\text {out}}(u) \cap \mathcal {I}(u, t)} q_a(t)\right) \\&+ \left( \sum _{a\in \delta ^{\text {in}}(u) \cap \mathcal {O}(u, t)} q_a(t) - \sum _{a\in \delta ^{\text {out}}(u) \cap \mathcal {O}(u, t)} q_a(t)\right) \\ =&\sum _{a\in \mathcal {I}(u, t)} |{q_a(t)}| - \sum _{a\in \mathcal {O}(u, t)} |{q_a(t)}|. \end{aligned} \end{aligned}$$

(27)

The same ideas applied to the thermal energy balance Eq. (25) lead to

$$\begin{aligned} \begin{aligned} 0 =&\sum _{a\in \delta ^{\text {in}}(u)} q_a(t) T_{a:u}(t) -\sum _{a\in \delta ^{\text {out}}(u)} q_a(t) T_{a:u}(t)\\ =&\left( \sum _{a\in \delta ^{\text {in}}(u) \cap \mathcal {I}(u, t)} q_a(t) T_{a:u}(t) - \sum _{a\in \delta ^{\text {out}}(u) \cap \mathcal {I}(u, t)} q_a(t) T_{a:u}(t)\right) \\&+ \left( \sum _{a\in \delta ^{\text {in}}(u) \cap \mathcal {O}(u, t)} q_a(t) T_{a:u}(t) - \sum _{a\in \delta ^{\text {out}}(u) \cap \mathcal {O}(u, t)} q_a(t) T_{a:u}(t)\right) \\ =&\sum _{a\in \mathcal {I}(u, t)} |{q_a(t)}| T_{a:u}(t) - \sum _{a\in \mathcal {O}(u, t)} |{q_a(t)}| T_{a:u}(t). \end{aligned} \end{aligned}$$

(28)

We now assume that the mixing Eqs. (10) hold. Using (27), we obtain

$$\begin{aligned} 0 =&\left( \sum _{a\in \mathcal {I}(u, t)} |{q_a(t)}| - \sum _{a\in \mathcal {O}(u, t)} |{q_a(t)}|\right) T_u(t)\\ =&\left( \sum _{a\in \mathcal {I}(u, t)} |{q_a(t)}|\right) T_u(t) - \left( \sum _{a\in \mathcal {O}(u, t)} |{q_a(t)}| T_u(t)\right) \\ =&\left( \sum _{a\in \mathcal {I}(u, t)} |{q_a(t)}|\right) \frac{\sum _{a\in \mathcal {I}(u, t)} |{q_a(t)}| T_{a:u}(t)}{\sum _{a\in \mathcal {I}(u, t)} |{q_a(t)}|} - \sum _{a\in \mathcal {O}(u, t)} |{q_a(t)}| T_{a:u}(t)\\ =&\sum _{a\in \mathcal {I}(u, t)} |{q_a(t)}| T_{a:u}(t) - \sum _{a\in \mathcal {O}(u, t)} |{q_a(t)}| T_{a:u}(t), \end{aligned}$$

which implies the thermal energy balance Eq. (25) by using (28).

Consider now an arc $a\in \delta ^{\text {out}}(u)$. Then, the temperature propagation Eq. (26a) is satisfied by using (10b),

$$\begin{aligned} v_{a}(t) |{T_{a:u}(t) - T_u(t)}|&= 0 \quad \text {if } a\in \mathcal {O}(u,t),\\ \underbrace{v_{a}(t)}_{\le 0} \underbrace{|{T_{a:u}(t) - T_u(t)}|}_{\ge 0}&\le 0 \quad \text {if } a\in \mathcal {I}(u,t). \end{aligned}$$

For an arc $a\in \delta ^{\text {in}}(u)$, the temperature propagation Eq. (26b) is also fulfilled,

$$\begin{aligned} v_{a}(t) |{T_{a:u}(t) - T_u(t)}|&= 0 \quad \text {if } a\in \mathcal {O}(u, t),\\ \underbrace{v_{a}(t)}_{\ge 0} \underbrace{|{T_{a:u}(t) - T_u(t)}|}_{\ge 0}&\ge 0 \quad \text {if } a\in \mathcal {I}(u, t), \end{aligned}$$

and hence, we have shown the first implication.

For the reverse implication, we assume that (25) and (26) hold. For $a\in \mathcal {O}(u, t)$, because of (26), we have

$$\begin{aligned} \begin{aligned} \underbrace{v_{a}(t)}_{>0} |{T_{a:u}(t) - T_u(t)}|&\le 0 \quad \text {if } a\in \delta ^{\text {out}}(u),\\ \underbrace{v_{a}(t)}_{<0} |{T_{a:u}(t) - T_u(t)}|&\ge 0 \quad \text {if } a\in \delta ^{\text {in}}(u). \end{aligned} \end{aligned}$$

Thus, $|{T_{a:u}(t) - T_u(t)}| = 0$ holds, which implies (10b).

Then, we use the thermal energy balance Eq. (25) to prove (10a)

$$\begin{aligned} \begin{aligned} 0 =&\sum _{a\in \delta ^{\text {in}}(u)} q_a(t) T_{a:u}(t) -\sum _{a\in \delta ^{\text {out}}(u)} q_a(t) T_{a:u}(t)\\ =&\sum _{a\in \mathcal {I}(u, t)} |{q_a(t)}| T_{a:u}(t) - \sum _{a\in \mathcal {O}(u, t)} |{q_a(t)}| T_{a:u}(t)\\ =&\sum _{a\in \mathcal {I}(u, t)} |{q_a(t)}| T_{a:u}(t) - \sum _{a\in \mathcal {O}(u, t)} |{q_a(t)}| T_u(t)\\ =&\left( \sum _{a\in \mathcal {I}(u, t)} |{q_a(t)}|\right) \frac{\sum _{a\in \mathcal {I}(u, t)} |{q_a(t)}| T_{a:u}(t)}{\sum _{a\in \mathcal {I}(u, t)} |{q_a(t)}|} - \left( \sum _{a\in \mathcal {O}(u, t)} |{q_a(t)}|\right) T_u(t)\\ =&\left( \sum _{a\in \mathcal {I}(u, t)} |{q_a(t)}|\right) \frac{\sum _{a\in \mathcal {I}(u, t)} |{q_a(t)}| T_{a:u}(t)}{\sum _{a\in \mathcal {I}(u, t)} |{q_a(t)}|} - \left( \sum _{a\in \mathcal {I}(u, t)} |{q_a(t)}|\right) T_u(t)\\ =&\left( \sum _{a\in \mathcal {I}(u, t)} |{q_a(t)}|\right) \left( \frac{\sum _{a\in \mathcal {I}(u, t)} |{q_a(t)}| T_{a:u}(t)}{\sum _{a\in \mathcal {I}(u, t)} |{q_a(t)}|} - T_u(t)\right) . \end{aligned} \end{aligned}$$

Since

$$\begin{aligned} \sum _{a\in \mathcal {I}(u, t)} |{q_a(t)}| > 0 \end{aligned}$$

holds by assumption, the mixing Eq. (10a) follows. $\square$

By introducing a new variable $\Delta T_{a, u}$ for all $u\in {V}$ and $a\in \delta (u)$ one can rewrite (26) to also avoid absolute values in the equations:

$$\begin{aligned} v_{a}(t) \Delta T_{a, u}(t)&\le 0,&u\in {V}, a\in \delta ^{\text {out}}(u), \end{aligned}$$

(29a)

$$\begin{aligned} \Delta T_{a, u}(t)&\ge T_{a:u}(t) - T_u(t),&u\in {V}, a\in \delta ^{\text {out}}(u), \end{aligned}$$

(29b)

$$\begin{aligned} \Delta T_{a, u}(t)&\ge T_u(t) - T_{a:u}(t),&u\in {V}, a\in \delta ^{\text {out}}(u), \end{aligned}$$

(29c)

$$\begin{aligned} v_{a}(t) \Delta T_{a, u}(t)&\ge 0,&u\in {V}, a\in \delta ^{\text {in}}(u), \end{aligned}$$

(29d)

$$\begin{aligned} \Delta T_{a, u}(t)&\ge T_{a:u}(t) - T_u(t),&u\in {V}, a\in \delta ^{\text {in}}(u), \end{aligned}$$

(29e)

$$\begin{aligned} \Delta T_{a, u}(t)&\ge T_u(t) - T_{a:u}(t),&u\in {V}, a\in \delta ^{\text {in}}(u). \end{aligned}$$

(29f)

We have the following result.

Theorem 2

System (29) is feasible if and only if the temperature propagation Eq. (26) are feasible.

Proof

It is easy to see that (29b) and (29c) are smooth and linear reformulations of

$$\begin{aligned} \Delta T_{a, u}(t) \ge |{T_{a:u}(t) - T_u(t)}|, \quad u\in {V}, \ a\in \delta ^{\text {out}}(u), \end{aligned}$$

and (29e) and (29f) are smooth and linear reformulations of

$$\begin{aligned} \Delta T_{a, u}(t) \ge |{T_{a:u}(t) - T_u(t)}|, \quad u\in {V}, \ a\in \delta ^{\text {in}}(u). \end{aligned}$$

Suppose now that (26) is feasible. Then,

$$\begin{aligned} \Delta T_{a, u}(t) :=|{T_{a:u}(t) - T_u(t)}|, \quad u\in {V}, a\in \delta ^{\text {out}}(u) \cup \delta ^{\text {in}}(u), \end{aligned}$$

satisfies (29).

Next, assume that (29) is feasible. For a node $u\in {V}$ and an outgoing arc $a\in \delta ^{\text {out}}(u)$, we have $v_{a}(t) \Delta T_{a, u}(t) \le 0$ by (29a). Thus, either $v_{a}(t) \le 0$ or $\Delta T_{a, u}(t) = 0$. In the first case, it follows that

$$\begin{aligned} v_{a}(t) |{T_{a:u}(t) - T_u(t)}| \le 0. \end{aligned}$$

In the second case, we obtain that

$$\begin{aligned} 0 \le |{T_{a:u}(t) - T_u(t)}| \le \Delta T_{a, u}(t) = 0, \end{aligned}$$

which implies $T_{a:u}(t) = T_u(t)$. Hence, (26a) is fulfilled. The case of a node $u\in {V}$ and an ingoing arc $a\in \delta ^{\text {in}}(u)$ can be handled analogously. $\square$

Using the reformulated constraints, we obtain the finite-dimensional NLP model

$$\begin{aligned} \begin{aligned} \min \quad&(18)\\ \text {s.t.}\quad&\text {Discretized Euler equation: } (16),\\&\text {Discretized thermal energy equation: } (17) \text { or } (19) \text { and } (20),\\&\text {Discretized mass balance equation: } (7),\\&\text {Discretized pressure continuity equations: } (8),\\&\text {Discretized thermal energy balance equation: } (25),\\&\text {Discretized temperature propagation equations: } (29),\\&\text {Discretized consumer constraints: } (11),\\&\text {Discretized depot constraints: } (12),\\&\text {Discretized bounds: } (13) \end{aligned} \end{aligned}$$

(30)

for optimizing the control of the district heating network.

The temperature propagation Eq. (29) still imply a complementarity structure similar to the complementarity constraints (23) of the MPCC-based mixing model. In particular, this means that for $v_a(t) = \Delta T_{a, u}(t) = 0$, the tangential cone of (30) restricted to the constraints (29) is nonconvex. In this case, the ACQ is not satisfied, which was also the case for the formulation discussed in Sect. 4.1. Nevertheless, the reformulation presented in this section results in a larger tangential cone; see Fig. 3. Later, in Sect. 6, we will see that this gain in constraint regularity can lead to significantly improved numerical results for some NLP solvers.

Fig. 3

Illustration of the tangential cones (thick blue axes and shaded area) of the MPCC- (left) and NLP-based (right) mixing model

5 Optimization techniques

In this section, we present several optimization techniques that allow to solve the challenging problem presented and discussed in the last sections.

5.1 An instantaneous control approach

The discretizations described in Sect. 3 lead to finite-dimensional but typically very large NLPs or MPCCs. Since the solution of these problems is very hard in practice, in this section we develop an instantaneous control approach. Instantaneous control has been frequently used for challenging control problems; cf., e.g., Choi et al. (1993, 1999) for flow control, and in Altmüller et al. (2010), Hinze (2002), Hundhammer and Leugering (2001) for the control of linear wave equations, of wave equations in networks, or of vibrating string networks, respectively. An application to traffic flows can be found in Herty et al. (2007) as well as to mixed-integer nonlinear gas transport networks models in Gugat et al. (2018), and for MPEC-type optimal control problems in Antil et al. (2017).

The basic idea of instantaneous control is the following. Starting from the first time period of the discretization and with a given initial state, we only solve the control problem for this first time period of our discretized time horizon. We then apply the resulting control, move one time period forward in time, solve the control problem restricted to the second period, etc. In other words, we solve a series of quasi-stationary problems while moving forward in time.

This heuristic control approach can be used in two different ways. First, if successful, i.e., if an overall feasible control is obtained, this resulting control can be applied directly in practice. However, this control typically will be far away from being optimal for the complete time horizon. Second, the resulting control can be used to initialize the full NLP (or MPCC) to obtain a feasible initial point, which usually helps significantly in solving the overall problem to (local) optimality.

Let us now formally describe the instantaneous control approach. To this end, we denote the fully discretized problem as

$$\begin{aligned} \min _x \quad&\sum _{i=1}^N f_i(x_i, x_{i-1}) \end{aligned}$$

(31a)

$$\begin{aligned} \text {s.t.}\quad&c_i^{\mathcal {E}}(x_i, x_{i-1}) = 0, \quad i = 1, \dotsc , N, \end{aligned}$$

(31b)

$$\begin{aligned}&c_i^{\mathcal {I}}(x_i, x_{i-1}) \ge 0, \quad i = 1, \dotsc , N, \end{aligned}$$

(31c)

$$\begin{aligned}&d_i^{\mathcal {E}}(x_i) = 0, \quad i = 1, \dotsc , N, \end{aligned}$$

(31d)

$$\begin{aligned}&d_i^{\mathcal {I}}(x_i) \ge 0, \quad i = 1, \dotsc , N, \end{aligned}$$

(31e)

where $x = (x_i)_{i=0}^N$ and $x_i$ contains all variables associated to the time point $t_i$. The super-indices $\mathcal E$, $\mathcal I$ stand for equality and inequality constraints. The constraints $c_i^{\mathcal {E}}$, $c_i^{\mathcal {I}}$ represent the constraints coupling the time points $t_{i-1}$ and $t_i$ and $d_i^{\mathcal {E}}$ and $d_i^{\mathcal {I}}$ couple all constraints that only depend on the single time point $t_i$.

Restricted to the time period $[t_{i-1}, t_i]$ and for given $x_{i-1} = \hat{x}_{i-1}$, this problem can be formulated as

$$\begin{aligned} \min _{x_i} \quad&f_i(x_i, \hat{x}_{i-1}) \end{aligned}$$

(32a)

$$\begin{aligned} \text {s.t.}\quad&c_i^{\mathcal {E}}(x_i, \hat{x}_{i-1}) = 0, \quad c_i^{\mathcal {I}}(x_i, \hat{x}_{i-1}) \ge 0, \end{aligned}$$

(32b)

$$\begin{aligned}&d_i^{\mathcal {E}}(x_i) = 0, \quad d_i^{\mathcal {I}}(x_i) \ge 0, \end{aligned}$$

(32c)

With this problem at hand, the instantaneous control method can be described as in Algorithm 1.

Note that this approach is usually very fast in practice because the variables $x_i$ in the NLP (32) can be reasonably initialized with the values $\hat{x}_{i-1}$. Note again that if Algorithm 1 is successful, i.e., if every problem in Line 2 is solved, the method results in an overall feasible control for the entire time horizon.

5.2 Penalty formulations

In this section, we consider the fully discretized version (31) of our problem. This problem is mainly governed by equality constraints from physics and has rather few controls. Thus, it contains only very few degrees of freedom, which renders the problem hard to solve in practice; see, e.g., (Schmidt et al. 2016), where the same phenomenon is discussed for the case of nonlinear gas network optimization models. One possible remedy in such situations is to consider the relaxed version

$$\begin{aligned} \min _{x,s \ge 0} \quad&\sum _{i=1}^N f_i(x_i, x_{i-1}) + \Vert Ws\Vert \end{aligned}$$

(33a)

$$\begin{aligned} \text {s.t.}\quad&c_i^{\mathcal {E}}(x_i, x_{i-1}) + s_i^{\mathcal {E},c,+} - s_i^{\mathcal {E},c,-} = 0,&i = 1, \dotsc , N, \end{aligned}$$

(33b)

$$\begin{aligned}&c_i^{\mathcal {I}}(x_i, x_{i-1}) + s_i^{\mathcal {I},c,+} \ge 0,&i = 1, \dotsc , N, \end{aligned}$$

(33c)

$$\begin{aligned}&d_i^{\mathcal {E}}(x_i) + s_i^{\mathcal {E},d,+} - s_i^{\mathcal {E},d,-} = 0,&i = 1, \dotsc , N, \end{aligned}$$

(33d)

$$\begin{aligned}&d_i^{\mathcal {I}}(x_i) + s_i^{\mathcal {I},d,+} \ge 0,&i = 1, \dotsc , N. \end{aligned}$$

(33e)

Here, every equality constraint $c_i^{\mathcal {E}}$ is equipped with a slack variable $s_i^{\mathcal {E},c,+}$ for the negative and a slack variable $s_i^{\mathcal {E},c,-}$ for the positive violation of the constraint. Obviously, inequality constraints only require slack variables for their negative violation and the constraints d are handled in the same way. The vector s in the objective function then denotes the vector of all slack variables used in the constraints and the matrix W is a diagonal matrix with positive diagonal entries representing scaling factors for the respective slack variables. Obviously, a solution with $s=0$ is also a solution of the original problem.

We also combine the penalty formulation with the instantaneous control approach described in the last section. In practice, it may happen that a sub-problem in the for-loop of Algorithm 1 cannot be solved to a feasible point. Thus, we also introduce a corresponding penalty formulation in every iteration of the instantaneous control algorithm. If, in an iteration, the slack variables are too large, then we consider the constraint violations of the infeasible point (for the original problem) and increase the respective weights in W in order to penalize the violation of the most violated constraints even stronger. Then, the sub-problem is solved again and the process is repeated until the sub-problem is solved to feasibility (or a maximum number of re-iterations is reached). Finally note that it is often preferable in practice to not equip all constraints with slack variables but only a subset of constraints, e.g., all nonlinear constraints. See Joormann et al. (2015) for a detailed discussion of relaxed penalty models in the related field of gas network optimization.

5.3 A preprocessing technique for fixing flow directions

Due to their complementarity structure, the temperature mixing equations of the MPCC-based mixing model as well as of the NLP-based mixing model usually lead to difficulties in the solution process. To avoid these difficulties, we first identify nodes with incident arcs on which the flow direction is known, which helps to reduce the hardness of the model. In addition to simplifying the mixing equations, one can also smoothen the friction term

$$\begin{aligned} \lambda _a\frac{|{v_a}| v_a\rho _a}{2D_a}(x,t) \end{aligned}$$

in the momentum Eq. (6) if the sign of the velocity $v_a$ is known a priori. This leads to a simple but powerful preprocessing strategy to identify arcs with fixed flow direction in Algorithm 2. The idea behind Algorithm 2 is to return the depot arc, all consumer arcs, and all arcs that are not contained in a cycle. Some arcs in cycles can also have a fixed flow direction as well. To detect such arcs, other algorithms would be needed, which we do not discuss.

Given the result of Algorithm 2, the velocity $v_a$ and mass flow $q_a$ of arcs $a$ in ${A}_{\text {pos}}$ or ${A}_{\text {neg}}$ can be bounded by zero from below or above, respectively.

$$\begin{aligned} v_a\ge 0, \quad q_a&\ge 0, \quad a\in {A}_{\text {pos}},\\ v_a\le 0, \quad q_a&\le 0, \quad a\in {A}_{\text {neg}}. \end{aligned}$$

Additionally, all friction terms in the momentum equations can be reformulated as

$$\begin{aligned} \lambda _a\frac{|{v_a}| v_a\rho _a}{2D_a}&= 0, \quad a\in \left( {A}_{\text {ff}}\cup {A}_{\text {bf}}\right) \setminus \left( {A}_{\text {pos}}\cup {A}_{\text {neg}}\right) , \\ \lambda _a\frac{v_a^2 \rho _a}{2D_a}&= 0, \quad a\in \left( {A}_{\text {ff}}\cup {A}_{\text {bf}}\right) \cap {A}_{\text {pos}},\\ - \lambda _a\frac{v_a^2 \rho _a}{2D_a}&= 0, \quad a\in \left( {A}_{\text {ff}}\cup {A}_{\text {bf}}\right) \cap {A}_{\text {pos}}, \end{aligned}$$

where, for better readability, we have omitted the dependence on x and t. In this way, the friction terms are smoothed for all arcs $a\in {A}_{\text {pos}}\cup {A}_{\text {neg}}$.

Consider now the MPCC-based mixing model. For arcs $a\in {A}_{\text {pos}}$, one can fix the variable for the negative part of the mass as $\gamma _a$ to 0 and for arcs $a\in {A}_{\text {neg}}$, one can fix the variable for positive part of the mass flow $\beta _a$ to 0. The MPCC-based mixing Eq. (22a) then turns into

$$\begin{aligned} T_u(t) = \frac{\sum _{a\in \delta ^{\text {in}}(u) \setminus {A}_{\text {neg}}} \beta _a(t) T_{a:u}(t) + \sum _{a\in \delta ^{\text {out}}(u) \setminus {A}_{\text {pos}}} \gamma _a(t) T_{a:u}(t)}{\sum _{a\in \delta ^{\text {in}}(u) \setminus {A}_{\text {neg}}} \beta _a(t) + \sum _{a\in \delta ^{\text {out}}(u) \setminus {A}_{\text {pos}}} \gamma _a(t)}, \quad t \in \mathcal {T}, \end{aligned}$$

and (22b) and (22c) can be simplified to

$$\begin{aligned} 0&= \beta _a(t)(T_{a:u}(t) - T_u(t)),&a\in \delta ^{\text {out}}(u) \setminus \left( {A}_{\text {pos}}\cup {A}_{\text {neg}}\right) ,\, t \in \mathcal {T}, \\ 0&= T_{a:u}(t) - T_u(t),&a\in \delta ^{\text {out}}(u) \cap {A}_{\text {pos}},\, t \in \mathcal {T}, \\ 0&= \gamma _a(t)(T_{a:u}(t) - T_u(t)),&a\in \delta ^{\text {in}}(u) \setminus \left( {A}_{\text {pos}}\cup {A}_{\text {neg}}\right) ,\, t \in \mathcal {T}, \\ 0&= T_{a:u}(t) - T_u(t),&a\in \delta ^{\text {in}}(u) \cap {A}_{\text {neg}},\, t \in \mathcal {T}. \end{aligned}$$

This means that for $a\in {A}_{\text {pos}}$, Eq. (22c) is not needed any more and for $a\in {A}_{\text {neg}}$, Eq. (22b) can be removed. Thus, every MPCC-mixing equation that contains an arc in ${A}_{\text {pos}}$ or ${A}_{\text {neg}}$ either gets simplified or is dropped. Moreover, the number of nonlinearities is reduced as well.

Similarly, for the NLP-based mixing model, we can simplify the temperature propagation Eq. (29) as

$$\begin{aligned} v_{a}(t) \Delta T_{a, u}(t)&\le 0,&u\in {V}, a\in \delta ^{\text {out}}(u) \setminus \left( {A}_{\text {pos}}\cup {A}_{\text {neg}}\right) ,\\ \Delta T_{a, u}(t)&\ge T_{a:u}(t) - T_u(t),&u\in {V}, a\in \delta ^{\text {out}}(u) \setminus \left( {A}_{\text {pos}}\cup {A}_{\text {neg}}\right) ,\\ \Delta T_{a, u}(t)&\ge T_u(t) - T_{a:u}(t),&u\in {V}, a\in \delta ^{\text {out}}(u) \setminus \left( {A}_{\text {pos}}\cup {A}_{\text {neg}}\right) ,\\ T_{a:u}(t) - T_u(t)&= 0,&u\in {V}, a\in \delta ^{\text {out}}(u) \cap {A}_{\text {pos}},\\ v_{a}(t) \Delta T_{a, u}(t)&\ge 0,&u\in {V}, a\in \delta ^{\text {in}}(u) \setminus \left( {A}_{\text {pos}}\cup {A}_{\text {neg}}\right) ,\\ \Delta T_{a, u}(t)&\ge T_{a:u}(t) - T_u(t),&u\in {V}, a\in \delta ^{\text {in}}(u) \setminus \left( {A}_{\text {pos}}\cup {A}_{\text {neg}}\right) ,\\ \Delta T_{a, u}(t)&\ge T_u(t) - T_{a:u}(t),&u\in {V}, a\in \delta ^{\text {in}}(u) \setminus \left( {A}_{\text {pos}}\cup {A}_{\text {neg}}\right) ,\\ T_{a:u}(t) - T_u(t)&= 0,&u\in {V}, a\in \delta ^{\text {in}}(u) \cap {A}_{\text {neg}}. \end{aligned}$$

Again, all equations in (29) that are defined on arcs in ${A}_{\text {pos}}$ or ${A}_{\text {neg}}$ either get simplified or dropped. The thermal energy balance Eq. (25) remains unchanged.

5.4 Initial conditions

Unfortunately, the exact state of a district heating network is usually not known in practice. However, our model requires reasonable initial conditions at $t = 0$. To obtain such conditions, we compute a stationary solution of the network for the first time step. The stationary model we use is the same as our standard model at $t=0$, except that all time derivatives are zero. In this case, the Euler momentum Eq. (6) becomes

$$\begin{aligned} \frac{p_a(L_a,0) - p_a(0,0)}{L_a} = - g\rho h'_a- \lambda _a\frac{|{v_a}| v_a\rho }{2D_a}(0), \quad a\in {A}_{\text {ff}}\cup {A}_{\text {bf}}, \end{aligned}$$

and the thermal energy Eq. (5) becomes

$$\begin{aligned} v_a(0) \frac{\partial T_a}{\partial x}(x,0) + \frac{4 U_a}{c_{\mathrm {p}}\rho _a(x,0) D_a}(T_a(x,0)-T_0) = 0, \quad a\in {A}_{\text {ff}}\cup {A}_{\text {bf}}. \end{aligned}$$

All algebraic equations stay the same but are only considered at $t=0$. The solution of this stationary model is then used to identify the initial conditions.

Note that the proposed method to generate reasonable initial conditions via solving a stationary variant of the model can be replaced by any other initialization, if required. For instance, if the state of the network is known, e.g., via measurements or proper state estimations, this state can be used directly instead of the one computed here.

6 Numerical results

In this section, we present and discuss numerical results for the models and techniques introduced in the previous sections. The models have been formulated using GAMS 25.1.2 (McCarl 2009). The resulting instances are solved using the solvers Ipopt 3.12 (Wächter and Biegler 2006), KNITRO 10.3.0 (Byrd et al. 2006), CONOPT4 4.06 (Drud 1994, 1995, 1996), and SNOPT 7.2-12.1 (Gill et al. 2005). We apply our technique to two different realistic district heating networks; the so-called AROMA network given in Fig. 4 and the so-called STREET network given in Fig. 5.

Fig. 4

The forward-flow part of the AROMA network

Fig. 5

The forward-flow part of the STREET network

Table 2 Parameters of the pipes in the AROMA network

Table 3 Fraction of the demand of every consumer regarding the total amount of demand given in Fig. 6

Table 4 Pressure and temperature bounds (above) and other parameters (below) of the AROMA network

The AROMA network consists of 18 nodes, 24 arcs (1 depot, 5 consumers, and 18 pipes), and one cycle each in the forward-flow and the backward-flow network. Its total pipe length is $7262.4\,\hbox {m}$. All parameters describing the AROMA network are given in Tables 2, 3, 4. The STREET network is a part of a real-world district heating network with 162 nodes, 195 arcs (1 depot, 32 consumers, and 162 pipes), and has a total pipe length of $7627.106\,\hbox {m}$. Both networks contain a cycle. Thus, not all flow directions are known in advance. The preprocessing technique described in Sect. 5.3 can fix the flow directions for 6 out of the 18 pipes of the AROMA network and for 150 out of the 162 pipes for the STREET network. The larger number of fixations for the STREET network follows from the fact that it only contains a small cycle whereas the major part of the network is tree-shaped. Let us also note that we used the $\ell _1$ norm throughout this section for the penalty terms in (33).

The remainder of this section is split up into two parts. In Sect. 6.1, we compare different variants of our model (namely the MPCC- and the NLP-based mixing model as well as the two different discretization schemes for the PDEs) and different NLP solvers. In Sect. 6.2 we then discuss properties of optimized heat and flow controls at the depot for the AROMA and the STREET network.

6.1 Comparison of model variants and NLP solvers

We now compare the performance of different NLP solvers applied to the two different spatial discretization schemes (the implicit Euler and the scheme based on central differences) as well as the two mixing models (the MPCC- and the NLP-based model). To this end, we consider the AROMA network with a time horizon of one day equipped with a time discretization using 30 minute intervals. The stepsize of the spatial discretization is $150 \,\hbox {m}$.

The numerical results are given in Table 5.

Table 5 Numerical results for all combination of model variants and NLP solvers for the AROMA network with $\Delta t= 1800\,\hbox {s}$ and $\Delta x_a= 150\,\hbox {m}$

The columns of the table contain the following information.

• Mixing: The mixing model; MPCC-based (Sect. 4.1) or NLP-based (Sect. 4.2).

• Discr.: The implicit Euler discretization (Sect. 3.1) or the discretization based on central differences (Sect. 3.2).

• t (all): The overall solution time including the initial value computation using the instantaneous control approach (Sect. 5.1). All running times in the table are given in seconds.

• t (NLP): The time to solve the NLP on the entire time horizon, which is initialized with the solution of the instantaneous control approach.

• t (IC): The time required to apply the instantaneous control approach.

• #IC: The total number of instantaneous control steps including re-iterations applied if the scaled max-norm of all slack values exceeds the tolerance of $10^{-2}$.

• Mean, Median, Min. Max.: The mean, median, minimum, and maximum time of all (re-)iterations of the instantaneous control approach.

• t (stat): The time required to compute the stationary solution that is used as an initial physical state (Sect. 5.4).

• #stat: The required number of re-iterations for computing the stationary solution.

• Obj.: The objective function value of the problem, which is the sum of the control costs and the scaled penalty terms. Here, “—” means that the final value of the max-norm of all scaled slack values exceeds the tolerance of $10^{-2}$.

• Cost: The control costs part of the objective function value; see (18).

If we first consider the overall time required to solve the problem (“t (all)”), we see that the results are highly heterogeneous w.r.t. the chosen NLP solver. The fastest approach (16.732s) is obtained by CONOPT4 applied to the MPCC-based mixing model and the implicit Euler discretization. In contrast, KNITRO applied to the MPCC-based mixing model and the discretization scheme based on central differences takes 933.063s, which corresponds to a factor larger then 55. Since every solver gets exactly the same models to be solved, this strongly indicates the hardness of the district heating network optimization problems.

It also strongly depends on the chosen solver whether the MPCC- or the NLP-based mixing model is used. For instance, KNITRO performs very poor on the MPCC-based model and significantly benefits from the NLP-based reformulation. On the other hand, for SNOPT it is exactly the other way around (although the difference in solution times is not as drastic as for KNITRO). The choice of the discretization scheme for the PDEs does not influence the solution times significantly. However, it may influence how the solvers are able to reduce the penalty terms in the objective function; see, e.g., KNITRO, which is not able to reduce the penalty terms so that the max-norm of all scaled slack values is below $10^{-2}$ if the implicit Euler scheme is used. A comparable behavior can also be seen in the instantaneous control approach: All solvers require more re-iterations to reduce the penalty terms for the implicit Euler discretization. The only exception is SNOPT applied to the NLP-based mixing model.

As expected, the instantaneous control approach is solved very fast for all solvers. The single iterations are all solved in less then a second on average. The only exception is Ipopt applied to the NLP-based mixing model and the implicit Euler discretization, where some convergence issues occur within the instantaneous control approach. The running times required to compute the stationary solution that we use as the initial physical state are in the same orders of magnitude as a single instantaneous control approach iteration but slightly longer, since no good initial point can be used by the NLP solvers.

Finally, let us also discuss the (local) optimal solutions obtained by the different NLP solvers applied to the different model variants. The objective function of the overall NLP consists of two parts: the original control costs and the scaled penalty terms. Scaling the penalty terms is always an issue in practical physical applications for which different penalty terms have different physical units. Obviously, the applicability of the obtained depot control strongly depends on the size of the penalty part of the objective, since large slack values correspond to violated physical or technical constraints. The table shows that different solvers find very different local optima of the problem. For instance, CONOPT4 is a rather fast solver but the obtained local optima also contain large slack values. Contrarily, KNITRO applied to the discretization based on central differences computes local optima with almost vanishing slack values. Compromising between the difference of the values in the last two columns (which is the size of the scaled penalty terms in the objective) and the solution times, KNITRO applied to the discretization based on central differences and the NLP-based mixing model seems to be the best combination of model variant and NLP solver.

6.2 Optimized depot controls

We now present some exemplary optimal depot controls. In Fig. 6 (top), the control profile is given for the AROMA network and the “winner setting” discussed in the last section. For the given profiles, we first assume that the amount of power generated by waste incineration is unbounded. This leads to a control (solid line) that mainly follows the aggregated consumption of the households (dashed line). Due to the heat losses in the transport network, the generated power at the depot is slightly larger than the aggregated consumption. Since pressure losses are small in the network, the pressure increase at the depot is almost negligible. The power control qualitatively changes if power generated by waste incineration is bounded; see the dashed-dotted line in Fig. 6 (bottom). Since aggregated power consumption is above this bound in some morning and evening hours, the optimized power control anticipates this and pre-heats the network in the hours before. This is obviously required because again simply following the aggregated consumption curve would result in hours where the power consumption would need to be curtailed. The same effect can be observed for the optimized depot control for the STREET network in Fig. 7. For the STREET network, our preliminary numerical experiments revealed that the NLP solver Ipopt applied to the NLP-based mixing model, the discretization scheme based on central differences as well as $\Delta t= 1800\,\hbox {s}$ and $\Delta x_a= 100\,\hbox {m}$ delivers the best results; cf. also the respective discussion for the AROMA network in Sect. 6.1.

Fig. 6

Aggregated power consumption (dashed curve), power generated by waste incineration at the depot (solid curve), and pressure increase at the depot (dotted curve) for the AROMA network without (top) and with (bottom) waste incineration bound

Fig. 7

Aggregated power consumption (dashed curve), power generated by waste incineration at the depot (solid curve), and pressure increase at the depot (dotted curve) for the STREET network with waste incineration bound (dashed-dotted line)

We now discuss the interplay between mass flow and water temperature on the example of the STREET network. Considering the power constraints of the consumers and the depot (11b) and (12d), we see that power consumption is mainly satisfied by the product of mass flow and temperature differences. Thus, to satisfy demand we can either increase the mass flow or the outlet temperature of the depot. These two values are shown in Fig. 8 for the entire time horizon. It can be seen that power consumption during night is mainly covered by high outlet temperatures at the depot. Here, this temperature is at its upper bound (403.15 K), which is obtained by waste incineration at the depot. Around 4 AM it is anticipated that in the morning hours high outlet temperatures will not be enough either due to the upper bound of the temperature or the upper bound on waste incineration. Thus, mass flows need to be increased, which then leads to outlet temperatures that can be decreased. During the remainder of the day it can be seen that mass flows and temperatures change in an opposed way—decreasing outlet temperatures require increased mass flows and vice versa.

Let us finally remark that the optimal control of the network is not unique due to the described interplay of mass flow and water temperature at the consumers. Throughout our numerical experiments we observed that larger mass flows can be replaced with larger temperature differences to satisfy demand and vice versa. However, for a fixed control at the depot, the remaining physical solution is unique.

Fig. 8

Outlet temperature and mass flow at the depot arc for the STREET network

7 Conclusion

In this paper, we presented an accurate dynamic optimization model for the control of district heating networks. The model is mainly governed by the nonlinear partial differential equations for water and heat flow as well as by nodal mixing models for tracking different water temperatures in the network. This results in a PDE-constrained MPCC or NLP model, depending on the chosen option for the genuinely nonsmooth mixing models. After applying suitable discretizations for the PDEs, we obtain a finite-dimensional but large and highly nonlinear MPCC or NLP, for which we develop different optimization techniques that then allow us to solve realistic instances. The applicability of the discussed models and techniques is illustrated by a numerical case study on different networks.

The literature on mathematical optimization for district heating networks is not as mature as for other utility networks like gas or water networks. Thus, many research topics remain to be addressed. In our future work, we plan to consider adaptive techniques as in Mehrmann et al. (2018) that are based on model hierarchies for the physics model. Here, port-Hamiltonian modeling frameworks seem to be favorable. A first step in this direction is already done in Hauschild et al. (2020). In terms of the application, we think that the most urgent research topics are to develop mathematical optimization techniques for dealing with uncertainties (especially w.r.t. the consumption of the households) as well as the coupling of district heating networks with power networks.