A concurrent implementation of the surrogate management framework with application to cardiovascular shape optimization

Abstract

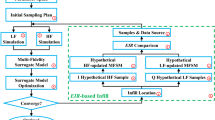
The surrogate management framework (SMF) is an effective approach for derivative-free optimization of expensive objective functions. The SMF is typically comprised of surrogate-based infill methods (SEARCH step) coupled to pattern search optimization (POLL step). Although the latter is easy to parallelize, parallelization of the SEARCH step requires surrogate-based strategies that generate multiple candidates at each iteration. The impact of such SEARCH methods on SMF performance remains poorly explored. In this paper, we extend the SMF to incorporate concurrent evaluations at the SEARCH step by comparing two different infill approaches: single search multiple error sampling and expected improvement constant liar approaches. These variants are generalized to address non-linearly constrained problems by the filter method. The proposed methods are benchmarked for different infill sizes, while accounting for the variability in initialization. We then demonstrate the proposed methods on two shape optimization problems motivated by hemodynamically-driven surgical design. Surrogate-based multiple-infill strategies outperform their single-infill counterparts for a fixed computational time budget on bound constrained problems. Insights drawn from this study have implications not only on future instances of the SMF, but also for other surrogate-based and hybrid parallel infill methods for derivative-free optimization.

Appendices

Analytical function set

This function set consists of 20 bound constrained test problems and 10 constrained test problems. These problems can be scaled to arbitrarily large dimensions. In this study, all bounds were rescaled to the unit hypercube. All strategies were initialized using 5 optimal Latin Hypercube Samples, containing 2d points each.

1.1 Bounded test function set

• 1. Sphere (Jamil and Yang 2013) :

  $$\begin{aligned} f^s_{1}(\varvec{x}) = \sum ^{d}_{i=1}{x^2_i}, \end{aligned}$$

  subject to $-1 \le x_i \le 1$. The global minimum is located at $x^*_i=0$.

• 2. Alpine-2 (Jamil and Yang 2013) :

  $$\begin{aligned} f^s_{2}(\varvec{x}) = \prod ^{d}_{i=1}{\sqrt{x_i}sin(x_i)}, \end{aligned}$$

  subject to $0 \le x_i \le 10$. The global minimum is located at $x^*_i=7.917$.

• 3. Brown (Jamil and Yang 2013) :

  $$\begin{aligned} f^s_{3}(\varvec{x}) = \sum ^{d-1}_{i=1}{ (x^2_i)^{(x^2_{i+1} + 1)} + (x^2_{i+1})^{(x^2_{i} + 1)} } \ \ , \end{aligned}$$

  subject to $-1 \le x_i \le 4$. The global minimum is located at $x^*_i=0$.

• 4. Chung-Reynolds (Jamil and Yang 2013) :

  $$\begin{aligned} f^s_{4}(\varvec{x}) = \left(\sum ^{d}_{i=1}{x^2_i}\right)^2 , \end{aligned}$$

  subject to $-100 \le x_i \le 100$. The global minimum is located at $x^*_i=0$.

• 5. Cosine Mixture (Breiman and Cutler 1993) :

  $$\begin{aligned} f^s_{5}(\varvec{x}) = \sum ^{d}_{i=1}{ (x^2_i - 0.1cos(5 \pi x_i)) } \ \ , \end{aligned}$$

  subject to $-1 \le x_i \le 1$. The global minimum is located at $x^*_i=0$.

• 6. Csendes (Jamil and Yang 2013) :

  $$\begin{aligned} f^s_{6}(\varvec{x}) = \sum ^{d}_{i=1}{x^6_i (2 + sin\left(\frac{1}{x_i})\right) }, \end{aligned}$$

  subject to $-1 \le x_i \le 1$. The global minimum is located at $x^*_i=0$.

• 7. Dixon & Price (Jamil and Yang 2013) :

  $$\begin{aligned} f^s_{7}(\varvec{x}) = (x_1 -1)^2 + \sum ^{d}_{i=2}{i(2 x^2_i - x_{i-1} )^2} \ \ , \end{aligned}$$

  subject to $-10 \le x_i \le 10$. The global minimum is located at $x^*_i=2^{(1 - \frac{1}{2^i})}$.

• 8. Giunta (Bossek 2017) :

  $$\begin{aligned} f^s_{8}(\varvec{x}) = 0.6 + \sum ^d_{i=1} \big [ sin^2(1-\frac{16}{15}x_i) - \frac{1}{50}sin(4-\frac{64}{15}x_i) - sin(1-\frac{16}{15}x_i) \big ] , \end{aligned}$$

  subject to $-1 \le x_i \le 1$. The global minimum is located at $x^*_i=0.46732$.

• 9. Levy-Montalvo (Levy and Montalvo 1985) :

  $$\begin{aligned} f^s_{9}(\varvec{x}) = sin^2(\pi w_1) + \sum ^{d-1}_{i=1}{(w_i-1)^2(1 + 10sin^2(\pi w_{i+1}))} + (w_d -1)^2 , \end{aligned}$$

  where

  $$\begin{aligned} w_i = 1 + \frac{x_i-1}{4}, \end{aligned}$$

  subject to $-10 \le x_i \le 10$. The global minimum is located at $x^*_i=1$.

• 10. Mishra-2 (Jamil and Yang 2013) :

  $$\begin{aligned} f^s_{10}(\varvec{x}) = (1+d - \sum _{i=1}^{d-1}{0.5(x_i+x_{i+1})})^{d-\sum _{i=1}^{d-1} 0.5(x_i + x_{i+1})} , \end{aligned}$$

  subject to $0 \le x_i \le 1$. The global minimum is located at $x^*_i=1$.

• 11. Paviani (Jamil and Yang 2013) :

  $$\begin{aligned} f^s_{11}(\varvec{x}) = \sum _{i=1}^{d} {( (ln(x_i-2))^2 + (ln(10-x_i))^2 )} - (\prod _{i=1}^{d} x_i)^{0.2} \ \ , \end{aligned}$$

  subject to $2.0001 \le x_i \le 9.9999$. The closed form minimizer for this function is not known and varies with d, however it lies in the hypercube : $8.2<= x^*_i <= 9.9999$, moving closer to $x^*_i <= 9.9999$ with increase in d.

• 12. Ripple-25 (Jamil and Yang 2013):

  $$\begin{aligned} f^s_{12}(\varvec{x}) = \sum _{i=1}^d -e^{-\frac{2log(2(x_i-0.1)^2)}{0.64}} (sin^6(5\pi x_i)), \end{aligned}$$

  subject to $0 \le x_i \le 1$. The global minimum is located at $x^*_i=0.1$.

• 13. Rosenbrock (Jamil and Yang 2013):

  $$\begin{aligned} f^s_{13}(\varvec{x}) = \sum _{i=1}^{d-1} [100(x_{i+1} - x_i^2)^2 + (x_i-1)^2 ] , \end{aligned}$$

  subject to $-30 \le x_i \le 30$. The global minimum is located at $x^*_i=1$.

• 14. Sargan (Jamil and Yang 2013) :

  $$\begin{aligned} f^s_{14}(\varvec{x}) = \sum _{i=1}^d d(x_i^2 + 0.4\sum _{j \ne i} x_i x_j) , \end{aligned}$$

  subject to $-100 \le x_i \le 100$. The global minimum is located at $x^*_i=0$.

• 15. Schwefel-25 (Jamil and Yang 2013) :

  $$\begin{aligned} f^s_{15}(\varvec{x}) = \sum _{i=1}^{d} (x_i-1)^2 + (x_1 - x_i^2)^2 \ \ , \end{aligned}$$

  subject to $0 \le x_i \le 10$. The global minimum is located at $x^*_i=1$.

• 16. Schwefel-26 (Jamil and Yang 2013) :

  $$\begin{aligned} f^s_{16}(\varvec{x}) = -\frac{1}{d} \sum _{i=1}^{d} x_i sin(\sqrt{|x_i |}) , \end{aligned}$$

  subject to $-500 \le x_i \le 500$. The global minimum is located at $x^*_i=420.968746$.

• 17. Styblinski-Tang: (Jamil and Yang 2013)

  $$\begin{aligned} f^s_{17}(\varvec{x}) = \frac{1}{2} \sum _{i=1}^{d} (x_i^4 - 16 x_i^2 + 5x_i) , \end{aligned}$$

  subject to $-5 \le x_i \le 5$. The global minimum is located at $x^*_i=-2.903534$.

• 18. Trid: (Jamil and Yang 2013)

  $$\begin{aligned} f^s_{18}(\varvec{x}) = \sum _{i=1}^d (x_i-1)^2 - \sum _{i=2}^d x_i x_{i-1} \ \ , \end{aligned}$$

  subject to $- \frac{1}{2}(d+1)^2 \le x_i \le \frac{1}{2}(d+1)^2$. The global minimum is the solution of the tridiagonal system

  $$\begin{aligned} T_d x^* = r_d , \end{aligned}$$

  where $T_d$ is a $d \times d$ tridiagonal matrix, given by :

  $$\begin{aligned} T_d = \left[ \begin{matrix} 1 &{} -0.5 &{} &{} 0\\ -0.5 &{} \ddots &{} \ddots &{} \\ &{} \ddots &{} \ddots &{} -0.5 \\ 0 &{} &{} -0.5 &{} 1 \end{matrix} \right] \end{aligned}$$

  (14)

  and $r_d$ is a $d \times 1$ vector, with $r_d^{\intercal } = \left[ 1, 1, \dots 1 \right]$.

• 19. Xin-She Yang-3 (Jamil and Yang 2013):

  $$\begin{aligned} f^s_{19}(\varvec{x}) = [ e^{\sum _{i=1}^d (\frac{x_i}{15})^{10}} - 2e^{-\sum _{i=1}^d(x_i)^2}. \prod _{i=1}^d cos^2 (x_i) ] \ \ , \end{aligned}$$

  subject to $-20 \le x_i \le 20$. The global minimum is located at $x^*_i=0$.

• 20. Zakharov (Jamil and Yang 2013):

  $$\begin{aligned} f^s_{20}(\varvec{x}) = \sum _{i=1}^d x_i^2 + \left( \frac{1}{2} \sum _{i=1}^d ix_i \right) ^2 + \left( \frac{1}{2} \sum _{i=1}^d ix_i \right) ^4 \ \ , \end{aligned}$$

  subject to $-5 \le x_i \le 10$. The global minimum is located at $x^*_i=0$.

1.2 Constrained test function set

For the constrained optimization problems, we consider a set of 10 scalable problems. These include 4 well known scalable multi-objective optimization problems ($f^c_7,f^c_8,f^c_9,f^c_{10}$), which were adapted to single-objective constrained optimization problems via an $\varepsilon$-constraint approach (Miettinen 1999). Since these multi-objective problems are scalable to a flexible number of objectives (up to dimension d), we set the number of objectives (M) to 4. This limits us to only consider dimensions $d>4$ for constrained optimization benchmarking. All strategies were initialized using 5 optimal Latin Hypercube Samples, containing 2d points each. Table 5 lists the number of initializations that were feasible for each (function,dimension) pair.

• 1. Sphere with one linear constraint :

  $$\begin{aligned} f^c_{1}(\varvec{x}) = \sum _{i=1}^d x_i^2 \end{aligned}$$

  subject to :

  $$\begin{aligned} 0.5 - \sum _{i=1}^d x_i \le 0, \end{aligned}$$

  and $-1 \le x_i \le 1$. The global minimum is located at $x^*_i=\frac{1}{2d}$.

• 2. Sphere with two disconnected feasible islands :

  $$\begin{aligned} f^c_{2}(\varvec{x}) = \sum _{i=1}^d x_i^2 \end{aligned}$$

  subject to :

  $$\begin{aligned} \bigg ( \sum _{i=1}^d (x_i-0.6)^2 - 0.09d \bigg ) \bigg ( \sum _{i=1}^d (x_i+0.2)^2 - 0.01d \bigg ) \le 0 \end{aligned}$$

  and $-1 \le x_i \le 1$. The global minimum is located at $x^*_i=-0.1$.

• 3. Rosenbrock (Jamil and Yang 2013) constrained within unit sphere:

  $$\begin{aligned} f^c_{3}(\varvec{x}) = \sum _{i=1}^{d-1} [100(x_{i+1} - x_i^2)^2 + (x_i-1)^2 ] , \end{aligned}$$

  subject to :

  $$\begin{aligned} \sum _{i=1}^d (x_i)^2 \le 1.0 \end{aligned}$$

  and $-30 \le x_i \le 30$. A closed form global minimum is not known.

• 4. Trid (Jamil and Yang 2013) with a 2-norm constraint :

  $$\begin{aligned} f^c_{4}(\varvec{x}) = \sum _{i=1}^d (x_i-1)^2 - \sum _{i=2}^d x_i x_{i-1} \end{aligned}$$

  subject to :

  $$\begin{aligned} \Vert \varvec{x}\Vert _2^2 \le d^3 \end{aligned}$$

  and$- \frac{1}{2}(d+1)^2 \le x_i \le \frac{1}{2}(d+1)^2$. A closed form solution is not known.

• 5. G02 (Koziel and Michalewicz 1999):

  $$\begin{aligned} f^c_{5} (\varvec{x}) = \left|\frac{\sum _{i=1}^d cos^4 (x_i) - \prod _{i=1}^d cos^2 (x_i) }{\sqrt{\sum _{i=1}^d ix_i^2}} \right|\end{aligned}$$

  subject to:

  $$\begin{aligned} 0.75 - \prod _{i=1}^d x_i\le & {} 0 , \\ \sum _{i=1}^d x_i - 7.5d\le & {} 0 \end{aligned}$$

  and $0 \le x_i \le 10$. A closed form solution is not known.

• 6. G03 (Koziel and Michalewicz 1999):

  $$\begin{aligned} f^c_{6} (\varvec{x}) = - (\sqrt{d})^d \prod _{i=1}^d x_i \end{aligned}$$

  subject to the relaxed equality constraint:

  $$\begin{aligned} \left|\bigg ( \sum _{i=1}^d x_i^2 \bigg ) -1 \right|\le \varepsilon \end{aligned}$$

  and $0 \le x_i \le 1$. We set $\varepsilon =0.025$, for which the global minimum is located at $x^*_i= \sqrt{\frac{0.975}{d}}$.

• 7. DTLZ1 (Deb et al. 2005), adapted as an $\varepsilon$-constraint problem:

  $$\begin{aligned} f^c_{7} (\varvec{x}) = \frac{1}{2} x_1 x_2 \ldots x_{M-1} (1 + g^c_7(\varvec{x}_{M:d})) \end{aligned}$$

  subject to :

  $$\begin{aligned} \frac{1}{2} x_1 x_2 \ldots x_{M-2} ( 1-x_{M-1} ) (1+g^c_7(\varvec{x}_{M:d}))\le & \varepsilon , \\ \frac{1}{2} x_1 x_2 \ldots (1 - x_{M-2}) (1+g^c_7(\varvec{x}_{M:d}))\le & \varepsilon , \ldots \\ \frac{1}{2} x_1 ( 1-x_{2} ) (1+g^c_7(\varvec{x}_{M:d}))\le & \varepsilon , \\ \frac{1}{2} (1 - x_1) (1+g^c_7(\varvec{x}_{M:d}))\le & \varepsilon , \end{aligned}$$

  and $0 \le x_i \le 1$. Here, we set $\varepsilon =\frac{1}{2M}$ and define the function $g^c_7(\varvec{x})$ as:

  $$\begin{aligned} g^c_7(\varvec{x}_{M:d}) = 100 \big ( d -M +1 + \sum _{i=M}^d \left[ (x_i-0.5)^2 - cos(20 \pi (x_i-0.5))\right] \big ). \end{aligned}$$

  The global minimum is $\varvec{x}_i = 1 -\frac{2\varepsilon }{(1-2(i-1)\varepsilon )}$ for $i=1,\ldots ,M-1$, and $\varvec{x}_{M:d}=0.5$.

• 8. DTLZ2 (Deb et al. 2005), adapted as an $\varepsilon$-constraint problem:

  $$\begin{aligned} f^c_{8} (\varvec{x}) = cos(\pi x_1/2) cos(\pi x_2/2) \ldots cos(\pi x_{M-2}/2) cos(\pi x_{M-1}/2) (1+g^c_8(\varvec{x}_{M:d})) \end{aligned}$$

  subject to :

  $$\begin{aligned} \bigg ( (1+g^c_8(\varvec{x}_{M:d}))cos(\pi x_1/2) cos(\pi x_2/2) \ldots cos(\pi x_{M-2}/2) sin(\pi x_{M-1}/2) \bigg )^2\le & \varepsilon , \\ \bigg ( (1+g^c_8(\varvec{x}_{M:d}))cos(\pi x_1/2) cos(\pi x_2/2) \ldots sin(\pi x_{M-2}/2) \bigg )^2\le & \varepsilon , \ldots \\ \bigg ( (1+g^c_8(\varvec{x}_{M:d}))cos(\pi x_1/2) sin(\pi x_2/2) \bigg )^2\le & \varepsilon , \\ \bigg ( (1+g^c_8(\varvec{x}_{M:d}))sin(\pi x_1/2) \bigg )^2\le & \varepsilon \end{aligned}$$

  and $0 \le x_i \le 1$. Here, we set $\varepsilon =\frac{1}{M}$ and define the function $g^c_8(\varvec{x})$ as: $g^c_8(\varvec{x}_{M:d}) = \sum _{i=M}^d (x_i-0.5)^2$. The global minimum is $\varvec{x}_i = \frac{2}{\pi }sin^{-1}\big (\frac{\varepsilon }{(1-(i-1)\varepsilon )} \big )$ for $i=1,\ldots ,M-1$, and $\varvec{x}_{M:d}=0.5$.

• 9. Modified DTLZ5 (Saxena et al. 2012) or DTLZ5(2,M), adapted as an $\varepsilon$-constraint problem:

  $$\begin{aligned} f^c_9 (\varvec{x}) = cos(\theta _1) cos(\theta _2) \ldots cos(\theta _{M-2}) cos(\theta _{M-1}) (1+g^c_9(\varvec{x}_{M:d})) \end{aligned}$$

  subject to :

  $$\begin{aligned} h_1(\varvec{x})= & (1+g^c_9(\varvec{x}_{M:d}))cos(\theta _1) cos(\theta _2) \ldots cos(\theta _{M-2}) sin(\theta _{M-1}) \le \varepsilon , \\ h_2(\varvec{x})= & (1+g^c_9(\varvec{x}_{M:d}))cos(\theta _1) cos(\theta _2) \ldots sin(\theta _{M-2}) \le \varepsilon , \ldots \\ h_{M-2}(\varvec{x})= & {} (1+g^c_9(\varvec{x}_{M:d}))cos(\theta _1) sin(\theta _2) \le \varepsilon , \\ h_{M-1}(\varvec{x})= & {} (1+g^c_9(\varvec{x}_{M:d}))sin(\theta _1) \le \varepsilon , \\ h_{M} (\varvec{x})= & {} 1 - h_{M-1}^2(\varvec{x}) - 2^{M-2} f^c_9 (\varvec{x}) \le 0 , \\ h_{M+1} (\varvec{x})= & {} 1 - h_{M-1}^2(\varvec{x}) - 2^{M-2} h_1 (\varvec{x}) \le 0 , \\ h_{M+2} (\varvec{x})= & {} 1 - h_{M-1}^2(\varvec{x}) - 2^{M-3} h_2 (\varvec{x}) \le 0 , \ldots \\ h_{2M-3} (\varvec{x})= & {} 1 - h_{M-1}^2(\varvec{x}) - 2^{2} h_{M-3} (\varvec{x}) \le 0 , \\ h_{2M-2} (\varvec{x})= & {} 1 - h_{M-1}^2(\varvec{x}) - 2^{1} h_{M-2} (\varvec{x}) \le 0 , \end{aligned}$$

  and $0 \le x_i \le 1$. Here, the function $g^c_9(\varvec{x})$ is defined as: $g^c_9(\varvec{x}_{M:d}) = \sum _{i=M}^d (x_i-0.5)^2$ , $\theta _0 = \pi x_1 /2$ and for $i=2,\ldots ,d$,

  $$\begin{aligned} \theta _i = \frac{\pi (1+2g(\varvec{x}_{M:d}x_i))}{4(1+g(\varvec{x}_{M:d})}. \end{aligned}$$

  $\varepsilon$ is set to 0.5. There exist a continuum of solutions that satisfy $\varvec{x}_{M:d}=0.5$ and $\varvec{x}_0 = \frac{2}{\pi } sin^{-1} (\varepsilon )$.

• 10. DTLZ9 (Deb et al. 2005), adapted as an $\varepsilon$-constraint problem:

  $$\begin{aligned} f^c_{10} (\varvec{x}) = \sum _{i=0}^{\lfloor d/M \rfloor } \varvec{x}_i^{p} \end{aligned}$$

  subject to :

  $$\begin{aligned} h_{1} (\varvec{x})= & {} \sum _{i=\lfloor d/M \rfloor }^{\lfloor 2d/M \rfloor } \varvec{x}_i^{p} \le \varepsilon , \\ h_{2} (\varvec{x})= & {} \sum _{i=\lfloor 2d/M \rfloor }^{\lfloor 3d/M \rfloor } \varvec{x}_i^{p} \le \varepsilon , \ldots \\ h_{M-1} (\varvec{x})= & {} \sum _{i=\lfloor (M-1)d/M \rfloor }^{d} \varvec{x}_i^{p} \le \varepsilon , \\ h_{M} (\varvec{x})= & {} 1 - h_{M-1}^2(\varvec{x}) - (f^c_{10} (\varvec{x}))^2 \le 0, \\ h_{M+1} (\varvec{x})= & {} 1 - h_{M-1}^2(\varvec{x}) - h_{1}^2 (\varvec{x}) \le 0, \\ h_{M+2} (\varvec{x})= & {} 1 - h_{M-1}^2(\varvec{x}) - h_{2}^2 (\varvec{x}) \le 0, \ldots \\ h_{2M-2} (\varvec{x})= & {} 1 - h_{M-1}^2(\varvec{x}) - h_{M-2}^2 (\varvec{x}) \le 0, \end{aligned}$$

  and $0 \le x_i \le 1$. We set $\varepsilon$ to 0.5 and $p=1$. The minimum is approximately $\varvec{x}_{1:d-1} = (\frac{\varepsilon }{\alpha })^{\frac{1}{p}}$, where $\alpha = \text {max}_j \big (\lfloor (j+1)d/M \rfloor \big ) - \big (\lfloor jd/M \rfloor \big )$. $\varvec{x}_d$ is the minimum value that satisfies $h_{M:2M-2}(\varvec{x})$.

Table 5 Number of Latin Hypercube initializations (5 total) that were feasible i.e. had at least one evaluation within initialization set which was feasible

Effect of Kriging stabilization strategies on surrogate performance

It is well known that the numerical stability of the Kriging procedure becomes a concern as number of observations increase (Diamond and Armstrong 1984). On the other hand, an artificial regression of the predictor to the mean may lead to uninformative surrogates (Li and Sudjianto 2005; Sasena 2002). To make the Kriging surrogate more robust, we consider two methods: (1) nuggeting (Sacks et al. 1989; Peng and Wu 2014; 2) $L_2$ penalized likelihood (Li and Sudjianto 2005). Nuggeting, in its simplest form, applies a small positive perturbation along the diagonal of the covariance matrix. Hence, it acts as a regularization in the vein of ridge regression. Penalized likelihood involves directly penalizing the maximum likelihood objective with a measure of the hyper-parameter size. This is favorable in situations of an insensitive likelihood function, leading to poor identifiability of hyper-parameters. Both methods have distinct benefits; the former ensures robustness in event of pile-up (Booker 2000) or clustering of design points that are close by, while the latter makes the estimation of hyper-parameters robust to artificially large hyper-parameter values.

The overall impact of these stabilization methods for the Surr-min SEARCH strategy applied to the benchmark set (Appendix A), is summarized in Fig. 19. A nugget value of $10^{-7}$ is applied for nuggeting. The performance and data profiles are drawn with $\tau =10^{-3}$. The overall performance of the optimization method is improved when both penalization and nuggeting are employed in conjunction. Both nuggeting and penalized likelihood show an improvement over Surr-min without stabilization, indicating that each method individually has a favorable impact on optimization. These strategies were integrated into the surrogate construction for all strategies studied.

Fig. 19

Performance (left) and data profiles (right) based on number of evaluations, for different stabilization methods: Nuggeting (nug), regularization via penalized likelihood (reg), with both nuggeting and penalized likelihood (nugreg) and no stabilization (nostab)