A game-theoretic optimisation approach to fair customer allocation in oligopolies

Abstract

Under the ever-increasing capital intensive environment that contemporary process industries face, oligopolies begin to form in mature markets where a small number of companies regulate and serve the customer base. Strategic and operational decisions are highly dependent on the firms’ customer portfolio and conventional modelling approaches neglect the rational behaviour of the decision makers, with regards to the problem of customer allocation, by assuming either static competition or a leader-follower structure. In this article, we address the fair customer allocation within oligopolies by employing the Nash bargaining approach. The overall problem is formulated as mixed integer program with linear constraints and a nonlinear objective function which is further linearised following a separable programming approach. Case studies from the industrial liquid market highlight the importance and benefits of the proposed game theoretic approach.

1 Introduction

1.1 Motivation

Current socioeconomic trends such as market globalisation, interconnectedness of firms and the ever-increasing capital intensive environment begin to lead to a paradigm shift on the market structure of process industries. Financial sustainability, competition elimination and market share growth are a few reasons that lead businesses in mature markets to form coalitions leading to oligopolistic market structures (Ziss 2007; Nagarajan and Sošić 2008). Oligopolies are formed when a limited number of companies rule in a particular market offering similar goods and typical examples from the process industry include the steel, food, pharmaceutical and specialty gases sector. Many of the strategic, tactical and operational decisions of industrial companies are directly related to the firms’ customer portfolio ranging from future investment planning to satisfying daily demands.

In this paper we study the problem of fair customer allocation in oligopolies for the case that new customers appear and provide market share growth opportunity for the firms from a decentralised game-theoretic viewpoint. The firms that comprise the oligopoly agree to allocate the new customers in a fair manner while at the same time they can re-assign existing ones so as to maximise their respective profits. The goal of this paper is: (i) to introduce a new approach for the problem of customer allocation in oligopolies and (ii) apply game-theoretic concepts to ensure the fair optimisation of the market under study.

The remaining of the paper is organised as follows: in Sect. 1.2 a literature review on the game theoretic optimisation of supply chain systems is conducted. Section 2 introduces the problem statement that is addressed in the present work whereas the key mathematical developments are detailed in Sect. 3. Next, in Sect. 4 two case studies are examined from the industrial liquids market and the key findings are discussed while conclusions and future research directions are outlined in Sect. 5.

1.2 Literature review

The progressive competition within supply chain systems along with the individual objectives and constraints of the supply chain participants have led many researchers to study the impact of such decentralisation in the optimal decision making (Papageorgiou 2009; Barbosa-Póvoa and Pinto 2018). In contrast to centralised modelling approaches, the interdependence of individual decisions, constraints and potentially conflicting objectives of the supply chain participants are explicitly taken into account (Shah 2005; Sahay and Ierapetritou 2013). Due to the nature of such systems, the formalisation of the optimisation problem needs to reflect the hierarchical structure of the market under study and to this end different methods have been employed such as bilevel programming, tailor-made iterative frameworks as well as Nash equilibrium methods to name a few.

Sherali and Leleno (1988) studied the existence, characterisation and computation of a two-stage oligopolistic network and they provided theoretical results that should hold for a market equilibrium to exist. The multi-period resource allocation problem was treated by Klein et al. (1992) with a lexicographic minimax algorithm that the authors proposed. Within the lexicographic minimax methods the concept of fairness is closely related to that of Pareto optimality, i.e. the solution returned from these methods is Pareto optimal in the sense that no preference by the decision maker was taken into account and also the optimal decision vector is non-dominated. Lexicographic minimax optimisation has also been applied successfully to location problems (Ogryczak 1997) in order to compute fair non-dominated solutions.

Later on, Nash strategies among multi-enterprise supply chains for the fair optimisation of transfer prices were proposed by Gjerdrum et al. (2001, 2002). In a series of papers, the authors considered the problem of transfer price and inventory optimisation and two different solution approaches were presented. A separable programming approach with exact linearisation of bilinear terms and a spatial and binary branch and bound procedure that solved the original MINLP problem as a series of MILPs (Gjerdrum et al. 2001).

Levis and Papageorgiou (2007) derived analytical formulae for the Nash equilibrium of Bertrand games for the special case of single product duopolies. Apart from the analytical formulae, an iterative algorithm for game theoretic price optimisation of multi-product competing companies was proposed and allowed the computation of the corresponding Nash equilibrium. Erkut et al. (2008) reported a multi-objective optimisation approach for the solution of the location-allocation problem in solid waste management and applied their methodology in a case study from Greece. The authors seeked for fair solutions in a Pareto-optimality fashion and devised an approach for the iterative solution of the resulting lexicographic minimax problem. It is interesting to note that their approach is applicable for either convex or nonconvex decision spaces. Zhao et al. (2010) as well as Cao et al. (2013) studied the cooperative game of decentralised supply chain between manufacturer and retailers under demand disruptions. In the first study a Nash approach was employed whereas in the second the authors followed the Stackelberg approach. In general, the Stackelberg approach is employed in cases of hierarchical games with a certain leader and a number of followers while such assumption in the Nash setting is not required. The construction of Pareto-optimal fair solution in a game theoretic context has been proposed by Zamarripa et al. (2012) where the authors computed the pay-off matrix of the game through a series of multi-objective MILPs.

Cooperative allocation of cost savings in decentralised supply chains using different methods from cooperative game theory was proposed by Lozano et al. (2013). Berglund and Kwon (2014), studied the facility location problem of a Stackelberg firm in the case of a Cournot-Nash game. The price functions of the different firms are modelled via inverse demand correlation while the cost function is convex and monotonically increasing with the amount manufactured by each firm. The overall problem was formulated as a mixed integer program with variational inequalities that enforce the achievement of Nash equilibrium for the competing firms. While exhaustive enumeration approaches had been proposed in the past, the authors proposed a heuristic approach that has at its core the simulated annealing paradigm. Zhang et al. (2014) employed the minimax approach for the fair cost distribution of homes that belong to a microgrid. Yue and You (2014a) studied a three-echelon supply chain system where decisions about its design and operation were made by solving a monolithic non-convex MINLP. Their work assumes a single leader, i.e. the manufacturer, and multiple followers, i.e suppliers and customers. The authors model the interaction between manufacturer and suppliers using the Nash bargaining approach while a bilevel formulation is employed to model the arrangements among suppliers and customers. The case of capacity planning in a competitive environment has recently been addressed from Grossmann and co-workers both from a bilevel and a trilevel scope (Garcia-Herreros et al. 2016; Florensa et al. 2017). Game theoretic optimisation of decentralised supply chains under uncertain environment was recently studied by Hjaila et al. (2017). The authors formulated the problem as a non-cooperative, non-zero sum game where apart from the leader/follower set, their interactions with third parties were also considered. The Stackelberg approach was employed and at the end a set “Pareto solutions” were computed and analysed through the solution of a series of non-convex MINLPs. Key decisions in this work were the transfer prices and resource amounts exchanged between the players while Monte Carlo simulations were conducted for the evaluation of uncertainty regarding a set of product prices and demand. The strategic planning of petroleum refineries was recently studied through a game theoretic perspective by Tominac and Mahalec (2017). The authors formulated the problem as a potential game where a number of refineries engaged in a Cournot oligopoly game and solved the resulting non-convex (MI)NLP. Yue and You (2017), proposed a decomposition framework for the solution of a mixed integer bilevel programming (MIBP) problems with application on Stackelberg games for supply chain design and operation. The authors considered the discrete, apart from continuous, decisions of the follower and the leader resulting in computational difficulties for the solution of a single level optimisation problem. To circumvent this issue, initially the discrete decisions of the follower are enumerated thus allowing for the introduction of the KKT conditions of the follower’s problem and then an iterative procedure is employed to avoid complete enumeration. Later on, Liu and Papageorgiou (2018) examined the fair profit allocation of an active ingredient supply chain through the solution of a Nash bargaining game and lexicographic maximin optimisation. Finally, Gao and You (2019) incorporated uncertainty considerations in the game theoretic optimisation of multi-stakeholder supply chains.

2 Problem statement

We study the problem of fair customer allocation in existing oligopolies. It is assumed that the firms which form the oligopoly are rational and that a firm has estimates of the other firms’ information . The fair customer allocation problem is formulated as a static MINLP following the Nash bargaining approach so as to compute the resulting firm profits in the equilibrium along with the assignment of the customers. The MINLP model is then linearised into an MILP using a separable programming approach. Concisely, the problem statement has as follows:

Given:

• Customer portfolio including existing and new customers

• Average customer demand per demand tank and liquid product

• Delivery cost to the customer’s demand tank from firm

• Customer acquisition/forfeit variable and fixed costs

• Third-party production outsourcing costs and tiers

• Product demand swap costs between firms

• Liquid products production capacities of the firms

• Product prices per customer and firm

• Cost of electricity

Compute:

• Optimal customer assignment to the firms

• Optimal production levels of the firms

• Optimal product demand outsourcing levels for the firms

• Optimal product demand swap levels for the firms

So as to:

• Maximise fairly the firms’ profit

As shown by Fig. 1, each company has an existing set of customers (and their tanks) that they serve and each customer is served by only one company. In the next section, we introduce the mathematical model for the fair customer allocation in such oligopolistic markets with emphasis on the industrial liquids industry.

Fig. 1

Conceptual representation of an oligopoly comprised by three companies that serve a number of customer tanks

3 Mathematical developments

In this section, first the model formulation for the customer allocation in oligopolies is presented and next the game-theoretic framework for its fair optimisation is introduced. The nomenclature of the mathematical developments is provided at the end of the article. The key assumptions in the present work are summarised as follows: (i) firms will participate in the game only if they can achieve greater profit than their current one, (ii) deterministic production and service cost, (iii) customer demands are given as their deterministic average values, (iv) firms should serve all customers and (v) decentralised decision making.

3.1 Model formulation

3.1.1 Customer assignment and demand satisfaction

Customers can only be assigned to one firm which should satisfy their entire product demand. To model this, Eq. (1) is employed and the binary variable $X_{cf}$ indicates the assignment of customer c to firm f.

$$\begin{aligned}&\underset{f}{\sum }X_{cf}=1 \qquad \forall c \end{aligned}$$

(1)

The customer’s (c) tank demand (t) for product (i) of each firm (f) can be satisfied either by (i) in-house production ($Q_{ictf}$), (ii) product swaps with competitor ($SF_{ictf^{\prime}f}$) or (iii) product acquisition from spot-market ($O_{ictf}$) as illustrated in Fig. 2.

Fig. 2

Demand satisfaction mechanisms

This is modelled using Eq. (2). The in-house production levels ($Q_{ictf}$) and amount of production swaps to other firms ($SF_{ictff^{\prime}}$) are restricted by the firm’s plant capacity as shown by Eq. (3).

$$\begin{aligned}&Q_{ictf}+\underset{f^{\prime}\ne f}{\sum }SF_{ictf^{\prime}f}+O_{ictf}=D_{ict}X_{cf}\qquad \forall i,c,t\in cti, f \end{aligned}$$

(2)

$$\begin{aligned}&Q_{ictf}+\underset{f^{\prime}\ne f}{\sum }SF_{ictff^{\prime}}\le Cap_{if}\qquad \forall i,c,t\in cti, f \end{aligned}$$

(3)

Note that the in-house capacity for each of the products ($Cap_{if}$) will be dictated by the short cut model that is introduced next.

3.1.2 Plant production short-cut model

Air separation plants are energy intensive and utilise air as raw material in order to produce gaseous nitrogen ($\mathrm {GNI}$), gaseous oxygen ($\mathrm {GOX}$) as well as liquid nitrogen ($\mathrm {LNI}$), oxygen ($\mathrm {LOX}$) and argon ($\mathrm {LAR}$) among others. Even though the main focus of the present work is regarded with the liquid products, the underlying characteristics of the air separation unit (ASU) directly affect the production capacity of the firm so as to satisfy customer demand. In order to incorporate the production capacity and electricity consumption considerations, we employ a surrogate model that captures the interdependence of manufacturing the different liquid products as well as the energy required. The general form of the model is given by Eqs. (4)–(5).

$$\begin{aligned}&PW_{f}= f(V^{f}_{air}, V^{f}_{GNI}, V^{f}_{LNI},V^{f}_{GOX},V^{f}_{LOX},V^{f}_{LAR}) \qquad \forall f \end{aligned}$$

(4)

$$\begin{aligned}&g(V^{f}_{air}, V^{f}_{GNI}, V^{f}_{LNI},V^{f}_{GOX},V^{f}_{LOX},V^{f}_{LAR})\le 0 \qquad \forall f \end{aligned}$$

(5)

where ${PW_{f}}$ is the electricity power consumed and ${V^{f}_{air}, V^{f}_{GNI}, V^{f}_{LNI},V^{f}_{LOX}}$, ${V^{f}_{GOX}}$, $V^{f}_{LAR}$ stand for the volumetric flows of the air and the different gaseous and liquid products. A graphical representation of the main flows that are tracked using the short-cut model, in which no gaseous oxygen is produced, is given by Fig. 3 whereas the key equations are summarised below.

Fig. 3

Main component flows tracked by the short-cut ASU model

$$\begin{aligned}&V^{f}_{NI}= \delta ^{f}_{1}V^{f}_{air} \qquad \forall f \end{aligned}$$

(6)

$$\begin{aligned}&V^{f}_{LNI^{ASU}}+V^{f}_{LNI}=\delta ^{f}_{2}V^{f}_{GNI^{Liq}}\qquad \forall f \end{aligned}$$

(7)

$$\begin{aligned}&V^{f}_{LNI^{ASU}}=\delta ^{f}_{3}V^{f}_{LOX}\qquad \forall f \end{aligned}$$

(8)

$$\begin{aligned}&V^{f}_{GNI^{Vent}}=V^{f}_{NI} + V^{f}_{LNI^{ASU}} - V^{f}_{GNI^{Pip}}-V^{f}_{GNI^{Liq}}\qquad \forall f \end{aligned}$$

(9)

$$\begin{aligned}&{\underline{V}}^{f}_{GNI^{Pip}}\le V^{f}_{GNI^{Pip}}\le {\overline{V}}^{f}_{GNI^{Pip}}\qquad \forall f \end{aligned}$$

(10)

$$\begin{aligned}&{\underline{V}}^{f}_{GNI^{Liq}}\le V^{f}_{GNI^{Liq}}\le {\overline{V}}^{f}_{GNI^{Liq}}\qquad \forall f \end{aligned}$$

(11)

$$\begin{aligned}&{\underline{V}}^{f}_{air}\le V^{f}_{air}\le {\overline{V}}^{f}_{air}\qquad \forall f \end{aligned}$$

(12)

$$\begin{aligned}&V^{f}_{LOX}\le {\overline{V}}^{f}_{LOX}\qquad \forall f \end{aligned}$$

(13)

$$\begin{aligned}&V^{f}_{LAR} = \delta ^{f}_{4}V^{f}_{air} \qquad \forall f \end{aligned}$$

(14)

Equation (6) models the amount of nitrogen in air that is recoverable as a product. Equations (7)–(9) are mass balances of the ASU, liquefier and pipeline, respectively. The lower (${\underline{V}}^{f}_{GNI^{Pip}}$) and upper (${\overline{V}}^{f}_{GNI^{Pip}}$) levels on the flow of gaseous nitrogen through the pipelines of the plant are established by Eq. (10); similar bounds for the flow of gaseous nitrogen in the liquefier, air in the ASU and output of liquid oxygen is are given by Eqs. (11)–(13). Finally, for the calculation of liquid argon (LAR) production, it is assumed that the quantity can be calculated as a proportion ($\delta ^{f}_{4}$) of the argon recoverable from the volume of the air processed as shown by Eq. (14). Notice that parameters $\delta ^{f}_{i} \, \forall i=1,2,3,4$ are dependent on the plant design of each firm (f).

3.1.3 Spot market product acquisition

Product acquisition from spot market is allowed at higher costs. To model this, the positive variable O_ictf is introduced to express the quantity of product i that is acquired from spot market by firm f. Acquiring product amounts from the spot market incurs in general higher costs to the firm and it is assumed that the relevant costing mechanism follows a piecewise constant paradigm as shown by Fig. 4. We assume (b) different, not necessarily continuous tiers, and each tier has its respective lower and upper bounds ($\gamma _{b}^{L},\gamma _{b}^{U}$) in terms of spot market capacities along with the corresponding spot market premium costs ($OC_{icftb}$). Mathematically this is modelled using SOS1 integer formulation as shown by Eqs. (15)–(18). The positive variable ${\hat{O}}_{ictfb}$ is employed to model the disaggregated counterpart, per tier, of $O_{ictf}$.

Fig. 4

Spot market product acquisition piecewise constant modelling

$$\begin{aligned}&O_{ictf}=\underset{b}{\sum }{\hat{O}}_{ictfb}\qquad \forall i,c,t \in cti ,f\end{aligned}$$

(15)

$$\begin{aligned}&\gamma _{b}^{L}Y_{ifb}\le \underset{c,t\in cti}{\sum }{\hat{O}}_{ictfb}\le \gamma _{b}^{U}Y_{ifb}\qquad \forall i,f,b\end{aligned}$$

(16)

$$\begin{aligned}&\underset{b}{\sum }{\hat{O}}_{ictfb}\le D_{ict}X_{cf}\qquad \forall i,c,t \in cti,f\end{aligned}$$

(17)

$$\begin{aligned}&\underset{b}{\sum }Y_{ifb}\le 1\qquad \forall i,f \end{aligned}$$

(18)

Equation (15) is employed to dissaggregate the overall outsource amount into different tiers and the lower and upper bounds of each tier are given by Eq. (16). Equation (17) is a logic constraint which implies that customer demand can be acquired by the spot market only if the customer is currently served by the firm and finally Eq. (18) defines that at most one tier can be selected for spot market acquisition of product demand for each product type (i) and firm (f).

3.1.4 Inter-firm swap agreements

Another way for a firm to satisfy customer demand that exceeds its current in-house capacity, is to hold a swap agreement with another firm. In contrast to acquiring products from the spot-market, the firms which swap product demand hold a bilateral contract with specified terms and conditions on the amount of products and cost mechanisms. It is assumed that there exists an upper bound ($U_{i}$) on the amount of product demand that can be swapped ($SF_{ictff^{\prime}}$) as shown by Eq. (19). Furthermore, a firm cannot request to swap customer demand unless the related customer is assigned to them as indicated by Eq. (20).

$$\begin{aligned}&\underset{c,t\in cti,f^{\prime}\ne f}{\sum }SF_{ictff^{\prime}}\le U_{i} \qquad \forall i, f \end{aligned}$$

(19)

$$\begin{aligned}&SF_{ictff^{\prime}}\le D_{ict}X_{cf^{\prime}} \qquad \forall i,c,t \in cti, f,f^{\prime}\ne f \end{aligned}$$

(20)

We also assume that there is a condition on the swapping agreement that requires the two companies to swap products of equal amount as shown by Eq. (21).

$$\begin{aligned}&\underset{i,c,t \in cti}{\sum }SF_{ictff^{\prime}}=\underset{i,c,t \in cti}{\sum }SF_{ictf^{\prime}f}\qquad \forall f, f\ne f^{\prime} \end{aligned}$$

(21)

3.1.5 Customer service cost

The customer service cost (${SC_{f}}$) accounts for the different demand satisfaction mechanisms under consideration. Firstly the unit service cost of serving a specific customer tank (${USC_{icf}}$) is calculated as ${USC_{ictf}=\frac{DC_{ictf}}{Dem_{ict}}}$, where ${DC_{ictf}}$ is the average delivery cost of firm f for serving customer’s c tank t. The first term as shown by Eq. (22) reflects the monthly average delivery cost for the case of in-house production. The second term reflects the cost incurred by the swaps, where a swap premium is involved (${SWC_{iff^{\prime}}}$) and is assumed to involve $\eta _{f^{\prime}f}-$times higher costs, depending on the inter-firms contracts established, for the firm compared to the in-house production and delivery as shown by Eq. (23). The last term of Eq. (22) reflects the cost of spot market product acquisition, where similarly to the swap’s cost, a spot market premium is considered depending on the related tier. Each tier is associated with a different premium (UOC_b).

$$\begin{aligned} SC_{f}= & {} \underset{i,c,t \in cit}{\sum }USC_{ictf}Q_{ictf} +\underset{i,c,t \in cit,f^{\prime}\lnot f}{\sum }SWC_{icf^{\prime}f}SF_{ictf^{\prime}f} \nonumber \\&+ \underset{i,c,t \in cit,b}{\sum }OC_{icfb}{\hat{O}}_{ictfb}\qquad \forall f \end{aligned}$$

(22)

$$\begin{aligned} SWC_{icf^{\prime}f}= & {} \eta _{f^{\prime}f} USC_{icf}\qquad \forall i,c,f^{\prime}\ne f \end{aligned}$$

(23)

$$\begin{aligned} OC_{icfb}= & {} UOC_{b}(USC_{icf}+UPC_{i})\qquad \forall i,c,f,b \end{aligned}$$

(24)

3.1.6 Customer acquisition cost

The customers that are not served by any company provide market share growth opportunity. On top of that, if a customer is dropped by a company, it can be acquired by the competitors. In order to acquire new customers, companies have to pay a fixed (${FNC_{cf}}$) and a variable cost (${VNC_{ctf}}$) to cover expenses related to the installation and maintenance of the new tanks. Eq. (25) is employed to model the overall cost of acquiring new customers.

$$\begin{aligned} NC_{f}=\underset{c\notin C_{f}}{\sum }FNC_{cf}X_{cf} + \underset{i,c,t \in cti \wedge \notin C_{f}}{\sum }VNC_{ctf}D_{ict}\qquad \forall f \end{aligned}$$

(25)

Notice that in Eq. (25), only the customers that are not already served by the firm are considered using the set $C_{f}$ which is the set of firms’ existing customers. This is achieved by excluding the customers that belong to the set $C_{f}$ from the related summations in Eq. (25).

3.1.7 Customer forfeit cost

A firm is allowed to forfeit a customer it already serves but this results in a fixed, ($FDC_{cf}$), and a variable penalty, ($VDC_{ctf}$). The variable penalty is dependent and proportional to the demand of the customer and the overall cost of dropping a customer for a company is given Eq. (26).

$$\begin{aligned} RC_{f}=\underset{c\in C_{f}}{\sum }FDC_{cf}(E_{cf}-X_{cf})+\underset{c\in C_{f}}{\sum }VDC_{ctf}\underset{i}{\sum }D_{ict}\cdot (E_{cf}-X_{cf})\qquad \forall f \end{aligned}$$

(26)

3.1.8 Power consumption cost

The operation of ASU plants is an energy intensive process and the electricity costs involved are significant. Their calculation is based on Eq. (27).

$$\begin{aligned} EC_{f}=EPC\cdot MT\cdot PW_{f}\qquad \forall f \end{aligned}$$

(27)

where EPC is the average electricity unit price, MT is the average operating uptime of the ASU plant.

3.1.9 Profit calculation

The profit of each firm f is calculated as the difference between the revenue and the total costs incurred by the customers’ activity. The revenue is calculated as the selling price of product i multiplied by the resulting product demand from customers served by each firm. The profit $\pi _{f}$ for each firm f is given by Eq. (28).

$$\begin{aligned} \pi _{f}=\underset{i,c,t\in cit}{\sum }P_{ictf}\cdot D_{ict}X_{cf}-SC_{f}-RC_{f}-NC_{f}-EC_{f} \quad \forall f \end{aligned}$$

(28)

3.2 Nash game-theoretic solution

The structure of the market, information availability and outlook of the players on cooperativeness are critical parameters within a game-theoretic setting. The Nash bargaining approach was introduced by Nash (1951) for the case of two-person game with fixed disagreement payoffs and was generalised to the n-person case (Nash 1951; Harsanyi and Selten 1972). Within this framework, the players have defined objective functions which constitute the game’s payoff vector. The payoff space is assumed to be compact so that a finite solution exists and it is convex for the solution payoffs to be unique. From a game theoretic perspective a game is governed by a number of axioms and these are: (i) individual rationality, (ii) Pareto optimality, (iii) symmetry, (iv) linear invariance and (v) independence of irrelevant alternatives. This full set of axioms results in a unique solution which is commonly referred to as the Nash Equilibrium. Mathematically, the axiom of individual rationality can be expressed as follows: given a status quo point that refers to player’s payoff under disagreement, i.e. the case that no game is established, each player will enter the game only if they can achieve a payoff greater than this point. In the problem under study, this means that a firm will agree on entering the game and its resulting equilibrium solution only if they can achieve profit greater than their current one ($\pi ^{sq}$) as shown by Eq. (29)

$$\begin{aligned} \pi _{f} \ge \pi ^{sq}_{f} \quad \forall f \end{aligned}$$

(29)

For the problem of interest the status quo profits of each firm are computed by fixing the assignment of existing customers and assume that no new customers can be taken by any firm. With this given status quo, the Nash equilibrium of the game is computed as the maximum value of the Nash product which is given by Eq. (30) and can be visualised, for a two-firm game, by Fig. 5.

$$\begin{aligned} \varPhi = \varPi _{f}(\pi _{f}-\pi ^{sq}_{f})^{\alpha _{f}} \end{aligned}$$

(30)

The parameter $\alpha _{f}$ represents the negotiation power of each firm f and the summation of the negotiation power over all the firms equals to 1. By manipulating the value of the parameter $\alpha _{f}$ it is possible to investigate scenarios when the players have an advantage over the other competitors. For example, in the case of a duopoly, setting the the negotiation power of a player close to 1 and the other player’s close to zero, emulates a leader-follower setting.

Fig. 5

Conceptual representation of the Nash bargaining solution for the case of duopoly with firms A and B

The Nash bargaining approach is inherently nonlinear and nonconvex due to its objective function, i.e. Eq. (30) which can result in computationally demanding problems. In order to alleviate the related computational complexity, Gjerdrum et al. (2001) proposed a separable programming approach so as to linearise approximately the Nash product. Initially, the logarithmic transformation is applied on Eq. (30) resulting in Eq. (31).

$$\begin{aligned}&\varPsi = ln\varPhi = \underset{f}{\sum }\alpha _{f}ln(\pi _{f}-\pi ^{sq}_{f}) \end{aligned}$$

(31)

Equation (31) is still nonlinear but now the objective function is strictly concave. Hence, it can be approximated via the piecewise linear function ${\tilde{\varPsi }}$ over a number of k grid points as shown by Eq. (32).

$$\begin{aligned}&{\tilde{\varPsi }}= \underset{f}{\sum }\underset{k}{\sum }\alpha _{f}ln({\tilde{\pi }}_{fk}-\pi ^{sq}_{f})\lambda _{fk} \end{aligned}$$

(32)

where the parameter ${\tilde{\pi }}_{fk}$ stands for the profit of firm f at grid point k and $\lambda _{fk}$ is a SOS2 variable Williams (2013) which implies that only two adjacent grid points take nonzero values and satisfy Eq. (33). Effectively, following this approach one discretises the strictly concave function over the number of grid points and the true solution can approximated as the convex combination two adjacent grid points over a line segment. Increasing the number of grid points, results in finer discretisation and thus error reduction with the number of grid points increasing until sufficient accuracy is achieved. The profit of each company can be calculated by Eq. (34).

$$\begin{aligned}&\underset{k}{\sum }\lambda _{fk}=1\qquad \forall f \end{aligned}$$

(33)

$$\begin{aligned}&\pi _{f} = \underset{k}{\sum }{\tilde{\pi }}_{fk}\lambda _{fk} \qquad \forall f \end{aligned}$$

(34)

Overall, the proposed mathematical model comprises of Eqs. (1)–(29) and is formulated as an MINLP with objective function Eq. (30) and as an MILP by substituting Eq. (30) with Eqs. (32)–(33). In the next section, the proposed approach is employed for two cases studies involving a duopoly and an oligopoly. In order to further compare the value of the game theoretic solution, we compare it with two alternative centralised formulations, namely Naive (I) & Naive (II). The Naive (I) formulation maximises the overall profit of the market as shown by Eq. (35) subject to Eqs. (1)–(28). The Naive (II) formulation also maximises the overall market profit, i.e. Eq. (35), subject to Eqs. (1)–(28) but also imposes that each player should achieve a resulting profit at least as high as its current status quo, i.e. Eq. (29). Notice that the Naive formulations, indicate the centralised decision-making setting, where a single decision-maker optimises the supply chain problem under study by optimising the overall profit. An overview of the proposed mathematical models is given in Table 1

$$\begin{aligned}&\varOmega = \underset{f}{\sum }\pi _{f}\qquad \end{aligned}$$

(35)

Table 1 Scope and mathematical formulations of the proposed mathematical models

4 Case studies

To demonstrate the proposed modelling and solution framework, we present two case studies on the fair customer allocation in industrial liquid oligopolistic markets. Firstly, the case of a duopoly is examined to illustrate the efficiency of the proposed framework and results from the sensitivity analysis with regards to the firms’ negotiation power are presented. Next, the case of an oligopoly comprised by three firms is investigated. All the computations were performed using a Dell workstation with Intel$\circledR$ Core^TM i7-5600 CPU @ 2.60 GHz and 16.00 GB RAM. The implementation and computations were executed using GAMS 25.1.2 (Rosenthal 2012). CPLEX 12.8 was used for solving the MILP while BARON 18.5.8 (Tawarmalani and Sahinidis 2005) for the global solution of the single-level MINLP problem.

For the customers that have monthly demand between 0 and 14,000 m³ the variable cost of acquisition is $VNC_{ctf}$, for customers that have demand levels between 14,000 and 28,000 m³ is $2\times VNC_{ctf}$ and for the customers that demand more than 28,000 m³ the variable cost of acquisition is $2.5\times VNC_{ctf}$ . The fixed acquisition cost is assumed to be $FNC_{cf}$ while the fixed forfeit cost is $FDC_{cf}=2\times FNC_{cf}$. The variable dropping cost for each customer ($VDC_{ctf}$), depending on the total customer’s demand, is assumed to be 2%, 5% and 10% of their unit service cost.

4.1 Liquid market duopoly

In this case study, the fair customer allocation in a duopoly was considered. Each customer can be served by a number of storage tanks and places orders for LOX and LNI- there is no LAR demand. Initially, firm A serves 44 customers and firm B 38 customers while there exist 16 new customers that provide opportunity for market share growth.

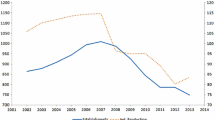
The companies can acquire products from spot market and the tiers considered herein are (i) [0–50,000 m³], (ii) [51,000–450,000 m³], (iii) [460,000–7,500,000 m³] with related spot market premiums ($UOC_{b}$) being 1.6, 1.4 and 1.3. The average plant up-time is considered to be 672 h per month while the unit electricity cost is 40 $/MWh. The production envelopes of the two firms can be envisaged in Fig. 6 where the values have been normalised. Fig. 7 illustrates the market product demand as it is currently covered by firms A and B along with the one resulting from the new customers.

Fig. 6

Production envelopes for the two firms of the duopoly case study

Fig. 7

Product demand for LOX and LNI among firm A and B and the demand placed by new and existing customers

First, the model is run with fixed customer assignment decisions and no new customers are allowed to be allocated so as to compute the status quo profits of the firms. The market share of each company is computed as the percentage of the firm’s profit with respect to the overall profit generated by the market. Firm A holds 63.1% of the market share while Firm B 36.9%, based solely on the customers served.

4.1.1 Nash equilibrium results

With the status quo profits computed, the game-theoretic model is subsequently solved both as an MINLP and MILP and the related results are compared. The MINLP model comprises of 2,669 equations, 4,003 continuous variables and 208 binary variables and is solved to global optimality using BARON 18.5.8 within 62.5 CPU (s). The Nash equilibrium results in a 7.3% profit increase for firm A while firm’s B profit is increased by 34.2% compared to their status quo values and a 55/45% market share allocation for the two firms respectively. Acquisition of new customers is one of the two main causes for the profit increase while the other one is the reallocation of existing customers among the firms which leads to reduction in distribution costs.

The importance of the game theoretic solution is further underlined when compared to the naive approach where one would seek maximisation of the overall profit generated by the two firms regardless of the decentralised structure of the market. Such a “naive approach”, results in significant market share reductions for firm A down to 50.6% while firm’s B market share is increased to 49.4%. However such case is not realisable since it benefits greatly the weak player of the game who increases their profit by 72% when firm A achieves merely 3.2% profit increase in this case. A graphical illustration of the aforementioned results is given in Fig. 8.

An interesting insight with regards to the effect of negotiation power and the game theoretic solution on the overall profit generated by the duopoly is given by Fig. 8. The highest overall profit is achieved when the decentralised nature of the market is completely neglected and the naive optimisation is employed. The biggest impact on the overall profit is attributed the negotiation power of the firm with the highest market share before the game, in this case firm A. As indicated by the graph in Fig. 8, when A is assumed to be the follower, i.e. when its negotiation power is assumed to be negligible ($\alpha _{A}=0$), the profit approaches the one computed by the naive approach and it is the second highest.

On the other hand, when firm A is the leader, i.e. its negotiation power is assumed to be absolute, the overall profit is the lowest as it completely disregards the synergies that can be exploited by the collaboration between the two companies of the duopoly through the exploitation of inter-firm swaps. The Nash approach provides the third highest overall profit, a reflection of the trade-off between the decentralised decision making in the duopoly and the fair profit generation.

Fig. 8

Impact of negotiation power and game theoretic solution on the overall profit generated by the duopoly

Considering the costs incurred by the customer demand a comparative analysis was conducted for the Nash equilibrium and the solution computed by the naive approach. As shown in Fig. 9, following the naive approach the different firms do not forfeit any of their customers while on the Nash equilibrium both firms do with firm’s B forfeit costs being twice as high as firm’s A. Higher utilisation of the inter-firm swap agreements is achieved in the Nash equilibrium which subsequently reduces the absolute value of power consumption cost for firm A. Finally, only firm A acquires products from the spot market in both cases and following the Nash approach the related costs are 37% higher compared to the naive. With regards to customer allocation in the Nash equilibrium, firm A forfeits 13 of its customers which are acquired by firm B while firm B forfeits 5 customers and that are acquired by firm A. As shown in Table 2, 5 of the new customers are acquired by firm A and 11 by firm B. The resulting overall customer allocation is 47 for firm A and 51 for firm B. It is interesting to note that on the equilibrium even though firm A acquires fewer customers than firm B, its new customers provide higher profit margin compared to the ones forfeited. Next, the MILP model was solved for varying numbers of grid points so as to quantify the trade-off between computational savings and approximation error in comparison to the MINLP model. Table 3 summarises the key results for four different levels of discretisation. In the beginning, 10 grid points were employed for the piecewise linear approximation of the Nash objective; the model comprised of 2673 equations, 4013 continuous variables and 208 binary variables with a considerable approximation error of 3.6%. As indicated in Table 3, increasing the number of grid points improves significantly the quality of the approximation without resolving in extensive computational times. More precisely, the MILP model with 100 grid points computes in 0.75s a solution almost identical to the global optimum of the original MINLP model with an approximation error of 0.054%.

Fig. 9

Firms’ costs for the allocation and service of customer demand in the duopoly case study

Table 2 Customer allocation and flows between firms on the Nash equilibrium for the duopoly case study

In addition to the error related to the objective function, the Hamming distance between the approximate and the global MINLP solution was computed. The Hamming distance is an information theory based similarity criterion that measures the minimum number of substitutions for two binary arrays to be identical (Norouzi et al. 2012). In our case, the binary arrays compared were the optimal allocation binary array ($X_{c,f}$) between the approximate and the global solution. As the number of grid points (k) increases the hamming distance is reduced and notice that in the case of k=100 even though the overall difference in customer allocation between the two firms is 1, the corresponding Hamming distance is 3 meaning that two more customers have been assigned differently. Finally, we implement the Branch and Refine (B&R) algorithm proposed by Bergamini et al. (2008) through which the global optimisation of the logarithmic objective function can be achieved via successive outer approximations (Yue and You 2014b). We initiate the algorithm with two grid-points and then grid is propagated using the bisection method. The algorithm converges in 2.84s with 9 iterations and a total of 11 grid points are used as shown in Fig. 10. The interested readers can find more details on the specifics of the algorithm in the works of Bergamini et al. (2008) and Yue and You (2014b).

Fig. 10

Branch and Refine algorithm’s convergence for the liquid market duopoly. The upper bound is derived by solving the outer approximation MILP of the original problem while the lower bound is updated by evaluating the original nonlinear objective function on the solution space of the MILP

Table 3 Comparison of the MILP and MINLP model results

4.1.2 Negotiation power sensitivity analysis

As mentioned in the Sect. 3.2, the Nash bargaining approach can facilitate the case where the different players have unequal negotiation power by adjusting the parameter $\alpha _{f}$ so as to indicate the hierarchy of the market. In order to evaluate the effect of the negotiation power on the resulting Nash equilibrium sensitivity analysis was conducted with varying the negotiation power of each player from 0 to 1.

Figure 11 illustrates the effect of the negotiation power of each firm on their resulting market share at the Nash equilibrium. An interesting observation is that when firm B has negotiation power greater than 0.8, i.e. when firm B is strongly the leader, its market share approaches the one computed by the naive approach. The general trend as expected indicates that the bigger negotiation power a firm has the better market share it can achieve at the Nash equilibrium. In the case study examined however, firm A achieves consistently to hold more market share compared to firm B even in the cases that it has little to none negotiation power. This can be attributed to its advantageous position at the status quo before the game.

Fig. 11

Effect of the firms’ negotiation power on their market share in the Nash equilibrium. Notice that the case where $\alpha _f=0.5$ is the default scenario of the game theoretic approach (MINLP model results)

Similar trends were observed with regards to the effect of the negotiation power on the equilibrium customer allocation among the firms and this can be envisioned by Fig. 12. However, the absolute number that a firm serves can be a misleading indicator of the firm’s market position and this can be observed for instance when firm A is assumed to have 0.7 negotiation power while firm B 0.3 with the resulting customer allocation being 38 and 60 respectively. Comparing this with the firms’ market share one can see that even though firm B serves more customers than firm A its market share is considerably less (45%) and this is related to the customer’s profit margin that each firm serves.

Fig. 12

Sensitivity analysis results on the customer allocation among the duopoly firms for varying negotiation power (MINLP model results)

4.2 Liquid market oligopoly

In the present case study the fair customer allocation among 3 different firms was examined. A total of 81 customers were considered with 119 storage tanks and demand for LOX, LNI and LAR of whom 13 are new. Initially, firm A serves 21 customers, firm B 17 and firm C 30. In the status quo, before the allocation of the new customers, 56% of the market share is held by firm C while firms A and B hold 24% and 20% respectively. Moreover, firm B is assumed to have an on-site customer with GNI demand. The operational envelopes of the firms can be envisaged in Fig. 13. The operational envelopes in this case study can provide some insights with regards to the firms’ participation in the game. For instance, Firm A has rather constrained production flexibility which may hinder its negotiation potential while the same can be speculated for firm B which despite having the nominally bigger operational envelope, has an onsite customer which constraints its operational flexibility.

Fig. 13

Production envelopes for the oligopoly case study

First, the Nash model of the case study was formulated so as compute the resulting equilibrium. The MINLP model consists of 1,990 equations, 2,815 continuous variables and 270 binary variables and is solved to global optimality in 116.65 CPU(s). On the Nash equilibrium, the profit increase is 71.4%, 83.4% and 24.9% for firms A, B and C respectively while related market share percentages are 27%, 25% and 48%. Compared to their status quo values, as shown in Fig. 14, it is seen that the Nash approach benefits the firms proportionally and allows for firm B to achieve higher improvement in its resulting market share due to its considerably higher production capability. Notice that the change in the market shares of the firms between the status quo and the other model formulations is due to the increase of the overall supply chain profit due to the entry of new customers. At the status quo, no new customers are assigned to the firms and firm C holds 55% of the market. After the status quo, new customers are allowed to be allocated among the firms and that leads to firm C holding 48% in the Nash equilibrium while still making more profit that its status quo due to the newly added customers.

Fig. 14

Market share allocation for the oligopoly case study following different naive approaches and the Nash approach

Next, in this case study two variants of the naive approach, where the objective is to maximise the overall profit of the market, were examined. In the naive approach (I) each player neglects their status quo profits while in the second case (naive approach (II)) each player requires their resulting profit to be increased with regards to their status quo values. As indicated by Fig. 14, the naive approach (I) benefits greatly the weaker firm (B) while the strongest firm (C) loses a significant amount of its profit. This instance is unrealistic as no firm would engage in a game where it will lose their profit for the sake of market equality. From an operational point of view, firm B before the game utilises only 15% of its LOX capacity and 50% of its LNI capacity capabilities while firm A is on average at 70% production capacity and firm C 60%. Following the naive approach (I) firm A reaches capacity bound on its LOX production capability while due its advantageous position, firm B manages to reach 55.5% of its LOX and 65% of its LNI production capacity.

A more realistic, yet still not realisable, market allocation is given by the naive approach (II) where again firms A and C even though having a slight increase in their profit (11.4% for firm A and 0.01% for firm C) their market share is decreased. It is worth mentioning that in this instance the overall profit increase for firm B was 233.9%, a clear indicator of the lack of fairness in profit allocation.

Fig. 15

Cost breakdown for the oligopoly case study following following the Nash and naive (II) approach

Comparing even further the Nash solution to the second variant of the naive approach, no significant changes are found on the power consumption costs for the different firms. On the other hand the overall allocation of the acquisition and forfeit costs are different reflecting the customer allocation shift among the two approaches. The allocation of the different costs among the three firms is shown in Fig. 15. In both of the cases, no firm resorts to spot market acquisition while on the Nash equilibrium the overall power consumption costs are 0.4% lower compared to the naive (II) approach. In terms of overall costs, the Nash approach inflicts 3% higher costs on the market compared to the naive (II) approach. The final allocation of the customers between the three firms is given in Table 4. Firm A gains 5 customers from firm C, 1 from firm B and 5 new customers. Firm B gains 4 new customers and 1 from firm C while firm C gains 5 from firm A, 2 from firm B and 4 new customers. On the Nash equilibrium, thus, firm A serves 27 customers, firm B 19 and firm C 35.

Table 4 Customer allocation and flows between firms on the Nash equilibrium for the oligopoly case study

Figure 16 provides an in-depth insight of the financial motivation on the customer allocation between the firms that comprise the oligopoly. As shown by Fig. 16 the general trend indicates that customers are allocated, following the Nash approach, to the firms for whom they provide the highest profit margin. The curved arrows indicate re-assignment of existing customers from their status quo firm to their Nash equilibrium firm while the star signed bars indicate the allocation of new customers to the firms. When customers are re-assigned to different firms they tend to be allocated to firms that provide better profit margin with the exception when the new company is the one with the majority of market share, e.g. customers c2 and c5. The re-allocation of customer c16 is another example that highlights the value of game theoretic solution since it is assigned to firm A for which higher profit can be achieved compared to the negative margin for the case of firm C.

Fig. 16

Normalised customer margin allocation for the different firms on the Nash equilibrium for new customers ($\displaystyle \star$) and customers that were re-assigned ($\displaystyle \curvearrowleft /\curvearrowright$)

Finally, the effect of operational flexibility on a firm’s resulting market share at the Nash equilibrium was examined. As shown by Fig. 17, the flexibility of the firm’s liquifier loading requirements appears to have significant negative impact on the firm’s resulting market share. The firm’s liquifier loading requirements was altered by manipulating the parameter ${\underline{V}}^{f}_{GNI^{Liq}}$ as shown by Eq. (11). As indicated by Fig. 13, firm B in the nominal case has the biggest production flexibility compared to the other two firms. By increasing the minimum load of the liquifier its production envelope reduces and thus its ability to achieve high market share on the equilibrium is reduced. The gas product demand commitments of the firm have an inverse proportional impact on the market share since their reduction allows the firm to achieve improved market share due to increased flexibility. More specifically, by decreasing the GNI demand by 20% the firm achieves 5% higher market share compared to the nominal case.

Fig. 17

Sensitivity analysis results of varying operational flexibility of Firm’s B and its Nash equilibrium market share

5 Concluding remarks

Considering explicitly the decentralised nature of contemporary supply chain systems when optimal strategic decisions are sought is of great importance. In this paper the problem of fair customer allocation in oligopolies was addressed with emphasis on the industrial liquid markets. A novel single-period mathematical model was introduced for the problem under study and in order to address the fairness considerations the Nash bargaining was proposed. The nonlinear nature of the Nash approach resulted in the model formulation as an MINLP for which globally optimal solutions were computed. A separable programming approach was also discussed for its approximate solution as an MILP with considerable computational savings. As shown by the case studies examined the MILP model solution asymptotically converges to the global solution of the MINLP as the number of points increases. The results indicate the computation of more realistic solutions that account for market power dynamics when the Nash approach is employed in comparison to a centralised naive profit maximisation of the entire system. Future work aims at the extension of the model to the multi-period case in order to account for capacity expansion considerations and the impact of customer contract design on the fair allocation as well as the exploration of uncertainty considerations through the proposed MILP formulation.