1 Introduction

Process optimization is one key component in order to achieve the level of efficiency that is required today in process plants. Among the many different ways in which optimization can be used in the management and control of a plant, operating it in the best possible way is one of the most challenging and, at the same time, rewarding problems because of its complexity and impact on the efficiency and results of the company.

Decisions about the production and operation of a process plant are organized hierarchically in a set of layers, as in Fig. 1 by Darby et al. (2011). This is a simplified schematic not covering other important features, but represents the main elements for the purpose of the paper.

Fig. 1
figure 1

Hierarchical decision layers for process control and operation

Full size image

Basic control is in charge of keeping safety and stability of the plant under control, implementing the control room operators’ or upper layers decisions. The Model Predictive Control (MPC) layer targets improving control by considering the interactions, disturbances and operation constraints associated to process units or small plants. Within the MES/MOM layer, the main element for the purpose of this paper is Real Time Optimization (RTO), which aims at computing the operation points of the process units that optimize production according to a certain criterion while satisfying process constraints. A RTO system normally uses large non-linear models covering a whole plant, section or complex process unit maximizing or minimizing a target limited to that scope. At this point, besides the “local” optimization of process units, RTO has to consider the interactions between the different plants and relevant process units that compose a process factory. If not computed by the RTO layer, the variables associated to the global functioning are normally decided by the plant managers according to experience or heuristics, but these decisions are difficult to take due to the complexity of the problem, lack of information or adequate models, affecting negatively the plant performance.

Of course, at the ERP level, the production planning tools may generate global targets for the different sections of a plant, but these are “averaged” targets to be taken as references for several days or weeks, that are not useful for real-time operation where, due to the variability of products, external disturbances, dynamic decisions are required in order to avoid creating bottlenecks, violating constraints or risking the safe operation of the plant, while being as close as possible to the optimum operating point of the whole plant.

The standard architecture of Fig. 1, with an RTO layer that uses non-linear steady-state models to generate fix targets for the MPC for periods of the order of hours does not manage properly the dynamic aspects above mentioned. Alternatively, the RTO and MPC layers can be combined in an economic MPC or optimal dynamic operation problem as in Engell (2007) and Gonzalez et al. (2001). This approach solves the inconsistency problem between layers that may appear due to the use of different models in RTO and MPC, and it is well stablished for continuous processes, but requires solving large-scale dynamic optimization problems in long computation times in order to allow for real-time implementation, which may be a significant obstacle for its implementation.

This paper proposes another way of considering the joint operation of large-scale RTO with MPC, and illustrates the methodology in a case study corresponding to the hydrogen network of an oil refinery involving the joint operation of 18 plants, first introduced by de Prada et al. (2017), discussing its implementation and results. In addition, uncertainty in the hydrogen demand is incorporated in the nonlinear optimization problem as an extension of the deterministic RTO (with and without risk considerations), analyzed and compared against deterministic results. Furthermore, particular attention is given to discussing the advantages and shortcomings of the two-stage stochastic formulations presented, i.e. risk-neutral and risk-averse.

The paper is organized as follows. After the introduction, Sect. 2 describes the hydrogen network under consideration and the formulation of the optimization problem. Then, Sect. 3 presents the architecture of the system implemented in the refinery and discuss some results. Next, Sect. 4 is devoted to formulate and discuss the stochastic problem considering two alternative aims, risk-neutral and risk-averse. The paper ends with conclusions and references sections.

2 Hydrogen network

2.1 Process description

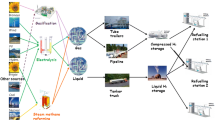
Hydrogen is used in oil refineries with two main purposes: converting heavy hydrocarbons into lighter ones in order to improve the profitability of the business, and removing sulphur from hydrocarbons in order to comply with environmental regulations. Because of that, it has become one key utility in the operation of the refineries. Hydrogen is obtained either from an external supplier or internally from steam reforming plants, as well as a sub-product from the platformer plants used to increase the octane number of gasolines and then it is distributed to the consumer plants through pipelines forming a complex network. A general overview of hydrogen supply chain for general purposes is explored by Ochoa Bique and Zondervan (2018).

In the particular refinery under consideration the network involves 18 plants: two producers of fresh hydrogen, two platformer plants and 14 consumer plants, most of them hydrodesulphurizers connected by means of several headers that operate at different pressures and hydrogen purities as in Fig. 2. Notice that a consumer plant can be fed from different sources.

Fig. 2
figure 2

Source: Gomez (2016)

Schematic of the hydrogen network with producer (grey boxes) and consumer (light grey boxes) plants connected by several headers, among them H4 (red), H3 (light purple) and LPH (blue).

Full size image

A simplified schematic of a typical hydrodesulphuration plant can be seen in Fig. 3. The high sulphur hydrocarbon (HC) feed is mixed with treatment gas (typically around 85–90% hydrogen content, and high pressure) coming from different sources (high and low purity headers, HPH and LPH respectively). This cold mixed stream is heated to reaction temperature, around 300–350 °C, by heat exchangers and a furnace (load heating subsystem, LHS) before going into the reactor. This untreated hot stream reacts on the catalyst fixed bed of the reactor, where the actual desulphurization and other side reactions take place. Due to exothermicity of the reactions, the outlet stream is used to preheat the cold stream load in the heat exchangers within the LHS. The next stage of the process is the separation of gas and liquid, for this purpose the high pressure separator (HPS) is fed with the cooled reactor outlet, and produces two outlets:

  • High pressure sour gas (rich in hydrogen sulphide),

  • Medium or low pressure mixed gas and HC.

Fig. 3
figure 3

Simplified schematic of a generic hydrodesulphuration (HDS) plant. HPH high purity gas header, LPH low purity gas header, HC liquid hydrocarbon, MU make-up, FG fuel gas, HPS high pressure gas/HC separator, LPS low pressure gas/HC separator

Full size image

The mixed stream goes into a stripper to remove the remaining gases, which typically go to fuel gas (FG) after some gas treating aimed at absorbing hydrogen sulphide. The liquid outlet (treated HC) at this stage is ready to be cooled and dried to be pumped into the blending system or stored in tanks.

In the high pressure circuit, gas is recycled back through a compressor, after being sweetened in a gas absorber (hydrogen sulphide removal). In addition, high pressure gas can be fed into a permeation membrane to purify its hydrogen (H2) content, or purged to the LPH (circa 5% less than treatment gas, e.g.: 75–85%).

One important aspect of the operation is the fact that preserving catalyst lifecycle requires hydrogen excess at all times, regardless of the demand. Since hydrogen is a product that is very difficult to store and the plants have variable hydrogen demand according to the type and flow of the hydrocarbons being processed, the producer plants always generate more hydrogen than what is consumed in order to guarantee that enough hydrogen is available under any circumstance. This policy is aimed at protecting catalysts, which are not only an expensive material but also require a plant shutdown to be replaced. Thereby, minimum H2 purity figures are operational constraints, subjected to change over time (e.g.: start of run, or end of run) mainly due to catalyst and load quality conditions. All excess gases across the network end up in the fuel gas header (basic pressure control at plant level), which complemented with natural gas and liquid petroleum gas (LPG) is used to fuel the gas burners plant-wide. As hydrogen is expensive to produce, a good management of the network should coordinate the operation of all plants, matching demand and production in order to minimize losses of hydrogen to FG.

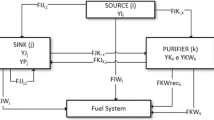
Another key point related to the operation of the reactors is purity management. As mentioned before, the gas recycled from the separation units (HPS) has a lower purity than the treatment gas fed to the reactor, but its purity can be increased using permeation membranes or, after being sent to LPH, reused in other plants either directly or mixed with fresh hydrogen to increase its purity. As a result, the hydrogen network operates with several headers at different purities and pressures as represented in the simplified schematic shown in Fig. 4, which displays two producer units with their corresponding headers, supplying hydrogen to three consumer plants that deliver or consume recycled gas from the LPH, and may also send low purity gas excess to the FG network by it local pressure control valve.

Fig. 4
figure 4

Schematic showing the different types of headers found in a hydrogen network: high purity headers (blue and green), low purity header (brown), fuel gas header (black)

Full size image

Proper management of the network requires deciding in real-time, according to the hydrogen demands from the reactors and variable hydrogen flows generated by the platformer plants, how much fresh hydrogen should be produced by each producer plant, and how to distribute the hydrogen through the network and internally in the consumer plants so that the losses to FG, or in general costs, are minimized. In addition, the operation of the network has to consider as the most important economic target the maximization of the hydrocarbon loads processed in the hydrodesulphurization plants, which may be limited by the hydrogen available and the production aims stablished by the planning of the refinery for the period under consideration. Notice that reducing losses of hydrogen to FG may increase the hydrocarbon processing if hydrogen is the limiting factor, which provides additional value to the optimal management of the network. Of course, optimal decisions must satisfy all process constrains imposed by the equipment, operation, safety, targets or quality.

2.2 Models and data reconciliation

Optimization of the complex system requires proper network and plant models validated against process data. One of the main obstacles in developing these models is the lack of reliable information about many streams and compositions besides the nature of hydrogen. Most of the hydrogen flow measurements are volumetric ones that must be compensated using pressure, temperature and molecular weight of the stream to obtain mass flows. Nevertheless, hydrogen purity measurements are not always available and, even when it is measured, the molecular weight of the stream is unknown and unreliable. This is due to the fact that the gas stream contains impurities (undesired light HC of various sources) of unknown and changing molecular weight much larger than the one of hydrogen (mainly methane and ethane), which is only 2 (g/mol). For example, a stream with purity 90%, where one half of the impurities change composition, for instance from methane to propane, can change the molecular weight of the stream in 41%. Notice that besides flows and compositions, other important variables, such as hydrogen demand in the reactors, are not measured and change over time with the composition of hydrocarbons being processed.

This means that, before any optimization can be performed, a procedure to obtain reliable information from the plant using the plant measurements should be implemented. Data reconciliation can be used for this purpose as it offers a way of estimating the values of all variables and model parameters coherent with a process model and as close as possible to the measurements. Data reconciliation is formulated as a large optimization problem searching for the values of variables and parameters that satisfy the model equations and constraints and that, simultaneously, minimize a function of the deviations (e) between model and measurements, properly normalized.

In our case study, a first principles model of the hydrogen behavior in the network and associated plants was available from previous works by Sarabia et al. (2012) and Gomez (2016). This model is based on mass balances of hydrogen (H2) and light ends (considered altogether as a single pseudo-component, LIG) at all nodes (N) of the network as in the pipelines, headers, and units as in (1a–1d), where F stands for gas flows, X are hydrogen purities, and MW refers to molecular weights. Each k node has outlets i and inlets j streams.

In addition, the model incorporates other first principle and reduced order equations for reactors (2a–2e), membranes (3a–3e), separation units (4a–4f), compressors and headers (1a–1d). Reduced order models are used for permeation membranes fitting their parameters to historical plant data to determine explicitly (3a), following previous works methodologies (Galan et al. 2018; de Prada et al. 2017; Gomez 2016). Table 1 presents a description of all variable and subscripts, while engineering units used in this study are provided in Table 2.

Table 1 Descriptions of variables and subscripts
Full size table
Table 2 Engineering units used, unless explicitly stated otherwise
Full size table

At all nodes N within the network:

$$\mathop \sum \limits_{i, out} F_{k,i} = \mathop \sum \limits_{j,in} F_{k,j} \quad \forall k \in N$$
(1a)
$$X_{H2, k} { \cdot }\mathop \sum \limits_{i,out} F_{k,i} = \mathop \sum \limits_{j,in} X_{H2,k,j} { \cdot }F_{k,j} \quad \forall k \in N$$
(1b)
$$MW_{k} { \cdot }\mathop \sum \limits_{i,out} F_{k,i} = \mathop \sum \limits_{j,in} MW_{ k, j} { \cdot }F_{k,j} \quad \forall k \in N$$
(1c)
$$100{ \cdot }MW_{k} = MW_{H2} { \cdot }X_{H2, k} + (100 - X_{H2, k} ){ \cdot }MW_{LIG, k} \quad \forall k \in N$$
(1d)

At all reactors r within the network:

$$F_{in, r} = F_{out, r} + RD_{H2, r} - RD_{LIG, r}$$
(2a)
$$F_{in, r} \frac{{X_{in, r,H2} }}{100} = F_{out, r} \frac{{X_{out, r,H2} }}{100} + RD_{H2, r}$$
(2b)
$$F_{in, r} MW_{in,r} = F_{out, r} MW_{out,r} + RD_{H2, r} MW_{H2} - RD_{LIG, r} MW_{LIG,r}$$
(2c)
$$RD_{H2, r} = HC_{in, r} { \cdot }rd_{H2, r}$$
(2d)
$$\begin{aligned} & RD_{LIG, r} = HC_{in, r} { \cdot }rd_{LIG,r} \\ & \forall r \in Reactors \\ \end{aligned}$$
(2e)

At all permeation membranes z within the network:

$$F_{in,z} = F_{o,z} + F_{pg,z}$$
(3a)
$$F_{in, z} \frac{{X_{in, z,H2} }}{100} = F_{o, z} \frac{{X_{o, z,H2} }}{100} + F_{pg, z} \frac{{X_{pg, z,H2} }}{100}$$
(3b)
$$F_{in, z} MW_{in,z} = F_{o, z} MW_{o,z} + F_{pg, z} MW_{pg,z}$$
(3c)
$$X_{o, z,H2} = a\frac{{F_{pg,z} }}{{F_{in,z} }} + b{ \cdot }X_{in, z,H2} + c$$
(3d)
$$\begin{aligned} & MW_{in, z,LIG} = MW_{o, z,LIG} \\ & \forall z \in Permeation\;membranes \\ \end{aligned}$$
(3e)

At all separators (high and low pressure) se within the network:

$$ksol_{se,gasHC} = \frac{{22.415{ \cdot }G_{out,se} \left( {Y_{out,se,H2} + Y_{out,se,LIG} } \right)}}{{G_{out,se} Y_{out,se,HC} \left( {\frac{{MW_{HC} }}{{\rho_{HC} }}} \right)}}$$
(4a)
$$ksol_{se,H2LIG} = \frac{{X_{out,se,H2} }}{{Y_{out,se,H2} }}{ \cdot }\frac{{Y_{out,se,LIG} }}{{X_{out,se,LIG} }}$$
(4b)
$$ksol_{se,MWLIG} = \frac{{MW_{out,se,LIG} }}{{MW_{Gout,se,LIG} }}$$
(4c)
$$G_{in, se} \left( {100 - Y_{in,HC} } \right) = F_{out, se} + G_{out, se} \left( {100 - Y_{out,se,HC} } \right)$$
(4d)
$$G_{in, se} Y_{in,se,H2} = F_{out, se} X_{out,se,H2} + G_{out, se} Y_{out,se,H2}$$
(4e)
$$\begin{aligned} & G_{in, se} \left( {100 - Y_{in,HC} } \right)MW_{Gin,se} = F_{out, se } MW_{out,se} + G_{out, se} \left( {100 - Y_{out,se,HC} } \right)MW_{Gout,se} \\ & \forall se \in Separators \\ \end{aligned}$$
(4f)

It must be noticed that, further details such as operation constraints (e.g.: compressors’ capacities and constraints on pipelines), and actual process units’ flow diagrams are confidential, thereby not available for disclosure. However, those are incorporated into the model and its constraints appropriately.

Taking into account the much faster dynamics of the hydrogen compared to the dynamics of the reactors, the hydrogen distribution model is static and contains flows (F), purities (XH2 and XLIG), molecular weights of hydrogen and light ends (MWH2 and MWLIG, respectively) of all streams and hydrogen consumption in the reactors as main variables.

For the sake of clarity, the deterministic model of the process network refers to Eqs. (1a–1d, 2a–2e, 3a–3e, 4a–4f) (or 1–4 for short), and other equations, which are undisclosed for confidentiality reasons. Altogether represent the full plant mathematical model used in this work.

The data reconciliation problem requires a certain degree of redundancy in the measurements and is formulated as the following Non-Linear Programming (NLP) problem:

$$\mathop {\hbox{min} }\limits_{{F_{i} ,X_{i} ,MW_{i} ,\varepsilon_{i} }} \mathop \sum \limits_{j \in M} \alpha_{j} c^{2} \left[ {\frac{{\left| {e_{j} } \right|}}{c} - \log \left( {1 + \frac{{\left| {e_{j} } \right|}}{c}} \right)} \right] + \mathop \sum \limits_{i \in S} \alpha_{i} \varepsilon_{i}^{2} + \mathop \sum \limits_{k \in M} \alpha_{k} Reg_{k}$$
(5a)

s.t.

process network model (1–4)

operational and range constraints

$$F_{i, min} - \varepsilon_{Fi} \le F_{i} \le F_{i,max} + \varepsilon_{Fi} \varepsilon_{Fi} \ge 0$$
(5b)
$$X_{i, min} - \varepsilon_{Xi} \le X_{i} \le X_{i,max} + \varepsilon_{Xi} \varepsilon_{Xi} \ge 0$$
(5c)
$$MW_{LIG, i, min} - \varepsilon_{MWi} \le MW_{LIG, i} \le MW_{LIG, i,max} + \varepsilon_{MWi} \varepsilon_{MWi} \ge 0$$
(5d)

where

$$e_{j} = \eta_{j} \left( {F_{rec, j} - \beta_{j} { \cdot }F_{j, mea} } \right)\quad j \in M$$
(5e)
$$e_{m} = \eta_{m} \left( {X_{rec, m} - X_{m, mea} } \right)\quad m \in M$$
(5f)
$$\beta_{j} = \sqrt {\frac{{T_{d} + 273}}{{\left( {P_{d} + 1} \right){ \cdot }MW_{j} }}} \sqrt {\frac{{\left( {P_{j} + 1} \right){ \cdot }MW_{d} }}{{T_{j} + 273}}}$$
(5g)

The above NLP minimizes the function (5a) of the errors ej between the measured flows Fj,mea and purities Xm,mea, and the same magnitudes computed with the model under the links imposed by the model (1–4) and other operational and range constraints. The coefficients β represent the compensation factors, and the variables ε are slack variables to ensure feasibility in the range constraints, while Reg are regularization terms to avoid sharp changes. Index i expands to all streams (S) across the network model, while indices j and m refer to plant measurements within set M. Notice that instead of the common sum of squares of the errors, a robust M-estimator (a.k.a.: maximum-likelihood type estimators) as the Fair function has been used, which is similar in shape to the sum of squared errors for small values of the error but grows slower for larger ones limiting the effect of gross errors in the data (Özyurt and Pike 2004; Huber 2011; Arora and Biegler 2001; Nicholson et al. 2013).

The data reconciliation problem is a large-scale NLP that is formulated and solved with a simultaneous approach in the General Algebraic Modeling System (GAMS) using IPOPT (Wächter and Biegler 2005) as the optimization algorithm. The implementation involves more than 4400 variables and 4700 equality and inequality constraints. It takes less than five Central Processing Unit (CPU) minutes in a PC with i7 processor and 8 Gb RAM, giving robust results against gross errors and helping to detect faulty instruments.

2.3 Network RTO

Once a sensible model and reliable corrected measurements are available, one can formulate the network optimization problem (6) as finding the production and redistribution of H2 in the network and the value of the hydrocarbon loads to the consumer plants that maximizes the value associated to the loads taking into account the cost of generating hydrogen, which corresponds to the cost function:

$$\mathop {\hbox{max} }\limits_{{HC_{1, \ldots ,4} ,F_{H2, 1, \ldots ,2} ,R_{1, \ldots ,4} }} \mathop \sum \limits_{i = 1}^{4} \left( {p_{HCi} HC_{i} - p_{Ri} R_{i} } \right) - \mathop \sum \limits_{j = 1}^{2} p_{H2} F_{H2,j}$$
(6)

where p represent prices HC are hydrocarbon loads, F fresh hydrogen and R deals with the compression cost of the recycled one.

This function is maximized respecting all constraints and without changing the way the reactors are operated, that is:

  • Maintaining the current specific consumption of H2 (rdH2), LIG generation (rdLIG) and their properties (purity and molecular weight) at each reactor,

  • Maintaining solubility coefficients at separators (ksolgasHC, ksolH2LIG, ksolMWLIG) and its properties (purity and molecular weight).

These values are estimated every 2 h from the data reconciliation step and are expected to be the same in the (near) future, if there is no change in hydrocarbon feed quality.

In the optimization, besides the network model, the main constraints refer to the process operation (e.g.: ranges, H2/HC, compressors capacity and maximum purity) and refinery planning specifications. Main decision variables include production of fresh hydrogen, feeds to consumer plants, hydrogen flows and recirculation, purges, purities and membranes operation.

The RTO is solved as an NLP problem in the GAMS system. It involves nearly 2000 variables and more than 1800 equality and inequality constraints and is solved with a simultaneous approach and the IPOPT algorithm in less than 1 min CPU time.

3 System architecture for optimization

The data reconciliation and network RTO are implemented according to the architecture displayed in Fig. 5.

Fig. 5
figure 5

Schematic of the system’s architecture displaying the DR-RTO module on the left hand side, the PI system in the center and process and other control and planning elements on the right hand side

Full size image

Data and measurements from the hydrogen network are stored regularly in the real-time information system of the refinery (PI system). Values of each of them are read every 2 h from the PI system to be processed in the DR-RTO application which resides in a dedicated PC. The application is composed of several modules as shown in the left hand side of Fig. 5. The data acquisition module reads 171 flows and 18 purity measurements, plus other variables and configuration parameters from the PI system (temperatures, pressures, valve openings, etc.) totaling around 1000 variables, averaging them in 2-h periods to smooth the effects of transients and disturbances. Data treatment is a critical component that contains a set of rules dedicated to detect faults and information inconsistences in the raw data and decides which options, variable ranges, etc. are the most adequate ones in the mathematical formulation of the problems. In addition, this module detects when a plant is out of service or a hydrogen header has modified its connectivity, such that its associated equations should be removed or changed in the network models. To implement this variable structure operation, the models are formulated as a superstructure that includes binary variables such that, according to the analysis of the data treatment module, the model can be adapted automatically to the state and configuration of the plants and headers.

Then, the treated data and constraints are sent to the data reconciliation module that solves the corresponding optimization problem and provides updated and reliable information and parameters to the network optimization module (named as Optimal Redistribution in Fig. 5). Finally, the information from the data reconciliation (DR) and the network optimization are used to compute some Resource Efficiency Indicators (REIs), and all of them are sent back to the PI system, where they are available to all potential users. Further details of REIs implementation and their usefulness for decision support in refinery hydrogen network are presented by Galan et al. (2017). A detailed description of REIs and their role in real-time monitoring and optimization in the process industry is covered by Krämer and Engell (2017), while comprehensive guide for REIs development is presented by Kujanpää et al. (2017).

A first benefit of the system is providing improved process information and, in particular:

  • An indication of possible faulty instruments

  • Reliable balances of hydrogen.

  • Values for unmeasured quantities (purities, molecular weights, hydrogen consumption,…) not available previously.

  • Data for computing REIs that allow better monitoring of the operation of the network.

Regarding the implementation of the solutions of the optimizer, ideally, the optimal values calculated should be sent as set-points to the network control system, either directly to the flow controllers or following the traditional architecture as in Fig. 1. Nevertheless, the static nature of the RTO and the low frequency of its execution brings several problems as the implementation of the optimal values has to be applied to the process taking into account the time evolution of variables. In particular, HC loads and hydrogen production have to be changed dynamically at a higher frequency to balance hydrogen production and consumption. In the same way, due to the presence of disturbances, changing aims, etc., constraints’ fulfilment requires dynamic actions to be performed at a higher rate, and changes in hydrogen flows may interact among them so that a proper implementation of the RTO solution would require multivariable control to take care of the interactions. Because of that, a different approach has been considered.

3.1 Implementing network optimization in real-time

A direct way of incorporating dynamics into the system, solving simultaneously the problem of possible inconsistencies between the non-linear RTO model and the linear one typically used in the MPC layer, is to formulate a single integrated dynamic optimization problem as mentioned in the introduction. Nevertheless, it is not realistic maintaining and operating in real-time a dynamic data reconciliation and dynamic RTO system involving 18 plants due to its large scale.

A different alternative, somewhere in the middle between sending set-points from a RTO to a MPC and direct dynamic optimization with economic aim, was considered and implemented in the refinery. For implementation, it takes advantage of the fact that some commercial MPCs, e.g. DMC+, are actually composed of two layers: a Dynamic Matrix Controller (DMC) to compute control actions, and a local optimizer on top that, using Linear Programming (LP) and sharing the same linear dynamic models as the DMC, computes on-line targets for the multivariable controller minimizing a user defined economic function.

The methodology is represented in Fig. 6, and basically consists of analyzing the network RTO solutions and extract from them optimal policies that are consistently recommended by the optimizer. This means, understanding the logic behind the solutions and identifying variables that should be maximized or minimized to achieve an overall network optimal management. Nonetheless, variable specific set-points depend on the process constraints or planning specifications. Therefore, the decision-making process, rather than being automatically translated downstream in the control pyramid, provides operation directions to the optimization layer of the DMC. These policies, or directions, represent targets (variables), which are maximized or minimized in the LP layer of the DMC considering controlled and manipulated variables’ specific weights. These weights reflect the priorities and costs of the steady state process. The LP determines the optimal values compatible with the actual process model, process state and constraints and generates the corresponding set points to the DMC controller, which, finally, taking into account systems dynamics and interactions, will compute current and future hydrogen and hydrocarbon set points to be given to the individual low level flow controllers of the DCS of the control room. A comprehensive description and discussion of the integration of the RTO and DMC in this process network is addressed by de Prada et al. (2017).

Fig. 6
figure 6

Schematic representing the methodology for on-line implementation of RTO policies

Full size image

In the case considered, the optimal policies identified were:

  • Losses from the HPS of a plant to fuel gas, required to avoid LIG accumulation, should be made at the lowest hydrogen purity compatible with the one required at the reactor input and the H2/HC minimum ratio, but the LPH purity should be maximized to increase hydrogen re-use. It must be noticed that, the higher the purity in the LPH, the more utilization of that gas for the process units.

  • The hydrogen unbalance in the network, that is, hydrogen generated minus hydrogen consumed in the reactors, reflects in the LPH pressure, so losses to fuel gas from this header should be minimized with a minimum to guarantee unsaturated operation of the pressure controller. This is a typical operational constraint, basically linked to the pressure valve controller.

  • Maximization of the hydrocarbon load to the consumer plants, which is the most important target, and can be made until either maximum hydrogen capacity is reached or another technical constraint is active.

  • Sending higher purity hydrogen (H4) to LPH should be minimized as purity degrades.

The system was implemented at the refinery shown in Fig. 5, but with the DMC controlling only the six most important plants from the hydrogen use point of view as a compromise between maintenance and development costs and potential benefits as in Fig. 7. A detailed description of the validation process of this deployment is addressed by Galan et al. (2018), and de Prada et al. (2017) present an analysis of the integration of the RTO and MPC applications in this case study.

Fig. 7
figure 7

Diagram of the DMC controlling the operation of two hydrogen producers H3 and H4 and four consumers G1, G3, G4 and HD3, with the main controlled hydrogen flows and HC loads

Full size image

The DMC controller manages two hydrogen producers (H3, H4) and four consumer plants (G1, G3, G4, HD3) and was developed and implemented by the refinery team. It is based on linear models obtained by identification using data from step-tests that forms a dynamic matrix involving 12 manipulated variables and 29 controlled ones. The main manipulated variables refer to the set points of hydrocarbon loads to the consumer units, fresh hydrogen production, hydrogen feed to the consumers from the high purity header, and supply of hydrogen from one of the platformer plants. The main controlled variables are hydrogen partial pressure in the reactors of the consumer plants, losses to fuel gas from the LPH (valve opening), recycle purity and HP losses to FG from some plants, hydrocarbon loads and valve openings to avoid control saturation.

The cost function at the LP layer combines four targets that together synthesize the solution of the RTO:

  • Maximize hydrocarbon loads to the consumer plants

  • Minimize losses from the LPH to FG.

  • Minimize hydrogen purity in the recycles of the consumer plants.

  • Minimize hydrogen transfers from higher to lower purity headers.

The corresponding variables are linked to the manipulated variables through the linear process model, so that the optimization problem is linear and can be solved in a short time. The LP/DMC runs with a sampling time of 1 min, giving consistent results for many months. In parallel, the network RTO is executed every 2 h being operated as a DSS for the whole network and allowing the supervision of the DMC application. As an example of results, Fig. 8 (bottom) presents the total optimal and actual hydrocarbon load to the HDS plants for a period of ten days, showing good performance. However, in the same time window it is seen still a gap in the H2 sent to FG when comparing the reconciled value to the optimal (Fig. 8, top). This gap is mainly explained by the fact that, the purification membranes across the network are operated manually and are out of the scope of the DMC, though considered in the RTO. These results showcase the importance of the optimal operation of purification membranes at network level (ideally automated), and their impact in the economy of the process. A thorough discussion of this finding is addressed by Galan et al. (2018).

Fig. 8
figure 8

Evolution of optimum (orange) and reconciled (blue) plant-wide figures over ten days. Top: hydrogen sent to FG header (%reference). Bottom: total hydrocarbons processed (%reference)

Full size image

4 Two-stage stochastic (TSS) optimization

In Fig. 8 (top and bottom), is seen that the optimal conditions change significantly over time. In fact, the refinery is subjected to potentially large changes every two to three days when it receives new crude oil from ships, not to mention new production targets imposed by market demands.

In this section, uncertainty in the hydrogen demand at reactors is considered in the decision-making process explicitly. For this purpose, network dynamics considerations are proposed such that, slower plants’ (low frequency dynamics) variables are to be decided ahead of time (here-and-now decisions), compared to faster plant’s (high frequency dynamics) variables. For instance, set-point changes on production units (i.e.: H3 and H4) typically take around 2 h to actually impact in the consumer unit. Thereby, actual gas demand at reactors should have been met and produced at hydrogen units 2 h earlier than actual consumption. Otherwise, an excess or defect in hydrogen demand, along with its economic consequences, is faced. Based on this sequence, it is possible to formulate a two-stage stochastic framework for the hydrogen network management problem with uncertain parameters. This approach is introduced and analyzed by Gutierrez et al. (2018) in a previous work over this case study.

Changes in the crude oil reflect in changes in the hydrogen consumption of the reactors of the HDS plants that are difficult to predict, creating transients where the performance of the network may suffer degradation. One may wonder if incorporating this uncertainty explicitly in the decision making process would improve significantly the results obtained.

At the RTO level, this is done updating the model and network information at regular intervals by means of data reconciliation. Nevertheless, it is well known that, even with data reconciliation, if the model has structural errors the optimum computed with the model may not correspond to the real process optimum. Alternatively, we can consider different possible values of the uncertain variables and optimize considering the worst case, following a robust optimization approach (Ben-Tal and Nemirovski 2002). This option chooses the values of the decision variables that guarantee fulfilment of all constraints in all scenarios, but provides very conservative solutions as they are fitted to the worse case. Another alternative approach may be multi-stage stochastic optimization, which takes into account that some decisions that influence the future behavior of the process have to be made at current time (here-and-now) without knowing the value of the uncertain parameters (e.g.: H2 demand at reactors) but, in the future, new information can be available that reveals the value of the uncertainty, so that particular correction actions (recourse) can be made in the future according to the specific scenario that may take place.

The concept is illustrated in Fig. 9, where a scenario tree is represented for a two-stage stochastic model. On the left hand side (a) the system has a state x at time t0 and a decision u0 (with some variables known as first-stage ones) has to be made considering all possible values ξi of the uncertainty, a scenario is defined as the arc between nodes. After applying u0, the system will evolve in t1 to different states depending on the specific value of ξi, but if this value were know at t1, we could compute a specific optimal decision u1(ξi) for each value of ξi in the period of time starting at t1 for the remaining variables (recourse variables), as in Fig. 9b. This section studies the value of the stochastic approach applied to the hydrogen network in order to evaluate the interest of its implementation.

Fig. 9
figure 9

Schematic of the main concepts behind two-stage stochastic optimization and scenario tree representation

Full size image

4.1 Formulation of the TSS problem

Main elements in the formulation of the optimal management of the hydrogen network as a two-stage stochastic optimization problem are: the identification of the uncertainty source, the scenarios definition with their likelihood of realization, and selection of meaningful first and second stage variables. Regarding the objective function, the simplest approach is to formulate the deterministic equivalent problem (DEP) of the minimization as in (7a–7f). A detailed discussion on alternative formulations of TSS problem could be found in Birge and Louveaux (2011).

$$\mathop {\hbox{min} }\limits_{{u_{F,} u_{{S\left( {\xi_{i} } \right)}} }} J_{F} \left( {u_{F} } \right) + {\mathbb{E}}\left\{ {J_{S} \left( {u_{F} ,u_{S} \left( {\xi_{i} } \right),x_{S} \left( {\xi_{i} } \right)} \right)} \right\}$$
(7a)
$$\begin{aligned} & {\text{s}} . {\text{t}} .: \\ & {\mathbb{E}}\left\{ {J_{S} \left( {u_{F} ,u_{S} \left( {\xi_{i} } \right),x_{S} \left( {\xi_{i} } \right)} \right)} \right\} = \mathop \sum \limits_{i = 1}^{n} J_{S} \left( {u_{F} ,u_{S} \left( {\xi_{i} } \right),x_{S} \left( {\xi_{i} } \right)} \right){ \cdot }\pi \left( {\xi_{i} } \right) \\ \end{aligned}$$
(7b)
$$h_{F} \left( {x_{F} ,u_{F} } \right) = 0,$$
(7c)
$$g_{F} \left( {x_{F} ,u_{F} } \right) \le 0,$$
(7d)
$$h_{S} \left( {x_{F} ,u_{F} ,u_{S} \left( {\xi_{i} } \right),x_{S} \left( {\xi_{i} } \right) } \right) = 0\quad \forall \xi_{i} \in \varXi ,$$
(7e)
$$g_{S} \left( {x_{F} ,u_{F} ,x_{S} \left( {\xi_{i} } \right),u_{S} \left( {\xi_{i} } \right)} \right) \le 0 \quad \forall \xi_{i} \in \varXi$$
(7f)

where (·)F refers to variables or functions in the first stage and (·)S denotes the ones in the second stage, while the decision variables are denoted as u and the remaining variables as x. The uncertainty is represented by the parameters ξi that can take values within a set Ξ according to a certain discrete probability distribution, for which the probability of occurrence (π(ξi)) is known (7b). This set is discrete and finite with n elements, (i.e.: ξi, i = 1,2,3,…,n of elements is considered). These n elements constitute the scenarios that will represent the uncertainty realizations. In the objective function the sum over all scenarios i represents the expected value of the objective function over the second stage variables (7b).

The cost function is composed of two terms: The first one, JF, is the cost in the first stage which depends on the first stage decisions uF. These are decisions that are taken and applied at current time without knowing the particular realization of the uncertainty ξ and will be maintained over the time horizon covered by the optimization problem. Consequently, they are the same for all values of ξi. Nevertheless, we can correct the effects of the uF decisions once the value of the ξi parameters are revealed, using the recourse variables uS(ξ) that take a particular value for each realization of the uncertainty (ξi). The second term of the cost the weigthed summation over all the scenarios with corresponding probabilities πi, represents the effect of these second stage corrections on the total value of the cost function, which also depend on the uF decisions.

The variables of the problem have to satisfy the constraints imposed by the model h(.) and additional inequality constraints g(.) in every stage for all possible scenarios considered (n). In (7), the corresponding equations, that depend on the stochastic parameter ξ, should be interpreted as being satisfied with probability one.

4.1.1 Uncertainty source description

Hydrogen gas in a refinery is basically a utility, for it is demanded and consumed in process units and it should be enough to satisfy the process requirements at all times. The deterministic problem tackles the optimal hydrogen management problem assuming that hydrogen demand of each plant is to be calculated exactly using the results of the DR problem. However, this concept does not hold when the refinery is facing crude oil changes, which typically imply hydrogen demand swings as well. In these situations, predictions of hydrogen demand at the plant level are usually inaccurate due to the fact that hydrocarbon cuts properties may be estimated with large errors, which make them the main source of uncertainty. Figure 10 presents a simplified oil refinery schematic representing the different intermediate cuts fed to hydrogen consumer units (i.e.: HDS, HDT, HDC), which will be impacted by changes in the hydrocarbon properties and ultimately lead to hydrogen demand changes. Therefore, a scenario tree representation is applicable in this context as seen in Fig. 9. In addition, in most case hydrogen demand affects all consumers in the same direction (i.e.: increase or decrease) as a consequence being fed by a unique crude oil source (see Fig. 10). It must be present that refinery hydrogen networks are very specific due to all the features described before. Other gas networks case studies available in literature, such as the one by Li et al. (2017) for natural gas networks, may differ in most of the assumptions and features, though the stochastic approach still holds in all.

Fig. 10
figure 10

Simplified schematic of an oil refinery, identifying the main intermediate cuts fed to process units. CDU crude distillation unit, VDU vacuum distillation unit, HDS hydrodesulphurization unit, HDC heavy oil desulphurization unit. FCC fluidized catalytic cracking, CR catalytic reforming, MX merox sweetening, LPG liquefied petroleum gas, Kero kerosene, LN/HN light and heavy naphta, respectively, AR atmospheric residue, VR vacuum residue, Gas gasoline, Jet aviation jet fuel, GO commercial gasoil, FO fuel oil, AS asphalt. 1Major hydrogen consumer

Full size image

4.1.2 Scenarios definition

Given different potential hydrogen demands at plant level is possible to link those to a probability of occurrence (π(ξi)), which will be revealed only after the first stage decisions are due. Therefore, each scenario is identified with a likelihood of realization of a hydrogen demand at plant level. It should be borne in mind that this idea narrows down the search for first and second stage variables, since the former remain equal at all scenarios.

4.1.3 First and second stage variables

As a consequence of the network dynamics, explained in Sect. 2, hydrogen production decisions at generation units (i.e.: H3 and H4) precede actual plant demand at consumer units by around 2 h. In other words, hydrogen demand at any given time should be met by the hydrogen production rates of the past 2 h. However, consumer plants have much faster dynamics and cope with most of the changes in feed quality within minutes. Due to the fact that the uncertainty source is from feed quality, which in turn reflects into hydrogen demand at the plant level, scenarios affect all consumer plant variables and headers. Additionally, hydrogen production has to be set 2 h before it is actually demanded. Therefore, in the TSS formulation the first stage variables are all related to the hydrogen production units, H3 and H4. The rest of the network variables are all subjected to scenarios hence defined as recourse or second stage variables.

4.1.4 Problem statement

Given the hydrogen network of an oil refinery, with production and consumption of hydrogen, and hydrocarbons processed in consumer plants. The problem is to determine the hydrogen production rate at time t0 of each producer, such that plants demands’ are satisfied for all possible scenarios, complying with operational restrictions. The objective is to maximize the expected profit of the network operation (8), considering hydrogen production costs and revenues from hydrocarbon processing at all scenarios.

$$\mathop {\hbox{max} }\limits_{{F_{{H_{2} ,}} HC_{i} \left( {\xi_{i} } \right),R_{i} \left( {\xi_{i} } \right)}} J_{F} \left( {\mathop \sum \limits_{i = 1}^{2} p_{{H_{2} i}} { \cdot }F_{{H_{2} i}} } \right) + {\mathbb{E}}\left\{ {J_{S} \left( {\mathop \sum \limits_{j = 1}^{4} p_{{HC_{i} }} { \cdot }HC_{i} \left( {\xi_{j} } \right) - p_{{R_{i} }} { \cdot }R_{i} \left( {\xi_{j} } \right)} \right)} \right\}$$
(8)

Here the process model and constraints are the same as in the deterministic case (i.e.: h(·) and g(·)), but evaluated for every scenario (7b–7f), which largely increases the number of variables and equations. The first stage cost (JF) corresponds to the production cost of fresh hydrogen, while the second stage (JS) includes the expected value of the hydrocarbons processed and the cost of the hydrogen recycles. The aim is to maximize the hydrocarbon load (HC) to consumer plants, minimize the use of fresh hydrogen generated in the steam reforming plants (FH) and minimize the internal recycles of hydrogen (R) in the consumer plants, considering all possible values of the uncertainty. uS refers to the remaining variables of the model.

This TSS formulation is known as deterministic equivalent problem (DEP) since it is solved as a single monolithic optimization problem over all the scenarios.

4.2 Evaluation of the value of the stochastic solution

4.2.1 Scenarios assessed

In particular, a formulation with nine scenarios is presented as case study in this paper. Table 3 displays details of scenarios conditions, which represent feasible transitions towards a higher hydrogen demand resulting from higher sulphur content crude oil. In fact, the key representation of these scenarios in the model is by multiplying (2d) and (2e) by their corresponding change coefficient at each scenario (9a–9b). The rest of the model equations remain unchanged, except for the addition of the scenario dimension to each second stage variable. It is assumed that other realizations are negligible. Therefore, these nine scenarios represent all meaningful ξi, such that the probability of occurrence (π) of the sum of all equals one (10). All values are presented in per one units (e.g.: 1.1 implies 10% increase).

$$RD_{H2, r,\xi } = HC_{in, r,\xi } { \cdot }\left( {rd_{H2, r} { \cdot }H_{2DEM,\xi } } \right)_{r,\xi }$$
(9a)
$$\begin{aligned} & RD_{LIG, r,\xi } = HC_{in, r,\xi } { \cdot }\left( {rd_{LIG, r} { \cdot }LIG_{GEN,\xi } } \right)_{r,\xi } \\ & \forall \xi \in \varXi \\ \end{aligned}$$
(9b)
$$\mathop \sum \limits_{i = 1}^{9} \pi \left( {\xi_{i} } \right) = 1$$
(10)
Table 3 Scenario specific hydrogen demand (H2DEM(Si)), light ends generation (LIGGEN(Si)) and probability of occurrence (π(Si)), for each scenario (Si). H2DEM(Si), LIGGEN(Si) and π(Si) values are presented in per one fractions
Full size table

4.2.2 Typical stochastic formulations

The two-stage stochastic programming problem where the first and second stage variables are considered together resulting in the deterministic equivalent (7), can be interpreted as the recourse problem (RP). In the RP the first stage variables are decided taking into account all possible scenarios, which enlarges the problem as much as scenarios are evaluated. A simplified approach is to consider each scenario separately, assuming the information on the each will be certain once the decision is to be made. Therefore, “perfect information” is assumed for each scenario and computing them separately and weighting the cost function by the corresponding π(ξi) represents the best theoretical outcome in the long run (PI, a.k.a: wait-and-see). Finally, a second simplification neglects the randomness of the uncertainty and assumes it equal to its weighted average. As a consequence, the realizations of the second stage variables are fixed and the optimization problem becomes a regular deterministic problem, which determines the first stage variables. However, in reality the second stage will reveal all the scenarios in the long run, and at that point one will have to cope with the actual hydrogen demand and previously set hydrogen production. This solution is named the expectation of the expected value problem (EEVP), and is a usual simplification of the TSS problem. A thorough discussion of these approaches and their value in addressing a real-world optimization problem considering stochastic uncertainty, including several examples, is provided by Birge and Louveaux (2011).

It is usually interesting to assess whether the two-stage programming stochastic offers an advantage over the two simplified approaches. For this purpose, Birge and Louveaux (2011) proposed the so called value of the stochastic solution (VSS) that is used in this study, as well as the expected value of perfect information (EVPI). The former quantifies the gain in the objective function resulting from considering the randomness of the uncertainty (i.e.: RP), versus its weighted average (i.e.: EEVP). The formula is presented in (11). The latter (12) compares the RP against a theoretical case where demand is certain and known beforehand (i.e.: PI), although this is not realistic.

$$VSS = RP - EEVP$$
(11)
$$EVPI = PI - RP$$
(12)

4.2.3 Case-study results

Considering actual plant data from a DR solution (discussed in Sect. 2.2), the TSS solutions for the RP, EEVP and PI problem are shown in Table 4. The problem RP involved 15,958 variables and 14,925 constraints, and required 76.38 CPU seconds (Intel® Core™ i7 2.50 GHz and 16.0 GB of RAM). In terms of computational efficiency the results are suitable for the online application. Moreover, typical techniques of decomposition (see for reference: Li et al. 2012; You and Grossmann 2013) were dismissed as alternative formulations due to the satisfactory results of the monolithic RP formulation. In addition, the EVPI and VSS are presented in the same table to analyze the value of considering uncertainty explicitly. Due to confidentiality reasons, representative but fictitious prices of hydrogen costs and HC loads are used in this study.

Table 4 Results of the implementation of the TSS formulation over the typical stochastic assumptions, i.e.: perfect information (PI), recourse problem (RP), expectation of the expected value problem (EEVP)
Full size table

It is interesting to notice that with an EVPI of less than 1% it does not seem to be worth investing in additional information from hydrogen demand or light ends generation of the network. It should be considered that, more information it almost surely, requires equipment investment to undertake better analysis at the refinery laboratory or allocate more resources to the hydrocarbon cuts’ properties predictions. However, the VSS shows an improvement of circa one order of magnitude compared to the EVPI, which is due to the incorporation of the stochastic uncertainty in the whole decision-making process from the beginning. In other words, if the uncertainty is estimated when deciding how much hydrogen should be produced and then corrected once the uncertainty reveals (i.e.: EEVP), the objective function is around ten k€ per hour worse than considering the uncertainty from the first stage (i.e.: RP). That is the “price” of simplifying the uncertainty when deciding on the hydrogen production, and neglecting the stochastic nature of hydrogen demand and LIG generation.

The same analysis applies when HC loads of EEVP and RP solutions are compared. For example, if the major hydrogen consumer is analyzed (i.e.: HD3) it could be seen how in most of the scenarios the RP outperforms EEVP (Fig. 11). The most favorable results for EEVP are at scenarios S1, S4 and S7, where HD3 maximum load capacity is reached. The rest of the scenarios require HC load to be below HD3 maximum to cope with hydrogen demands. However, RP is capable of meeting hydrogen demand at all scenarios without sacrifice of HC load. This translates directly to the objective function, where HC loads weight around 1000 times more than hydrogen production in volume (8).

Fig. 11
figure 11

RP and EEVP solutions for HC loads of process unit HD3

Full size image

In addition, RP solution improves LPH purity at all scenarios, except for S7 (Fig. 12), which translates into more effective usage of recycled gases across the network contributing to economy of the process network. The particularity seen at S7 is related to the efficiency in the LPH purity management. This underpins in the concept that it only makes sense to hold high purity if that is required to satisfy H2 demand at reactors, for instance HD3 in this case. In other words, once the network demand has been met the best decision is to save hydrogen production costs. That is exactly the case of scenario S7, where H2 demand itself has not changed, only LIG generation (see Table 3). By not considering the stochasticity of the uncertainty the EEVP solution shows higher LPH purity (unnecessarily), impacting in the production costs negatively.

Fig. 12
figure 12

Low purity header hydrogen purity at scenarios S1–S9 applying RP and EEVP

Full size image

4.3 Considering risk in the decision making process

The previous approach holds when the decisions do not take into account the risk associated to the objective function, a.k.a. risk-neutral. Therefore, in the long run the expected valued is maximized regardless of the shape of the probability distribution of the objective function. This sub-section analyzes the formulation and results of applying a TSS approach with a risk measure as objective function.

4.3.1 Conditional value-at-risk

First of all, it is important to present the definition of value-at-risk (VaR) as in (13). This risk measurement simply defines a value ω which is the least value of the random variable Ξ, where the likelihood is less than a confidence level 1 − α. Another popular risk measure is the conditional value-at-risk (CVaR) defined as in (14), which is actually more useful in optimization for its convexity and other properties such as subadditivity (Pflug 2000). Equation (15) shows how CVaR and VaR relate to each other, being trivial to see that CVaR is greater than VaR. More details on the characteristics of VaR and CVaR can be found in Rockafellar and Uryasev (2000, 2002) and Pflug (2000).

$$VaR_{1 - \alpha } \left( {J\left( \varXi \right)} \right)\mathop = \limits^{\text{def}} \mathop {\inf }\limits_{{\omega \in {\mathbb{R}}}} \left\{ {\omega |P\left( {J\left( \varXi \right) \le \omega } \right) \ge 1 - \alpha } \right\}$$
(13)
$$CVaR_{1 - \alpha } \left( {J\left( \varXi \right)} \right)\mathop = \limits^{\text{def}} \mathop {\inf }\limits_{{\omega \in {\mathbb{R}}}} \left\{ {\omega + \frac{1}{\alpha }{\mathbb{E}}\left[ {J\left( \varXi \right) - \omega } \right]_{ + } } \right\}$$
(14)
$$CVaR_{1 - \alpha } \left( {J\left( \varXi \right)} \right) = VaR_{1 - \alpha } \left( {J\left( \varXi \right)} \right) + \alpha^{ - 1} {\mathbb{E}}\left[ {J\left( \varXi \right) - VaR_{1 - \alpha } \left( {J\left( \varXi \right)} \right)} \right]_{ + }$$
(15)
$$\mathop {\hbox{min} }\limits_{{u_{F} ,u_{S} \left( \cdot \right)}} CVaR_{1 - \alpha } \left[ {J\left( {u_{F} ,u_{S} \left( \varXi \right),x\left( \varXi \right)} \right)} \right] \Leftrightarrow \mathop {\hbox{min} }\limits_{{u_{F} ,u_{S} \left( \cdot \right), \omega }} {\mathbb{E}}\left[ {\omega + \alpha^{ - 1} \varphi \left( \varXi \right)} \right]$$
(16a)
$$\begin{aligned} & {\text{s}} . {\text{t}} .\\ & \quad J\left( {u_{F} ,u_{S} \left( \xi \right),x\left( \xi \right)} \right) - \omega \le \varphi \left( \xi \right) \quad \forall \xi \in \varXi , \\ \end{aligned}$$
(16b)
$$\varphi \left( \xi \right) \ge 0 \forall \xi \in \varXi ,$$
(16c)

(7b–7f)

(9a–9b)

A practical formulation of the CVaR objective function is presented in (16a–16c), the full deduction is illustrated by Artzner et al. (1999). Table 5 shows the results for CVaR and VaR considering the same scenarios presented for RP at two confidence levels 1 − α (99% and 95%), and risk-neutral. Notice that in this case the hydrogen problem is formulated as a minimization problem instead of a maximization as in the previous examples. This is only for practicality of formulation for the CVaR, and does not affect the reasoning behind the analysis.

Table 5 Results of CVaR, VaR and hydrogen plant H4 at confidence levels 95% and 99%
Full size table

According to Table 5 it could be deemed that changing risk from a confidence of 95–99% changes very little the detriment in profit for the process, CVaR and VaR in all cases. Moreover, the same change of confidence level (95–99%) shows a negligible impact in the hydrogen production at H4, although it is around 800 Nm3/h (about 2%) higher than the RP solution, see Table 5. In other words, decreasing by 5% the risk of the network profit will be almost indistinguishable in terms of extra hydrogen production. It must be borne in mind that, HC load to hydrogen consumer is at its maximum in all scenarios and confidence levels considered, therefore improvement of profit in scenarios should come from better hydrogen distribution and fresh hydrogen saving from H4. Certainly, this solution is case specific and greatly depends on the actual hydrogen demand circumstances.

An interesting point of view is to compare profit at each scenario for CVaR and risk-neutral (i.e.: RP) solutions. Figure 13 presents those results. It is important to highlight that considering risk (99 and 95% of confidence level) presents a more stable profit across scenarios, at the price of being less on average than the RP. In particular, scenarios six and nine are the ones that RP profit is less than CVaR profits. In the rest, RP profit is greater than CVaR profit. It must be borne in mind that, these figures are illustrative for the analysis, and not real in terms of profit amounts. Furthermore, the difference between profits is still very narrow and long term results should be analyzed for delivering a more robust discussion regarding the actual significance of these figures within the refinery business context. Certainly, the viewpoint and contribution of decision-makers, such as line managers, and business managers, is deemed of key importance in order for that analysis to be meaningful with respect to business impact for a certain risk level.

Fig. 13
figure 13

Profit results over scenarios for RP (risk-neutral), CVaR0.05 and CVaR0.01

Full size image

In overall, the minimization of the weighted average cost of all scenarios considered in the RP does not stop the results obtained in a particular scenario to differ significantly from the optimized average, as the formulation does not include any constraint on the spread or variance of that cost function. To avoid this situation, a measure of the risk of obtaining a cost function significantly worse than the average can be use as objective function instead. However, this so called risk-averse solution comes at the price of lower expected profit in the long run, as it was mentioned before (see Fig. 13).

5 Conclusions

This paper presents the optimization and control system of a hydrogen network in an oil refinery of the Repsol group. It combines data reconciliation and RTO with the implementation of the optimal policies in a commercial DMC+ control system. The optimal policies appear as a set of targets to maximize or minimize within constraints in the LP layer of the DMC+ and are extracted from the analysis of the process and the optimization results proposed by the RTO. This way of implementing RTO has proven to be very effective and allows dealing with dynamics and disturbances as it is executed in real-time with the sampling time of the DMC predictive controller. In addition, the familiarity of the personnel with the DMC interface facilitates the adoption and use of the system and, being based on the DMC models, avoids the possible incoherencies with the ones of the RTO.

In addition this paper studies the advantages of incorporating uncertainty explicitly in the decision making process as a way to deal with the unknown and variable hydrogen demands created by the processing of different crudes. For this purpose, several scenarios were defined and Two-stage stochastic optimization was applied to the problem of optimal hydrogen distribution. On order to evaluate the improvement, two indexes were considered, the Expected Value of Perfect Information, EVPI, and the Value of Stochastic Solution, VSS. The former suggests that little gain is obtained by improving the knowledge on the quality (hydrogen demands) of the hydrocarbon loads being processed, but the VSS indicates that it may be worth to use the Two-stage stochastic optimization in the RTO. Although the results presented are for a particular 2-h period of time, similar conclusions are obtained when studying larger time periods. Finally, the use of an alternative objective function, risk of having a value of the cost function far from what expected, instead of the expected value over all scenarios was considered. More specifically, the Conditional Value-at-Risk, CVaR, was used. The results show a decrease in the cost function as expected. If the risk factor compensates this, is something that will require a deeper analysis, engaging business decision-makers at different levels in the organization in order for it to be representative of the actual business impact.