Multistage stochastic capacity planning of partially upgraded bitumen production with hybrid solution method

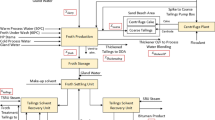
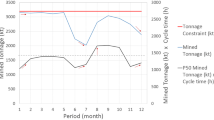
Abstract

Partial upgrading technologies have received a great amount of attention as a promising and economic solution for Canadian oil sands bitumen processing. In this paper, the optimal planning of capital and expansion capacities for partial upgrading of bitumen is studied. We propose a multistage stochastic planning model with consideration of various sources of uncertainties. The main challenge of the stochastic model is the presence of terms in which an uncertain parameter is multiplied by an adjustable dynamic decision variable. To solve the problem, two hybrid methods are proposed: in method 1, the uncertain parameter is modeled with an uncertainty set and the dynamic variable is modeled as scenario dependent variables; in method 2, the uncertain parameter is modeled with samples and the dynamic variable is modeled using the decision rule-based approximation. Finally, results obtained from both hybrid models are compared based on different criteria: (1) computational time, (2) solution performance, and (3) solutions for representative scenarios.

Appendix

In this appendix, deterministic counterpart derivation of the proposed hybrid models are explained. This includes the robust counterpart derivation of the semi-infinite constraints and the derivation of the expectation based objective function.

1.1 Deriving the robust counterpart for H1

Notice that in hybrid model 1, $\xi = [\xi ^{\alpha _1},\ldots ,\xi ^{\alpha _6}, \xi ^{\beta _1},\ldots ,\xi ^{\beta _6}, \xi ^{\phi _1},\ldots ,\xi ^{\phi _6}, \xi ^{\gamma }]^\top$. In order to map the associated uncertainties of out of the general uncertainty vector $\xi$, vector $P^{\alpha _i}$, $P^{\beta _i}$, $P^{\phi _i}$, and $P^{\gamma }$ can be used. For example, $P^{\alpha _1}$ = [1,0,…,0] can be used to get $\xi ^{\alpha _1}$ : $\xi ^{\alpha _1}= P^{\alpha _1} \xi$.

1.1.1 Counterpart of constraint 3d

• 1. Introduce appropriate truncate matrices to generalize the uncertainties as $\xi$, $\sum _{i\in I} \overline{\beta }_i \cdot (1 + P^{\beta _i} \cdot \xi ) \cdot C_i \le \overline{\gamma } \cdot (1 + P^{\gamma } \cdot \xi )$.

• 2. Arrange the uncertain variables in left-hand-side and derive the robust counterpart, $\Bigg \{\underset{\xi \in \varXi }{\text {max}} \quad \bigg [ \sum _{i\in I} \overline{\beta }_i \cdot P^{\beta _i} \cdot C_i - \overline{\gamma } \cdot P^{\gamma } \bigg ] \cdot \xi \Bigg \} \le \bigg [ \overline{\gamma } - \sum _{i\in I} \overline{\beta }_i \cdot C_i \bigg ].$

• 3. Introduce the uncertainty set,

  $$\left\{ \begin{array}{cc} \max \quad \bigg [ \sum _{i\in I} \overline{\beta }_i \cdot P^{\beta _i} \cdot C_i - \overline{\gamma } \cdot P^{\gamma } \bigg ] \cdot \xi \\ s.t. \quad - W \cdot \xi \le - h \end{array} \right\} \le \bigg [ \overline{\gamma } - \sum _{i\in I} \overline{\beta }_i \cdot C_i \bigg ]$$

• 4. Introduce dual variable $\varLambda ^d$ and apply duality to the inner LP problem,

  $$\left\{ \begin{array}{cc} \min \quad - h ^ T \cdot \varLambda ^d \\ s.t. \quad - W ^ T \cdot \varLambda ^d = \bigg [ \sum _{i\in I} \overline{\beta }_i \cdot P^{\beta _i} \cdot C_i - \overline{\gamma } \cdot P^{\gamma } \bigg ]^T \\ 0 \le \varLambda ^d \\ \end{array} \right\} \le \bigg [ \overline{\gamma } - \sum _{i\in I} \overline{\beta }_i \cdot C_i \bigg ]$$

• 5. Drop the min operator,

  $$\left\{ \begin{array} {lll} - h ^ T \cdot \varLambda ^d \le \bigg [ \overline{\gamma } - \sum _{i\in I} \overline{\beta }_i \cdot C_i \bigg ] \\ - W ^ T \cdot \varLambda ^d = \bigg [ \sum _{i\in I} \overline{\beta }_i \cdot P^{\beta _i} \cdot C_i - \overline{\gamma } \cdot P^{\gamma } \bigg ]^T \\ 0 \le \varLambda ^d \\ \end{array} \right.$$

1.1.2 Counterpart of constraint 3e

• 1. Introduce appropriate truncate matrices to generalize the uncertainties as $\xi$, $\sum _{i\in I} \overline{\beta }_i \cdot (1 + P^{\beta _i} \cdot \xi ) \cdot X_{i,s} \le \overline{\gamma } \cdot (1 + P^{\gamma } \cdot \xi ) ~ \quad \forall s \in {S}_{-1}$.

• 2. Arrange the uncertain variables in left-hand-side and derive the robust counterpart, $\Bigg \{\underset{\xi \in \varXi }{\text {max}} \quad \bigg [ \sum _{i\in I} \overline{\beta }_i \cdot P^{\beta _i} \cdot X_{i,s} - \overline{\gamma } \cdot P^{\gamma } \bigg ] \cdot \xi \Bigg \} \le \bigg [ \overline{\gamma } - \sum _{i\in I} \overline{\beta }_i \cdot X_{i,s} \bigg ] ~ \quad \forall s \in {S}_{-1}$.

• 3. Introduce the uncertainty set,

  $$\left\{ \begin{array}{cc} \max \quad \bigg [ \sum _{i\in I} \overline{\beta }_i \cdot P^{\beta _i} \cdot X_{i,s} - \overline{\gamma } \cdot P^{\gamma } \bigg ] \cdot \xi \\ s.t. \quad - W \cdot \xi \le - h \end{array} \right\} \le \bigg [ \overline{\gamma } - \sum _{i\in I} \overline{\beta }_i \cdot X_{i,s} \bigg ] \quad \forall s \in {S}_{-1}$$

• 4. Introduce dual variable $\varLambda ^e_s$ and apply duality to the inner LP problem,

  $$\begin{aligned}&\left\{ \begin{array}{cc} \min \quad - h ^ T \cdot \varLambda ^e_s \\ s.t. \quad - W ^ T \cdot \varLambda ^e_s = \bigg [ \sum _{i\in I} \overline{\beta }_i \cdot P^{\beta _i} \cdot X_{i,s} - \overline{\gamma } \cdot P^{\gamma } \bigg ]^T \\ 0 \le \varLambda ^e_s \\ \end{array} \right\} \\&\quad \le \bigg [ \overline{\gamma } - \sum _{i\in I} \overline{\beta }_i \cdot X_{i,s} \bigg ] \quad \forall s \in {S}_{-1} \end{aligned}$$

• 5. Drop the min operator,

  $$\left\{ \begin{array} {lll} - h ^ T \cdot \varLambda ^e_s \le \bigg [ \overline{\gamma } - \sum _{i\in I} \overline{\beta }_i \cdot X_{i,s} \bigg ] \quad \forall s \in {S}_{-1} \\ - W ^ T \cdot \varLambda ^e_s = \bigg [ \sum _{i\in I} \overline{\beta }_i \cdot P^{\beta _i} \cdot X_{i,s} - \overline{\gamma } \cdot P^{\gamma } \bigg ]^T \quad \forall s \in {S}_{-1} \\ 0 \le \varLambda ^e_s \quad \forall s \in {S}_{-1} \\ \end{array} \right.$$

1.1.3 Counterpart of constraint 3f

• 1. Introduce appropriate truncate matrices to generalize the uncertainties as $\xi$, $\varPhi \cdot \sum _{i\in I} (C_i + \sum _{s' \in P(s)} X_{i,s'}) \le \sum _{i\in I} \overline{\phi _i} \cdot (1 + P^{\phi _i} \cdot \xi ) \cdot (C_i + \sum _{s' \in P(s)} X_{i,s'}) ~ \quad \forall s \in {L}$.

• 2. Arrange the uncertain variables in left-hand-side and derive the robust counterpart, $\Bigg \{\underset{\xi \in \varXi }{\text {max}} \quad \bigg [ - \sum _{i\in I} \overline{\phi _i} \cdot P^{\phi _i} \cdot (C_i + \sum _{s' \in P(s)} X_{i,s'}) \bigg ] \cdot \xi \Bigg \} \le \bigg [ \sum _{i\in I} \bigg ( \overline{\phi _i} \cdot (C_i + \sum _{s' \in P(s)} X_{i,s'}) - \varPhi \cdot (C_i + \sum _{s' \in P(s)} X_{i,s'}) \bigg ) \bigg ] ~ \quad \forall s \in {L}$.

• 3. Introduce the uncertainty set,

  $$\begin{aligned}&\left\{ \begin{array}{cc} \max \quad \bigg [ - \sum _{i\in I} \overline{\phi _i} \cdot P^{\phi _i} \cdot (C_i \\ + \sum _{s' \in P(s)} X_{i,s'}) \bigg ] \cdot \xi \\ s.t. \quad - W \cdot \xi \le - h \end{array} \right\} \nonumber \\&\quad \le \bigg [ \sum _{i\in I} \bigg ( \overline{\phi _i} \cdot (C_i + \sum _{s' \in P(s)} X_{i,s'}) - \varPhi \cdot (C_i + \sum _{s' \in P(s)} X_{i,s'}) \bigg ) \bigg ] \quad \forall s \in {L} \end{aligned}$$

• 4. Introduce dual variable $\varLambda ^f_s$ and apply duality to the inner LP problem,

  $$\begin{aligned}&\left\{ \begin{array}{cc} \min \quad - h ^ T \cdot \varLambda ^f_s \\ s.t. \quad - W ^ T \cdot \varLambda ^f_s = \bigg [ - \sum _{i\in I} \overline{\phi _i} \cdot P^{\phi _i} \cdot (C_i \\ + \sum _{s' \in P(s)} X_{i,s'}) \bigg ]^T \\ 0 \le \varLambda ^f_s \\ \end{array} \right\} \nonumber \\&\quad \le \begin{array}{cc} \bigg [ \sum _{i\in I} \bigg ( \overline{\phi _i} \cdot (C_i + \sum _{s' \in P(s)} X_{i,s'}) \\ - \varPhi \cdot (C_i + \sum _{s' \in P(s)} X_{i,s'}) \bigg ) \bigg ] \end{array} \quad \forall s \in {L} \end{aligned}$$

• 5. Drop the min operator,

  $$\left\{ \begin{array} {lll} - h ^ T \cdot \varLambda ^f_s \le \bigg [ \sum _{i\in I} \bigg ( \overline{\phi _i} \cdot (C_i + \sum _{s' \in P(s)} X_{i,s'}) - \varPhi \cdot (C_i + \sum _{s' \in P(s)} X_{i,s'}) \bigg ) \bigg ] \quad \forall s \in {L} \\ - W ^ T \cdot \varLambda ^f_s = \bigg [ - \sum _{i\in I} \overline{\phi _i} \cdot P^{\phi _i} \cdot (C_i + \sum _{s' \in P(s)} X_{i,s'}) \bigg ]^T \quad \forall s \in {L} \\ 0 \le \varLambda ^f_s \quad \forall s \in {L} \\ \end{array} \right.$$

1.2 Deriving the robust counterpart for H2

Notice that in hybrid model 2, uncertainty vector is defined as $\xi = [1,\xi ^{\nu _1},\ldots ,\xi ^{\nu _T}]^\top$. Vector $P_t^{\nu }$ is used to simplify the expression ${\tilde{\nu }}_t = \sum _{t'=1}^t \xi ^{\nu _{t'}} = P_t^{\nu } \cdot \xi$. Matrix $P_t$ is used to convert $\xi$ to $\xi _{[t]}$: $\xi _{[t]} = P_t \cdot \xi$.

1.2.1 Counterpart of constraint 6b

• 1. Introduce appropriate truncate matrices to generalize the uncertainties as $\xi$, $P_t^{\nu } \cdot \xi \le \sum _i O_{i,t} \cdot P_{t} \cdot \xi ~ \quad \forall t \in {T}, \xi \in \varXi$.

• 2. Arrange the uncertain variables in left-hand-side and derive the robust counterpart, $\Bigg \{\underset{\xi \in \varXi }{\text {max}} \quad (P_t^{\nu } - \sum _i O_{i,t} \cdot P_{t}) \cdot \xi \Bigg \} \le 0 ~ \quad \forall t \in {T}$.

• 3. Introduce the uncertainty set,

  $$\left\{ \begin{array}{cc} \max \quad \bigg [ P_t^{\nu } - \sum _i O_{i,t} \cdot P_{t} \bigg ] \cdot \xi \\ s.t. \quad - M \cdot \xi \le - l \end{array} \right\} \le 0 \quad \forall t \in {T}$$

• 4. Introduce dual variable $\varPi ^b_t$ and apply duality to the inner LP problem,

  $$\left\{ \begin{array}{cc} \min \quad - l ^ T \cdot \varPi ^b_t \\ s.t. \quad - M ^ T \cdot \varPi ^b_t = \bigg [ P_t^{\nu } - \sum _i O_{i,t} \cdot P_{t} \bigg ]^T \\ 0 \le \varPi ^d_t \\ \end{array} \right\} \le 0 \quad \forall t \in {T}$$

• 5. Drop the min operator,

  $$\left\{ \begin{array} {lll} - l ^ T \cdot \varPi ^b_t \le 0 \quad \forall t \in {T} \\ - M ^ T \cdot \varPi ^b_t = \bigg [ P_t^{\nu } - \sum _i O_{i,t} \cdot P_{t} \bigg ]^T \quad \forall t \in {T} \\ 0 \le \varPi ^b_t \quad \forall t \in {T} \\ \end{array} \right.$$

1.2.2 Counterpart of constraint 6c

Part one:

• 1. Introduce appropriate truncate matrices to generalize the uncertainties as $\xi$, $0.75 \cdot (C_i + \sum _{t' \le t-1} X_{i,t'} \cdot P_{t'} \cdot \xi ) \le O_{i,t} \cdot P_t \cdot \xi ~ \quad \quad \forall i \in {I}, t \in {T}, \xi \in \varXi$.

• 2. Arrange the uncertain variables in left-hand-side and derive the robust counterpart, $\Bigg \{\underset{\xi \in \varXi }{\text {max}} \quad \bigg [ 0.75 \cdot \sum _{t' \le t-1} (X_{i,t'} \cdot P_{t'}) - O_{i,t} \cdot P_t \bigg ] \cdot \xi \Bigg \} \le -0.75 \cdot C_i ~ \quad \forall i \in {I}, t \in {T}$.

• 3. Introduce the uncertainty set,

  $$\left\{ \begin{array}{cc} \max \quad \bigg [ 0.75 \cdot \sum _{t' \le t-1} (X_{i,t'} \cdot P_{t'}) - O_{i,t} \cdot P_t \bigg ] \cdot \xi \\ s.t. \quad - M \cdot \xi \le - l \end{array} \right\} \le -0.75 \cdot C_i \quad \forall i \in {I}, t \in {T}$$

• 4. Introduce dual variable $\varPi ^{c_1}_{i,t}$ and apply duality to the inner LP problem,

  $$\begin{aligned}&\left\{ \begin{array}{cc} \min \quad - l ^ T \cdot \varPi ^{c_1}_{i,t} \\ s.t. \quad - M ^ T \cdot \varPi ^{c_1}_{i,t} = \bigg [ 0.75 \cdot \sum _{t' \le t-1} (X_{i,t'} \cdot P_{t'}) - O_{i,t} \cdot P_t \bigg ]^T \\ 0 \le \varPi ^{c_1}_{i,t} \\ \end{array} \right\} \quad \le -0.75 \cdot C_i \quad \forall i \in {I}, t \in {T} \end{aligned}$$

• 5. Drop the min operator,

  $$\left\{ \begin{array} {lll} - l ^ T \cdot \varPi ^{c_1}_{i,t} \le -0.75 \cdot C_i \quad \forall i \in {I}, t \in {T} \\ - M ^ T \cdot \varPi ^{c_1}_{i,t} = \bigg [ 0.75 \cdot \sum _{t' \le t-1} (X_{i,t'} \cdot P_{t'}) - O_{i,t} \cdot P_t \bigg ]^T \quad \forall i \in {I}, t \in {T} \\ 0 \le \varPi ^{c_1}_{i,t} \quad \forall i \in {I}, t \in {T} \\ \end{array} \right.$$

Part two:

• 1. Introduce appropriate truncate matrices to generalize the uncertainties as $\xi$, $O_{i,t} \cdot P_t \cdot \xi \le C_i + \sum _{t' \le t-1} X_{i,t'} \cdot P_{t'} \cdot \xi ~ \quad \quad \forall i \in {I}, t \in {T}, \xi \in \varXi$.

• 2. Arrange the uncertain variables in left-hand-side and derive the robust counterpart, $\Bigg \{\underset{\xi \in \varXi }{\text {max}} \quad \bigg [ O_{i,t} \cdot P_t - \sum _{t' \le t-1} X_{i,t'} \cdot P_{t'} \bigg ] \cdot \xi \Bigg \} \le C_i ~ \quad \forall i \in {I}, t \in {T}$.

• 3. Introduce the uncertainty set,

  $$\left\{ \begin{array}{cc} \max \quad \bigg [ O_{i,t} \cdot P_t - \sum _{t' \le t-1} X_{i,t'} \cdot P_{t'} \bigg ] \cdot \xi \\ s.t. \quad - M \cdot \xi \le - l \end{array} \right\} \le C_i \quad \forall i \in {I}, t \in {T}$$

• 4. Introduce dual variable $\varPi ^{c_2}_{i,t}$ and apply duality to the inner LP problem,

  $$\left\{ \begin{array}{cc} \min \quad - l ^ T \cdot \varPi ^{c_2}_{i,t} \\ s.t. \quad - M ^ T \cdot \varPi ^{c_2}_{i,t} = \bigg [ O_{i,t} \cdot P_t - \sum _{t' \le t-1} X_{i,t'} \cdot P_{t'} \bigg ]^T \\ 0 \le \varPi ^{c_2}_{i,t} \\ \end{array} \right\} \le C_i \quad \forall i \in {I}, t \in {T}$$

• 5. Drop the min operator,

  $$\left\{ \begin{array} {lll} - l ^ T \cdot \varPi ^{c_2}_{i,t} \le C_i \quad \forall i \in {I}, t \in {T} \\ - M ^ T \cdot \varPi ^{c_2}_{i,t} = \bigg [ O_{i,t} \cdot P_t - \sum _{t' \le t-1} X_{i,t'} \cdot P_{t'} \bigg ]^T \quad \forall i \in {I}, t \in {T} \\ 0 \le \varPi ^{c_2}_{i,t} \quad \forall i \in {I}, t \in {T} \\ \end{array} \right.$$

1.2.3 Counterpart of constraint 6e

• 1. Introduce appropriate truncate matrices to generalize the uncertainties as $\xi$, $\sum _{i\in I} \beta _{i,k} \cdot X_{i,t} \cdot P_t \cdot \xi \le \gamma _k ~ \quad \forall k \in {K}, t \in {T}, \xi \in \varXi$.

• 2. Arrange the uncertain variables in left-hand-side and derive the robust counterpart, $\Bigg \{\underset{\xi \in \varXi }{\text {max}} \quad \bigg [ \sum _{i\in I} \beta _{i,k} \cdot X_{i,t} \cdot P_t \bigg ] \cdot \xi \Bigg \} \le \gamma _k ~ \quad \forall k \in {K}, t \in {T}, \xi \in \varXi$.

• 3. Introduce the uncertainty set,

  $$\left\{ \begin{array}{cc} \max \quad \bigg [ \sum _{i\in I} \beta _{i,k} \cdot X_{i,t} \cdot P_t ) \bigg ] \cdot \xi \\ s.t. \quad - M \cdot \xi \le - l \end{array} \right\} \le \gamma _k \quad \forall k \in {K}, t \in {T}$$

• 4. Introduce dual variable $\varPi ^e_{k,t}$ and apply duality to the inner LP problem,

  $$\left\{ \begin{array}{cc} \min \quad - l ^ T \cdot \varPi ^e_{k,t} \\ s.t. \quad - M ^ T \cdot \varPi ^e_{k,t} = \bigg [ \sum _{i\in I} \beta _{i,k} \cdot X_{i,t} \cdot P_t \bigg ]^T \\ 0 \le \varPi ^e_{k,t} \\ \end{array} \right\} \le \gamma _k \quad \forall k \in {K}, t \in {T}$$

• 5. Drop the min operator,

  $$\left\{ \begin{array} {lll} - l ^ T \cdot \varPi ^e_{k,t} \le \gamma _k \quad \forall k \in {K}, t \in {T} \\ - M ^ T \cdot \varPi ^e_{k,t} = \bigg [ \sum _{i\in I} \beta _{i,k} \cdot X_{i,t} \cdot P_t \bigg ]^T \quad \forall t \in {T} \\ 0 \le \varPi ^e_{k,t} \quad \forall k \in {K}, t \in {T} \\ \end{array} \right.$$

1.2.4 Counterpart of constraint 6f

• 1. Introduce appropriate truncate matrices to generalize the uncertainties as $\xi$, $\varPhi \le \dfrac{ \sum _{i\in I} \phi _{i,k} \cdot (C_i + \sum _{t \in {T}} X_{i,t} \cdot P_t \cdot \xi )}{ \sum _{i\in I}( C_i + \sum _{t \in {T}} X_{i,t} \cdot P_t \cdot \xi )} ~ \quad \forall k \in {K}, \xi \in \varXi$.

• 2. Arrange the uncertain variables in left-hand-side and derive the robust counterpart, $\Bigg \{\underset{\xi \in \varXi }{\text {max}} \quad \bigg [ \varPhi \cdot \sum _{i\in I} \sum _{t \in {T}} X_{i,t} \cdot P_t - \sum _{i\in I} \phi _{i,k} \cdot \sum _{t \in {T}} X_{i,t} \cdot P_t \bigg ] \cdot \xi \Bigg \} \le \sum _{i\in I} \phi _{i,k} \cdot C_i - \varPhi \cdot \sum _{i\in I} C_i ~ \quad \forall k \in {K}, \xi \in \varXi$.

• 3. Introduce the uncertainty set,

  $$\begin{aligned}&\left\{ \begin{array}{cc} \max \quad \bigg [ \varPhi \cdot \sum _{i\in I} \sum _{t \in {T}} X_{i,t} \cdot P_t - \sum _{i\in I} \phi _{i,k} \cdot \sum _{t \in {T}} X_{i,t} \cdot P_t \bigg ] \cdot \xi \\ s.t. \quad - M \cdot \xi \le - l \end{array} \right\} \\&\quad \le \sum _{i\in I} \phi _{i,k} \cdot C_i - \varPhi \cdot \sum _{i\in I} C_i \quad \forall k \in {K} \end{aligned}$$

• 4. Introduce dual variable $\varPi ^f_k$ and apply duality to the inner LP problem,

  $$\left\{ \begin{array}{cc} \min \quad - l ^ T \cdot \varPi ^f_k \\ s.t. \quad - M ^ T \cdot \varPi ^f_k = \bigg [ \varPhi \cdot \sum _{i\in I} \sum _{t \in {T}} X_{i,t} \cdot P_t \\ - \sum _{i\in I} \phi _{i,k} \cdot \sum _{t \in {T}} X_{i,t} \cdot P_t \bigg ]^T \\ 0 \le \varPi ^f_k \\ \end{array} \right\} \le \sum _{i\in I} \phi _{i,k} \cdot C_i - \varPhi \cdot \sum _{i\in I} C_i \quad \forall k \in {K}$$

• 5. Drop the min operator,

  $$\left\{ \begin{array} {lll} - l ^ T \cdot \varPi ^f_k \le \sum _{i\in I} \phi _{i,k} \cdot C_i - \varPhi \cdot \sum _{i\in I} C_i \quad \forall k \in {K} \\ - M ^ T \cdot \varPi ^f_k = \bigg [ \varPhi \cdot \sum _{i\in I} \sum _{t \in {T}} X_{i,t} \cdot P_t - \sum _{i\in I} \phi _{i,k} \cdot \sum _{t \in {T}} X_{i,t} \cdot P_t \bigg ]^T \quad \forall k \in {K} \\ 0 \le \varPi ^f_k \quad \forall k \in {K} \\ \end{array} \right.$$

1.2.5 Counterpart of constraint 6h

Part one:

• 1. Introduce appropriate truncate matrices to generalize the uncertainties as $\xi$, $\underline{\varOmega } \cdot Y^X_{i,t} \le X_{i,t} \cdot P_t \cdot \xi ~ \quad \forall i \in {I}, t \in {T}, \xi \in \varXi$.

• 2. Arrange the uncertain variables in left-hand-side and derive the robust counterpart, $\Bigg \{\underset{\xi \in \varXi }{\text {max}} \quad \bigg [ - X_{i,t} \cdot P_t \bigg ] \cdot \xi \Bigg \} \le - \underline{\varOmega } \cdot Y^X_{i,t} ~ \quad \forall i \in {I}, t \in {T}$.

• 3. Introduce the uncertainty set,

  $$\left\{ \begin{array}{cc} \max \quad \bigg [ - X_{i,t} \cdot P_t \bigg ] \cdot \xi \\ s.t. \quad - M \cdot \xi \le - l \end{array} \right\} \le - \underline{\varOmega } \cdot Y^X_{i,t} \quad \forall i \in {I}, t \in {T}$$

• 4. Introduce dual variable $\varPi ^{h_1}_{i,t}$ and apply duality to the inner LP problem,

  $$\left\{ \begin{array}{cc} \min \quad - l ^ T \cdot \varPi ^{h_1}_{i,t} \\ s.t. \quad - M ^ T \cdot \varPi ^{h_1}_{i,t} = \bigg [ - X_{i,t} \cdot P_t \bigg ]^T \\ 0 \le \varPi ^{h_1}_{i,t} \\ \end{array} \right\} \le - \underline{\varOmega } \cdot Y^X_{i,t} \quad \forall i \in {I}, t \in {T}$$

• 5. Drop the min operator,

  $$\left\{ \begin{array} {lll} - l ^ T \cdot \varPi ^{h_1}_{i,t} \le - \underline{\varOmega } \cdot Y^X_{i,t} \quad \forall i \in {I}, t \in {T} \\ - M ^ T \cdot \varPi ^{h_1}_{i,t} = \bigg [ - X_{i,t} \cdot P_t \bigg ]^T \quad \forall i \in {I}, t \in {T} \\ 0 \le \varPi ^{h_1}_{i,t} \quad \forall i \in {I}, t \in {T} \\ \end{array} \right.$$

Part two:

• 1. Introduce appropriate truncate matrices to generalize the uncertainties as $\xi$, $X_{i,t} \cdot P_t \cdot \xi \le \overline{\varOmega } \cdot Y^X_{i,t} ~ \quad \forall i \in {I}, t \in {T}, \xi \in \varXi$.

• 2. Arrange the uncertain variables in left-hand-side and derive the robust counterpart, $\Bigg \{\underset{\xi \in \varXi }{\text {max}} \quad \bigg [ X_{i,t} \cdot P_t \bigg ] \cdot \xi \Bigg \} \le \overline{\varOmega } \cdot Y^X_{i,t} ~ \quad \forall i \in {I}, t \in {T}$.

• 3. Introduce the uncertainty set,

  $$\left\{ \begin{array}{cc} \max \quad \bigg [ X_{i,t} \cdot P_t \bigg ] \cdot \xi \\ s.t. \quad - M \cdot \xi \le - l \end{array} \right\} \le \overline{\varOmega } \cdot Y^X_{i,t} \quad \forall i \in {I}, t \in {T}$$

• 4. Introduce dual variable $\varPi ^{h_2}_{i,t}$ and apply duality to the inner LP problem,

  $$\left\{ \begin{array}{cc} \min \quad - l ^ T \cdot \varPi ^{h_2}_{i,t} \\ s.t. \quad - M ^ T \cdot \varPi ^{h_2}_{i,t} = \bigg [ X_{i,t} \cdot P_t \bigg ]^T \\ 0 \le \varPi ^{h_2}_{i,t} \\ \end{array} \right\} \le \overline{\varOmega } \cdot Y^X_{i,t} \quad \forall i \in {I}, t \in {T}$$

• 5. Drop the min operator,

  $$\left\{ \begin{array} {lll} - l ^ T \cdot \varPi ^{h_2}_{i,t} \le \overline{\varOmega } \cdot Y^X_{i,t} \quad \forall i \in {I}, t \in {T} \\ - M ^ T \cdot \varPi ^{h_2}_{i,t} = \bigg [ X_{i,t} \cdot P_t \bigg ]^T \quad \forall i \in {I}, t \in {T} \\ 0 \le \varPi ^{h_2}_{i,t} \quad \forall i \in {I}, t \in {T} \\ \end{array} \right.$$