Abstract
In this paper, we present a review of deterministic software for solving convex MINLP problems as well as a comprehensive comparison of a large selection of commonly available solvers. As a test set, we have used all MINLP instances classified as convex in the problem library MINLPLib, resulting in a test set of 335 convex MINLP instances. A summary of the most common methods for solving convex MINLP problems is given to better highlight the differences between the solvers. To show how the solvers perform on problems with different properties, we have divided the test set into subsets based on the continuous relaxation gap, the degree of nonlinearity, and the relative number of discrete variables. The results also provide guidelines on how well suited a specific solver or method is for particular types of MINLP problems.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Mixed-integer nonlinear programming (MINLP) combines the modeling capabilities of mixed-integer linear programming (MILP) and nonlinear programming (NLP) into a versatile modeling framework. By using integer variables, it is possible to incorporate discrete decisions, e.g., to choose between some specific options, into the optimization model. Furthermore, by using both linear and nonlinear functions it is possible to accurately model a variety of different phenomena, such as chemical reactions, separations, and material flow through a production facility. The versatile modeling capabilities of MINLP means there are a wide variety of real-world optimization problems that can be modeled as MINLP problems, e.g., block layout design problems (Castillo et al. 2005), cancer treatment planning (Cao and Lim 2011), design of water distribution networks (Bragalli et al. 2012), portfolio optimization (Bonami and Lejeune 2009), nuclear reactor core fuel reloading (Quist et al. 1999), process synthesis (Grossmann et al. 1999), pooling problems in the petrochemical industry (Misener and Floudas 2009), and production planning (Sahinidis and Grossmann 1991). More of MINLP applications are described by, e.g., Floudas (1995), Biegler and Grossmann (2004), Boukouvala et al. (2016) and Trespalacios and Grossmann (2014). For a recent review on MINLP methods see D’Ambrosio and Lodi (2013) and Bonami et al. (2012).
MINLP is often considered as a “difficult” class of optimization problems. However, there has been significant progress in the field during the last twenty years and there are several good solvers for MINLP problems available today (Bussieck and Vigerske 2010). Here we will focus on convex MINLP, which is a specific subclass with some desirable properties, e.g., it is possible to decompose a convex MINLP problem into a finite sequence of tractable subproblems. An MINLP problem is often considered as convex when its continuous relaxation yields a convex NLP problem. In recent years there has been significant progress within the field of MILP and NLP (Achterberg and Wunderling 2013; Bazaraa et al. 2013) which is also reflected onto the field of MINLP since decomposition techniques for MINLP problems often rely on solving these types of subproblems. It is also possible to solve certain classes of nonconvex MINLP problems, such as problems with signomial or general twice-differentiable constraints, by reformulating them into convex MINLP problems (Pörn et al. 1999; Lundell et al. 2009; Lundell and Westerlund 2017; Nowak et al. 2018), further motivating the study of efficient methods for convex MINLP.
The intention of this paper is to give an overview of commonly available deterministic solvers for convex MINLP problems and to present a thorough numerical comparison of the most common solvers. Most optimization solvers are connected to one or more of the well-established modeling environments for MINLP optimization, such as, AIMMS (Bisschop 2006), AMPL (Fourer et al. 1993), and GAMS (Brook et al. 1988). In recent years, there has also been a growing interest in optimization modeling in Python and Julia (Bezanson et al. 2012); JuMP is a modeling environment for optimization embedded in Julia (Dunning et al. 2017), and Pyomo is a similar environment in Python (Hart et al. 2012). Several MINLP solvers also offer interfaces to MATLAB, and through OPTI Toolbox it is also possible to access several solvers in MATLAB (Currie et al. 2012).
The solvers considered in the numerical comparison are AlphaECP, Antigone, AOA, BARON, BONMIN, Couenne, DICOPT, Juniper, KNITRO, LINDO, Minotaur, Muriqui, Pavito, SBB, SCIP, and SHOT. These were chosen based on criteria like availability, active development, and support for a file format available in MINLPLib (MINLPLib 2018). Some of these are global solvers and therefore not limited to convex problems. However, most of the global solvers have convexity identification techniques or manual strategy settings that can be set by the user to allow them to more efficiently deal with convex problems. The convex solvers can also often be used as heuristic methods without guarantee for finding the optimal solution for nonconvex MINLP problems.
In Sect. 2, the convex MINLP problem is defined and a general overview of the most common algorithms for such problems are given in Sect. 3. Most solvers in the comparison utilize one or more of these solution methods, as described in Sect. 4, which contains a summary of the solvers considered. Section 5 describes the benchmark in detail, and the numerical results are, finally, presented in Sect. 6.
2 Convex MINLP problem formulation
A convex MINLP problem can, without loss of generality, be written as
where the sets N, L and Y are given by
and \(L\cap Y\) is assumed to be a compact set. The upper and lower bounds on the integer variables \(y_i\) are denoted as \({\overline{y}}_i\) and \({\underline{y}}_i\). To ensures convergence of methods such as outer approximation, it is assumed that all the integer variables are bounded either by the variables bounds or by the linear constraints, since unbounded variables can, e.g., cause some of the subproblems to be unbounded. Most solvers do not require the variables to be bounded, however, to avoid such issues some solvers automatically assigns large bounds to unbounded variables. Generally, problem (P-MINLP) is considered as convex if all the nonlinear functions \(g_j\) are convex in the variables \({\mathbf {x}}\) and the relaxed integer variables \({\mathbf {y}}\). There has recently been an interest in nonsmooth convex MINLP, and some solution techniques have been presented see e.g., Eronen et al. (2017) and Eronen et al. (2014). However, most of the commonly available solvers only have guaranteed convergence for smooth problems and therefore we limit this study to problems where the nonlinear functions \(g_j\) are continuously differentiable.
3 Methods
This section describes the most commonly used algorithms for convex MINLP. The methods described are branch and bound, extended cutting plane, extended supporting hyperplane, outer approximation, generalized Benders decomposition, and LP/NLP-based branch and bound. This summary is not intended to give an in-depth analysis of the algorithms, but to better exemplify the differences between the solvers. For a more detailed discussion about the algorithms see, e.g., D’Ambrosio and Lodi (2013), Belotti et al. (2013), Grossmann (2002), and Floudas (1995).
3.1 Branch and bound
Branch and bound (BB) was first presented as a technique for solving MILP problems by Land and Doig (1960). A few years later it was noted by Dakin (1965) that MINLP problems can be solved with a similar branch and bound approach, although the paper focused on linear problems. Solving convex MINLP problems with a BB approach was also studied by Gupta and Ravindran (1985).
In the basic form, BB solves the MINLP problem by relaxing the integer restrictions of the original problem and solving continuous (convex) NLP relaxations. Solving a continuous relaxation of problem (P-MINLP) results in a solution \(({\mathbf {x}}^{k},{\mathbf {y}}^{k})\), which provides a valid lower bound. If all components of \({\mathbf {y}}^{k}\) take on integer values, then it is also an optimal solution to the MINLP problem. Otherwise, the continuous relaxation is divided (branched) into two new NLP subproblems by adding the constraints \(y_i \le {\lfloor }{ y_i^k}{\rfloor }\) and \(y_i \ge {\lceil }{ y_i^k}{\rceil }\) to the relaxed problem. The branching variable \(y_i\) is a variable that takes on a fractional value and usually chosen based on some criteria, e.g., the variable furthest away from an integer value. A new lower bound can be obtained by solving the new subproblems (child nodes), and in case one of the subproblems returns an integer solution it also provides a valid upper bound. The search procedure is often represented by a tree, where the nodes are connected to their parent node and represent the subproblems. If one of the nodes does not provide an integer solution, then it is branched into two new nodes creating two new subproblems. In case one of the nodes obtains an optimum worse than the upper bound or in case the subproblem is infeasible, then the node can be pruned since an optimal solution cannot exist in that part of the search space. This approach of solving convex NLP problems in each node is often referred to as NLP-based branch and bound (NLP-BB).
Obtaining a tight continuous relaxation is of great importance within BB to avoid large search trees. Stubbs and Mehrotra (1999) presented a branch and cut method for convex MINLP problems that uses cutting planes to strengthen the continuous relaxation. Several techniques have been proposed for obtaining cuts to strengthen the continuous relaxation for MINLP problems, e.g., lift-and-project cuts (Kılınç et al. 2017; Zhu and Kuno 2006; Balas et al. 1993), Gomory cuts (Çezik and Iyengar 2005; Gomory et al. 1958), and perspective cuts (Frangioni and Gentile 2006).
Compared to BB techniques for MILP problems, NLP-BB involves computationally more demanding subproblems; it is often not unusual to explore more than 100,000 nodes for a modest-sized problem! Techniques to efficiently integrate the NLP solver and not solving all subproblems to optimality have also been proposed by Borchers and Mitchell (1994) and Leyffer (2001). Another BB approach is to solve LP relaxations in the nodes and construct a polyhedral approximation of the nonlinear constraints. A polyhedral branch and cut technique, solving LP relaxations in the nodes, was presented by Tawarmalani and Sahinidis (2005).
Many important details on BB such as branching strategies have been left out for the sake of brevity. For more details on BB see, e.g., Bonami et al. (2011) and Floudas (2000).
3.2 Extended cutting plane
The extended cutting plane (ECP) algorithm was first presented by Westerlund and Petterson (1995), and can be seen as an extension of Kelley’s cutting plane method for convex NLP problems presented by Kelley (1960). In its original form the ECP method is intended for convex MINLP problems, and by some modifications, given the name generalized alpha ECP (GAECP), it can be applied to pseudoconvex problems as shown by Westerlund and Pörn (2002).
The ECP algorithm uses linearization of the nonlinear constraints to construct an iteratively improving polyhedral outer approximation of the set N. The trial solutions are obtained by solving the following MILP subproblems,
where the set \(\hat{N_k}\) is given by
Here \(A_i\) is an index set containing the indices of either the most violated or all violated constraints in iteration i. Set \(\hat{N_k}\) is, thus, a polyhedral approximation of set N, constructed by first-order Taylor series expansions of the nonlinear constraints generated at the trial solutions \(({\mathbf {x}}^{k},{\mathbf {y}}^{k})\). The linearizations defining \(\hat{N_k}\) is usually referred to as cutting planes since they cut off parts of the search space that cannot contain the optimal solution. Due to convexity, \(N\subseteq \hat{N_k}\) and therefore, the solution of problem (MILP-k) provides a valid lower bound of problem (P-MINLP).
In the first iteration, the set \(\hat{N_0}\) can simply be defined as \({\mathbb {R}}^{n+m}\). New trial solutions are then obtained by solving subproblem (MILP-k), and the procedure is repeated until a trial solution satisfies all the constraints within a given tolerance. Once a trial solution satisfies all nonlinear constraints it is also the optimal solution, since the solution was obtained by minimizing the objective within a set containing the entire feasible region. For more details on the ECP algorithm see, e.g., Westerlund and Petterson (1995) or Westerlund and Pörn (2002).
3.3 Extended supporting hyperplane
The extended supporting hyperplane (ESH) algorithm was presented by Kronqvist et al. (2016) as an algorithm for solving convex MINLP problems. The ESH algorithm uses the same technique as the ECP algorithm for obtaining trial solutions, but uses a different technique for generating the polyhedral outer approximation \(\hat{N_k}\). It has been observed that the cutting planes used to construct the polyhedral outer approximation in the ECP algorithm are, in general, not as tight as possible, see Kronqvist et al. (2016). By using a one dimensional root search, the ESH algorithm is able to obtain supporting hyperplanes to the set N at each iteration, and use these to construct a polyhedral outer approximation \(\hat{N_k}\).
First, a strict interior point \(\left( {\mathbf {x}}_\text {int},{\mathbf {y}}_\text {int}\right)\) is obtained by solving the following convex NLP problem
The interior point should preferably be as deep as possible within the interior of N, which is here approximated by minimizing the \(l_\infty\)-norm of the nonlinear constraints.
Similar to the ECP algorithm, the trial solutions \(\left( {\mathbf {x}}^k_\text {MILP},{\mathbf {y}}^k_\text {MILP}\right)\) are obtained by solving problem (MILP-k). These solutions provide a valid lower bound on the optimal solution of problem (P-MINLP). However, they will not be directly used to construct the set \(\hat{N_k}\) as in the ECP method.
To construct the polyhedral outer approximation, we define a new function F as the point-wise maximum of the nonlinear constraints, according to
A new sequence of points \(\left( {\mathbf {x}}^k,{\mathbf {y}}^k\right)\) is now defined as
where the interpolation parameters \(\lambda ^k\) are chosen such that \(F({\mathbf {x}}^k,{\mathbf {y}}^k)=0\). The interpolation parameters \(\lambda ^k\) can be obtained by a simple one-dimensional root search. The points \(\left( {\mathbf {x}}^k,{\mathbf {y}}^k\right)\) are now located on the boundary of the feasible region, and linearizing the active nonlinear constraints at this point results in supporting hyperplanes to the set N. The set \(\hat{N_k}\) is, thus, constructed according to Eq. (2) using the points \(\left( {\mathbf {x}}^k,{\mathbf {y}}^k\right)\).
The ESH algorithm also uses a preprocessing step to obtain supporting hyperplanes of the set N by solving linear programming (LP) relaxations. The procedure of solving MILP subproblems and generating supporting hyperplanes is repeated until a trial solution satisfies all nonlinear constraints. The tighter polyhedral outer approximation usually gives the ESH algorithm an advantage over the ECP algorithm. It has been shown in Eronen et al. (2017), that the ESH algorithm can also be successfully applied to nonsmooth MINLP problems with pseudoconvex constraint functions.
3.4 Outer approximation
The outer approximation (OA) method was first presented by Duran and Grossmann (1986), with additional properties for convex MINLP problems described in Fletcher and Leyffer (1994). Some modifications of the OA method have been presented to handle nonconvex problems more efficiently, see, e.g., Kocis and Grossmann (1988) and Viswanathan and Grossmann (1990). For more details on the basic convex approach discussed in this paper see, e.g., Grossmann (2002).
OA is a decomposition technique, which obtains the optimal solution of the original problem by solving a sequence of MILP and NLP subproblems. Similar to both ECP and ESH, OA also constructs an iteratively improving polyhedral outer approximation \(\hat{N_k}\) of the nonlinear feasible region defined by the set N. However, OA only uses the polyhedral approximation for choosing the integer combination \({\mathbf {y}}^k\), while the corresponding continuous variables \({\mathbf {x}}^k\) are chosen by solving a convex NLP subproblem.
In each iteration, the polyhedral outer approximation is used to construct problem (MILP-k), referred to as the MILP master problem. A new integer combination \({\mathbf {y}}^k\) is then obtained by solving problem (MILP-k). Once the integer combination \({\mathbf {y}}^k\) is obtained, the following NLP subproblem is formed
If problem (NLP-fixed) is feasible, a valid upper bound can be obtained from the solution \(({\mathbf {x}}^{k},{\mathbf {y}}^{k})\), and the solution is used to improve the polyhedral approximation according to Eq. (2). The polyhedral outer approximation is updated by either linearizing all constraints or only the active constraints.
Problem (NLP-fixed) may also be infeasible in some iteration. If \({\mathbf {y}}^{k}\) is an infeasible integer combination, the corresponding continuous variables can be obtained by solving the following convex subproblem
which minimizes the constraint violation with respect to the \(l_\infty\)-norm. The solution to problem (NLP-feasibility) does not provide a lower bound. However, using the infeasible solution \(({\mathbf {x}}^{k},{\mathbf {y}}^{k})\) to update the polyhedral outer approximation according to Eq. (2), ensures that the infeasible integer combination \({\mathbf {y}}^{k}\) cannot be obtained again by the MILP master problem, cf. Fletcher and Leyffer (1994).
The OA algorithm is usually initiated by solving a continuous relaxation of the MINLP problem, giving an initial lower bound and a solution that can be used to construct the polyhedral approximation \(\hat{N_0}\) (Viswanathan and Grossmann 1990). It is also possible to use integer cuts to exclude specific integer combinations, as suggested by Duran and Grossmann (1986). Solving the MILP master problems (MILP-k) provides a lower bound on the optimum, and the procedure is repeated until the upper and lower bound is within a given tolerance.
In general, OA results in tighter polyhedral outer approximations than the ECP algorithm, and may, therefore, require fewer iterations. For a feasible integer combination, OA will in general result in a tighter polyhedral outer approximation than ESH, but for an infeasible integer combination, ESH can give a tighter approximation. OA may thus require fewer iterations than both ESH and ECP to solve certain problems. However, since each iteration is somewhat more computationally demanding, the methods are difficult to compare directly.
3.5 Generalized Benders decomposition
Generalized Benders decomposition (GBD) was first presented by Geoffrion (1972) and is a generalization of Benders decomposition, a partitioning procedure for solving MILP problems (Benders 1962). As noted by Quesada and Grossmann (1992), GBD is closely related to OA and the main difference is the derivation of the master problem. In GBD, the master problem is projected onto the space defined by the integer variables and the master problem is, thus, only expressed in the integer variables. Here we will not present the full derivation of GBD, but use the same approach as Grossmann (2002) to derive the master problem. For more details on GBD see, e.g., Grossmann and Kravanja (1997) or Floudas (1995).
Given an integer combination \({\mathbf {y}}^{k}\), the corresponding continuous variables can be obtained by solving either one of the problems (NLP-fixed) or (NLP-feasibility). If problem (NLP-fixed) is feasible, it provides a valid upper bound, as well as values for the continuous variables \({\mathbf {x}}^{k}\) and the optimal Lagrangean multipliers \(\lambda ^k\) and \(\mu ^k\). A valid cut is then given by
where \(\nabla _{\mathbf {y}}\) denotes the gradient with respect to the integer variables. Here, \(\alpha\) is a new auxiliary variable used for describing the objective function of the MILP subproblems. Note that the left-hand side of Eq. (6) is a first order Taylor series expansion of the Lagrangean function of problem (NLP-fixed) at the point \(({\mathbf {x}}^{k},{\mathbf {y}}^{k},\lambda ^k,\mu ^k)\) with respect to the \({\mathbf {x}}\) and \({\mathbf {y}}\) variables, and that the gradient with respect to the \({\mathbf {x}}\) variables will be zero. The cut in Eq. (6) can be shown to be a surrogate constraint of the linearization in Eq. (2) in which the continuous variables \({\mathbf {x}}\) are projected out, cf. Quesada and Grossmann (1992) or Grossmann (2002).
If problem (NLP-fixed) is infeasible with the integer combination \({\mathbf {y}}^{k}\), problem (NLP-feasibility) is solved to obtain the continuous variables \({\mathbf {x}}^{k}\) as well as the optimal multipliers \(\lambda ^k\) and \(\mu ^k\). A valid cut in the integer space is then given by,
For more details on the cuts see, e.g., Quesada and Grossmann (1992). The master problem for obtaining new integer combinations, is then given by,
where \(K_f\) contains the indices of all iterations where problem (NLP-fixed) is feasible and the index set K contains all iterations. Solving the master problem provides a lower bound on the optimal solution and gives a new integer combination \({\mathbf {y}}^{k+1}\). The procedure is repeated until the upper and lower bounds are within the desired tolerance.
Since the cuts obtained by equations (6) and (7) can be viewed as surrogate cuts of the linear constraints included in the OA master problem, GBD generates weaker cuts than OA at each iteration and usually requires more iterations to solve a given problem. However, the master problems in GBD may be easier to solve since they contain fewer variables compared to OA and only one cut is added in each iteration.
A compromise between OA and GBD has been proposed by Quesada and Grossmann (1992), where the continuous variables are classified into linear or nonlinear based on how they are involved in the original MINLP problem. By projecting out the nonlinear continuous variables, one can derive a Lagrangean cut in a similary way as with GBD while still retaining the linear constraints involving continuous variables in the master problem. The given method has been coined as partial surrogate cuts (PSC), and as proved in Quesada and Grossmann (1992), it results in a tighter linear relaxation compared to GBD while still only adding one cut per iteration.
3.6 LP/NLP-based branch and bound
When solving a convex MINLP problem with either ECP, ESH, GBD or OA, most of the total solution time is usually spent on solving the MILP subproblems. The MILP problems are also quite similar in consecutive iterations since they only differ by a few linear constraints. To avoid constructing many similar MILP branch and bound trees, Quesada and Grossmann (1992) presented a method which integrates OA within BB, called LP/NLP-based branch and bound (LP/NLP-BB). The main idea is to only construct one branch and bound tree, where the MILP master problem is dynamically updated.
An initial polyhedral outer approximation is constructed by solving a continuous relaxation and linearizing the constraints at the relaxed solution, as in OA. The polyhedral outer approximation is used to construct the first MILP master problem and the branch and bound procedure, where an LP relaxation is solved in each node, is initiated. Once an integer solution is obtained at a given node, the integer combination is used as in OA. If the NLP problem (NLP-fixed) with the given integer combination is feasible, it provides an upper bound and new linearizations are generated. If it is infeasible, new linearizations can be obtained by solving the feasibility problem (NLP-feasibility). The new linearizations are then added to all open nodes, and the LP relaxation is resolved for the node which returned the integer combination. The branch and bound procedure continues normally by solving LP relaxations, which now give a more accurate approximation of the nonlinear constraints. Here, the search must continue down each node until either the LP relaxation returns an integer solution that satisfies all nonlinear constraints, the LP relaxation obtains an objective value worse than the upper bound, or until the LP relaxation becomes infeasible. As in normal BB, a lower bound is provided by the lowest optimal solution of the LP relaxations in all open nodes, and the search continues until the upper and lower bounds are within a given tolerance. The LP/NLP-BB procedure, thus, only generates a single branch and bound tree, and is sometimes referred to as a single-tree OA.
Numerical results have shown that LP/NLP-BB technique can result in significantly fewer nodes than the total number of nodes explored in the multiple MILP master problems in OA (Duran and Grossmann 1986; Leyffer 1993). Implementations of the LP/NLP-BB algorithm have shown promising results, cf. Abhishek et al. (2010), Bonami et al. (2008) or Mahajan et al. (2017).
3.7 Solver enhancement techniques
Most solvers are not based on a single algorithm but combines several techniques to improve its performance. In this section, we briefly describe some preprocessing techniques and primal heuristics that can be integrated with all the previously mentioned methods to improve the practical performance. Other important techniques to improve the performance include various cutting planes as well as different branching rules. For more details on cutting planes for convex MINLP see, e.g., Belotti et al. (2013), Bonami (2011) and (Kılınç et al. 2017). Overviews of branching rules are given by Linderoth and Savelsbergh (1999) and Achterberg et al. (2005).
3.7.1 Preprocessing
Preprocessing includes various techniques for modifying the problem into a form more favorable for the actual solver. The preprocessing procedures can result in tighter relaxations or reduce the problem size. Belotti et al. (2013) classified MINLP presolving techniques into two major categories: housekeeping and reformulations. Housekeeping includes techniques such as bound tightening and removal of redundant constraints, while reformulations can include techniques such as improvement of coefficients in the constraints and disaggregation of constraints.
There are two main approaches for tightening the variable bounds, feasibility-based bound tightening (Shectman and Sahinidis 1998; Belotti et al. 2010), and optimization-based bound tightening (Liberti and Maculan 2006). Feasibility-based bound tightening analyzes the constraints sequentially to improve the variable bounds, whereas optimization-based bound tightening solves a sequence of relaxed problems where each individual variable is maximized and minimized to obtain optimal bounds.
By reformulating the original problem, it is in some cases possible to obtain significantly tighter relaxations. Within MILP it is well known that different problem formulations can result in a tighter or weaker continuous relaxations; the uncapacitated facility location problem is a good example of when disaggregation of some constraints leads to a tighter continuous relaxation (Wolsey 1998). Similar techniques can also be used to obtain tighter relaxations for MINLP problems. Some types of nonlinear constraints can also be disaggregated to obtain a lifted reformulation of the problem, where the nonlinear constraint is split into several constraints by the introduction of new variables. Such lifted reformulations were proposed by Tawarmalani and Sahinidis (2005), where it was shown that a lifted reformulation results in tighter polyhedral outer approximations. In a recent paper by Kronqvist et al. (2018b), it was shown that the performance of several MINLP solvers, based on ECP, ESH, and OA, could be drastically improved by utilizing a reformulation technique based on lifting. Lifted reformulations of MINLP problems have also been studied by Hijazi et al. (2013), and Lubin et al. (2016). Some further reformulation techniques for MINLP problems are also presented in Liberti (2009).
3.7.2 Primal heuristics
Primal heuristics is a common term for algorithms and techniques intended to obtain good feasible solutions with relatively little computational effort compared to solving the original problem. The use of primal heuristics began in the field of MILP, and for instance Fischetti and Lodi (2011) claimed that primal heuristics were one of the most important improvements in MILP solvers within the last decade. In recent years, there has also been an interest in primal heuristics for MINLP problems and several algorithms have been proposed for this task. Such algorithms are, e.g., undercover (Berthold and Gleixner 2014), feasibility pumps (Bonami et al. 2009), rounding heuristics (Berthold 2014b), and the center-cut algorithm (Kronqvist et al. 2018a). Another technique for obtaining feasible solutions in solvers based on ECP, ESH or OA, is to check the alternative solutions in the solution pool provided by the MILP solver (Kronqvist et al. 2016). A detailed summary of several primal heuristics for MINLP problems is given by Berthold (2014a) and D’Ambrosio et al. (2012).
Finding a good feasible solution to an MINLP problem can improve the performance of MINLP solvers, as shown by the numerical results in Berthold (2014a) and Bernal et al. (2017). Having a good feasible solution can, e.g., reduce the size of the search tree in BB-based solvers and provide a tight upper bound. Obtaining a tight upper bound is especially important in solvers based on the ECP or ESH algorithm, because neither of the algorithms will in their basic form obtain a feasible solution before the very last iteration.
4 Solvers
This section is intended as an introduction to commonly available MINLP solvers, and to describe their main properties. Most of the solvers are not based on a single “pure” algorithm but they combine several techniques and ideas to improve their performance. On top of this, MINLP solver technology has evolved from the more mature NLP and MILP fields, and most MINLP solvers rely heavily on such subsolvers. Among the MILP solvers, the most recognized commercial solvers are CPLEX (IBM ILOG CPLEX Optimization Studio 2017), Gurobi (Gurobi 2018), and XPRESS (FICO 2017). The solvers GLPK (Makhorin 2008) and Cbc (Forrest 2005), the latter is a part of the COIN-OR initiative (Lougee-Heimer 2003), and are among the most recognized open-source solvers for MILP. All of these solvers implement an arsenal of methods within a branch and cut framework. In the NLP case, solvers like CONOPT (Drud 1994), Knitro (Byrd et al. 2006), Mosek (Andersen and Andersen 2000), and SNOPT (Gill et al. 2005) are well-known commercial options, and IPOPT (Wächter and Biegler 2006) is a well-known open-source solver (also part of the COIN-OR initiative). There exists more variability in the algorithms behind NLP solvers, e.g., CONOPT implements a Generalized Reduced Gradient (GRG) method, while IPOPT, Knitro, and Mosek use an interior-point method, and SNOPT uses a sequential quadratic programming (SQP) approach; see Biegler (2010) for a review in NLP.
Besides convexity, some of the solvers mentioned here also require an algebraic formulation of the problem. By analyzing the problem structure and applying different reformulations for instance it is, e.g., possible to obtain tighter relaxations. Furthermore, some of the NLP solvers also require the nonlinear functions to be twice continuously differentiable to guarantee convergence, which in turn imposes additional restrictions on some of the MINLP solvers.
In this section, we only mention the main features of the solvers, and for more details see the references given in the solver sections. A summary of solvers and software for MINLP problems was previously also given by Bussieck and Vigerske (2010). The solvers are implemented in a variety of programming languages, either available as standalone executables or libraries accessible from algebraic modeling software like GAMS, AMPL, and AIMMS. Other solvers have been implemented directly in the same programming languages as their modeling systems, e.g., MATLAB, Python-Pyomo, Julia-JuMP. The solvers used in the numerical comparison are listed in alphabetical order below.
4.1 AlphaECP
- License type: :
-
Commercial
- Interfaces: :
-
GAMS, NEOS
- URL: :
AlphaECP (Alpha Extended Cutting Plane) is a solver based on the \(\alpha \hbox {ECP}\) algorithm developed by T. Westerlund’s research group at Åbo Akademi University and implemented in GAMS by T. Lastusilta. By using the GAECP algorithm (Westerlund and Pörn 2002) the solver also has guaranteed convergence for pseudoconvex MINLP problems. AlphaECP mainly solves a sequence of MILP subproblems to generate a polyhedral outer approximation through cutting planes, but to speed-up convergence, it occasionally solves NLP subproblems with fixed integer variables as well. To improve the capabilities of handling nonconvex problems, the algorithm also employs some heuristic techniques described in Lastusilta (2011). An important feature of AlphaECP is the technique to initially only solve MILP problems to feasibility Westerlund and Pörn (2002). This often results in a significant reduction in total solution time since fewer MILP subproblems are solved to optimality. AlphaECP can use all the NLP and MILP subsolvers available in GAMS.
4.2 ANTIGONE
- License type: :
-
Commercial
- Interfaces: :
-
GAMS, NEOS
- URL: :
ANTIGONE (Algorithms for coNTinuous / Integer Global Optimization of Nonlinear Equations) is a global optimization solver developed by R. Misener and C. A. Floudas at Princeton University. As a global solver, ANTIGONE is not limited to only convex problems but is also able to solve a variety of nonconvex problems. It uses reformulations and decomposes nonlinear functions into constant, linear, quadratic, signomial, linear fractional, exponential, and other general nonconvex terms. Convex relaxations are then generated for the decomposed nonconvex terms and the relaxations are solved in a branch and cut framework (Misener and Floudas 2014, 2013). ANTIGONE uses the local solvers CONOPT or SNOPT for finding feasible solutions and CPLEX for lower bounding MILP relaxations. The solver also uses both feasibility- and optimality-based bound tightening to reduce the search space and obtain tighter relaxations.
4.3 AOA
- License type: :
-
Commercial (source code available)
- Interfaces: :
-
AIMMS
- URL: :
AOA (AIMMS Outer Approximation) is a module implemented in the AIMMS language (Hunting 2011). As the name suggests, the solver is based on OA and implements both normal OA and the LP/NLP-BB methods. The latter is the recommended one for convex problems and generates linearizations as lazy constraints utilizing MILP solver callbacks. To improve the performance and its capabilities for solving nonconvex problems, AOA may use nonlinear preprocessing and a multi-start technique. The source code of AOA is included in AIMMS, so the user can fully customize the algorithm (Roelofs and Bisschop 2018). Since the AOA algorithm utilizes MILP callbacks, only CPLEX and Gurobi are available as linear subsolvers. For solving NLP problems CONOPT, IPOPT, Knitro, Minos and SNOPT can be used.
4.4 BARON
- License type: :
-
Commercial
- Interfaces: :
-
Standalone; AIMMS, AMPL, GAMS, JuMP, MATLAB, NEOS, Pyomo, YALMIP
- URL: :
BARON (Branch and Reduce Optimization Navigator) is a global MINLP solver developed by N. V. Sahinidis’s research group (Ryoo and Sahinidis 1996; Tawarmalani and Sahinidis 2005). The solver uses a polyhedral branch and bound technique, and thus, solves LP relaxations in the BB nodes. However, BARON also uses MILP relaxations as described by Zhou et al. (2018) and Kılınç and Sahinidis (2018) and nonlinear relaxations (Khajavirad and Sahinidis 2018). Nonconvex problems are handled by generating convex underestimators and concave overestimators in combination with a spatial branch and bound technique. The solver utilizes automatic reformulations and convexity identification to decompose nonconvex functions into simpler functions with known convex or concave relaxations. The reformulations can also result in tighter lifted polyhedral outer approximations as shown by Tawarmalani and Sahinidis (2005). BARON also uses advanced bound tightening and range reduction techniques to reduce the search space and uses local search techniques as primal heuristics. BARON includes IPOPT, FilterSD or FilterSQP for solving NLP subproblems, and it can also utilize any available NLP solver in GAMS. Cbc, CPLEX or Xpress can be used as LP and MILP subsolvers.
4.5 BONMIN
- License type: :
-
Open-source (EPL 1.0)
- Interfaces: :
-
Standalone; AMPL, C++, GAMS, JuMP, MATLAB, NEOS, OS, Pyomo, YALMIP
- URL: :
BONMIN (Basic Open-source Nonlinear Mixed Integer Programming) is an open-source solver for MINLP problems developed by P. Bonami in a collaboration between Carnegie Mellon University and IBM Research as part of the COIN-OR initiative (Bonami et al. 2008). The solver implements several algorithms, and the user is able to choose between NLP-BB, LP/NLP-BB, OA, feasibility pump, OA-based branch and cut, and a hybrid approach. Some computational results, as well as detailed descriptions of the main algorithms, are given by Bonami et al. (2008) and Bonami and Lee (2007). As subsolvers, BONMIN uses IPOPT for NLP and Cbc or CPLEX for MILP problems.
4.6 Couenne
- License type: :
-
Open-source (EPL 1.0)
- Interfaces: :
-
Standalone; AMPL, C++, GAMS, JuMP, NEOS, OS, Pyomo
- URL: :
Couenne (Convex Over and Under Envelopes for Nonlinear Estimation) is a global open-source solver for MINLP problems. It was developed as part of the COIN-OR initiative by P. Belotti in a collaboration between Carnegie Mellon University and IBM Research. The solver implements an LP-based spatial branch and bound technique as its main algorithm, in addition to bound reduction techniques and primal heuristics (Belotti et al. 2009; Belotti 2010). Couenne features routines for calculating valid linear outer approximations of nonconvex constraints. It is currently the only global MINLP solver available in the COIN-OR Optimization Suite. Couenne uses IPOPT as NLP subsolver, CBC or CPLEX as MILP subsolver and CLP, CPLEX, Gurobi, SoPlex or Xpress as LP subsolver.
4.7 DICOPT
- License type: :
-
Commercial
- Interfaces: :
-
GAMS, NEOS
- URL: :
DICOPT (Discrete Continuous Optimizer) is a solver based on the OA method, developed by I. E. Grossmann’s research group at Carnegie Mellon University. The solver implements the equality relaxation and augmented penalty methods in combination with OA (Viswanathan and Grossmann 1990). In the equality relaxation, the nonlinear equality constraints are relaxed as inequalities using the signs of the corresponding Lagrangean multipliers, given by one of the NLP subproblems. The augmented penalty method relaxes the linearizations with slack variables which are penalized in the objective of the MILP master problem of OA. Both methods are intended as heuristics for nonconvex MINLP problems, although if the equality constraints relax as convex inequalities the methods become rigorous. A feasibility pump algorithm is implemented as a primal heuristic to improve the solver’s performance (Bernal et al. 2017). DICOPT can use any available MILP and NLP subsolvers available in GAMS.
4.8 Juniper
- License type: :
-
Open-source (MIT)
- Interfaces: :
-
JuMP
- URL: :
Juniper is an open-source MINLP solver implemented in Julia. It is developed by O. Kröger, C. Coffrin, H. Hijazi, and H. Nagarajan at Los Alamos National Laboratory. The solver implements an NLP-BB method with branching heuristics and primal heuristics, such as the feasibility pump (Kröger et al. 2018). The solver also uses parallelization capabilities available in Julia to solve multiple NLP subproblems in parallel. For nonconvex problems, it acts as a heuristic. It can use any NLP solver available in JuMP for solving subproblems, and it can optionally use a MIP solver for its feasibility pump.
4.9 Knitro
- License type: :
-
Commercial
- Interfaces: :
-
AIMMS, AMPL, C++, C#, Fortran, Java, JuMP, GAMS, NEOS, Pyomo, Python, YALMIP
- URL: :
Knitro is a commercial optimization software currently developed by Artelys (Byrd et al. 2006). Knitro includes several algorithms for dealing with continuous problems, such as interior-point and active-set algorithms. The solver uses BB techniques for problems with discrete variables, and the solver has three methods for dealing with MINLP problems. The first method uses an NLP-BB algorithm, and the second method is based on the LP/NLP-BB algorithm. The third method, based on a sequential quadratic programming approach, is mainly intended for problems with expensive function evaluations and can handle MINLP problems where the discrete variables are not relaxable, e.g., functions given by black-box simulators (Artelys 2018). By using default settings the solver will automatically choose which method to use.
4.10 LINDO
- License type: :
-
Commercial
- Interfaces: :
-
C, C++, Delphi, Excel/What’s Best!, Fortran, Java, JuMP, GAMS, LINGO, MATLAB, NEOS, .NET, Ox, Python, R
- URL: :
LINDO is a global solver developed by LINDO Systems Inc. (Lin and Schrage 2009). It includes specific algorithms for solving LP, quadratic programming (QP), conic programming, semidefinite programming (SDP), and general NLP problems. For mixed-integer problems, LINDO uses a branch and cut approach (LINDO Systems Inc. 2017). The solvers deal with nonconvex problems by using reformulations and convex relaxations within a BB framework. LINDO also performs preprocessing in combination with bound tightening and uses several local search techniques to quickly find good solutions. Non-smooth functions such as abs, min, floor, etc. are dealt with automatically via reformulation techniques. The solver is able to recognize convex quadratic, conic, and SDP terms, and an option for turning off the global search strategies, i.e., for convex problems, is available. To solve general nonlinear problems LINDO requires the NLP solver CONOPT. Furthermore, if the solver Mosek is available, it is used for efficiently solving conic and SDP problems.
4.11 Minotaur
- License type: :
-
Open-source
- Interfaces: :
-
Standalone; AMPL, C++
- URL: :
Minotaur (Mixed-Integer Nonlinear Optimization Toolkit: Algorithms, Underestimators, and Relaxations) is an open-source toolkit for solving MINLP problems developed in collaboration between Argonne National Laboratory, Indian Institute of Technology Bombay, and the University of Wisconsin-Madison (Mahajan et al. 2017). It implements several different algorithms in a common framework. Currently, Minotaur has two main approaches for convex MINLP based on the NLP-BB and LP/NLP-BB algorithms. It also has a global strategy for quadratically constrained QP. Minotaur implements both a nonlinear presolver and a feasibility pump heuristic. Minotaur is able to use both filterSQP and IPOPT as NLP subsolvers and CLP or CPLEX as LP subsolvers.
4.12 Muriqui
- License type: :
-
Open-source (MIT)
- Interfaces: :
-
Standalone; AMPL, C++
- URL: :
Muriqui is an open-source MINLP solver developed by W. Melo, M. Fampa, and F. Raupp, recently presented by Melo et al. (2018b). The solver has several algorithms implemented, e.g., ECP, ESH, OA, LP/NLP-BB, and NLP-BB, as well as some heuristics approaches (Melo et al. 2018a). The solver provides a platform for using the most common algorithms for convex MINLP with several customizable parameters for the end user. For solving the resulting MILP and NLP subproblems, Muriqui can use CPLEX, Gurobi, Xpress (FICO 2017), Mosek, Glpk (Makhorin 2008), IPOPT and Knitro. Muriqui also utilizes callback functionality and so-called lazy constraints in CPLEX and Gurobi to perform the single-tree search in LP/NLP-BB and in the hybrid algorithm.
4.13 Pavito
- License type: :
-
Open-source (MPL 2.0)
- Interfaces: :
-
JuMP
- URL: :
Pavito is an open-source solver for convex MINLP implemented in Julia by C. Coey, M. Lubin and J. P. Vielma. Its functionality was previously part of the Pajarito solver for conic MINLP, but the NLP functionality was recently moved into the Pavito solver (Coey et al. 2018). Contrary to the other solvers presented in this manuscript, Pajarito uses a conic problem formulation and is based on a conic outer approximation algorithm (Lubin et al. 2016). Conic MINLP formulations can be built using the Disciplined Convex Programming (DCP) modeling paradigm, which may require a reformulation of the test instances. Because of this, Pajarito is left out of the numerical comparison and only Pavito is included. Pavito is based on an OA algorithm and has the functionality to perform a single-tree search similar to LP/NLP-BB by utilizing callbacks to the MILP subsolver. Pavito can use any MILP and NLP subsolver available in JuMP for solving subproblems.
4.14 SBB
- License type: :
-
Commercial
- Interfaces: :
-
GAMS, NEOS
- URL: :
SBB (Simple Branch and Bound) is a solver in GAMS based on NLP-BB, developed by ARKI Consulting and Development A/S. SBB is based on a BB method that solves nonlinear relaxations in the form of NLP problems at each node. For nonconvex MINLP problems it works as a heuristic approach without convergence guarantees. For improved robustness the solver has functionality for dealing with NLP solver failures, by changing either subsolver or subsolver parameters. The solver also uses primal heuristics through the GAMS Branch-Cut-and-Heuristic facility (GAMS 2018). SBB can use any of the available NLP solvers in GAMS for solving the relaxed subproblems. However, it works best with solvers that take advantage of a near-optimal starting point such as CONOPT, Minos and SNOPT.
4.15 SCIP
- License type: :
-
Free for academic use (ZIB academic license); commercial
- Interfaces: :
-
Standalone; AMPL, C, GAMS, JuMP, MATLAB, NEOS, Java, Pyomo, Python
- URL: :
SCIP (Solving Constraint Integer Programs) was originally developed by T. Achterberg at the Zuse Institute Berlin in cooperation with TU Darmstadt, RWTH Aachen, and University of Erlangen-Nürnberg, as a general framework based on branching for constraint integer and mixed-integer programming using branch-cut-and-price, cf. Achterberg (2009). The solver is intended to be modular and it utilizes plugins to make it easy to modify (Gleixner et al. 2018). SCIP was extended by Vigerske and Gleixner (2018) to solve convex and nonconvex MINLP problem by utilizing polyhedral outer approximations and a spatial branch and bound technique. The solver uses LP relaxations and cutting planes to provide strong dual bounds, while using Constraint Programming to handle arbitrary (non-linear) constraints and propagation to tighten domains of variables. A variety of primal heuristics and bound tightening techniques are also utilized in the solver. SCIP includes SoPlex for solving the LP subproblems, but can also utilize, CLP, CPLEX, Gurobi, Mosek or XPress if available. Furthermore, the solver uses IPOPT for solving NLP subproblems in the nonlinear strategy.
4.16 SHOT
- License type: :
-
Open-source (EPL 2.0)
- Interfaces: :
-
Standalone; C++, GAMS
- URL: :
SHOT (Supporting Hyperplane Optimization Toolkit) is an open-source solver for convex MINLP developed by A. Lundell, J. Kronqvist and T. Westerlund at Åbo Akademi University (Lundell et al. 2018; Kronqvist et al. 2016). The solver utilizes polyhedral outer approximations, generated mainly by the ESH method, and iteratively constructs an equivalent MILP problem for its lower bound. For the upper bound, SHOT utilizes primal heuristics such as solving fixed NLP problems. If either CPLEX and Gurobi are used as MILP subsolver, SHOT can use a single-tree approach similar to the LP/NLP-BB technique. The supporting hyperplanes are then dynamically added by utilizing callbacks and lazy constraints, enabling the MILP solver to continue without rebuilding the branch and bound tree. If Cbc is used as MILP subsolver, a multi-tree strategy is used. The tight integration with the MILP solvers enables SHOT to fully benefit from their cut generating procedures, advanced node selection, and branching techniques. SHOT also includes the functionality to solve MIQP subproblems with CPLEX and Gurobi. The NLP problems are solved with either IPOPT or any of the applicable solvers in GAMS. A version of SHOT with reduced functionality, e.g., only utilizing the multi-tree approach, is also available for Wolfram Mathematica (Lundell et al. 2017).
4.17 Other MINLP solvers
Besides the solvers mentioned above, there are a few others solvers capable of solving convex MINLP problems that the authors are aware of. It should be noted that the solvers left out of the numerical comparison are not necessarily inferior compared to the other solvers. These solvers have been left out of the comparison due to one of the following reasons: not publicly available, not maintained within the last years, or not able to read the problem formats available in MINLPlib.
bnb is a MATLAB implementation of NLP-BB by K. Kuipers at the University of Groningen. The solver uses the fmincon routine in MATLAB’s Optimization Toolbox for solving the integer relaxed subproblems. The MATLAB code for the solver can be downloaded from www.mathworks.com/matlabcentral/fileexchange/95-bnb.
FICO Xpress-SLP is a solver currently developed by FICO (FICO 2017) and is available as both standalone binaries and a FICO Xpress-MOSEL module. The solver has an interface to Python and can be used in several other programming environments through the BCL Builder Component Library (FICO 2017). Xpress-SLP is a local solver designed for large scale nonconvex problems, and global optimality is only guaranteed for convex problems. For general MINLP problems, the solver uses a mixed integer successive linear programming (MISLP) approach. With the MISLP approach, it is, e.g., possible to use an NLP-BB technique where the NLP subproblem at each node is solved using a successive linear programming (SLP) technique. For certain types of problems, such as convex MIQP, MIQCQCP and MISOCP, the solver detects convexity and automatically reverts to FICO Xpress’s purpose written solvers. The solver also includes some heuristic approaches for quickly obtaining solutions. More information about FICO and its solvers can be found at www.fico.com/en/products/fico-xpress-optimization.
FilMINT is an MINLP solver developed by K. Abhishek, S. Leyffer and J. Linderoth based on the NLP/LP-BB algorithm (Abhishek et al. 2010). The solver is built on top of the MILP solver MINTO (Nemhauser et al. 1994) and uses filterSQP (Fletcher and Leyffer 1998) for solving NLP relaxations. By utilizing functionality in MINTO, FilMINT is able to combine the NLP/LP-BB algorithm with features frequently used by MILP solvers, such as cut generation procedures, primal heuristics, and enhanced branching and node selection rules. There is an AMPL interface available for FilMINT and the solver can also be used through the NEOS server. For more details, we refer to Abhishek et al. (2010).
fminconset is an implementation of NLP-BB in MATLAB by I. Solberg. The NLP subproblems are solved with MATLAB’s fmincon routine in the Optimization Toolbox. The solver is available to download from www.mathworks.com/matlabcentral/fileexchange/96-fminconset.
GAECP (Generalized Alpha Extended Cutting Plane) is a solver based on the GAECP algorithm (Westerlund and Pörn 2002) developed by T. Westerlund. The solver also uses supporting hyperplanes as in the ESH algorithm and is able to guarantee convergence for MINLP problems with nonsmooth pseudoconvex functions. The solver is described in detail in Westerlund (2018).
MILANO (Mixed-Integer Linear and Nonlinear Optimizer) is a MATLAB-based MINLP solver developed by H. Y. Benson at Drexel University. There are two versions of the solver available; one uses an NLP-BB technique and the other is based on OA. The NLP-BB technique version uses an interior point NLP solver with warm-starting capabilities described in Benson (2011). The solver can be downloaded from www.pages.drexel.edu/~hvb22/milano.
MindtPy (Mixed-Integer Nonlinear Decomposition Toolbox in Pyomo) is an open-source software framework implemented in Python for Pyomo by the research group of I. Grossmann at Carnegie Mellon University. This toolbox implements the ECP, GBD, and OA algorithms, together with primal heuristics. It relies on Pyomo to handle the resulting MILP and NLP subproblems, allowing any of the solvers compatible with Pyomo to be used with MindtPy (Bernal et al. 2018). The toolbox is available in the following repository www.github.com/bernalde/pyomo/tree/mindtpy.
MINLP_BB was developed by S. Leyffer and R. Fletcher as a general solver for MINLP problems (Leyffer 1999). The solver is based on NLP-BB and uses filterSQP for solving the continuous relaxations. There are interfaces to AMPL and Fortran. Furthermore, the solver can also be used in MATLAB through the TOMLAB optimization environment (Holmström 1999). More information about the solver is available at wiki.mcs.anl.gov/leyffer.
MINOPT (Mixed Integer Nonlinearl Optimizer) was developed by C.A. Schweiger and C.A. Floudas as a modelling language for a wide range of optimization problems (Schweiger and Floudas 1998). For MINLP problems MINOPT offered several algorithms, such as variants of OA and GBD.
MISQP (Mixed-Integer Sequential Quadratic Programming) is a solver based on a modified sequential quadratic programming (SQP) algorithm for MINLP problems presented by Exler and Schittkowski (2007). The solver is developed by K. Schittkowski’s research group and the University of Bayreuth. MISQP is intended for problems where function evaluations may be expensive, e.g., where some function values are obtained by running a simulation. Unlike some of the other solvers, MISQP does not need to evaluate functions at fractional values for integer variables which can be an important property, e.g., for simulation-based optimization tasks. There is an interface in MATLAB through TOMLAB as well as a standalone Fortran interface. A more detailed description of the solver is available at tomwiki.com/MISQP.
Finally, there are a few other deterministic solvers that the authors are aware of, capable of handling convex MINLP problems but mainly focusing on nonconvex MINLP. These solvers are: Decogo (DECOmposition-based Global Optimizer; Nowak et al. (2018)), NOMAD (Le Digabel 2011), POD (Piecewise convex relaxation, Outer-approximation, and Dynamic discretization; Nagarajan et al. (2017)), LaGO (Lagrangian Global Optimizer; Nowak et al. (2002)). For more details on nonconvex MINLP see, e.g., Tawarmalani and Sahinidis (2002), Liberti and Maculan (2006) and Floudas (2000).
5 Benchmark details
The objective of the forthcoming two sections is to compare some of the convex MINLP solvers mentioned in the previous section by applying them on a comprehensive set of test problems. There are some benchmarks available in literature, e.g., Kronqvist et al. (2016), Bonami et al. (2012), Lastusilta (2011) and Abhishek et al. (2010). However, these are limited to only a few of the solvers considered here or used a smaller set of test problems. The goal here is to give a comprehensive up-to-date comparison of both open-source and commercial solvers available in different environments. The main interest has been to study how the solvers perform on a desktop computer, and all the benchmarks were performed on a Linux-based PC with an Intel Xeon 3.6 GHz processor with four physical cores (able to process eight threads at once) and 32 GB memory. We have allowed the solvers to use a maximum of eight threads to replicate a real-world situation where one tries to solve the problems with all the available resources. However, it is worth mentioning that the solvers and subsolvers utilize parallelism to different extents.
In the comparison, we have included three versions of BONMIN: BONMIN-OA based on OA, BONMIN-BB based on NLP-BB, and BONMIN-HYB, which is a variant of the LP/NLP-BB algorithm. We have also included two versions of Minotaur: Minotaur-QG based on the LP/NLP-BB algorithm, and Minotaur-BB based on NLP-BB. Two version of Knitro where considered: Knitro-QG based on LP/NLP-BB and Knitro-BB based on NLP-BB. These different versions of the same solver were included since they represent different approaches for solving the MINLP problems and their performance vary significantly. The solvers in the comparison are implemented in and used from different environments (GAMS, AIMMS, and Julia/JuMP), and the subsolvers available may vary. Where possible, we have tried to use CONOPT and IPOPT as the NLP solver, and CPLEX as the (MI)LP solver. The linear solver used in IPOPT was MA27 (HSL 2018) which is the default if available. For all applicable solvers, the latest version of CPLEX (12.8) was used; the exception is Minotaur which we only got working with version 12.6.3. Couenne warns against using another LP solver than CLP, which we respected since it actually improved performance significantly. For Minotaur, filterSQP was used as NLP subsolver as it is recommended over IPOPT, and overall performed better. A full list of solvers and subsolvers used are given in Table 1.
The termination criteria used with the solvers is the relative objective gap between the upper and lower objective bounds, where we used a tolerance of 0.1% with all the solvers. To make sure that the solvers did not terminate prematurely due to other built-in termination criteria and to avoid clear solver failures, some specific solver options were given; these are listed in Appendix B. Except for these, default settings were used for all solvers. Furthermore, a wall clock time limit of 900 s was also used with all solvers. Even with the 15-min time limit per problem, the total running time for the experiments was more than two weeks.
5.1 Problem sets
The problems considered here are from the problem library MINLPLib (MINLPLib 2018), which as of July 2018 consists of 1534 instances. These instances originate from many different sources and applications as indicated in the library. Out of the instances, we have chosen all problems that satisfy the following criteria: classified as convex, containing at least one discrete variable and some nonlinearity (either in the objective function or in the constraints). We also excluded the instance meanvarxsc utilizing semicontinuous variables not supported by all of the solvers. The smallinvSNPr* instances were also excluded, since they recently lost their convex classification in MINLPLib due to rounding errors in the problem format that actually made them slightly nonconvex. In total, there were 335 instances that satisfied the given criteria, and these constitute our master benchmark test set. Some statistics of the problems are available in Table 2
The problems selected represent a variety of different types of optimization problems with different properties such as number of variables, number of discrete variables, and number of nonlinear terms. Some of the problems also represent different formulations of the same problems, e.g., both big-M and convex hull formulation of disjunctions. It is therefore of interest to compare the solvers not only on the entire test set but also on smaller subsets with specific properties. We have partitioned the test set into groups, representing both integer and nonlinear properties, to compare both the solvers and algorithms for the different types of problems. The following criteria were used to partition the test problems into subsets:
5.1.1 Continuous relaxation gap
By solving a continuous relaxation of the MINLP problem and comparing the optimal objective value of the relaxed problem with the actual optimal objective value, we are able to determine the continuous relaxation gap. To avoid differences due to scaling, we use a relative value calculated as
where \(z^*\) denotes the optimal objective value and \(\bar{z}\) denotes to optimum of the continuous relaxation. The continuous relaxation gap varies significantly for the test problems: some instances have a gap larger than 1000% and for some instances it is smaller than 1%. Based on the gap, given by Eq. (8), we have divided the test problems into two subsets: problems with a large gap (\(\ge 50\%\)) and problems with a small gap (\(<50\%\)). According to this classification, there are 151 problems with a large gap (average gap 188%) and 184 with a small gap (average gap 7.2%).
5.1.2 Nonlinearity
Some of the test problems are almost linear with only a few nonlinear terms, whereas some test problems are nonlinear in each variable. The test problems are here classified based on the following nonlinearity measure
where \(n_\text {nonlin}\) is the number of variables involved in a nonlinear term and \(n_\text {tot}\) is the total number of variables. The test problems are divided into the following two categories: problems with high degree of nonlinearity (\(\ge 50\%\)), and problems with low degree of nonlinearity (\(<50\%\)). The set with high degree of nonlinearity contains 103 problems with an average nonlinearity measure of 89%, while the set with low degree of nonlinearity contains 232 problems with an average nonlinearity measure of 14%.
5.1.3 Discrete density
The number of discrete variables also varies significantly in the test problems. Some problems contain only a few discrete variables, while others contain only discrete variables. To avoid a division based mainly on the problem size, we have chosen to divide the problems based on the following measure
Here \(n_\text {int}\) and \(n_\text {bin}\) are the number of integer and binary variables, and \(n_\text {tot}\) is the total number of variables. Again the test problems are divided into two subsets: problems with a high discrete density (\(\ge 50 \%\)) and problems with a low discrete density (\(< 50 \%\)). The first category contains 120 problems with an average discrete density of 81%, and the second category contains 215 problems with an average density of 27%.
A list of the problems in each category is given in “Appendix A”, which also shows the continuous relaxation gap, degree of nonlinearity, and discrete density for each test problem. Scatter plots are also presented in “Appendix A” that show there is little to no correlation between the problem categories.
5.2 Reporting
All the results were analyzed using PAVER (Bussieck et al. 2014), which is a tool for comparing the performance of optimization solvers and analyzing the quality of the obtained solutions. The reports generated by PAVER, as well as all the results obtained by the individual solvers are available at andreaslundell.github.io/minlpbenchmarks. The parameters used for generating the reports are also available within the reports.
A comment must be made regarding the choice of the parameter gaptol in PAVER, which was set to the value \(1.002\times 10^{-3}\) instead of the value used as termination criteria (\(1\times 10^{-3} = 0.1\%\)). The small perturbation is needed due to differences in how the relative gap is calculated by the solvers. Some of the solvers calculate the relative gap by dividing the gap by the lower bound, whereas others divide by the smallest absolute value of either the upper or lower bound. For example, BARON and ANTIGONE would, without the small perturbation, seem to terminate prematurely on a large number of instances and these would all be marked as failed by PAVER.
PAVER also calculates so-called virtual best and virtual worst solvers. The virtual best solver is the best (in our graphs the fastest) successful solver selected for each individual problem instance, and the virtual worst is then the slowest for each instance. These virtual solvers provide a good comparison for how good or bad an individual solver is compared to all the solvers.
Since MINLPLib also provides a list of known optimal objective values, as well as upper and lower objective bounds, PAVER is able to compare the obtained solutions by the known bounds in MINLPLib. PAVER is, thus, also able to calculate the so-called primal gap, i.e., the difference between the obtained solution and the best-known integer solution, which can be used to analyze the quality of the obtained solutions. For example, there are cases where the solver returns the optimal solution, but it has not been able to verify optimality within the time limit. PAVER also uses known objective bounds available in MINLPLib to check whether the solvers obtained correct solutions and bounds for the test problems.
6 Results
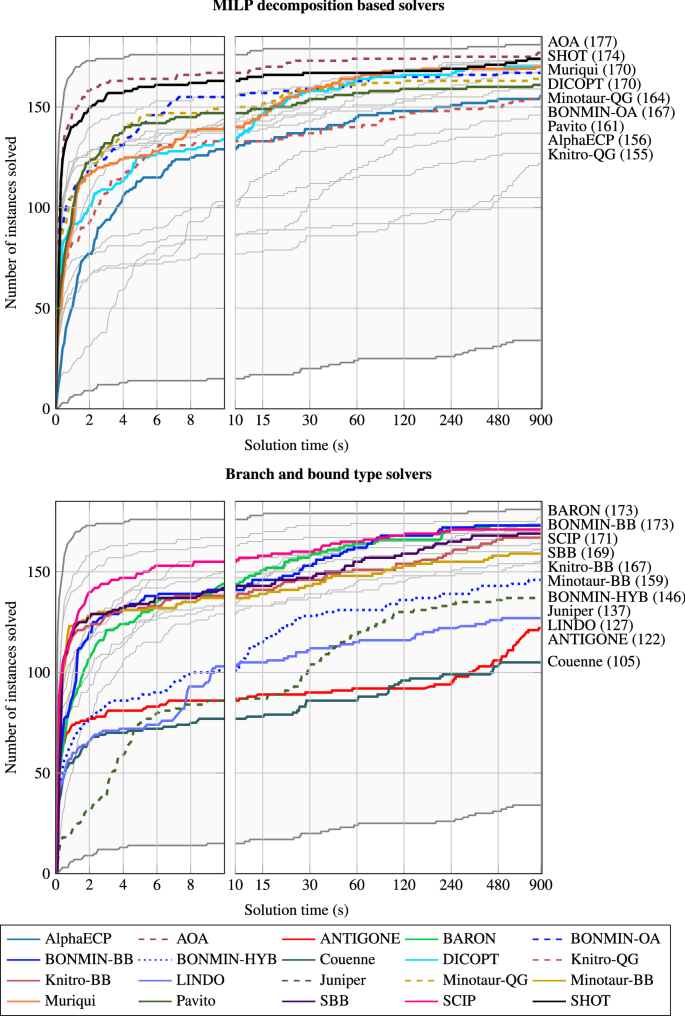
The solution profile indicates the number of solved convex MINLP instances in MINLPLib (MINLPLib 2018) as a function of time. A problem is regarded as solved if the relative objective gap, as calculated by PAVER (Bussieck et al. 2014), is \(\le 0.1\%\). The border lines on top/below the shaded area indicates the virtual best/worst solver
The solution profile indicates the number of solved convex MINLP instances in MINLPLib (MINLPLib 2018) as a function of time. A problem is regarded as solved if the relative objective gap, as calculated by PAVER (Bussieck et al. 2014), is \(\le 0.1\%\). The border lines on top/below the shaded area indicates the virtual best/worst solver
The results are presented using solution profiles showing the number of individual problems that a solver is able to solve as a function of time. Note that the profiles do not represent the cumulative solution time, but shows how many individual problems the solvers can solve within a specific time. We have not used performance profiles where the time is normalized with respect to best solver (Dolan and Moré 2002) since these are not necessarily good for comparing several solvers as noted by Gould and Scott (2016).
In all solution profiles in this section, we have chosen to divide the solvers into two categories to make the solution profiles more easily readable. The solvers are divided into MILP decomposition-based solvers and BB-based solvers. The division is not completely straightforward since some of the solvers could fit into both categories. However, the division is only intended to make it easier to read the results. The solvers classified as MILP decomposition-based solvers are AlphaECP, AOA, BONMIN-OA, DICOPT, Knitro-QG, Minotaur-QG, Muriqui, Pavito, and SHOT. Solvers classified as BB-based solvers are ANTIGONE, BARON, BONMIN-BB, BONMIN-HYB, Couenne, Juniper, Knitro-BB, LINDO, Minotaur-BB, SBB, and SCIP. The time scales are also divided into two parts to better highlight differences between the solvers, and it is linear in the first 10 s, and logarithmic between 10 and 900 s. In each plot, the solvers in the nonactive group are indicated with thin gray lines, while the others are as shown in the respective legends. The same line style is used for a specific solver in all figures. If there are several different strategies used with the same solvers, different line types (solid, dashed, dotted) are used while the color remain the same. In the right margin of each profile, the solvers are ranked according to the number of solved problems (as indicated within parenthesis). The virtual best and virtual worst solvers are shown in the figures as the top and bottom thick gray lines, and the region between them is shaded.
Figures 1 and 2 show the solution profiles when applying the solvers on the complete set of test problems. As mentioned, the solution profiles indicate the number of problems that have been solved by the individual solvers as a function of time. A problem is defined as solved in this set of experiments if the relative objective gap, as calculated by PAVER, is \(\le\) 0.1002% (see note above). To better examplify the differences between the solvers, the same data is used for generating Table 3 which shows “snapshots” of the solution profile for different levels of the number of solved problems.
Out of the BB-based solvers, BARON is able to solve the most instances (306) within the time limit followed by SCIP (295) and Minotaur-BB (258). SHOT is able to solve the most problems out of the MILP decomposition-based solvers (312), closely followed by AOA (310) and Muriqui (301). SHOT and AOA are overall the fastest solvers for the test set. The virtual best solver is able to solve 326 of the problems while the virtual worst only manages to solve 39. The virtual best and worst solvers indicate a huge spread in the solvers’ performance for different problems and highlight the importance of choosing a solver well suited for the problem type. The virtual best solver also shows that a large portion of the test problems are manageable for at least one of the solvers, while judging by the virtual worst solver, it is clear the test set is challenging.
Figure 3 presents statistics regarding the termination of the solvers, e.g., how many errors and timeouts occurred. These values are as reported by the solver, but also include solver crashes where no solution was returned. PAVER also verifies if the solver runs were completed successfully, e.g., by comparing the objective values returned to known values or bounds; if there is a discrepancy, these instances are given the status failed. Statistics on instances marked as failed are shown in Fig. 4.
Figure 5 shows the number of problems where the solver was able to obtain a solution within 0.1% and 1% of the best-known solution, but not necessarily able to verify optimality. The figure shows that none of the solvers was able to obtain a solution within 1% of the best-known solution for all of the problems, given the 900 s time limit. For example, BARON was able to obtain a solution within 1% of the optimum for 317 problems, and SHOT obtained such a solution for 320 problems.
The number of instances solved to a relative objective gap, i.e., difference between the upper and lower objective bound, of 0.1%, 1% and 10%, per solver is shown in Fig. 6. By comparing Figs. 5 and 6, it can be observed that some of the solvers are able to obtain a solution within 0.1% of the optimum to significantly more problems than they are able to verify as optimal. For example, AlphaECP and ANTIGONE seems to be struggling with obtaining a tight lower bound for some of the problems, since they are able to obtain solutions within 0.1% for 300 (AlphaECP) and 275 (ANTIGONE) problems, while only verifying optimality for 276 and 236 instances respectively. Since ANTIGONE is a global solver without a user-selected convex strategy, it might fail to recognize some of the problems as convex, and therefore, generate weaker relaxations. This would explain the difference between the number of optimal solutions found and number of solutions verified as optimal.
Since it may be difficult to draw more detailed conclusions from the results in Figs. 1 and 2, the next sections consider subsets of test problems with specific properties. A summary of the results for the different subsets is given in Sect. 6.4.
6.1 Impact of the continuous relaxation gap
In this section, we consider problems with a large continuous relaxation gap and problems with a small continuous relaxation gap. Figure 7 shows the solution profiles of the solvers for the problems with a large gap, and Fig. 8 shows the solution profiles for those with a small gap. By comparing the figures, there is a clear difference for the solvers based on a BB approach, as these clearly perform better on the problems with a small gap compared to those with a large continuous relaxation gap. For example, BONMIN-BB is one of the most efficient solvers for the problems with a small gap, both in terms of speed and number of solved problems, while it is clearly out-performed by several solvers for the problems with a large gap.
The NLP-BB-based solvers, BONMIN-BB, Juniper, Knitro-BB, Minotaur-BB, and SBB solve significantly fewer problems with a large gap than the solvers based on either an ECP, ESH or OA (AlphaECP, BONMIN-OA, DICOPT, and SHOT). For problems with a large continuous relaxation gap, the BB trees may become larger and the more expensive subproblems in each node may make the NLP-BB-based solvers suffer performance-wise. Using a polyhedral approximation within a BB framework, BARON and SCIP are not as strongly affected by the relaxation gap; this could partially be due to having simpler subproblems at each node.
Overall, the MILP decomposition-based solvers seem to be less affected by the continuous relaxation gap then the BB-based ones. Several of the MILP decomposition-based solvers, such as AOA and SHOT, are closely integrated with the MILP subsolver (CPLEX in this case), and rely on it for handling the integer requirements. This close integration enables the usage of several advanced features from the more mature MILP solvers, while NLP-BB-based solvers often need to manage branching, handling the BB tree, cut generation, and other techniques on their own. One can expect this advantage to be more important for problems that are challenging due to the integer requirements, which is often a trait of problems with large continuous relaxation gaps. As an example of the impact on the performance of a MILP decomposition-based solver that handle the integer requirements itself, consider Minotaur-QG (as it only uses CPLEX as a LP subsolver): The performance difference between Minotaur-QG and AOA are significant, even though they utilize the same basic algorithm.
6.2 Impact of nonlinearity
In this section, problem types with a high and low degree of nonlinearity are compared, and the results are shown in Figs. 9 and 10. Several of the solvers use linearizations to approximate the nonlinear functions in some steps of the solution procedure, whereas solvers using an NLP-BB approach directly treats the nonlinearity in each node of the BB tree. As expected, most of the solvers utilizing linearizations perform significantly better on the problems with a low degree of nonlinearity, since BONMIN-OA, DICOPT, and SCIP are among the most efficient solvers in terms of both speed and number of problems solved. However, for problems with a high degree of nonlinearity they are outperformed by the NLP-BB-based solvers BONMIN-BB, Knitro-BB, Minotaur-BB, and SBB.
SHOT and the LP/NLP-BB-based solvers AOA, Minotaur-QG and Muriqui have quite similar behavior for both types of problems and perform well in both categories. These solvers rely on linearizations of the nonlinear constraints and one would, thus, expect them to be negatively affected by the degree of nonlinearity. However they all use a quite similar single-tree approach where NLP subproblems are solved in some of the nodes, which may help them to cope with problems with a high degree of nonlinearity. The LP/NLP-BB-based solver Knitro-QG also performs quite well for problems with a high degree of nonlinearity.
Most affected by the degree of nonlinearity seem to be the NLP-BB-based solvers. For problems with a high degree of nonlinearity they performed overall well, with several of the NLP-BB-based solvers being among the most efficient ones. Thus, in this case there seems to be a clear advantage of directly treating the nonlinearities. For the problems with a low degree of nonlinearity, however, the NLP-BB-based solvers did not perform as well in comparison with the other solvers.
6.3 Impact of discrete density
Finally, we compare how the solvers are affected by the relative number of discrete variables, i.e., integer and binary variables. Figures 11 and 12 show how the solvers perform for problems with high and low discrete density.
The MILP decomposition-based solvers perform similarly for both types of problems, and no obvious conclusions can be drawn from the results. However, again there is a clear difference for the NLP-BB-based solvers, and surprisingly many of these solvers performed better than the other ones on the high discrete density set of problems. One could expect a correlation between the discrete density and continuous relaxation gap, and that a high discrete density would result in a high continuous relaxation gap. However, as shown in Fig. 13 in “Appendix A”, there is basically no correlation between the two for this set of test problems. Thus, by analyzing the results there is no clear reason for why the NLP-BB-based solvers perform better for the problems with a high discrete density, but one should keep in mind that the test set is somewhat limited.
Both BARON and SHOT perform well on both sets of test problems, while they perform somewhat better on problems with a low discrete density. The OA approach seems to be well suited for the problems with a low discrete density, where DICOPT is one of the most efficient solvers and BONMIN-OA also manages to solve a large portion of the problems. AOA and Muriqui, both integrating the LP/NLP-BB method through callbacks and lazy constraints with the MILP solver, also perfoms well on both categories.
6.4 Summary of the results
How the solvers are affected by the continuous relaxation gap, degree of nonlinearity and discrete density is summarized in Table 4. The table shows the number of problems solved within each category as well as an indicator of how the solvers’ performances were affected by the specific properties. The performance indicator tries to show how the performance of a solver is affected by the problem properties with respect to the other solvers. If a solver clearly performed better in a category, with respect to speed and number of solved problems, it is indicated by ‘+’, and similarly ‘−’ indicates that solver performed worse for that category of problems. If the performance is similar within both categories it is indicated by ‘\(\sim\)’. Each performance indicator has been chosen by comparing how a specific solver performed in both the high and low category with respect to the other solvers. Note that a ‘–’ sign does not necessarily indicate that the solver performed poorly, it simply states that the solver did not perform as well as in the other category. For example, for the problems with a low degree of nonlinearity DICOPT is overall one of the fastest solvers. For the problems with a high degree of nonlinearity DICOPT also performs well, but not as well as in the other category, and this is indicated by a ‘+’ and ‘−’ sign in Table 4. That there are no significant changes for the performance of AOA with respect to both categories is indicated by ‘\(\sim\)’ sign.
These indicators were obtained by carefully analyzing the performance profiles, and are not intended as a grade of the solver but to show how it is affected by different problem properties. The results presented in Table 4 indicates that BB-based solvers seem to be more affected by the problem properties considered here compared to the MILP decomposition-based solvers. One possible explanation for the differences between the two types of solvers is that several of the MILP decomposition-based solvers rely heavily on the MILP subsolver, and benefits from several advanced features from the MILP solver.
Comparing the global solvers (ANTIGONE, BARON, Couenne, LINDO, and SCIP) with the convex solvers is not completely fair since the global solvers are able to solve a wider class of problems. In the numerical comparison, one should keep in mind that these global solvers are intended for a different (more general) type of problems. Some of these solvers do not have a convex option, and thus, they have access to less information about the problem and might treat it as nonconvex. For example, the performance difference of ANTIGONE and Couenne compared to BARON and SCIP, may be explained with the solvers treating some of the convex functions as nonconvex, and therefore, generate unnecessarily weak relaxations. BARON seems to be very efficient at identifying convex problems since it is able to deal with the problems in the benchmark set in such an efficient manner. Even if it is a global solver, capable of handling a variety of nonconvex problems, it is also one of the most efficient solvers for convex problems.
Furthermore, one should not draw any conclusions on how the solvers perform on nonconvex problems based solely on the results presented in this paper. For example, the convex strategies in AOA and SHOT, the two most efficient solvers for this set of problems, do not necessarily work well for nonconvex problems, and in fact there is another strategy in AOA intended as an heuristic for nonconvex problems. Some of the nonglobal solvers may actually work quite well as heuristics for nonconvex problems, of course without any guarantee of finding the global or even a feasible solution.
7 Conclusions
The comparisons presented in this paper are mainly intended to help the readers make informed decisions about which tools to use when dealing with different types of convex MINLP problems. In the previous sections, we have shown how 16 different solvers performed on a test set containing 335 MINLP instances. By comparing the solvers on MINLP instances with different properties we noticed significant differences in the solvers’ performance. For example, the solvers based on NLP-BB were strongly affected by both the continuous relaxation gap and the degree of nonlinearity. Several of the solvers are based on the same main algorithms, although they differ significantly in terms of speed and number of problems solved. The differences are mainly due to different degrees of preprocessing, primal heuristics, cut generation procedures, and different strategies used by the solvers. The performance differences highlight the importance of such techniques for an efficient solver implementation.
For the test set considered here, SHOT and AOA were the overall fastest solvers. Both of the solvers are based on a single-tree approach closely integrated with the MILP solver by utilizing callbacks to add the linearizations as lazy constraints. The results show the benefits of such a solution technique and support the strong belief in the single-tree approach by Abhishek et al. (2010) and Belotti et al. (2013). The close integration with the MILP solver allows AOA and SHOT to benefit from different techniques integrated within the MILP solver, such as branching heuristics, cut generation procedures, and bound tightening.
Overall, several of the solvers performed well on the test set and were able to solve a large portion of the problems. The most instances any solver could solve within the time limit was 312 instances, and by combining all the solvers we where able solve 326 of the 335 MINLP problems to a 0.1% guaranteed optimality gap. However, it should be noted that many of the test instances are quite small and simple compared to industry-relevant problems. Still today, real-world problems must often be simplified and reduced in size to obtain tractable formulations, in the process limiting the practical benefits of MINLP. Thus, in order to fully benefit from convex MINLP as a tool for design and decision-making, both further algorithmic research and solver software development are required. We also hope that this paper encourages MINLP users to submit their problems to the instances libraries, e.g., MINLPLib and www.minlp.org, to benefit both MINLP solver developers and end users.
References
Abhishek K, Leyffer S, Linderoth J (2010) FilMINT: an outer approximation-based solver for convex mixed-integer nonlinear programs. INFORMS J Comput 22(4):555–567
Achterberg T (2009) SCIP: solving constraint integer programs. Math Program Comput 1(1):1–41
Achterberg T, Koch T, Martin A (2005) Branching rules revisited. Oper Res Lett 33(1):42–54
Achterberg T, Wunderling R (2013) Mixed integer programming: analyzing 12 years of progress. In: Jünger M, Reinelt G (eds) Facets of combinatorial optimization. Springer, pp 449–481
Andersen ED, Andersen KD (2000) The MOSEK optimization software. EKA Consulting ApS, Copenhagen
Artelys (2018) Artelys Knitro User’s Manual. https://www.artelys.com/tools/knitro_doc/2_userGuide.html
Balas E, Ceria S, Cornuéjols G (1993) A lift-and-project cutting plane algorithm for mixed 0–1 programs. Math Program 58(1–3):295–324
Bazaraa MS, Sherali HD, Shetty CM (2013) Nonlinear programming: theory and algorithms. Wiley, New York
Belotti P (2010) Couenne: a user’s manual. https://www.coin-or.org/Couenne/couenne-user-manual.pdf
Belotti P, Lee J, Liberti L, Margot F, Wächter A (2009) Branching and bounds tightening techniques for non-convex MINLP. Optim Methods Softw 24:597–634
Belotti P, Cafieri S, Lee J, Liberti L (2010) Feasibility-based bounds tightening via fixed points. In: Wu W, Daescu O (eds) International conference on combinatorial optimization and applications. Springer, New York, pp 65–76
Belotti P, Kirches C, Leyffer S, Linderoth J, Luedtke J, Mahajan A (2013) Mixed-integer nonlinear optimization. Acta Numer 22:1–131
Benders JF (1962) Partitioning procedures for solving mixed-variables programming problems. Numer Math 4(1):238–252
Benson HY (2011) Mixed integer nonlinear programming using interior-point methods. Optim Methods Softw 26(6):911–931
Bernal DE, Chen Q, Gong F, Grossmann IE (2018) Mixed-integer nonlinear decomposition toolbox for Pyomo (MindtPy). http://egon.cheme.cmu.edu/Papers/Bernal_Chen_MindtPy_PSE2018Paper.pdf
Bernal DE, Vigerske S, Trespalacios F, Grossmann IE (2017) Improving the performance of DICOPT in convex MINLP problems using a feasibility pump. http://www.optimization-online.org/DB_HTML/2017/08/6171.html
Berthold T (2014a) Heuristic algorithms in global MINLP solvers. Ph.D. thesis, Technische Universität Berlin
Berthold T (2014b) RENS: the optimal rounding. Math Program Comput 6(1):33–54
Berthold T, Gleixner AM (2014) Undercover: a primal MINLP heuristic exploring a largest sub-MIP. Math Program 144(1–2):315–346
Bezanson J, Karpinski S, Shah VB, Edelman A (2012) Julia: a fast dynamic language for technical computing. arXiv preprint: 1209.5145
Biegler LT (2010) Nonlinear programming: concepts, algorithms, and applications to chemical processes. SIAM, Philadelphia
Biegler LT, Grossmann IE (2004) Retrospective on optimization. Comput Chem Eng 28(8):1169–1192
Bisschop J (2006) AIMMS optimization modeling. www.Lulu.com
Bonami P (2011) Lift-and-project cuts for mixed integer convex programs. In: International conference on integer programming and combinatorial optimization. Springer, pp 52–64
Bonami P, Lee J (2007) BONMIN user’s manual. Numer Math 4:1–32
Bonami P, Lejeune MA (2009) An exact solution approach for portfolio optimization problems under stochastic and integer constraints. Oper Res 57(3):650–670
Bonami P, Biegler LT, Conn AR, Cornuéjols G, Grossmann IE, Laird CD, Lee J, Lodi A, Margot F, Sawaya N, Wächter A (2008) An algorithmic framework for convex mixed integer nonlinear programs. Discrete Optim 5(2):186–204
Bonami P, Cornuéjols G, Lodi A, Margot F (2009) A feasibility pump for mixed integer nonlinear programs. Math Program 119(2):331–352
Bonami P, Kilinç M, Linderoth J (2012) Algorithms and software for convex mixed integer nonlinear programs. In: Lee J, Leyffer S (eds) Mixed integer nonlinear programming. Springer, pp 1–39
Bonami P, Lee J, Leyffer S, Wächter A (2011) More branch-and-bound experiments in convex nonlinear integer programming. Optimization. http://www.optimization-online.org/DB_FILE/2011/09/3191.pdf
Borchers B, Mitchell JE (1994) An improved branch and bound algorithm for mixed integer nonlinear programs. Comput Oper Res 21(4):359–367
Boukouvala F, Misener R, Floudas CA (2016) Global optimization advances in mixed-integer nonlinear programming, MINLP, and constrained derivative-free optimization, CDFO. Eur J Oper Res 252(3):701–727
Bragalli C, DAmbrosio C, Lee J, Lodi A, Toth P (2012) On the optimal design of water distribution networks: a practical MINLP approach. Optim Eng 13(2):219–246
Brook A, Kendrick D, Meeraus A (1988) GAMS, a user’s guide. ACM Signum Newslett 23(3–4):10–11
Bussieck MR, Vigerske S (2010) MINLP solver software. In: Wiley encyclopedia of operations research and management science. Wiley Online Library
Bussieck MR, Dirkse SP, Vigerske S (2014) PAVER 2.0: an open source environment for automated performance analysis of benchmarking data. J Global Optim 59(2):259–275
Byrd RH, Nocedal J, Waltz RA (2006) Knitro: an integrated package for nonlinear optimization. Large-scale nonlinear optimization. Springer, New York, pp 35–59
Cao W, Lim GJ (2011) Optimization models for cancer treatment planning. In: Wiley encyclopedia of operations research and management science. Wiley Online Library
Castillo I, Westerlund J, Emet S, Westerlund T (2005) Optimization of block layout design problems with unequal areas: a comparison of MILP and MINLP optimization methods. Comput Chem Eng 30(1):54–69
Çezik MT, Iyengar G (2005) Cuts for mixed 0–1 conic programming. Math Program 104(1):179–202
Coey C, Lubin M, Vielma JP (2018) Outer approximation with conic certificates for mixed-integer convex problems. arXiv preprint: 1808.05290
Currie J, Wilson DI et al (2012) OPTI: lowering the barrier between open source optimizers and the industrial MATLAB user. Found Comput Aided Process Oper 24:32
Dakin RJ (1965) A tree-search algorithm for mixed integer programming problems. Comput J 8(3):250–255
D’Ambrosio C, Lodi A (2013) Mixed integer nonlinear programming tools: an updated practical overview. Ann Oper Res 204(1):301–320. https://doi.org/10.1007/s10479-012-1272-5
D’Ambrosio C, Frangioni A, Liberti L, Lodi A (2012) A storm of feasibility pumps for nonconvex MINLP. Math Program 136(2):375–402
Dolan ED, Moré JJ (2002) Benchmarking optimization software with performance profiles. Math Program Ser B 91(2):201–213
Drud AS (1994) CONOPT—a large-scale GRG code. ORSA J Comput 6(2):207–216
Dunning I, Huchette J, Lubin M (2017) JuMP: a modeling language for mathematical optimization. SIAM Rev 59(2):295–320
Duran MA, Grossmann IE (1986) An outer-approximation algorithm for a class of mixed-integer nonlinear programs. Math Program 36(3):307–339
Eronen VP, Mäkelä MM, Westerlund T (2014) On the generalization of ECP and OA methods to nonsmooth convex MINLP problems. Optimization 63(7):1057–1073
Eronen VP, Kronqvist J, Westerlund T, Mäkelä MM, Karmitsa N (2017) Method for solving generalized convex nonsmooth mixed-integer nonlinear programming problems. J Global Optim 69(2):443–459
Exler O, Schittkowski K (2007) A trust region SQP algorithm for mixed-integer nonlinear programming. Optim Lett 1(3):269–280
FICO (2017) FICO Xpress-SLP manual. https://www.artelys.com/uploads/pdfs/Xpress/Xpress_SLP_2795MS.pdf
FICO (2017) Xpress-optimizer reference manual. https://www.artelys.com/uploads/pdfs/Xpress/Xpress_Optimizer_2447PS.pdf
Fischetti M, Lodi A (2011) Heuristics in mixed integer programming. In: Wiley encyclopedia of operations research and management science. Wiley Online Library
Fletcher R, Leyffer S (1994) Solving mixed integer nonlinear programs by outer approximation. Math Program 66(1):327–349
Fletcher R, Leyffer S (1998) User manual for filterSQP. Numerical analysis Report NA/181. Department of Mathematics, University of Dundee, Dundee
Floudas CA (2000) Deterministic global optimization: Theory, methods and applications. Nonconvex optimization and its applications, vol 37. Springer, US. https://doi.org/10.1007/978-1-4757-4949-6
Floudas CA (1995) Nonlinear and mixed-integer optimization: fundamentals and applications. Oxford University Press, Oxford
Forrest J (2005) Cbc user’s guide. https://projects.coin-or.org/Cbc
Fourer R, Gay D, Kernighan B (1993) AMPL. Boyd & Fraser, Danvers
Frangioni A, Gentile C (2006) Perspective cuts for a class of convex 0–1 mixed integer programs. Math Program 106(2):225–236
GAMS (2018) Branch-and-cut-and-heuristic facility. https://www.gams.com/latest/docs/UG_SolverUsage.html. Accessed 18 May 2018
Geoffrion AM (1972) Generalized Benders decomposition. J Optim Theory Appl 10(4):237–260
Gill PE, Murray W, Saunders MA (2005) SNOPT: an SQP algorithm for large-scale constrained optimization. SIAM Rev 47(1):99–131
Gleixner A, Bastubbe M, Eifler L, Gally T, Gamrath G, Gottwald RL, Hendel G, Hojny C, Koch T, Lübbecke ME, Maher SJ, Miltenberger M, Müller B, Pfetsch ME, Puchert C, Rehfeldt D, Schlösser F, Schubert C, Serrano F, Shinano Y, Viernickel JM, Walter M, Wegscheider F, Witt JT, Witzig J (2018) The SCIP optimization suite 6.0. Technical report, Optimization. http://www.optimization-online.org/DB_HTML/2018/07/6692.html
Gomory RE et al (1958) Outline of an algorithm for integer solutions to linear programs. Bull Am Math Soc 64(5):275–278
Gould N, Scott J (2016) A note on performance profiles for benchmarking software. ACM Trans Math Softw (TOMS) 43(2):15
Grossmann IE (2002) Review of nonlinear mixed-integer and disjunctive programming techniques. Optim Eng 3(3):227–252
Grossmann IE, Kravanja Z (1997) Mixed-integer nonlinear programming: a survey of algorithms and applications. In: Biegler LT, Coleman TE, Conn AR, Santosa FN (eds) Large-scale optimization with applications. Springer, New York
Grossmann IE, Caballero JA, Yeomans H (1999) Mathematical programming approaches to the synthesis of chemical process systems. Korean J Chem Eng 16(4):407–426
Gupta OK, Ravindran A (1985) Branch and bound experiments in convex nonlinear integer programming. Manag Sci 31(12):1533–1546
Gurobi (2018) Gurobi optimizer reference manual. Gurobi Optimization, LLC. http://www.gurobi.com/documentation/8.0/refman.pdf
Hart WE, Laird CD, Watson JP, Woodruff DL, Hackebeil GA, Nicholson BL, Siirola JD (2012) Pyomo-optimization modeling in Python, vol 67. Springer, New York
Hijazi H, Bonami P, Ouorou A (2013) An outer-inner approximation for separable mixed-integer nonlinear programs. INFORMS J Comput 26(1):31–44
Holmström K (1999) The TOMLAB optimization environment in Matlab. Citeseer. http://citeseerx.ist.psu.edu/viewdoc/summary?doi=10.1.1.134.5714
HSL (2018) A collection of Fortran codes for large-scale scientific computation. http://www.hsl.rl.ac.uk
Hunting M (2011) The AIMMS outer approximation algorithm for MINLP. Tech. rep. AIMMS B.V
IBM ILOG CPLEX Optimization Studio (2017) CPLEX Users Manual, version 12.7. IBM
Kelley JE Jr (1960) The cutting-plane method for solving convex programs. J Soc Ind Appl Math 8(4):703–712
Khajavirad A, Sahinidis NV (2018) A hybrid LP/NLP paradigm for global optimization relaxations. Math Program Comput 10(3):383–421
Kılınç MR, Sahinidis NV (2018) Exploiting integrality in the global optimization of mixed-integer nonlinear programming problems with BARON. Optim Methods Softw 33(3):540–562
Kılınç MR, Linderoth J, Luedtke J (2017) Lift-and-project cuts for convex mixed integer nonlinear programs. Math Program Comput 9(4):499–526
Kocis GR, Grossmann IE (1988) Global optimization of nonconvex mixed-integer nonlinear programming (MINLP) problems in process synthesis. Ind Eng Chem Res 27(8):1407–1421
Kröger O, Coffrin C, Hijazi H, Nagarajan H (2018) Juniper: an open-source nonlinear branch-and-bound solver in Julia. arXiv preprint: 1804.07332
Kronqvist J, Lundell A, Westerlund T (2016) The extended supporting hyperplane algorithm for convex mixed-integer nonlinear programming. J Global Optim 64(2):249–272
Kronqvist J, Bernal D, Lundell A, Westerlund T (2018a) A center-cut algorithm for quickly obtaining feasible solutions and solving convex MINLP problems. Comput Chem Eng. https://doi.org/10.1016/j.compchemeng.2018.06.019
Kronqvist J, Lundell A, Westerlund T (2018b) Reformulations for utilizing separability when solving convex MINLP problems. J Global Optim 71(3):571–592. https://doi.org/10.1007/s10898-018-0616-3
Land AH, Doig AG (1960) An automatic method of solving discrete programming problems. Econom J Econom Soc 28:497–520
Lastusilta T (2011) GAMS MINLP solver comparisons and some improvements to the AlphaECP algorithm. PhD thesis, Åbo Akademi University
Le Digabel S (2011) Algorithm 909: Nomad: nonlinear optimization with the mads algorithm. ACM Trans Math Softw (TOMS) 37(4):44
Leyffer S (1993) Deterministic methods for mixed integer nonlinear programming. Ph.D. University of Dundee
Leyffer S (1999) User manual for MINLP BB. Technical Report, University of Dundee numerical analysis report
Leyffer S (2001) Integrating SQP and branch-and-bound for mixed integer nonlinear programming. Comput Optim Appl 18(3):295–309
Liberti L (2009) Reformulation techniques in mathematical programming. HDR thesis
Liberti L, Maculan N (2006) Global optimization: from theory to implementation, vol 84. Springer Science & Business Media, New York
Lin Y, Schrage L (2009) The global solver in the LINDO API. Optim Methods Softw 24(4–5):657–668
Linderoth JT, Savelsbergh MW (1999) A computational study of search strategies for mixed integer programming. INFORMS J Comput 11(2):173–187
LINDO Systems Inc (2017) LINDO User’s Manual. https://www.lindo.com/downloads/PDF/LindoUsersManual.pdf
Lougee-Heimer R (2003) The common optimization interface for operations research: Promoting open-source software in the operations research community. IBM J Res Dev 47(1):57–66
Lubin M, Yamangil E, Bent R, Vielma JP (2016) Extended formulations in mixed-integer convex programming. In: Louveaux Q, Skutella M (eds) 18th International conference integer programming and combinatorial optimization: IPCO 2016. Springer International Publishing, pp 102–113
Lundell A, Westerlund T (2017) Solving global optimization problems using reformulations and signomial transformations. Comput Chem Eng 116:122–134
Lundell A, Westerlund J, Westerlund T (2009) Some transformation techniques with applications in global optimization. J Global Optim 43(2–3):391–405
Lundell A, Kronqvist J, Westerlund T (2017) SHOT—a global solver for convex MINLP in Wolfram Mathematica. Comput Aided Chem Eng 40:2137–2142
Lundell A, Kronqvist J, Westerlund T (2018) The supporting hyperplane optimization toolkit—a polyhedral outer approximation based convex MINLP solver utilizing a single branching tree approach. Optimization. http://www.optimization-online.org/DB_HTML/2018/06/6680.html
Mahajan A, Leyffer S, Linderoth J, Luedtke J, Munson T (2017) Minotaur: a mixed-integer nonlinear optimization toolkit. Optimization. http://www.optimization-online.org/DB_FILE/2017/10/6275.pdf
Makhorin A (2008) GLPK (GNU linear programming kit). http://www.gnu.org/software/glpk/
Melo W, Fampa M, Raupp F (2018a) First steps to solve MINLP problems with Muriqui Optimizer. http://www.wendelmelo.net/muriqui/manual_muriqui-ing3.pdf. Accessed 18 May 2018
Melo W, Fampa M, Raupp F (2018b) An overview of MINLP algorithms and their implementation in Muriqui Optimizer. Ann Oper Res. https://doi.org/10.1007/s10479-018-2872-5
MINLPLib (2018) Mixed-integer nonlinear programming library. http://www.minlplib.org/. Accessed 27 May 2018
Misener R, Floudas CA (2009) Advances for the pooling problem: modeling, global optimization, and computational studies. Appl Comput Math 8(1):3–22
Misener R, Floudas CA (2013) GloMIQO: global mixed-integer quadratic optimizer. J Global Optim 57(1):3–50
Misener R, Floudas CA (2014) ANTIGONE: algorithms for continuous/integer global optimization of nonlinear equations. J Global Optim 59(2–3):503–526
Nagarajan H, Lu M, Wang S, Bent R, Sundar K (2017) An adaptive, multivariate partitioning algorithm for global optimization of nonconvex programs. arXiv preprint: 1707.02514
Nemhauser GL, Savelsbergh MW, Sigismondi GC (1994) MINTO, a MIxed INTeger optimizer. Oper Res Lett 15(1):47–58
Nowak I, Alperin H, Vigerske S (2002) LaGO–an object oriented library for solving MINLPs. In: Bliek C, Jermann C, Neumaier A (eds) International workshop on global optimization and constraint satisfaction. Springer, Berlin, pp 32–42
Nowak I, Breitfeld N, Hendrix EM, Njacheun-Njanzoua G (2018) Decomposition-based inner-and outer-refinement algorithms for global optimization. J Global Optim 72(2):305–321. https://doi.org/10.1007/s10898-018-0633-2
Pörn R, Harjunkoski I, Westerlund T (1999) Convexification of different classes of non-convex MINLP problems. Comput Chem Eng 23(3):439–448
Quesada I, Grossmann IE (1992) An LP/NLP based branch and bound algorithm for convex MINLP optimization problems. Comput Chem Eng 16(10–11):937–947
Quist A, Van Geemert R, Hoogenboom J, Ílles T, Roos C, Terlaky T (1999) Application of nonlinear optimization to reactor core fuel reloading. Ann Nuclear Energy 26(5):423–448
Roelofs M, Bisschop J (2018) AIMMS—the language reference. https://download.aimms.com/aimms/download/manuals/AIMMS3_LR.pdf
Ryoo HS, Sahinidis NV (1996) A branch-and-reduce approach to global optimization. J Global Optim 8(2):107–138
Sahinidis N, Grossmann IE (1991) MINLP model for cyclic multiproduct scheduling on continuous parallel lines. Comput Chem Eng 15(2):85–103
Schweiger C, Floudas C (1998) Minopt: a modeling language and algorithmic framework for linear, mixed-integer, nonlinear, dynamic, and mixed-integer nonlinear optimization. Princeton University. http://titan.princeton.edu/MINOPT
Shectman JP, Sahinidis NV (1998) A finite algorithm for global minimization of separable concave programs. J Global Optim 12(1):1–36
Stubbs RA, Mehrotra S (1999) A branch-and-cut method for 0–1 mixed convex programming. Math Program 86(3):515–532
Tawarmalani M, Sahinidis NV (2002) Convexification and global optimization in continuous and mixed-integer nonlinear programming: Theory, algorithms, software, and applications, vol 65. Springer Science & Business Media, New York
Tawarmalani M, Sahinidis NV (2005) A polyhedral branch-and-cut approach to global optimization. Math Program 103:225–249
Trespalacios F, Grossmann IE (2014) Review of mixed-integer nonlinear and generalized disjunctive programming methods. Chem Ing Tech 86(7):991–1012
Vigerske S, Gleixner A (2018) SCIP: global optimization of mixed-integer nonlinear programs in a branch-and-cut framework. Optim Methods Softw 33(3):563–593
Viswanathan J, Grossmann IE (1990) A combined penalty function and outer-approximation method for MINLP optimization. Comput Chem Eng 14(7):769–782
Wächter A, Biegler LT (2006) On the implementation of an interior-point filter line-search algorithm for large-scale nonlinear programming. Math Program 106(1):25–57
Westerlund T (2018) Users guide for GAECP, an interactive solver for generalized convex MINLP-problems using cutting plane and supporting hyperplane techniques. http://users.abo.fi/twesterl/GAECPDocumentation.pdf
Westerlund T, Petterson F (1995) An extended cutting plane method for solving convex MINLP problems. Comput Chem Eng 19:131–136
Westerlund T, Pörn R (2002) Solving pseudo-convex mixed integer optimization problems by cutting plane techniques. Optim Eng 3(3):253–280
Wolsey LA (1998) Integer programming. Series in discrete mathematics and optimization. Wiley-Interscience, New Jersey
Zhou K, Kılınç MR, Chen X, Sahinidis NV (2018) An efficient strategy for the activation of MIP relaxations in a multicore global MINLP solver. J Global Optim 70(3):497–516
Zhu Y, Kuno T (2006) A disjunctive cutting-plane-based branch-and-cut algorithm for 0–1 mixed-integer convex nonlinear programs. Ind Eng Chem Res 45(1):187–196
Acknowledgements
Open access funding provided by Abo Akademi University (ABO). First, we want to thank the developers of the solvers for their support to the comparison, and we also want to thank both AIMMS (especially M. Hunting) and GAMS (especially S. Vigerske and M. Bussieck) for their support. D. E. Bernal and I. E. Grossmann would like to thank the Center for Advanced Process Decision-making (CAPD) for its financial support. A. Lundell wants to express his gratitude for the financial support from the Magnus Ehrnrooth Foundation, as well as the Ruth and Nils-Erik Stenbäck Foundation. The authors want to acknowledge the Dagstuhl Seminar 18081 on Designing and Implementing Algorithms for Mixed-Integer Nonlinear Optimization, which provided valuable insight into the current status of MINLP software. Finally, we want to thank the anonymous reviewers for their valuable comments which helped to improve the paper significantly.
Author information
Authors and Affiliations
Corresponding author
Appendices
Appendix A
The following table contains the problem names and their classifications with regards to the different benchmark sets in Sect. 5.1. Correlation between the categories are shown in Fig. 13.
Instance name | Relaxation | Nonlinearity | Discreteness | |||
|---|---|---|---|---|---|---|
Gap (%) | Cat. | Measure (%) | Cat. | Measure (%) | Cat. | |
alan | 0.89 | Low | 38 | Low | 50 | High |
ball_mk2_10 | – | High | 100 | High | 100 | High |
ball_mk2_30 | – | High | 100 | High | 100 | High |
ball_mk3_10 | – | High | 100 | High | 100 | High |
ball_mk3_20 | – | High | 100 | High | 100 | High |
ball_mk3_30 | – | High | 100 | High | 100 | High |
ball_mk4_05 | – | High | 100 | High | 100 | High |
ball_mk4_10 | – | High | 100 | High | 100 | High |
ball_mk4_15 | – | High | 100 | High | 100 | High |
batch | 9.2 | Low | 48 | Low | 52 | High |
batch0812 | 5.6 | Low | 40 | Low | 60 | High |
batchdes | 3.9 | Low | 53 | High | 47 | Low |
batchs101006m | 4.5 | Low | 18 | Low | 46 | Low |
batchs121208m | 3.1 | Low | 15 | Low | 50 | High |
batchs151208m | 2.8 | Low | 14 | Low | 46 | Low |
batchs201210m | 1.7 | Low | 12 | Low | 45 | Low |
clay0203h | 100 | High | 20 | Low | 20 | Low |
clay0203m | 100 | High | 20 | Low | 60 | High |
clay0204h | 100 | High | 15 | Low | 20 | Low |
clay0204m | 100 | High | 15 | Low | 62 | High |
clay0205h | 100 | High | 12 | Low | 19 | Low |
clay0205m | 100 | High | 13 | Low | 63 | High |
clay0303h | 100 | High | 27 | Low | 21 | Low |
clay0303m | 100 | High | 18 | Low | 64 | High |
clay0304h | 100 | High | 20 | Low | 20 | Low |
clay0304m | 100 | High | 14 | Low | 64 | High |
clay0305h | 100 | High | 16 | Low | 20 | Low |
clay0305m | 100 | High | 12 | Low | 65 | High |
cvxnonsep_normcon20 | 0.34 | Low | 100 | High | 50 | High |
cvxnonsep_normcon20r | 0.34 | Low | 50 | High | 25 | Low |
cvxnonsep_normcon30 | 0.54 | Low | 100 | High | 50 | High |
cvxnonsep_normcon30r | 0.54 | Low | 50 | High | 25 | Low |
cvxnonsep_normcon40 | 0.78 | Low | 100 | High | 50 | High |
cvxnonsep_normcon40r | 0.78 | Low | 50 | High | 25 | Low |
cvxnonsep_nsig20 | 0.16 | Low | 100 | High | 50 | High |
cvxnonsep_nsig20r | 0.16 | Low | 50 | High | 25 | Low |
cvxnonsep_nsig30 | 0.11 | Low | 100 | High | 50 | High |
cvxnonsep_nsig30r | 0.12 | Low | 50 | High | 25 | Low |
cvxnonsep_nsig40 | 0.16 | Low | 100 | High | 50 | High |
cvxnonsep_nsig40r | 0.16 | Low | 50 | High | 25 | Low |
cvxnonsep_pcon20 | 0.55 | Low | 100 | High | 50 | High |
cvxnonsep_pcon20r | 0.55 | Low | 51 | High | 26 | Low |
cvxnonsep_pcon30 | 0.47 | Low | 100 | High | 50 | High |
cvxnonsep_pcon30r | 0.47 | Low | 51 | High | 25 | Low |
cvxnonsep_pcon40 | 0.39 | Low | 100 | High | 50 | High |
cvxnonsep_pcon40r | 0.39 | Low | 51 | High | 25 | Low |
cvxnonsep_psig20 | 0.08 | Low | 100 | High | 50 | High |
cvxnonsep_psig20r | 0.09 | Low | 50 | High | 24 | Low |
cvxnonsep_psig30 | 0.32 | Low | 100 | High | 50 | High |
cvxnonsep_psig30r | 0.32 | Low | 50 | High | 24 | Low |
cvxnonsep_psig40 | 0.34 | Low | 100 | High | 50 | High |
cvxnonsep_psig40r | 0.29 | Low | 50 | High | 24 | Low |
du-opt | 1.2 | Low | 100 | High | 65 | High |
du-opt5 | 51 | High | 100 | High | 65 | High |
enpro48pb | 6.9 | Low | 19 | Low | 60 | High |
enpro56pb | 15 | Low | 19 | Low | 57 | High |
ex1223 | 15 | Low | 64 | High | 36 | Low |
ex1223a | 2.0 | Low | 43 | Low | 57 | High |
ex1223b | 15 | Low | 100 | High | 57 | High |
ex4 | 104 | High | 14 | Low | 69 | High |
fac1 | 0.11 | Low | 73 | High | 27 | Low |
fac2 | 23 | Low | 82 | High | 18 | Low |
fac3 | 30 | Low | 82 | High | 18 | Low |
flay02h | 25 | Low | 4.3 | Low | 8.7 | Low |
flay02m | 25 | Low | 14 | Low | 29 | Low |
flay03h | 37 | Low | 2.5 | Low | 10 | Low |
flay03m | 37 | Low | 12 | Low | 46 | Low |
flay04h | 43 | Low | 1.7 | Low | 10 | Low |
flay04m | 43 | Low | 10 | Low | 57 | High |
flay05h | 46 | Low | 1.3 | Low | 10 | Low |
flay05m | 46 | Low | 8.1 | Low | 65 | High |
flay06h | 48 | Low | 1.1 | Low | 11 | Low |
flay06m | 48 | Low | 7.0 | Low | 70 | High |
fo7 | 100 | High | 12 | Low | 37 | Low |
fo7_2 | 100 | High | 12 | Low | 37 | Low |
fo7_ar2_1 | 100 | High | 13 | Low | 38 | Low |
fo7_ar25_1 | 100 | High | 13 | Low | 38 | Low |
fo7_ar3_1 | 100 | High | 13 | Low | 38 | Low |
fo7_ar4_1 | 100 | High | 13 | Low | 38 | Low |
fo7_ar5_1 | 100 | High | 13 | Low | 38 | Low |
fo8 | 100 | High | 11 | Low | 38 | Low |
fo8_ar2_1 | 100 | High | 11 | Low | 39 | Low |
fo8_ar25_1 | 100 | High | 11 | Low | 39 | Low |
fo8_ar3_1 | 100 | High | 11 | Low | 39 | Low |
fo8_ar4_1 | 100 | High | 11 | Low | 39 | Low |
fo8_ar5_1 | 100 | High | 11 | Low | 39 | Low |
fo9 | 100 | High | 10 | Low | 40 | Low |
fo9_ar2_1 | 100 | High | 10 | Low | 40 | Low |
fo9_ar25_1 | 100 | High | 10 | Low | 40 | Low |
fo9_ar3_1 | 100 | High | 10 | Low | 40 | Low |
fo9_ar4_1 | 100 | High | 10 | Low | 40 | Low |
fo9_ar5_1 | 100 | High | 10 | Low | 40 | Low |
gams01 | 97 | High | 22 | Low | 76 | High |
gbd | 0.00 | Low | 25 | Low | 75 | High |
hybriddynamic_fixed | 10 | Low | 15 | Low | 14 | Low |
ibs2 | 0.22 | Low | 100 | High | 50 | High |
jit1 | 0.37 | Low | 48 | Low | 16 | Low |
m3 | 100 | High | 23 | Low | 23 | Low |
m6 | 100 | High | 14 | Low | 35 | Low |
m7 | 100 | High | 12 | Low | 37 | Low |
m7_ar2_1 | 100 | High | 13 | Low | 38 | Low |
m7_ar25_1 | 100 | High | 13 | Low | 38 | Low |
m7_ar3_1 | 100 | High | 13 | Low | 38 | Low |
m7_ar4_1 | 100 | High | 13 | Low | 38 | Low |
m7_ar5_1 | 100 | High | 13 | Low | 38 | Low |
meanvarx | 0.41 | Low | 20 | Low | 40 | Low |
netmod_dol1 | 49 | Low | 0.3 | Low | 23 | Low |
netmod_dol2 | 16 | Low | 0.3 | Low | 23 | Low |
netmod_kar1 | 79 | High | 0.9 | Low | 30 | Low |
netmod_kar2 | 79 | High | 0.9 | Low | 30 | Low |
no7_ar2_1 | 100 | High | 13 | Low | 38 | Low |
no7_ar25_1 | 100 | High | 13 | Low | 38 | Low |
no7_ar3_1 | 100 | High | 13 | Low | 38 | Low |
no7_ar4_1 | 100 | High | 13 | Low | 38 | Low |
no7_ar5_1 | 100 | High | 13 | Low | 38 | Low |
nvs03 | 49 | Low | 100 | High | 100 | High |
nvs10 | 0.74 | Low | 100 | High | 100 | High |
nvs11 | 0.41 | Low | 100 | High | 100 | High |
nvs12 | 0.41 | Low | 100 | High | 100 | High |
nvs15 | 89 | High | 100 | High | 100 | High |
o7 | 100 | High | 12 | Low | 37 | Low |
o7_2 | 100 | High | 12 | Low | 37 | Low |
o7_ar2_1 | 100 | High | 13 | Low | 38 | Low |
o7_ar25_1 | 100 | High | 13 | Low | 38 | Low |
o7_ar3_1 | 100 | High | 13 | Low | 38 | Low |
o7_ar4_1 | 100 | High | 13 | Low | 38 | Low |
o7_ar5_1 | 100 | High | 13 | Low | 38 | Low |
o8_ar4_1 | 100 | High | 11 | Low | 39 | Low |
o9_ar4_1 | 100 | High | 10 | Low | 40 | Low |
portfol_buyin | 3.9 | Low | 47 | Low | 47 | Low |
portfol_card | 4.0 | Low | 47 | Low | 47 | Low |
portfol_classical050_1 | 3.2 | Low | 33 | Low | 33 | Low |
portfol_classical200_2 | 13 | Low | 33 | Low | 33 | Low |
portfol_roundlot | 0.00 | Low | 47 | Low | 47 | Low |
procurement2mot | 37 | Low | 1.5 | Low | 7.5 | Low |
ravempb | 15 | Low | 25 | Low | 48 | Low |
risk2bpb | 1.0 | Low | 0.6 | Low | 3.0 | Low |
rsyn0805h | 5.0 | Low | 2.9 | Low | 12 | Low |
rsyn0805m | 63 | High | 1.8 | Low | 41 | Low |
rsyn0805m02h | 3.1 | Low | 2.6 | Low | 21 | Low |
rsyn0805m02m | 160 | High | 1.7 | Low | 41 | Low |
rsyn0805m03h | 1.7 | Low | 2.6 | Low | 21 | Low |
rsyn0805m03m | 104 | High | 1.7 | Low | 41 | Low |
rsyn0805m04h | 0.46 | Low | 2.6 | Low | 21 | Low |
rsyn0805m04m | 57 | High | 1.7 | Low | 41 | Low |
rsyn0810h | 3.8 | Low | 5.2 | Low | 12 | Low |
rsyn0810m | 72 | High | 3.2 | Low | 40 | Low |
rsyn0810m02h | 4.0 | Low | 4.6 | Low | 21 | Low |
rsyn0810m02m | 298 | High | 2.9 | Low | 41 | Low |
rsyn0810m03h | 2.8 | Low | 4.6 | Low | 21 | Low |
rsyn0810m03m | 206 | High | 2.9 | Low | 41 | Low |
rsyn0810m04h | 0.93 | Low | 4.6 | Low | 21 | Low |
rsyn0810m04m | 113 | High | 2.9 | Low | 41 | Low |
rsyn0815h | 6.7 | Low | 8.0 | Low | 12 | Low |
rsyn0815m | 104 | High | 5.4 | Low | 39 | Low |
rsyn0815m02h | 4.2 | Low | 6.9 | Low | 21 | Low |
rsyn0815m02m | 277 | High | 4.7 | Low | 40 | Low |
rsyn0815m03h | 3.1 | Low | 6.9 | Low | 21 | Low |
rsyn0815m03m | 186 | High | 4.7 | Low | 40 | Low |
rsyn0815m04h | 1.7 | Low | 6.9 | Low | 21 | Low |
rsyn0815m04m | 230 | High | 4.7 | Low | 40 | Low |
rsyn0820h | 7.3 | Low | 10 | Low | 12 | Low |
rsyn0820m | 239 | High | 6.5 | Low | 39 | Low |
rsyn0820m02h | 1.2 | Low | 8.2 | Low | 21 | Low |
rsyn0820m02m | 536 | High | 5.5 | Low | 41 | Low |
rsyn0820m03h | 3.6 | Low | 8.2 | Low | 21 | Low |
rsyn0820m03m | 335 | High | 5.5 | Low | 41 | Low |
rsyn0820m04h | 2.4 | Low | 8.2 | Low | 21 | Low |
rsyn0820m04m | 380 | High | 5.5 | Low | 41 | Low |
rsyn0830h | 10 | Low | 12 | Low | 13 | Low |
rsyn0830m | 380 | High | 8.0 | Low | 38 | Low |
rsyn0830m02h | 6.1 | Low | 10 | Low | 21 | Low |
rsyn0830m02m | 674 | High | 6.5 | Low | 40 | Low |
rsyn0830m03h | 3.0 | Low | 10 | Low | 21 | Low |
rsyn0830m03m | 470 | High | 6.5 | Low | 40 | Low |
rsyn0830m04h | 2.0 | Low | 10 | Low | 21 | Low |
rsyn0830m04m | 392 | High | 6.5 | Low | 40 | Low |
rsyn0840h | 8.2 | Low | 14 | Low | 13 | Low |
rsyn0840m | 753 | High | 10 | Low | 37 | Low |
rsyn0840m02h | 5.8 | Low | 12 | Low | 21 | Low |
rsyn0840m02m | 876 | High | 7.8 | Low | 40 | Low |
rsyn0840m03h | 2.3 | Low | 12 | Low | 21 | Low |
rsyn0840m03m | 266 | High | 7.8 | Low | 40 | Low |
rsyn0840m04h | 2.1 | Low | 12 | Low | 21 | Low |
rsyn0840m04m | 508 | High | 7.8 | Low | 40 | Low |
slay04h | 13 | Low | 5.7 | Low | 17 | Low |
slay04m | 13 | Low | 18 | Low | 55 | High |
slay05h | 5.9 | Low | 4.3 | Low | 17 | Low |
slay05m | 5.9 | Low | 14 | Low | 57 | High |
slay06h | 7.0 | Low | 3.5 | Low | 18 | Low |
slay06m | 7.0 | Low | 12 | Low | 59 | High |
slay07h | 4.6 | Low | 2.9 | Low | 18 | Low |
slay07m | 4.6 | Low | 10 | Low | 60 | High |
slay08h | 4.9 | Low | 2.5 | Low | 18 | Low |
slay08m | 4.9 | Low | 8.7 | Low | 61 | High |
slay09h | 4.3 | Low | 2.2 | Low | 18 | Low |
slay09m | 4.3 | Low | 7.7 | Low | 62 | High |
slay10h | 8.1 | Low | 2.0 | Low | 18 | Low |
slay10m | 8.1 | Low | 6.9 | Low | 62 | High |
smallinvDAXr1b010-011 | 1.8 | Low | 97 | High | 97 | High |
smallinvDAXr1b020-022 | 0.36 | Low | 97 | High | 97 | High |
smallinvDAXr1b050-055 | 0.10 | Low | 97 | High | 97 | High |
smallinvDAXr1b100-110 | 0.04 | Low | 97 | High | 97 | High |
smallinvDAXr1b150-165 | 0.03 | Low | 97 | High | 97 | High |
smallinvDAXr1b200-220 | 0.01 | Low | 97 | High | 97 | High |
smallinvDAXr2b010-011 | 1.8 | Low | 97 | High | 97 | High |
smallinvDAXr2b020-022 | 0.36 | Low | 97 | High | 97 | High |
smallinvDAXr2b050-055 | 0.10 | Low | 97 | High | 97 | High |
smallinvDAXr2b100-110 | 0.04 | Low | 97 | High | 97 | High |
smallinvDAXr2b150-165 | 0.03 | Low | 97 | High | 97 | High |
smallinvDAXr2b200-220 | 0.01 | Low | 97 | High | 97 | High |
smallinvDAXr3b010-011 | 1.8 | Low | 97 | High | 97 | High |
smallinvDAXr3b020-022 | 0.36 | Low | 97 | High | 97 | High |
smallinvDAXr3b050-055 | 0.10 | Low | 97 | High | 97 | High |
smallinvDAXr3b100-110 | 0.04 | Low | 97 | High | 97 | High |
smallinvDAXr3b150-165 | 0.03 | Low | 97 | High | 97 | High |
smallinvDAXr3b200-220 | 0.01 | Low | 97 | High | 97 | High |
smallinvDAXr4b010-011 | 1.8 | Low | 97 | High | 97 | High |
smallinvDAXr4b020-022 | 0.36 | Low | 97 | High | 97 | High |
smallinvDAXr4b050-055 | 0.10 | Low | 97 | High | 97 | High |
smallinvDAXr4b100-110 | 0.04 | Low | 97 | High | 97 | High |
smallinvDAXr4b150-165 | 0.03 | Low | 97 | High | 97 | High |
smallinvDAXr4b200-220 | 0.01 | Low | 97 | High | 97 | High |
smallinvDAXr5b010-011 | 1.8 | Low | 97 | High | 97 | High |
smallinvDAXr5b020-022 | 0.36 | Low | 97 | High | 97 | High |
smallinvDAXr5b050-055 | 0.10 | Low | 97 | High | 97 | High |
smallinvDAXr5b100-110 | 0.04 | Low | 97 | High | 97 | High |
smallinvDAXr5b150-165 | 0.03 | Low | 97 | High | 97 | High |
smallinvDAXr5b200-220 | 0.01 | Low | 97 | High | 97 | High |
squfl010-025 | 51 | High | 96 | High | 3.8 | Low |
squfl010-040 | 43 | Low | 98 | High | 2.4 | Low |
squfl010-080 | 49 | Low | 99 | High | 1.2 | Low |
squfl015-060 | 58 | High | 98 | High | 1.6 | Low |
squfl015-080 | 57 | High | 99 | High | 1.2 | Low |
squfl020-040 | 53 | High | 98 | High | 2.4 | Low |
squfl020-050 | 57 | High | 98 | High | 2.0 | Low |
squfl020-150 | 59 | High | 99 | High | 0.7 | Low |
squfl025-025 | 60 | High | 96 | High | 3.8 | Low |
squfl025-030 | 60 | High | 97 | High | 3.2 | Low |
squfl025-040 | 61 | High | 98 | High | 2.4 | Low |
squfl030-100 | 66 | High | 99 | High | 1.0 | Low |
squfl030-150 | 63 | High | 99 | High | 0.7 | Low |
squfl040-080 | 65 | High | 99 | High | 1.2 | Low |
sssd08-04 | 62 | High | 6.7 | Low | 73 | High |
sssd12-05 | 61 | High | 5.3 | Low | 79 | High |
sssd15-04 | 62 | High | 4.5 | Low | 82 | High |
sssd15-06 | 65 | High | 4.5 | Low | 82 | High |
sssd15-08 | 63 | High | 4.5 | Low | 82 | High |
sssd16-07 | 63 | High | 4.3 | Low | 83 | High |
sssd18-06 | 63 | High | 4.0 | Low | 84 | High |
sssd18-08 | 67 | High | 4.0 | Low | 84 | High |
sssd20-04 | 63 | High | 3.7 | Low | 85 | High |
sssd20-08 | 62 | High | 3.7 | Low | 85 | High |
sssd22-08 | 62 | High | 3.4 | Low | 86 | High |
sssd25-04 | 64 | High | 3.1 | Low | 88 | High |
sssd25-08 | 61 | High | 3.1 | Low | 88 | High |
st_e14 | 15 | Low | 64 | High | 36 | Low |
st_miqp1 | 15 | Low | 100 | High | 100 | High |
st_miqp2 | 382 | High | 50 | High | 100 | High |
st_miqp3 | 0.00 | Low | 50 | High | 100 | High |
st_miqp4 | 0.05 | Low | 50 | High | 50 | High |
st_miqp5 | 0.00 | Low | 29 | Low | 29 | Low |
st_test1 | \(3 \cdot 10^6\) | High | 80 | High | 100 | High |
st_test2 | 9.5 | Low | 83 | High | 100 | High |
st_test3 | 24 | Low | 38 | Low | 100 | High |
st_test4 | 11 | Low | 33 | Low | 100 | High |
st_test5 | 104 | High | 70 | High | 100 | High |
st_test6 | 30 | Low | 100 | High | 100 | High |
st_test8 | 0.00 | Low | 100 | High | 100 | High |
st_testgr1 | 0.11 | Low | 100 | High | 100 | High |
st_testgr3 | 0.63 | Low | 100 | High | 100 | High |
st_testph4 | 3.1 | Low | 100 | High | 100 | High |
stockcycle | 1.7 | Low | 10 | Low | 90 | High |
syn05h | 0.03 | Low | 21 | Low | 12 | Low |
syn05m | 37 | Low | 15 | Low | 25 | Low |
syn05m02h | 0.02 | Low | 17 | Low | 19 | Low |
syn05m02m | 19 | Low | 10 | Low | 33 | Low |
syn05m03h | 0.02 | Low | 17 | Low | 19 | Low |
syn05m03m | 20 | Low | 10 | Low | 33 | Low |
syn05m04h | 0.01 | Low | 17 | Low | 19 | Low |
syn05m04m | 20 | Low | 10 | Low | 33 | Low |
syn10h | 0.03 | Low | 23 | Low | 13 | Low |
syn10m | 58 | High | 17 | Low | 29 | Low |
syn10m02h | 0.08 | Low | 19 | Low | 21 | Low |
syn10m02m | 104 | High | 11 | Low | 36 | Low |
syn10m03h | 0.05 | Low | 19 | Low | 21 | Low |
syn10m03m | 103 | High | 11 | Low | 36 | Low |
syn10m04h | 0.04 | Low | 19 | Low | 21 | Low |
syn10m04m | 103 | High | 11 | Low | 36 | Low |
syn15h | 0.12 | Low | 26 | Low | 12 | Low |
syn15m | 97 | High | 20 | Low | 27 | Low |
syn15m02h | 0.10 | Low | 21 | Low | 20 | Low |
syn15m02m | 66 | High | 13 | Low | 35 | Low |
syn15m03h | 0.07 | Low | 21 | Low | 20 | Low |
syn15m03m | 74 | High | 13 | Low | 35 | Low |
syn15m04h | 0.06 | Low | 21 | Low | 20 | Low |
syn15m04m | 91 | High | 13 | Low | 35 | Low |
syn20h | 0.32 | Low | 26 | Low | 13 | Low |
syn20m | 221 | High | 22 | Low | 31 | Low |
syn20m02h | 0.30 | Low | 21 | Low | 21 | Low |
syn20m02m | 179 | High | 13 | Low | 38 | Low |
syn20m03h | 0.27 | Low | 21 | Low | 21 | Low |
syn20m03m | 178 | High | 13 | Low | 38 | Low |
syn20m04h | 0.20 | Low | 21 | Low | 21 | Low |
syn20m04m | 179 | High | 13 | Low | 38 | Low |
syn30h | 6.1 | Low | 25 | Low | 13 | Low |
syn30m | 932 | High | 20 | Low | 30 | Low |
syn30m02h | 2.9 | Low | 20 | Low | 21 | Low |
syn30m02m | 677 | High | 13 | Low | 38 | Low |
syn30m03h | 2.0 | Low | 20 | Low | 21 | Low |
syn30m03m | 593 | High | 13 | Low | 38 | Low |
syn30m04h | 1.6 | Low | 20 | Low | 21 | Low |
syn30m04m | 613 | High | 13 | Low | 38 | Low |
syn40h | 17 | Low | 26 | Low | 13 | Low |
syn40m | 2608 | High | 22 | Low | 31 | Low |
syn40m02h | 2.4 | Low | 21 | Low | 21 | Low |
syn40m02m | 1072 | High | 13 | Low | 38 | Low |
syn40m03h | 5.6 | Low | 21 | Low | 21 | Low |
syn40m03m | 1467 | High | 13 | Low | 38 | Low |
syn40m04h | 2.0 | Low | 21 | Low | 21 | Low |
syn40m04m | 917 | High | 13 | Low | 38 | Low |
synthes1 | 87 | High | 33 | Low | 50 | High |
synthes2 | 101 | High | 36 | Low | 45 | Low |
synthes3 | 78 | High | 35 | Low | 47 | Low |
tls12 | 98 | High | 19 | Low | 82 | High |
tls2 | 86 | High | 16 | Low | 89 | High |
tls4 | 79 | High | 19 | Low | 85 | High |
tls5 | 89 | High | 19 | Low | 84 | High |
tls6 | 91 | High | 20 | Low | 83 | High |
tls7 | 96 | High | 16 | Low | 86 | High |
unitcommit1 | 1.6 | Low | 25 | Low | 75 | High |
watercontamination0202 | 52 | High | 3.8 | Low | 0.0 | Low |
watercontamination0202r | 100 | High | 48 | Low | 3.6 | Low |
watercontamination0303 | 64 | High | 4.2 | Low | 0.0 | Low |
watercontamination0303r | 100 | High | 48 | Low | 3.6 | Low |
Appendix B
The options provided to the solvers (and subsolvers) in the benchmark are listed below. All other settings are the default values as provided by the individual solvers. Note that we have not tried to fine-tune any of the solvers; however, if there is a convex strategy, or recommended convex parameters we have used those. We have also modified limits and other parameters when it is apparent that implementation issues are the cause of, e.g., premature termination of a solver on some problem instances or numerical instability. For example, without adding the CONOPT option specified below, DICOPT and SBB fails to solve all the smallinv-instances in MINLPLib. Therefore, we believe that it is motivated to use these, since this problem occurs in the subsolver.
Name | Value | Description |
|---|---|---|
General GAMS | ||
MIP | CPLEX | Uses CPLEX as MIP solver |
Threads | 8 | Max amount of threads |
optCR | 0.001 | Relative termination tolerance |
optCA | 0 | Absolute termination tolerance |
nodLim | \(10^8\) | To avoid premature termination |
domLim | \(10^8\) | To avoid premature termination |
iterLim | \(10^8\) | To avoid premature termination |
resLim | 900 | Time limit |
AlphaECP | ||
ECPmaster | 1 | Activates convex strategy |
TOLepsg | \(10^{-6}\) | Constraint tolerance |
AOA | ||
IsConvex | 1 | Activates convex strategy |
IterationMax | \(10^7\) | Maximal number of iterations |
RelativeOptimalityTolerance | 0.1 | Relative termination tolerance (in %) |
TimeLimit | 900 | Time limit |
BONMIN | ||
bonmin.algorithm | B-OA | Selects the main algorithm |
B-HYB | ||
B-BB | ||
milp_solver | CPLEX | uses CPLEX as MILP solver |
bonmin.time_limit | 900 | Sets the time limit |
Couenne | ||
lp_solver | Clp | Uses Clp as LP solver (as recommended in the manual) |
DICOPT | ||
convex | 1 | Activates convex strategy |
stop | 1 | Convex stopping criterion |
maxcycles | \(10^8\) | iteration limit |
infeasder | 1 | Add cutting planes from infeasible NLP (convex recommendation) |
nlpoptfile | 1 | To use the CONOPT options below |
Juniper | ||
fp_cpx | Use CPLEX for the feasibility pump | |
processors | 8 | Max number of threads |
mip_gap | 0.001 | Relative termination tolerance |
time-limit | 900 | Time limit |
LINDO | ||
USEGOP | 0 | Deactivates global strategy |
SPLEX_ITRLMT | \(-\) 1 | Simplex iteration limit |
MIP_ITRLIM | \(-\) 1 | MILP iteration limit |
The iteration limits are set as infinite to avoid premature termination | ||
Minotaur | ||
lp_engine | OsiCpx | Use CPLEX as MIP solver |
obj_gap_percent | 0.1 | Relative termination tolerance (in %) |
bnb_time_limit | 900 | Time limit |
threads | 8 | Max amount of threads (does not seem to have any effect as it only uses one thread) |
Muriqui | ||
MRQ_LP_NLP_BB_OA_BASED_ALG | Use LP/NLP based algorithm | |
in_assume_convexity | 1 | Use convex strategy |
in_absolute_convergence_tol | 0 | Absolute termination tolerance |
in_relative_convergence_tol | 0.001 | Relative termination tolerance |
in_absolute_feasibility_tol | \(10^{-6}\) | Constraint tolerance |
in_integer_tol | \(10^{-5}\) | Integer tolerance |
in_max_time | 900 | Time limit |
in_milp_solver | MRQ_CPLEX | Use CPLEX as MIP solver |
in_nlp_solver | MRQ_IPOPT | Use IPOPT as NLP solver |
in_number_of_threads | 8 | Max amount of threads |
Pavito | ||
mip_solver | CplexSolver | Use CPLEX as MILP solver; with one thread since multiple threads are not supported with callbacks |
cont_solver | IpoptSolver | Use IPOPT as NLP solver |
mip_solver_drives | True | Let MILP solver manage tree |
rel_gap | 0.001 | Relative termination tolerance |
timeout | 900 | Time limit |
SBB | ||
memnodes | \(5 \times 10^7\) | To avoid premature termination, but not too large, since memory is preallocated |
rootsolver | CONOPT.1 | To use the CONOPT options below |
SCIP | ||
constraints/nonlinear/assumeconvex | True | Activates convex strategy |
SHOT | ||
Dual.MIP.NumberOfThreads | 8 | Max number of threads |
Dual.MIP.Solver | 0 | Use CPLEX as MIP solver |
Primal.FixedInteger.Solver | 2 | To use GAMS NLP solvers |
Subsolver.GAMS.NLP.Solver | CONOPT | Use CONOPT as GAMS NLP solver |
Termination.ObjectiveGap.Absolute | 0 | Absolute termination tolerance |
Termination.ObjectiveGap.Relative | 0.001 | Relative termination tolerance |
Termination.TimeLimit | 900 | Time limit |
CONOPT (GAMS) | ||
RTMAXV | \(10^{30}\) | To avoid problems with unbounded variables in DICOPT and SBB |
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Kronqvist, J., Bernal, D.E., Lundell, A. et al. A review and comparison of solvers for convex MINLP. Optim Eng 20, 397–455 (2019). https://doi.org/10.1007/s11081-018-9411-8
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11081-018-9411-8