1 Introduction

The extent of price rigidity is a central feature of modern macro models, with strong implications for choosing optimal monetary policy regimes. In this paper we discuss how this central issue has failed to be resolved by empirical estimation and testing due to the imposition of strong priors about the degree of price flexibility.

There is a long tradition of assuming general price flexibility in thinking about the economy as a whole. This included Austrian economics (White 2003), classical macroeconomics pre-Keynes and Real Business Cycle theory (Kydland and Prescott 1982). Under fully flexible prices and general equilibrium; supply/demand shocks affect output but the effects are dampened by immediate equilibrating price reactions. This tradition was interrupted by the Keynesian revolution after the Great Depression, in which a general presumption was that prices and wages were slow to adjust. Under this wage and price rigidity, demand drives output; price reactions occur later, affecting demand, which then further drives output.

It may be noted that full price flexibility is not intended to mean that prices change continuously but rather that markets clear continuously at prevailing prices, including the effects of accompanying strategies with elements such as advertising, loyalty rewards, store offers, and financing deals, which between them create an ‘effective price’. It might be thought that the extensive micro data on prices (Le et al. 2021) showing that many prices change infrequently with a minority changing with high frequency settles this controversy in favour of price rigidity models. However, the price flexibility model is potentially consistent with this micro data, because market-clearing is not directly observable while the non-price elements above are in practice not surveyed regularly like prices; thus the model makes no predictions about price change frequency, merely that whatever effective price changes occur achieve market-clearing. Furthermore, the models we are dealing with apply to macro data and use micro-founded assumptions about the actions of representative agents designed to predict average, i.e. macro, behaviour on an ‘as if’ basis (Friedman 1953). These models can therefore only be tested on their ability to mimic macro behaviour.

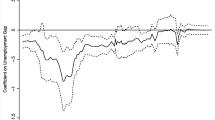
The significance of different assumptions about the degree of price flexibility can be illustrated by considering the impulse response functions of various shocks on output under the two contrasting assumptions of standard New Keynesian price/wage rigidity and full price/wage flexibility where there is no delay in price adjustment to changing marginal costs or in wage adjustment to the changing marginal utility of leisure. We show in Fig. 1 the differing output effects of a large selection of shocks under both assumptions (a replica of Fig. 6 from Le et al. 2021). Notice how output reacts more and for longer under rigidity to shocks that affect demand.

Fig. 1
figure 1

Output IRFs to various shocks under NK and Flex-Price models

Full size image

2 Empirical Evidence

These responses are so strikingly different that it is important to establish the degree of price flexibility empirically. Empirical estimation of these various models was led by Keynesian modellers after WW2. For ‘Old Keynesian’ models the main example is Project Link (Klein 1976) where models were estimated by a wide variety of methods: OLS/IV single equation, FIML, 3SLS. In this estimation process, Keynesian theory, including wage/price rigidity, was imposed on the data.

In later New Keynesian models (e.g. Smets and Wouters 2007), Bayesian NK priors have been imposed in estimation.

On the other hand, models with price flexibility were generally calibrated from micro data estimates, not estimated on macro data — just imposed. The main examples of this can be found in Kydland and Prescott-type RBC models, such as Kydland and Prescott (1982).

Neither side of the price rigidity debate therefore tests its own prior beliefs; each estimates or calibrates models imposing these beliefs. Both sides reject the other; for example Chari et al. (2009) say trenchantly: “Some think New Keynesian models are ready to be used for quarter-to-quarter quantitative policy advice. We do not. Focusing on the state-of-the-art version of these models, we argue that some of its shocks and other features are not structural or consistent with microeconomic evidence. Since an accurate structural model is essential to reliably evaluate the effects of policies, we conclude that New Keynesian models are not yet useful for policy analysis.”

Yet it has been shown that neither side’s model fits the data — Le et al. (2011) estimated both a flexprice model and a New Keynesian model of the US on postwar US data from the 1950s. Both were strongly rejected on the indirect inference test. Both models failed to replicate the sample’s data behaviour from their massive failure to mirror inflation experience alone. The flexprice model showed heavily excessive inflation variance, NK showed far too little. The failure of each to reflect the joint behaviour of the three central variables, output, inflation and interest rates is revealed by the overall p-values of each model version being close to zero and therefore being rejected.

The situation has not been changed by the arrival of micro-founded models since Lucas’ (1976) critique was taken to heart. These DSGE models have simply been specified either within a sticky-price or a flexprice environment, with again no testing in either case. In these models’ specification, this environment is the key driver of behaviour; the parameters of consumption, investment and monetary policy are of secondary importance, it turns out according to the findings of Le et al. (2011) that the Bayesian-estimated New Keynesian model of Smets and Wouters (2007) — a seminal paper — is strongly rejected by a powerful indirect inference test because of its assumptions on price rigidity. Hence it seems to be of great importance to establish good estimates of the degree of price rigidity in macro models. This paper therefore focuses on how this has been and might be done. Examples of macro model estimation include Smets and Wouters (2007)’s use of Bayesian methods, Ireland (2011)’s use of FIML (where he reports finding very high rigidity which he overrules in the final version), and Le et al. (2011)’s use of Indirect Inference. In this paper we examine the consequences of using each method, using an extended Monte Carlo experiment.

3 Aim of this Paper

This paper addresses the question of how we can settle this major controversy in macroeconomics by estimating and testing the rival models against the data. For this purpose we use an extended Monte Carlo experiment to check out rival methods of estimation and testing. We assume that there is a true model to be discovered and assess the likelihood of discovering it by using various available methods of estimation. In particular we consider Bayesian estimation where the prior distributions may differ from the values of the parameters of the model generating the data; maximum likelihood estimation; and indirect estimation.

The estimation of macroeconomic models by Bayesian methods has been facilitated by the development of computer programs such as Dynare (Adjemian et al. 2011) which is freely available and requires little knowledge of econometrics. The use of Bayesian methods was initially an attempt to improve on the use of calibration by combining prior beliefs with data instead of relying just on prior beliefs. In calibration the values of parameters are simply imposed on a model derived from theory; often they are based on estimated micro relationships. Validation of calibrated models was by an informal form of indirect inference in which the simulated moments of key variables were roughly compared with their data counterparts. Originally calibration was a response to what Sargent has referred to in an interview with Evans and Honkapohja (2005) as the rejection of too many “good” models using maximum likelihood (ML) estimation. Calibration is now most commonly used to explore the properties of a theoretical model where the calibration is regarded as providing a numerical representation of the model, and not an estimate of the model. The prior distributions in Bayesian estimation provide a constraint on the influence of the data in determining a model’s coefficients. Roughly speaking, the prior beliefs and the data are weighted in proportion to the precision of their information. In calibration the prior beliefs are treated as exact. In Bayesian estimation they are expressed through (non-degenerative) probability distributions and so provide a stochastic constraint on the data.

If a Bayesian estimated model is rejected by a test, it could be because the choice of prior distributions has produced very misleading posterior (i.e. Bayesian) estimates. Another possibility is that the model is mis-specified. In this paper we are concerned with the implications of the choice of prior distribution and model mis-specification. We examine these issues by formulating a ‘true’ model, generate data from the model and then estimate the model’s parameters using different choices of the prior distributions, including choosing priors from a different model specification. While our primary focus is on the effective estimation of the price rigidity parameters, our experiment also has relevance to the estimation of the other parameters of the model as all contribute to the behaviour of the model in response to policy regime choices. However, where previous work has found that certain parameters have a clear range of values, and there is no controversy over this, we use Bayesian priors for these parameters.

Our focus is on the rigidity parameters because of their central role in macroeconomic behaviour, as we have seen. Their controversial nature lends support to using new sample information which might help to settle the controversy. Using strong Bayesian priors could downgrade this information. In this paper we explore by Monte Carlo experiment just how large this downgrading is. We assume there is no controversy on the other parameters, which is broadly the case, and estimate these with prior means that correspond to the true values. However, we allow the true model to have rigidity parameters that lie at the extremes implied by the controversy. We examine how far setting the wrong Bayesian priors for these can bias their posterior estimates away from their true values. Plainly, if Bayesian studies whose priors favour New Keynesian models predominate in the literature, any such bias will produce posterior estimates that support the use of New Keynesian models, and vice versa. Similarly, priors favouring flexprice models will, if there is a bias, tend to support the use of flexprice models.

One alternative to using fixed priors is to use empirical Bayesian estimates where the posterior distribution is used as the new prior distribution. This would provide a more data-based prior but, if this is repeated, the resulting posterior would converge on the ML estimates based just on the data. Consequently, this procedure is effectively ML estimation. Hence we focus solely on fixed priors in Bayesian estimation, and consider ML estimation separately.

If a drawback to using Bayesian estimation is having to choose prior distributions, is there a better way to estimate the model? We consider two alternatives: ML and indirect estimation. Whereas Bayesian estimated models tend to be tightly specified with limited dynamics and restricted error processes, models estimated by ML tend either to produce biased estimates of tightly restricted models, or to be weakly identified, having unrestricted time series error processes in order to improve fit. Both may be attributed to model mis-specification. Sims (1980) argued that macroeconomic models tend to be under-identified, not over-identified as implied by their conventional specification and as required for the use of ML estimation. In consequence he doubted the findings from ML estimation. Instead, he proposed the use of unrestricted VAR (or VARMA) models which always provide a valid representation of the data. An over-identified macro model would imply a VAR with coefficient restrictions.

Indirect estimation involves simulating a structural model for given values of its parameters and then using the simulated data to estimate an auxiliary model whose role is to represent characteristics of the data. Sample moments are an example of an auxiliary model, as are sample scores (derivatives of the likelihood function). Another convenient way of capturing the characteristics of the data is an unrestricted VAR, which we will use in what follows; Meenagh et al. (2019) show that these auxiliary models all yield equivalent results. The estimates of the auxiliary model using the simulated data are then compared with estimates of the auxiliary model obtained from observed data. The given values of the structural parameters are revised until the estimates of the auxiliary model based on the simulated data converge on those from the observed data. Even with an auxiliary model with unrestricted parameters, the estimates of its parameters reflect the structural model’s restrictions through the simulated data. The indirect estimates are asymptotically equivalent to maximum likelihood estimates; but in the small samples that in practice we are normally faced with, and are our focus here, the Indirect and ML estimators behave quite differently, as we will see. One reason for using a VAR (or VARMA) as the auxiliary model is that the solution to a linearised DSGE model is a VAR (or VARMA) with coefficient restrictions. Testing these restrictions provides a test of the structural model. This is known as an indirect test. In a series of papers, we and other co-authors have proposed the use of indirect testing for Bayesian-estimated models, see Le et al. (2011, 2016), and Meenagh et al. (2019) who report that a variety of auxiliary models, including moments, impulse response functions and VARs give results with similar properties.

The model we use to make our comparisons is the New Keynesian model of the US constructed by Christiano et al. (2005), which was estimated by Bayesian methods by Smets and Wouters (2007). In this model the US is treated as a closed continental economy. In essence it is a standard Real Business Cycle model but with the addition of sticky wages and prices which allows monetary policy feedback to affect the real economy. Although Smets and Wouters found that their estimated model forecasted more accurately than unrestricted VAR models, we note that such forecast tests have been shown to have little power (Minford et al. 2015).

In our first set of comparisons we specify a New Keynesian (NK) model with high rigidity. A second set assumes the same model but with virtually full wage/price flexibility — where the Calvo chances of resetting effective wages and prices is a shade short of 100%; we label this a “flexprice” (FP) model. In all other respects, for maximum simplicity and transparency, the two models are the same. This allows us to focus narrowly on the implications of these various estimation methods for determining the extent of rigidity in macro models.

In all of our experiments we take the NK model as the “true” model (or DGM) and generate 1000 samples from it. Two versions of the model are considered, one with wage/price rigidities and the other with flexible wages and prices, as just explained. In our first set of experiments we examine the effects of the choice of prior. We obtain Bayesian estimates of each model for each sample using two different priors: a prior with wage/price rigidities (a high rigidity, or HR prior) and a prior with flexible wages and prices (an FP prior). We obtain the very striking result that the choice of prior distribution strongly biases the posterior estimates towards the prior whatever version of the model generates the simulated data; this bias can be reduced by ‘flattening’ the prior distribution (raising its variance) and centering it closer to the true mean, but it cannot be eliminated. We also compare ML and Indirect estimates of the NK version of the model. It would seem from these findings that the reliance on Bayesian estimation in support of the dominant NK model of the US post-war economy is highly vulnerable to the choice of prior distributions. This might help to explain why these models are rejected by Indirect Inference tests; the tests might be implicitly rejecting the NK priors instead of (or as well as) the specification of the model.

We compare the use of Bayesian estimation with two classical estimators: ML and Indirect estimation. We find that the ML estimates are also highly biased while the Indirect estimates have low bias. This suggests that a better general strategy than using Bayesian estimation might be the use of Indirect estimation.

In the next section we show how the choice of prior and biases in the maximum likelihood estimator may affect the posterior estimates in Bayesian estimation. The consequences for the Bayesian estimates of the New Keynesian model of alternative choices of the prior distributions are reported in the following section. We also report the biases when using instead ML and Indirect estimators. A brief summary of our results and their broader implications are reported in the concluding section.

4 Bias in Bayesian Estimation — The Role of Priors and Data

The effect on the posterior distribution of the choice of prior distribution and of biases in the ML estimator can be illustrated as follows. In classical estimation with data x and T observations we choose \(\theta\) to maximise the log likelihood function \(\ln L(x/\theta )\); i.e.

$$\begin{aligned} \underset{\theta }{\arg \max }\ln L(x/\theta ) \end{aligned}$$

The ML estimator \(\widehat{\theta }\) is obtained by solving

$$\begin{aligned} \frac{\partial \ln L(x/\theta )}{\partial \theta }|_{\theta =\widehat{\theta }}=0. \end{aligned}$$

In Bayesian estimation either we estimate \(\theta\) using the mean of the posterior distribution, or we use the mode of the posterior distribution \(\widetilde{\theta }\). For a symmetric posterior distribution the mean and the mode are the same. In general, computationally, it is easier to find the mode. To obtain the mode we maximise the posterior distribution; i.e.

$$\begin{aligned} \underset{\theta }{\arg \max }p(\theta /x)\equiv \underset{\theta }{\arg \max }\ln p(\theta /x) \end{aligned}$$

As

$$\begin{aligned} \ln p(\theta /x)=\ln L(x/\theta )+\ln p(\theta )-\ln f(x) \end{aligned}$$

and the last term doesn’t contain \(\theta\), we can ignore it. Hence

$$\begin{aligned} \underset{\theta }{\arg \max }\ln p(\theta /x)\equiv \underset{\theta }{\arg \max }[\ln L(x/\theta )+\ln p(\theta )]. \end{aligned}$$

The mode of the posterior distribution is obtained from

$$\begin{aligned}{}[\frac{\partial \ln L(x/\theta )}{\partial \theta }+\frac{\partial \ln p(\theta )}{\partial \theta }]_{\theta =\widetilde{\theta }}=0. \end{aligned}$$
(1)

We note that solving \(\frac{\partial \ln L(x/\theta )}{\partial \theta }=0\) for \(\theta\) gives the mode of the likelihood function (i.e. the ML estimator), and solving \(\frac{\partial \ln p(\theta )}{\partial \theta }=0\) for \(\theta\) gives the mode of the prior distribution. The posterior mode is obtained by solving the sum of the two.

If \(\ln L(x/\theta )\) is flat then the data are uninformative about \(\theta\) and \(\frac{\partial \ln L(x/\theta )}{\partial \theta }\) is close to zero for a range of values of \(\theta\). It then follows that the Bayesian estimator is dominated by the prior. If \(p(\theta )\) is flat (i.e. the prior is a uniform distribution) then \(\frac{\partial \ln p(\theta )}{\partial \theta }=\frac{1}{p(\theta )}\frac{\partial p(\theta )}{\partial \theta }=0\) and so the data dominate.

To find the posterior mode \(\widetilde{\theta }\) consider an expansion of Eq. (1) about \(\theta _{0}\) which gives

$$\begin{aligned} &\frac{\partial \ln L(x/\theta )}{\partial \theta }+\frac{\partial \ln p(\theta )}{\partial \theta }\simeq [\frac{\partial \ln L(x/\theta )}{\partial \theta }+\frac{\partial \ln p(\theta )}{\partial \theta }]_{\theta =\theta _{0}}\\ &+[\frac{\partial ^{2}\ln L(x/\theta )}{\partial \theta \partial \theta ^{\prime }}+\frac{\partial ^{2}\ln p(\theta )}{\partial \theta \partial \theta ^{\prime }}]_{\theta =\theta _{0}}(\theta -\theta _{0}). \end{aligned}$$

Setting this to zero and solving for \(\theta =\widetilde{\theta }\) gives

$$\begin{aligned} \widetilde{\theta }-\theta _{0}=-[\frac{\partial ^{2}\ln L(x/\theta )}{\partial \theta \partial \theta ^{\prime }}+\frac{\partial ^{2}\ln p(\theta )}{\partial \theta \partial \theta ^{\prime }}]_{\theta =\theta _{0}}^{-1}[\frac{\partial \ln L(x/\theta )}{\partial \theta }+\frac{\partial \ln p(\theta )}{\partial \theta }]_{\theta =\theta _{0}}. \end{aligned}$$

We can obtain \(\widetilde{\theta }\) through an interative process. For interation r we have \(\theta =\widetilde{\theta }_{(r)}\), \(\theta _{0}=\widetilde{\theta }_{(r-1)}\). As

$$\begin{aligned} p\lim T^{-1}\frac{\partial ^{2}\ln L(x/\theta )}{\partial \theta \partial \theta ^{\prime }}= & {} -p\lim T^{-1}\frac{\partial \ln L(x/\theta )}{\partial \theta }\frac{\partial \ln L(x/\theta )}{\partial \theta ^{\prime }} \\ p\lim T^{-1}\frac{\partial ^{2}\ln p(\theta )}{\partial \theta \partial \theta ^{\prime }}= & {} -p\lim T^{-1}\frac{\partial \ln p(\theta )}{\partial \theta }\frac{\partial \ln p(\theta )}{\partial \theta ^{\prime }} \end{aligned}$$

it follows that

$$\begin{aligned} &\widetilde{\theta }-\theta _{0}\simeq [\frac{\partial \ln L(x/\theta )}{\partial \theta }\frac{\partial \ln L(x/\theta )}{\partial \theta ^{\prime }}+\frac{\partial \ln p(\theta )}{\partial \theta }\frac{\partial \ln p(\theta )}{\partial \theta ^{\prime }}]_{\theta =\theta _{0}}^{-1}\\ &[\frac{\partial \ln L(x/\theta )}{\partial \theta }+\frac{\partial \ln p(\theta )}{\partial \theta }]_{\theta =\theta _{0}} \end{aligned}$$
(2)

If \(\theta _{0}\) is the true value of \(\theta\) then asymptotically the mode of the posterior distribution has the distribution

$$\begin{aligned} \widetilde{\theta }\sim & {} N(\theta ,\widetilde{\Sigma }) \nonumber \\ \widetilde{\Sigma }= & {} p\lim T[\frac{\partial \ln L(x/\theta )}{\partial \theta }\frac{\partial \ln L(x/\theta )}{\partial \theta ^{\prime }}+\frac{\partial \ln p(\theta )}{\partial \theta }\frac{\partial \ln p(\theta )}{\partial \theta ^{\prime }}]^{-1}{}_{\theta =\theta _{0}} \end{aligned}$$
(3)

It follows from Eqs. (1), (2) and (3) that the posterior mode is approximately a weighted average of the score \(\frac{\partial \ln L(x/\theta )}{\partial \theta }\) and \(\frac{\partial \ln p(\theta )}{\partial \theta ^{\prime }}\). The weights are proportional to the precision of the ML estimator \(p\lim T[\frac{\partial \ln L(x/\theta )}{\partial \theta }\frac{\partial \ln L(x/\theta )}{\partial \theta ^{\prime }}]_{\theta =\theta _{0}}^{-1}\) and the variance of the prior distribution \(p\lim T[\frac{\partial \ln p(\theta )}{\partial \theta }\frac{\partial \ln p(\theta )}{\partial \theta ^{\prime }}]^{-1}{}_{\theta =\theta _{0}}\). The more precise these estimators the more they determine the posterior mode.

We can now see the effect on the posterior mode of the choice of prior and biases in the ML estimator. If the mode of the prior distribution differs from the true value of \(\theta\) then this will affect \(\frac{\partial \ln p(\theta )}{\partial \theta }\) and hence \(\widetilde{\theta }\). If the ML estimator is biased then this will affect \(\frac{\partial \ln L(x/\theta )}{\partial \theta }\) and hence \(\widetilde{\theta }\). Replacing \(\frac{\partial \ln p(\theta )}{\partial \theta }\) and \(\frac{\partial \ln L(x/\theta )}{\partial \theta }\) in Eq. (2) by these differences gives an approximate idea of their effects. The biases will be weighted by the relevant measure of precision. We conclude that the greater the biases and the measure of precision, the larger will be the effect of these two biases on \(\widetilde{\theta }\).

5 The Monte Carlo Experiment

5.1 Bayesian Estimation

In this section, using Monte Carlo experiments, we explore the consequences for Bayesian estimation of the New Keynesian model of alternative choices of the prior distributions. We take the Smets-Wouters model with their estimated parameters to be the true model and generate 1000 samples of data from it. These are treated as the observed data in the Bayesian estimation. We perform two experiments. In the first we set the true model so that the degree of wage and price stickiness parameters (\(\xi _{w}\) and \(\xi _{p}\)) are equal to the values estimated by Smets-Wouters (approximately 0.7), which we refer to as the high-rigidity (HR), typical New Keynesian, version. In the second, we set the true model so that both \(\xi _{w}\) and \(\xi _{p}\) are set to 0.05, and call it the flexible price (FP) version, which implies that the probability that effective prices and wages are fixed is close to zero — thereby eliminating its typical New Keynesian properties. In each experiment we use two sets of priors: high-rigidity priors (HR) and flexible price (FP) priors. For the HR priors we set the mean to be 0.5 and the standard deviation to be 0.1, the same distribution as Smets-Wouters. For the FP priors the mean and standard deviation are set to 0.05 and 0.1 with a minimum lower bound of 0.001 to ensure the model solves. In each case one of these is the false set. For all the other parameters whose values are not critical to whether the model is HR or FP, we used the same priors as in SW.

The results for the first experiment (HR true) are reported in columns 2 and 3 of Table 1. We show the average estimates for the 1000 samples of the key parameters \(\xi _{w}\) and \(\xi _{p}\) for each prior distribution together with the standard deviations of these 1000 estimates.

Table 1 Average Estimates and their standard deviations (over 1000 samples) of the Wage and Price Stickiness Parameters for the NK and FP models with NK and FP Priors
Full size table
Fig. 2
figure 2

Histograms of the rigidity of wage (\(\xi _{w}\)) and price (\(\xi _{p}\)) coefficients and under HR and FP priors

Full size image

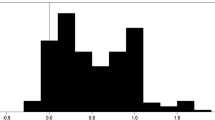
In the HR case, the true parameter values for both \(\xi _{w}\) and \(\xi _{p}\) are approximately 0.7. The average Bayesian estimates based on the HR prior distribution are close to, and not significantly different from, their true values. For the FP priors centred on 0.05 they are a long way below, and highly significantly different from, the true values of 0.7. The top row of Fig. 2 shows the histograms of the \(\xi _{w}\) and \(\xi _{p}\) parameters for this HR case under both HR and FP priors. Under HR priors the parameters are centred approximately around the true value of 0.7. Under FP priors the parameters are centred approximately around 0.1; but a large number of the estimates are spread above this.

The corresponding results for the second experiment where FP is the true model are reported in columns 4 and 5 of Table 1. For the FP priors the estimate of \(\xi _{p}\) is close to, and not significantly different from its “true” value of 0.05. The estimate of \(\xi _{w}\) is further from 0.05, but still not significantly different. For the HR priors the estimates of both parameters are close to their prior means of 0.7, but they are significantly far from their true values of 0.05.

The bottom row of Fig. 2 shows the histograms of the \(\xi _{w}\) and \(\xi _{p}\) parameters for this FP model version under both HR and FP priors. With FP priors the histograms are centred close to 0.05. With HR priors the distributions of both \(\xi _{w}\) and \(\xi _{p}\) are centred around 0.7, far from the true values of 0.05.

One response to these results might be that they are due to excessively tight prior distributions. Perhaps greater flexibility could allow Bayesian estimation to give less biased results? Accordingly we show how the results remain largely unaffected as we allow the mean of the prior distributions to vary while still differentiating the priors meaningfully from the truth. Essentially what we find is that the priors act powerfully to distort the posterior estimates of price rigidity away from the true values. Nor do we find that substituting the mean for the mode alters our findings; estimating the mean rather than the mode is far more time-consuming but gives essentially the same results (as widely noted, e.g. by Smets and Wouters 2007).

In the following exercise we simulated the HR and FP models, then treated each simulation as the data and estimated the parameters with a set prior mean. The top panel of Table 2 shows the results when the HR model is treated as the true model and the bottom panel when the FP model is treated as the true model. What is clear is that as the prior mean changes from low to high values the mean of the posterior mode of the rigidity parameters also increases.

Table 2 Estimating the mode with shifting priors
Full size table

These two experiments show with startling clarity how the choice of prior distribution affects the posterior estimates. The most striking result, which holds in both experiments, is that the posterior estimates are completely dominated by the prior distributions. Whether the data are generated by an HR or an FP model is immaterial as here the data play little role. It might be argued that this is what Bayesian econometrics aims to achieve, i.e. incorporate prior beliefs. The danger, of course, is that it will be inferred that the model is correct no matter how flawed it may be. This is why we have urged in several papers that Bayesian estimated models be tested.

5.2 ML and Indirect Estimation

If the use of Bayesian estimation is suspect, what other method of estimation might be preferable? We compare two classical estimators: ML and Indirect estimation. As noted above, the use of Bayesian estimation was in part a response to the deficiencies of ML estimation. ML estimation — which can also be interpreted as Bayesian estimation with uninformative, uniform priors — seeks to choose parameter values that give the best in-sample forecasting performance by the model. This can produce highly biased parameter estimates, especially if the model is mis-specified; the estimator compensates for the mis-specification by distorting the parameters, thereby improving the forecasts.

In contrast, Indirect estimation (II) chooses the model parameters to generate data from the structural model that gives estimates of an auxiliary model closest to those using the observed data. In a recent paper Le et al. (2016) carried out small sample Monte Carlo experiments which showed that the Indirect estimator has low bias and the associated Indirect test — based on the significance of differences between estimates of the parameters of the auxiliary model from data simulated from the structural estimates and the observed data — has very high power against a mis-specified model such as the FP version of the NK model. The ML estimator by contrast was highly biased and had no power against a mis-specified model.

We now go on to apply ML and II here to the estimation of the price rigidity parameters in our Monte Carlo experiment. We produce 1000 simulations from both the HR and FP models, then estimate only the price rigidity parameters (keeping all other parameters fixed) treating each simulation as the data. What we find is consistent with those of Le et al. (2016). Table 3 shows that the ML estimate is seriously biased, while the II bias is very small. When we treat the HR model as the true model we find II has very low bias of approximately 1-2%, compared to 4-13% for ML. When the FP model is treated as the truth the difference in bias is much greater. The bias for II is approximately 1-5% compared to the massive bias of 1200-1700% for the ML estimates.Footnote 1

Table 3 Bias of ML and II estimators
Full size table

6 Conclusions

In this paper we have explored the estimation of price rigidity in macro models; the degree of rigidity is central to the behaviour of the economy in these models and there has been a long-running debate in macroeconomics about the appropriateness of assuming price rigidity as opposed to flexible prices. Yet it has not been resolved by estimation or testing against the data — with rival schools of thought on price rigidity either imposing their approach a priori, which avoids testing altogether, or using Bayesian estimation with price rigidity being treated as a prior. We have investigated the consequences of this Bayesian method for the resulting estimates of the price rigidity parameter. Our central finding is that in Bayesian estimation of the New Keynesian model the choice of prior distribution tends to distort the posterior estimates of this parameter, causing it to be substantially biased. A further result is that Maximum Likelihood estimates of it are also highly biased and that Indirect estimates have much lower bias.

The broader significance of these findings is that the Bayesian estimation of macro models may give very misleading results by placing too much weight on prior information compared to observed data and that a better method may be Indirect estimation. While our extended example has focused narrowly on the price/wage rigidity parameters because of their central importance in DSGE models, the conclusion applies to all the parameters of the model, which all have some bearing on the welfare assessment of policy regimes within the economy; all should be estimated with minimum bias, which can be achieved in small samples by Indirect estimation — as found already by Le et al. (2016) across all the parameters of a DSGE model. The reason this is an important finding is the widespread use of Bayesian estimation in macroeconomics which has been facilitated by Dynare. This has resulted in a failure to resolve the central controversy over the degree of price rigidity in the economy but also the emergence of a majority view in favour of the New Keynesian model with highly sticky wages and prices, in spite of its rejection by indirect inference tests in favour of a hybrid model whose rigidity varies with the evolution of shocks — as found recently on US data by Le et al. (2021). The danger for macroeconomics is that this majority view becomes an orthodox opinion that is not supported by scientific evidence, while also being rejected by a significant minority. Eventually, of course, theories not supported by the evidence will be rejected, much as the Great Depression overturned classical macroeconomics. Such overturning is however bad for the reputation of economics as a science. Rather than protect a theory by biasing estimation results in its favour — for example, through using strong priors — it is better to submit theories to ongoing tests of their consistency with the data, and so achieve a resolution of the central controversy in macroeconomics over price rigidity.